A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model
Abstract
:1. Introduction
- CoCr Alloy/UHWMPE
- Ti6Al4V/Ti6Al4V
- Si3N4-TiN/Si3N4-TiN
2. Materials and Methods
2.1. Numerical Modeling
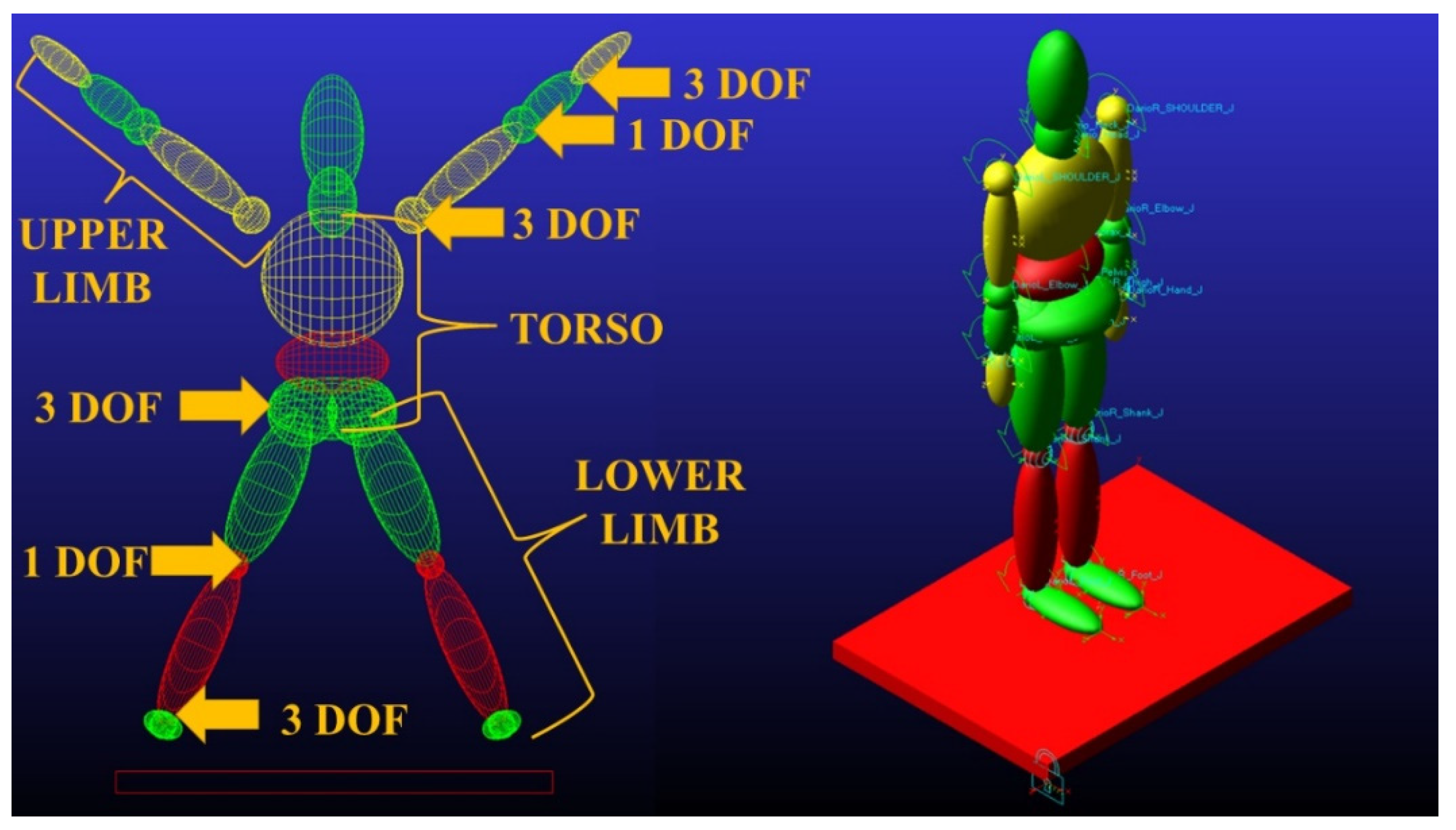
2.2. Parametric Human Model
- Lower limbs: Left/Right Thigh, Left/Right Shank, Left/Right Foot.
- Upper limbs: Left/Right Upper arm, Left/Right Forearm, Left/Right Hand.
- Torso: Pelvis, Abdomen, Thorax.
- Weight: 85 kg
- Standing Height: 1755 mm
- Seated Height: 918 mm
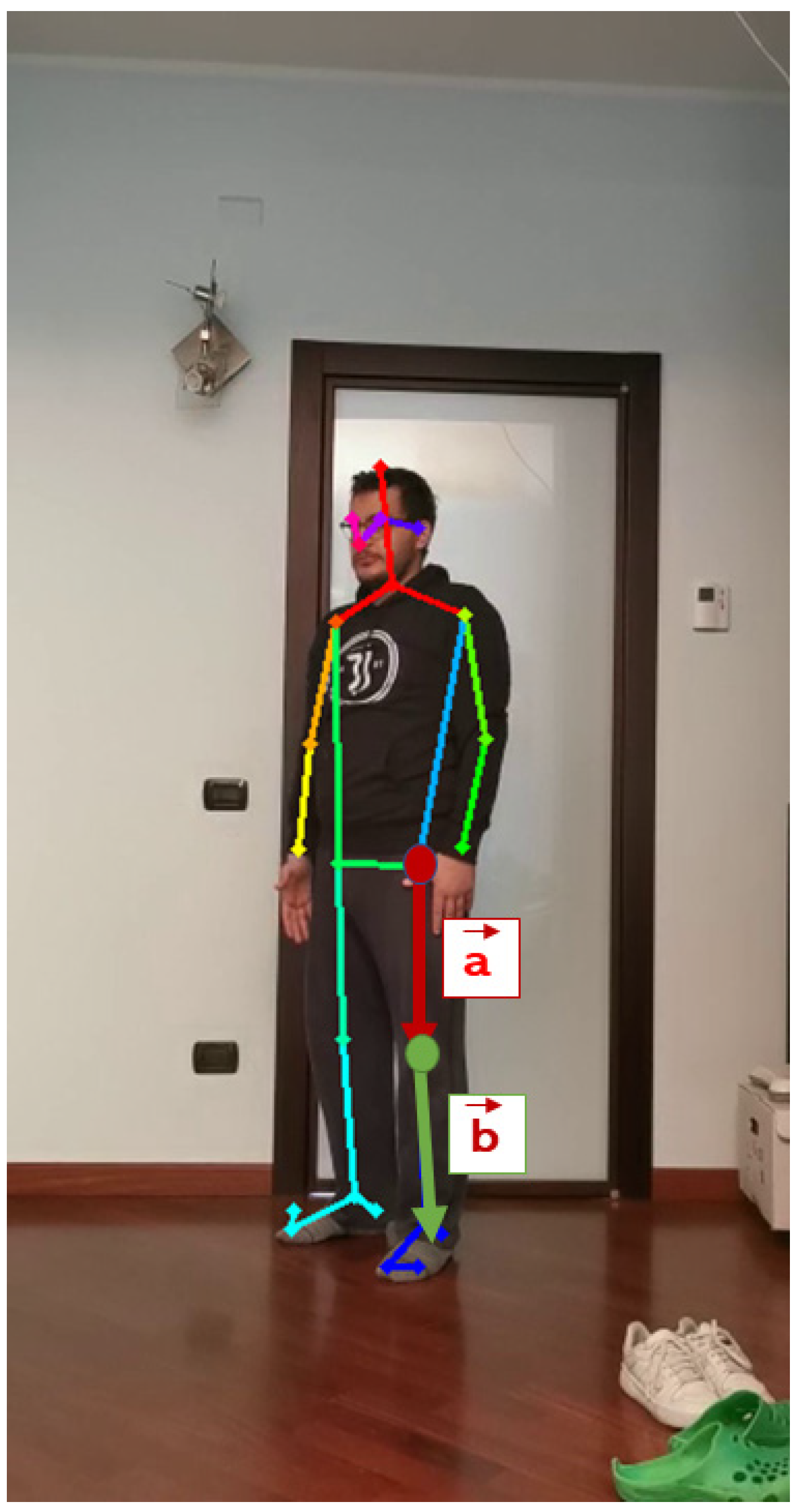
2.3. Motion Capture
- MPI can estimate a total of 15 key points.
- COCO can estimate a total of 18 points.
- BODY_25 can estimate a total of 25 points.
2.4. Experimental Tests
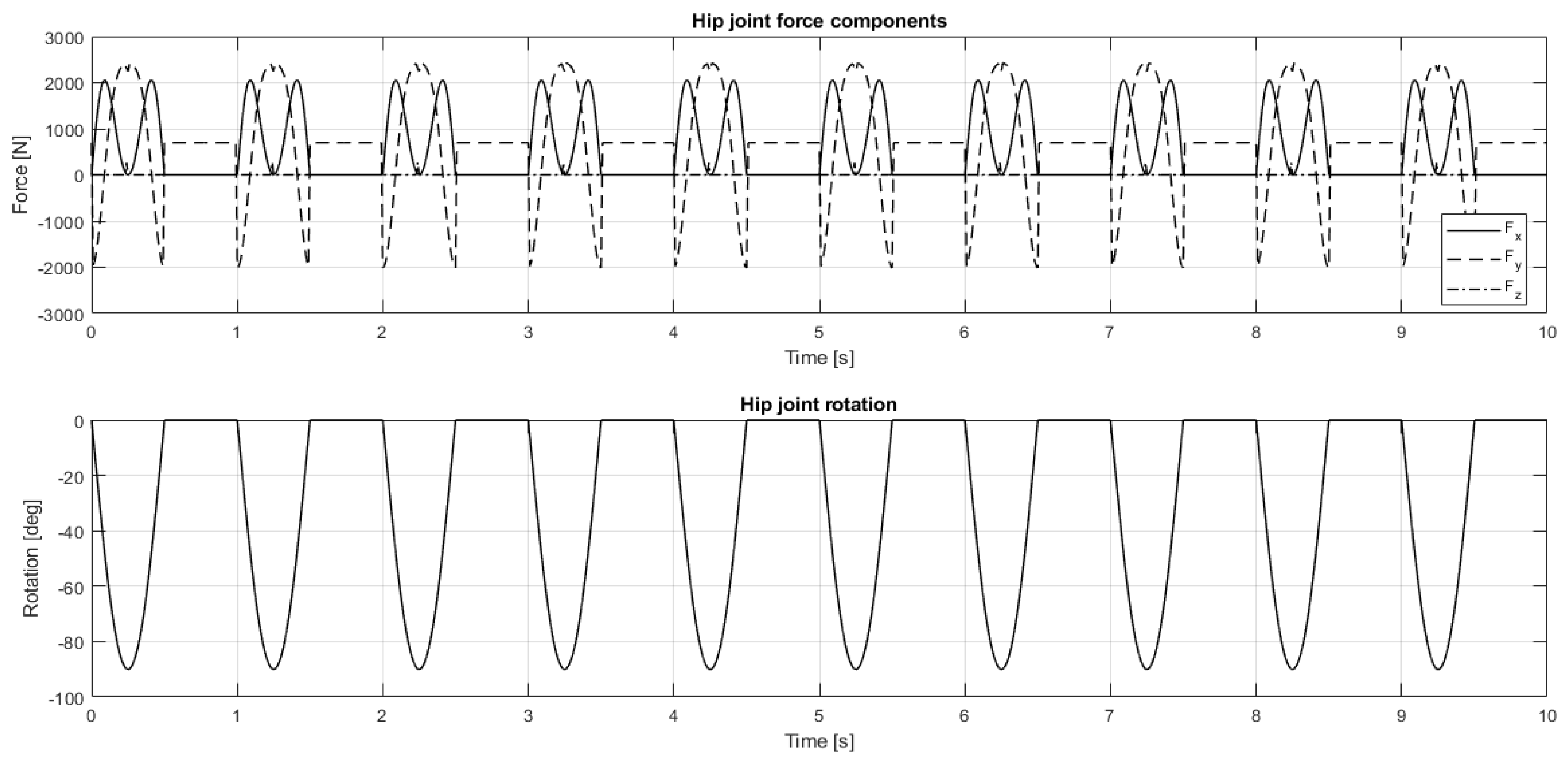
2.4.1. Sit-to-Stand Movement
2.4.2. Motion Acquisition and Multibody Analysis
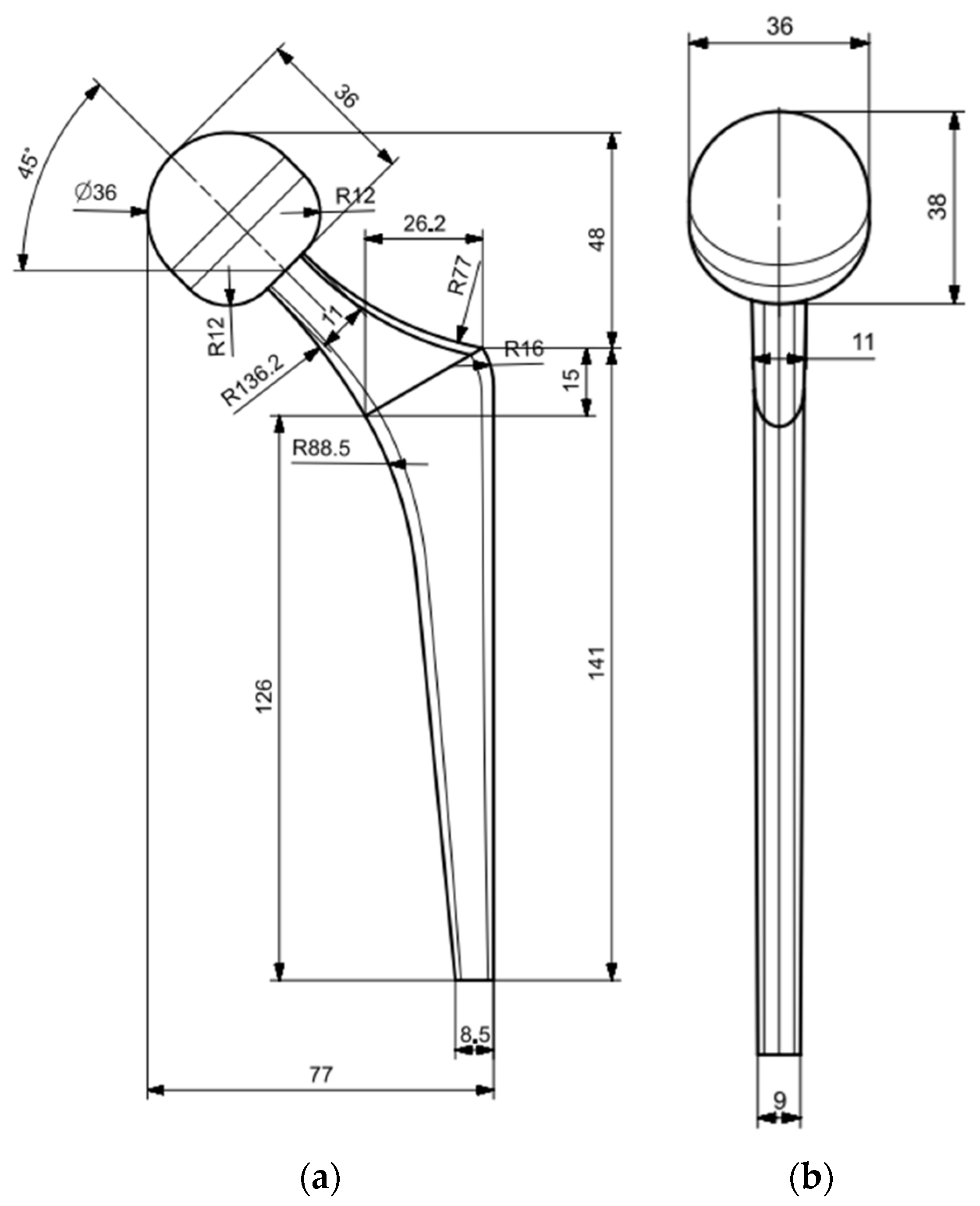
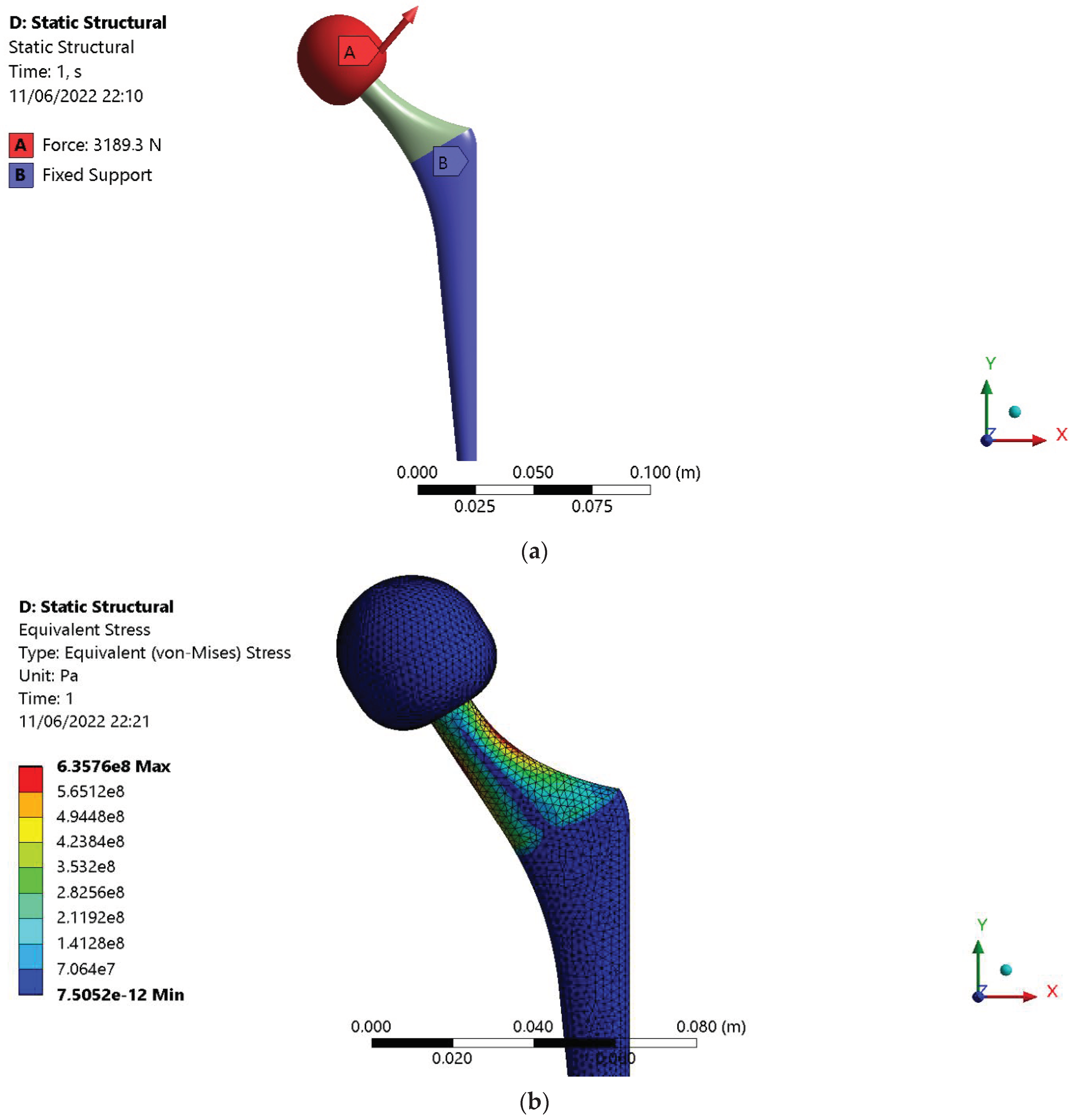
2.5. Hip Prosthesis Finite Element Model (FEM)
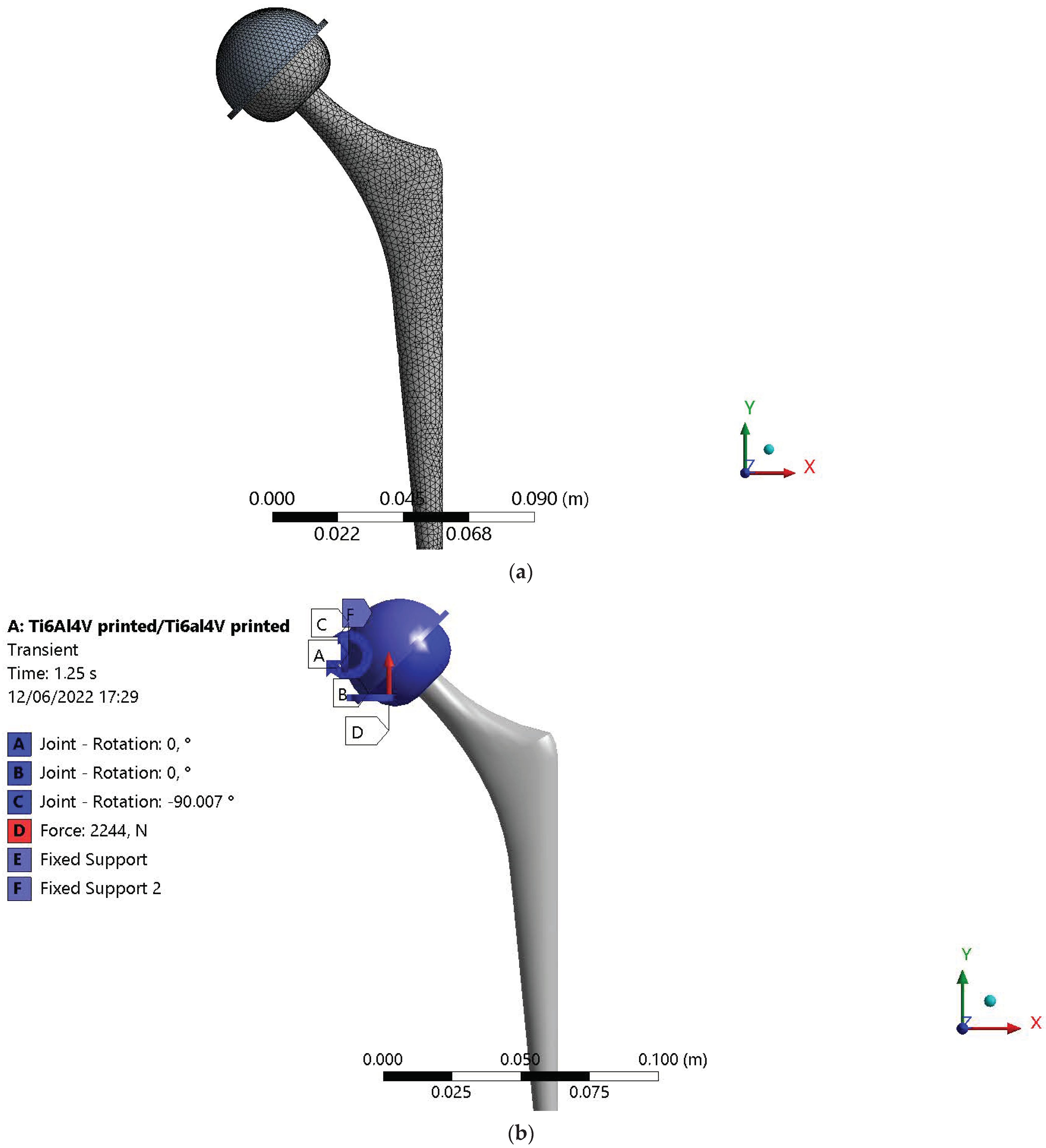
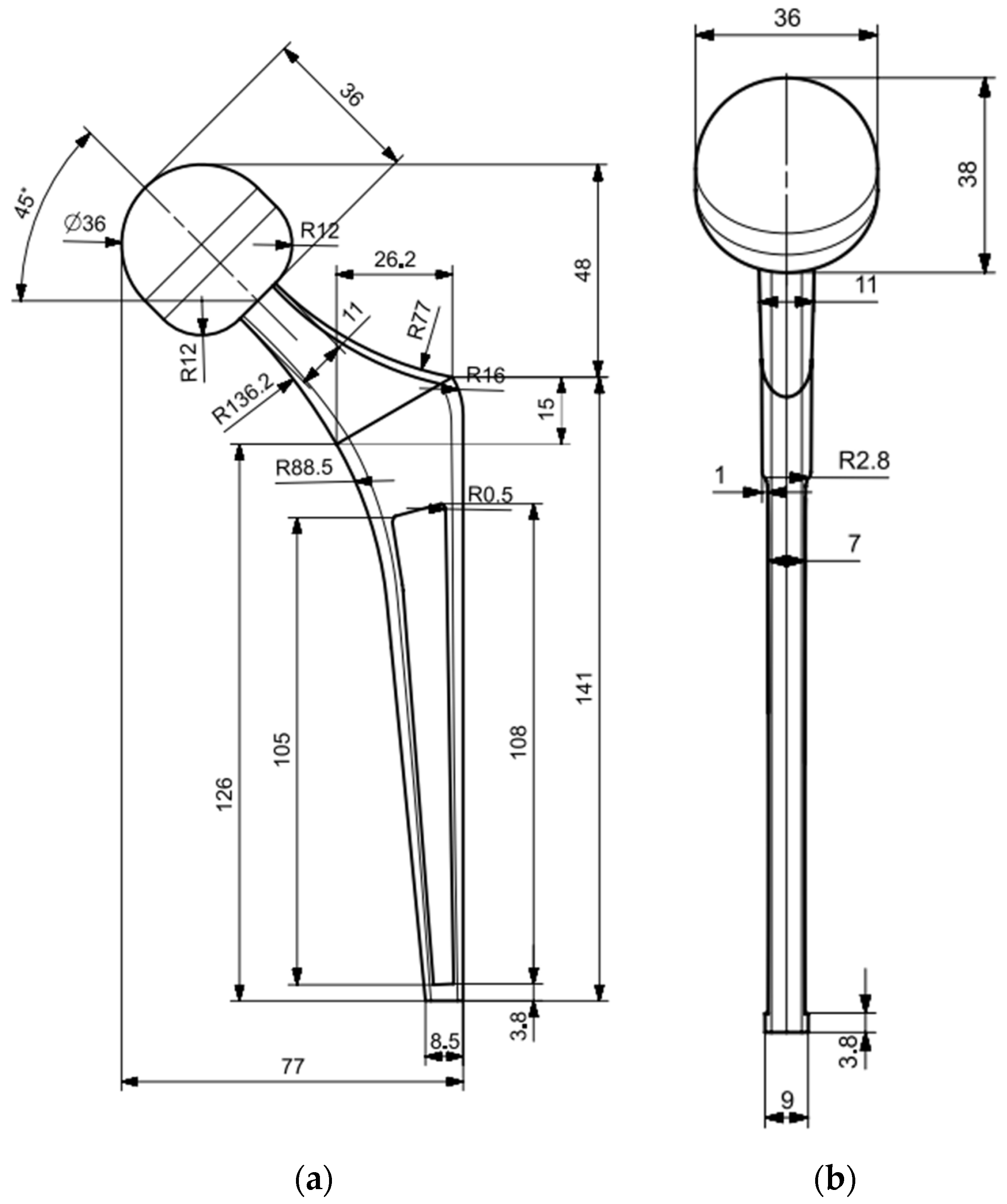
2.5.1. Geometry, Mesh, and Boundary Condition Definition
2.5.2. Archard’s Wear Law Implementation
- CoCr Alloy (femoral head)/UHWMPE (acetabular cup)
- Ti6Al4V (femoral head)/Ti6Al4V (acetabular cup)
- Si3N4-TiN (femoral head)/Si3N4-TiN (acetabular cup)
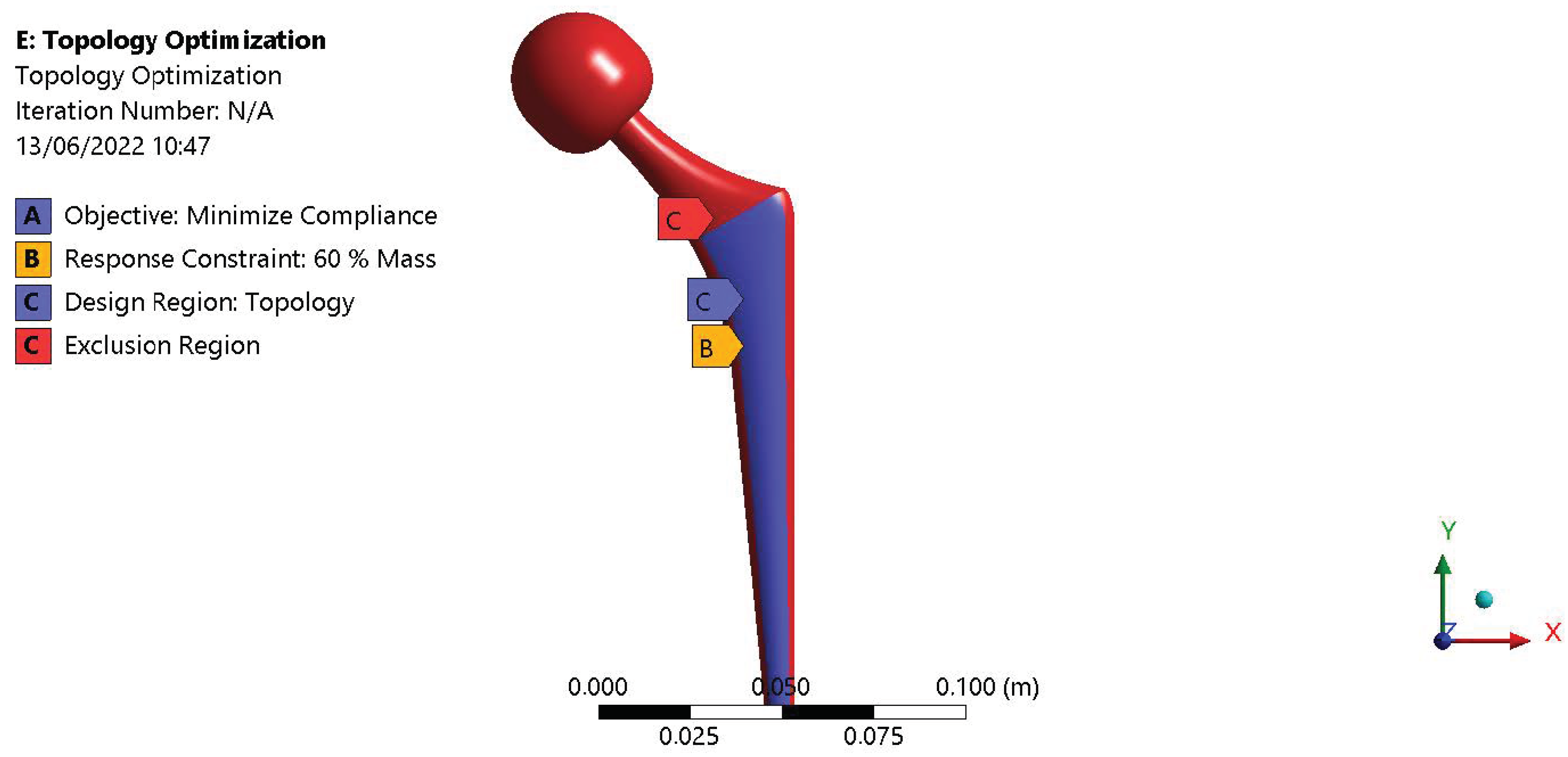
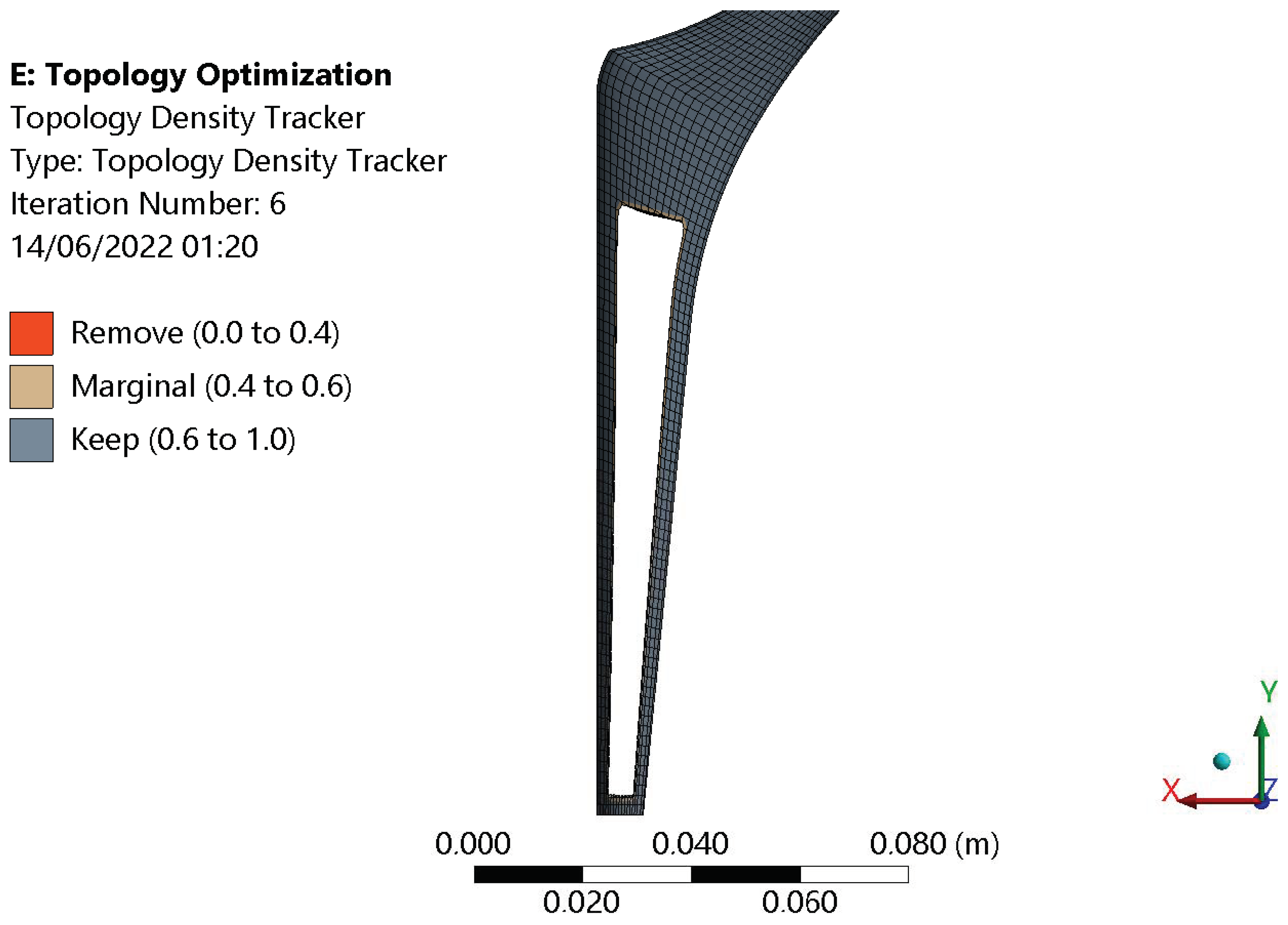
2.5.3. Topology Optimization
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cucinotta, F.; Guglielmino, E.; Longo, G.; Risitano, G.; Santonocito, D.; Sfravara, F. Topology Optimization Additive Manufacturing-Oriented for a Biomedical Application; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Volume 1, ISBN 9783030123468. [Google Scholar]
- D’Andrea, D.; Risitano, G.; Guglielmino, E.; Piperopoulos, E.; Santonocito, D. Correlation between Mechanical Behaviour and Microstructural Features of AISI 316L Produced by SLM. Procedia Struct. Integr. 2022, 41, 199–207. [Google Scholar] [CrossRef]
- Epasto, G.; Palomba, G.; D’Andrea, D.; Guglielmino, E.; Di Bella, S.; Traina, F. Ti-6Al-4V ELI Microlattice Structures Manufactured by Electron Beam Melting: Effect of Unit Cell Dimensions and Morphology on Mechanical Behaviour. Mater. Sci. Eng. A 2019, 753, 31–41. [Google Scholar] [CrossRef]
- Epasto, G.; Palomba, G.; Andrea, D.D.; Di Bella, S.; Mineo, R.; Guglielmino, E.; Traina, F. Experimental Investigation of Rhombic Dodecahedron Micro-Lattice Structures Manufactured by Electron Beam Melting. Mater. Today Proc. 2019, 7, 578–585. [Google Scholar] [CrossRef]
- Fellah, M.; Labaiz, M.; Assala, O.; Dekhil, L.; Iost, A. Tribological Behavior of Biomaterials for Total Hip Prosthesis. Trends Biomater. Artif. Organs 2015, 29, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Banchet, V.; Fridrici, V.; Abry, J.C.; Kapsa, P. Wear and Friction Characterization of Materials for Hip Prosthesis. Wear 2007, 263, 1066–1071. [Google Scholar] [CrossRef]
- Unsworth, A.; Hall, R.M.; Burgess, I.C.; Wroblewski, B.M.; Streicher, R.M.; Semlitsch, M. Frictional Resistance of New and Explanted Artificial Hip Joints. Wear 1995, 2, 226–231. [Google Scholar] [CrossRef]
- Saikko, V.O. A Three-Axis Hip Joint Simulator for Wear and Friction Studies on Total Hip Prostheses. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1996, 210, 175–185. [Google Scholar] [CrossRef]
- Shankar, S.; Nithyaprakash, R.; Abbas, G.; Naveen Kumar, R.; Pramanik, A.; Kumar Basak, A.; Prakash, C. Tribological Behavior of Zirconia-Toughened Alumina (ZTA) against Ti6Al4V under Different Bio-Lubricants in Hip Prosthesis Using Experimental and Finite Element Concepts. Mater. Lett. 2022, 307, 131107. [Google Scholar] [CrossRef]
- Mattei, L.; Di, F.; Ciulli, E.; Pauschitz, A. Tribology International Experimental Investigation on Wear Map Evolution of Ceramic-on-UHMWPE Hip Prosthesis. Tribol. Int. 2020, 143, 106068. [Google Scholar] [CrossRef]
- Kourra, N.; Warnett, J.M.; Attridge, A.; Dibling, G.; McLoughlin, J.; Muirhead-Allwood, S.; King, R.; Williams, M.A. Computed Tomography Metrological Examination of Additive Manufactured Acetabular Hip Prosthesis Cups. Addit. Manuf. 2018, 22, 146–152. [Google Scholar] [CrossRef]
- Murr, L.E. Additive Manufacturing of Biomedical Devices: An Overview. Mater. Technol. 2018, 33, 57–70. [Google Scholar] [CrossRef]
- Cortis, G.; Mileti, I.; Nalli, F.; Palermo, E.; Cortese, L. Additive Manufacturing Structural Redesign of Hip Prostheses for Stress-Shielding Reduction and Improved Functionality and Safety. Mech. Mater. 2022, 165, 104173. [Google Scholar] [CrossRef]
- Kashyap, V.; Ramkumar, P. Comprehensive Analysis of Geometrical Parameters of Crosshatched Texture for Enhanced Tribological Performance under Biological Environment. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2021, 235, 434–452. [Google Scholar] [CrossRef]
- Allen, Q.; Raeymaekers, B. The Effect of Texture Floor Profile on the Lubricant Film Thickness in a Textured Hard-on-Soft Bearing with Relevance to Prosthetic Hip Implants. J. Tribol. 2021, 143, 021801. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, V.; Ramkumar, P. DLC Coating over Pre-Oxidized and Textured Ti6Al4V for Superior Adhesion and Tribo-Performance of Hip Implant. Surf. Coat. Technol. 2022, 440, 128492. [Google Scholar] [CrossRef]
- Prince, R.M.R.; Selvakumar, N.; Arulkirubakaran, D.; Singh, S.C.E.; Das, M.C.; Bannaravuri, P.K.; Prabha, R.M.R.; Raj, J.A.; Robert, R.B.J. ZrC-Impregnated Titanium-Based Coating as an Effective Lubricating Barrier for Artificial Hip Prosthesis. Mater. Perform. Charact. 2021, 10, 189–205. [Google Scholar] [CrossRef]
- Senatore, A.; Risitano, G.; Scappaticci, L.; D’andrea, D. Investigation of the Tribological Properties of Different Textured Lead Bronze Coatings under Severe Load Conditions. Lubricants 2021, 9, 34. [Google Scholar] [CrossRef]
- Khaskhoussi, A.; Risitano, G.; Calabrese, L.; D’Andrea, D. Investigation of the Wettability Properties of Different Textured Lead/Lead-Free Bronze Coatings. Lubricants 2022, 10, 82. [Google Scholar] [CrossRef]
- D’Andrea, D.; Pistone, A.; Risitano, G.; Santonocito, D.; Scappaticci, L.; Alberti, F. Tribological Characterization of a Hip Prosthesis in Si3N4-TiN Ceramic Composite Made with Electrical Discharge Machining (EDM). Procedia Struct. Integr. 2021, 33, 469–481. [Google Scholar] [CrossRef]
- Ploof, G.; Alqahtani, B.; Alghamdi, F.; Flynn, G.; Yang, C.X. Center of Mass Estimation Using Motion Capture System. In Proceedings of the 2017 IEEE 15th Intl Conf on Dependable, Autonomic and Secure Computing, 15th Intl Conf on Pervasive Intelligence and Computing, 3rd Intl Conf on Big Data Intelligence and Computing and Cyber Science and Technology Congress (DASC/PiCom/DataCom/CyberSciTech), Orlando, FL, USA, 6–10 November 2017; pp. 287–292. [Google Scholar] [CrossRef]
- D’andrea, D.; Cucinotta, F.; Farroni, F.; Risitano, G.; Santonocito, D.; Scappaticci, L. Development of Machine Learning Algorithms for the Determination of the Centre of Mass. Symmetry 2021, 13, 401. [Google Scholar] [CrossRef]
- Tanaka, R.; Takimoto, H.; Yamasaki, T.; Higashi, A. Validity of Time Series Kinematical Data as Measured by a Markerless Motion Capture System on a Flatland for Gait Assessment. J. Biomech. 2018, 71, 281–285. [Google Scholar] [CrossRef] [PubMed]
- Fadela, A.; Habib, L.; Abderrahmane, B. Finite Element Analysis of Stress State in the Cement of Total Hip Prosthesis with Elastomeric Stress Barrier. Frat. Integrità Strutt. 2021, 15, 281–290. [Google Scholar] [CrossRef]
- Bhawe, A.K.; Shah, K.M.; Somani, S.; Shenoy, B.S.; Bhat, N.S.; Zuber, M.; KN, C. Static Structural Analysis of the Effect of Change in Femoral Head Sizes Used in Total Hip Arthroplasty Using Finite Element Method. Cogent Eng. 2022, 9, 2027080. [Google Scholar] [CrossRef]
- D’Andrea, D.; Risitano, G.; Desiderio, E.; Quintarelli, A.; Milone, D.; Alberti, F. Artificial Neural Network Prediction of the Optimal Setup Parameters of a Seven Degrees of Freedom Mathematical Model of a Race Car: IndyCar Case Study. Vehicles 2021, 3, 300–329. [Google Scholar] [CrossRef]
- Mahyudin, F.; Hermawan, H. Biomaterials and Medical Devices. Adv. Struct. Mater. 2016, 58, 207–234. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Afif, I.Y.; Maula, M.I.; Winarni, T.I.; Tauviqirrahman, M.; Akbar, I.; Basri, H.; van der Heide, E.; Jamari, J. Tresca Stress Simulation of Metal-on-Metal Total Hip Arthroplasty during Normal Walking Activity. Materials 2021, 14, 7554. [Google Scholar] [CrossRef]
- Uddin, M.S.; Zhang, L.C. Predicting the Wear of Hard-on-Hard Hip Joint Prostheses. Wear 2013, 301, 192–200. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Huber, N.; Kraft, O. Finite Element Based Simulation of Dry Sliding Wear. Model. Simul. Mater. Sci. Eng. 2005, 13, 57–75. [Google Scholar] [CrossRef]
- Stanković, M.; Marinković, A.; Grbović, A.; Mišković, Ž.; Rosić, B.; Mitrović, R. Determination of Archard’s Wear Coefficient and Wear Simulation of Sliding Bearings. Ind. Lubr. Tribol. 2019, 71, 119–125. [Google Scholar] [CrossRef]
- Ruggiero, A.; Sicilia, A. Lubrication Modeling and Wear Calculation in Artificial Hip Joint during the Gait. Tribol. Int. 2020, 142, 105993. [Google Scholar] [CrossRef]
- Barber, H.; Kelly, C.N.; Abar, B.; Allen, N.; Adams, S.B.; Gall, K. Rotational Wear and Friction of Ti-6Al-4V and CoCrMo against Polyethylene and Polycarbonate Urethane. Biotribology 2021, 26. [Google Scholar] [CrossRef]
- Sharma, D.; Kamran, M.; Paraye, N.K.; Anant, R. Insights into the Wear Behaviour of Electron Beam Melted Ti–6Al–4V Alloy in the as-Built and the Heat-Treated Conditions. J. Manuf. Process. 2021, 71, 669–678. [Google Scholar] [CrossRef]
- Wang, L.; Isaac, G.; Wilcox, R.; Jones, A.; Thompson, J. Finite Element Analysis of Polyethylene Wear in Total Hip Replacement: A Literature Review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 1067–1088. [Google Scholar] [CrossRef] [PubMed]
- Moskaljuk, A.; Vee, P.; Lee, S.; Dimitroulis, G.; Ackland, D.C.; Hart, C. Ackland Etal 2015 TMJ Prosthesis Loading After Temporomandibular Joint Replacement Surgery: A Musculoskeletal Modeling Study. J. Biomech. Eng. 2015, 137. [Google Scholar] [CrossRef]
- Gröning, F.; Jones, M.E.H.; Curtis, N.; Herrel, A.; O’Higgins, P.; Evans, S.E.; Fagan, M.J. The Importance of Accurate Muscle Modelling for Biomechanical Analyses: A Case Study with a Lizard Skull. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [Green Version]
- Langenbach, G.E.J.; Hannam, A.G. The Role of Passive Muscle Tensions in a Three-Dimensional Dynamic Model of the Human Jaw. Arch. Oral Biol. 1999, 44, 557–573. [Google Scholar] [CrossRef]
- Shi, J.; Curtis, N.; Fitton, L.C.; O’Higgins, P.; Fagan, M.J. Developing a Musculoskeletal Model of the Primate Skull: Predicting Muscle Activations, Bite Force, and Joint Reaction Forces Using Multibody Dynamics Analysis and Advanced Optimisation Methods. J. Theor. Biol. 2012, 310, 21–30. [Google Scholar] [CrossRef]
- D’Andrea, D.; Milone, D.; Nicita, F.; Risitano, G.; Santonocito, D. Qualitative and Quantitative Evaluation of Different Types of Orthodontic Brackets and Archwires by Optical Microscopy and X-Ray Fluorescence Spectroscopy. Prosthesis 2021, 3, 342–360. [Google Scholar] [CrossRef]
- Milone, D.; Nicita, F.; Cervino, G.; Santonocito, D.; Risitano, G. Finite Element Analysis of OT Bridge Fixed Prosthesis System. Procedia Struct. Integr. 2021, 33, 734–747. [Google Scholar] [CrossRef]
- May, B.; Saha, S.; Saltzman, M. A Three-Dimensional Mathematical Model of Temporomandibular Joint Loading. Clin. Biomech. 2001, 16, 489–495. [Google Scholar] [CrossRef]
- Cervino, G.; Cicciù, M.; Fedi, S.; Milone, D.; Fiorillo, L. FEM Analysis Applied to OT Bridge Abutment with Seeger Retention System. Eur. J. Dent. 2020, 15, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Cicciù, M.; Cervino, G.; Milone, D.; Risitano, G. Materials FEM Analysis of Dental Implant-Abutment Interface Overdenture Components and Parametric Evaluation of Equator ® and Locator ® Prosthodontics Attachments. Materials 2019, 12, 592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paschold, H. Whole-Body Vibration. In Proceedings of the ASSE Professional Development Conference and Exposition 2009, San Antonio, TX, USA, 28 June–1 July 2009. [Google Scholar]
- Young, S.N.; VanWye, W.R.; Wallmann, H.W. Sport Simulation as a Form of Implicit Motor Training in a Geriatric Athlete after Stroke: A Case Report. Physiother. Theory Pract. 2018, 36, 524–532. [Google Scholar] [CrossRef] [PubMed]
- Cameron, P.W.; Soltero, N.C.; Byers, J. Effects of a 60 Minute on Ice Game Simulation on the Balance Error Scoring System. Int. J. Exerc. Sci. 2018, 11, 462. [Google Scholar] [PubMed]
- Chung, H.-J. Optimization Based Dynamic Human Motion Prediction with Modular Exoskeleton Robots as Interactive Forces: The Case of Weight Lifting Motion. In Collaborative and Humanoid Robots [Working Title]; IntechOpen: London, UK, 2021. [Google Scholar]
- Cheng, H.; Obergefell, L.; Rizer, A. The Development of the GEBOD Program. In Proceedings of the 1996 Fifteenth Southern Biomedical Engineering Conference, Dayton, OH, USA, 29–31 March 1969; pp. 251–254. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J. Discover Internet of Things Research on College Gymnastics Teaching Model Based on Multimedia Image and Image Texture Feature Analysis. Discov. Internet Things 2021, 1, 15. [Google Scholar] [CrossRef]
- Erdmann, W.S.; Kowalczyk, R. Basic Inertial Quantities Including Multi-Segment Trunk of Fit, Young Males Obtained Based on Personalized Data. J. Biomech. 2020, 106. [Google Scholar] [CrossRef] [PubMed]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s Segment Inertia Parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 43, 172–186. [Google Scholar] [CrossRef] [Green Version]
- Feng, B. Marker-Less Motion Capture System Using OpenPose. Proc. SPIE 2022, 12101, 84–93. [Google Scholar] [CrossRef]
- Simon, T.; Joo, H.; Matthews, I.; Sheikh, Y. Hand Keypoint Detection in Single Images Using Multiview Bootstrapping. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2016; pp. 4645–4653. [Google Scholar] [CrossRef]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional Pose Machines. In Proceedings of the IEEE Computer Society Conference Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4724–4732. [Google Scholar] [CrossRef]
- Pagnon, D.; Domalain, M.; Reveret, L. Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness. Sensors 2021, 21, 6530. [Google Scholar] [CrossRef]
- Hidalgo, G.; Raaj, Y.; Idrees, H.; Xiang, D.; Joo, H.; Simon, T.; Sheikh, Y. Single-Network Whole-Body Pose Estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6982–6991. [Google Scholar]
- Riley, P.O.; Schenkman, M.L.; Mann, R.W.; Hodge, W.A. Mechanics of a Constrained Chair-Rise. J. Biomech. 1991, 24, 77–85. [Google Scholar] [CrossRef]
- Jones, C.J.; Rikli, R.E.; Beam, W.C. A 30-s Chair-Stand Test as a Measure of Lower Body Strength in Community-Residing Older Adults. Res. Q. Exerc. Sport 2013, 70, 113–119. [Google Scholar] [CrossRef]
- Kerr, K.; White, J.; Barr, D.; Mollan, R. Analysis of the Sit-Stand-Sit Movement Cycle: Development of a Measurement System. Gait Posture 1994, 2, 173–181. [Google Scholar] [CrossRef]
- Kerr, K.; White, J.; Barr, D.; Mollan, R. Standardization and Definitions of the Sit-Stand-Sit Movement Cycle. Gait Posture 1994, 2, 182–190. [Google Scholar] [CrossRef]
- Tveter, A.T.; Dagfinrud, H.; Moseng, T.; Holm, I. Health-Related Physical Fitness Measures: Reference Values and Reference Equations for Use in Clinical Practice. Arch. Phys. Med. Rehabil. 2014, 95, 1366–1373. [Google Scholar] [CrossRef] [PubMed]
- Viswakumar, A.; Rajagopalan, V.; Ray, T.; Parimi, C. Human Gait Analysis Using OpenPose. In Proceedings of the 2019 fifth international conference on image information processing (ICIIP), Shimla, India, 15–17 November 2019; pp. 310–314. [Google Scholar] [CrossRef]
- Jamari, J.; Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Prakoso, A.T.; Basri, H.; van der Heide, E. Computational Contact Pressure Prediction of CoCrMo, SS 316L and Ti6Al4V Femoral Head against UHMWPE Acetabular Cup under Gait Cycle. J. Funct. Biomater. 2022, 13, 64. [Google Scholar] [CrossRef]




| Reference Number | Dimension | Reference Number | Dimension |
|---|---|---|---|
| 0 | Weight | 16 | Hip Breadth, Standing |
| 1 | Standing Height | 17 | Shoulder to Elbow Length |
| 2 | Shoulder Height | 18 | Forearm-Hand Length |
| 3 | Armpit Height | 19 | Biceps Circumference |
| 4 | Waist Height | 20 | Elbow Circumference |
| 5 | Seated Height | 21 | Forearm Circumference |
| 6 | Head Length | 22 | Waist Circumference |
| 7 | Head Breadth | 23 | Knee Height, Seated |
| 8 | Head to Chin Height | 24 | Thigh Circumference |
| 9 | Neck Circumference | 25 | Upper Leg Circumference |
| 10 | Shoulder Breadth | 26 | Knee Circumference |
| 11 | Chest Depth | 27 | Calf Circumference |
| 12 | Chest Breadth | 28 | Ankle Circumference |
| 13 | Waist Depth | 29 | Ankle Height, Outside |
| 14 | Waist Breadth | 30 | Foot Breadth |
| 15 | Buttock Depth | 31 | Foot Length |
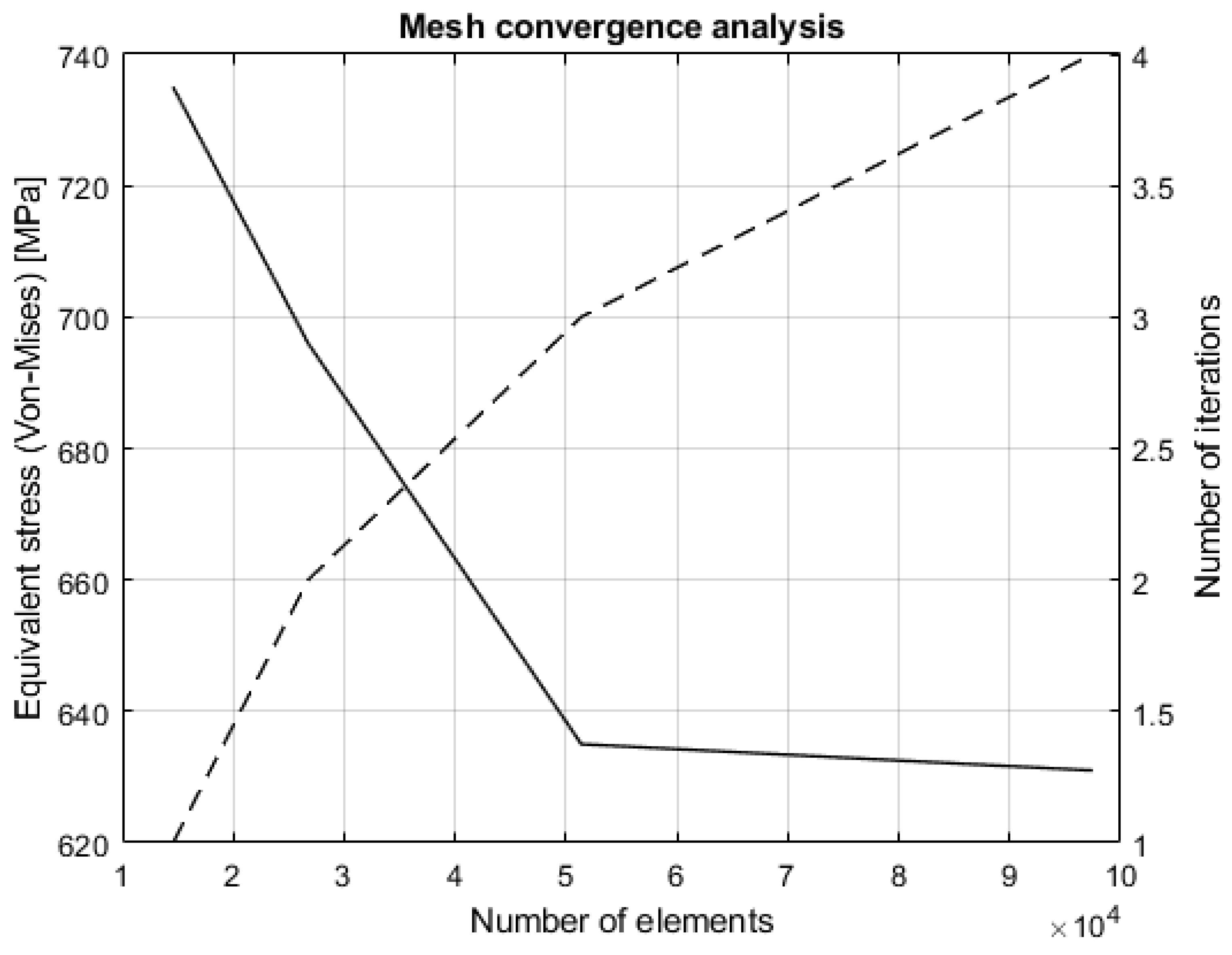
| Number of Iterations | Element Size | Number of Elements | Equivalent Stress |
|---|---|---|---|
| 1 | 10 mm | 14,574 | 735 MPa |
| 2 | 5 mm | 26,745 | 669 MPa |
| 3 | 2 mm | 51,379 | 635 MPa |
| 4 | 1 mm | 97,475 | 631 MPa |
| Pairs | Friction Coefficient | Wear Coefficient | Hardness | m, Pressure Exponent | n, Sliding Velocity Exponent | Poisson Ratio |
|---|---|---|---|---|---|---|
| CoCr alloy/UHMWPE | 0.11 | 1.22 GPa | 1 | 1 | 0.3 | |
| Si3N4-TiN/Si3N4-TiN | 0.14 | 14.7 GPa | 1 | 1 | 0.3 | |
| Ti-6Al-4V/Ti-6Al-4V | 0.53 | 1.09 GPa | 1 | 1 | 0.3 |
| Pairs | Volume Loss Due to Wear |
|---|---|
| CoCr alloy/UHMWPE | |
| Si3N4-TiN/Si3N4-TiN | |
| Ti-6Al-4V/Ti-6Al-4V |
| Original Mass | Optimized Mass | Mass Reduction |
|---|---|---|
| 0.41 kg | 0.32 kg | −28.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milone, D.; Risitano, G.; Pistone, A.; Crisafulli, D.; Alberti, F. A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model. Lubricants 2022, 10, 160. https://doi.org/10.3390/lubricants10070160
Milone D, Risitano G, Pistone A, Crisafulli D, Alberti F. A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model. Lubricants. 2022; 10(7):160. https://doi.org/10.3390/lubricants10070160
Chicago/Turabian StyleMilone, Dario, Giacomo Risitano, Alessandro Pistone, Davide Crisafulli, and Fabio Alberti. 2022. "A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model" Lubricants 10, no. 7: 160. https://doi.org/10.3390/lubricants10070160
APA StyleMilone, D., Risitano, G., Pistone, A., Crisafulli, D., & Alberti, F. (2022). A New Approach for the Tribological and Mechanical Characterization of a Hip Prosthesis Trough a Numerical Model Based on Artificial Intelligence Algorithms and Humanoid Multibody Model. Lubricants, 10(7), 160. https://doi.org/10.3390/lubricants10070160






