Study on the Lubricating Characteristics of the Oil Film of the Slipper Pair in a Large Displacement Piston Pump
Abstract
:1. Introduction
2. Modeling of Oil Film Thickness of Slipper Pair of LDPP
2.1. Force Analysis of Slipper Pair
2.2. Oil Film Thickness Model of Slipper Pair
3. Analysis of Effect Factors on Lubrication Characteristics of Slipper Pair Oil Film
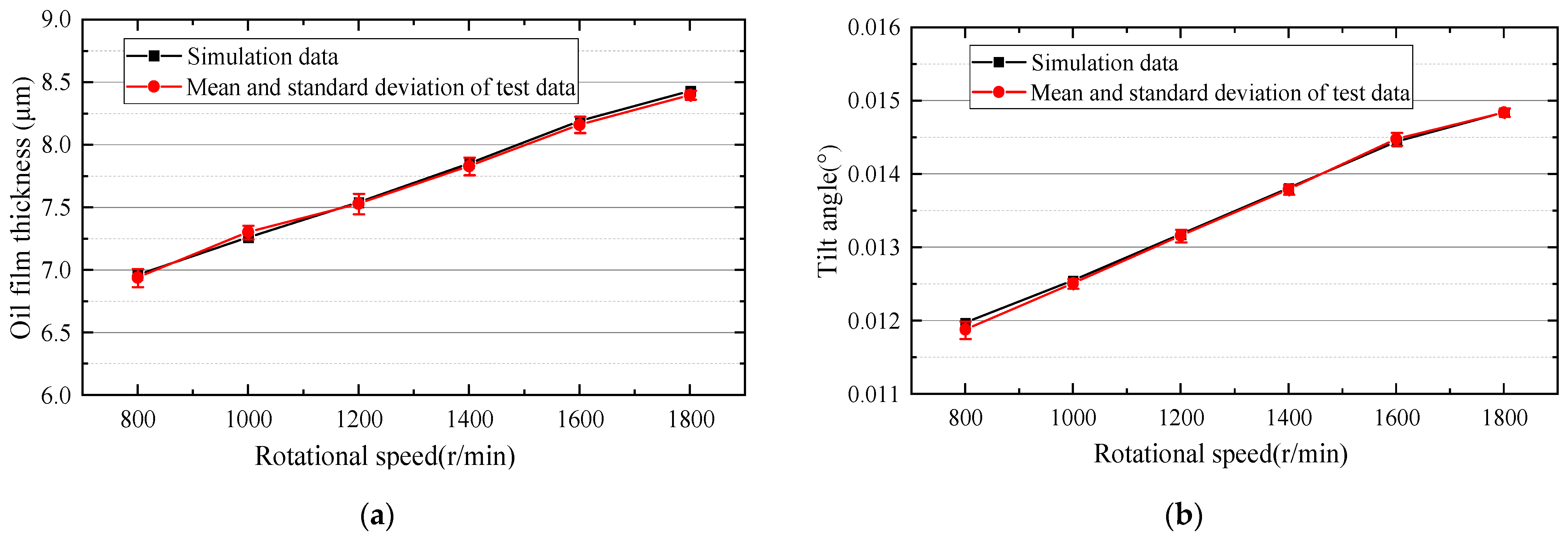
3.1. Effect of Rotational Speed on the Oil Film Thickness of the Slipper Pair
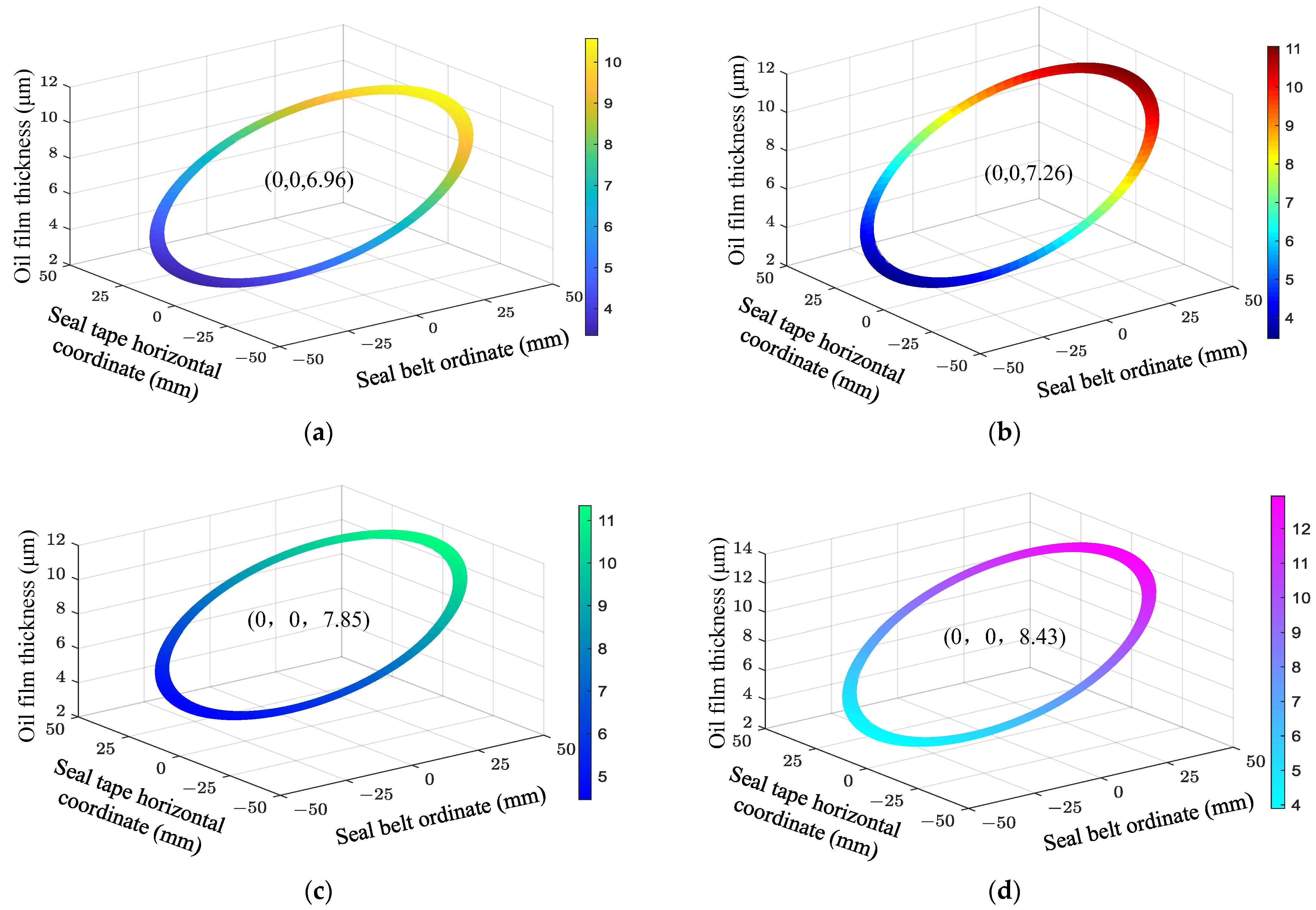
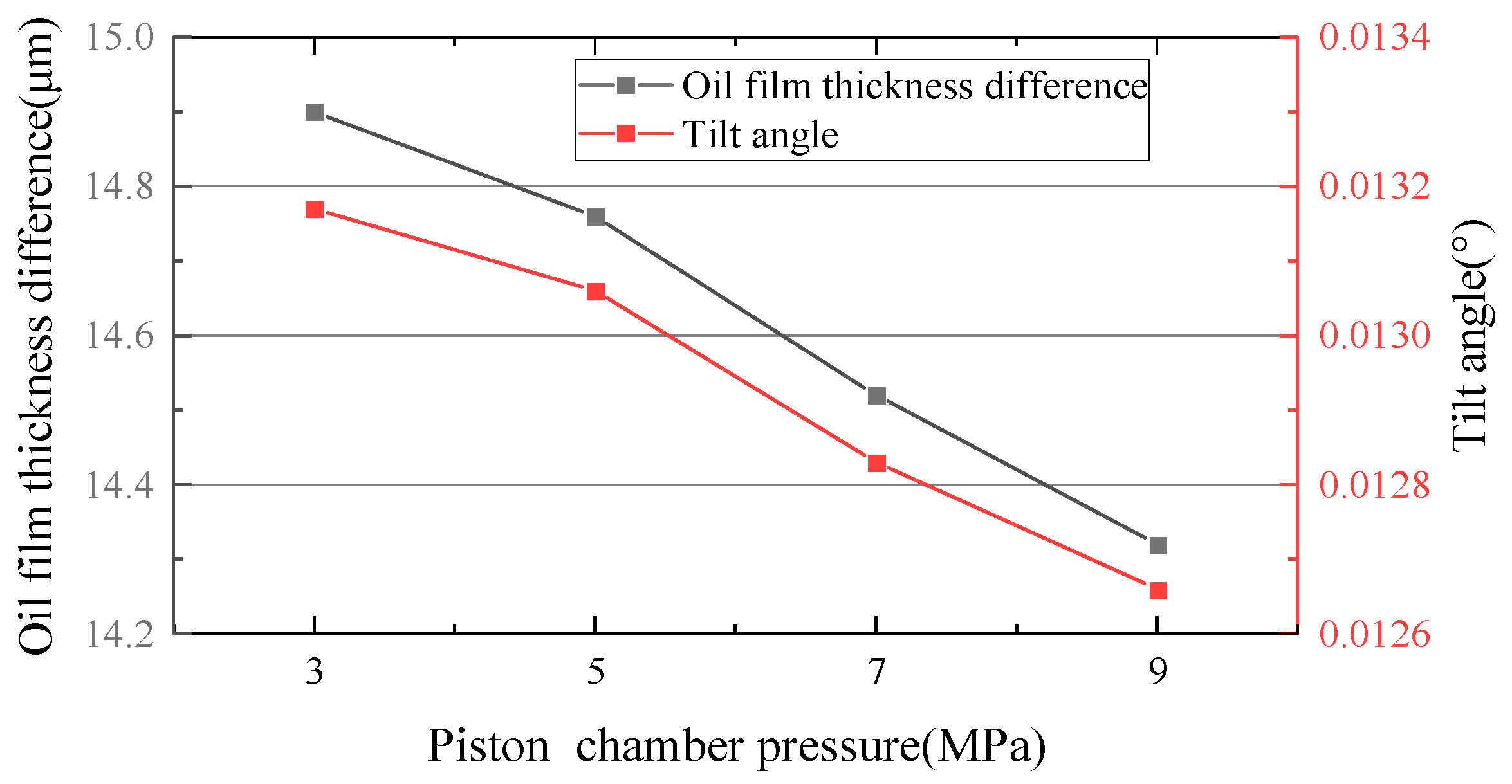
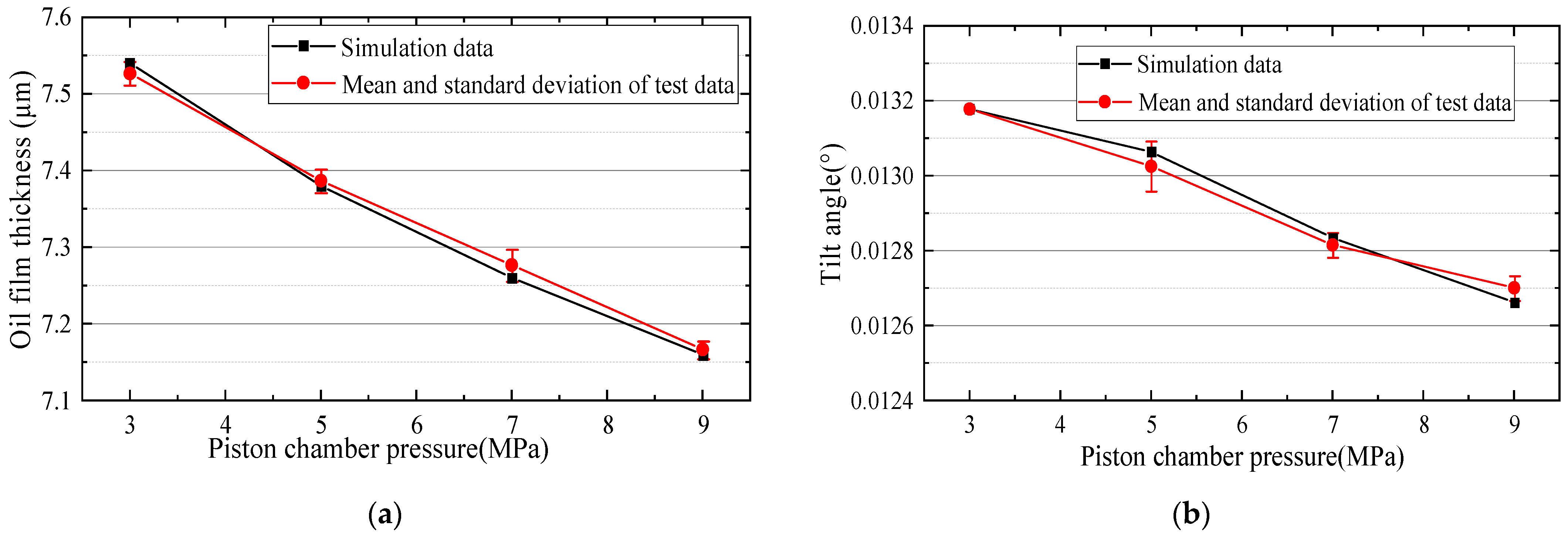
3.2. Effect of Piston Chamber Pressure on the Oil Film Thickness of the Slipper Pair
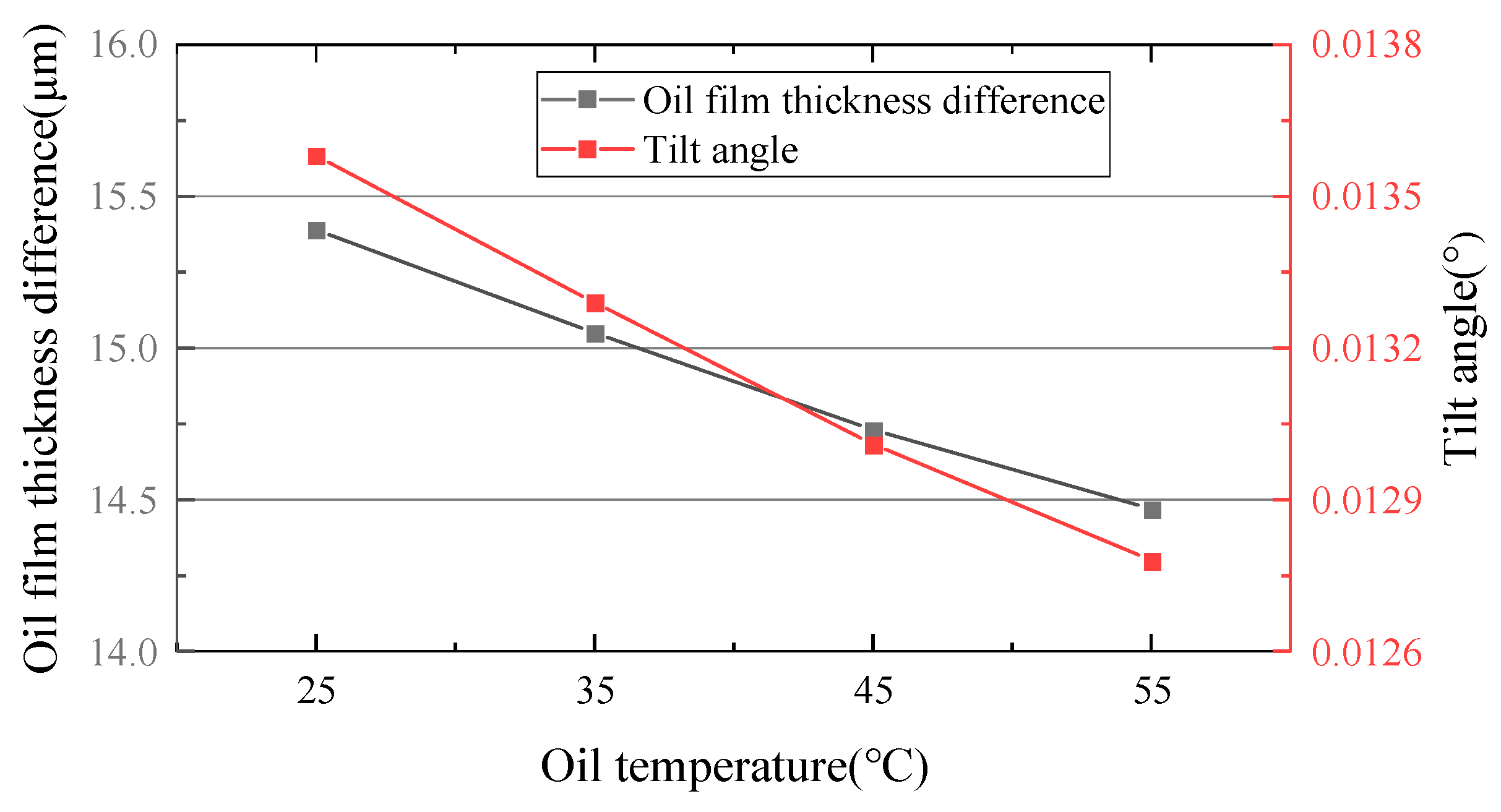
3.3. Effect of Oil Temperature on the Oil Film Thickness of the Slipper Pair
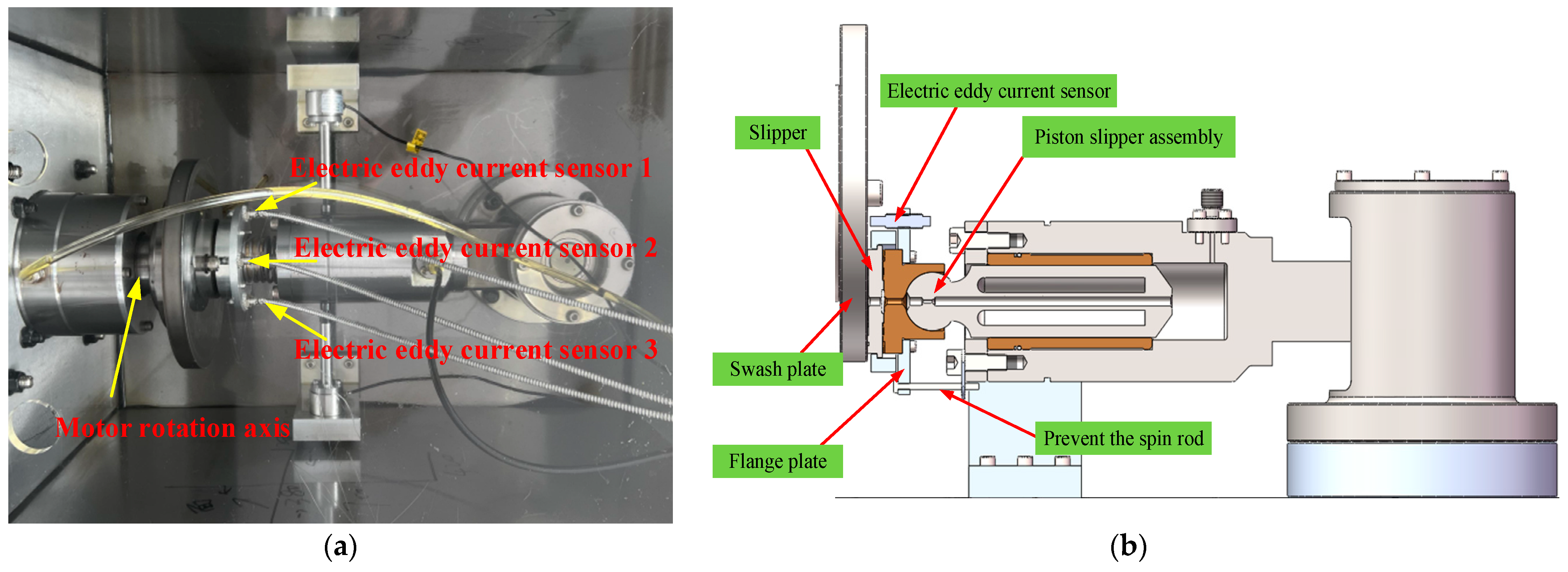
4. Experimental Contrastive Analysis
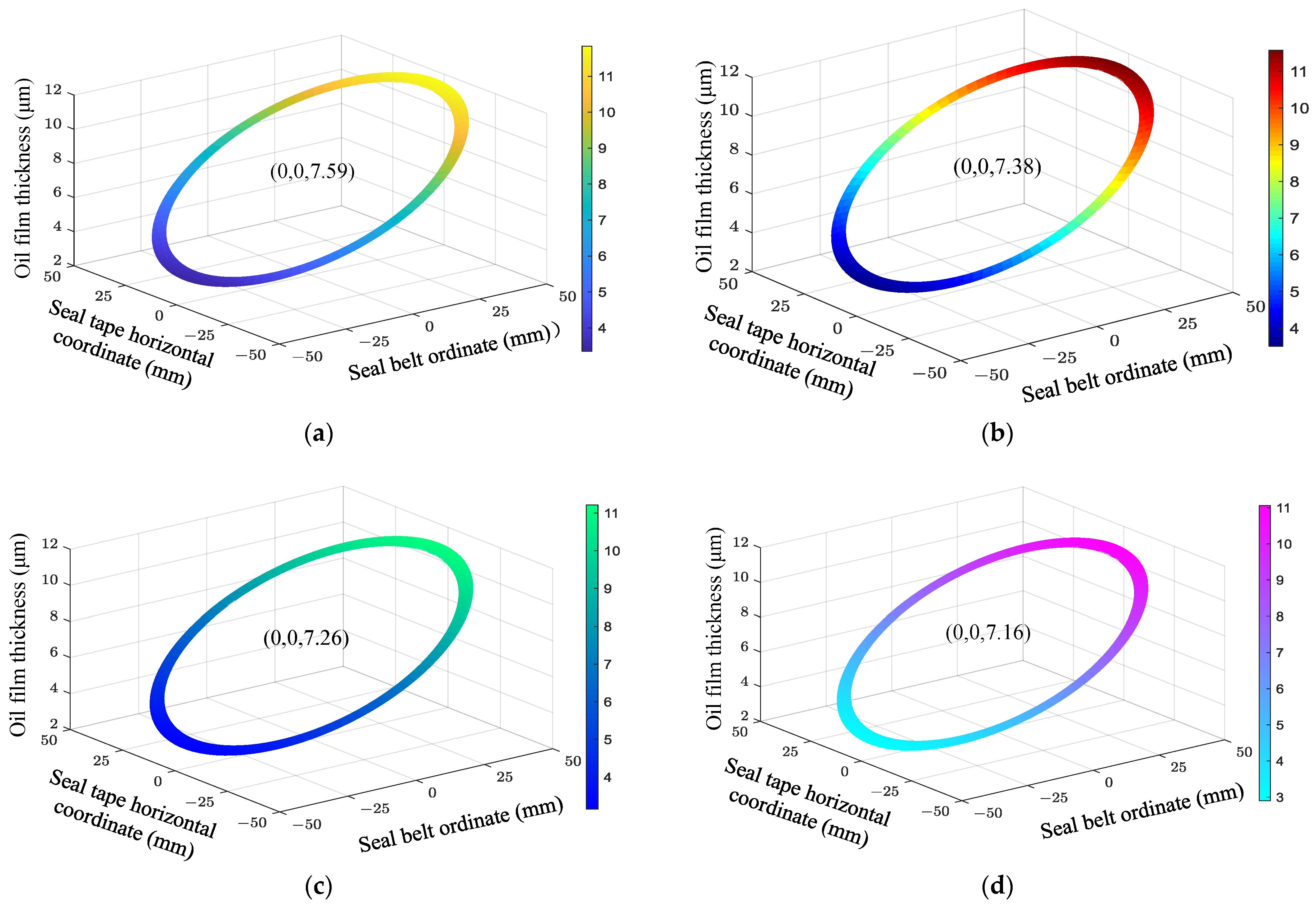
4.1. Comparison of the Effect of Rotational Speed
4.2. Comparison of the Effect of Piston Chamber Pressure
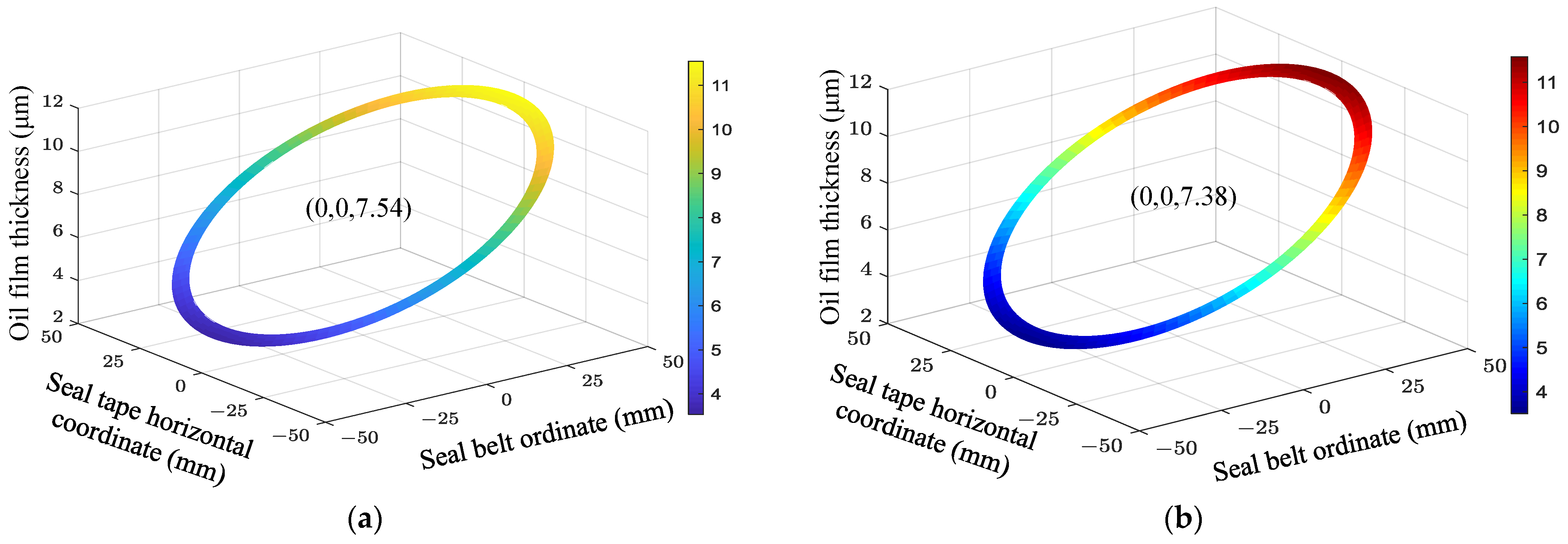
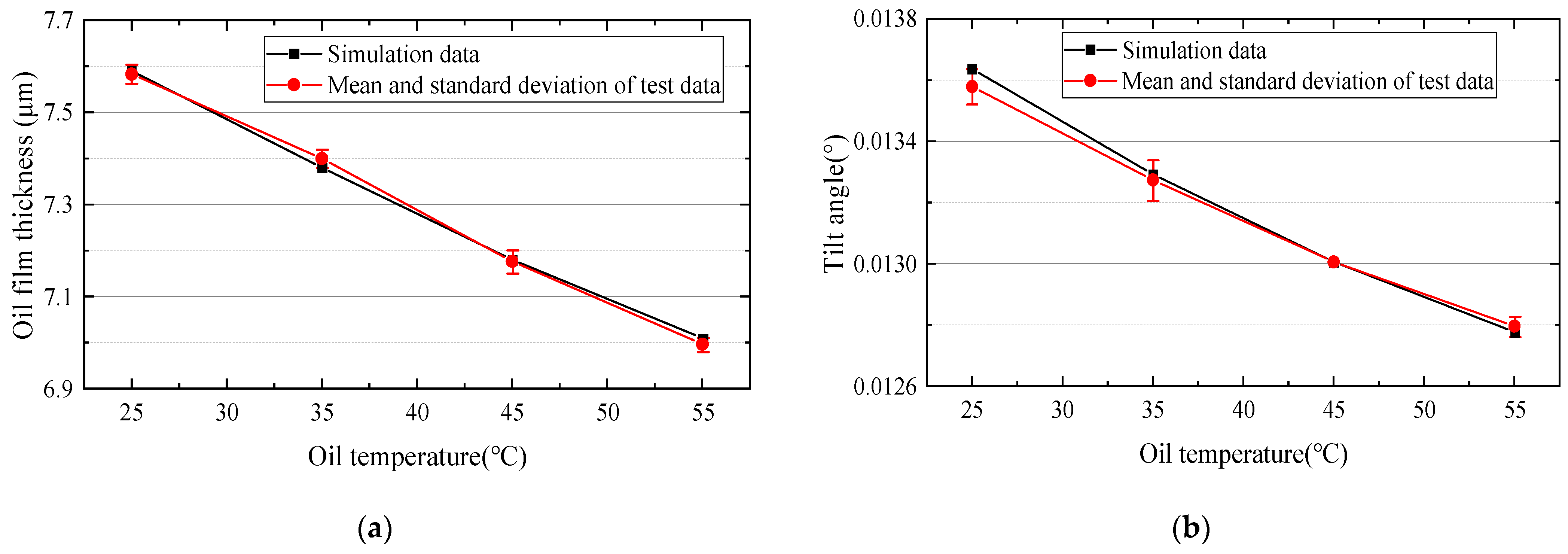
4.3. Comparison of Effects of Oil Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Zhao, L.; Ni, S.; He, Y. Study on friction performance and mechanism of slipper pair under different paired materials in high-pressure axial piston pump. Friction 2020, 8, 957–969. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Wang, Q.; Lyu, F.; Li, K. Integrated slipper retainer mechanism to eliminate slipper wear in high-speed axial piston pumps. Front. Mech. Eng. 2022, 17, 1. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.; Chen, C.; Wang, D.; Li, S. Oil film lubrication state analysis of piston pair in piston pump based on coupling characteristics of the fluid thermal structure. Eng. Fail. Anal. 2022, 140, 106521. [Google Scholar] [CrossRef]
- Yin, F.; Chen, Y.; Ma, Z.; Nie, S.; Ji, H. Investigation on mixed thermalelstohydrodynamic lubrication behavior of slipper/swash plate interface in water hydraulic axial piston pump. Tribol. Int. 2023, 189, 108896. [Google Scholar] [CrossRef]
- Wu, J.; Ma, L.; An, G.; Han, H. Squeeze Film Effect and Its Influence on the Lubrication Characteristics of Slipper Oil Film under Pressure Pulse. Shock Vib. 2023, 2023, 2731176. [Google Scholar] [CrossRef]
- Liu, S.; Li, Z.; Sun, W.; Ai, C.; Zhang, W.; Zhang, Y.; Chen, Z. A Mixed Lubrication Model for Predicting the Lubrication Performance Degradation Behavior of Slipper Pair in Early Wear Failure. IEEE Access 2023, 11, 100479–100494. [Google Scholar] [CrossRef]
- Wang, H.; Shi, G. Lubrication characteristics of the worn slipper in the slipper-swashplate pair. Ind. Lubr. Tribo 2021, 73, 1037–1044. [Google Scholar] [CrossRef]
- Hashemi, S.; Friedrich, H.; Bobach, L.; Bartel, D. Validation of a thermal elastohydrodynamic multibody dynamics model of the slipper pad by friction force measurement in the axial piston pump. Tribol. Int. 2017, 115, 319–337. [Google Scholar] [CrossRef]
- Xu, L.; Sun, H.; Xu, S. Fracture mechanism analysis on the slipper retainer in axial piston pumps. Eng. Fail. Anal. 2017, 80, 378–385. [Google Scholar] [CrossRef]
- Gaston, H.; Wang, D. Analysis of Damage and Failure mechanism under a lubricated slipper/swashplate interface in Axial Piston Machines. Sci. Direct 2022, 35, 124–131. [Google Scholar]
- Xu, B.; Li, Y.; Zhang, B.; Zhang, J. Numerical simulation of overturning phenomenon of axial piston pump slipper pair. J. Mech. Eng. 2010, 46, 161–168. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Q.; Zhang, J. Effect of case drain pressure on slipper/swashplate pair within axial piston pump. J. Zhejiang Univ.-Sci. A 2015, 16, 1001–1014. [Google Scholar] [CrossRef]
- Mo, H.; Hu, Y.; Quan, S. Thermo-Hydrodynamic Lubrication Analysis of Slipper Pair Considering Wear Profile. Lubricants 2023, 11, 190. [Google Scholar] [CrossRef]
- Bergada, J.; Watton, J.; Haynes, J.M.; Davies, D.L. The hydrostatic/hydrodynamic behaviour of an axial piston pump slipper with multiple lands. Meccanica 2010, 45, 585–602. [Google Scholar] [CrossRef]
- Schenk, A.; Ivantysynova, M. A Transient Thermoelastohydrodynamic Lubrication Model for the Slipper/Swashplate in Axial Piston Machines. J. Tribol. 2015, 137, 031701. [Google Scholar] [CrossRef]
- Rokala, M.; Calonius, O.; Koskinen, K.T.; Pietola, M. Study of lubrication conditions in slipper-swashplate contact in water hydraulic axial piston pump test rig. In Proceedings of the JFPS International Symposium on Fluid Power; The Japan Fluid Power System Society: Tokyo, Japan, 2008; pp. 91–94. [Google Scholar]
- Tang, H.; Ren, Y.; Xiang, J. A novel model for predicting thermoelastohydrodynamic lubrication characteristics of slipper pair in axial piston pump. Int. J. Mech. Sci. 2017, 124, 109–121. [Google Scholar] [CrossRef]
- Tang, H.; Yin, Y.; Ren, Y.; Xiang, J.; Chen, J. Impact of the thermal effect on the load-carrying capacity of a slipper pair for an aviation axial-piston pump. Chin. J. Aeronaut. 2018, 31, 395–409. [Google Scholar] [CrossRef]
- Zhao, K.; He, T.; Wang, C.; Chen, Q.; Li, Z. Lubrication characteristics analysis of slipper pair of digital valve distribution axial piston pump. Adv. Mech. Eng. 2022, 14, 16878132221085442. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Z.; Li, G. The impact of slipper microstructure on slipper-swashplate lubrication interface in axial piston pump. IEEE Access 2020, 8, 222865–222875. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Z. Optimization and influence of micro-chamfering on oil film lubrication characteristics of slipper/swashplate interface within axial piston pump. Energies 2021, 14, 1961. [Google Scholar] [CrossRef]
- Song, Y.; Zeng, S.; Ma, J.; Hou, J. Failure analysis of graphite stationary ring utilized in one type of mechanical seal. Eng. Fail. Anal. 2020, 108, 104259. [Google Scholar] [CrossRef]
- Shi, C.; Wang, S.; Wang, X.; Zhang, Y. Variable load failure mechanism for high-speed load sensing electro-hydrostatic actuator pump of aircraft. Chin. J. Aeronaut. 2018, 31, 949–964. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, J.; Jing, C. Experimental research on the dynamic lubricating performance of slipper/swash plate interface in axial piston pumps. Chin. J. Mech. Eng. 2020, 33, 25. [Google Scholar] [CrossRef]
- Ma, J.; Chen, J.; Li, J.; Li, Q.; Ren, C. Wear analysis of swash plate/slipper pair of axis piston hydraulic pump. Tribol. Int. 2015, 90, 467–472. [Google Scholar] [CrossRef]
- Zhang, J.; Chao, Q.; Wang, Q.; Xu, B.; Chen, Y.; Li, Y. Experimental investigations of the slipper spin in an axial piston pump. Measurement 2017, 102, 112–120. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, H.; Chen, J.; Huang, W.; Huang, X.; Lyu, F.; Xu, B.; Pan, M.; Su, Q. Modeling and Analysis of the tilt behavior of the cylinder block in a high-speed axial piston pump. Mech. Mach. Theory 2022, 170, 25. [Google Scholar]
- Shen, R.; Pan, Y. Friction characteristic analysis of slipper pair in A11VO190 axial piston pumps. Chin. J. Eng. Design 2014, 21, 51–55. [Google Scholar]
- Tang, H.; Yan, Y.; Li, J. Lubrication characteristics analysis of slipper bearing in axial piston pump considering thermal effect. Lubr. Sci. 2016, 28, 107–124. [Google Scholar]
- Yu, S. Characteristics Analysis and Structure Optimization of Slipper with Static and Dynamic Pressure Support Used in the Axial Piston Pump. Master’s Thesis, Harbin Institute of Technology, Harbin, China, July 2013. [Google Scholar]
- Sun, Y. Testing System Research for Investigating the Properties of Slipper Pair in High Speed and High Pressure Axial Piston Pump. Master’s Thesis, Zhejiang University, Hangzhou, China, March 2016. [Google Scholar]
- Xu, B.; Sun, Y.; Zhang, J.; Sun, T.; Mao, Z. A new design method for the transition region of the valve plate for an axial piston pump. J. Zhejiang Univ.-Sci. A 2015, 16, 229–240. [Google Scholar] [CrossRef]
- Tang, H.; Yan, Y.; Li, J.; Wang, Z. Thermohydrodynamic Lubrication Analysis of Slipper Pair in Axial Piston Pump Considering Surface Deformation. Chin. J. Mech. Eng. 2017, 53, 168–176. [Google Scholar] [CrossRef]
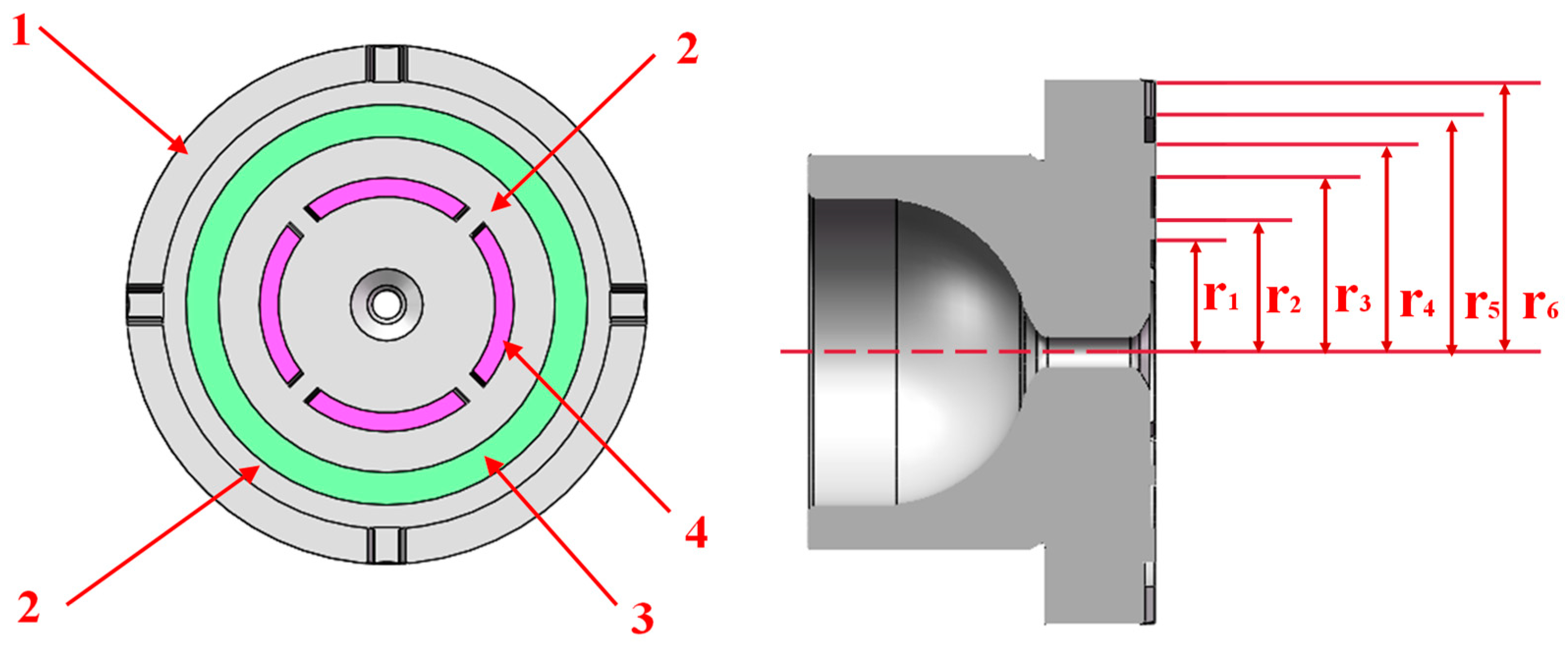

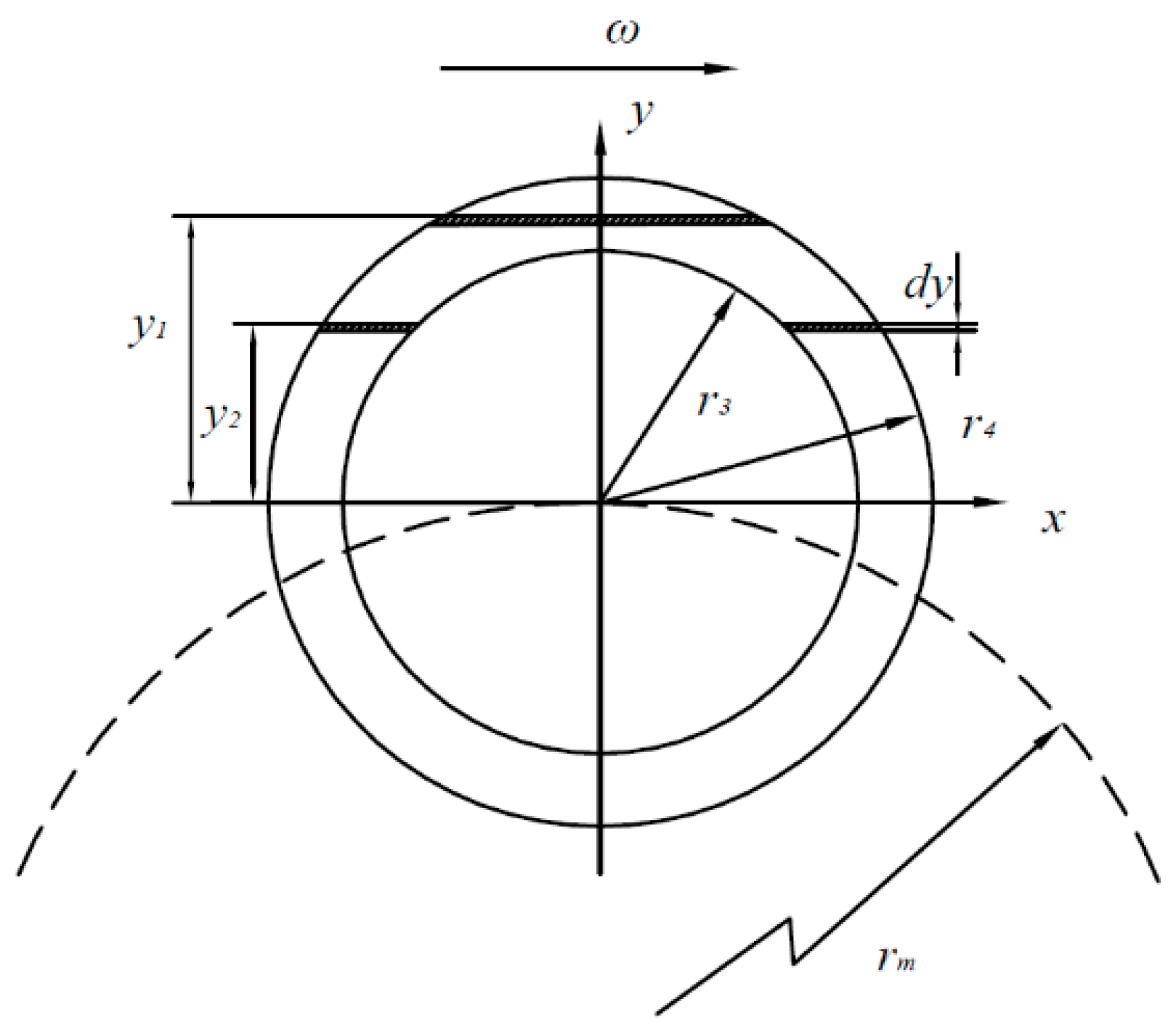
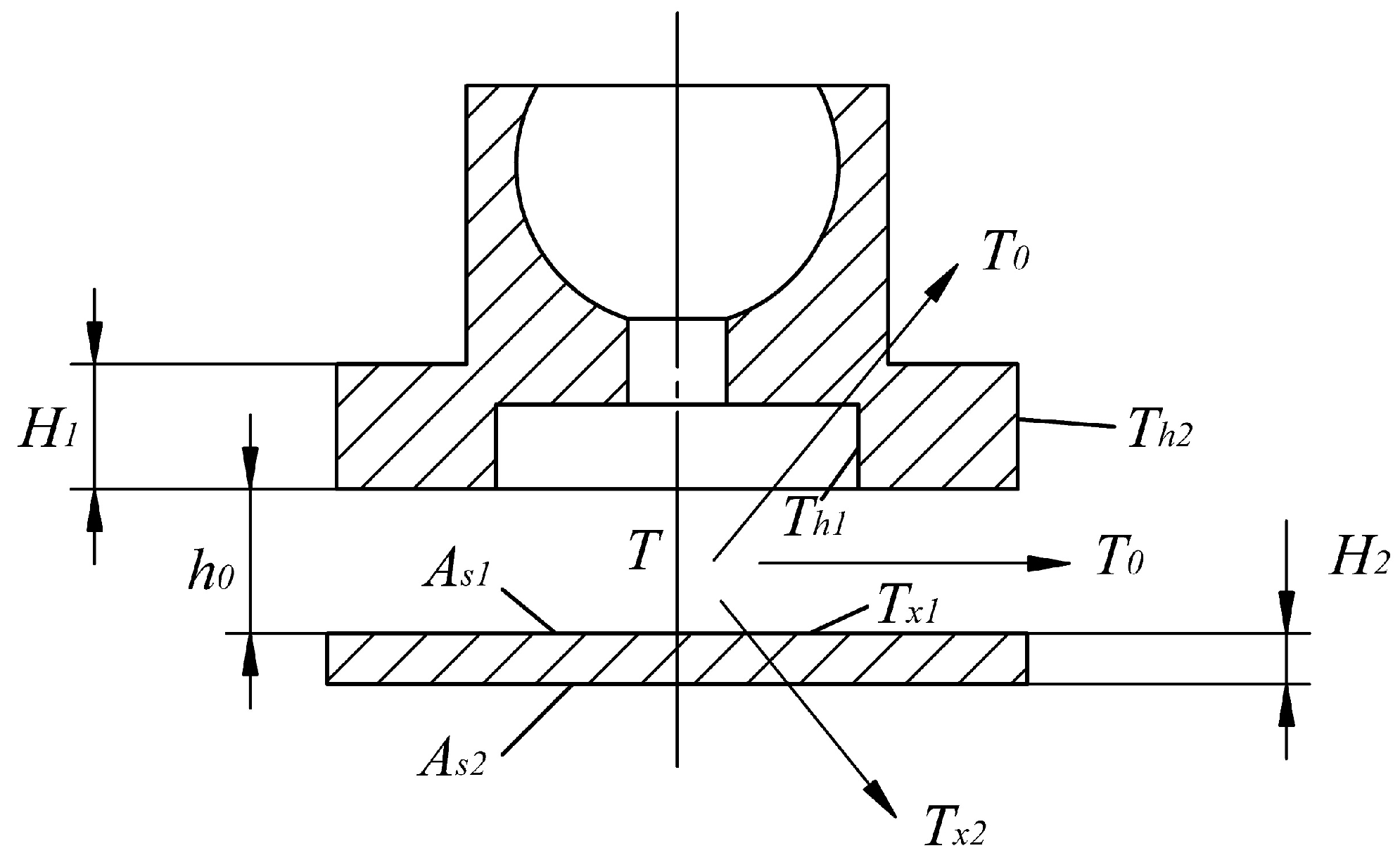
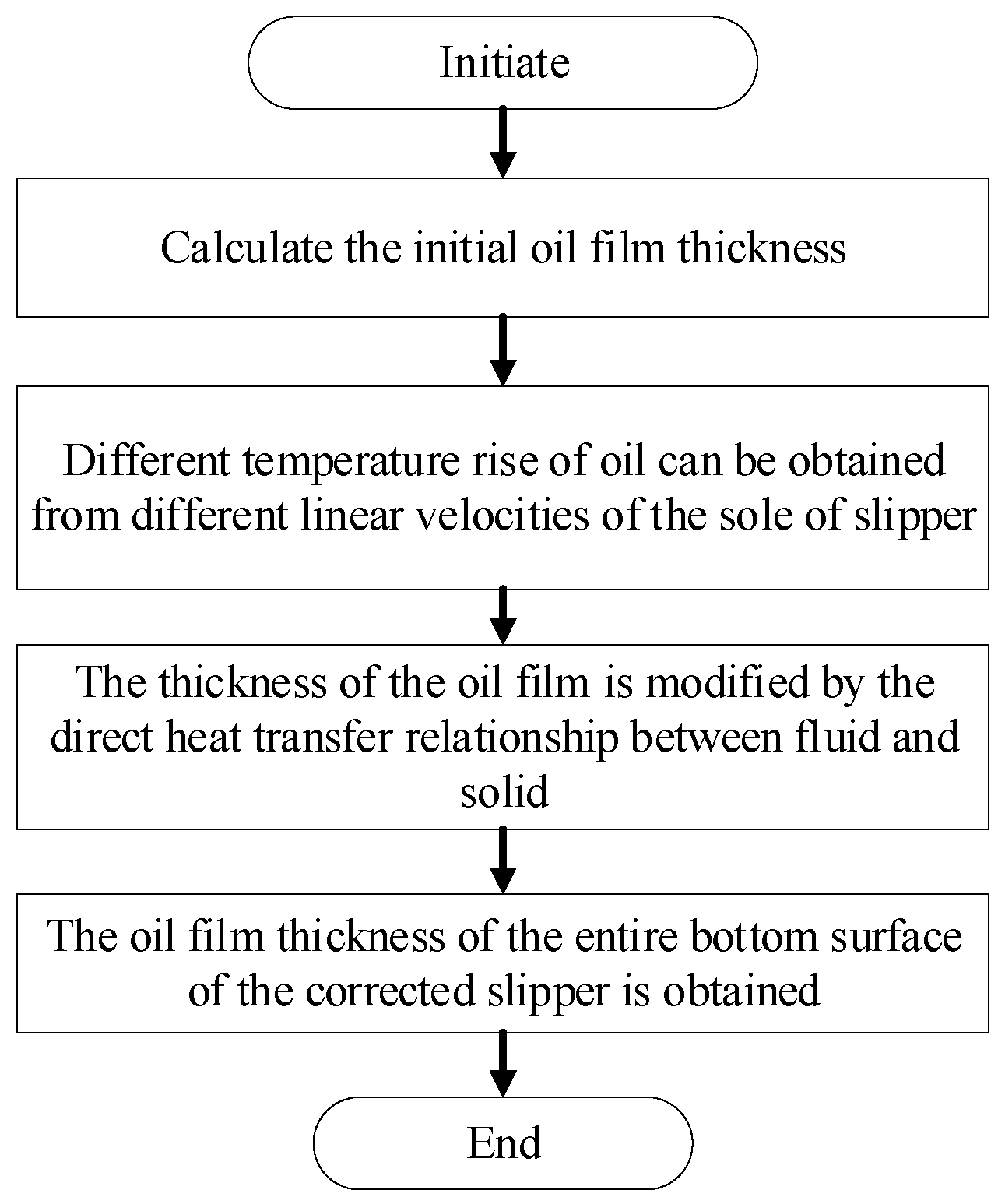



| Correlation Parameter | Numerical Value |
|---|---|
| Inner diameter of slipper auxiliary ring | 13.3 mm |
| Outer diameter of slipper inner auxiliary ring | 15.85 mm |
| Slipper seal with inner diameter | 20.05 mm |
| Slipper seal with outer diameter | 24.85 mm |
| Inside diameter of slipper outer auxiliary ring | 27.6 mm |
| Outer diameter of slipper auxiliary ring | 32.4 mm |
| Diameter of damping tube | 2 mm |
| Damping tube length | 6 mm |
| Piston distribution circle radius | 100 mm |
| Piston diameter | 45 mm |
| Quality of single piston assembly | 1.7 kg |
| Volume expansion coefficient of oil | |
| The density of oil | 860 kg/m3 |
| Specific heat capacity of oil | |
| Acceleration of gravity | 9.8 m/s2 |
| Oil dynamic viscosity coefficient | |
| Thermal equivalent | 481.2 J |
| Precompression force | 30 N |
| Thermal conductivity | |
| Linear expansion coefficient of slipper | |
| Slipper material thickness | 11 mm |
| Linear expansion coefficient of swash plate | |
| Swash plate material thickness | 18 mm |
| Thermal conductivity | |
| Thermal conductivity | |
| Swash plate roughness | Ra 0.8 |
| Slipper roughness | Ra 1.6 |
| Swash plate inclination | |
| Piston dip angle | |
| Half angle of the cone | |
| Dynamic viscosity of hydraulic oil 25 °C | 85 mm2/s |
| Dynamic viscosity of hydraulic oil 35 °C | 50 mm2/s |
| Dynamic viscosity of hydraulic oil 45 °C | 40 mm2/s |
| Dynamic viscosity of hydraulic oil 55 °C | 25 mm2/s |
| Range | Combined Error | Precision | Operating Temperature |
|---|---|---|---|
| 0–1 mm | 0.01 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Chen, J.; Li, D.; Zhang, L.; Jia, Y.; Guo, F.; Li, J. Study on the Lubricating Characteristics of the Oil Film of the Slipper Pair in a Large Displacement Piston Pump. Lubricants 2023, 11, 521. https://doi.org/10.3390/lubricants11120521
Xu L, Chen J, Li D, Zhang L, Jia Y, Guo F, Li J. Study on the Lubricating Characteristics of the Oil Film of the Slipper Pair in a Large Displacement Piston Pump. Lubricants. 2023; 11(12):521. https://doi.org/10.3390/lubricants11120521
Chicago/Turabian StyleXu, Liping, Jiaheng Chen, Donglin Li, Liang Zhang, Yaowei Jia, Fuhang Guo, and Jian Li. 2023. "Study on the Lubricating Characteristics of the Oil Film of the Slipper Pair in a Large Displacement Piston Pump" Lubricants 11, no. 12: 521. https://doi.org/10.3390/lubricants11120521





