Study on Sealing Characteristics of Compliant Foil Face Gas Seal under Typical Hypervelocity Gas Effects
Abstract
:1. Introduction
2. Theoretical Model
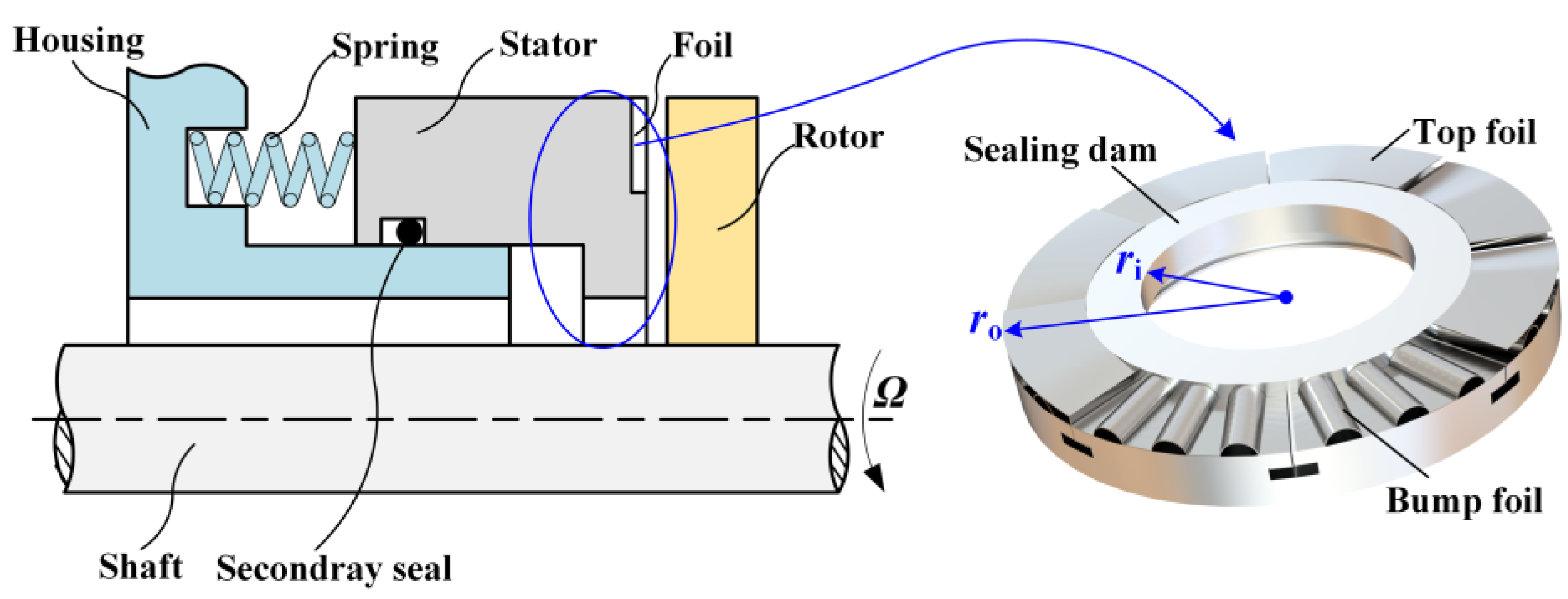
2.1. Structure of CFFGS
2.2. Control Equation of Film Pressure
2.3. Control Equation of Film Thickness
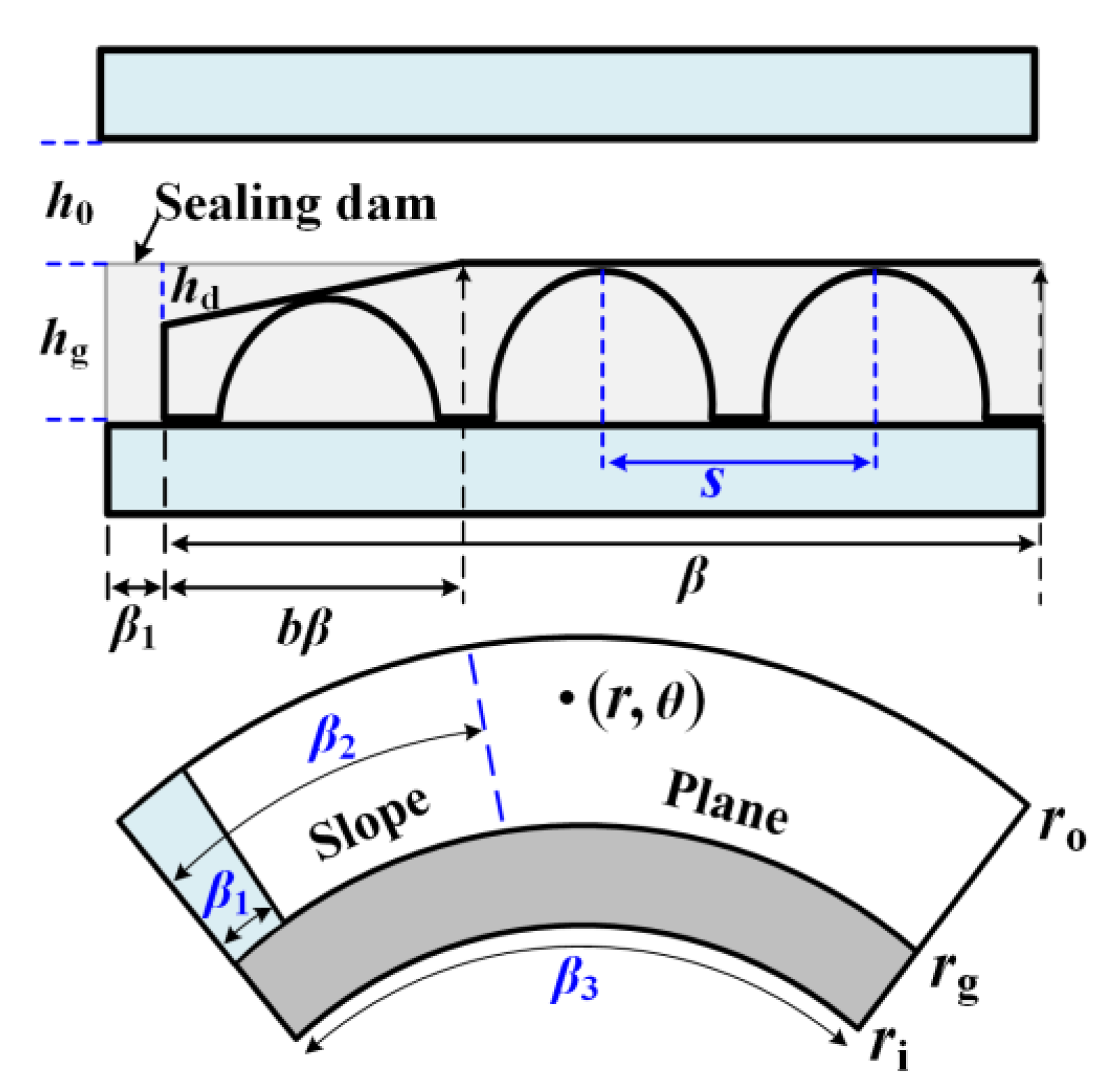
2.3.1. Establishment of Film Thickness Equation
2.3.2. Mechanical Model of Foil Deformation
2.4. Pressure Boundary Conditions
2.5. Calculation of Sealing Performance Parameters
3. Results and Discussion
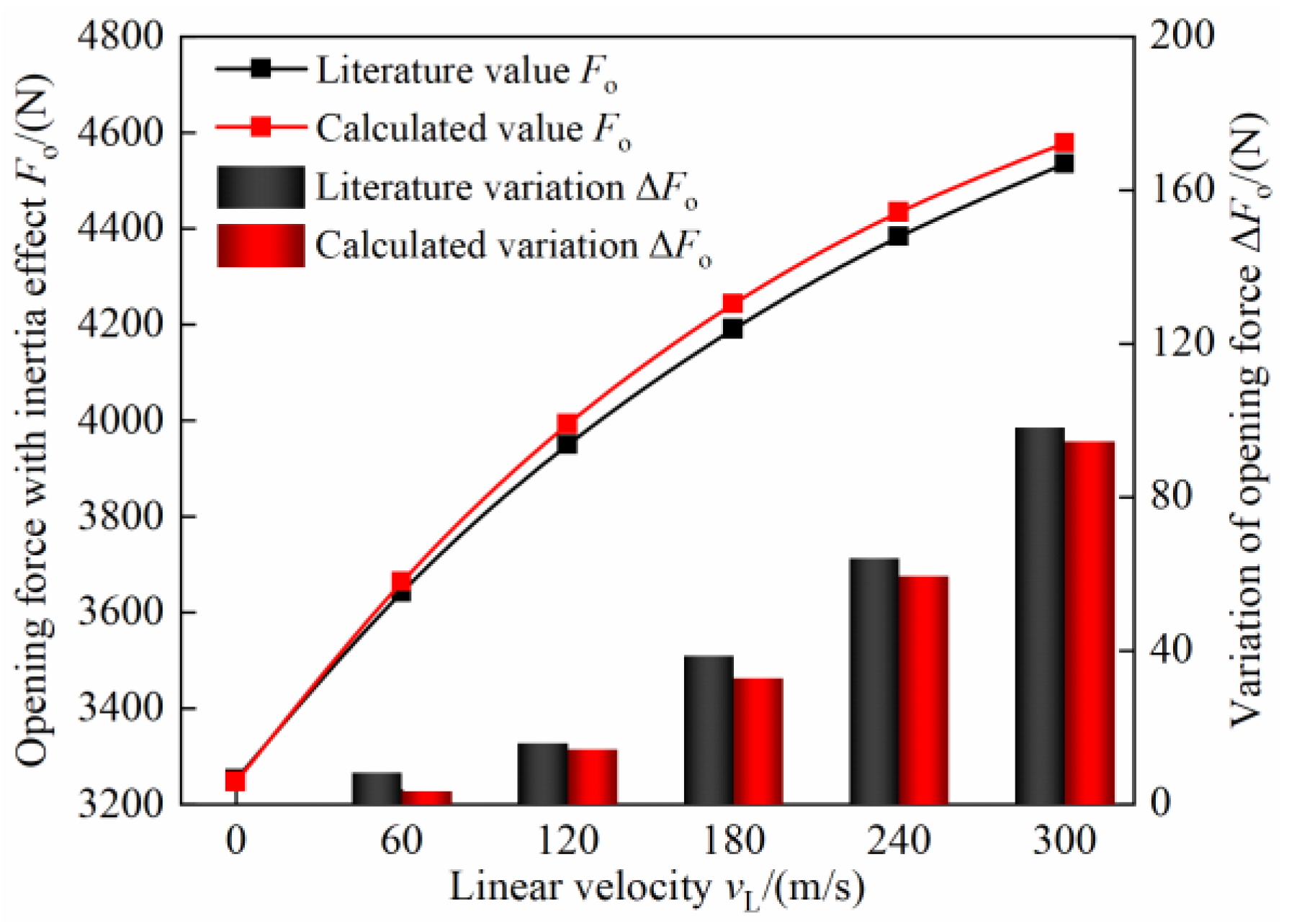
3.1. Correctness Verification of Calculation Program
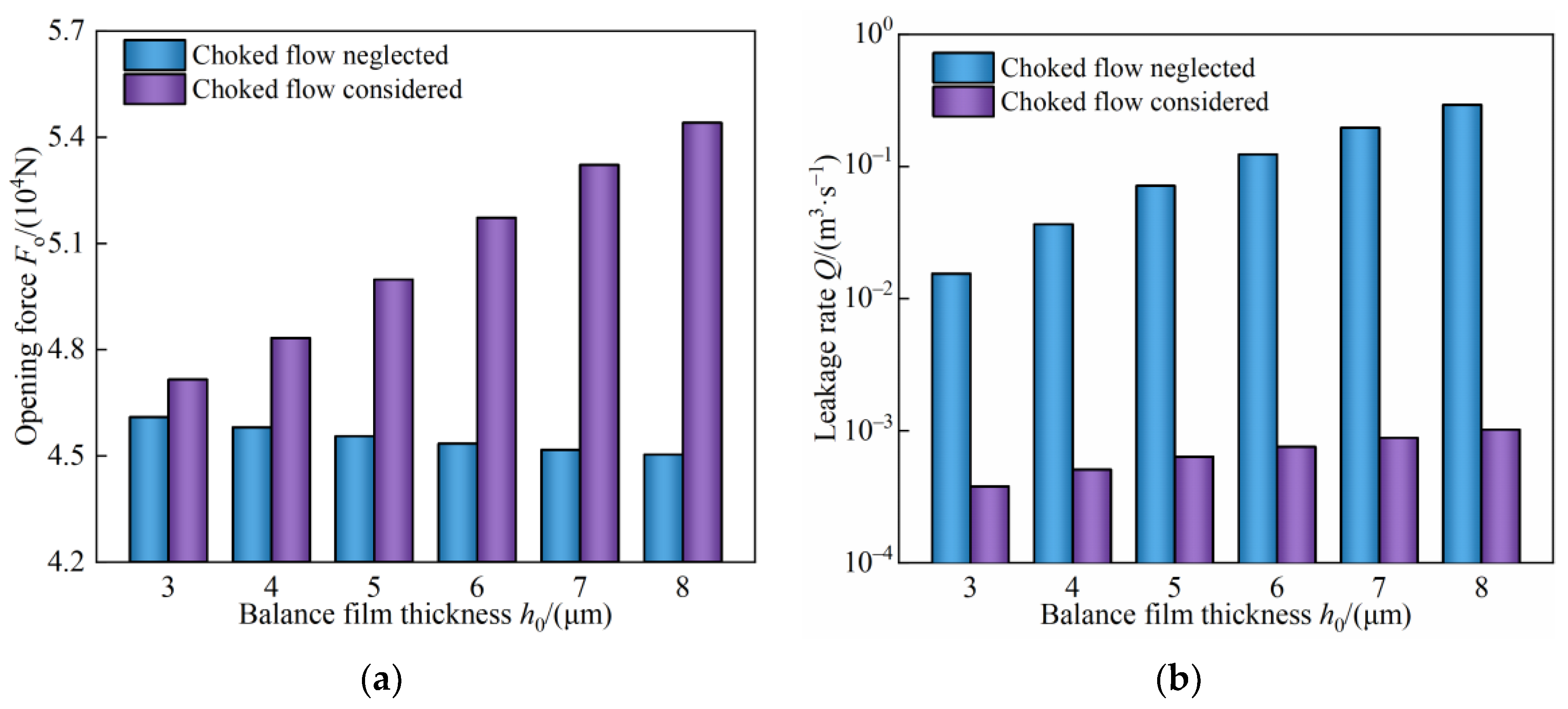
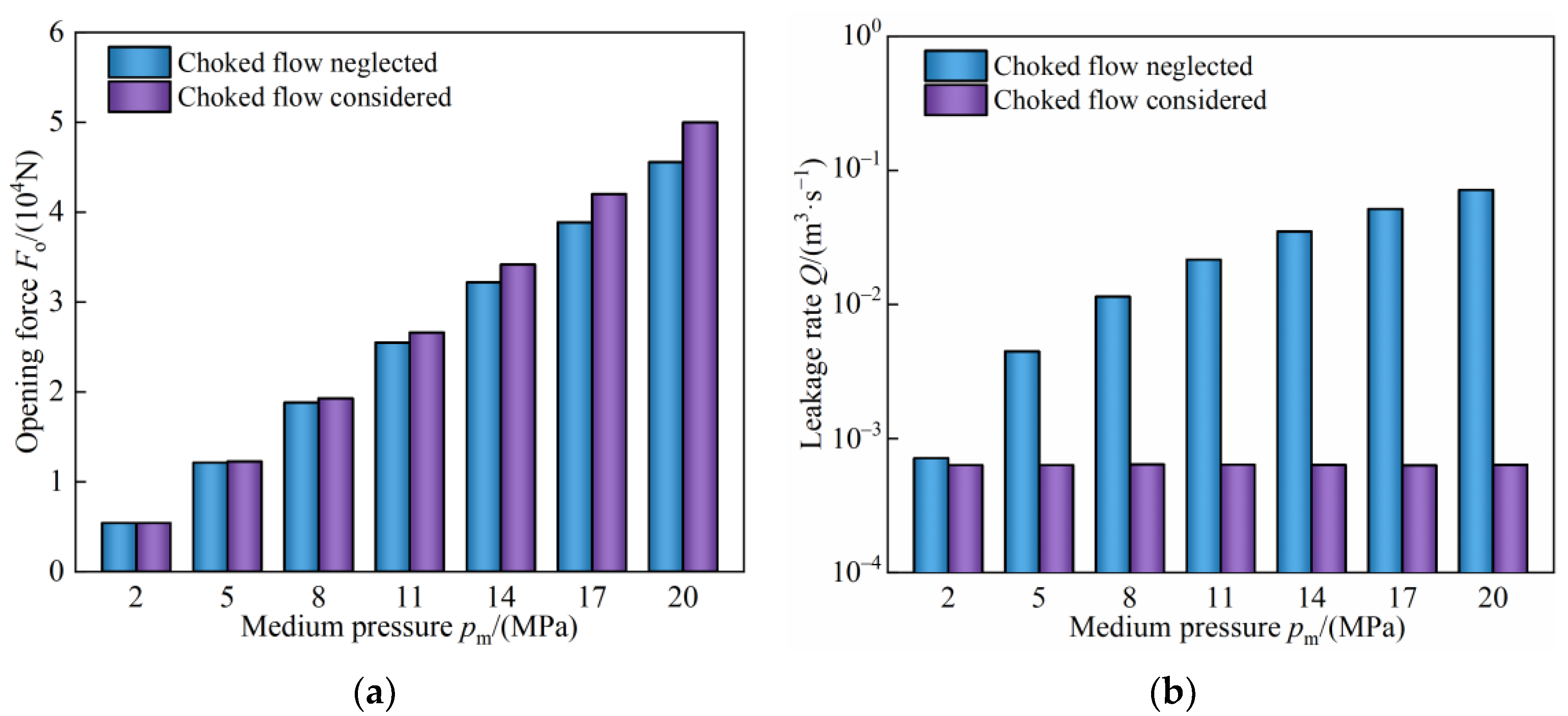
3.2. Influence of Choked Flow on Sealing Characteristics
3.2.1. Influence of Choked Flow on Flow Field of Dynamic Lubrication
3.2.2. Influence of Choked Flow on Sealing Performance
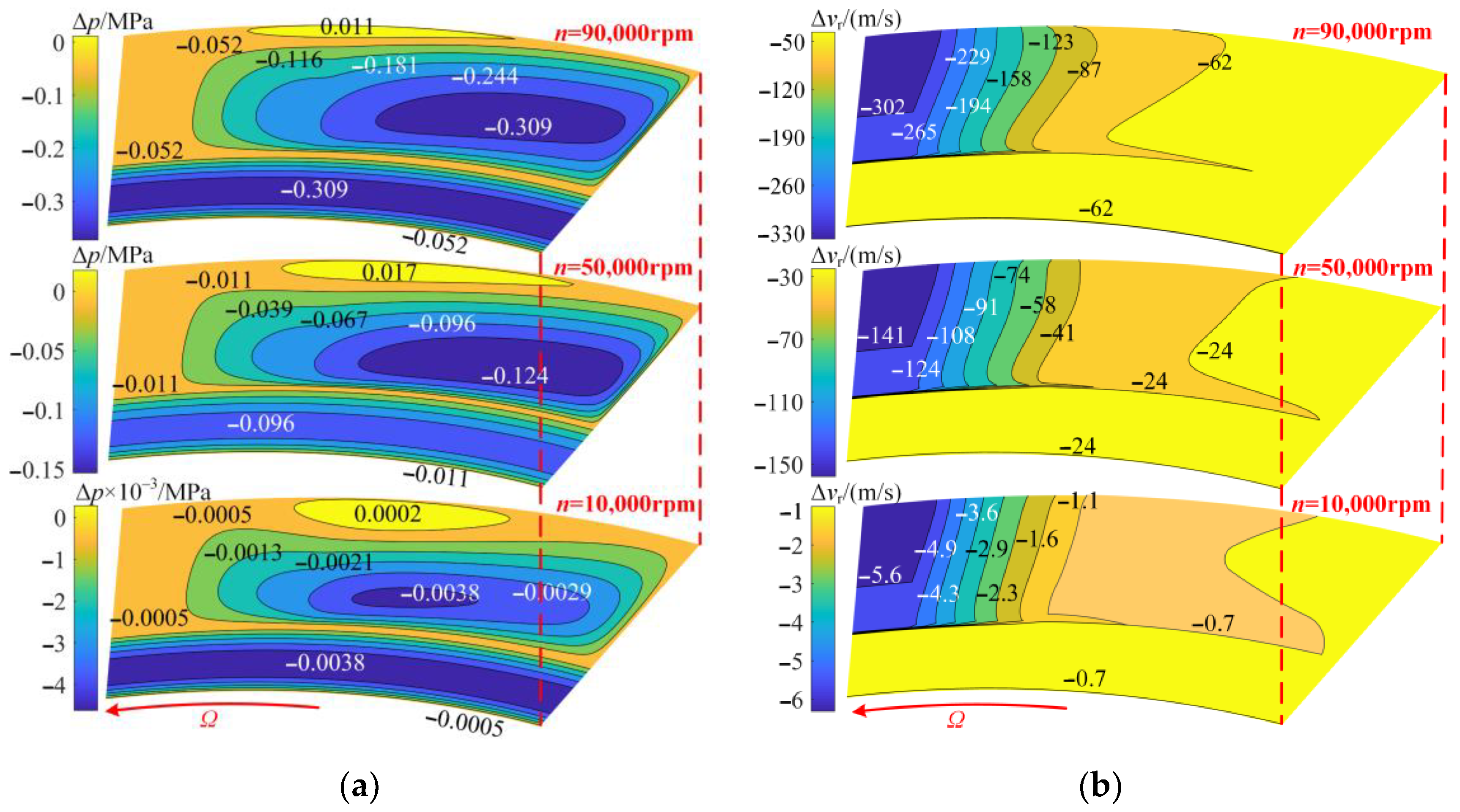
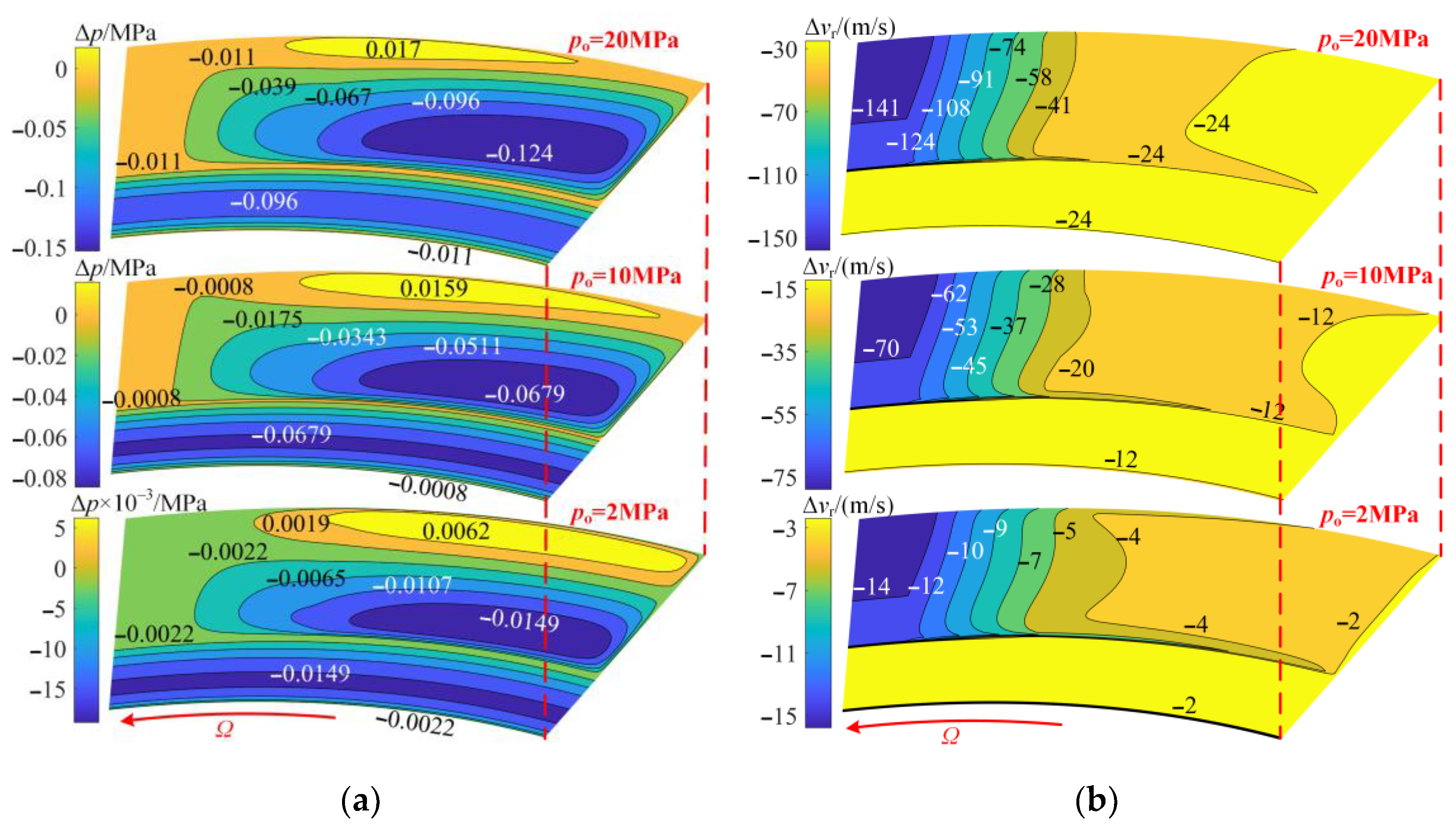
3.3. Influence of Inertia Effect on Sealing Characteristics
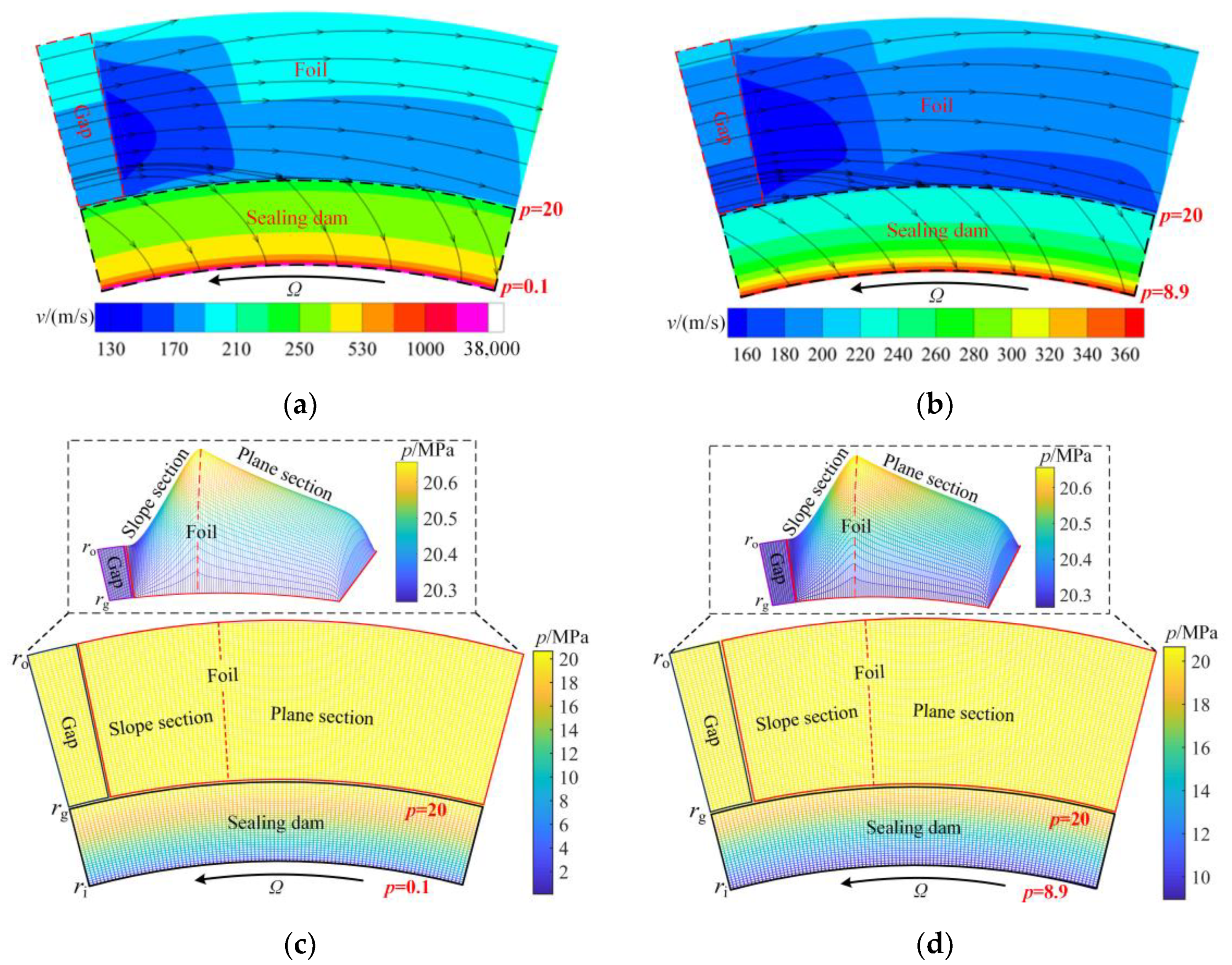
3.3.1. Influence of Inertia Effect on Flow Field of Dynamic Lubrication
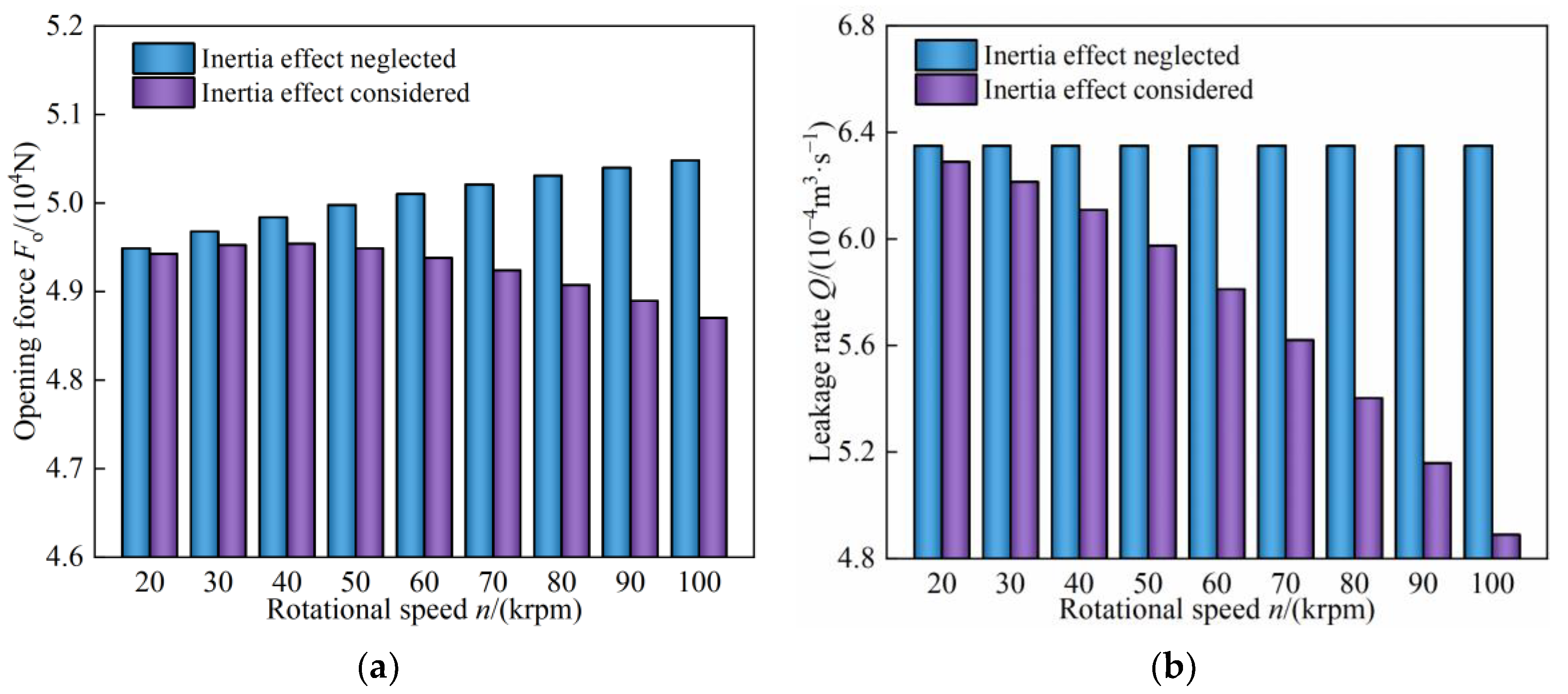
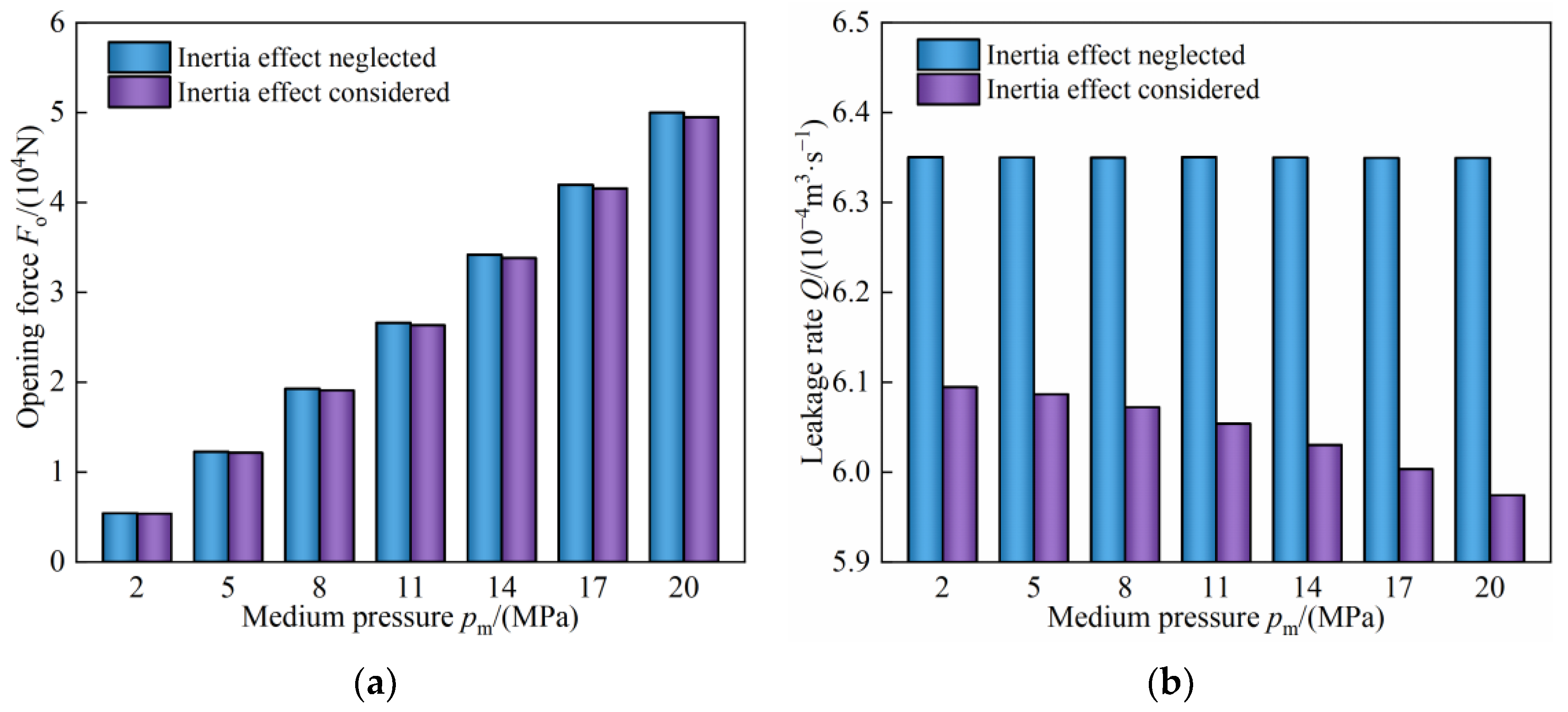
3.3.2. Influence of Inertia Effect on Sealing Performance
4. Scientific Contribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Slope ratio |
| Fo | Opening force |
| h, h0, hg, hd | Film thickness, balance film thickness, depth of gap section, wedge height |
| kb, Kb | Unit transverse stiffness, dimensionless axial deformation stiffness of bump foil |
| n, N | Rotational speed of shaft, number of foil |
| p, pa, pm | Film pressure, atmospheric pressure, pressure of high-pressure medium |
| pi, po | Pressure at inner radius, pressure at outer radius |
| Pθ | Dimensionless film pressure at the end of top foil |
| Q | Steady-state volume leakage rate |
| r, rg, ri, ro | Radius, outer radius of sealing dam, inner radius, and outer radius of seal face |
| Rg | Gas constant |
| s | Length of bump foil unit |
| T | Temperature |
| u | Axial deformation |
| v, vr | Fluid velocity and radial velocity of fluid |
| α | Compliance coefficient |
| β, β1, β2, β3 | Angle of single foil and gap section, angle of slope section and plane section |
| θ | Angle |
| µ | Gas viscosity |
| Λ1 | Compressibility number |
| Ω | Angular velocity of shaft |
References
- He, Q.; Huang, W.F.; Hu, G.Y.; Li, Y.J.; Liu, Y.; Wang, Y.M. Research status of the film-riding gas seal technologies in aeroengine. Aeroengine 2021, 4, 106–113. [Google Scholar]
- Chen, Y.; Jiang, J.B.; Peng, X.D.; Yan, T.H.; Li, Y.T.; Li, X.L.; Li, J.Y. Analysis of the interaction between the dynamic performance of the dry gas seal mechanical system and its influencing factors. Tribology 2019, 3, 269–278. [Google Scholar]
- Keller, D.; Jacobs, G.; Neumann, S. Development of a low-friction radial shaft seal: Using cfd simulations to optimise the microstructured sealing lip. Lubricants 2020, 8, 41. [Google Scholar] [CrossRef] [Green Version]
- Heshmat, H.; Ren, Z.; Hunsberger, A.; Walton, J.; Jahanmir, S. The emergence of compliant foil bearing and seal technologies in support of 21st century compressors and turbine engines. In Proceedings of the ASME 2010 International Mechanical Engineering Congress & Exposition, Vancouver, BC, Canada, 12–18 November 2010; pp. 95–103. [Google Scholar]
- Munson, J.H. Foil face seal testing. In Proceedings of the NASA Seal/Secondary Air System Workshop, Indianapolis, IN, USA, 1 November 2009; pp. 131–137. [Google Scholar]
- Li, C.; Du, J.; Li, J.; Xu, Z. Investigations on the frictional hysteresis effect of multi-leaf journal foil bearing: Modeling, predictions and validations. Lubricants 2022, 10, 261. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Du, J. The fluid-structure-thermal performance analysis of gas foil thrust bearing by using computational fluid dynamics. Lubricants 2022, 10, 294. [Google Scholar] [CrossRef]
- Heshmat, H. Advanced development of air-lubricated foil thrust bearings. Lubr. Eng. 1984, 1, 21–26. [Google Scholar]
- Heshmat, H. Compliant Foil Seal. U.S. Patent 6,505,837, 14 January 2003. [Google Scholar]
- Agrawal, G.L.; Patel, K.H.; Munson, J.H. Hydrodynamic Foil Face Seal. U.S. Patent 7,261,300, 28 August 2007. [Google Scholar]
- Munson, J.H.; Grant, D.; Agrawal, G.L. Foil face seal development. In Proceedings of the 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Salt Lake City, UT, USA, 8–11 July 2001; p. 3483. [Google Scholar]
- Munson, J.H.; Grant, D.; Agrawal, G.L. Foil film riding face seal proof-of-concept testing. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, IN, USA, 7–10 July 2002; p. 3791. [Google Scholar]
- Heshmat, H.; Walton, J. Innovative High-temperature compliant surface foil face seal development. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 4505. [Google Scholar]
- Bai, C.B.; Liu, M.H.; Sun, J.F.; Dai, D. Research on support structure performance of cylindrical gas film seal based on fluid-structure interaction. Lubr. Eng. 2020, 9, 64–70. [Google Scholar]
- Zhao, C.Y.; Liu, M.H.; Sun, J.F.; Wei, Q.F.; Xu, D.W. Research on mechanical properties of cylindrical gas film sealed bubbling supporting structure. Agric. Equip. Veh. Eng. 2021, 9, 32–37. [Google Scholar]
- Chen, Y.; Chen, K.; Peng, X.D.; Wang, B.; Li, X.; Jin, J. Research on the operation mechanism and performance of bump-type compliant foil face gas seal. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 325. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Q.G.; Peng, X.D.; Li, Y.; Wang, B.; Jin, J. Flow field and sealing performance analysis of compliant foil face gas seal. Adv. Mech. Eng. 2022, 6, 1–16. [Google Scholar] [CrossRef]
- Wang, Q.G.; Chen, Y.; Peng, X.D.; Li, Y.; Li, X.; Wang, B.; Jin, J. Analysis on dynamic characteristics of compliant foil face gas seal with three degrees of freedom perturbation. China Mech. Eng. 2022, 15, 1828–1840. [Google Scholar]
- Sun, J.F.; Liu, M.H.; Xu, Z.; Liao, T.; Hu, X.; Li, Y.; Wang, J. Coupled fluid–solid numerical simulation for flow field characteristics and supporting performance of flexible support cylindrical gas film seal. Aerospace 2021, 4, 97. [Google Scholar] [CrossRef]
- Wang, X.L.; Liu, M.H. The seal performance of compliant foil gas seal based on multi-scale analysis. Processes 2022, 6, 1123. [Google Scholar] [CrossRef]
- Wang, X.L.; Liu, M.H.; Kao-Walter, S.; Hu, X. Numerical evaluation of rotordynamic coefficients for compliant foil gas seal. Appl. Sci. 2020, 11, 3828. [Google Scholar] [CrossRef]
- Zuk, J.; Ludwig, L.P.; Johnson, R.L. Compressible flow across shaft face seals. In Proceedings of the Fifth International Conference on Fluid Sealing, Coventry, UK, 8–12 September 1971. [Google Scholar]
- Zuk, J. Analysis of face deformation effects on gas film seal performance. ASLE Trans. 1973, 4, 267–275. [Google Scholar] [CrossRef]
- Arghir, M.; Defaye, C.; Frêne, J. The lomakin effect in annular gas seals under choked flow conditions. J. Eng. Gas Turbines Power 2007, 4, 1028–1034. [Google Scholar] [CrossRef]
- Thomas, S.; Brunetière, N.; Tournerie, B. Numerical modeling of high pressure gas face seals. J. Tribol. 2006, 128, 396–405. [Google Scholar] [CrossRef]
- Thomas, S.; Brunetière, N.; Tournerie, B. Thermoelasto-hydrodynamic behavior of mechanical gas face seals operating at high pressure. J. Tribol. 2007, 129, 841–850. [Google Scholar] [CrossRef]
- Thatte, A.; Zheng, X. Hydrodynamics and sonic flow transition in dry gas seals. In Proceedings of the ASME Turbo Expo, Fairfield, CT, USA, 16–20 June 2014. [Google Scholar]
- Pinkus, O.; Lund, J.W. Centrifugal effects in thrust bearings and seals under laminar conditions. J. Tribol. 1981, 1, 126–136. [Google Scholar] [CrossRef]
- Yu, T.; Sadeghi, F. Groove effects on thrust washer lubrication. J. Tribol. 2001, 2, 295–304. [Google Scholar] [CrossRef]
- Garratt, J.E.; Hibberd, S.; Cliffe, K.A.; Power, H. Centrifugal inertia effects in high-speed hydrostatic air thrust bearings. J. Eng. Math. 2012, 1, 59–80. [Google Scholar] [CrossRef]
- Fairuz, Z.; Jahn, I. The influence of real gas effects on the performance of supercritical CO2 dry gas seals. Tribol. Int. 2016, 102, 333–347. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.J.; Song, P.Y.; Mao, W.Y.; Deng, Q.; Sun, X. Analysis on inertia effect of carbon dioxide dry gas seal at high speed and pressure under laminar condition. CIESC J. 2018, 10, 4311–4323. [Google Scholar]
- Shen, W.; Peng, X.D.; Jiang, J.B.; Li, J.Y.; Zhao, W.J. The influence of inertia effect on steady performance and dynamic characteristic of super high-speed tilted gas face seal. Tribology 2019, 4, 452–462. [Google Scholar]
- Yang, Q.; Sun, X.H.; Hao, M.M.; Mei, B.; Li, Z.; Ren, B. Study on dynamic characteristics of supercritical carbon dioxide dry gas seal considering inertia effect. Lubr. Eng. 2022, 1, 44–52. [Google Scholar]
- Heshmat, C.A.; Xu, D.S.; Heshmat, H. Analysis of gas lubricated foil thrust bearings using coupled finite element and finite difference methods. J. Tribol. 2000, 122, 199–204. [Google Scholar] [CrossRef]
- Xu, H.J.; Song, P.Y.; Mao, W.Y.; Deng, Q. The performance of spiral groove dry gas seal under choked flow condition considering the real gas effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 4, 554–566. [Google Scholar] [CrossRef]
- Jiang, J.B.; Zhao, W.J.; Peng, X.D.; Li, J. A novel design for discrete surface texture on gas face seals based on a superposed groove model. Tribol. Int. 2020, 147, 106269. [Google Scholar] [CrossRef]
- Xu, H.J. Dynamic Characteristics of DRY Gas Seal Influenced by the Real Gas, Choked Flow and Inertia Effects; Kunming University of Science and Technology: Kunming, China, 2019. [Google Scholar]
- Shen, W. Surface Groove Design and Inertia Effect and Turbulent Effect Analysis of High Parameter Dry Gas Seal; Zhejiang University of Technology: Hangzhou, China, 2019. [Google Scholar]





| Parameters | Symbol | Values |
|---|---|---|
| Inner radius of seal | ri | 58.42 mm |
| Outer radius of seal | ro | 77.78 mm |
| Temperature | T | 298 K |
| Gas viscosity | µ | 0.018 mPa·s |
| Atmospheric pressure | pa | 0.1 MPa |
| Sealed medium pressure | pm | 20 MPa |
| Rotational speed of shaft | n | 50,000 rpm |
| Length of bump foil unit | s | 5 mm |
| Depth of gap section | hg | 0.5 mm |
| Balance film thickness | h0 | 5 µm |
| Wedge height | hd | 10 µm |
| Slope ratio | b | 0.3 |
| Compliance coefficient | α | 0.1 |
| Number of foils | N | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, Q.; Li, Y.; Li, X.; Wang, B.; Jin, J. Study on Sealing Characteristics of Compliant Foil Face Gas Seal under Typical Hypervelocity Gas Effects. Lubricants 2023, 11, 46. https://doi.org/10.3390/lubricants11020046
Chen Y, Wang Q, Li Y, Li X, Wang B, Jin J. Study on Sealing Characteristics of Compliant Foil Face Gas Seal under Typical Hypervelocity Gas Effects. Lubricants. 2023; 11(2):46. https://doi.org/10.3390/lubricants11020046
Chicago/Turabian StyleChen, Yuan, Qinggang Wang, Yuntang Li, Xiaolu Li, Bingqing Wang, and Jie Jin. 2023. "Study on Sealing Characteristics of Compliant Foil Face Gas Seal under Typical Hypervelocity Gas Effects" Lubricants 11, no. 2: 46. https://doi.org/10.3390/lubricants11020046





