A Mixed Lubrication Model of Piston Rings on Cylinder Liner Contacts Considering Temperature-Dependent Shear Thinning and Elastic–Plastic Contact

Abstract

This work develops a numerical methodology for predicting the performance of an automotive piston ring system by considering contact and lubrication mechanics. The rough surface contact mechanics and lubrication occurs on a scale much smaller than the size of the piston rings and therefore the key aspect of the model is an algorithm that simultaneously solves the multiple mechanisms at different scales. The finite element method will be used to model the mechanical deformations of the piston ring surfaces at large scales. The quasi-steady state model includes heat generation due to solid and viscous friction. This heat generation will then be used to predict the temperature rise and thermal effects in the lubricant and component. A statistical rough surface method that renders asperities as elastic–plastic wavy surfaces predicts the solid contact area. The modified Reynolds equation will be solved to consider the effects of mixed hydrodynamic lubrication while using flow factors formulated for actual piston and ring surfaces. The lubricant viscosity depends both on temperature and shear rate. This will allow for the regimes of boundary, mixed, and full-film lubrication to be considered. The model predicts friction for various loads and speeds that are then compared to experimental measurements. Although the contacts operate mostly in the mixed lubrication regime, the model and experiments show changes in friction with load, speed, and temperature.

1. Introduction

Combustion engines are still the most common source of power for vehicles at 97% of the vehicle market in 2021 [1]. Electric vehicles will displace some combustion vehicles, but it will take many years for them to overtake combustion vehicles in number. The rate at which this is predicted to occur varies drastically depending on the organization making the prediction (between 20% and 90% of vehicles by 2050) [2]. The adoption of electric vehicles will also be slower in developing countries [1]. Certain applications and types of vehicles, such as heavy trucks, will also mostly consist of combustion powered vehicles for a longer period. Therefore, combustion will arguably be a significant part of the market for many years.

Piston assembly is also the largest source of friction loss in combustion engines [3]. Therefore, there has been a great deal of work on reducing the friction in the piston ring–cylinder liner interface using such things and coatings and textures, as will be discussed briefly below. To evaluate possible technologies, it is also advantageous to have models capable of predicting the friction. Therefore, this work aims at creating a model that compares well to experimental measurements of a piston ring to cylinder liner interface. The model will consist of a rough surface contact and hydrodynamic lubrication modules and therefore a brief background of these areas is also provided. While many models for the individual modules exist, there are few models that combine all these aspects at once. This work creates a model that combines wavy elastic–plastic rough surface contact and hydrodynamic lubrication and evaluates three variants, two of which introduce frictional heating.

1.1. Prior Works on the Piston Ring–Cylinder Liner Interface

Many methods and techniques have been used in the past to predict the frictional losses of a piston ring–cylinder liner interface in an engine [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. The piston ring–cylinder liner interface system includes several variables such as surface topography, transient lubrication, and exhaust flow rate that interact with each other. Prior works have generally focused on only one variable at a time. Furuhama and Sumi’s [4] analysis of compression ring linings is one of the first investigations on the subject. Ma et al. [5] analyzed lubricant transport and found that cylinder liner surface and ring movement significantly influence tribological behavior. Akalin and Newaz [6] analyzed the mixed lubrication regime using the Reynolds equation with flow factors. They found that hydrodynamic lubrication occurs during most parts of the stroke, but the friction coefficient increases greatly at top and bottom dead center when the sliding speed is too low for the lubricant to support much of the load. Their analysis did not calculate flow factors for a specific surface or consider elastic–plastic asperity contact, nor did they perform experiments to validate their model. Jeng [7] analyzed the lubrication conditions at the ring contact surface. Furuhama and Sasaki [8] derived a new technique to measure friction forces for small engines. Previously, this was a difficult task because they could not be isolated from much larger gas and inertia forces. Taking into account torsion, film thickness changes, and ring wear, Tian [9] studied piston ring dynamics numerically and experimentally. Harigaya et al. and Rahmani et al. investigated temperature effects on the friction and piston ring lubrication [10,11].

In recent years, several studies have focused on improving internal combustion engine efficiency. Morris et al. [12] optimized the piston ring to minimize energy losses, incidence of asperity contact, and ring mass. Bewsher et al. [13] applied atomic force microscopy to measure the boundary asperity shear strength and thus calculate localized values of frictional losses on real engine components. Howell-Smith et al. [14] tested lubricant coatings and surface textures for friction reduction. They found that surface modifications of the liner at top dead center (TDC) reduces friction by creating additional lubricant reservoirs there. In turn, this increases the power output of the engine by up to 4%. Li et al. [15] found that laser finishing could reduce the friction coefficient and weight loss of an Al-Si alloy cylinder liner by removing the aluminum layer and exposing rounded edges of silicon particles.

Efficiency can also be improved by changing the surface texture. Senatore et al. [16] studied a bronze coating with different surface textures and found that an appropriate texture geometry improves the friction coefficient and wear. Wang et al. [17] tested the effects of dimples on brass discs. They found that only a small dimple pattern reduced the friction—for large dimples, the friction coefficient actually increased. Kligerman et al. [18] developed an analytical model for partial laser surface texturing to reduce the friction in the piston ring–cylinder liner system. They found an optimal percentage of the textured portion and dimple depth depending on operating conditions. Spencer [19] developed simulations to evaluate a cross-hatched cylinder liner to reduce oil consumption, wear, and friction. Lu and Wood [20] observed an 82% reduction in piston ring–cylinder liner friction when texture grooves were normal to the sliding direction. Abril et al. [21] studied the effects of dimples and the honing groove in the cylinder liner. A slight increase in dimple density increased the minimum film thickness and reduced the friction force. Comparable increases in minimum film thickness could be obtained with deeper, larger dimples. Their honing groove analysis found that a 15 degree increase in honing angle reduced the friction coefficient by more than 14%. However, friction increased when the honing groove density was too high.

1.2. Rough Surface Contact

Contact between rough surfaces is a ubiquitous problem that can be applied to numerous phenomena such as friction, wear, and contact resistance. This work employs a statistical model in which mathematical parameters describing the surface are used to calculate probabilities and determine the contact area and load. This model was initially developed by Greenwood and Williamson [22] (GW model). They considered the interaction between a perfectly flat, rigid plane and a plane covered with spherical asperities of varying heights. They assumed that asperities behave independently of each other, and that deformation is limited to the asperities. However, they only assumed elastic contact, so other models were subsequently derived when yielding occurs at larger loads. Jackson and Green (JG) [23] derived a statistical elastic–plastic deformation model in which they established the load required for plastic deformation. As contact pressure increases, the internal stress within asperities increases as well. This results in yielding and plastic deformation. The JG model, while it includes varying fully plastic pressure not captured by most other models, is limited to small deformations where the contact radius is no more than 41% of the radius of curvature. Note that wavy asperities also result in a varying fully plastic pressure with load and can also be incorporated into statistical rough surface contact models [24].

Statistical models are reliable and easily implemented, but shortcomings exist. Those previously described assume a homogenous radius of curvature over an entire region, neglect the effects of different scales of features, and do not couple the deformation between asperities and the substrate. Bush et al. [25] developed a statistical model that accounts for variable asperity radius, but they still assumed negligible adjacent or lateral asperity interaction. Ciavarella et al. developed a model that accounts for lateral asperity interaction [26]. Afferrante et al. followed up with a coalescing asperity model, while Vakis expanded it below the mean asperity height [27,28]. These works are similar to the wavy asperity model used in this work that includes lateral asperity interaction. A recent work compared spherical and wavy asperity-based statistical models to a deterministic prediction. The wavy asperity model compared best and will therefore be implemented here [29].

1.3. Hydrodymanic Lubrication

To calculate the hydrodynamic load in modeling viscous flow of lubricant between the cylinder wall and the piston ring, the modified Reynolds Equation is used. It is a second-order partial differential equation derived from the Navier–Stokes equations assuming a Newtonian fluid, negligible inertia and body forces, negligible pressure variation across the film, laminar flow, and negligible curvature [30]. It can take many forms, depending on the physical mechanisms involved in the system.

Flow Factors are a method to determine roughness effects on lubrication flow in any of the three regimes: full film lubrication, mixed lubrication, and boundary lubrication. These regimes are depicted in Figure 1.

Boundary lubrication, which is characterized by high surface abrasion and wear, is on the left side. On the right side, the lubricant separates the surfaces sufficiently such that no solid contact occurs. The lubrication regimes can be categorized by the Stribeck curve, a plot of friction coefficient against the dimensionless bearing number, shown in Figure 2. It is used to determine transitions between flow regimes.

Lubricants interact at both the macroscopic and the microscopic scales; the latter is especially important for the surfaces. Using the Reynolds equation to determine the pressure at each asperity is possible akin to a deterministic contact model, but it becomes computationally unfeasible for a sufficiently large surface resolution. Flow past individual asperities is too computationally and numerically difficult to model, so the simpler method of flow factors added to the Reynolds equation is used instead. Patir and Cheng [32] were the first to determine the effects of surface roughness on flow between three-dimensional surfaces. They derived statistical flow factors added to the Reynolds equation as follows:

$$\frac{\partial }{\partial x}\left({\phi }_x\frac{\rho h^2}{12\mu }\frac{\partial p}{dx}\right)+\frac{\partial }{\partial z}\left({\phi }_z\frac{\rho h^2}{12\mu }\frac{\partial p}{dz}\right)=\frac{\overline{U}}{2}\frac{\partial \rho h}{\partial x}+\frac{\partial \rho h}{\partial t}+\frac{\partial {\phi }_s}{\partial x}$$

(1)

This modified Reynolds equation produces a more accurate solution that accounts for microscopic surface features. In this equation, φ_z and φ_x measure the flow resistance across asperities in the flow direction and the transverse direction, respectively, while φ_s measures lubricant transport due to shear effects. The flow factors depend on the film thickness, the RMS surface roughness, and the Peklenik number, γ. This number can be calculated from auto-correlation functions derived from the surface topography [33].

The flow factors calculated by Patir and Cheng were based off a statistically generated surface whose asperities were purely transverse, isotropic, or purely longitudinal. However, their flow factors are not totally accurate for a real surface that is not perfectly Gaussian. Other researchers tried methods to improve upon Patir and Cheng’s work to find a more accurate model for specific cases. Wilson and Marsault derived an alternate form of the Reynolds equation applicable for high contact area ratios [34]. Peeken et al. investigated flow factors for sintered bearing surfaces [35]. Hu and Zheng considered different boundary conditions and numerical methods to calculate flow factors but still considered theoretical surfaces [36]. Morales-Espejel derived a transformation to calculate flow factors for a non-Gaussian surface from their counterparts for a Gaussian surface [37]. Sahlin et al. devised a new way to calculate flow factors that accounts for contact mechanics and used measured surfaces to do so [38]. Their results agreed with those of Patir and Cheng for longitudinal asperities but differed substantially for cross-hatched surfaces. Others applied various numerical and analytical methods [39,40,41]. The methodology used here is similar to work by Leighton et al. [42], who derived surface-specific flow factors for a piston ring–cylinder liner interface.

Previous studies of surface roughness effects on lubrication flow was mostly limited to stochastic concepts such as those first introduced by Tzeng and Saibel [43]. Patir and Cheng [24,44] derived a new method based on numerically solving the Reynolds equation over a randomly generated surface and calculating an average equation from flow quantities. Their method assumes that rough surface heights are a perfect Gaussian distribution though. This work uses the flow factors Locker et al. [45] derived for an actual cross-hatched cylinder wall by combining stochastic concepts with Peklinik’s signal processing theory [33].

2. Model Methodology

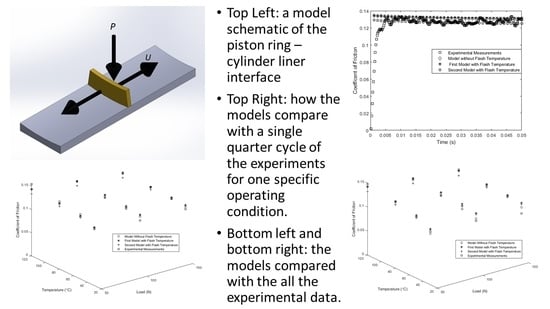
Figure 3 shows the overview of the iterative axisymmetric model of the piston ring–cylinder liner interface. While a full 3D model would be ideal, that was deemed to be too computationally expensive due to the number of iterations and finite element analyses required. The model is also pseudo-steady state, meaning it does not consider transient or dynamic effects, but it does consider different sliding speeds, U (see Figure 4). As shown in Figure 3, the problem is solved iteratively by updating the forces, deformations, and surface separation with each iteration. On the inner radius of the ring, the applied load, P, (50, 100, or 150 N) was converted to a pressure using the area on the inside. This mimics the loads applied in the experiment and those experienced in an actual engine (see Figure 3). Combining the applied load on the inside with the contact and fluid pressures on the outside gives an equation that relates net radial force and surface separation. The location of the ring was numerically solved for a net zero radial force. The contact and hydrodynamic forces that solve the equilibrium equation are written in an Abaqus™ input file that creates the mesh shown later. The input file is then run in Abaqus™, and the toolbox abaqus2matlab is used to transfer the displacements back to MATLAB™. These displacements are then used to alter the piston ring profile, and the process is repeated until convergence is reached. The problem is considered converged when the difference in the forces between iterations is less than 0.5%. Additional details are provided in the following sections.

A profilometer was used to measure the surface height of a 1 mm² sample area from a cylinder liner and a piston ring. The diamond stylus employed has a tip radius of 2 μm and a resolution of 1 nm. Due to the profilometer’s sensitivity, it was operated on a self-leveling pneumatic vibration isolation table to ensure steadiness. The surface profiles are shown in Figure 5, Figure 6, Figure 7 and Figure 8. As shown in Figure 5 and Figure 6, the cylinder liner surface has a cross-hatched finishing. The ring surface (Figure 7 and Figure 8) also possesses some dimples by design. All surface parameters for the lubrication and the statistical rough surface contact modules were calculated from these measurements. Additional details about the parameter calculations are provided later.

2.1. Rough Surface Contact

This work uses the Greenwood–Williamson statistical model [22] as a base for predicting the effects of rough surface contact. The equations to find the total contact load and area are

$$P\left(h\right)=A_n\eta {\displaystyle \underset{h}{\overset{\infty }{\int }}\overline{P}\left(z-h\right)\varphi \left(z\right)dz}$$

(2)

$$A\left(d\right)=A_n\eta {\displaystyle {\int }_d^{\infty }\overline{A}\left(z-h\right)\cdot \varphi \left(z\right)\cdot dz}$$

(3)

P is the total contact force, A_n is the nominal area of contact (neglecting roughness), h is the mean surface separation, η is the areal asperity density, and ϕ is the asperity height distribution. Asperities are assumed to be homogenous and evenly distributed; their RMS (root mean square) height is σ_s. To calculate the statistical parameters, asperities were manually counted by scanning the surface profile and identifying points whose height was higher than any of the eight surrounding points. The radius of curvature of each asperity was calculated in two orthogonal directions, using

$$r_x=\frac{{\left[1+\frac{dh}{dx}\right]}^{\frac{3}{2}}}{\frac{d^{2}h}{d{x}^2}}$$

(4)

and

$$r_y=\frac{{\left[1+\frac{dh}{dy}\right]}^{\frac{3}{2}}}{\frac{d^{2}h}{d{y}^2}}$$

(5)

The two values were averaged to estimate asperity’s radius of curvature r. This parameter was calculated for every asperity, and then it was averaged to find R for all the asperities. The asperity density η was found by dividing the number of asperities counted by the area scanned. The original G–W model assumes elastic Hertz contact and a constant value of R. Different equations are used here because this work assumes the asperities are sinusoidal in nature and the loads are large enough for yielding to occur. The following relations were used to convert the asperity radius and density to frequency and amplitude:

$$f=\sqrt{\frac{\eta }{2}}$$

(6)

$$\Delta =\frac{1}{4R{\left(f\pi \right)}^2}$$

(7)

For a single $\lambda \times \lambda$ (λ = 1/f) wavy asperity area to reach complete elastic contact, the pressure required is given by [46]

$$p^{*}=\sqrt{2}\pi E\text{'}f\Delta$$

(8)

where the effective elastic modulus to account for the deformations of both surfaces is given by

$$\frac{1}{E\text{'}}=\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}$$

(9)

assuming plane strain. Assuming an average contact pressure of $\overline{p}$, a required pressure p* for complete contact, and letting

$$P_e=\frac{\overline{p}}{p^{*}}$$

(10)

The following asymptotic solutions were found by Johnson, Greenwood, and Higginson [46]:

$${\left({\overline{A}}_{JGH}\right)}_1=\pi {\lambda }^2{\left[\frac{3P_e}{8\pi }\right]}^{\frac{2}{3}}$$

(11)

for small values of P_e and

$${\left({\overline{A}}_{JGH}\right)}_2=\frac{{\lambda }^2}{2}\left(1-\frac{3}{2\pi }\left[1-P_e\right]\right)$$

(12)

when P_e approached unity.

Jackson and Streator [47] fitted a polynomial combining these equations using experimental data from Johnson et al. [46]:

$$\tilde{A}=\{\begin{array}{c}{\left({\overline{A}}_{JGH}\right)}_1\left(1-P_e{}^{0.51}\right)+{\left({\overline{A}}_{JGH}\right)}_2{P}_e{}^{1.04},P_e<0.8\\ {\left({\overline{A}}_{JGH}\right)}_2,P_e\ge 0.8\end{array}$$

(13)

These equations neglect asperity yielding, so the elastic–plastic model developed by Krithivasan and Jackson is used instead. They derived an expression for the contact area above which elastic–plastic contact occurs. This was derived from spherical contact, so this work uses a model developed by Jackson et al. [48] that computes the critical interference above which elastic–plastic relations are used. That expression from Ghaednia et al. [49] is

$${\Delta }_c=\frac{\sqrt{2}{S}_y}{E\text{'}f\pi \left[3e^{-\frac{2}{3}\left(\nu +1\right)}+2\left(\frac{1-2\nu }{1-\nu }\right)\right]}$$

(14)

Using this value of critical interference, the following equation was fitted to the FEM data of Krithivasan and Jackson [24] that links the pressures required for complete contact under elastic and elastic–plastic loading:

$$\frac{P^{*}{}_{ep}}{p^{*}}={0.992}^{\left[{\left\{\frac{\Delta }{{\Delta }_c}\right\}}^{\frac{10}{3}{\left(\frac{\Delta }{{\Delta }_c}\right)}^{-0.39}+\frac{9}{4}{\nu }^4+0.64}-1\right]}$$

(15)

The contact area for low loads is found using

$$A_p=2{\left(\frac{A_c}{2}\right)}^{\frac{1}{1+d}}{\left(\frac{3\overline{p}}{4C{f}^2{S}_y}\right)}^{\frac{d}{1+d}}$$

(16)

where

$$d=3.8{\left(\frac{E\text{'}f\Delta }{S_y}\right)}^{0.11}$$

(17)

and

$$A_c=\frac{2}{\pi }{\left(\frac{C{S}_y}{8E\text{'}{f}^2\Delta }\right)}^2$$

(18)

is the critical contact area at which elastic–plastic contact begins.

The equation that links the contact area for low and high loads is

$$\overline{A}=A_p\left(1-P_{ep}{}^{1.51}\right)+{\left({\overline{A}}_{JGH}\right)}_2{P}_{ep}{}^{1.04}$$

(19)

In this equation, ${\left({\overline{A}}_{JGH}\right)}_2$ is calculated by replacing P_e with P_ep in Equations (12) and (16).

To apply sinusoidal asperities to the GW model, the surface separation needs to be calculated. Rostami and Jackson [50] derived expressions by averaging the surface separation from a finite element model. Their fitted equations for the dimensionless surface separation G are

$$G={\left(1-\sqrt{P_e}\right)}^{2.5}$$

(20)

for elastic contact and

$$G={\left(1-P_{ep}{}^{A_1{P}_{ep}+A_2}\right)}^{2.5}$$

(21)

for elastic–plastic contact. In these equations,

$$G=\frac{g}{\Delta },$$

(22)

$$A_1=-0.08\ln B^{*}$$

(23)

$$A_2=\frac{1}{15}{\left(B^{*}-1\right)}^{0.44}+{0.99}^{0.41\left\{B^{*}-1\right\}}-0.5$$

(24)

and

$$B^{*}=\frac{\Delta }{{\Delta }_c}$$

(25)

The integrals in Equations (2) and (3) were numerically evaluated for specified values of surface separation. To find the corresponding load, Equation (19) for elastic contact or Equation (20) for elastic–plastic contact was solved numerically.

2.2. Fluid Lubrication Model

The piston ring–cylinder wall interface is not exclusively boundary lubrication; fluid film lubrication plays an integral role in the overall system behavior. To calculate the hydrodynamic lift, the modified Reynolds equation that considers roughness effects via flow factors is employed. For rough surfaces in the mixed lubrication regime, the modified Reynolds equation is given as Equation (1).

Locker et al. [45] used deterministic modeling of flow around the measured rough surfaces of a ring a cylinder to find the averaged flow factors over the entire surface and fitted empirical equations to the predicted flow factors:

$${\phi }_x=2.48{\left(\frac{h}{\sigma }\right)}^{-1.777}+1$$

(26)

$${\phi }_z=1-0.4824e^{-0.2477\left(\frac{h}{\sigma }\right)}$$

(27)

For the surfaces being studied, φ_x and φ_z are related through the film thickness, roughness, and surface anisotropy index as

$${\phi }_x\left(\frac{h}{\sigma },\gamma \right)={\phi }_z\left(\frac{h}{\sigma },\frac{1}{\gamma }\right)$$

(28)

Because the model predicted mostly hydrodynamic lubrication at very low sliding speeds, a shear thinning model was introduced. A version of the Carreau model adapted from Jang, Khonsari, and Bair [51] was introduced as follows:

$${\mu }_{eff}={\mu }_2+\left({\mu }_1-{\mu }_2\right){\left(1+{\left(\frac{{\mu }_{1}U}{hG}\right)}^2\right)}^{\frac{n-1}{2}}$$

(29)

μ₂ was set to zero, and a fit was generated at a temperature of 60 °C using the data in

Table 1. Lubricant Viscosity Dependence on Shear Rate (the first two measurements were conducted with a Cone and Plate Viscometer, while the other values were measured by a Tapered Bearing Simulator Viscometer and modified relative to ASTM D6616).

Shear Rate (1/s)	μ (Pa·s)
103	0.02
104	0.01921
104	0.01971
105	0.01777
106	0.01601
3.5 × 106	0.01537

below. Figure 9 shows the fit to the shear thinning data, and

Table 2. Coefficients Used in Equation (29).

G (Pa)	299
n	−0.0254

shows the values of G and n. Although there is a limited amount of data available, the usage of a well-accepted phenomenological equation should limit the uncertainty.

It was presumed that the coefficients remained valid for different temperatures. A shear factor that reflects the surface roughness was added later in the model’s development when predicting the shear stress and friction from viscous shearing:

$$\tau =\mu \frac{U_2-U_1}{h}\left({\varphi }_f\pm {\varphi }_{fs}\right)\pm \frac{h}{2}\frac{\partial p}{\partial x}$$

(30)

As an improved comparison to experimental data was sought, pressure and temperature viscosity effects were incorporated. This model uses the Barus equation to account for increased viscosity under loading.

$$\mu ={\mu }_0{e}^{\xi P}$$

(31)

Table 3. Pressure Viscosity Coefficient Values for the Lubricant.

Temperature (°C)	ξ (Pa·s)
25	2.05 × 10−8
100	1.248 × 10−8

lists the values used for the pressure viscosity coefficient. There are concerns in the literature about properly accounting for pressure viscosity and shear rate to viscosity relations, but this is more important for contacts where higher pressures are likely, such as in rolling element bearings. The issues are most with Roelands Equation for piezo-viscosity [52], which we are not using it for. The equations employed are well recognized in the literature and probably adequate for the limited ranges of temperature and pressure that are expected in this model.

With only two values provided, the coefficient was assumed to vary linearly. If the temperature was beyond the range of the provided values, the closer value was used without modification.

The Roelands equation was used to adjust the viscosity due to changes in temperature.

$$\frac{\mu }{{\mu }_0}=\frac{{\mu }_{\infty }}{{\mu }_0}{10}^{G_0{\left(1+\frac{t_m}{135}\right)}^{-S_0}}$$

(32)

Figure 10 illustrates the viscosity fit as a function of temperature.

2.3. Frictional Force Calculation

To determine the frictional force from rough surface contact, Amonton’s Law of Friction is used.

$$F_f=F_{contact}{\mu }_k$$

(33)

To determine the value of the friction coefficient, the following equation derived from a curve fit of the experimental data is used. Note that this description possesses a decrease in friction with load which is also predicted and observed by previous works [53,54,55,56].

$${\mu }_k=0.1565-0.2F_n^{*}$$

(34)

The frictional force from viscous shear, F_v, is calculated by multiplying the shear stress calculated from Equation (30) by the area on which it is applied. This was performed on the ring surface. The total frictional force can be calculated as follows:

$$F_t=F_v+F_f$$

(35)

2.4. Temperature Adjustments Due to Frictional Heating

Due to the high friction coefficient in boundary lubrication, a large amount of heat can be generated, especially when the load is large. On the local scale, this is known as flash temperature. The following equation can be used to calculate the generated heat.

$$Q={\mu }_{k}PV$$

(36)

The heat depends on the total frictional force and the velocity–higher speeds and/or loads will result in a greater amount of heat generated. That manifests itself in a temperature increase in the surfaces as given by Equation (37) for a moving surface and 38 for a stationary surface [57]. In the following equations, k is the thermal conductivity, r_c is the applicable contact area, and κ is the thermal diffusivity.

$$T-T_0=\frac{Q}{4.56r_{c}k\sqrt{0.66+Pe}}$$

(37)

$$T-T_0=\frac{Q}{4r_{c}k}$$

(38)

$$Pe=\frac{V{r}_c}{2\kappa }$$

(39)

Based off an analogy with electrical current, Equations (37) and (38) can be combined for the case in which neither surface is adiabatic [30]:

$$Q=4r_c{k}_1\left(T-T_0\right)+4r_c{k}_2\left(T-T_0\right)$$

(40)

Equation (38) for heat conduction away from the surfaces assumes a low sliding speed for both of them but can be easily adapted if either surface is sliding rapidly. Solving it for the temperature change results in

$$T-T_0=\frac{Q}{4.56r_{c}k\sqrt{0.66+Pe}+4r_{c}k}$$

(41)

There are several ways that the temperature will directly influence the model. First, the temperature will change the viscosity, as described by Equation (31). Second, the temperature could influence the strength of the material locally. The model incorporates the reduction in metals’ yield strength as the temperature increases modeled by Johnson and Cook [58]. This would result in the surfaces becoming more liquid-like and less resistant to flow, meaning that the predicted dry friction coefficient would decrease. This assumes the adhesive friction model mentioned previously [52,53]. Following how shear strength is lowered by Johnson and Cook, then the friction can be approximately modified by the following:

$${\mu }_k={\mu }_b\left(1-T^{*}\right)$$

(42)

$$T^{*}=\frac{T-T_{room}}{T_m-T_{room}}$$

(43)

2.5. Finite Element Model

The deformation of the surfaces is divided into two scales, the asperity and macro scale. The asperity-scale deformations of both surfaces are considered by the statistical rough surface contact model by using the effective elastic modulus E’ (Section 2.1), while the macro-scale deformation is considered by a finite element model. The combined surface contact pressure and oil hydrodynamic pressure deforms the ring, so the model is combined with a finite element analysis performed in Abaqus™. The abaqus2matlab toolbox is used to allow the MATLAB program to read the displacements from the finite element analysis to determine the new ring profile for the next iteration [59]. Figure 11 shows the axisymmetric mesh of the piston ring with 1726 linear CAX4R elements. In the finite element analysis, a known load is applied to the inside (left side of the figure) of the ring, while the balancing loads due to rough surface contact and hydrodynamic lift are applied to the outside (right side). Also applied are frictional forces that would induce ring tilt; the center of the ring is held stationary in the z-direction. As stated earlier, a three-dimensional model was considered to be too computationally expensive but could be implemented in future versions of the model. Due to the large variation in deformations observed at high loads, the relaxation factor was set to 0.2 to assist with convergence.

3. Results

This work assesses three slightly different models that predict the friction coefficient of the piston ring–cylinder liner system. The first model neglects the effects of thermal heating and does not incorporate Equations (36)–(43) at all. The second model includes thermal heating and Equations (39) and (41) to calculate the temperature increase. The third model reflects metals’ decreased yield strength by adding Equations (42) and (43). To determine the validity of the models, they are compared to experimental measurements of a reciprocating piston ring sliding against a cylinder liner in a Phoenix Tribology TE77 High Frequency Friction Machine [60,61] (see Figure 3 and Figure 12). The same ring, liner, and lubricant considered in the model is used in the experiment. The experiments featured loads of 50 N, 100 N, or 150 N that simulates actual forces applied to the piston ring, average sliding speeds of 0.3 or 0.6 m/s by running the machine with a stroke length of 0.15 m and a frequency of 5 or 10 Hz, and base oil temperatures of 30 °C, 50 °C, 80 °C, or 120 °C, that represent typical operating conditions of a combustion engine. This results in 24 different cases being experimentally measured and then predicted by the described model. Figure 12 shows the setup.

To compare to the experiments, the model was run over a range of sliding speeds as shown in Figure 13 and Figure 14. These represent the different sliding speeds of the piston during one-reciprocating stroke. Then, the average friction coefficients over the stroke are calculated. As shown, the model is weakest at predicting transient effects such as when the sliding velocity changes direction at 0 s. In these transition regions, the contacts might actually stick briefly due to mechanical play or the ring rotating. This behavior is ignored in the model. Then, the average friction coefficients for average piston speeds of 0.3 m/s and 0.6 m/s are calculated from the model for comparison to the experiments, as will be discussed next.

Figure 15 and Figure 16 show the overall comparisons. Overall, there is good agreement between the models and the experiments. The largest differences are at the extremities of load and speed.

Table 4. Average Friction Coefficient for a Mean Piston Speed of 0.3 m/s.

Data Set	Average	Standard Deviation
Experimental Measurements	0.1275	0.0143
No Adjustments for Frictional Heating	0.1280	0.0031
First Flash Temperature Model (Equation (41))	0.1302	0.0017
Second Flash Temperature Model (Equations (41)–(43))	0.1262	0.0016

,

Table 5. Average Friction Coefficient for a Mean Piston Speed of 0.6 m/s.

Model	Average	Standard Deviation
Experimental Measurements	0.1237	0.0164
No Adjustments for Frictional Heating	0.1235	0.0053
First Flash Temperature Model (Equation (41))	0.1280	0.0027
Second Flash Temperature Model (Equations (41)–(43))	0.1244	0.0023

,

Table 6. Average RMS Error Relative to the Experiments for a Mean Piston Speed of 0.3 m/s.

Model	RMS Error	Number of Cases For Which Model Was Closest to Experimental Average
No Adjustments for Frictional Heating	0.0014866	6
First Flash Temperature Model (Equation (41))	0.0018159	4
Second Flash Temperature Model (Equations (41)–(43))	0.0027476	2

and

Table 7. Average RMS Error Relative to the Experiments for a Mean Piston Speed of 0.6 m/s.

Model	RMS Error	Number of Cases For Which Model Was Closest to Experimental Average
No Adjustments for Frictional Heating	0.0011368	7
First Flash Temperature Model (Equation (41))	0.0021501	3
Second Flash Temperature Model (Equations (41)–(43))	0.0028841	2

compare the average means and rms error between the model versions and the experiments. These values were calculated by averaging every point in time during the repeating tests whose friction coefficient value was at least 10% of the maximum observed during its test. Based on these results, the adjustments for frictional heating, in particular metal softening with increasing temperature in the second flash temperature model, do not improve the model prediction. For a baseline temperature of 120 °C, the second flash temperature model predicts a much lower friction coefficient than the model that does not adjust for frictional heating at high temperatures. However, it predicts the highest friction coefficient at the lowest loads and temperatures. This is likely because the lower dry friction coefficient due to metal softening does not counteract the decreased load-carrying capacity of the lubricant due to the increased temperature and decreased viscosity.

4. Conclusions

This work presents three slightly different mixed lubrication and solid contact models of a piston ring–cylinder liner interface. The first model does not account for temperature changes at all due to frictional heating. The other two models increase the temperature due to the frictional force and account for that in different ways. One of those models decreases the solid friction coefficient due to metal softening with increasing temperature using Equations (41) and (42). This effect becomes more pronounced as the base temperature increases because the heating pushes the system towards the melting temperature. The models overall display good agreement with experimental measurements performed over a wide range of operating conditions, but larger discrepancies exist for low or high temperatures and high loads and speeds. This can partially be attributed to the shear thinning fit not working as well farther from the temperature from which it was found. The models predict an increase in friction coefficient as temperature increases or load or speed decreases. However, they do not predict as large an increase at high temperature and low load, the condition under which the largest friction coefficients were measured. Overall, these models can be used to design or evaluate friction-reduction technologies such as better lubricants or surface textures.