Study on a Novel Strategy for High-Quality Grinding Surface Based on the Coefficient of Friction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Equipment
2.2. Experimental Scheme
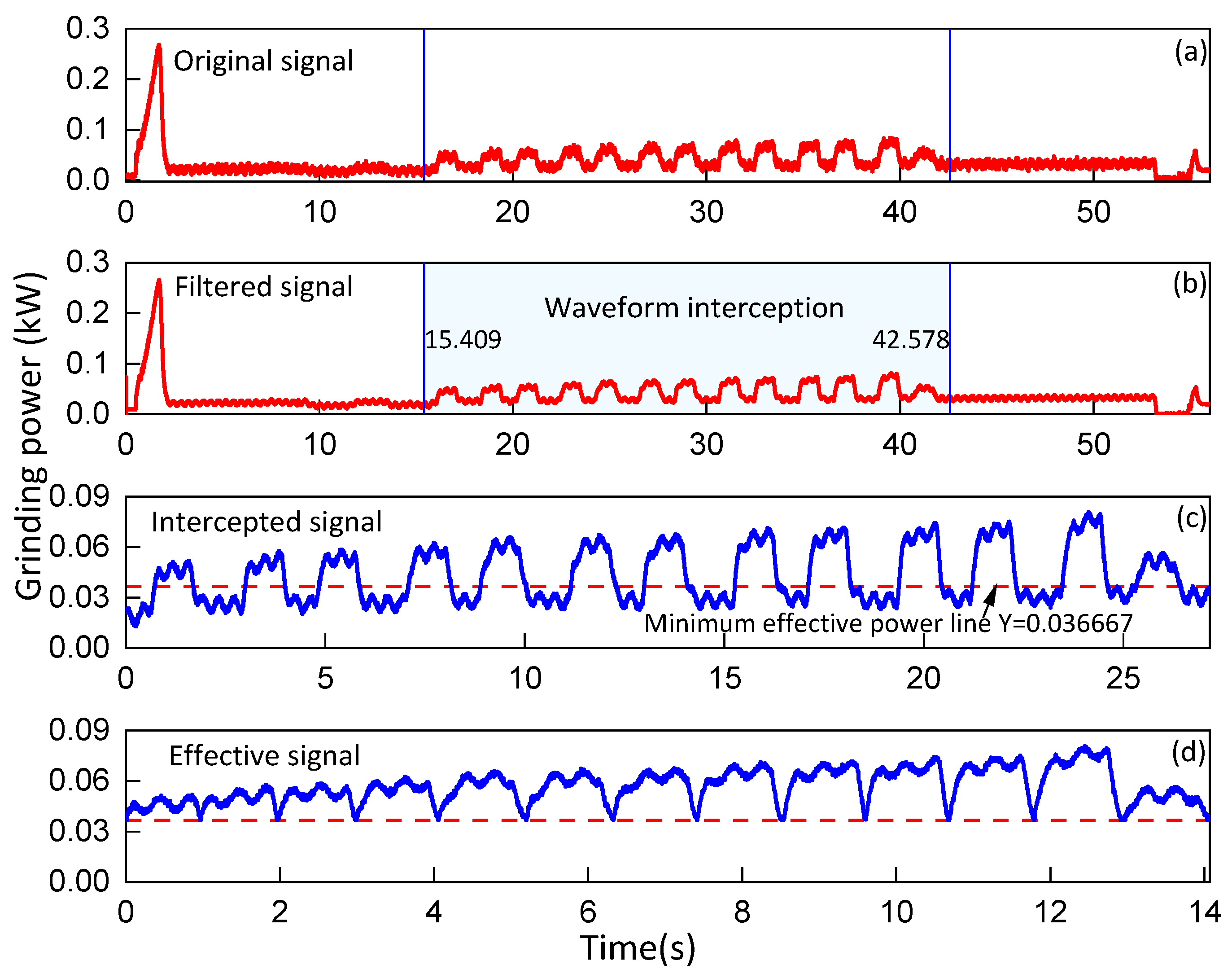
2.3. Signal Processing
2.3.1. Grinding Force Signal Processing
2.3.2. Grinding Power Signal Processing
3. Results
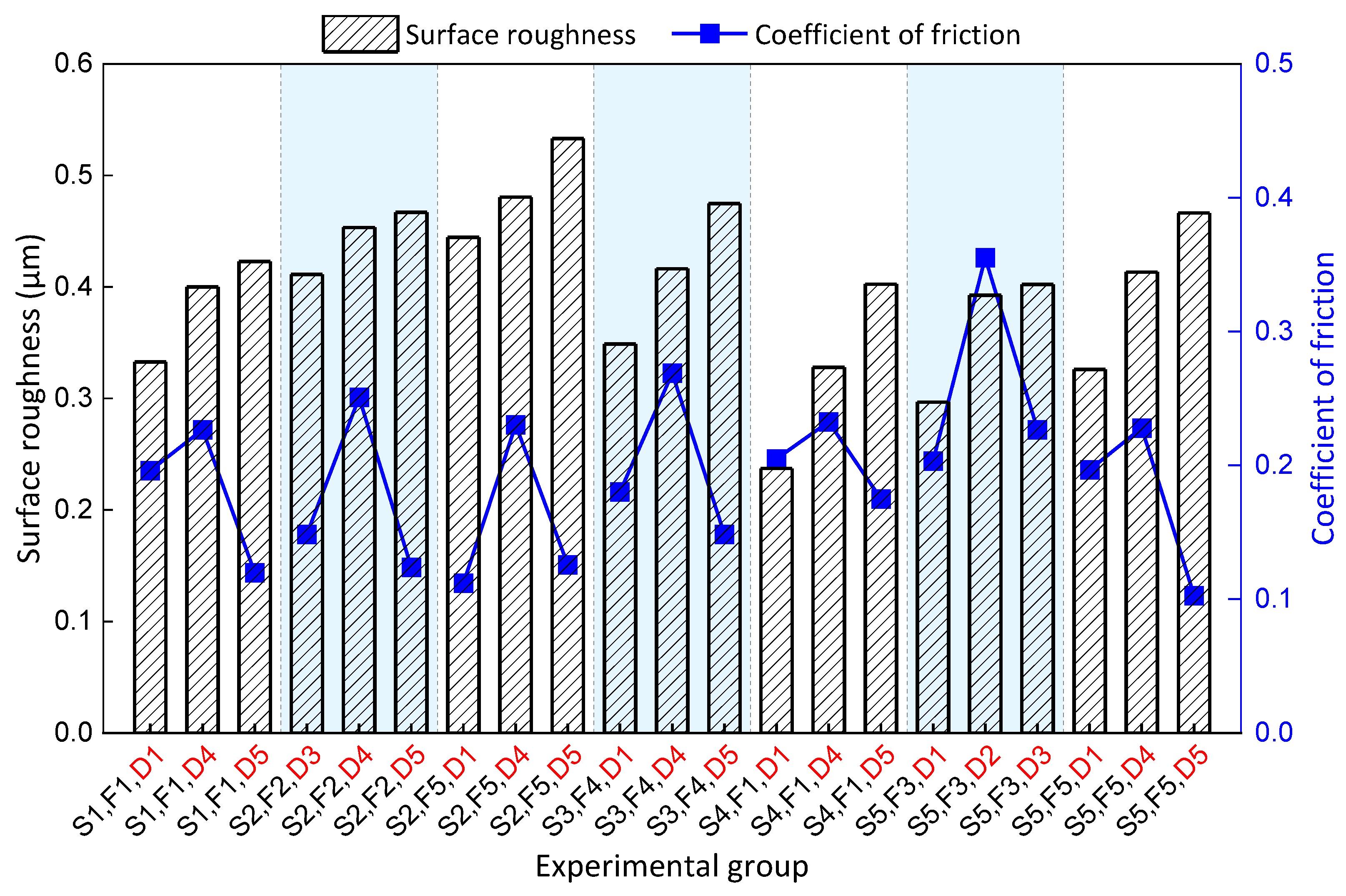
3.1. Experimental Results
3.2. Interaction among Evaluation Indicators
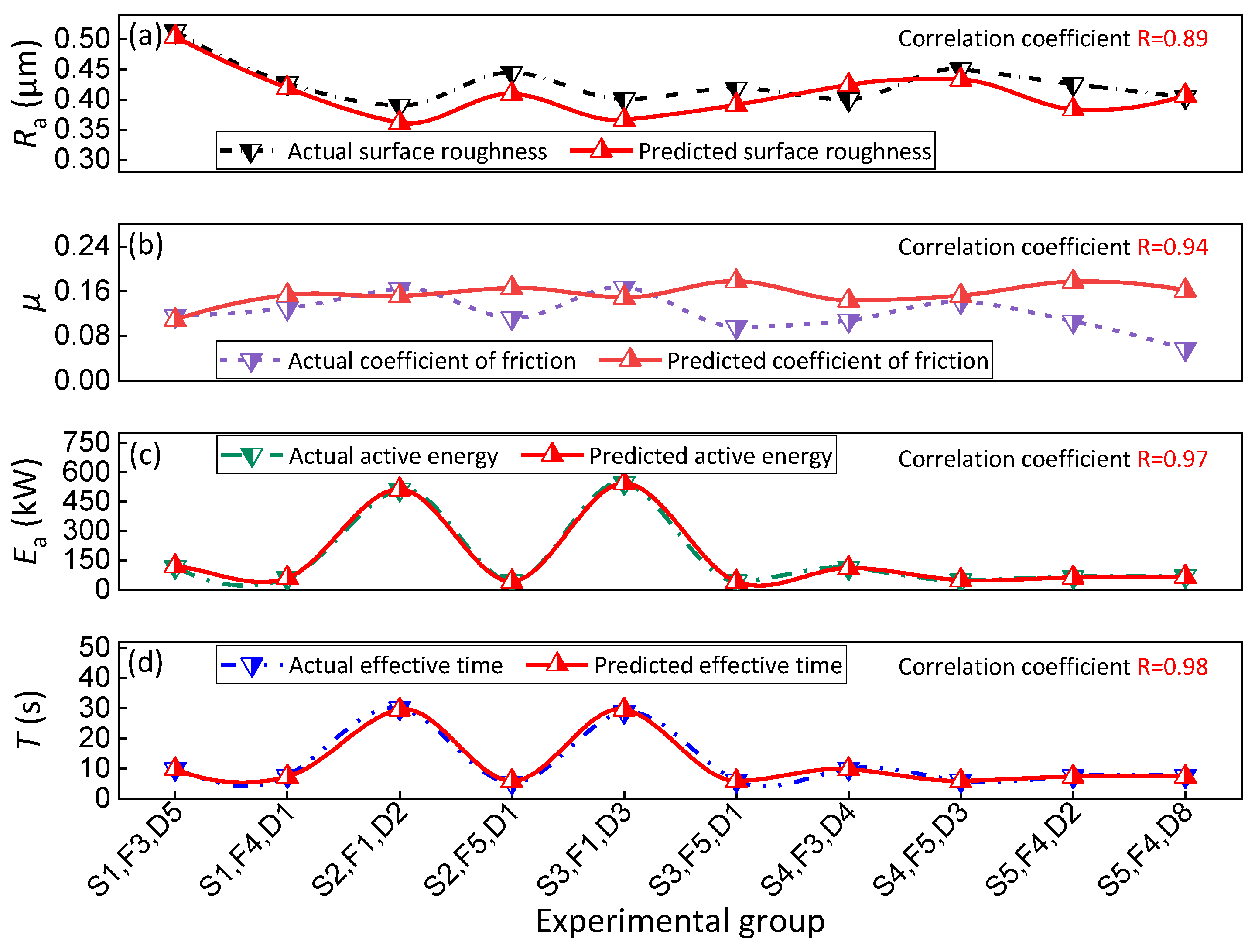
3.3. Mathematical Modeling
3.4. Mathematical Modeling Integration
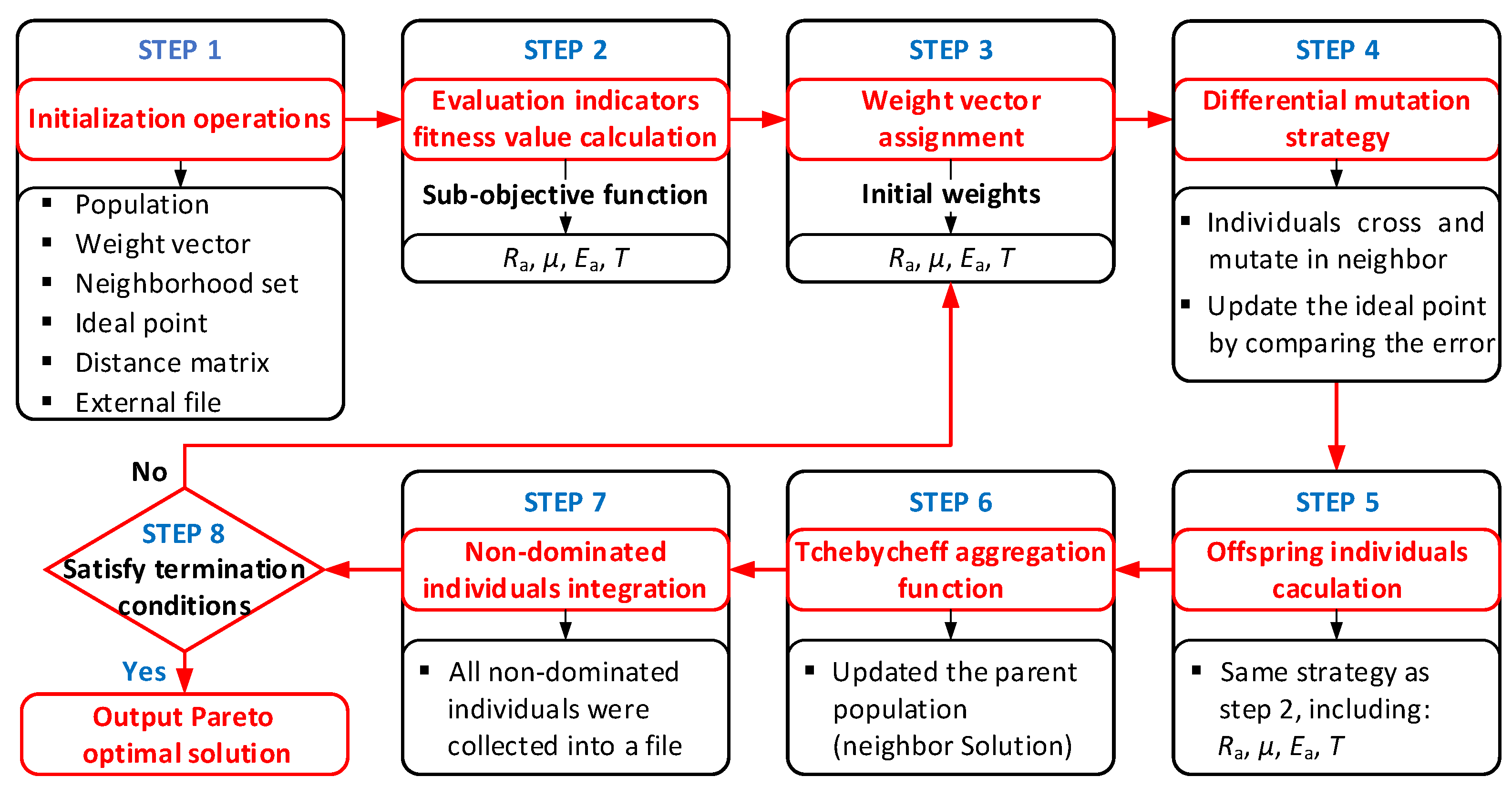
3.4.1. Weight Vector Generation and Aggregation Method for MOEA/D Algorithm
3.4.2. MOEA/D Algorithm Framework
3.5. Optimization Results for the Grinding Process
4. Discussion
4.1. Comprehensive Evaluation of Optimization Parameters
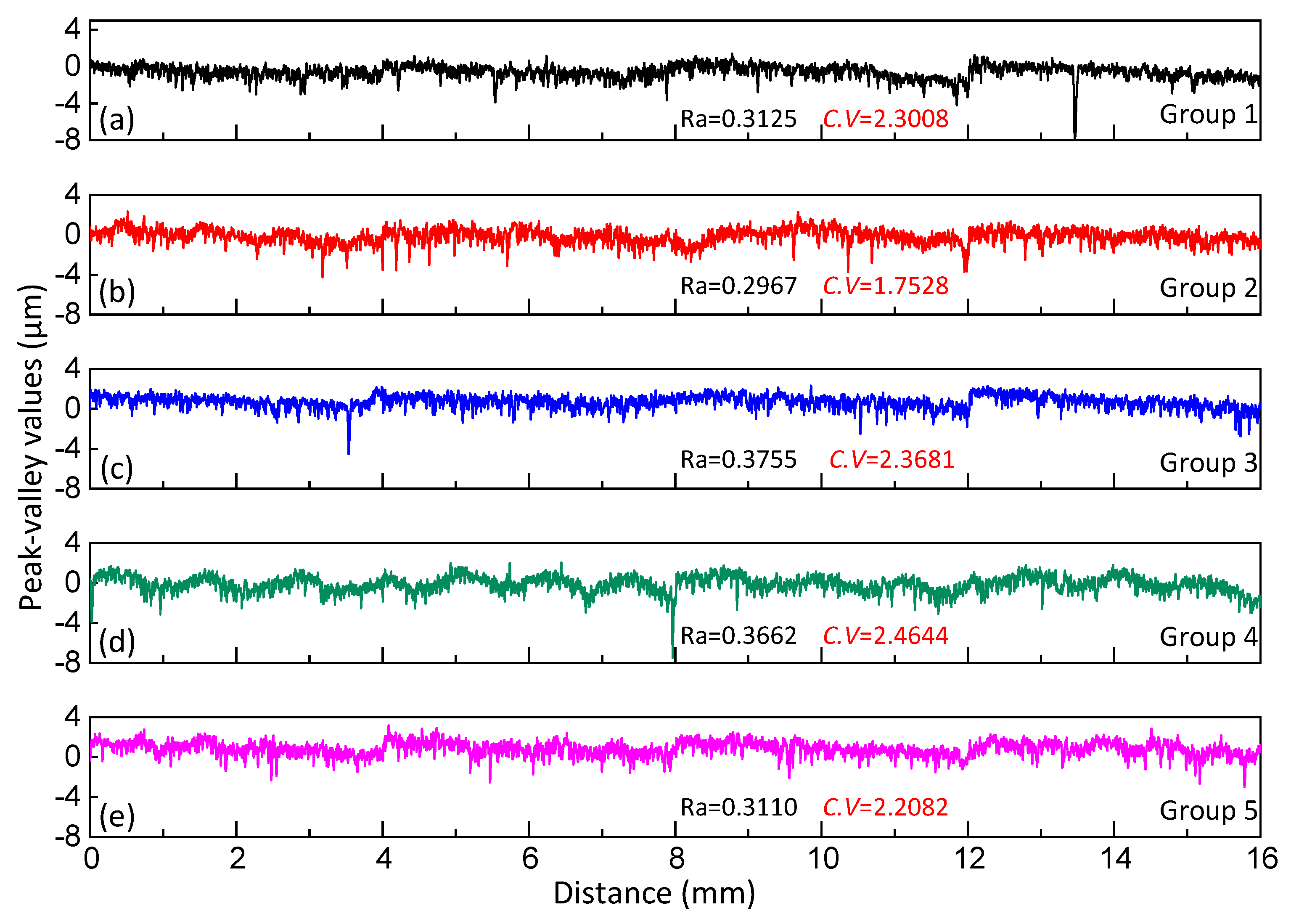
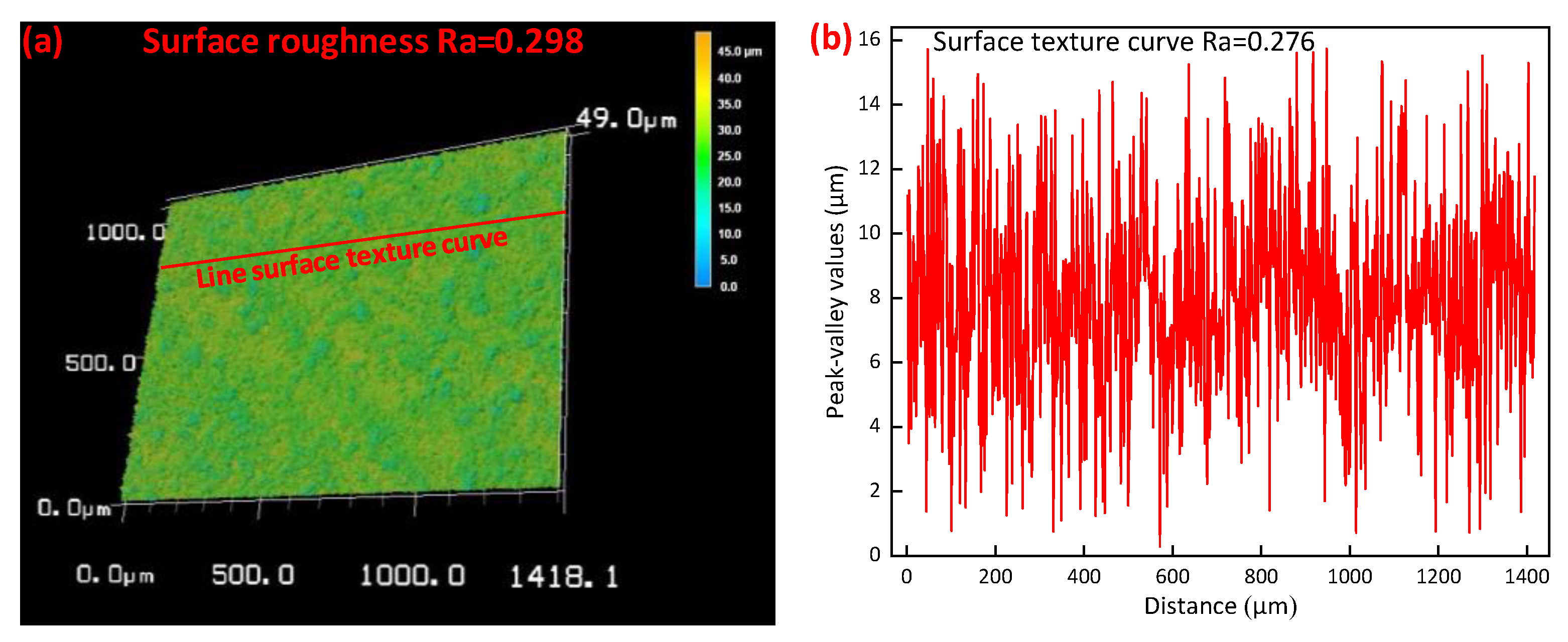
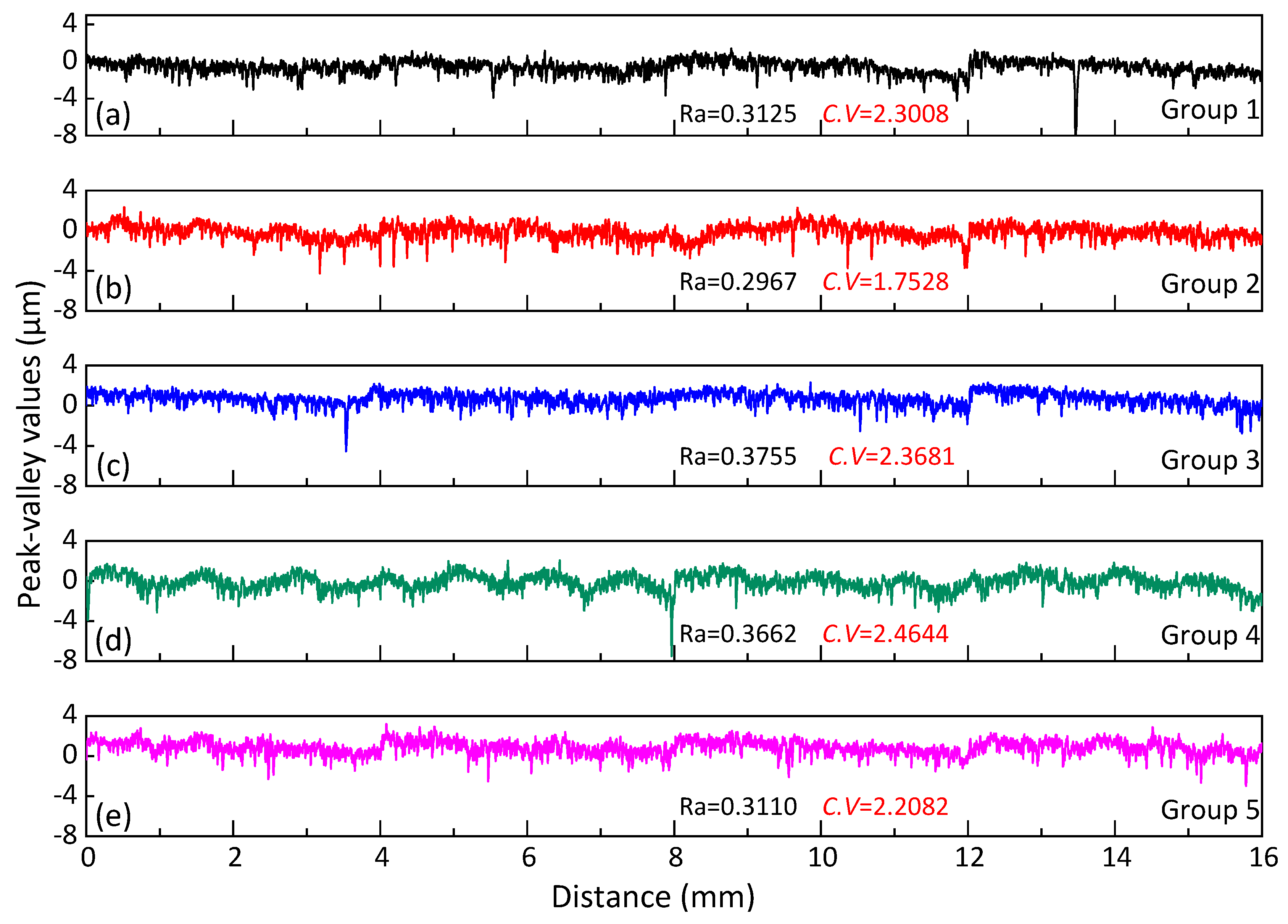
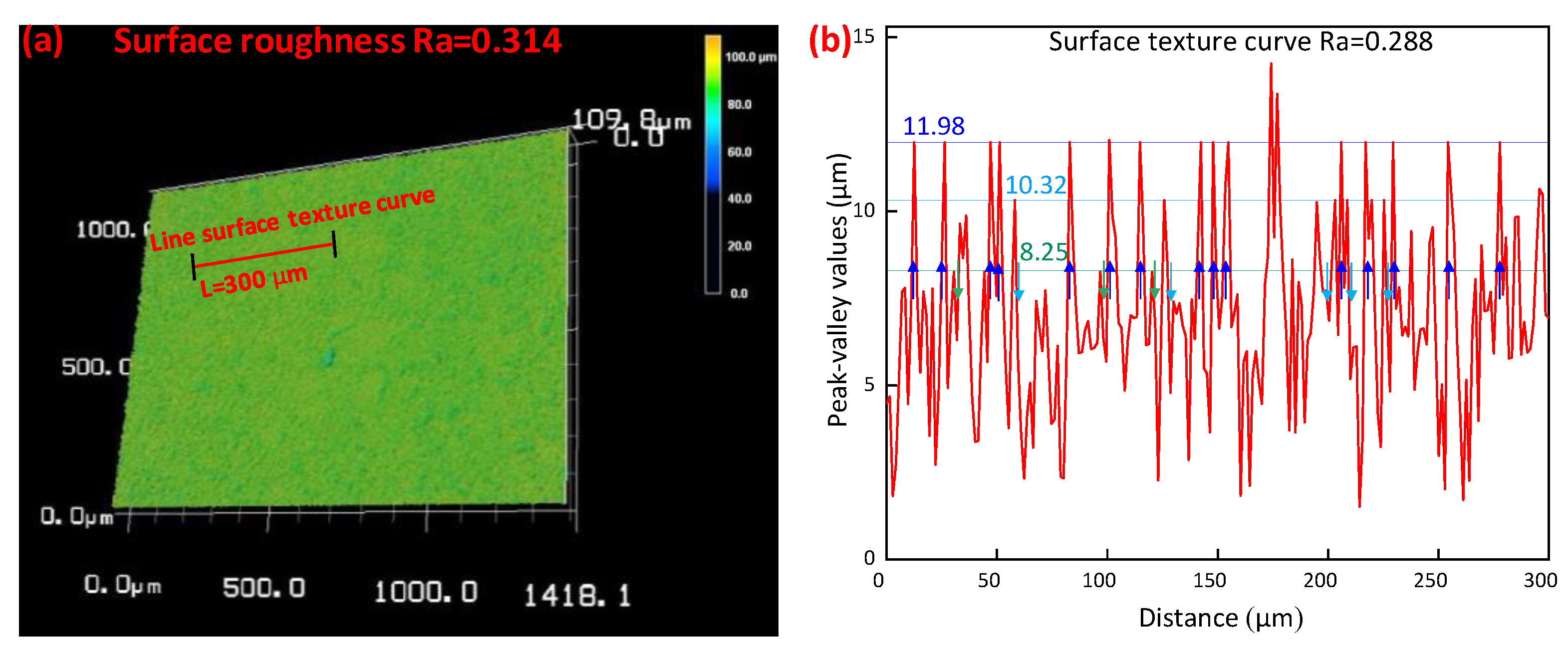
4.1.1. Variation Coefficient and Surface Profile Autocorrelation Analysis
4.1.2. Experimental Verification of Optimized Parameters
5. Conclusions
- i.
- The four sub-objective function models of surface roughness, coefficient of friction, active energy consumption, and effective grinding time are established with good accuracy. The correlation coefficients of them are high, with values of 0.89, 0.94, 0.97, and 0.98, respectively;
- ii.
- The weight vectors of sub-objective functions were optimized by the MOEA/D algorithm in the multi-objective numerical function and two sets of optimal weight vectors were obtained. The weight vectors of (Ra, µ, Ea, T) are (0.52, 0.34, 0.09, 0.05) and (0.56, 0.36, 0.05, 0.03). The surface roughness Ra and coefficient of friction µ show a relatively heavy weight;
- iii.
- Different working parameters were optimized by GA as grinding machine inputs. The optimal input parameters are experimentally verified to be (1638.38 m/min, 1033.60 mm/min, 4.06 μm) and (1724.23 m/min, 1286.83 mm/min, 4.10 μm). The surface roughness, coefficient of friction, active energy consumption, and effective grinding time obtained with the two sets of input parameters are (0.297 μm, 0.199, 441.773 J, 30.207 s) and (0.311 μm, 0.205, 318.769 J, 24.890 s), respectively;
- iv.
- The coefficient of friction with a range of 0.197~0.216 was beneficial to the surface quality of the workpiece. Whether the friction coefficient tends to 0.197 or 0.216 will produce knowledge of chaos and bifurcation. When the coefficient of friction value tends to be 0.197, the smaller the coefficient of variation of the surface profiles, the smaller the distribution distance deviation of the microscopic data points. The distribution of data points becomes uniform. When it tends to be 0.216, the surface profile shows more periodic characteristics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, B.; Wang, H.; Wei, J.; Sui, T. Diamond wheel grinding characteristics of 3D orthogonal quartz fiber reinforced silica ceramic matrix composite. Chin. J. Aeronaut. 2021, 34, 404–414. [Google Scholar] [CrossRef]
- Xia, L.; Lu, S.; Zhong, B.; Huang, L.; Yang, H.; Zhang, T.; Han, H.; Wang, P.; Xiong, L.; Wen, G. Effect of boron doping on waterproof and dielectric properties of polyborosiloxane coating on SiO2f/SiO2 composites. Chin. J. Aeronaut. 2019, 32, 2017–2027. [Google Scholar] [CrossRef]
- Dong, W.; Ma, H.; Liu, R.; Liu, T.; Li, S.; Bao, C.; Song, S. Fabrication by stereolithography of fiber-reinforced fused silica composites with reduced crack and improved mechanical properties. Ceram. Int. 2021, 47, 24121–24129. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, K.; Lin, C.; Zhang, J.; Wang, K.; Sun, P.; Xu, J. An analytical force and energy model for ductile-brittle transition in ultra-precision grinding of brittle materials. Int. J. Mech. Sci. 2022, 220, 107107. [Google Scholar] [CrossRef]
- Fernández-Hernán, J.P.; López, A.J.; Torres, B.; Rams, J. Influence of roughness and grinding direction on the thickness and adhesion of sol-gel coatings deposited by dip-coating on AZ31 magnesium substrates. A Landau–Levich equation revision. Surf. Coat. Technol. 2021, 408, 126798. [Google Scholar] [CrossRef]
- Zhu, S.Y.; Liu, Y.H.; Bai, T.B.; Shi, X.T.; Li, D.M.; Feng, L.B. High-efficient and robust fog collection through topography modulation. Surf. Coat. Technol. 2023, 468, 129747. [Google Scholar] [CrossRef]
- Qin, R.; Zhang, Z.; Hu, Z.; Du, Z.; Xiang, X.; Wen, G.; He, W. On-line evaluation and monitoring technology for material surface integrity in laser shock peening-A review. J. Mater. Process. Technol. 2023, 313, 117851. [Google Scholar] [CrossRef]
- Wen, J.R.; Fei, C.W.; Ahn, S.Y.; Han, L.; Huang, B.; Liu, Y.; Kim, H.S. Accelerated damage mechanisms of aluminized superalloy turbine blades regarding combined high-and-low cycle fatigue. Surf. Coat. Technol. 2022, 451, 129048. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Q.; Wu, T. An investigation of monitoring the damage mechanism in ultra-precision grinding of monocrystalline silicon based on AE signals processing. J. Manuf. Process. 2022, 81, 945–961. [Google Scholar] [CrossRef]
- Wang, S.; Sun, G.; Zhao, Q.; Yang, X. Monitoring of ductile-brittle transition mechanisms in sapphire ultra-precision grinding used small grit size grinding wheel through force and acoustic emission signals. Measurement 2023, 210, 112557. [Google Scholar] [CrossRef]
- Ling, L.G.; Luo, L.; Liu, F.S. Effects of grinding treatment on surface properties and deformation microstructure in alloy 304L. Surf. Coat. Technol. 2021, 408, 126850. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H.; Xu, J.; Song, X.; Wang, J.; Chen, X. A novel sound-based belt condition monitoring method for robotic grinding using optimally pruned extreme learning machine. J. Mater. Process. Technol. 2018, 260, 9–19. [Google Scholar] [CrossRef]
- Tian, Y.B.; Liu, F.; Wang, Y.; Wu, H. Development of portable power monitoring system and grinding analytical tool. J. Manuf. Process. 2017, 27, 188–197. [Google Scholar] [CrossRef]
- Feng, J.; Kim, B.S.; Shih, A.; Ni, J. Tool wear monitoring for micro-end grinding of ceramic materials. J. Mater. Process. Technol. 2009, 209, 5110–5116. [Google Scholar] [CrossRef]
- Qin, F.; Zhang, L.X.; Chen, P.; An, T.; Dai, Y.W.; Gong, Y.P.; Yi, Z.B.; Wang, H.M. In situ wireless measurement of grinding force in silicon wafer self-rotating grinding process. Mech. Syst. Signal Process. 2021, 154, 107550. [Google Scholar] [CrossRef]
- Warren, T.L.; Ting, C.; Qu, J.; Blau, P.J. A wavelet-based methodology for grinding wheel condition monitoring. Int. J. Mach. Tools Manuf. 2007, 47, 580–592. [Google Scholar] [CrossRef]
- Ma, L.; Gong, Y.; Chen, X. Study on surface roughness model and surface forming mechanism of ceramics in quick point grinding. Int. J. Mach. Tools Manuf. 2014, 77, 82–92. [Google Scholar] [CrossRef]
- Yao, Z.; Gu, W.; Li, K. Relationship between surface roughness and subsurface crack depth during grinding of optical glass BK7. J. Mater. Process. Technol. 2012, 212, 969–976. [Google Scholar] [CrossRef]
- Kong, D.D.; Zhu, J.J.; Duan, C.Q.; Lu, L.X.; Chen, D.X. Bayesian linear regression for surface roughness prediction. Mech. Syst. Signal Process. 2020, 142, 106770. [Google Scholar] [CrossRef]
- Meng, Q.; Guo, B.; Wu, G.; Xiang, Y.; Guo, Z.; Jia, J.; Zhao, Q.; Li, K.; Zeng, Z. Dynamic force modeling and mechanics analysis of precision grinding with microstructured wheels. J. Mater. Process. Technol. 2023, 314, 117900. [Google Scholar] [CrossRef]
- Lei, X.; Xiang, D.; Peng, P.; Liu, G.; Li, B.; Zhao, B.; Gao, G. Establishment of dynamic grinding force model for ultrasonic-assisted single abrasive high-speed grinding. J. Mater. Process. Technol. 2022, 300, 117420. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Dai, C.; Ding, W.; Zhu, Y.; Xu, J.; Yu, H. Grinding temperature and power consumption in high speed grinding of Inconel 718 nickel-based superalloy with a vitrified CBN wheel. Precis. Eng. 2018, 52, 192–200. [Google Scholar] [CrossRef]
- Wang, J.L.; Tian, Y.B.; Hu, X.T.; Li, Y.; Zhang, K.; Liu, Y.H. Predictive modelling and Pareto optimization for energy efficient grinding based on aANN-embedded NSGA II algorithm. J. Clean. Prod. 2021, 327, 129479. [Google Scholar] [CrossRef]
- Wang, J.L.; Tian, Y.B.; Zhang, K.; Liu, Y.H.; Cong, J.C. Online prediction of grinding wheel condition and surface roughness for the fused silica ceramic composite material based on the monitored power signal. J. Mater. Res. Technol. 2023, 24, 8053–8064. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.H.; Wang, J.L.; Wang, Y.; Tian, Y.B. Real-time monitoring of silica ceramic composites grinding surface roughness based on signal spectrum analysis. Ceram. Int. 2022, 48, 7204–7217. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, J.W.; Tian, Y.B.; Liu, Y.H.; Zhang, K. Methods of grinding power signal acquisition and dynamic power monitoring database establishment. Diam. Abras. Eng. 2022, 42, 356–363. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, Y.B.; Cong, J.C.; Liu, Y.H.; Yan, N.; Lu, T. Reduction grinding energy consumption by modified particle swarm optimization based on dynamic inertia weigh. Diam. Abras. Eng. 2020, 41, 71–75. [Google Scholar] [CrossRef]
- Wang, J.L.; Tian, Y.B.; Hu, X.T.; Han, J.G.; Liu, B. Integrated assessment and optimization of dual environment and production drivers in grinding. Energy 2023, 272, 127046. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2008, 11, 712–731. [Google Scholar] [CrossRef]
- Jaszkiewicz, A. On the performance of multiple-objective genetic local search on the 0/1 knapsack problem-a comparative experiment. IEEE Trans. Evol. Comput. 2000, 6, 402–412. [Google Scholar] [CrossRef]
- Wang, W.; Li, K.; Tao, X.; Gu, F. An improved MOEA/D algorithm with an adaptive evolutionary strategy. Inf. Sci. 2020, 539, 1–15. [Google Scholar] [CrossRef]
- Qin, S.; Sun, C.; Zhang, G.; He, X.; Tan, Y. A modified particle swarm optimization based on decomposition with different ideal points for many-objective optimization problems. Complex Intell. Syst. 2020, 6, 263–274. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.H.; Tian, Y.B.; Wang, Y.; Wang, J.L. Application of improved fireworks algorithm in grinding surface roughness online monitoring. J. Manuf. Process. 2022, 74, 400–412. [Google Scholar] [CrossRef]
- Jiang, J.; Ge, P.; Hong, J. Study on micro-interacting mechanism modeling in grinding process and ground surface roughness prediction. Int. J. Adv. Manuf. Technol. 2013, 67, 1035–1052. [Google Scholar] [CrossRef]
- Wang, Q.; Cong, W.; Pei, Z.J.; Gao, H.; Kang, R. Rotary ultrasonic machining of potassium dihydrogen phosphate (KDP) crystal: An experimental investigation on surface roughness. J. Manuf. Process. 2009, 11, 66–73. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Jia, D.; Li, B.; Wang, Y.; Yang, M.; Hou, Y.; Zhang, X. Experimental study on the effect of nanoparticle concentration on the lubricating property of nanofluids for MQL grinding of Ni-based alloy. J. Mater. Process. Technol. 2016, 232, 100–115. [Google Scholar] [CrossRef]
- Jiang, J.L.; Ge, P.Q.; Bi, W.B.; Zhang, L.; Wang, D.X.; Zhang, Y. 2D/3D ground surface topography modeling considering dressing and wear effects in grinding process. Int. J. Mach. Tools Manuf. 2013, 74, 29–40. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, Y.; Wang, Y.; Li, B.; Yang, M.; Guo, S.; Liu, G.; Zhang, N. Lubricating property of MQL grinding of Al2O3/SiC mixed nanofluid with different particle sizes and microtopography analysis by cross-correlation. Precis. Eng. 2017, 47, 532–545. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, Y.; Jia, D.; Li, B.; Wang, Y.; Yang, M.; Hou, Y.; Zhang, X. Performances of Al2O3/SiC hybrid nanofluids in minimum-quantity lubrication grinding. Int. J. Adv. Manuf. Technol. 2016, 86, 3427–3441. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| The linear speed of the grinding wheel vs (m/min) | 1000(S1), 1200(S2), 1400(S3), 1600(S4), 1800(S5) |
| Workpiece speed vw (mm/min) | 1000(F1), 2000(F2), 3000(F3), 4000(F4), 5000(F5) |
| Grinding depth ap (μm) | 4(D1), 6(D2), 8(D3), 10(D4), 12(D5) |
| No. | Inputs | Outputs | |||||
|---|---|---|---|---|---|---|---|
| vs (m/min) | vw (mm/min) | ap (μm) | Ra (μm) | u | Ea (J) | T (s) | |
| 1 | 1000 | 1000 | 4 | 0.333 | 0.196 | 520.824 | 29.945 |
| 2 | 1000 | 1000 | 10 | 0.400 | 0.227 | 538.088 | 29.690 |
| 3 | 1000 | 1000 | 12 | 0.423 | 0.120 | 626.641 | 29.963 |
| 4 | 1000 | 2000 | 4 | 0.426 | 0.159 | 119.739 | 14.982 |
| 5 | 1000 | 2000 | 6 | 0.419 | 0.236 | 147.500 | 14.956 |
| 6 | 1000 | 2000 | 8 | 0.424 | 0.181 | 168.877 | 15.019 |
| 7 | 1000 | 3000 | 6 | 0.433 | 0.106 | 72.429 | 10.004 |
| 8 | 1000 | 3000 | 8 | 0.465 | 0.132 | 83.263 | 9.987 |
| 9 | 1000 | 3000 | 12 | 0.513 | 0.116 | 116.740 | 9.934 |
| 10 | 1000 | 4000 | 4 | 0.427 | 0.130 | 58.609 | 7.510 |
| 11 | 1000 | 4000 | 10 | 0.436 | 0.164 | 95.176 | 7.389 |
| 12 | 1000 | 4000 | 12 | 0.529 | 0.156 | 115.372 | 7.481 |
| 13 | 1000 | 5000 | 6 | 0.462 | 0.069 | 72.429 | 5.975 |
| 14 | 1000 | 5000 | 8 | 0.466 | 0.177 | 76.690 | 6.342 |
| 15 | 1000 | 5000 | 12 | 0.539 | 0.144 | 96.517 | 5.958 |
| 16 | 1200 | 1000 | 4 | 0.305 | 0.140 | 486.283 | 30.353 |
| 17 | 1200 | 1000 | 6 | 0.390 | 0.140 | 511.823 | 30.042 |
| 18 | 1200 | 1000 | 8 | 0.401 | 0.134 | 567.206 | 29.926 |
| 19 | 1200 | 2000 | 8 | 0.411 | 0.148 | 167.374 | 11.738 |
| 20 | 1200 | 2000 | 10 | 0.453 | 0.251 | 216.624 | 15.019 |
| 21 | 1200 | 2000 | 12 | 0.467 | 0.124 | 317.837 | 15.034 |
| 22 | 1200 | 3000 | 4 | 0.440 | 0.053 | 63.669 | 9.980 |
| 23 | 1200 | 3000 | 10 | 0.464 | 0.112 | 71.240 | 9.780 |
| 24 | 1200 | 3000 | 12 | 0.479 | 0.111 | 202.890 | 9.967 |
| 25 | 1200 | 4000 | 6 | 0.469 | 0.126 | 69.445 | 7.453 |
| 26 | 1200 | 4000 | 8 | 0.501 | 0.127 | 102.964 | 7.454 |
| 27 | 1200 | 4000 | 12 | 0.491 | 0.126 | 108.551 | 7.365 |
| 28 | 1200 | 5000 | 4 | 0.445 | 0.112 | 44.026 | 5.310 |
| 29 | 1200 | 5000 | 10 | 0.481 | 0.230 | 46.059 | 5.754 |
| 30 | 1200 | 5000 | 12 | 0.533 | 0.126 | 69.332 | 5.961 |
| 31 | 1400 | 1000 | 6 | 0.376 | 0.107 | 518.141 | 29.710 |
| 32 | 1400 | 1000 | 8 | 0.400 | 0.167 | 544.445 | 28.751 |
| 33 | 1400 | 1000 | 12 | 0.415 | 0.135 | 568.541 | 28.738 |
| 34 | 1400 | 2000 | 4 | 0.313 | 0.071 | 136.096 | 12.854 |
| 35 | 1400 | 2000 | 10 | 0.397 | 0.303 | 146.993 | 13.189 |
| 36 | 1400 | 2000 | 12 | 0.437 | 0.260 | 159.001 | 14.559 |
| 37 | 1400 | 3000 | 6 | 0.394 | 0.060 | 162.067 | 9.769 |
| 38 | 1400 | 3000 | 8 | 0.432 | 0.149 | 189.511 | 9.805 |
| 39 | 1400 | 3000 | 12 | 0.440 | 0.131 | 144.624 | 9.943 |
| 40 | 1400 | 4000 | 4 | 0.349 | 0.180 | 73.428 | 7.117 |
| 41 | 1400 | 4000 | 10 | 0.416 | 0.269 | 91.638 | 7.341 |
| 42 | 1400 | 4000 | 12 | 0.475 | 0.149 | 130.246 | 7.446 |
| 43 | 1400 | 5000 | 4 | 0.418 | 0.096 | 43.957 | 6.001 |
| 44 | 1400 | 5000 | 6 | 0.430 | 0.218 | 67.381 | 5.984 |
| 45 | 1400 | 5000 | 8 | 0.452 | 0.155 | 84.441 | 5.334 |
| 46 | 1600 | 1000 | 4 | 0.237 | 0.205 | 468.124 | 29.853 |
| 47 | 1600 | 1000 | 10 | 0.328 | 0.233 | 548.139 | 30.351 |
| 48 | 1600 | 1000 | 12 | 0.403 | 0.175 | 564.990 | 30.643 |
| 49 | 1600 | 2000 | 6 | 0.366 | 0.098 | 138.741 | 15.092 |
| 50 | 1600 | 2000 | 8 | 0.388 | 0.343 | 151.043 | 15.099 |
| 51 | 1600 | 2000 | 12 | 0.419 | 0.135 | 178.248 | 15.042 |
| 52 | 1600 | 3000 | 4 | 0.311 | 0.064 | 97.888 | 9.906 |
| 53 | 1600 | 3000 | 10 | 0.400 | 0.108 | 111.350 | 9.979 |
| 54 | 1600 | 3000 | 12 | 0.440 | 0.081 | 125.653 | 9.958 |
| 55 | 1600 | 4000 | 4 | 0.341 | 0.102 | 27.717 | 7.381 |
| 56 | 1600 | 4000 | 6 | 0.434 | 0.112 | 37.726 | 7.533 |
| 57 | 1600 | 4000 | 8 | 0.432 | 0.143 | 89.867 | 7.475 |
| 58 | 1600 | 5000 | 8 | 0.450 | 0.141 | 47.901 | 6.010 |
| 59 | 1600 | 5000 | 10 | 0.480 | 0.146 | 63.151 | 5.969 |
| 60 | 1600 | 5000 | 12 | 0.471 | 0.141 | 76.120 | 5.944 |
| 61 | 1800 | 1000 | 6 | 0.371 | 0.142 | 492.783 | 30.104 |
| 62 | 1800 | 1000 | 8 | 0.393 | 0.154 | 510.063 | 29.023 |
| 63 | 1800 | 1000 | 12 | 0.344 | 0.059 | 688.878 | 30.22 |
| 64 | 1800 | 2000 | 4 | 0.287 | 0.139 | 116.907 | 14.702 |
| 65 | 1800 | 2000 | 10 | 0.373 | 0.469 | 144.436 | 14.891 |
| 66 | 1800 | 2000 | 12 | 0.416 | 0.174 | 165.680 | 14.857 |
| 67 | 1800 | 3000 | 4 | 0.297 | 0.203 | 71.907 | 9.950 |
| 68 | 1800 | 3000 | 6 | 0.393 | 0.355 | 74.378 | 10.046 |
| 69 | 1800 | 3000 | 8 | 0.402 | 0.227 | 75.018 | 10.102 |
| 70 | 1800 | 4000 | 6 | 0.426 | 0.106 | 66.879 | 7.464 |
| 71 | 1800 | 4000 | 8 | 0.404 | 0.147 | 69.806 | 7.546 |
| 72 | 1800 | 4000 | 12 | 0.419 | 0.137 | 112.556 | 7.619 |
| 73 | 1800 | 5000 | 4 | 0.326 | 0.197 | 45.776 | 5.534 |
| 74 | 1800 | 5000 | 10 | 0.413 | 0.228 | 62.568 | 6.008 |
| 75 | 1800 | 5000 | 12 | 0.466 | 0.103 | 78.477 | 5.927 |
| Grinding Elements | Weight Vector Grouping Categories | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| vs (m/min) | 1560.3760 | 1638.3838 | 1753.1953 | 1765.5965 | 1724.2324 |
| vw (mm/min) | 1094.4094 | 1033.6033 | 4708.3708 | 4647.1647 | 1286.8286 |
| ap (μm) | 4.1712 | 4.0624 | 4.3400 | 4.1208 | 4.1016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Jiao, L.; Liu, Y.; Tian, Y.; Qiu, T.; Zhou, T.; Wang, X.; Zhao, B. Study on a Novel Strategy for High-Quality Grinding Surface Based on the Coefficient of Friction. Lubricants 2023, 11, 351. https://doi.org/10.3390/lubricants11080351
Li Y, Jiao L, Liu Y, Tian Y, Qiu T, Zhou T, Wang X, Zhao B. Study on a Novel Strategy for High-Quality Grinding Surface Based on the Coefficient of Friction. Lubricants. 2023; 11(8):351. https://doi.org/10.3390/lubricants11080351
Chicago/Turabian StyleLi, Yang, Li Jiao, Yanhou Liu, Yebing Tian, Tianyang Qiu, Tianfeng Zhou, Xibin Wang, and Bin Zhao. 2023. "Study on a Novel Strategy for High-Quality Grinding Surface Based on the Coefficient of Friction" Lubricants 11, no. 8: 351. https://doi.org/10.3390/lubricants11080351
APA StyleLi, Y., Jiao, L., Liu, Y., Tian, Y., Qiu, T., Zhou, T., Wang, X., & Zhao, B. (2023). Study on a Novel Strategy for High-Quality Grinding Surface Based on the Coefficient of Friction. Lubricants, 11(8), 351. https://doi.org/10.3390/lubricants11080351







