Study on Thermal Characteristics of Angular Contact Ball Bearings Considering Roundness Error
Abstract
:1. Introduction
2. Calculation Method for Steady-State Heat Generation of Angular Contact Ball Bearings Considering Roundness Error
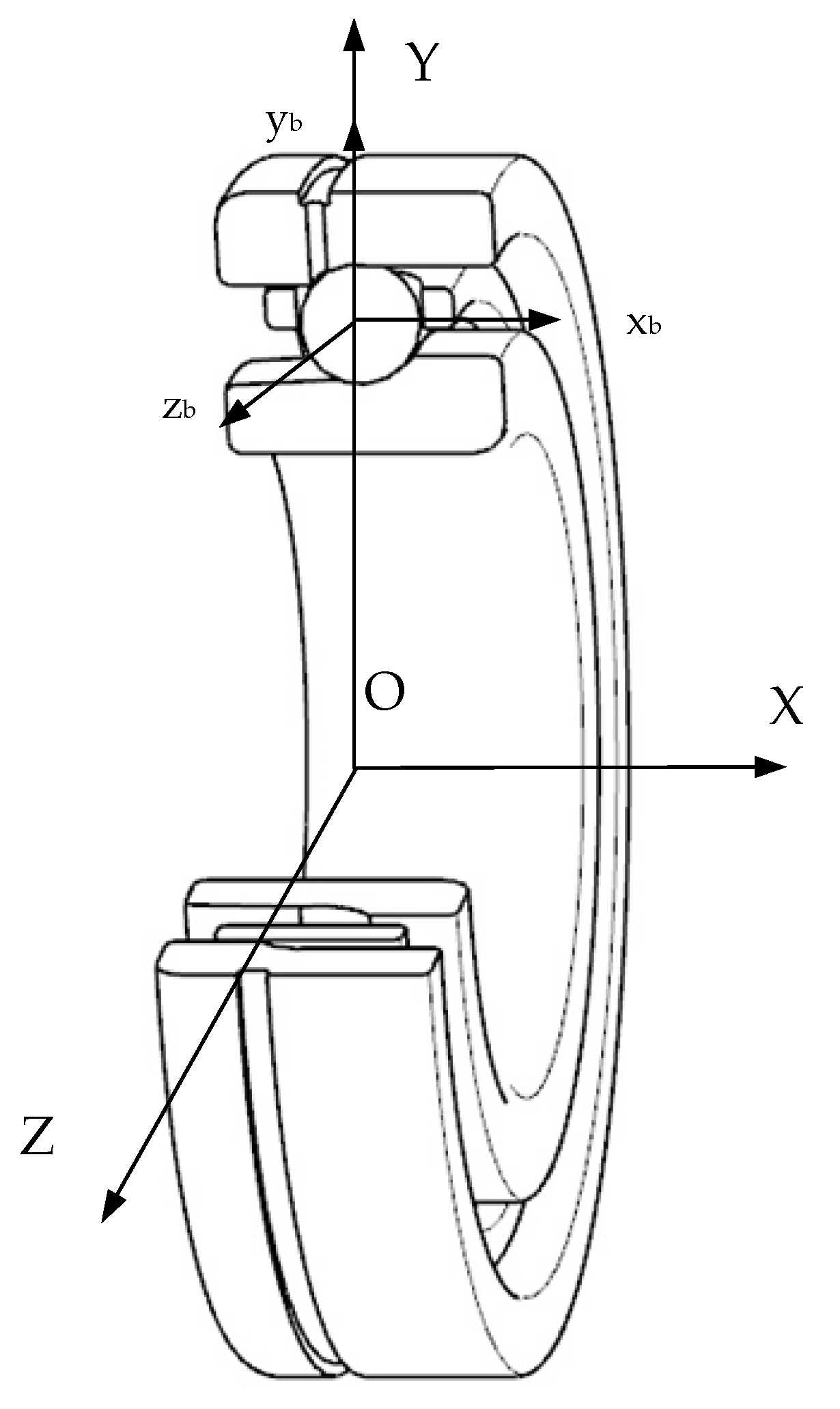
2.1. Quasi Dynamics of Angular Contact Ball Bearings Considering Roundness Error
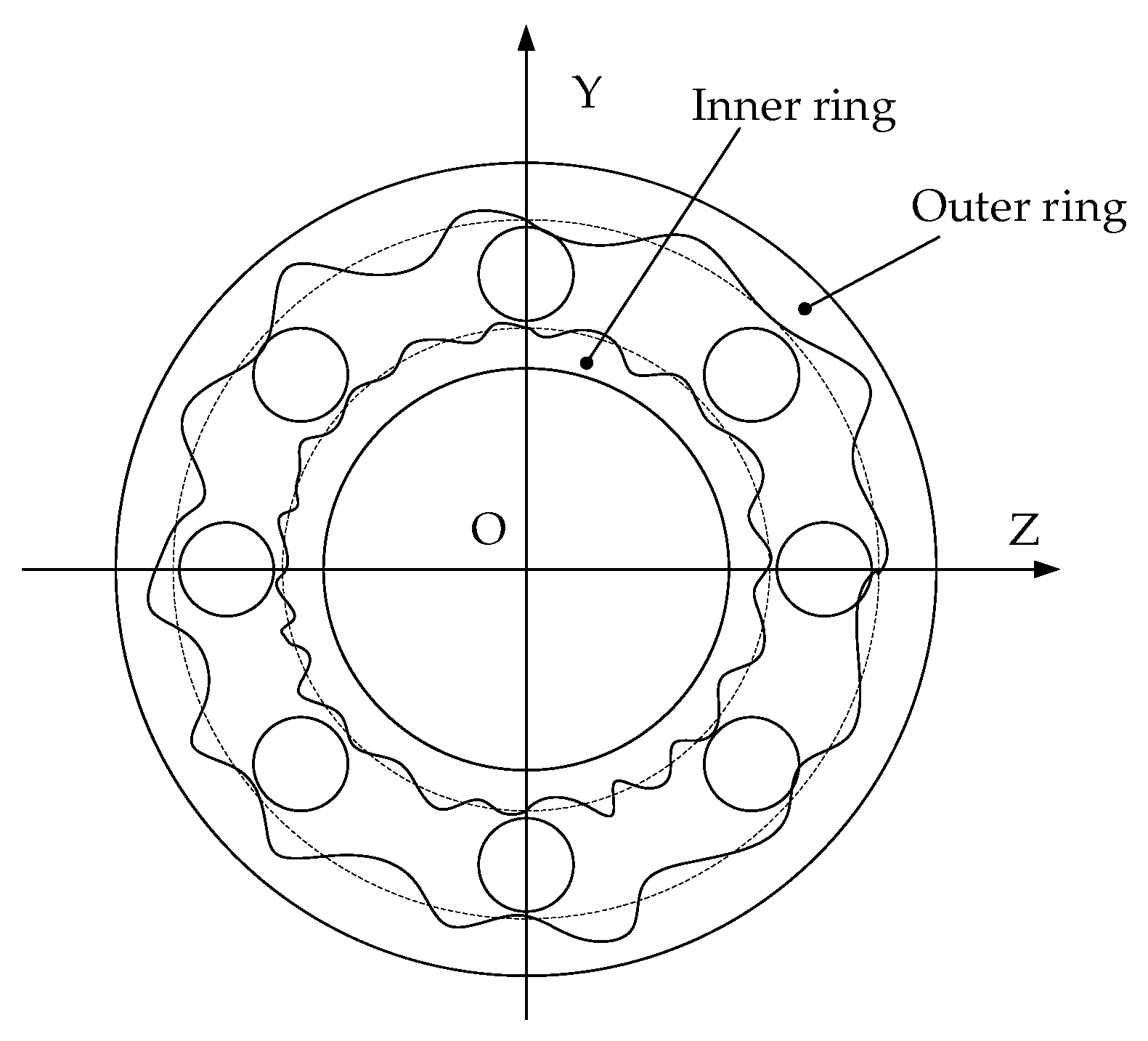
2.1.1. Channel Roundness Error of Angular Contact Ball Bearings
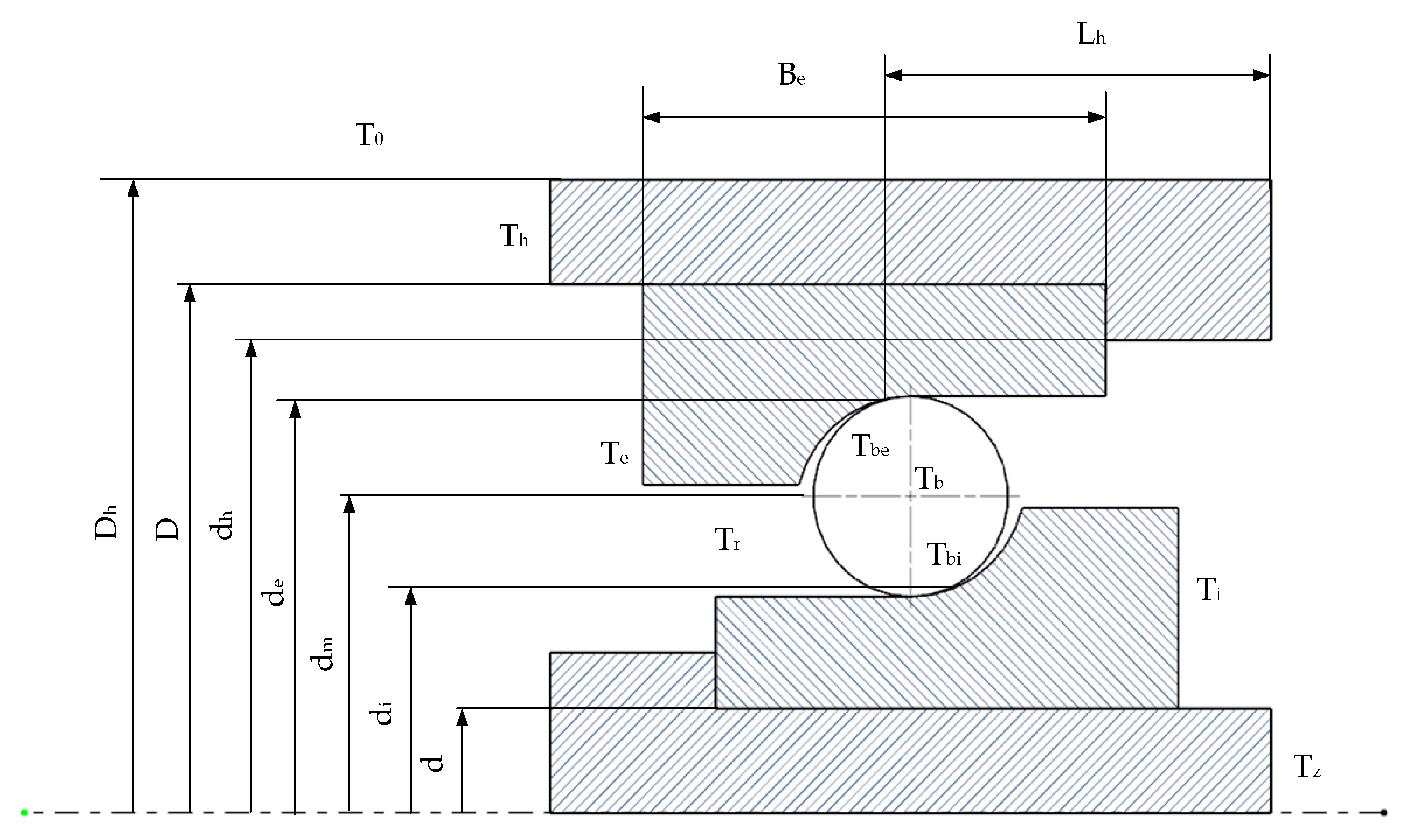
2.1.2. Quasi-Dynamic Model
2.2. Calculation of Friction Torque
2.2.1. Friction Torque Caused by Elastic Hysteresis
2.2.2. Lubricating Oil Viscous Friction Torque
2.2.3. Friction Torque Caused by Differential Sliding
2.2.4. Friction Torque Caused by Spin Slip
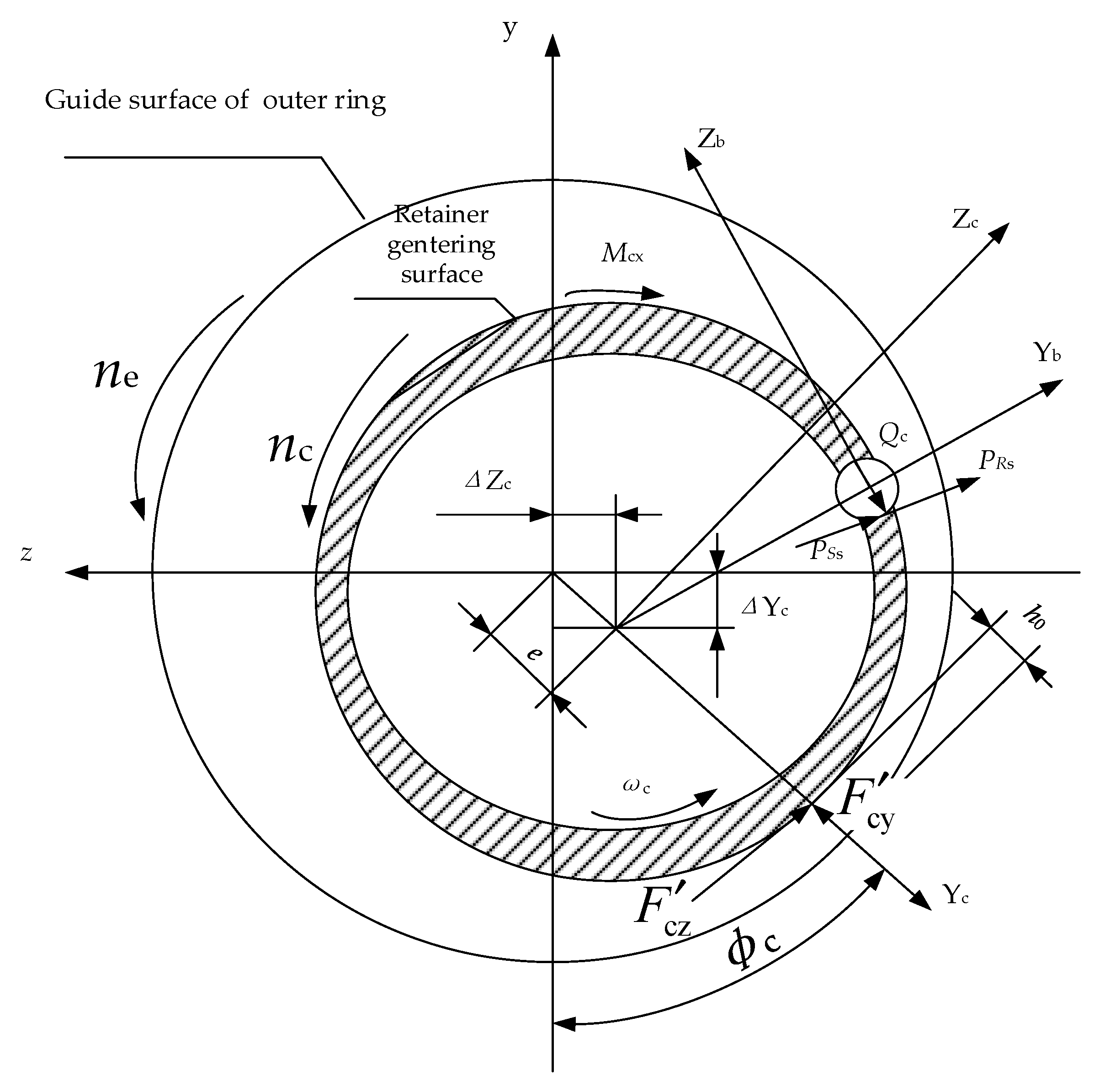
2.2.5. Friction Torque Caused by Friction between Rolling Element and Cage
2.2.6. Friction Torque Caused by Friction between Cage and Guide Ring
2.2.7. Total Friction Torque
2.3. Temperature Calculation by Thermal Network Method
3. Comparative Verification
4. Calculation Results and Analysis
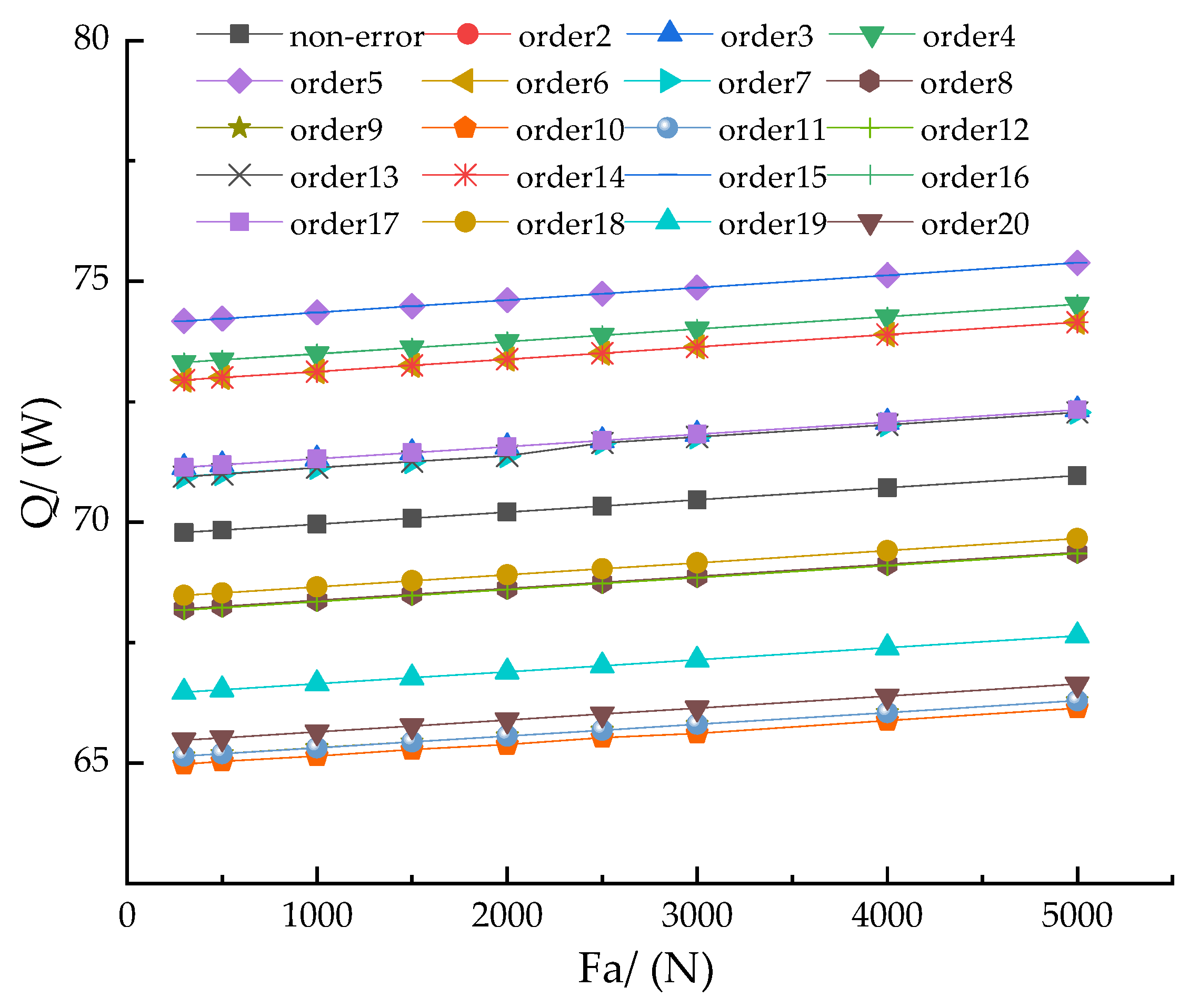
4.1. Influence of Bearing Working Conditions on Overall Heat Generation of Bearings
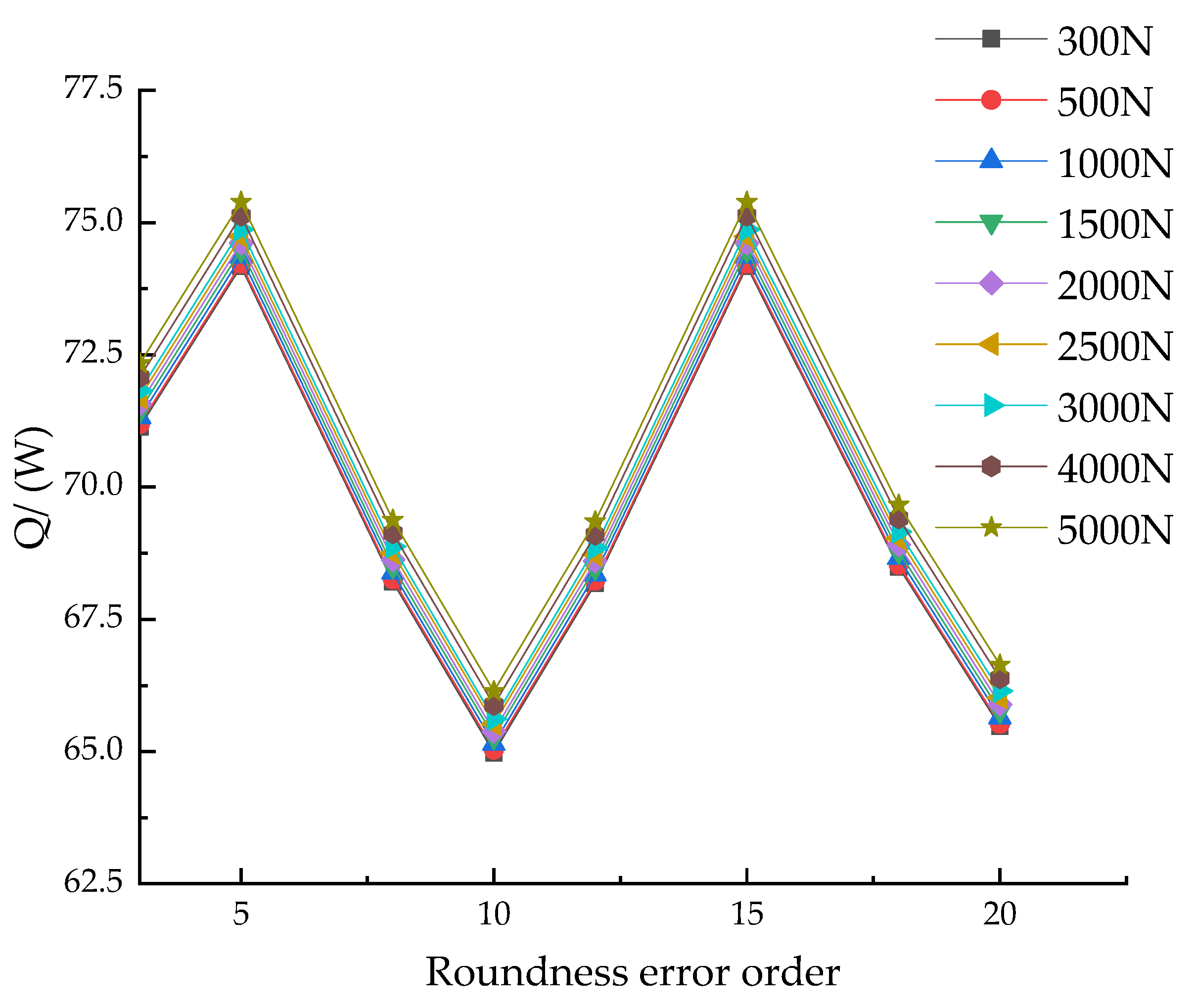
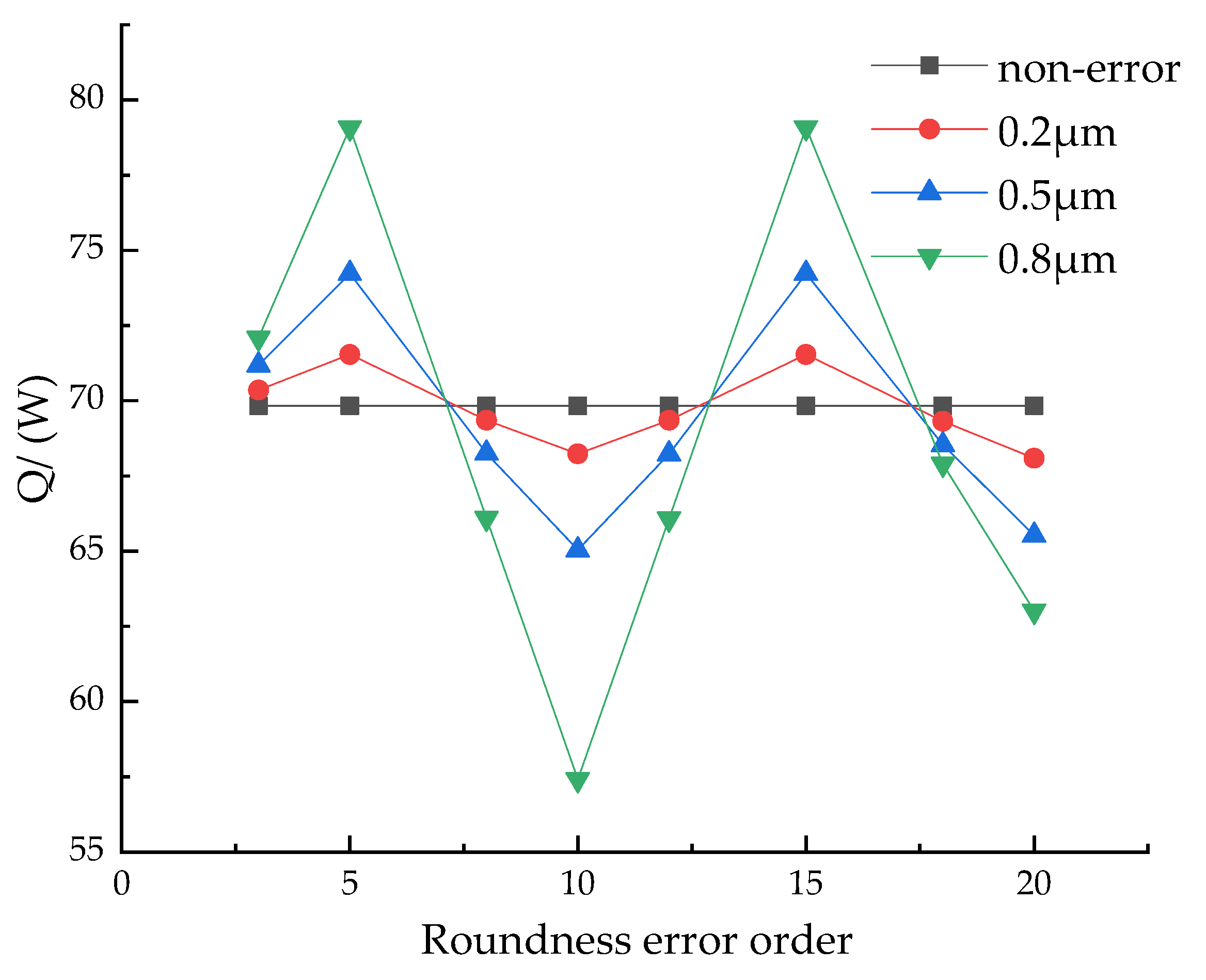
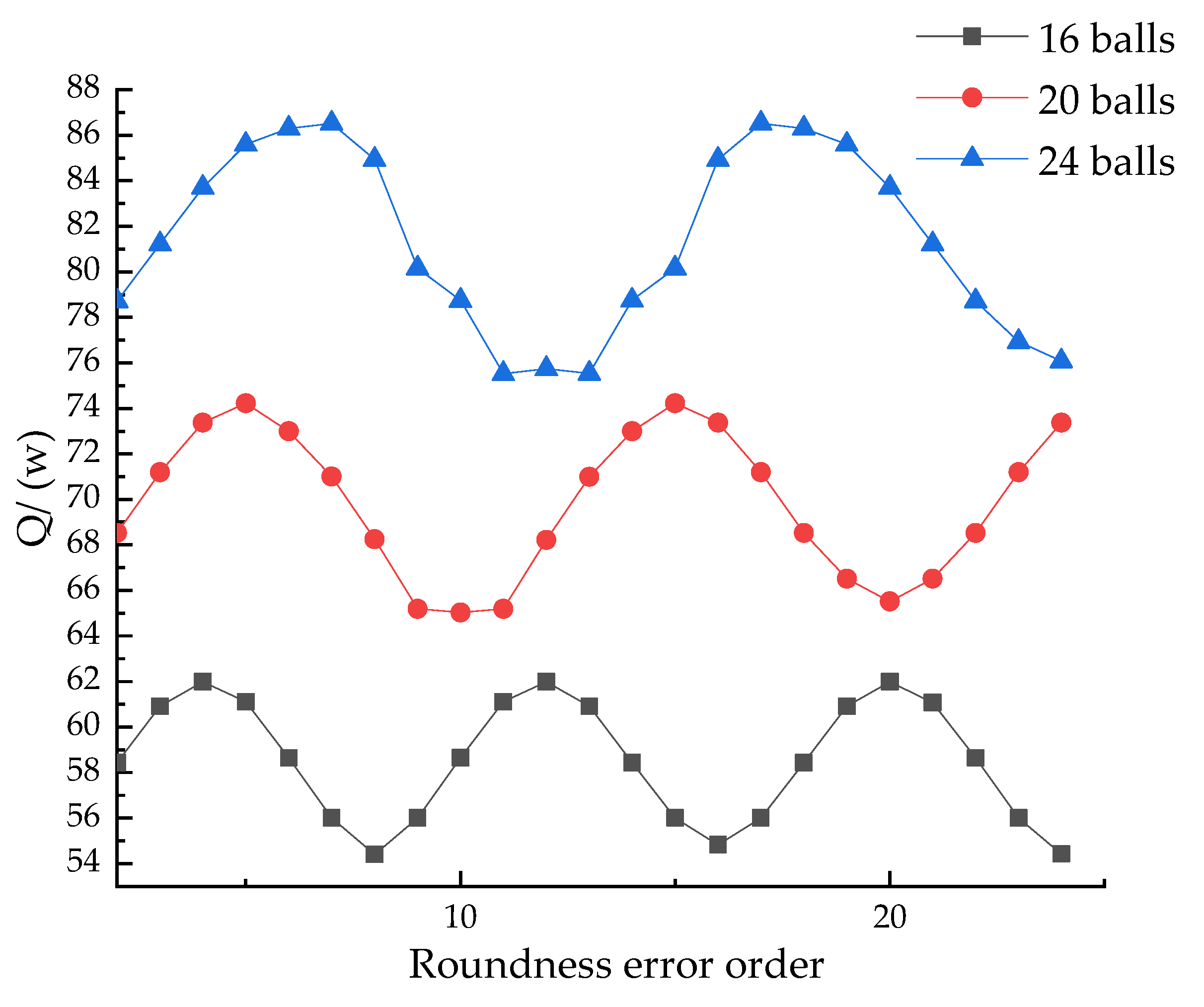
4.2. Influence of Roundness Error Order on the Whole Heat Generation of Bearings
5. Conclusions
- (1)
- As the speed and axial load increase, the overall heat generation linearly increases, and the increase in speed produces a more significant increase in heat generation compared to the axial load. When the order of the roundness error is equal to the number of balls n/2 ± 2 (where n = 1, 2, 3, …), the overall heat generation of the bearing is lower than when the roundness error is not considered. When the order of the roundness error is equal to the number of balls (2n − 1)/4 ± 2 (where n = 1, 2, 3, …), the overall heat generation of the bearing is higher than that without roundness error.
- (2)
- When the order of the roundness error is equal to the number of balls (2n − 1)/4 times (where n = 1, 2, 3, …), the overall heat generation of the bearing is maximum. When the order of the roundness error is equal to the number of balls n/2 times (where n = 1, 2, 3, …), the overall heat generation of the bearing is minimum.
- (3)
- As the order of the roundness error increases, the overall heat generation fluctuates. The faster the speed, the more obvious the trend of fluctuation. Under the same order of roundness error, the load has little effect on the overall heat generation, which increases with the increase in bearing speed.
- (4)
- The overall heat generation fluctuation of the bearing under steady state increases with the increase in the roundness error amplitude, and its fluctuation is proportional to the amplitude. The overall heat generation of the bearing exhibits periodic changes with the increase in the harmonic order of the roundness error, and the change period is mapped to the number of balls.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Palmgren, A. Ball and Roller Bearing Engineering; Svenska Kullager Fabriken (SKF) Industries Incorporation: Philadelphia, PA, USA, 1959. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology Rolling Bearing Analysis; CRC Press, Taylor Francis Group: New York, NY, USA, 2006. [Google Scholar]
- Kerrouche, R.; Dadouche, A.; Mamou, M.; Boukraa, S. Power Loss Estimation and Thermal Analysis of an Aero-Engine Cylindrical Roller Bearing. Tribol. Trans. 2021, 64, 1079–1094. [Google Scholar] [CrossRef]
- Pouly, F.; Changenet, C.; Ville, F.; Velex, P.; Damiens, B. Power loss predictions in high-speed rolling element bearings using thermal networks. Tribol. Trans. 2010, 53, 957–967. [Google Scholar] [CrossRef]
- Pouly, F.; Changenet, C.; Ville, F. Investigations on the Power Losses and Thermal Behavior of Rolling Element Bearings. J. Eng. Tribol. 2010, 224, 925–933. [Google Scholar]
- Zheng, D.; Chen, W.; Li, M. An optimized thermal network model to estimate thermal per formances on a pair of angular contact ball bearings under oil-air lubrication. Appl. Therm. Eng. 2018, 131, 328–339. [Google Scholar]
- Tarawneh, C.M.; Fuentes, A.A.; Kypuros, J.A.; Navarro, L.A.; Vaipan, A.G.; Wilson, B.M. Thermal Modeling of a Railroad Tapered-Roller Bearing Using Finite Element Analysis. J. Therm. Sci. Eng. Appl. 2012, 4, 031002. [Google Scholar] [CrossRef]
- Hong, Y.; Kou, W. Dynamic Simulation of the Slide Friction Heat Generation of Deep Groove Ball Bearing Based on Hertz Theory. Equip. Manuf. Technol. 2014, 12, 39–41. (In Chinese) [Google Scholar]
- Zheng, D.; Chen, W. Effect of structure and assembly constraints on temperature of high-speed angular contact ball bearings with thermal network method. Mech. Syst. Signal Process. 2020, 145, 106929. [Google Scholar] [CrossRef]
- Nicolás, J.A.M.; de León Hijes, F.C.G.; Alhama, F. Solution of temperature fields in hydrodynamics bearings by the numerical network method. Tribol. Int. 2007, 40, 139–145. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, Y.; Qiu, M.; Chen, F.; He, K. Analysis and experimental research of transient temperature rise characteristics of high-speed cylindrical roller bearing. Sci. Rep. 2024, 14, 711. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Su, B.; Zhang, S.; Yang, H.; Cui, Y. Dynamics-Based Thermal Analysis of High-Speed Angular Contact Ball Bearings with Under-Race Lubrication. Machines 2023, 11, 691. [Google Scholar] [CrossRef]
- Hassan, E. Rasheed, Effect of surface waviness on the hydrodynamic lubrication of a plain cylindrical sliding element bearing. Wear 1998, 223, 1–6. [Google Scholar]
- Rodionov, E.M. Moment Originating from Errors in the Form or Rolling Surfaces of a Ball Bearing; Technical Report FTD-HT-66-374; Foreign Technology Div.: Wright-Patterson AFB, OH, USA, 1966. [Google Scholar]
- Cui, L. Research on Dynamic Performances of High-Speed Rolling Bearing and Rotor System of Aeroenging. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, 2008. (In Chinese). [Google Scholar]
- Zheng, H.; Wang, F.; Ji, B. The Study for Effect of Outer Race Waviness on the Dynamic Behavior of Cylindrical Roller Bearing. Mach. Des. Manuf. 2014, 12, 82–84+88. (In Chinese) [Google Scholar]
- Yang, M.; Lu, H.; Zhang, X.; Duan, M.; Bao, L.; Wang, B.; Wu, W. Influence of Surface Waviness of Journal and Bearing Bush on the Static Characteristics of Hydrodynamic Bearing. Processes 2021, 9, 110. [Google Scholar] [CrossRef]
- Liu, J.; Pang, R.; Xu, Y.; Ding, S.; He, Q. Vibration analysis of a single row angular contact ball bearing with the coupling errors including the surface roundness and waviness. Sci. China Technol. Sci. 2020, 63, 943–952. [Google Scholar] [CrossRef]
- Deng, S.; Li, X.; Wang, J.; Wang, Y.; Teng, H. Analysis on the friction torque fluctuation of angular contact ball bearings. J. Mech. Eng. 2011, 23, 104–112. (In Chinese) [Google Scholar] [CrossRef]
- Gao, Y.; Deng, S.; Zheng, C.; Liang, B.; Li, J. Experimental study on effects of groove waviness on ball bearing friction torque. Bearing 2009, 10, 41–44. (In Chinese) [Google Scholar]
- Liu, J.; Yan, Z.; Shao, Y. An investigation for the friction torque of a needle roller bearing with the roundness error. Mech. Mach. Theory 2018, 121, 259–272. [Google Scholar] [CrossRef]
- Burton, R.A.; Staph, H.E. Thermally activated seizure of angular contact bearings. ASLE Trans. 1967, 10, 408–417. [Google Scholar] [CrossRef]
- Deng, S.; Li, X.; Wang, J. Friction al Torque Characteristic of Angular Contact Ball Bearings. J. Mech. Eng. 2011, 47, 114–120. (In Chinese) [Google Scholar] [CrossRef]
- Ai, S.; Wang, W.; Wang, Y.; Zhao, Z. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method. Tribol. Int. 2015, 87, 11–22. [Google Scholar] [CrossRef]
- Crecelius, W.J.; Pirvics, J. Computer Program Operation Manual on SHABERTH: A Computer Program for the Analysis of the Steady State and Transient Thermal Performance of Shaft-Bearing Systems; U.S. Air Force: Washington, DC, USA, 1976.


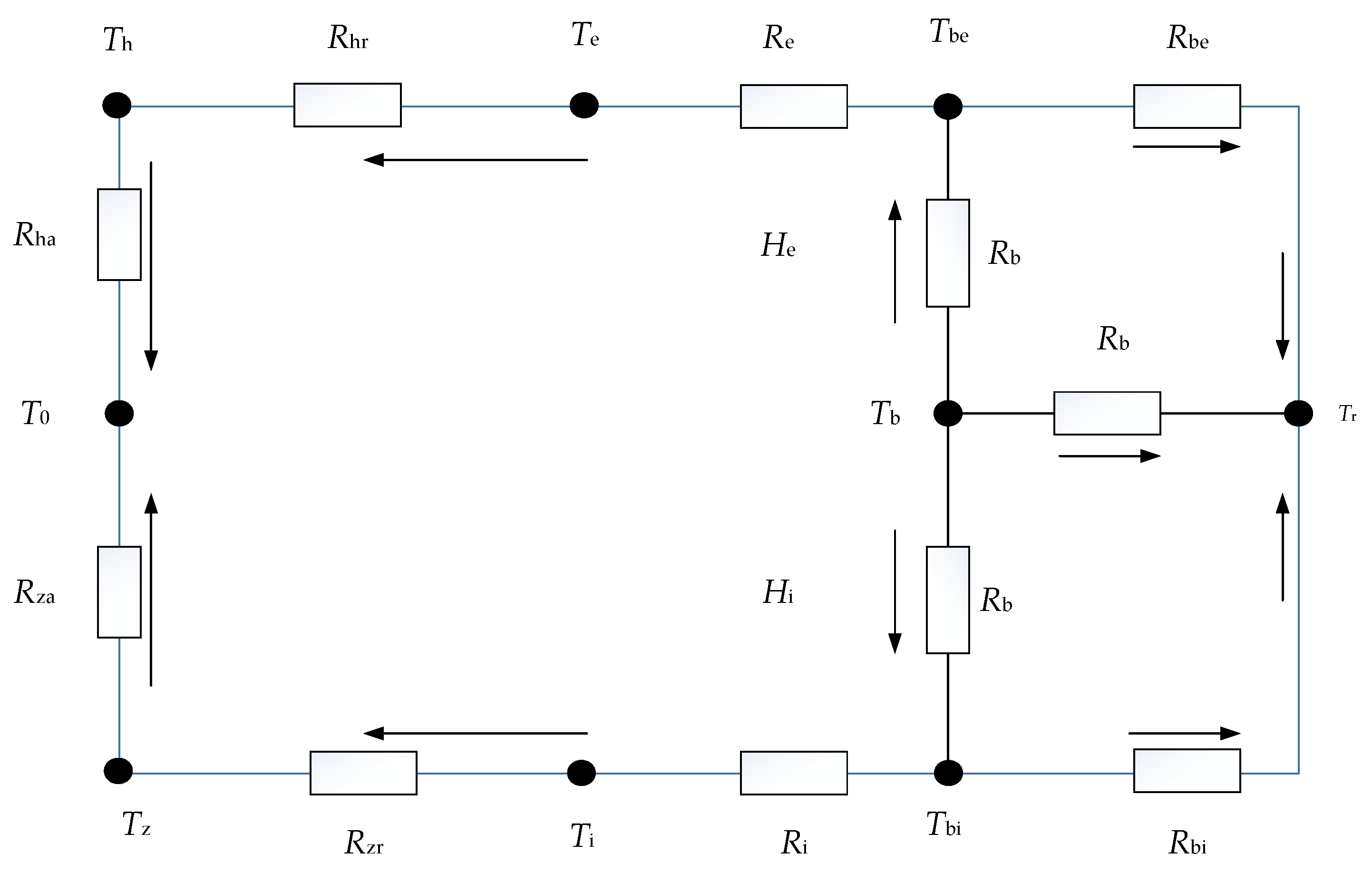

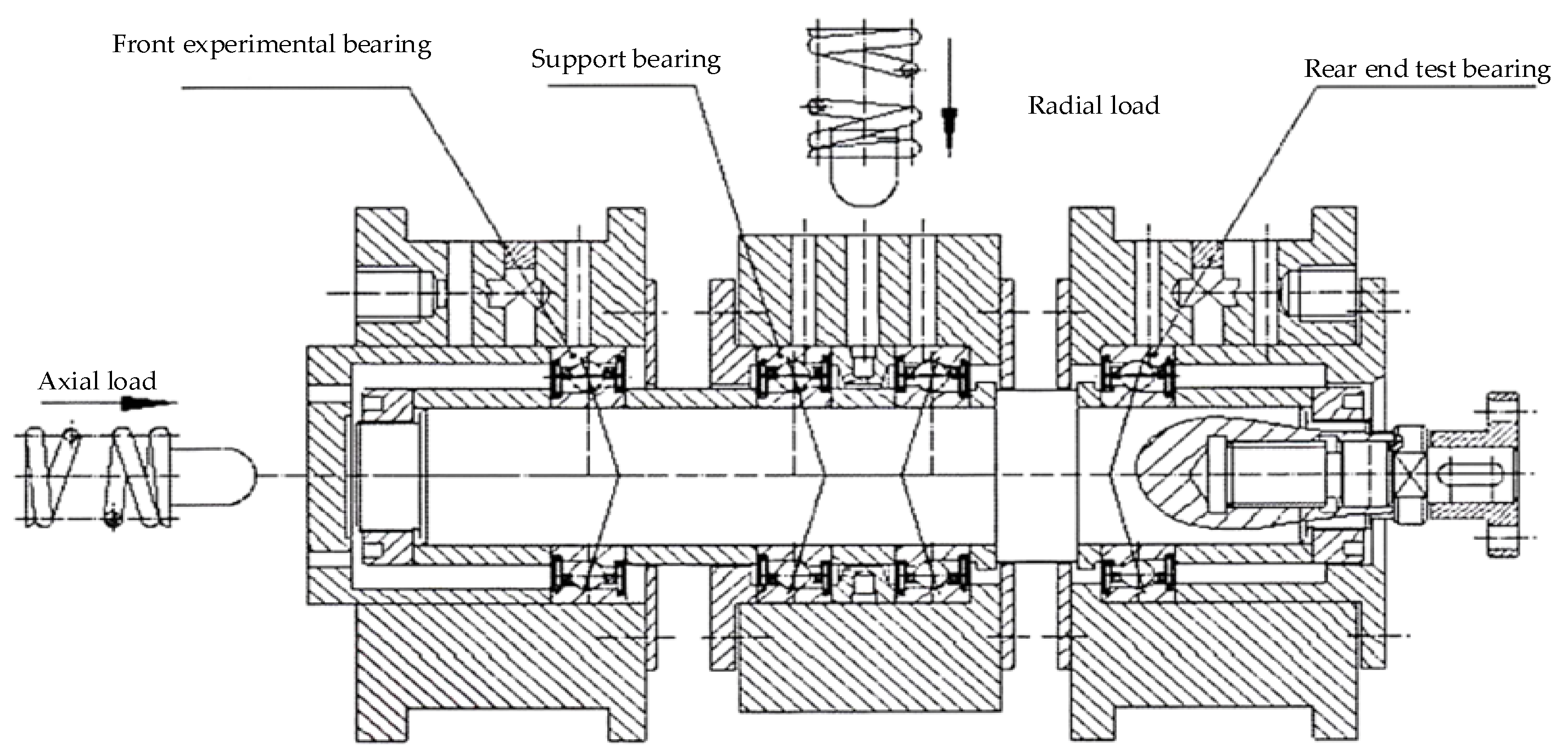

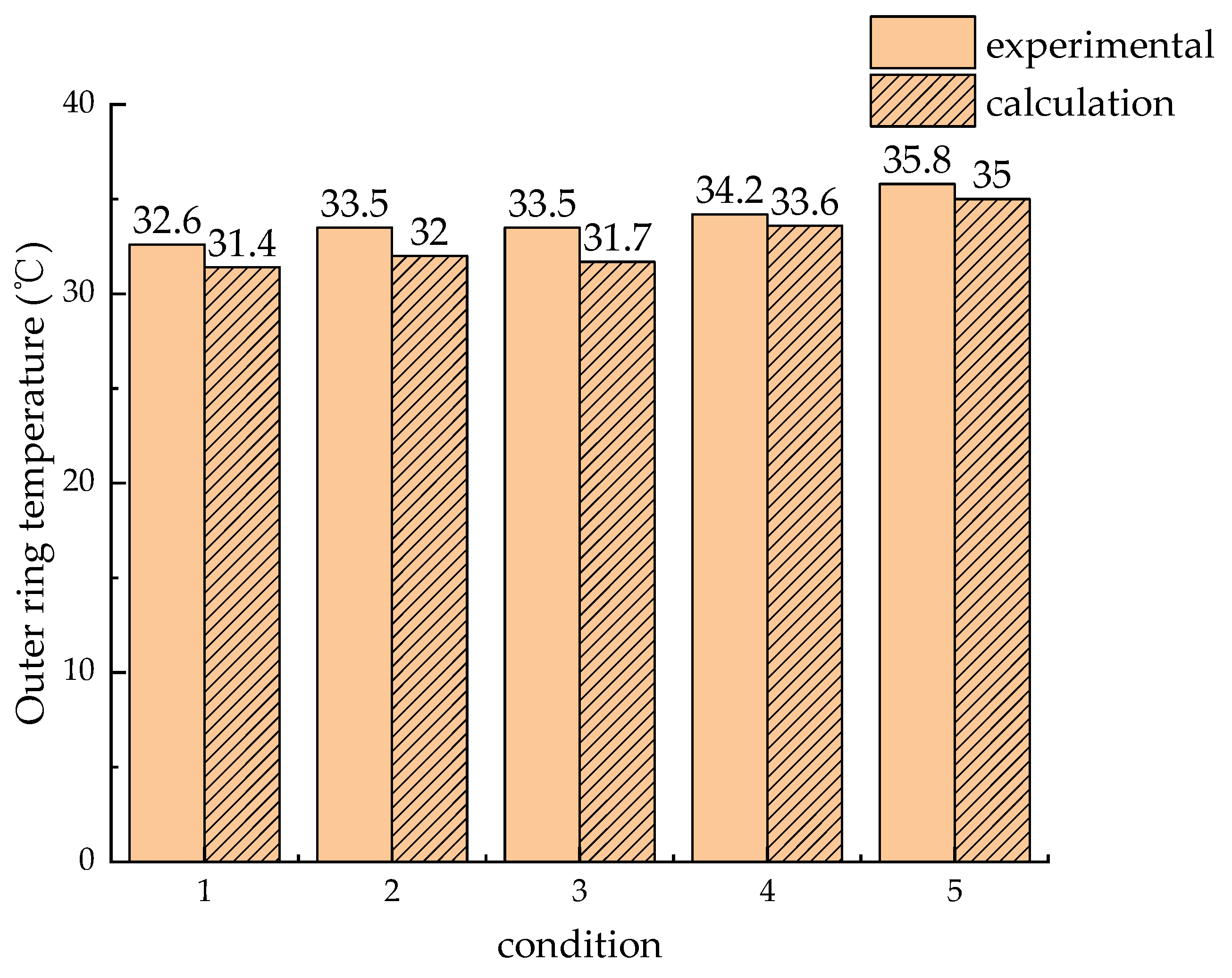
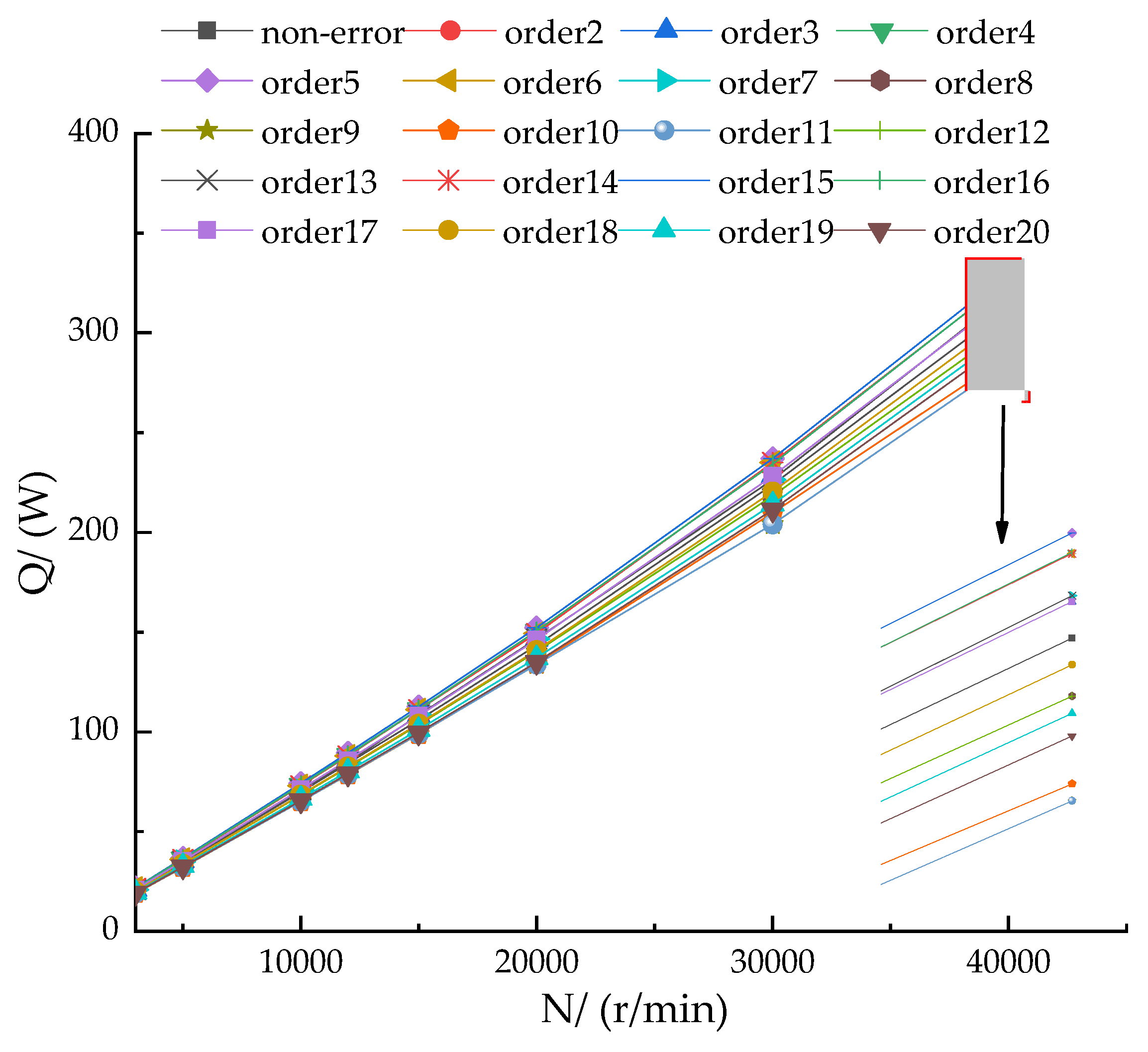

| Parameter | Value |
|---|---|
| Outside diameter (mm) | 55 |
| Inner diameter (mm) | 30 |
| Pitch diameter (mm) | 42.85 |
| Number of balls | 18 |
| Initial contact angle (°) | 16 |
| Spherical diameter (mm) | 5.5 |
| Width (mm) | 13 |
| Inner race groove diameter (mm) | 39.927 |
| Outer race groove diameter (mm) | 48.079 |
| Cage pocket hole diameter (mm) | 5.89 |
| Clearance (mm) | 0.15 |
| Cage width (mm) | 8.8 |
| Guide face diameter (mm) | 46.07 |
| Ceramic thermal conductivity (W/(m·K)) | 16.7 |
| Parameter | Value |
|---|---|
| Dynamic viscosity (Pa*s) | 0.055 |
| Coefficient of viscous pressure (×10−8 Pa−1) | 1.85 |
| Viscosity-temperature coefficient (°C−1) | 0.0315 |
| Coefficient of heat transfer (W/(m·K)) | 0.0966 |
| Condition | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Axial load Fa (N) | 300 | 500 | 200 | 400 | 600 |
| Radial load Fr (N) | 200 | 400 | 100 | 300 | 500 |
| Inner ring speed (r/min) | 6000 | 6000 | 10,000 | 10,000 | 10,000 |
| Elapsed time (min) | 10 | 10 | 10 | 10 | 10 |
| Parameter | Value |
|---|---|
| Outside diameter (mm) | 68 |
| Inner diameter (mm) | 40 |
| Pitch diameter (mm) | 53.98 |
| Number of balls | 20 |
| Initial contact angle (°) | 18 |
| Spherical diameter (mm) | 6.35 |
| Width (mm) | 15 |
| Inner race groove curvature radius (mm) | 3.49 |
| Outer race groove curvature radius (mm) | 3.3 |
| Cage pocket diameter (mm) | 6.73 |
| Cage pocket clearance (mm) | 0.19 |
| Cage width (mm) | 10 |
| Guide face diameter (mm) | 58.08 |
| Parameter | Value |
|---|---|
| Bearing Steel Modulus of Elasticity (N/m2) | 2.04 × 1011 |
| Holder elastic modulus (Polyamide, N/m2) | 2.32 × 109 |
| Bearing Steel Density (kg/m3) | 7805.6 |
| Cage density (kg/m3) | 1120 |
| Poisson’s ratio of bearing steel | 0.3 |
| Cage Poisson’s ratio | 0.34 |
| Heat conductivity coefficient of bearing steel (W/(m*K)) | 40.1 |
| Thermal expansion coefficient of bearing steel (1/°C) | 0.1224 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Ma, R.; Xue, Y.; Liu, Y. Study on Thermal Characteristics of Angular Contact Ball Bearings Considering Roundness Error. Lubricants 2024, 12, 43. https://doi.org/10.3390/lubricants12020043
Yu Y, Ma R, Xue Y, Liu Y. Study on Thermal Characteristics of Angular Contact Ball Bearings Considering Roundness Error. Lubricants. 2024; 12(2):43. https://doi.org/10.3390/lubricants12020043
Chicago/Turabian StyleYu, Yongjian, Ruixiang Ma, Yujun Xue, and Yonggang Liu. 2024. "Study on Thermal Characteristics of Angular Contact Ball Bearings Considering Roundness Error" Lubricants 12, no. 2: 43. https://doi.org/10.3390/lubricants12020043
APA StyleYu, Y., Ma, R., Xue, Y., & Liu, Y. (2024). Study on Thermal Characteristics of Angular Contact Ball Bearings Considering Roundness Error. Lubricants, 12(2), 43. https://doi.org/10.3390/lubricants12020043





