Application and Prospect of Wear Simulation Based on ABAQUS: A Review

Abstract

The finite element method(FEM) is a powerful tool for studying friction and wear. Compared to experimental methods, it has outstanding advantages, such as saving financial costs and time. In addition, it has been widely used in friction and wear research. This paper discusses the application of the FEM in the study of friction and wear in terms of the finite element modeling methods, factors affecting wear behavior, wear theory, and the practical application of the method. Finally, the latest progress of finite element simulation wear research is summarized, and the future research direction is proposed.

1. Introduction

Wear, an important factor affecting the service life and reliability of mechanical parts, is one of the most common topics in tribology, which is defined as the progressive loss of material due to the relative movement between the surfaces in contact [1]. Wear can make components lose the correct shape and size, leading to vibration, noise, and other undesirable effects. In addition, excessive wear may also cause early failure of parts, resulting in mechanical failure, economic losses, and safety hazards [2,3,4,5,6]. Therefore, the study of friction and wear behavior of materials is of great significance for improving machine performance and economic development.

The experimental method is the primary method in wear research. However, the cost of human, material, and financial resources required by the experimental method is high [1], and the experimental conditions are harsh. Wear simulation is an alternative technique for predicting wear characteristics based on experimental material properties. Among the simulation methods, the FEM is the most popular because of its wide applicability. FEM is used to simulate the wear characteristics under different conditions, which can effectively predict the wear characteristics. FEM is a powerful tool for wear prediction and parametric studies, which, compared to physical experiments, can provide a cost-effective solution for optimizing friction systems to reduce wear.

ABAQUS, one of the mainstream simulation software, has outstanding advantages in the nonlinear behavior of materials, such as plastic deformation, contact, and friction. ABAQUS can model the wear behavior of materials and consider the impact of wear on structural performance through coupling analysis. In addition, ABAQUS has powerful computing power and provides users with various subroutines. Based on the above advantages, ABAQUS has been widely applied in the field of wear research [7].

The purpose of this article is to review the latest methods and progress based on ABAQUS in friction and wear research. This article is divided into four parts: the establishment of finite element models, factors affecting wear behavior, wear theory, and application of wear simulation. On this basis, the future development direction of finite element friction and wear simulation research is proposed. The overall structure of this paper is shown in Figure 1.

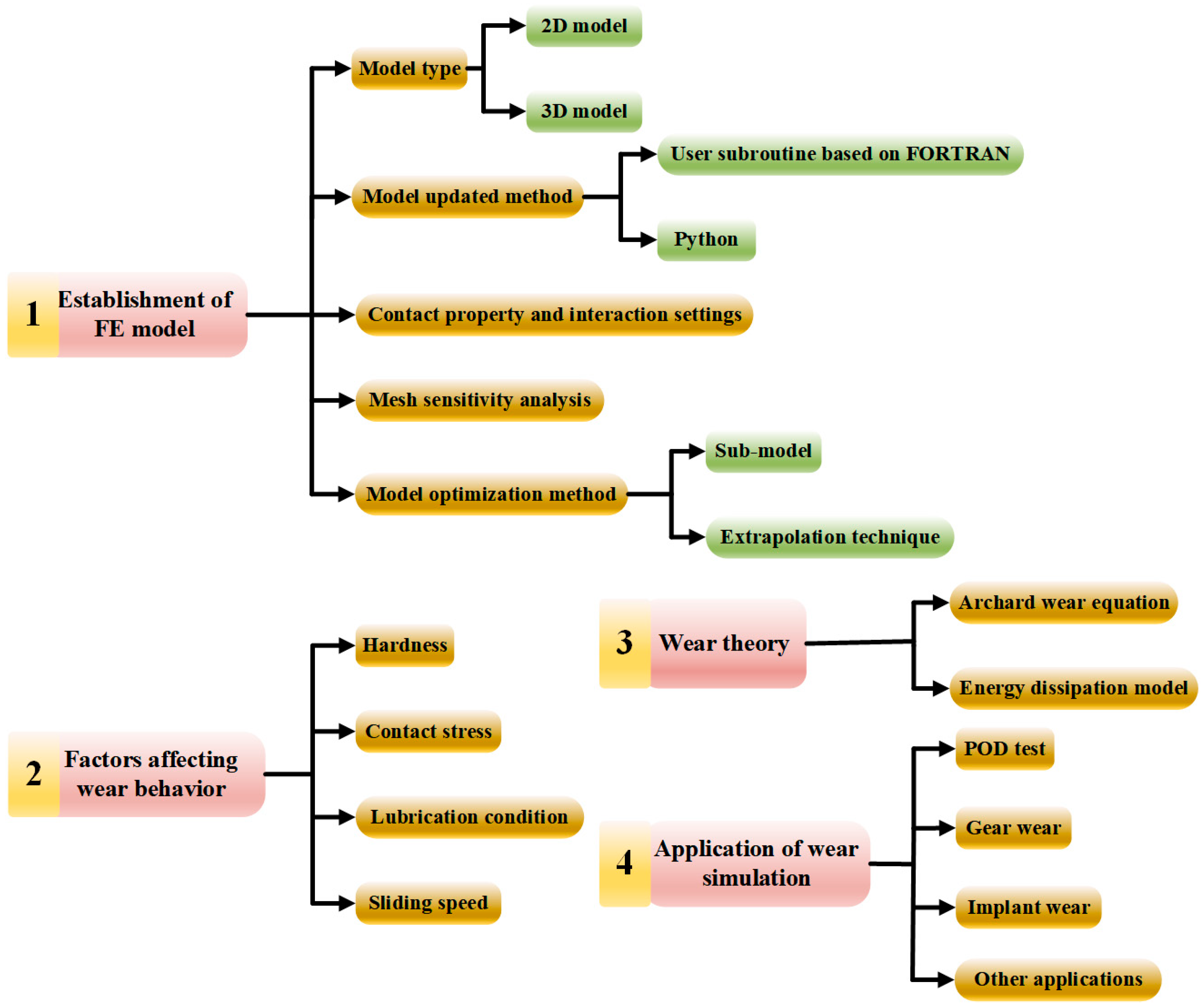
2. Finite Element Model

Establishing a finite element model is the first and crucial step in simulation. Factors such as the type of model, mesh division, and selection of element types directly affect the accuracy of the final results and the length of calculation time. On the premise of ensuring the accuracy of the calculation results, time cost is the biggest issue that scholars have focused on. A good finite element (FE) model can not only obtain accurate results but also have a short calculation time. The authors have summarized the research methods used in 34 articles related to wear simulation, as shown in

Table 1. Wear simulation research method statistics.

References	Model Type	Model Updating Method	Wear Theory	Model Optimization Method	Application
[8]	2D	UMESHMOTION	Energy dissipation model	Extrapolation technique	Fretting wear
[9]	2D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Service life prediction
[10]	2D/3D	Nope	Nope	Sub-model	Wear profile prediction
[11]	2D	UMESHMOTION	Energy dissipation model + Damage-coupled elastic–plastic constitutive model	Extrapolation technique	Service life prediction
[12]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Tribocorrosion
[13]	3D	Nope	Energy dissipation model	Nope	Wear mechanism auxiliary analysis
[14]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Wear profile prediction
[15]	3D	UMESHMOTION	Archard’s wear law	Sub-model	Fretting wear
[16]	3D	UMESHMOTION	Energy dissipation model	Extrapolation technique	Fretting wear
[17]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	POD tribometer wear prediction
[18]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Tire tread wear
[19]	2D	UMESHMOTION	Archard’s wear law	Nope	Casing wear
[20]	2D	UMESHMOTION	Archard’s wear law	Mesh and increment size optimization	Fretting wear
[2]	3D	UMESHMOTION	Power hardening law +Archard’s wear law	Extrapolation technique	Thermo-mechanical wear
[21]	3D	UMESHMOTION	Electrochemical equation + Archard’s wear law	Nope	Corrosive wear
[22]	3D	Python	Archard’s wear law	Nope	Orthopedic implant wear
[23]	3D	Python	Archard’s wear law	Nope	Orthopedic implant wear
[24]	2D/3D	Python	Usui’s tool wear model	Nope	Tool wear
[25]	3D	Python	Archard’s wear law	Extrapolation technique	POD tribometer wear prediction
[26,27]	3D	UMESHMOTION	Archard’s wear law	Sub-model	Orthopedic implant wear
[28]	3D	UMESHMOTION	Archard’s wear law	Sub-model	Orthopedic implant wear
[29]	2D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Pin wear prediction
[30]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	POD tribometer wear prediction
[31]	3D	UMESHMOTION	Archard’s wear law	Extrapolation technique	Dry sliding wear prediction
[1]	2D	UMESHMOTION	Archard’s wear law	Extrapolation technique	POD tribometer wear prediction
[32]	3D	UMESHMOTION	Archard’s wear law	Nope	Wear profile prediction
[33]	2D	UMESHMOTION	Archard’s wear law	Extrapolation technique	POD tribometer wear prediction
[34]	3D	UMESHMOTION	Archard’s wear law	Nope	Gear wear prediction
[35]	3D	UMESHMOTION	Archard’s wear law + shape functions and Newton–Raphson formulation	Nope	POD tribometer wear prediction
[36]	2D	UMESHMOTION	Energy dissipation model	Nope	Fretting wear
[37]	3D	UMESHMOTION	Energy dissipation model	Nope	Wear profile evolution
[38]	3D	UMESHMOTION	Energy dissipation model	Extrapolation technique	Wear simulation in automotive bush chain
[39]	3D	UMESHMOTION	Energy dissipation model	Extrapolation technique	Fretting wear

, and elaborated on model types, model updating methods, and model optimization methods. Figure 2 displays the frequency of commonly used research methods, including model updating methods and wear theories, as observed in 34 research papers.

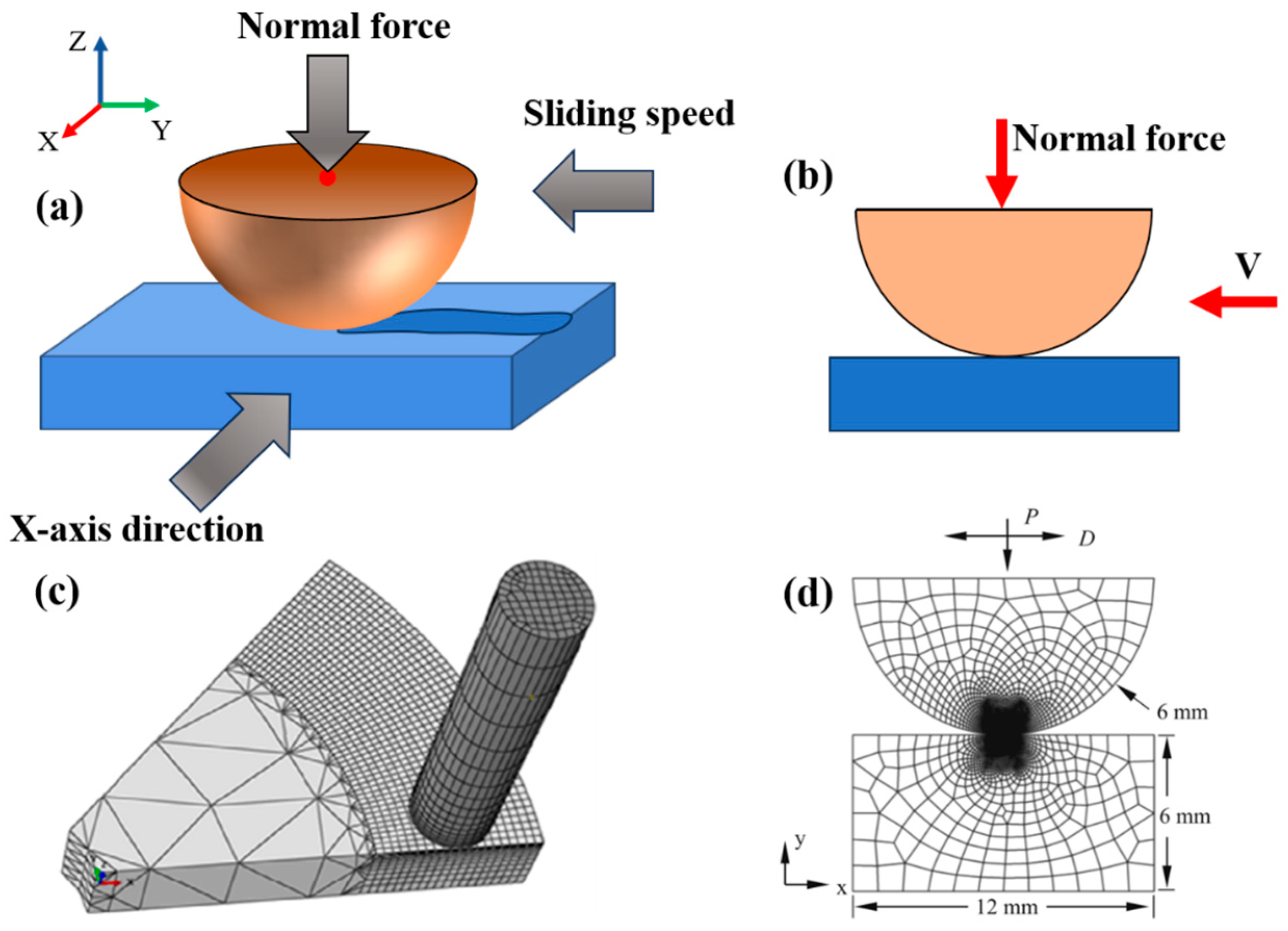
2.1. Model Type

2.1.1. 2D Model

Finite element models can be divided into two categories: 2D and 3D models. The types of FE models selected vary depending on the needs of practical problems. The 2D model is suitable for cases where there is no concern about the overall wear profile. Using this approach, the number of elements, nodes, degrees of freedom, and boundary conditions is reduced, thereby improving computational efficiency. In the field of friction and wear research, the pin-on-disk (POD) test is a typical example. The 2D and 3D FE models of the POD test are shown in Figure 3.

However, as shown in Table 1, a large number of studies used 3D FE models instead of 2D models. This is because, in practical engineering applications, many models are very complex, such as orthopedic implants, gears, and cutting tools. The 2D model cannot truly reflect its true structure and working conditions. Moreover, due to the simplification of conditions, the 2D model may cause significant computational errors. In this case, the 2D model is not applicable.

2.1.2. 3D Model

3D FE models have the advantage of more accurate calculation results. However, 3D FE models are not economical because of their complex geometric structure and long calculation time [15,17,41]. Hence, 3D FE models are often used in situations where the structure or the stress situation is complex and when the model cannot be simplified.

Sadeghi and Ahmadi [13] applied a 3D FE model to study the Hertz circular and line contacts. Compared to the results of fretting wear tests, the numerical results are well-confirmed. Bastola et al. [14] proposed a generalized 3D FEM to obtain the wear between the contacting components. The results were validated by the POD test.

From the above literature, it can be seen that the calculation results of the 3D FE models are more accurate. However, as mentioned at the beginning, the problem of long calculation time becomes more serious in 3D wear simulation. To solve this problem, scholars have proposed many solutions. Hegadekatte et al. [41] proposed an incremental implementation of Archard’s wear law, which greatly improved the computing efficiency. Bae et al. [15] used the sub-model method to reduce the complexity of the model and the significant computational time required for finite element analysis (FEA). Bose and Penchaliah [17] introduced a numerical wear simulation approximation technique based on the FEM to solve the problem. In addition, as shown in Table 1, the main model optimization methods include a substructure method and extrapolation technique, which will be discussed in Section 2.5.

2.2. Model Update Method

Wear is an accumulation process. The FEM is employed to simulate wear formation by updating the mesh model with moving nodes, enabling the determination of wear depth and volume for wear assessment. In ABAQUS-based wear simulation, two primary methods are utilized to update the mesh model: user subroutine based on programming languages, FORTRAN and Python. This section will elaborate on these two methods.

2.2.1. User Subroutine Based on FORTRAN

ABAQUS provides users with various subroutines, with the most commonly used in wear simulation research being the UMESHMOTION subroutine, which can be used to simulate the movement of nodes in an FE model [42]. During the wear process, as the number of wear cycles increases, material loss also increases, and the actual contact situation also changes. In order to simulate the actual wear process and obtain correct calculation results, it is necessary to continuously update node and mesh information during wear simulation. The UMESHMOTION subroutine provides the conditions for this process [43,44]. The process of wear simulation is shown in Figure 4. The determination of the initial parameters is a key step to ensure the accuracy and efficiency of the FE model, particularly for the parameter “$\mathsf{\Delta }N$”(step sizes). To tackle this problem, McColl proposed a method that has been widely applied in wear simulation [14,20].

In addition, the UMESHMOTION subroutine is always combined with the ALE (Arbitrary-Lagrangian-Eulerian) technique. The ALE technique is an adaptive mesh method in ABAQUS [42]. By incorporating the attributes of unadulterated Lagrangian and Eulerian examination, it permits the mesh to shift independently of the material [1]. This technique can automatically adjust the mesh according to the degree of distortion in the analysis of materials with large deformation or loss, ensuring high quality of the mesh and improving calculation accuracy and model stability. In wear simulation, UMESHMOTION is used to move the contact node by the amount of local wear increment. As the nodes move, the contact mesh model is updated, and preparations are made for the node update after the next wear increment. The movement of nodes may cause mesh distortion, thereby affecting the FEM results. This mesh distortion can be prevented through the ALE technique [1,9,45].

The majority of examples in Table 1 used the Archard wear equation to calculate the wear depth, which does not mean that the UMESHMOTION subroutine can only be bound to Archard’s wear equation. The UMESHMOTION subroutine only serves the purpose of moving nodes. The distance and mode of movement of nodes are determined by the wear model used. The Archard wear equation is only one of the methods for calculating the distance of node movement. The UMESHMOTION subroutine can also be used in conjunction with other theoretical models. Chemical corrosion is an important factor affecting wear [46], Fallahnezhad et al. [21] combined Archard’s wear law with chemical equations to study fretting corrosion wear of CoCr. Temperature is an important factor affecting wear [47,48]; Gan et al. [2] took into account the effect of temperature on wear by combining heat transfer analysis with Archard’s wear law. After verification through POD experiments, comparative analysis shows that friction heat and plasticity have a substantial effect on the progression of wear. Li et al. [49] proposed a wear equation, which combines the hydrodynamic lubrication wear with the thermochemical erosion to study the wear of artillery barrels under hydrodynamic friction. In addition, as shown in Figure 2, the energy dissipation model can also be used in conjunction with the UMESHMOTION subroutine to simulate wear.

2.2.2. Python

Except for the UMESHMOTION subroutine, Python is also an important way to update node information. By using Python scripts, the ABAQUS/CAE graphical user interface can be bypassed and the ABAQUS kernel can be directly operated to modify the finite element model and related parameters [42]. Figure 4 shows that the calculation process is similar to the UMESHMOTION subroutine. However, as shown in Table 1 and Figure 2, most studies apply the UMESHMOTION subroutine instead of Python. Compared to the UMESHMOTION subroutine, Python has lower accuracy in FEA. This is because the UMESHMOTION subroutine is usually used in conjunction with the ALE technique, resulting in good mesh quality. However, when using Python scripts, the mesh quality is poor, leading to increased stress concentration and convergence issues [50].

2.3. Contact Property and Interaction Settings

The setting of contact attributes and interactions is one of the important links to ensure the correctness of the solution. In ABAQUS, the contact surface interaction is established using the contact pair approach, which employs the master–slave algorithm to implement the contact constraints [20]. In addition, surface-to-surface contact discretization is utilized instead of node-to-surface contact discretization. When the contact geometry is well depicted, the surface-to-surface discretization produces more accurate stress and pressure outcomes [14]. Arbitrary separation, sliding, and rotation of the contact surfaces are allowed by the finite-sliding contact tracking approach [42]. The definitions of tangential and normal contact properties are needed. For the tangential behavior, constant penalty friction formulation is utilized with the coefficient of friction tested in the experiment. For normal behavior, “Hard” contact pressure-overclosure is applied. In addition, two constraint enforcement methods, augmented Lagrange and penalty, are selected [14]. Compared with augmented Lagrange, a lower error in the maximum contact pressure can be obtained by the penalty method [9]. However, the comparable pressure distribution throughout the contact region can be obtained by the augmented Lagrange method [14]. Both constraint enforcement methods can be applied in simulation.

2.4. Mesh Sensitivity Analysis

Meshing is also one of the important links to ensure the accuracy of the results. In general, a fine mesh is needed in the contact area. However, as the elements increase, the calculation cost will also increase, and the accuracy does not necessarily increase [14]. Therefore, mesh sensitivity analysis is of the essence, which plays a role in determining the size and number of elements [20]. Based on the literature survey, the Hertz formula is always used to validate the worn model [9,14,20,51].

The Hertz contact pressure distribution varies with ‘x’ as:

$$p(x)=p_0\sqrt{1-\frac{x^2}{a^2}}$$

(1)

where $a$ and $p_0$ are the half-width of the contact region and the maximum contact pressure, respectively, given by the following formulas:

$$a={\left(\frac{4PR}{\pi E^{*}}\right)}^{1/2}$$

(2)

$$p_0={\left(\frac{P{E}^{*}}{\pi R}\right)}^{1/2}$$

(3)

where P is the applied normal load and $E^{*}$ is the composite modulus of two contacting bodies. $E^{*}$ and R are given by:

$$E^{*}={\left(\frac{1-{\left(v^f\right)}^2}{E^f}+\frac{1-{\left(v^c\right)}^2}{E^c}\right)}^{-1}$$

(4)

$$R={\left(\frac{1}{R^f}+\frac{1}{R^c}\right)}^{-1}$$

(5)

where $v^f$, $v^c$ and $E^f$, $E^c$ are the Poisson’s ratios and the elastic modulus of flat and cylindrical bodies, respectively. $R^f$ and $R^c$ are the radii of the contacting surfaces.

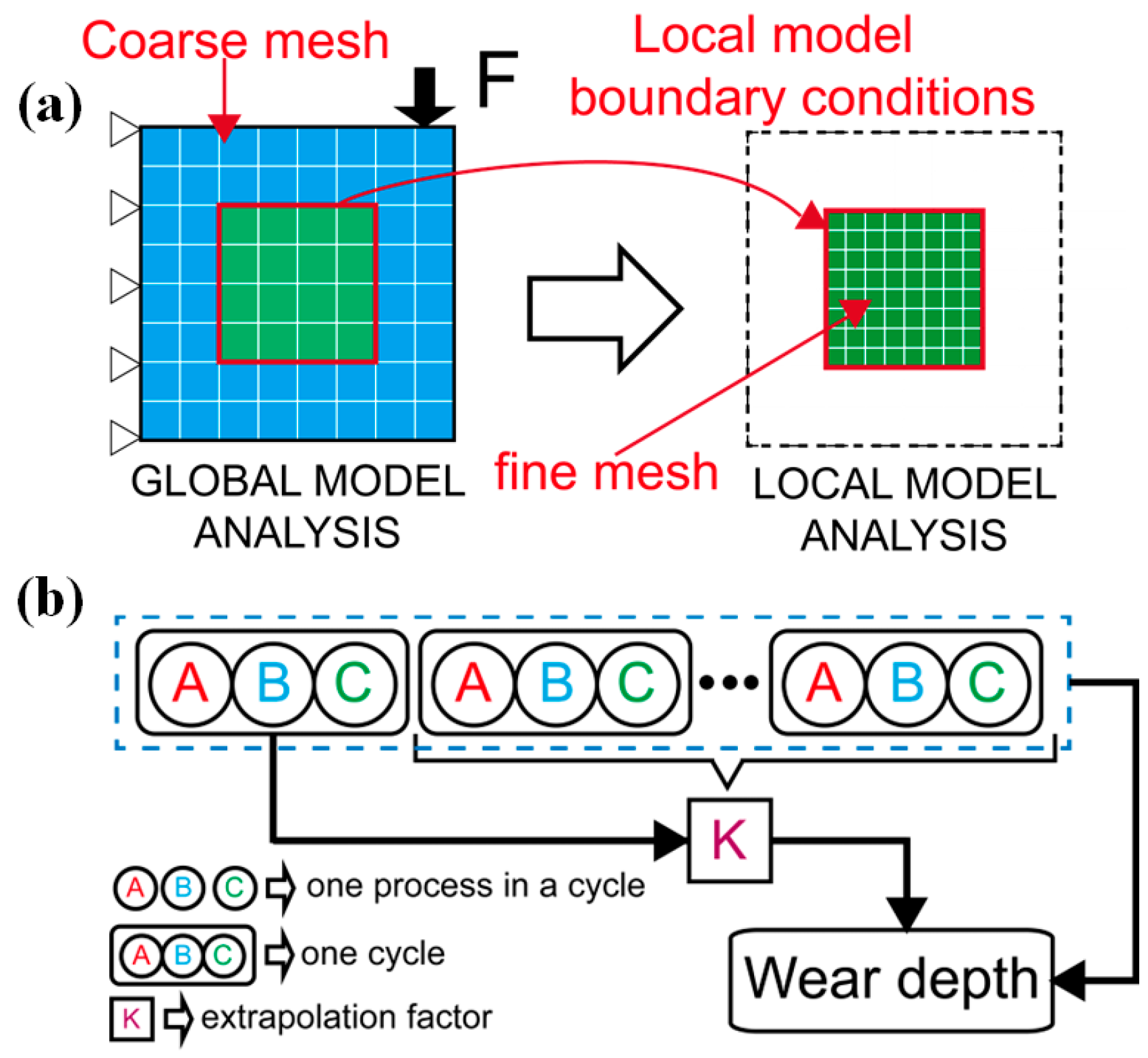
2.5. Model Optimization Method

The effectiveness and computational efficiency of a model are the two most concerned issues in FEA. With regard to ensuring the effectiveness of the model, the computational efficiency of the finite element model is the primary concern of scholars because faster calculation speed will bring better economic benefits. Currently, common methods for solving computational time problems include the sub-model method and extrapolation method. This section will elaborate on the two aspects mentioned above.

2.5.1. Sub-Model

The main idea of the sub-model method is to combine the global coarse model of the entire system with the local fine model of key regions, to minimize computational costs and provide accurate numerical results. When conducting finite element analysis on large and complex structures, the order of the equation and the computer resources required for calculation can be reduced, resulting in an improvement of the solving efficiency. Therefore, the sub-model method is suitable for wear analysis of large and complex structures. The program for the wear sub-model mainly consists of three steps [52], which are shown in Figure 5a. The first step is to determine the boundary conditions required for creating a detailed local model based on the initial rough FE global model. After checking the convergence of the quantity to be transmitted, the next step is to create the local model with the appropriately defined mesh. Eventually, the local model, to which boundary conditions from the global model are applied, is used to conduct the wear simulation. The research of Curreli et al. [52,53] on the substructure method showed that the sub-model method can greatly reduce the computational cost of FE wear simulation. In particular, in the biomedical field, complex finite element models result in high time costs [26]. Substructure technology provides an effective solution.

Using total hip arthroplasty (THA) as an example, Shankar et al. [26,27] applied this method to study the contact pressure and wear in hip joint prostheses made of metal, ceramic, and polycrystalline diamond materials, as well as the wear behavior of silicon nitride and Ti6Al4V alloy under the influence of five different biological lubricants during various gait activities. Prasad and Ramkumar [28] employed the sub-model method to investigate the wear performance of ceramic hip joint implants under dynamic edge loading conditions. The sub-model technique improves the computational efficiency of FEA in the above studies.

2.5.2. Extrapolation Technique

The extrapolation technique is one of the most commonly used methods, with the main idea involving the assumption that the state of multiple wear cycles is the same as the state of one cycle [52]. An extrapolation factor is introduced to calculate the wear depth after several wear cycles. As shown in Figure 5b and using Bose’s study as an example [9], each FEM wear cycle consists of 4 steps. In each cycle, the pin moves a sliding distance increment of 2 mm, which is called step size. Increasing the step size will lead to a decrease in the stability of the wear simulation. Therefore, in order to simulate a sliding distance of 200 m without using extrapolation techniques, 100,000 FEM cycles and 400,000 steps are required. Assuming a constant contact pressure in the extrapolation process, using an extrapolation factor of 100, the computer only needs 1000 FEM cycles and 4000 steps to simulate a sliding distance of 200 m, thus improving the computational efficiency of the finite element model and reducing time costs. The extrapolation factor depends on the applied load [1]. However, it should be noted that a large extrapolation factor can affect the stability and accuracy of the model [9,29,30,31], while a small extrapolation factor will result in higher utilization of computer resources. Even if an appropriate extrapolation size is selected at the beginning of the simulation, different sizes of extrapolation factors may be required at different stages of the simulation to maximize resource utilization [52]. Therefore, the key to the extrapolation technique lies in selecting the appropriate extrapolation factor to balance computational efficiency and simulation accuracy. According to current studies, there is no uniform method for determining the extrapolation factor.

Bose and Ramkumar [1] improved the extrapolation technique. They found that in the wear model of the POD model, point contact begins, and the contact stress is high. As the contact area increases, the contact pressure gradually decreases, and using a constant extrapolation factor will result in a large error. After several wear cycles, the contact pressure begins to stabilize, and at this moment, using extrapolation techniques will have a better effect. On this basis, they proposed the linear extrapolation technique. In comparison to the constant extrapolation technique, this method uses a small extrapolation factor at the beginning of the cycle, and as the number of wear cycles increases, the extrapolation factor also increases, demonstrating better efficiency and accuracy in wear simulation. The extrapolation method can be used in general wear simulation.

3. Factors Affecting Wear Behavior

Many factors affect the wear behavior, and the influence of the influencing factors on the wear is often not a single effect; there is an interaction between the influencing factors. This section will cover four aspects: material hardness, contact stress, lubrication, and sliding speed.

3.1. Hardness

Hardness is an important factor affecting the material wear rate. In general, the higher the material hardness, the stronger its surface wear resistance. When two material surfaces come into contact, they are subjected to stress and friction from the other surface. If the surface hardness is high, it often exhibits strong resistance to scratches and indentation, and the degree of wear caused by interaction between contacting surfaces is also small, thereby reducing the wear rate. On the contrary, if the surface hardness of the material is low, the surface is susceptible to scratches and indentation, leading to microstructure damage and material loss, resulting in a higher wear rate. The research of Rigney [54] shows that severe wear occurs when the hardness ratio range of the tested pin to disc is less than or equal to 1.0, and mild wear occurs when the hardness ratio is greater than 1.0. Lemm et al. [55] studied the effect of hardness in an AISI Type O1 steel-on-steel fretting contact. 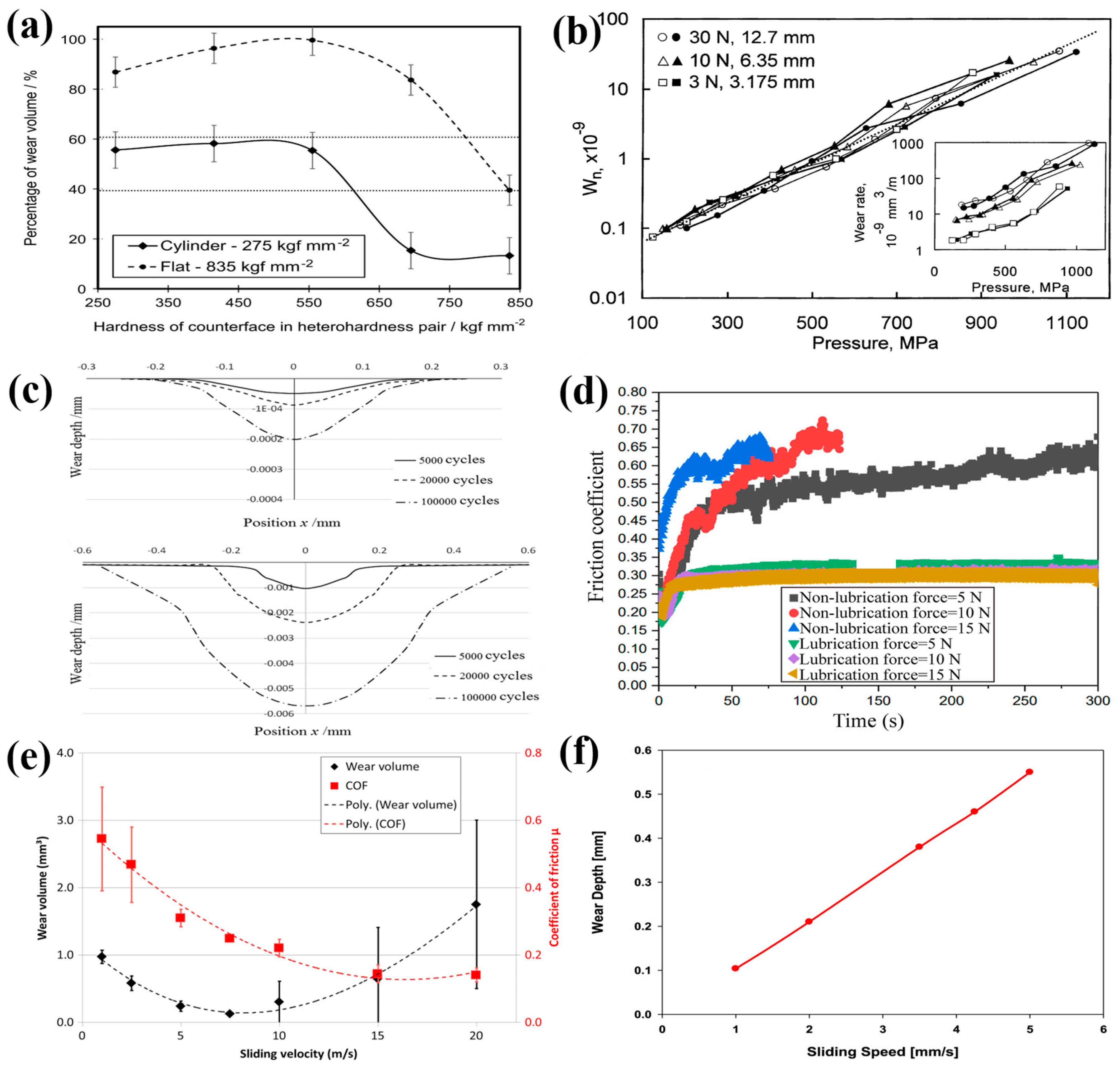As shown in Figure 6a, the wear rate initially increases and then decreases with increasing hardness.

3.2. Contact Stress

Contact stress has a greater impact on wear compared to other factors, and higher contact stress increases shear forces between contacting surfaces, thereby exacerbating wear. When the contact stress exceeds the strength limit of the material, it can cause plastic deformation and peeling on the surface of the material, further exacerbating wear. Ravikiran and Jahamir [56] studied the effects of contact pressure and load on the wear of alumina. As shown in Figure 6b, the result indicates that the wear rate increases with the increase of contact pressure, regardless of the applied load used in the test. Guo et al. [61] studied the effect of contact stress on the cyclic wear behavior of ceramic restorations. The result shows that the high contact stress promotes the veneer porcelain to enter a severe wear stage. On the contrary, lower contact stress can easily keep the veneered porcelain in a stable wear stage, thereby delaying the arrival of a severe wear stage. The contact area affects wear by affecting contact stress. Under the same load conditions, the larger the contact area, the smaller the contact stress, thereby reducing wear.

3.3. Lubrication Condition

Lubrication is a common method to reduce wear as lubricants can form a thin film between the surfaces of two objects in contact, avoiding direct contact, and thus reducing wear [62]. Lubricants can also absorb and dissipate the heat generated by friction between two contact objects, reducing the impact of temperature on material properties and thereby reducing material wear. Qin et al. [57] compared the simulated geometric shape of lubricated frictional contact and the effect of lubricants on friction and wear with experimental results. The result shown in Figure 6c indicates that oil lubrication can effectively reduce microwear and friction in low flexible contact while having little effect on high flexible contact. Zhao et al. [63] proposed that under mixed lubrication conditions, increasing the viscosity of lubricants can reduce the degree of wear on rough surfaces as it can reduce the direct contact area of rough surfaces. Cao et al. [58] established a wear model for all-metal progressive cavity pumps (AMPCP) based on Archard’s wear theory and studied the effects of factors such as rotational speed, lubrication, and clearance on wear behavior. As shown in Figure 6d, lubrication can significantly reduce wear and prolong the service life of AMPCP.

3.4. Sliding Speed

The impact of sliding speed on wear varies in different situations. Khader et al. [59] established a wear model for dry sliding contact between silicon nitride and nickel-based alloys. As shown in Figure 6e, the wear rate decreases with an increase in sliding speed, reaching a minimum value. Beyond this threshold, wear escalates as the sliding speed increases. The same behavior was also observed in the relationship between wear and friction. Okonkwo et al. [64] conducted a study on the influence of sliding speed on the wear of steel and tool steel pairs. The results show that at all sliding speeds, adhesive wear dominates on the surface of tool steel, with the highest amount of adhesion occurring at the slowest sliding speed. Moreover, temperature has a significant impact on wear, and a slight increase in contact interface temperature can lead to a significant change in wear rate. Arjmandi et al. [60] conducted parameterized research on the developed wear model to investigate the impact of key parameters on wear rate. The result shown in Figure 6f indicates that under higher normal loads and sliding speeds, the wear rate of three-dimensional woven textiles increases, but the change in friction coefficient has little effect. Chowdhury et al. [65] studied the effects of sliding speed and normal load on the friction and wear performance of aluminum. The study showed that the friction coefficient decreases with the increase of sliding speed and normal load, while the wear rate increases with the increase of sliding speed and normal load. Maintaining sliding speed and normal load at an appropriate low level helps to reduce wear.

4. Wear Theory

Wear is always one of the most complicated and difficult problems in tribology because there are numerous factors that affect wear, such as load, speed, temperature, surface roughness, mechanical properties, and microscopic flaws. Currently, there are over 300 wear-related equations [66], most of which are tailored to a specific situation and cannot be applied to other situations. These theories can be divided into two categories: mechanistic and phenomenological [14]. The mechanistic models aim to explore the potential mechanism, but multiple wear mechanisms occur simultaneously in a practical matter. Furthermore, the mechanistic models are also limited to specific length scales. The phenomenological models are easier, presented in mathematical equations based on the contact mechanics variables [67]. In the field of wear simulation based on FEM, the phenomenological type is preferred because it can be localized and provides an acceptable level of accuracy and reliability in tracking the wear process [67]. In this section, two commonly used wear equations are presented.

4.1. Archard’s Wear Law

Archard’s wear law is probably the most famous theory of wear analysis. This equation relates volume loss, normal load, sliding distance, and material hardness through a dimensionless coefficient, which lays the foundation for the establishment of wear simulation models. Archard deduced the relationship between the material wear volume (V), sliding distance (S), dimensionless wear coefficient (k), normal load ($F_N$), and hardness of the softer material (H) [41,60] in the two contacting materials, expressed as [68]:

$$V=k\cdot \frac{F_N}{H}\cdot S$$

(6)

It can be seen from the formula that the wear volume is proportional to the normal load, inversely proportional to the material hardness, and proportional to the sliding distance.

In the field of wear simulation, in order to simulate the evolution of the contact surface with the wear cycle, the wear depth at each contact node needs to be determined. Therefore, Equation (6) needs to be deformed. For very small contact areas ($\mathsf{\Delta }A$), the relationship between the incremental wear depth ($dh$) and the incremental slip distance ($dS$) can be expressed by dividing the left and right sides of Equation (6) by the contact area ($\mathsf{\Delta }A$):

$$\frac{dV}{\mathsf{\Delta }A}=k\cdot \frac{F_N}{H\cdot \mathsf{\Delta }A}\cdot dS$$

(7)

In this formula, $\frac{dV}{\mathsf{\Delta }A}$ is the wear increment $dh$, $\frac{F_N}{\mathsf{\Delta }A}$ is the local contact stress $p$, and $\frac{k}{H}$ is replaced by $k_D$; then, the above formula can be expressed as:

$$dh=k_D\cdot p\cdot dS$$

(8)

where $k_D$ is dimensional local wear coefficient, which is determined by multiple factors including contact size [69], temperature [66], sliding condition [70], and pressure [71]. There is no one explicit approach to obtain the value of $k_D$ during the wear process [14,20]. In wear simulation, the wear coefficient is always considered as a constant [8] and obtained from experimental results. The equation is given by:

$$k_D=\frac{V}{S\cdot F_N}$$

(9)

Archard’s wear equation provides a theoretical basis for node updates in wear simulation, and as shown in Table 1 and Figure 2, and it is now widely used [67,72,73,74,75,76]. However, as an empirical formula obtained from experiments, it has a weak theoretical foundation and cannot fully reflect actual wear behavior. The disadvantages are shown below [77,78,79,80]:

• Fatigue, corrosion, oxidation, and other wear mechanisms are ignored.
• The effects of temperature and lubrication on wear are not considered.
• The wear coefficient is set to constant in the simulation.
• The effect of transverse shear stress is not taken into account.

In view of the above shortcomings, many scholars have improved Archard’s wear theory. Most improvement methods are coupled with the addition of related factors to the analysis. For example, chemical corrosion [21], temperature [2,81,82], and Archard’s wear law are combined for coupling analysis.

For the effect of temperature, Yin et al. [83] proposed a comprehensive modeling approach to predict the thermomechanical tribological behaviors. In view of the lack of consideration of transverse shear stress, Wang [84] used the POD test and hip simulator wear test results to establish a wear model dependent on cross shear and contact pressure. However, for conventional non-crosslinked polyethylene, this model is not suitable, because applying the model without crosslinking would result in the prediction of infinite wear. Using a POD test, Kang et al. [85] showed that cross-shear ratio (CS) has significant effects on wear coefficient and established a wear model including cross-shear effect. In addition, Kang et al. [86] incorporated cross-shear motion and wear factors related to contact pressure into Archard’s law to establish an independent computational wear model to predict hip polyethylene wear. Goreham-Voss et al. [7] proposed an improved model considering the influence of transverse shear motion on the main molecular orientation of polyethylene joint surfaces. Shu et al. [50] developed an improved Archard’s wear theory by considering CS for wear prediction of total knee replacements.

4.2. Energy Dissipation Model

The energy-based wear theory was proposed by Fouvry et al. [87], which relates material volume loss with dissipated interfacial shear energy and considers the influence of interfacial shear work as an important wear parameter. The energy dissipation method is expressed as follows:

$$V=\alpha {\displaystyle \sum E_d}$$

(10)

where V, α, and $E_d$ represent the wear volume, energy wear coefficient, and accumulated dissipated energy, respectively. The factors affecting the value of α are the same as those determining the wear coefficient in Archard’s wear equation [67]. $E_d$ is given by:

$$E_d=Q\cdot S$$

(11)

where Q and S represent the shear force and the sliding distance. Based on Coulomb’s friction law, $E_d$ is given by:

$$E_d=\mu \cdot P\cdot S$$

(12)

where μ and P represent the coefficient of friction and the normal load. According to the equations from (10) to (12), the local wear depth for each wear cycle can be described as [39]:

$$dh(x)=\alpha \cdot q(x)\cdot ds(x)$$

(13)

where q is local shear stress and ds is the local sliding distance.

In the numerical simulation study of fretting wear, the energy wear model is considered better than the Archard-based approach, because it allows for the use of a single wear coefficient across a variety of fretting load-stroke combinations, encompassing both partial slip and gross sliding regimes [11,88,89]. Changes in the friction coefficient can be considered during the wear process [39]. Moreover, as shown in Equations (6) and (10), the wear coefficient in Archard’s wear equation equals the wear coefficient in the energy method divided by the coefficient of friction. Therefore, once one of them is known, both wear equations can be utilized in wear simulation [67]. Nowadays, many scholars use the energy dissipation model for wear simulation. Shen et al. [11] established a coupled damage elastoplastic constitutive model and developed a method to predict fretting fatigue life. The study used the energy dissipation model to simulate the evolution of contact geometry. Li et al. [36] introduced the friction coefficient as a function of fretting cycle numbers in numerical simulations, combining the energy consumption model with an adaptive mesh method to establish a wear model considering variable friction coefficients. Zhang et al. [37] proposed a finite element model for thread surface wear based on the energy dissipation model, simulating the phenomenon of self-loosening of bolted connections under transverse loads. Tandler et al. [38] simulated wear in automotive chain drive systems after high mileage using the energy dissipation model, and a comparison of the simulation data with experimental data demonstrated the effectiveness of the established model. Imran et al. [39] utilized the energy wear theory to establish a 3D FE model for simulating fretting wear in steel wire ropes used in coal mining processes. The influence of contact parameters on the fretting wear process during fretting cycles was examined.

5. Application of Wear Simulation

Wear simulation provides a dynamic representation of the changes in various parameters throughout the wear process. By leveraging the visualization capabilities of ABAQUS, the wear process can be vividly illustrated. This allows researchers to analyze wear behavior by referencing both the computational results and the actual conditions under which wear occurs. Utilizing wear simulation technology for analyzing wear mechanisms offers several distinct advantages:

(1)

Using wear simulation before physical experiments allows for early assessment of wear mechanisms, enabling product optimization and reducing the need for extensive testing and improvements.

(2)

Compared to physical experiments, wear simulation is a cost-effective, fast, and adaptable method. It allows for multiple calculations with adjustable parameters based on real working conditions.

(3)

Wear simulation, compared to physical experiments, provides an intuitive visualization of the distribution of contact stress, displacement, temperature, and more, making it easier for researchers to analyze.

As can be seen from Table 1 and

Table 2. Articles related to wear simulation applications.

Reference	Application Field	Year	Aim
[90]	Service life prediction	2023	The study proposed an approach based on FEM to predict the electrical contact resistance endurance of AgNi10 alloy.
[91]	Service life prediction	2015	The study predicted thrust bearing run-out, with the intention of using linear and non-linear wear models to predict bearing failure/life.
[4]	Service life prediction	2021	The study introduced a combined 3D wear and fatigue numerical method for fretting issues in ultra-high-strength steel wires.
[92]	Service life prediction	2022	The study analyzed the friction and wear conditions of dynamic and static metal wires inside the metal rubber.
[3]	Service life prediction Wear mechanism auxiliary analysis	2018	The study established a 3D FM model to simulate the failure process of self-lubricating spherical plain bearings under swinging wear conditions.
[5]	Service life prediction Wear mechanism auxiliary analysis	2022	The study investigated the fretting fatigue mechanism of WC-12Co coating through experiments and simulations.
[93]	Wear profile prediction	2023	The study aimed to predict the wear of a tenon connection structure by FEM.
[28]	Wear profile prediction	2023	A new fundamental FEM model was developed to predict wear for ceramic hip replacement bearings.
[94]	Wear mechanism auxiliary analysis	2009	The study examined the impact of normal load and attack angle of a conical indenter on wear mechanisms.
[88]	Wear mechanism auxiliary analysis	2023	The study aimed to explore the wear mechanism of Inconel 690 alloy and 403 stainless-steel anti-vibration strips.
[95]	Wear mechanism auxiliary analysis	2022	The impact of adding 3 wt.% of Y on the wear characteristics of ZK60 extruded alloy was studied.
[96]	Wear mechanism auxiliary analysis	2022	The study investigated the influence of loading frequency on fatigue performance and uncovered the wear mechanisms of bolted joints.

, wear simulation is widely used in wear research, which can be mainly divided into three aspects: service life prediction, wear profile prediction, and wear mechanism auxiliary analysis. This section will elucidate the application of wear simulation in three areas: POD test, gear wear, and wear of orthopedic implants.

5.1. POD Test

Fretting wear, resulting in component failures and financial loss, is defined as a surface degradation process when small amplitude oscillatory sliding occurs between two contacting surfaces [69]. To estimate fretting wear, the POD test, which is an essential approach to estimating the wear performance of a specific material, is always applied in fretting wear research. However, as previously mentioned, the cost of the test is high. The FEM, which has been widely used in POD simulation, has a distinct advantage in reducing cost [97]. This section will discuss the application of POD simulation in fretting wear.

The POD simulation in fretting wear is a typical case, as it shows the basic architecture of wear simulation, as shown in Figure 7. First, the FE model is established according to the test conditions. Then, the FE model is validated by the Hertz formula to ensure accuracy [9,98]. The outputs such as wear depth, wear rate, and wear profile are obtained in the final step. To track the wear process in fretting wear, two wear equations, Archard’s wear law and the energy dissipation model [67], are implemented through the UMESHMOTION subroutine. Since the FE model of the POD test is simple, the sub-model method is rarely applied. On the contrary, the number of wear cycles is generally large, and the extrapolation technique is always utilized to enhance the efficiency [1,14].

Wear profile prediction and wear mechanism analysis are the primary applications. McColl et al. [20] presented a 2D FE model based on Archard’s wear equation for fretting wear simulation. The study showed that measured and predicted wear profiles are well confirmed under the low normal load situation. However, under the high normal load condition, the results were overestimated. The same conclusion was obtained by several other studies [17,30,33]. McColl attributed this phenomenon to the fact that changes in the wear coefficient were not taken into account [20]. Despite this drawback, the depth of wear and the changing trend of the wear profile are generally consistent with the experimental results. The energy dissipation model is considered superior to the Archard wear equation [8,88]. Li et al. [97] presented a method based on the energy law to study the fretting wear of the double rough surfaces. The model was validated by Hertz’s theory and experiments. Zhang et al. [98] compared the significance of the Hertzian assumption to that of a rounded punch-on-flat in terms of fretting behavior. The model was validated by Hertz’s theory and experiments. Cai et al. [99] applied the energy dissipation model to simulate fretting wear under the ball on flat contacting conditions. The research demonstrated that the combined effect of the normal load and amplitude had an impact on the contact pressure and shear stress, which in turn influenced the kinetic behavior, wear behavior, and evolution of worn surfaces. Li et al. [8] studied the fretting wear performance of the Inconel 718 alloy-based energy wear approach. In addition, Bastola et al [14] showed that there is no FE method for describing the wear of two 3D bodies simultaneously using adaptive mesh. They presented a method to predict wear on both contact surfaces.

5.2. Gear Wear

Gears, integral to mechanical transmission, facilitate power and motion transfer between parallel and non-parallel axes. With their precise transmission ratio, extensive power range, high efficiency, and smooth operation, they find widespread use in diverse power transmission domains. Wear, a primary cause of gear failure, occurs on the tooth contact surface due to friction between meshing gears, excessive load, and unsuitable working conditions. Excessive wear can distort the gear tooth shape, resulting in increased noise, vibration, and reduced transmission efficiency. The reduction in the contact area between meshing gears exacerbates gear force conditions, increases contact stress, and accelerates other gear failure modes. Hence, gear wear research holds significant importance.

Numerous studies about gear wear in existing research are predicated on Archard’s wear theory [100,101,102,103,104,105]. As shown in Figure 8b, Xue et al. [103] used Archard’s wear law to calculate the slip distance of an aero-engine’s involute spline coupling. The typical simulation flow in gear wear simulation studies is shown in Figure 8a. For wear simulation, the ongoing gear meshing process is broken down into discrete steps, and the points of contact on the tooth profile are considered as the elastic contact of two cylinders based on Hertz’s contact theory [106,107]. Subsequently, the contact pressure is determined, and the wear at each discrete point on the tooth surface within the wear cycle is computed.

In gear wear calculations, factors such as positional tolerances and installation errors can modify the contact path, leading to accelerated tooth surface wear [109]. Therefore, gear tolerance modeling is crucial. Tooth Contact Analysis (TCA) is conducted to determine the contact path and meshing state of the gear pair. However, traditional TCA can lead to high nonlinearity when errors exist in all six degrees of freedom, reducing efficiency. To mitigate this, the Small Displacement Torsor (SDT) concept has been introduced in TCA [110,111]. Sun et al. [108] conducted an analysis of the wear law of the tooth surface by integrating Archard’s wear law with the SDT theory, tolerance theory, and TCA. Their approach involved the use of modeling and numerical simulation methods (Figure 8c). It was found that standard assembly of the gear pair results in an evenly distributed contact ellipse with a complete shape. However, installation errors can cause the contact area to become skewed, resulting in an incomplete contact ellipse and a smaller contact area, which leads to edge contact. As shown in Figure 8d, installation error results in a doubling of the contact surface stress. The results of their research can serve as a guide for the design and installation of a small module gear drive system.

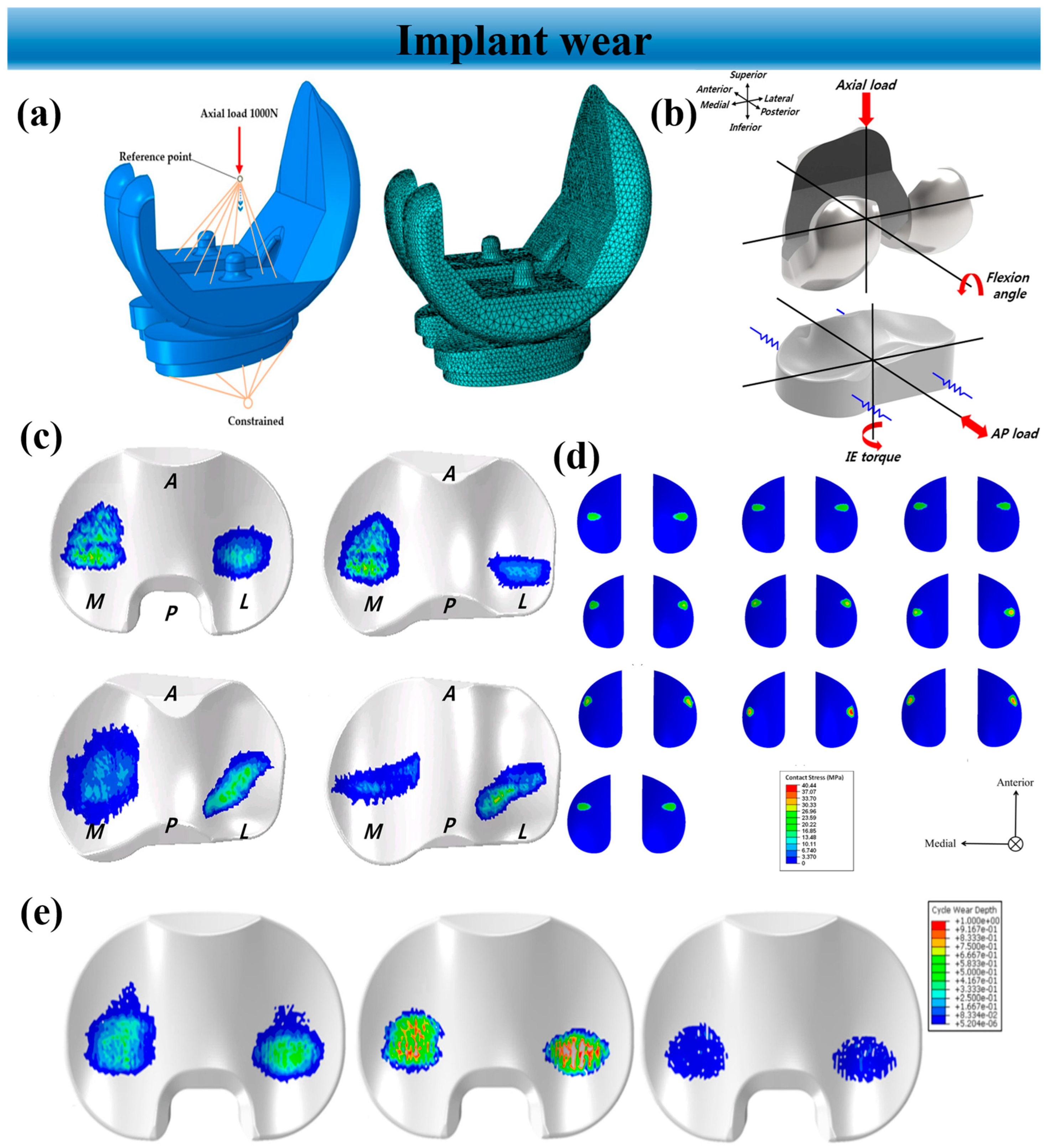
5.3. Implant Wear

Joint replacement technology, a pivotal treatment for orthopedic diseases, has revitalized patients immobilized by conditions like arthritis and fractures. With the maturation of this technology and a growing demand, surgical cases are on the rise. Despite its benefits, the technology has limitations, with implant wear being a primary concern. Excessive wear can lead to implant-bone loosening, patient discomfort, increased risk of revision surgery, and potential local inflammation due to wear debris [22,71,112,113,114,115]. Hence, implant wear research is crucial. Wear simulation technology offers a novel approach to study implant friction wear, outperforming physical experiments in certain aspects. This discussion will further illustrate this using total knee arthroplasty (TKA) as an example.

TKA is a surgical technique that replaces the worn-out native knee joint. The TKA schematic is shown in Figure 9b. Specifically, the articular surface consisting of cartilage, meniscus, and cartilage is substituted with an Ultra-High Molecular Weight Polyethylene (UHMWPE) insert in a metal backing [116]. In this field, wear prediction is still the primary application. Innocenti et al. [116] devised and validated a finite element model to anticipate wear in polyethylene-based TKA. Zhang et al. [117] studied how internal-external rotation and anterior-posterior translation affect the wear of knee implants. It was shown that both internal-external rotation and anterior-posterior movement were vital factors that influenced the contact mechanism and wear of total knee implants. Kang et al. [118] employed finite element analysis under gait cycle loading conditions to examine the effects of various surface characteristics on the femoral component’s weight loss, wear depth, and kinematics in TKA. Furthermore, Koh et al. [119] mitigated wear in personalized TKA through the design, optimization, and parameterization of a 3D finite element model, corroborated by experimental wear test outcomes.

The design of joint surface curvature is crucial in TKA for tibiofemoral kinematics and contact mechanics. Yet, the effects of this curvature on various designs remain underexplored [120]. Mukhtar et al. [120] optimized and personalized the design parameters of a knee implant using the Taguchi method. The constructed model and simulation results are shown in Figure 9a,d. Koh et al. [121] performed computational simulations to contrast wear performance between conventional and patient-specific TKA under gait loading conditions. They found that different TKA designs result in kinematic variations, with contact pressure and area not directly influencing wear performance, as shown in Figure 9c. Notably, conforming individualized TKA exhibited the highest volume wear and wear rate, with a 29% increase in volume wear compared to internally rotated center individualized TKA.

UHMWPE is frequently employed in knee joint replacements. However, research indicates that Polyether ether ketone (PEEK) and Carbon Fiber Reinforced PEEK (CFR-PEEK) could serve as alternatives. The wear particles of CFR-PEEK exhibit no cytotoxicity, suggesting minimal adverse tissue reactions. Koh et al. [122] constructed a finite element model using tomography and magnetic resonance imaging techniques, investigating the biomechanical implications of UHMWPE and CFR-PEEK on mobile bearing TKA. The findings revealed a significant reduction in wear volume and the depth of CFR-PEEK compared to UHMWPE, while PEEK showed an increase (Figure 9e). This underscores the potential of CFR-PEEK as a promising substitute for UHMWPE in tibial implants. Nonetheless, comprehensive orthopedic research is warranted for newly introduced biomaterials to ascertain their threshold conditions and appropriate applications.

5.4. Other Applications

In addition to the applications of wear simulation in the POD test, gear wear, and implant wear, wear simulation is also applied in many other fields, which can be seen in Figure 10, such as the wear of seal [123,124], chain [125], tire [126], cam [127], artillery barrel [128], pump [129], metal wire [4] and so on. However, it can be observed that regardless of the field where wear simulation is applied, the main functions of wear simulation are wear profile prediction, service life prediction, and wear mechanism auxiliary analysis. Moreover, the wear simulation processes are similar across different research subjects and issues. Another striking feature can also be observed, such that Archard’s wear law is widely applied in different situations: electrical contact under fretting wear [90], tribocorrosion [125], thermal-mechanical coupling wear [130], and so on. However, as mentioned in Section 4.1, in many cases, Archard’s wear law needs to be combined with other models to accurately capture the wear process. The same applies to the energy dissipation wear model.

Except for the features discussed above, an outstanding disadvantage can be observed, such that the wear processes, in practical situations, include a variety of wear mechanisms. However, this complex process is described only by Archard’s theory or the energy dissipation theory. Wear simulation lacks some rationality in this aspect. Therefore, it can be concluded that the application of FEM in wear simulation is still in the research stage.

6. Summary

This paper presents the research methodology and application of ABAQUS in wear simulation, covering aspects such as FE model construction, factors influencing wear behavior, wear theory, and the practical application of wear simulation. The main conclusions of this paper are as follows:

(1)

The FE model can be categorized into two types: 2D and 3D. The 2D model is suitable for cases where there is no concern about the overall wear profile, offering high computational efficiency. On the other hand, the 3D model is used for complex structures and situations with complex boundary conditions and loading, providing more accurate computational results at the cost of higher computational resources and time.

(2)

To maintain contact in the model and simulate the real wear process, the model needs to be updated after each incremental step. Common methods for this include the UMESHMOTION subroutine and Python scripts. The element quality updated by the UMESHMOTION is better than what is updated by the Python script, reducing the possibility of stress concentration and convergence issues.

(3)

Computational efficiency is a significant concern in finite element analysis. Two commonly used methods to address this issue are the sub-model and extrapolation method. The sub-model method is often used for large and complex structures, while the extrapolation method can be applied to general wear problems, effectively improving computational efficiency. However, it is important to note that the extrapolation method requires finding an appropriate extrapolation factor to avoid significant errors. These two optimization methods can be used in combination based on actual situations.

(4)

There are many factors that influence wear behavior, which can be broadly categorized into two aspects: material properties and working conditions. These factors include hardness, roughness, lubrication, contact stress, sliding speed, and others. The effects of these factors on wear behavior are not singular, and they can also interact with each other. Therefore, it is challenging to propose a wear model that encompasses all influencing factors. Archard proposed a widely accepted theoretical model based on experiments, but it still has limitations. Many scholars have made improvements to Archard’s wear law through coupled analysis. In addition to this theory, the energy dissipation theory is another wear theory that is increasingly used in current wear research. Furthermore, the results obtained from the energy dissipation model show better agreement with the experimental results compared to Archard's wear law.

(5)

In practical applications, wear simulation technology can be utilized in various research fields, primarily focusing on predicting service life, wear profile, and wear mechanisms. This article provides an overview of the application of wear simulation in the POD test, gear wear, orthopedic implant wear, and other applications, leading to the following conclusions: Wear simulation technology can serve as an initial tool for product development and failure analysis, providing researchers with relatively reliable reference data.

(6)

The wear simulation presented in this paper is capable of capturing micron-scale wear processes and can provide a reasonable initial estimate of material loss. However, the subtle features of a specific wear mechanism cannot be obtained.

(7)

At present, the application of FEM in wear simulation is still in the research stage.

7. Perspectives

Based on the preceding discussions, it is evident that wear simulation technology holds vast potential for future applications. In this context, a future perspective on its development is provided below:

(1)

Development of more precise and accurate wear models to enhance the accuracy of finite element wear analysis.

(2)

Advancement of more efficient and accurate computational methods and algorithms to reduce computational costs and time.

(3)

Integration of new technologies such as machine learning to optimize and improve wear models, thereby enhancing predictive capabilities.

These developments are expected to significantly enhance the effectiveness and applicability of wear simulation technology across various industrial and scientific domains. As computational capabilities continue to evolve, these advancements will play a crucial role in addressing wear-related challenges and driving innovation in engineering and materials science.