Parameter Effects on the Static Characteristics of the Multi-Foil Aerodynamic Journal Bearing with Bump-Backing Foils

Abstract

Due to the complexity of lubricating characteristics in the variable-sectional and multiscale clearance, the absence of an effective prediction method and theoretical basis of multi-foil aerodynamic journal bearing with bump-backing foils needs to be further developed. Hence, a modified efficient static characteristics model has been established, of which the one-dimensional curved beam theory is integrated and the elasto-hydrodynamic influence is intelligently concerned. It can be used to well predict the influential mechanisms of operational, geometric, and physical parameter effects on the static characteristics, and the important variation laws are systemically clarified. It aims to furnish a more effective and computationally efficient method and theoretical foundation for this significant type of bearing and promote its engineering design and performance optimization.

1. Introduction

As for aerodynamic journal bearings, if merely relying on the rigid contact surfaces, several challenges will be faced, such as excessively high demands for processing accuracy and rigorous material properties [1]. Once contact friction happens, severe damage may occur to the bearing structure; hence, the operational stability, bearing capacity, and service life can be negatively affected [2,3]. In order to overcome the shortage of rigid aerodynamic bearing, the elastic metal foils are introduced and partially installed on the bearing house in practical engineering applications, thus resulting in the emergence of the so-called foil aerodynamic journal bearings. It offers inherent advantages, for instance, appropriate processing precision, reduced costs, and feasible quality control in engineering manufacture [4,5]. Moreover, due to the foil elastic deformation, the operational stability, bearing capacity, and service life of this type of bearing are also improved [6,7,8].

However, with the introduction of the foils, the foil elastic deformation may happen under high-speed conditions; hence, the lubrication flow in the complex variable cross-section clearance will become more complicated. Then, it will be more difficult to predict the static and dynamic characteristics of the bearing [9,10].

As reported in previous literature, many scholars have attempted to deal with these problems via different methods [11,12,13]. Heshmat et al. [14] early proposed a numerical model for the equivalent transformation of supporting bump foil by using the linear spring coefficients. In this model, the elastic deformation is considered, and the dimensionless Reynolds equation is solved coupled with the gas film thickness equation. The influence of evaluation parameters on bearing performance is analyzed, and the foil deformation is calculated through flexibility coefficient. The convergence speed of this model is fast, which makes it still popular among scholars; however, it still focuses on the relatively simple type of Hydresill ring foil aerodynamic journal bearing (shown in Figure 1a). However, the relevant results for the multi-foil aerodynamic journal bearings (shown in Figure 1b) need to be improved.

Subsequently, the finite difference method (FDM) coupled with the finite element method (FEM) was introduced to solve the Reynolds equation [15], and static characteristics of the relatively simple type of bump-foil aerodynamic thrust bearings were investigated. The distributions of gas film thickness, pressure, and stiffness were yielded. In this method, the influence of the coupling elastic effect of top and bump foils is considered, which accelerates the convergence speed of this numerical method, and can provide reference for the current research. Based on the assumptions of gas compressibility and isothermal condition, several scholars [16] performed numerical analyses on the flow characteristics of elastic foil aerodynamic bearings. In order to achieve more precise static characteristics, a foil structure model containing the bending deformation of top foils and the interactions between bump foils was established [17]. It reveals that when the bearing house and bump foils were frictionally superimposed, the foil stiffness at the fixed end is larger than that of the free end. However, it still primarily centered on the relatively simple type of Hydresill aerodynamic journal bearings, and the relevant investigations on multi-foil aerodynamic journal bearings still needed to be further strengthened.

Meanwhile, some scholars compared the advantages and disadvantages of different numerical models and their calculation algorithms. Andres and Kim [18], Andres and Chirathadam [19] successively proposed two FEM models for top foils in multi-foil aerodynamic journal bearings. One is the two-dimensional shell model, the other is the one-dimensional beam model that incorporated foil elastic deformation, deflection, and lubrication fluid mechanics. By comparison, it was found that the latter model showed better alignment with the experimental results. Zhang and Liu [20] introduced the trajectory method to analyze the bearing capacity, orbit of shaft center, and frequency spectrum and bifurcation characteristics. In a separate investigation, Hou et al. [21] numerically studied the interactions between gas pressure and foil deformation in aerodynamic bearings. It was based on the hypotheses of isothermal and iso-viscous conditions, and the perturbation method was introduced to linearize the Reynolds equation, which showed that the static characteristics were significantly influenced with the increase in bearing number and eccentricity ratio, and could be deteriorated by the unevenness of stiffness distribution. Nevertheless, the study was focused on the foil thrust bearing, and the relevant mechanism for the multi-foil aerodynamic bearing needs to be further explained. Later, Larsen et al. [22] conducted a comparative study to evaluate the nonlinear time domain simulation and the linearized frequency domain simulation with a perturbation of Reynolds equation. It reveals that the flexibility of the bump foil structure significantly affects the lateral stability of the bearing shaft. Furthermore, as the flexibility increased or under heavier bearing loads, the difference would become more pronounced. Larsen et al. [22] emphasized that when tackling aerodynamic bearing problems, it is crucial to consider both programming simplicity and ease of use of program. This study provides valuable insights for improving the accuracy and efficiency of bearing analysis methods in future research.

Recently, a novel fully coupled elastic hydrodynamics model has been proposed to analyze the static characteristics of aerodynamic bearings [23]. It showed that the model incorporating the separation between top and bump foils exhibits better alignment with the engineering practices. Furthermore, Xu et al. [24] introduced a frictional structure model and studied the bump foil gas bearing based on contact mechanics. The static characteristics were focused, and the influence of foil layouts and structural parameters were explored. They urged that the properties be enhanced via precise adjustment of bump foil layout. However, it was cautioned that the growth of maximum bearing load capacity could be negatively affected if under excessively high foil stiffness.

It has been observed that, on the one hand, the studies with respect to the foil bearing parameters were mainly focused on the relatively simple structural Hydresill-type ring foil aerodynamic journal bearing. The insights of the important and relatively complex structural multi-foil aerodynamic journal bearings need to be further improved. On the other hand, the previous studies mainly emphasized the mechanical properties, for instance, elastic deformation, rotor dynamics, vibration characteristics, and foil stiffness. However, the insights of the flow characteristics of lubricating gas film in the variable cross-section clearance, and their solid–liquid coupling influence on the bearing operational performances, still requires further enrichment. Thus, the absence of an effective prediction method of multi-foil aerodynamic journal bearing with bump-backing foils needs to be further developed. Also, the research of parameter effects on the static characteristics will not only lay theoretical basis and design guidelines for the multi-foil aerodynamic journal bearing with bump-backing foils but also can be used to optimize the operation stability and bearing capacity.

In this study, a modified more efficient static characteristics model of the multi-foil aerodynamic journal bearing with bump-backing foils has been established. In this model, the one-dimensional curved beam theory is integrated, and the elasto-hydrodynamic influence is mainly concerned. The relatively simple and convenient FDM is adopted. It can be used to well predict the influential mechanisms. The change rules of the operational, geometric, and physical parameters on the static characteristics are systemically exhibited. The interesting three-dimensional and two-dimensional gas film pressure and thickness distributions on each foil are innovatively demonstrated. Additionally, the variations in bearing capacity, friction torque, and azimuth angle are depicted and discussed. It aims to supply a more effective method and theoretical foundation for the static characteristics prediction and contributes to the improvement of engineering design and performance optimization of the specific significant type of bearing.

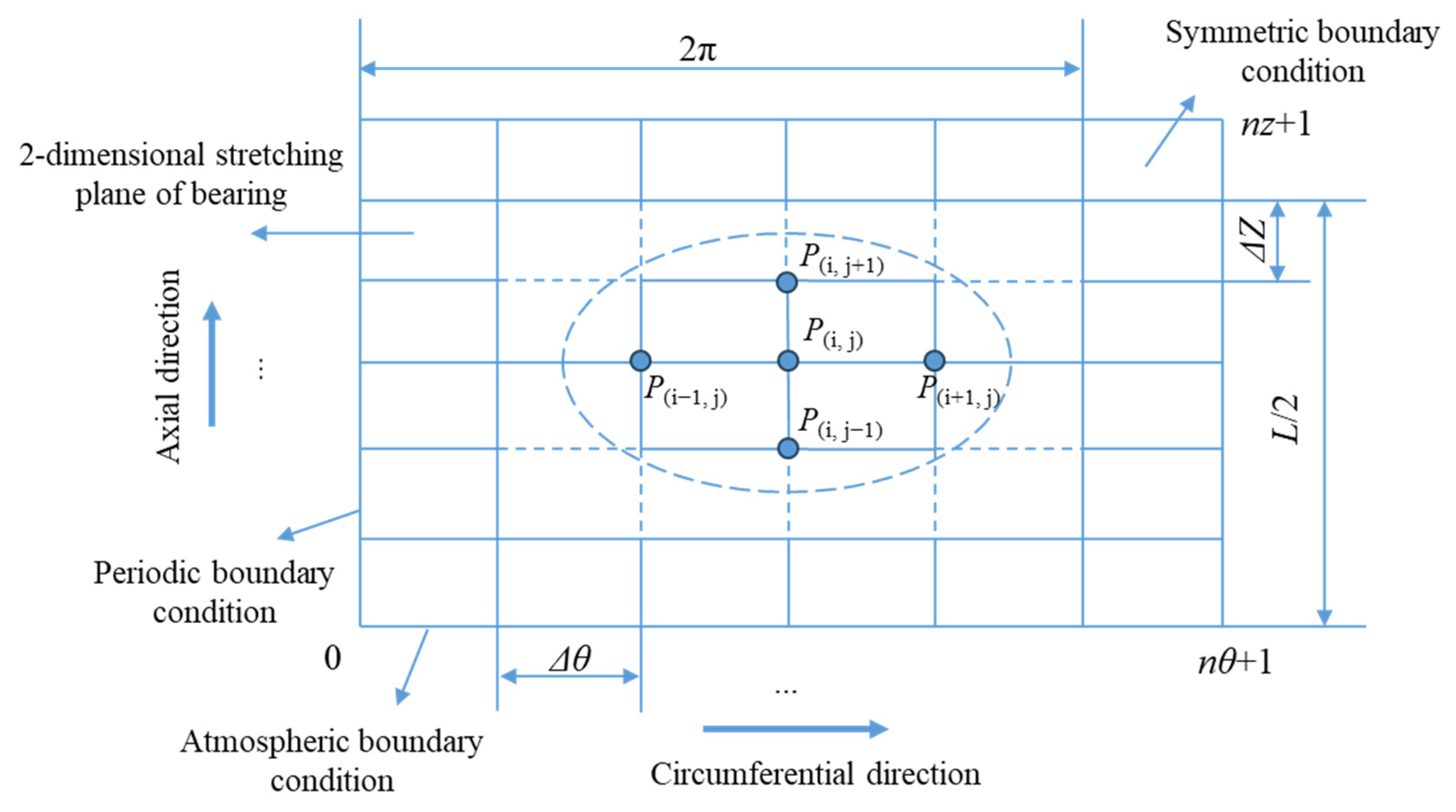
2. Numerical Models

The configuration of multi-foil aerodynamic journal bearing is depicted in Figure 2. The compressible Reynolds equation coupled with the gas film thickness equation was adopted to determine the pressure and thickness distribution of lubrication gas film in the complex elastic variable cross-section clearance. Meantime, the foil deformation was considered, and the FDM was used to compute the static characteristics, which include the bearing capacity, friction torque, and other relevant parameters.

2.1. Reynolds Equation

In this study, the lubrication gas in the bearing clearance is assumed as the isothermal ideal gas, and the pressure distribution can be described by the dimensionless Reynolds equation, expressed as follows [25]:

$$\frac{\partial }{\partial \theta }\left(P{H}^3\frac{\partial P}{\partial \theta }\right)+{\left(\frac{2R}{L}\right)}^2\frac{\partial }{\partial Z}\left(P{H}^3\frac{\partial P}{\partial Z}\right)=\Lambda \frac{\partial \left(PH\right)}{\partial \theta }+2\Lambda \gamma \frac{\partial }{\partial {\tau }_s}\left(PH\right)$$

(1)

where

$$\theta =\frac{x}{R};Z=\frac{z}{0.5L};P=\frac{p}{p_a};H=\frac{h}{C};\Lambda =\frac{6\mu \omega }{pa}{\left(\frac{R}{C}\right)}^2;\gamma =\frac{{\omega }_s}{\omega };\overline{t}={\omega }_{s}t$$

θ represents the circular angle coordinates in radians, Z denotes the dimensionless bearing length, L is the bearing length in meters, P represents the dimensionless pressure, p_a is the circumstance pressure in Pa, and H denotes the dimensionless gas film thickness. Additionally, Λ signifies the bearing number, μ represents the dynamic viscosity in Pa/s, and ω denotes the bearing speed in rpm. Additionally, γ represents the vortex frequency, $\overline{t}$ signifies the dimensionless time, and ω_s denotes the oscillation angular frequency in rad/s.

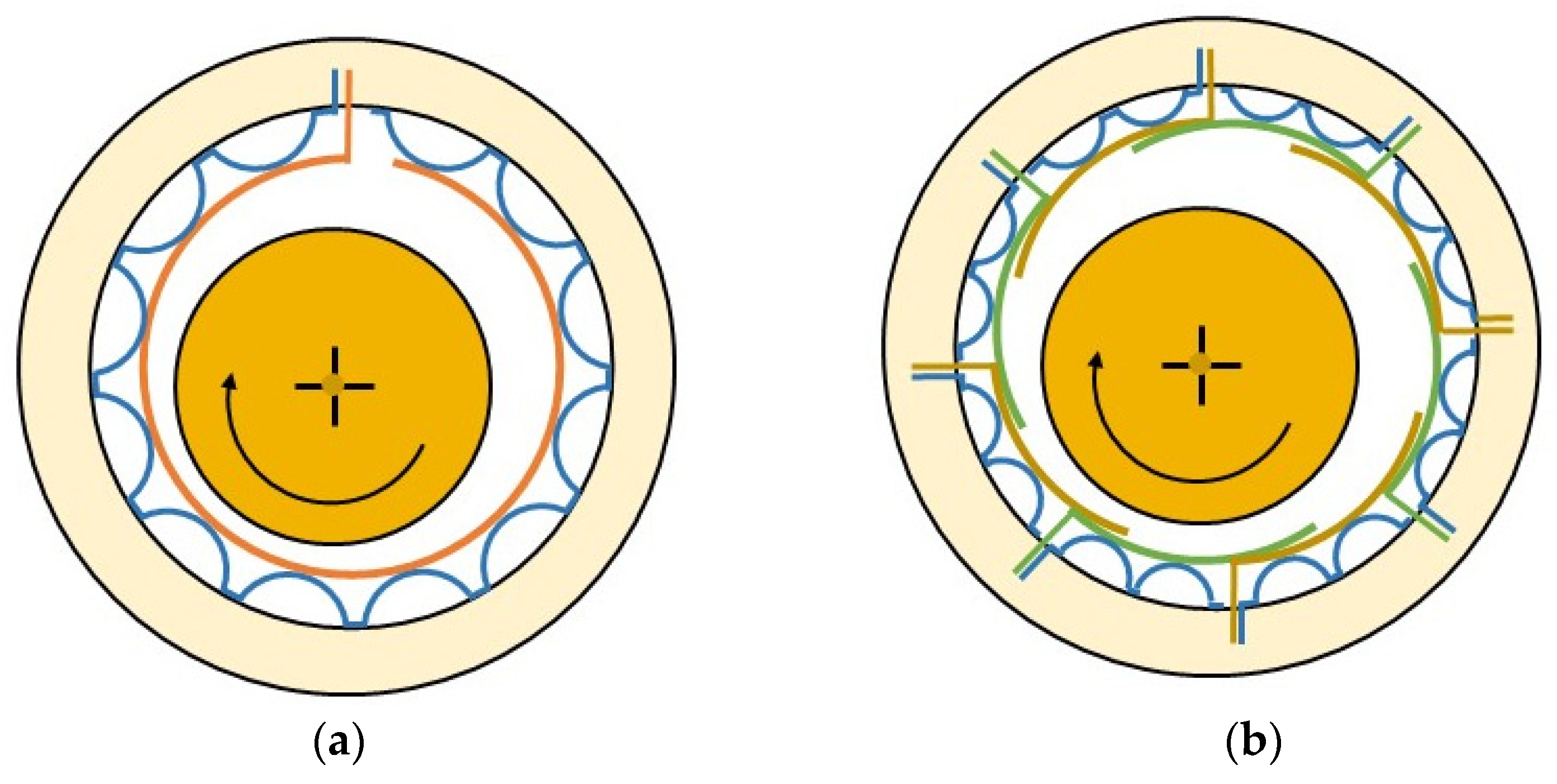
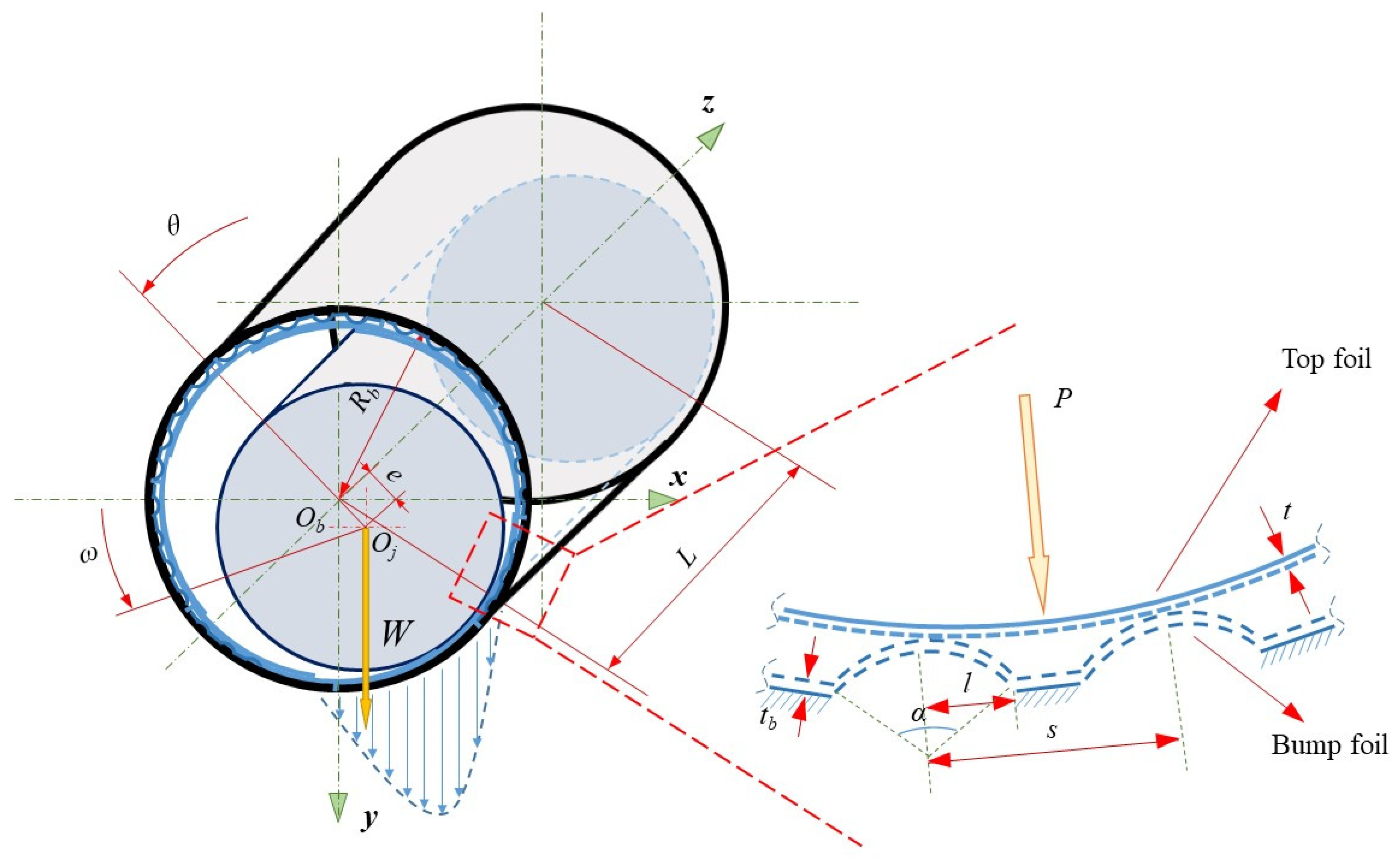
2.2. Gas Film Thickness Equation

The dimensionless gas film thickness in the clearance can be mathematically expressed as follows:

$$H=\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$C$}\right.=\left(h_0+u\right)/C=H_0+U$$

(2)

where h₀ denotes the initial gas film thickness in meters, u represents the foil radial deformation, H₀ signifies the dimensionless initial gas film thickness, and U corresponds to the dimensionless foil radial deformation.

The schematic diagram of a multi-foil aerodynamic journal bearing in the rotating coordinate system x₁Oy₁ is illustrated in Figure 3, where the corresponding fixed Cartesian coordinate system is represented as xOy. The shaft rotates anticlockwise, and the structural parameters of a randomly selected top foil are depicted. As shown in Figure 3, the symbols O_b, O_l, and O_j denote the centers of the bearing house, top foil, and bearing shaft, respectively. Additionally, R_b, R_f, and R_p represent the radii of the bearing house, top foil, and tangent circle of the top foil, respectively. Additionally, e signifies the eccentricity in meters, φ represents the deflection angle in radians, T_p denotes the tangential point of top foil, and N signifies the quantity of top foils. Furthermore, Γ and β_f correspond to the developing angle and installation angle of the top foil in radians, respectively. Then, it can be easily inferred from the geometric relationships that Γ can be expressed as follows [26]:

$$\Gamma =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\sqrt{\left[{\left(R_f-\frac{1}{2}{R}_p\right)}^2-\frac{1}{4}{R}_b^2\right]\left(R_b^2-R_p^2\right)}}{R_f\left(R_f-R_p\right)}+\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left[\left(1-\frac{R_p}{R_f}\right)sin\frac{\pi }{N}\right]-\left(1-\frac{2}{N}\right)\frac{\pi }{2}$$

(3)

Considering the impact of top foil thickness on initial gas film distribution, the angle $\mathrm{\angle }C{O}_{1}O$ is equal to $\mathrm{\angle }{BO}_{1}O$, and the corresponding spread angle α_c at the overlap point C can be expressed as follows:

$${\alpha }_c={\alpha }_T-\left(\Gamma -{\alpha }_T\right)$$

(4)

For any arbitrary point P located on the top foil, within the rotating coordinate system x₁Oy₁, the following formulas can be established:

$$\left(\begin{array}{c}{x}_{1O_1}\\ y_{1O_1}\end{array}\right)=\left(\begin{array}{c}-R_{f}sin\left({\beta }_f\right)\\ R_{f}cos\left({\beta }_f\right)-R_b\end{array}\right)$$

(5)

$$\left(\begin{array}{c}{x}_{1p}\\ y_{1p}\end{array}\right)=\left(\begin{array}{c}{x}_{1O_1}\\ y_{1O_1}\end{array}\right)+\left(\begin{array}{c}{R}_f\sin ({\alpha }_p+{\beta }_f)\\ {-R}_{f}cos{({\alpha }_p+\beta }_f)\end{array}\right)$$

(6)

$$\left(\begin{array}{c}{x}_{1C_p}\\ y_{1C_p}\end{array}\right)=\left(\begin{array}{c}{x}_{1O_1}\\ y_{1O_1}\end{array}\right)+\left(\begin{array}{c}{R}_f\sin ({\alpha }_c+{\beta }_f)\\ {-R}_{f}cos{({\alpha }_c+\beta }_f)\end{array}\right)$$

(7)

where α_p denotes the spread angle corresponding to point P, C_p represents the overlap point between the top foils, and O_l signifies the circle center of the arc of a top foil.

For the foil mounting angles α_T and β_f, the formulas can be set up:

$$\beta =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{R_f^2+R_b^2-{\left(R_f-R_p\right)}^2}{2R_f{R}_b}$$

(8)

$${\alpha }_T=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{R_f^2+{\left(R_f-R_p\right)}^2-R_b^2}{2R_f\left(R_f-R_p\right)}$$

(9)

Then, the coordinate system x₁Oy₁ can be transformed into xOy by rotating Ψ degrees counterclockwise. Mathematically, the conversion can be expressed as follows:

$$\left(\begin{array}{c}{x}_{O_p}\\ y_{O_p}\end{array}\right)=\mathit{T}\left(\Psi \right)\left(\begin{array}{c}{x}_{1O_p}\\ y_{1O_p}\end{array}\right)$$

(10)

$$\mathit{T}\left(\Psi \right)=\left(\begin{array}{cc}cos\psi & -sin\psi \\ sin\psi & cos\psi \end{array}\right)$$

(11)

$$\psi =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(-\frac{x_{1C_p}}{y_{1C_p}}\right)$$

(12)

where T (Ψ) represents the rotation matrix. Obviously, in the same coordinate system, the center of the journal O_j can be expressed in the following form:

$$\left(\begin{array}{c}{x}_{O_j}\\ y_{O_j}\end{array}\right)=\left(\begin{array}{c}esin\psi \\ -ecos\psi \end{array}\right)$$

(13)

Then, the vector $\mathit{a}$ and arbitrary vector $\mathit{b}$ depicted in Figure 3 can be mathematically represented as:

$$\mathit{a}=\overrightarrow{O_i{O}_j}=\left(x_{o_l}-x_{o_j},y_{o_l}-y_{o_j}\right);\mathit{b}=\overrightarrow{p{O}_j}=\left(x_{o_p}-x_{o_j},y_{o_p}-y_{o_j}\right)$$

(14)

Given that each top foil can be regarded as an integral component of a full-circle radial bearing, hence the gas film thickness at arbitrary point p can be expressed as follows:

$$h=\left(R_f-R\right)+\left|\mathit{a}\right|\frac{\mathit{a}·\mathit{b}}{\left|\mathit{a}\right|\left|\mathit{b}\right|}$$

(15)

Additionally, the center O_i of an arbitrary top foil within the bearing can be represented in the following form:

$$\left(\begin{array}{c}{x}_{O_i}\\ y_{O_i}\end{array}\right)=\left[\mathit{T}\left(-\left(i-1\right)\frac{2\pi }{N}\right)\right]\left(\begin{array}{c}{x}_{O_l}\\ y_{O_l}\end{array}\right)$$

(16)

Therefore, the gas film thickness corresponding to the rest of the foils can be calculated by utilizing the aforementioned method. Ultimately, the gas film thickness h₀ can be derived. Notably, it differs from the conventional single-ring bump foil bearing in that the multi-foil bearing sustains the complex mutual interactions, which is exerted by the deformation of the multi-foil structure and the self-eccentric action of the bearing shaft.

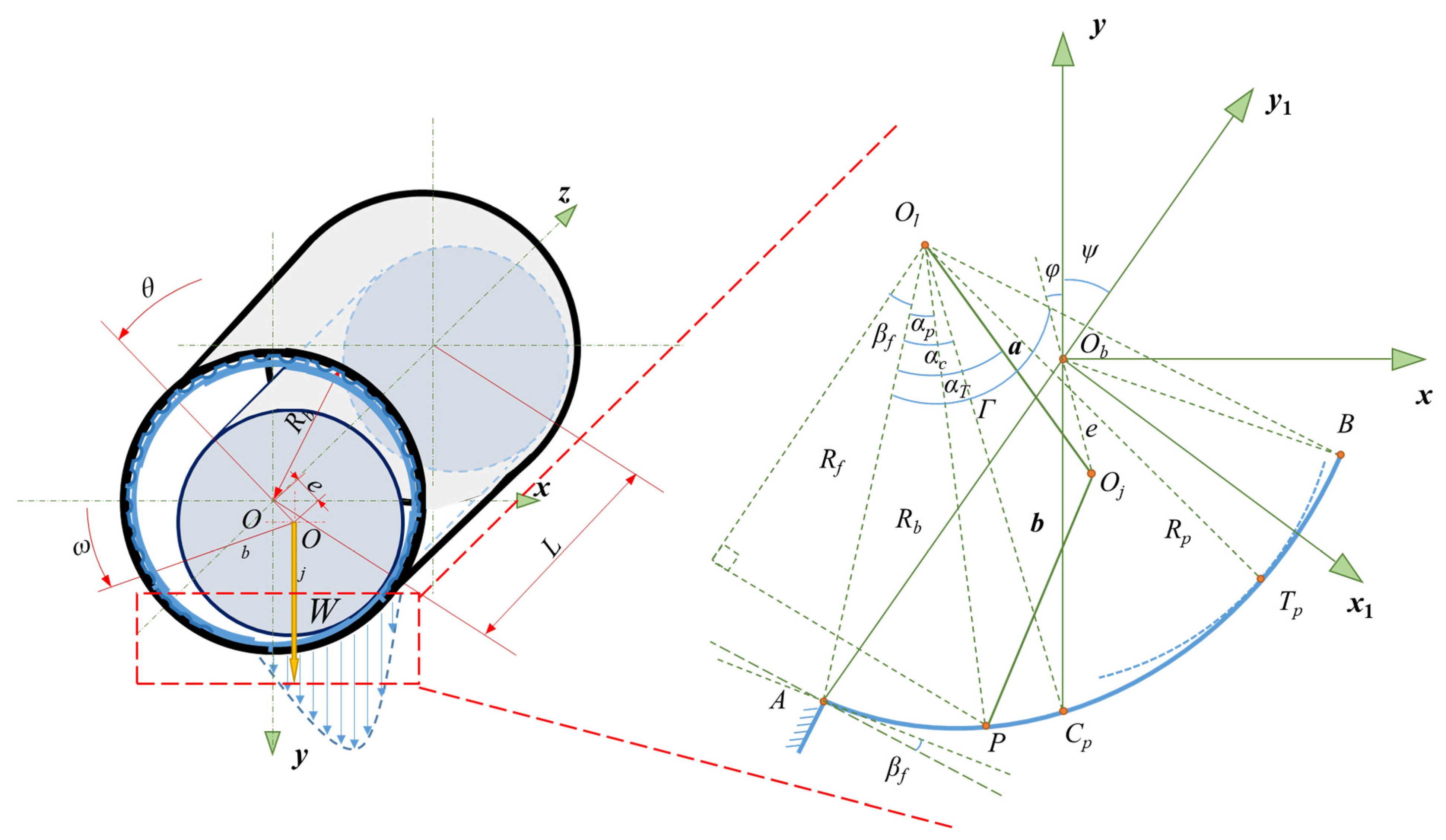
2.3. The Amount of Foil Deformation

To investigate the static characteristics of the bearing, it is crucial to calculate the foil deformations. The top foil is considered as a curved beam [27], and its structural configuration is illustrated in Figure 4.

As for the structural configuration of the curved beam [27] depicted in Figure 4, the following relationships are defined:

$$\begin{gathered} D_1=EA\frac{R-r_n}{r_n};D_2=\frac{r_n}{G{A}_s};D_3=\frac{EA}{r_n};D_4=\frac{r_n{D}_3-D_1\left(1-D_2{D}_3\right)}{-r_n{D}_3-D_1\left(1+D_2{D}_3\right)}; \\ {D}_5=1-D_4-D_2{D}_3\left(1+D_4\right);D_5=D_1{D}_5,D_7=D_4\left(1+D_4\right) \end{gathered}$$

(17)

Then, the bending stiffness matrix can be expressed as:

$$\widetilde{k_i}=\mathit{QS}$$

(18)

where

$$Q=\left[\begin{array}{cccccc}0& 0& 0& 0& -D_7& 0\\ 0& 0& 0& 0& 0& -D_7\\ 0& -D_1& 0& 0& -D_{6}cos\beta & 0\\ 0& 0& 0& 0& D_7& 0\\ 0& 0& 0& 0& 0& D_7\\ 0& D_1& 0& 0& D_{6}cos\beta & D_{6}cos\beta \end{array}\right]$$

(19)

$$S=\left(m_1,m_2,m_3,m_4,m_5,m_6\right)$$

(20)

where

$$\begin{gathered} m_1={\left(0,-\frac{D_{5}sin\beta }{{∆}_1},\frac{1}{2},\frac{\left[D_{5}sin\beta \left(\beta sin\beta +cos\beta \right)-\beta D_4{cos}^2\beta \right]}{{∆}_1},\frac{\beta }{{∆}_1},0\right)}^{\mathrm{T}} \\ {m}_2={\left(-\frac{D_{5}sin\beta }{{∆}_2},0,-\frac{\left(D_2{sin}^2\beta -D_5{cos}^2\beta \right)}{{∆}_2},-\frac{1}{2},0,\frac{1}{{∆}_2}\right)}^{\mathrm{T}} \\ {m}_3={\left(-\frac{r_n\left(D_{4}cos\beta sin\beta -\beta \right)}{{∆}_2},\frac{r_n\left(D_{4}cos\beta sin\beta +\beta \right)}{{∆}_1},\frac{r_n\left(D_{4}sin\beta -\beta cos\beta \right)}{{∆}_2},-\frac{r_n\left[\beta D_{4}cos\beta +\beta \left(\beta sin\beta +cos\beta \right)\right]}{{∆}_1},-\frac{r_n\left(sin\beta -\beta cos\beta \right)}{{∆}_1},-\frac{\left(r_{n}sin\beta \right)}{{∆}_2}\right)}^{\mathrm{T}} \\ {m}_4={\left(0,\frac{D_{5}sin\beta }{{∆}_1},\frac{1}{2},-\frac{\left[D_{4}cos\beta +\beta \left(\beta sin\beta +cos\beta \right)\right]}{{∆}_1},-\frac{\beta }{{∆}_1},0\right)}^{\mathrm{T}} \\ {m}_5={\left(\frac{D_{5}cos\beta }{{∆}_1},0,-\frac{\left(D_5{cos}^2\beta -D_4{sin}^2\beta \right)}{{∆}_2},-\frac{1}{2},0,-\frac{1}{{∆}_2}\right)}^{\mathrm{T}} \\ {m}_6={\left(-\frac{r_n\left(D_{4}cos\beta sin\beta -\beta \right)}{{∆}_2},-\frac{r_n\left(D_{4}cos\beta sin\beta +\beta \right)}{{∆}_1},\frac{r_n\left(D_{4}sin\beta -\beta cos\beta \right)}{{∆}_2},\frac{r_n\left[\beta D_{4}cos\beta +\beta \left(\beta sin\beta +cos\beta \right)\right]}{{∆}_1},\frac{r_n\left(sin\beta -\beta cos\beta \right)}{{∆}_1},-\frac{\left(r_{n}sin\beta \right)}{{∆}_2}\right)}^{\mathrm{T}} \end{gathered}$$

(21)

where

$${∆}_1=2D_5{sin}^2\beta -2\beta \left(D_4+D_5\right)cos\beta sin\beta -2{\beta }^2;{∆}_2=2\left(D_4+D_5\right)cos\beta sin\beta -2\beta$$

(22)

Define the coordinate transformation matrix as follows:

$$T^i=\left[\begin{array}{cccccc}cosxX& cosxZ& 0& 0& 0& 0\\ coszX& coszZ& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& cosxX& cosxZ& 0\\ 0& 0& 0& coszX& coszX& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]$$

(23)

where x, y, and z are the local coordinates of the bending element of the curved beam, and X, Y, and Z are the global coordinates.

Then, the stiffness matrix of the selected curved beam under the global coordinate can be expressed as:

$${k_i}_{\left(6\times 6\right)}=T_i^T\widetilde{k_i}{T}_i$$

(24)

Taking the bending element 1 for instance, the relationship between the force F₁, F₂ and the deformation u₁, u₂ is as follows:

$$\left\{\begin{array}{c}{F}_1\\ F_2\end{array}\right\}=\left\{\begin{array}{cc}{k}_1& {-k}_1\\ -k_1& k_1\end{array}\right\}\left\{\begin{array}{c}{u}_1\\ u_2\end{array}\right\}$$

(25)

If we divide one top foil into 30 curved beam elements, then there will be 31 nodes. Depending on the superposition method, the relationship between the overall stiffness K_top and the deformation u of the top foil under the action of force F can be expressed as follows:

$${\mathit{F}=\mathit{K}}_{top}\mathit{u}$$

(26)

Expanding the above formula, the foil structure deformation model can be obtained as follows:

$$\left\{\begin{array}{c}{F}_1\\ F_2\\ F_3\\ ⋮\\ F_{29}\\ F_{30}\\ F_{31}\end{array}\right\}={\left\{\begin{array}{ccc}\begin{array}{ccc}{k}_1& -k_1& \\ -k_1& k_1+k_2& {-k}_2\\ & {-k}_2& k_2{+k}_3\end{array}& \cdots & \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ & 0& 0\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{ccc}0& 0& \\ 0& 0& 0\\ 0& 0& 0\end{array}& \cdots & \begin{array}{ccc}{k}_{29}{+k}_{30}& {-k}_{29}& 0\\ {-k}_{29}& k_{30}+k_{31}& {-k}_{30}\\ 0& {-k}_{30}& k_{31}\end{array}\end{array}\right\}\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\\ ⋮\end{array}\\ u_{29}\\ u_{30}\\ u_{31}\end{array}\right\}}_{\left(93\times 93\right)}$$

(27)

Because the load of multi-foil aerodynamic journal bearing with backing foil is relatively large, it is necessary to consider the lap state between the top foil as the surface contact to better meet the actual situation. Through superimposing the stiffness matrix of each top foil in the lap area, K_top-all, the overall stiffness matrix of the entire top foil can be obtained. As for the bump foil, the surface stiffness can usually be calculated by the FDM or empirical formula. In order to improve the calculation efficiency and optimize the calculation process, here, the Iordanoff empirical formula [28] is adopted, which can be expressed as follows:

$$\left\{\begin{array}{c}{k}_b^{fw}=\frac{E_b{t}_b^3{sin}^3\left(\frac{\alpha }{2}\right)}{12l^{3}sJ\left(\eta ,\alpha \right)\left(1-{\nu }_b^2\right)}\\ k_b^{ff}=\frac{E_b{t}_b^3{sin}^3\left(\frac{\alpha }{2}\right)}{6l^{3}sI\left(\eta ,\alpha \right)\left(1-{\nu }_b^2\right)}\end{array}\right.$$

(28)

where E_b and v_b represent the elastic modulus and Poisson’s ratio of bump foil, respectively. In addition, as depicted in Figure 2, α denotes the field angle, s represents the unit length, l corresponds to the half-bump length, and t_b signifies the thickness of bump foil.

$$\left\{\begin{array}{c}J\left(\eta ,{\alpha }_b\right)=y_a\left[\left(cos\frac{{\alpha }_b}{2}-1\right)\left(sin\frac{{\alpha }_b}{2}+\eta cos\frac{{\alpha }_b}{2}\right)+\frac{\eta \left(1-cos{\alpha }_b\right)}{4}\right]+\left(1-y_a\right)\left(\frac{{\alpha }_b}{4}-\frac{sin{\alpha }_b}{4}\right)\\ I\left(\eta ,{\alpha }_b\right)=\left(A^2+\frac{1+{\eta }^2}{2}\right)\frac{{\alpha }_b}{2}-\frac{\left(1-{\eta }^2\right)sin{\alpha }_b}{4}-\frac{\eta \left(1-cos{\alpha }_b\right)}{2}-2A\left[1-cos\frac{{\alpha }_b}{2}+\eta sin\frac{{\alpha }_b}{2}\right]\end{array}\right.$$

(29)

$$\left\{\begin{array}{c}{y}_a=\frac{-\left(\frac{3sin{\alpha }_b}{4}-\frac{{\alpha }_b}{4}-sin\frac{{\alpha }_b}{2}\right)}{\alpha sin\frac{{\alpha }_b}{2}\left(sin\frac{{\alpha }_b}{2}+\eta cos\frac{{\alpha }_b}{2}\right)-2\eta {sin}^2\left(\frac{{\alpha }_b}{2}\right)+\frac{{\alpha }_b}{2}-\frac{sin{\alpha }_b}{2}}\\ A=sin\frac{{\alpha }_b}{2}+\eta cos\frac{{\alpha }_b}{2}\end{array}\right.$$

(30)

Then, the stiffness of each individual top foil can be calculated, and the overall stiffness matrix K_bump of bump foils can be derived through integration. By matrixing and combining to the corresponding node of the global stiffness matrix K_top of top foil, the comprehensive top–bump foil global stiffness matrix K_all can be obtained.

$${\mathit{K}}_{all}={\mathit{K}}_{top}+{\mathit{K}}_{bump}$$

(31)

Due to the restricted displacement of foil at the fixed end, it exists that:

$${\mathit{K}}_{all}{\mathit{U}}_{all}={\mathit{F}}_{all}$$

(32)

where ${\mathit{F}}_{all}$ denotes the gas film pressure vector exerting on the top foil surface, ${\mathit{F}}_{all}=\left\{0,\right.\left.F_{p1},0,F_{p2},\dots \right\}$, F_pi (i = 1, 2,…), which is related to the gas film pressure at each node. Additionally, ${\mathit{U}}_{all}$ represents the foil deformation, ${\mathit{U}}_{all}=\left\{u_{fx1},\right.\left.u_{fx2},\dots \right\}$, u_fxi, u_fyi (i = 1, 2,…), which corresponds to the displacement of each node. Through extracting the lateral displacement u_fxi of all nodes, the foil radial deformation u_f can be calculated.

Hence, the method can be established by means of Equations (15) and (19), which can be used to describe the gas film thickness distribution within the complex clearance, with the superposition of top-bump multi-foils being considered.

The mesh and computation domain are illustrated in Figure 5. Additionally, the boundary conditions of the Reynolds equation are as follows:

$$\left\{\begin{array}{c}whenZ=\pm 1,P=1\\ whenZ=0,\frac{\partial P}{\partial Y}=0\\ P\left(\theta =0\right)=P\left(\theta =2\pi \right)\end{array}\right.$$

(33)

The convergence criteria can be expressed as follows:

$$\left\{\begin{array}{c}\sqrt{\sum _{i=0}^{n\theta }\sum _{j=0}^{nZ}{\left(\frac{{\delta }_{i,j}}{P_{i,j}}\right)}^2}\le {10}^{-6}\\ \sqrt{\sum _{i=0}^{n\theta }\sum _{j=0}^{nZ}{\left(\frac{{∆P}_{i,j}}{P_{i,j}}\right)}^2}\le {10}^{-6}\end{array}\right.$$

(34)

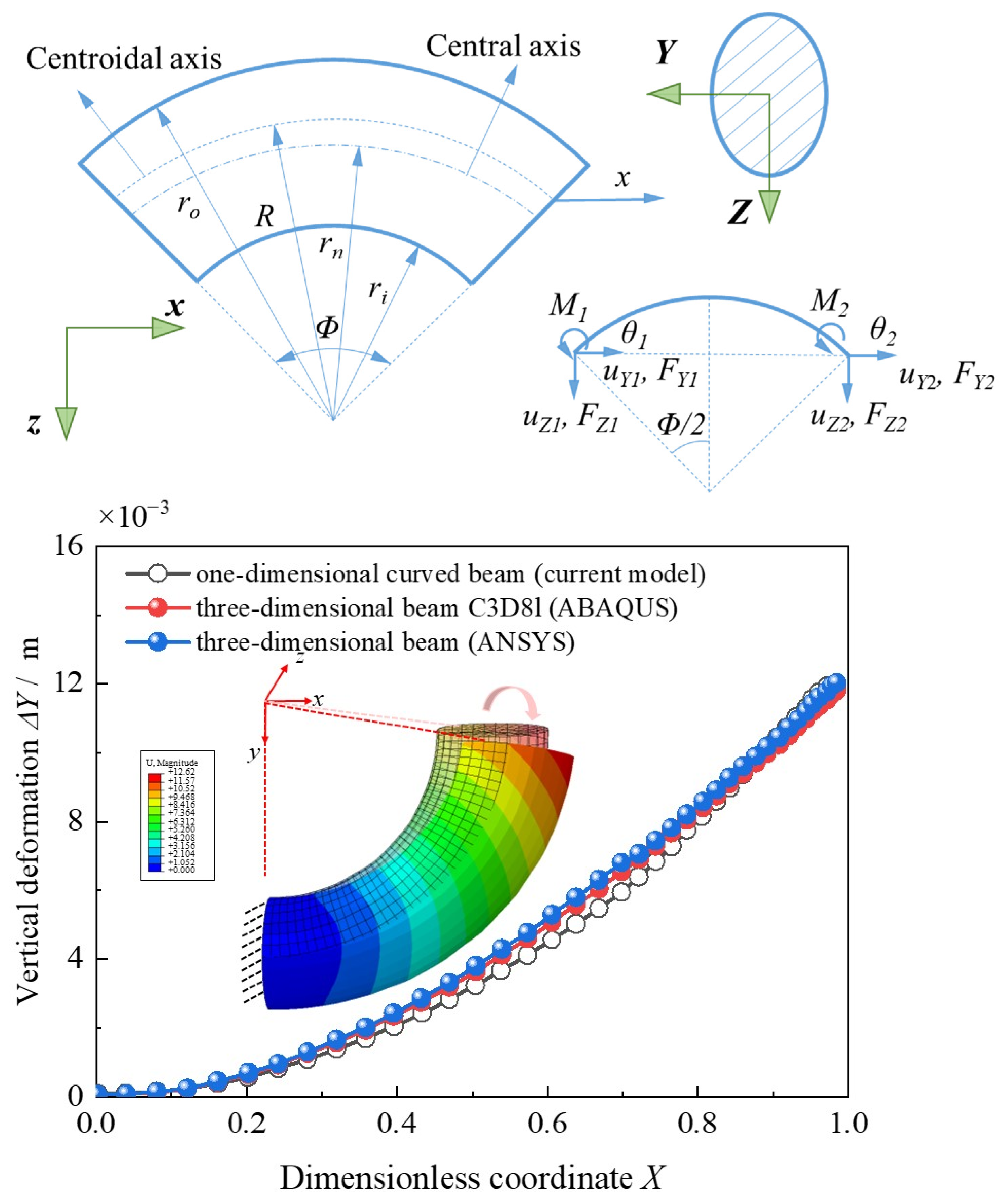
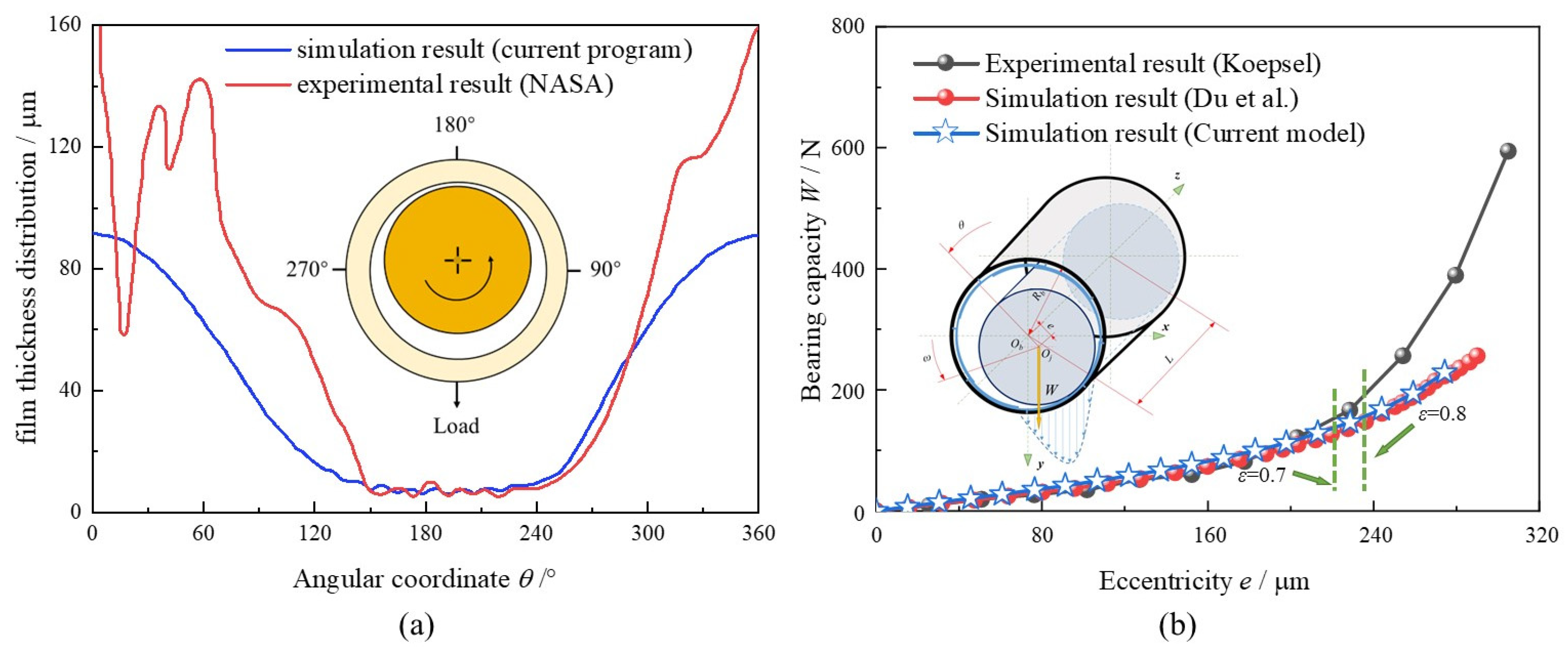
2.4. Validation of Model

In this section, the proposed model will be validated. To ensure both the accuracy and applicability, the model was employed to simulate the variations between bearing capacity and eccentricity of shaft center of the multi-foil aerodynamic journal bearings. Valuable work towards the multi-foil aerodynamic journal bearing was performed by early researchers [29,30,31]. The relevant parameters of bearing in the literature in [29] and [30,31] are listed in

Table 1. Parameters of experimental bearing in the literature (NASA).

Parameter Name	Value
Bearing length (L)	38.1 × 10−3 m
Shaft radius (Rj)	19.05 × 10−3 m
Bearing clearance (C)	20 × 10−5 m
Foil thickness (t)	10.16 × 10−5 m
Foil elastic modulus (Eb)	2.14 × 1011 Pa
Foil Poisson’s ratio (υb)	0.3
Ambient pressure (pa)	1.01325 × 105 Pa
Dynamic viscosity of gas (μ)	1.932 × 10−5 Pa·s
Bearing capacity (W)	134.1 N
Bearing speed (ω)	3.0 × 104 rpm

and

Table 2. Parameters of bearing in the literature [30,31].

Parameter Name	Value
Bearing length (L)	15.24 × 10−3 m
Shaft radius (Rj)	57.15 × 10−3 m
Bearing radius (Rb)	57.9628 × 10−3 m
Incircle radius (Ri)	57.4548 × 10−3 m
Foil radius (Rf)	59.50 × 10−3 m
Foil thickness (t)	25.40 × 10−4 m
Foil elastic modulus (Eb)	2.0685 × 1011 Pa
Foil number (N)	8
Ambient pressure (pa)	1.01325 × 105 Pa
Dynamic viscosity of gas (μ)	2.953 × 10−5 Pa·s
Bearing clearance (C)	30.48 × 10−5 m
Bearing speed (ω)	3.3 × 104 rpm

, respectively. Moreover, the parameters of bearing in current research are listed in

Table 3. Relevant parameters of bearing in current research.

Parameter Name	Value
Bearing length (L)	30.0 × 10−3~70.0 × 10−3 m
Shaft radius (Rj)	23.49 × 10−3 m
Bearing radius (Rb)	26.25 × 10−3 m
Incircle radius (Ri)	23.5 × 10−3 m
Foil radius (Rf)	25.25 × 10−3 m
Foil thickness (t)	1.0 × 10−4~2.5 × 10−4 m
Foil elastic modulus (Eb)	2.00 × 1011~2.20 × 1011 Pa
Foil number (N)	4~8
Ambient pressure (pa)	1.01325 × 105 Pa
Dynamic viscosity of gas (μ)	1.932 × 10−5 Pa·s
Specific heat ratio of gas (Cp/Cv)	1.401
Eccentricity ratio (ε)	0.1~0.7
Bearing speed (ω)	3.0 × 104~1.2 × 105 rpm
Foil Poisson’s ratio (υb)	0.3
Span of bump foil (s)	4.2 × 10−3 m
Half-length of bump foil (l)	1.75 × 10−3 m
Thickness of bump foil (tb)	1.016 × 10−4 m

. The comparison of film thickness distribution with experimental results in the literature [29] is illustrated in Figure 6a. The calculated results in the minimum film thickness area by the current program are highly consistent with that of experimental results by NASA [29]. To some extent, the accuracy of the solution method in this paper is verified. Additionally, as depicted in Figure 6b, the simulated results were compared with the experimental and numerical results in the literature under identical working conditions. Specifically, the black spherical curve represents the experimental data by Koepsel [30]; meanwhile, the red spherical curve corresponds to numerical simulation results reported by Du et al. [31]. In contrast, the blue curve denoted by blue stars represents the simulation results obtained via the current model. Notably, when the eccentricity ratio does not exceed 0.7, the simulated results by the current model are highly consistent with both the experimental and numerical data in the literature. The maximum deviation between the numerical and experimental results is less than −7.1%, and the accuracy of the current model surpasses that reported in the literature under most conditions.

When the eccentricity ratio ranges between 0.7 and 0.8, the deviation will be increased to −12.1%. Notably, the precision of all simulated results calculated by the current model surpass that in the literature. However, when the eccentricity ratio attains 0.8, the deviation will surge to −25.2% with increasing trend, which indicates that the accuracy of the current model is degraded. It can be attributed to the inadequate consideration of surface contact constraints between the foil and the inner wall of the bearing house at higher eccentricity ratios. These constraints play a role in restriction of the foil deformation and enhancement of the foil stiffness, ultimately bolstering the bearing capacity. Thus, the deviation between simulated and experimental results amplifies rapidly as the eccentricity ratio exceeds 0.8. Considering the actual operational state, the current model can still well satisfy the investigative requirements for most bearing operational conditions. Furthermore, in order to ensure the precision and reliability of the results, in the subsequent investigations the eccentricity ratio will be controlled, not surpassing 0.7.

3. Results and Discussion

As detailed in this section, the influence of the operating parameters (for instance, eccentricity ratio and bearing speed) on the bearing lubrication performance was initially studied, and the variation rules were derived. Subsequently, the impact of foil structure and physical parameters (including foil thickness and elasticity modulus) on critical performance indicators (such as pressure and thickness distribution, bearing capacity, friction torque, and azimuth angle) were systematically investigated. Finally, the influence of bearing geometry parameters (the length–diameter ratio) and bearing numbers on the bearing static characteristics were discussed. It aims to provide a comprehensive understanding of the characteristics and limiting factors of multi-foil aerodynamic journal bearings under varying operational and design parameters.

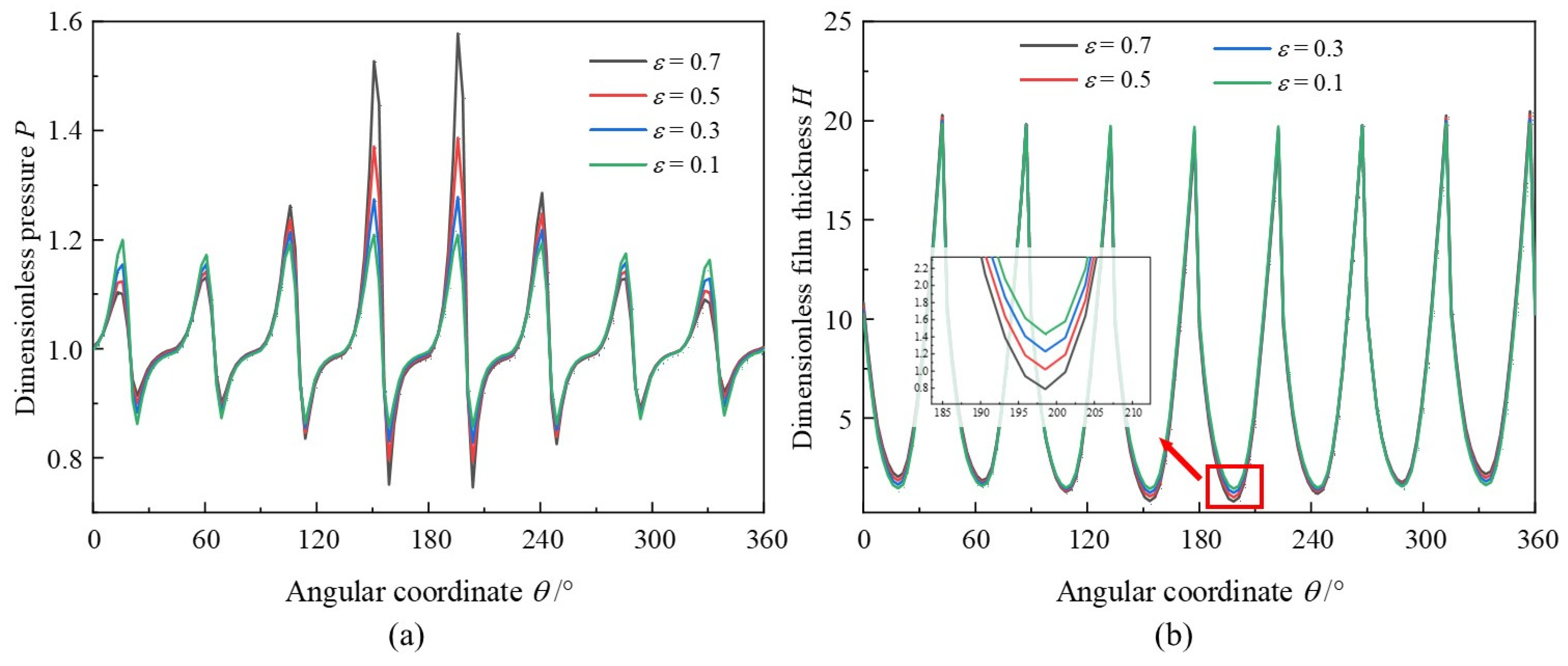
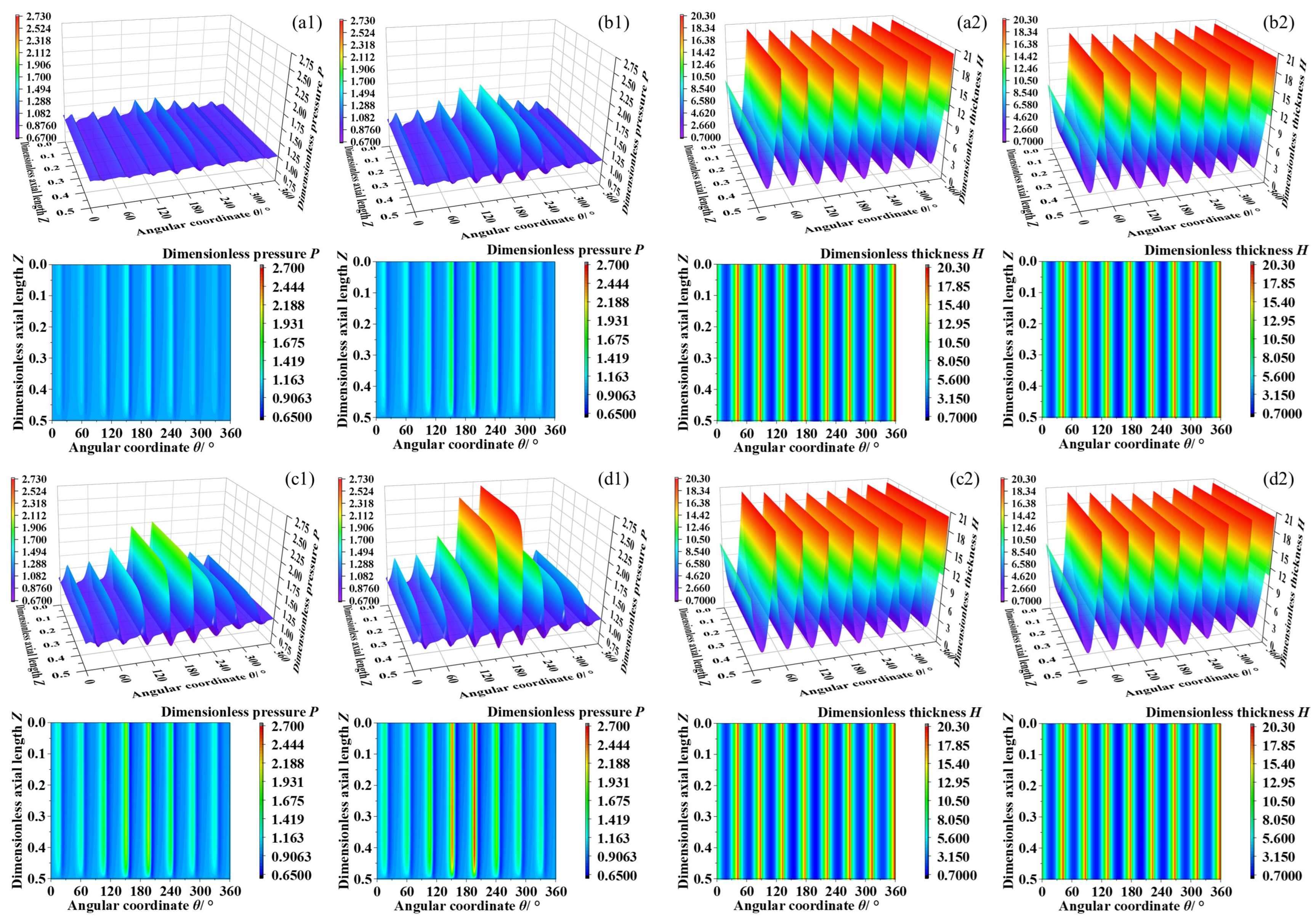
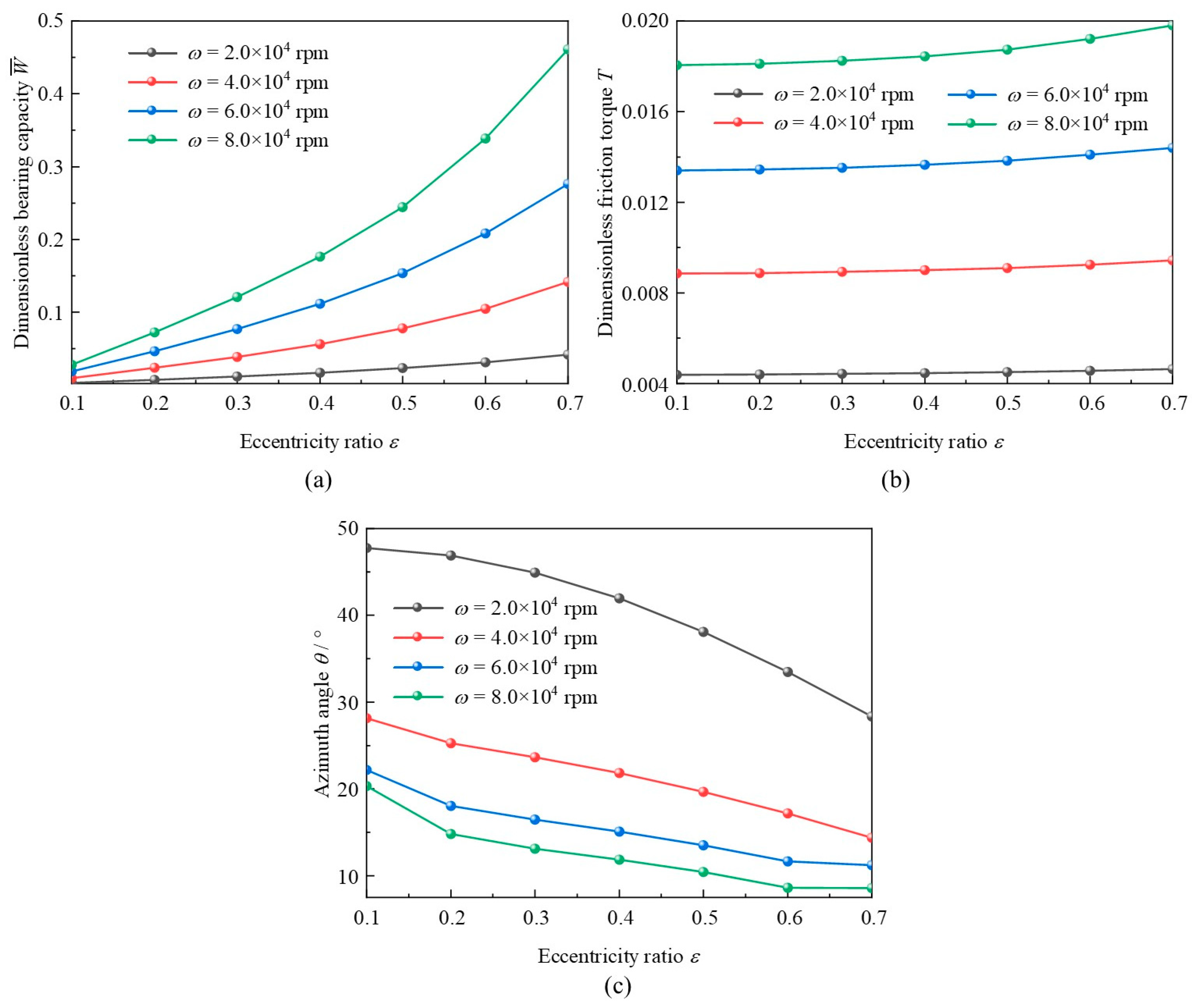
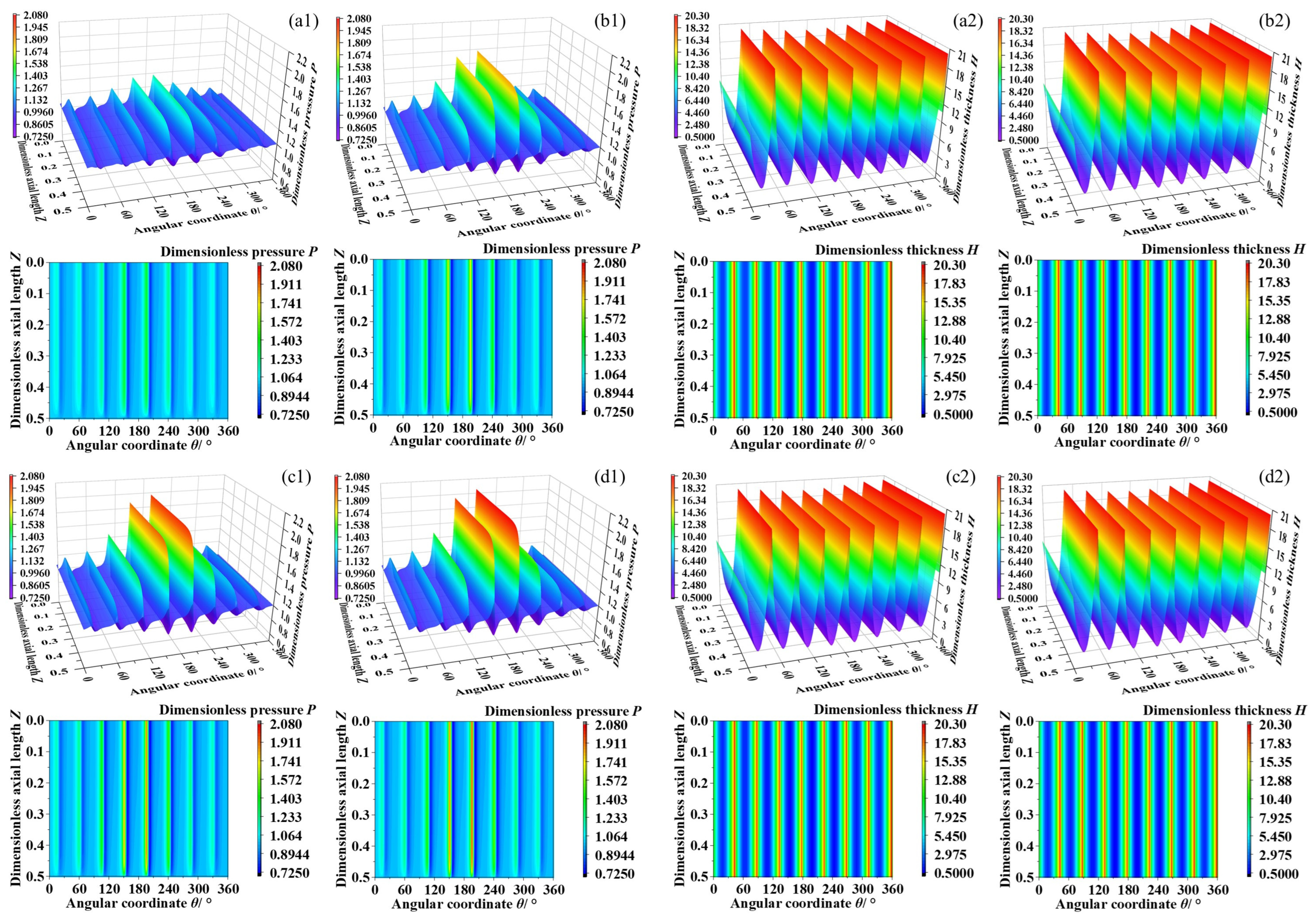
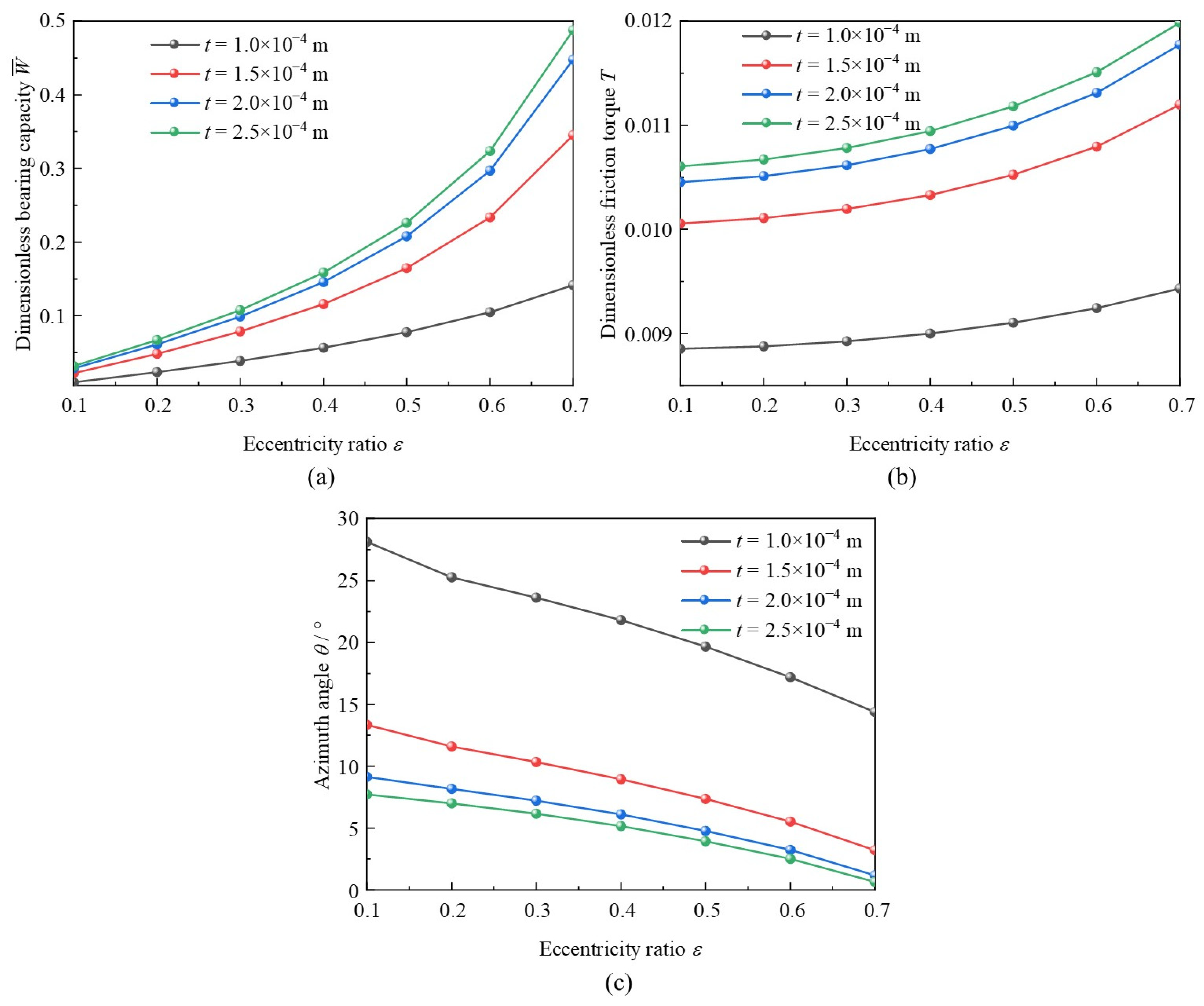
3.1. Eccentricity Ratio

It is well known that the eccentric action plays an important role in the lubrication and bearing characteristics of gas bearings. Therefore, the gas film pressure and thickness under different eccentricity ratios were initially simulated, then the bearing capacity, friction torque, and azimuth angle were calculated. Due to the symmetrical relationship, the axial midsection was taken as the symmetry plane, and half the length of shaft and corresponding circumferential position was chosen as the calculation area. The three-dimensional and two-dimensional variation distributions of the gas film pressure and thickness are depicted in Figure 7. As shown in Figure 7, when the eccentricity ratio increases from 0.1 to 0.7, the air film pressure on the foil surface near the minimum clearance is significantly higher than that of other foils. The difference expands obviously, which indicates that it could be where the bearing capacity mainly roots in. Moreover, the gas film thickness on each side is higher than that of the middle and differs at a gradually increasing trend. It illustrates that the foil near the minimum clearance could be squeezed by the load and deformed. Comparing the two-dimensional top view with the three-dimensional distribution under the same eccentricity ratio, it can be observed that the peak pressure exists close to the minimum film thickness and exhibits mutual correspondence. It suggests that the gas film is resisting accelerated pressurization at the convergence wedge, which is formed by the interaction between the foil and journal. Subsequently, as the film thickness increases, the gas film undergoes decelerating depressurization at the divergent wedge. As depicted in Figure 8, when the eccentricity ratio increases, the peak pressures demonstrate outward expanding trends, whereas the maximum peak pressure exhibits more pronounced variation. In contrast, the minimum film thickness gradually diminishes at an amplitude of variation, which is not as conspicuous as the pressure peak. It can be attributed to more substantial aerodynamic influence being exerted by the foil deformation on the squeezing action. Additionally, the foil thickness is far less than that of the initial bearing clearance by orders of magnitude; thus, the impact on film thickness is comparatively unobvious. Figure 9 illustrates the variations in bearing capacity, friction torque, and azimuth angle with respect to bearing numbers under different eccentricity ratios. As seen from Figure 9a, the bearing capacity is pronouncedly enhanced at higher eccentricity ratio. The friction torque demonstrates an almost linear ascent with the rise in bearing numbers. It indicates that the influence of eccentricity ratio on the foil bearing is not as remarkable as that of traditional rigid bearings or rolling bearings, which can be primarily attributed to the increase in gas film thickness caused by foil deformation. Additionally, the azimuth angle exhibits a decrement with the increase in eccentricity ratio and bearing numbers. However, at larger eccentricity ratio and bearing number, for instance ε = 0.7 and Λ = 30, respectively, the decreasing trend of the azimuth angle slows down. It suggests that when under larger bearing number, the reinforcement effect by the increased eccentricity ratio on bearing operational stability could be receded.

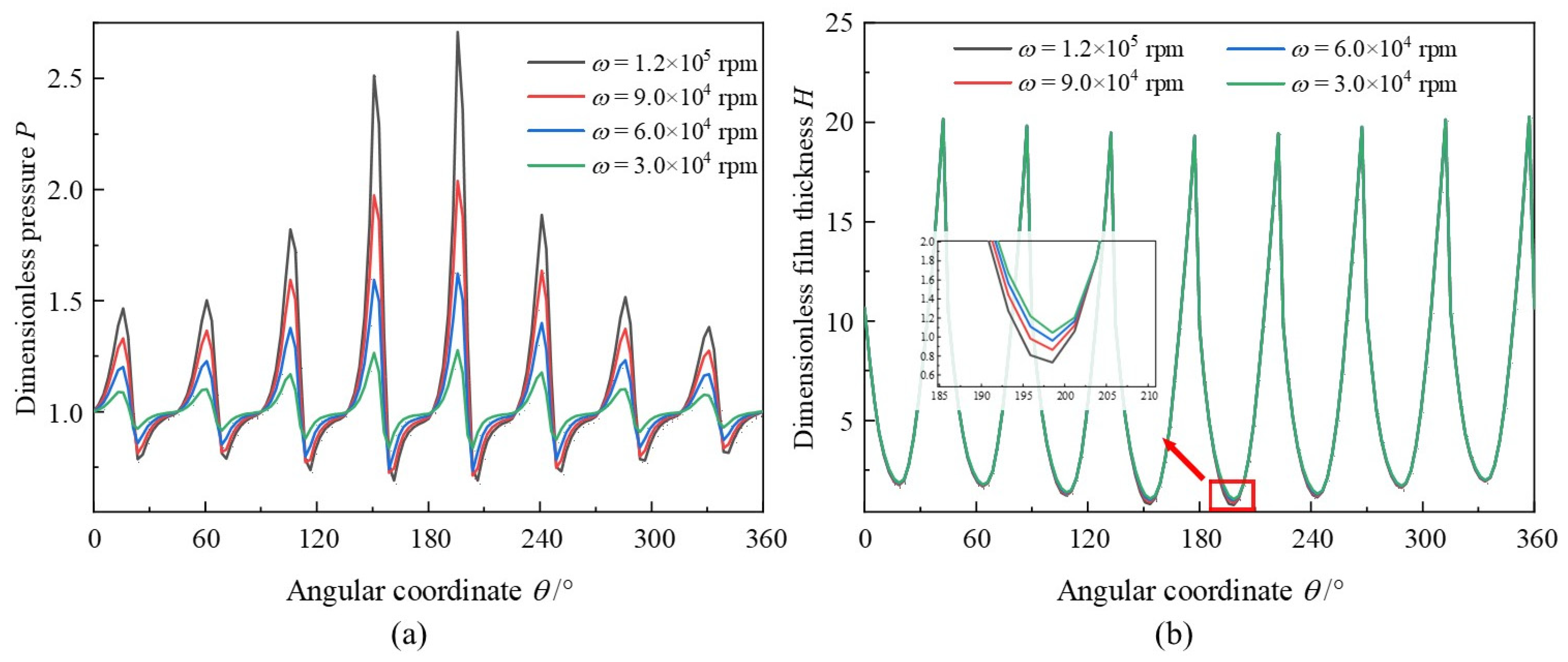
3.2. Bearing Speed

As illustrated in the three-dimensional distribution of gas pressure in Figure 10, with the increase in bearing speed, the gas pressure close to the minimum clearance on the foil surface shows a notable augmentation, and the difference in pressure peaks gradually expands. In contrast, the gas film thickness exhibits a downward concave trend at the minimum clearance and an upward bulge at each end. In general, the difference in film thickness is not as obvious as gas pressure, whereas the influence of bearing speed is more distinct than the eccentricity ratio. As seen from Figure 11, when the bearing speed is accelerated from ω = 3.0 × 10⁴ rpm to ω = 1.2 × 10⁵ rpm, the maximum pressure peak is rapidly increased. Nevertheless, the decrease in film thickness is not so obvious, which indicates that the foil deformation may not be the primary cause for the variation in film thickness. Figure 12 depicts the variations in bearing capacity, friction torque, and azimuth angle versus different bearing speeds. It is observed that the bearing capacity is lifted with the increase in bearing speed, and the effect is more evident at larger eccentricity ratio. In contrast, the friction torque remains stable until the eccentricity ratio exceeds a certain threshold at higher bearing speed, with a slight increase being exhibited. It could be attributed to the foil deformation caused by the increased bearing speed. Additionally, the interesting relationship of the azimuth angle with bearing speed and eccentricity ratio is observed. Within the research parameters, the azimuth angle is decreased with the increase in bearing speed and exhibits an overall decline trend with the increase in eccentricity ratio, which indicates that the operational stability of the bearing is improved. It is worth noting that when exceeding certain high bearing speeds, such as ω = 6.0 × 10⁴ rpm, the decrease in azimuth angle with increasing eccentricity ratio is affected. It could be ascribed to the fact that when under high eccentricity ratio, the potential for further compression of lubrication gas film in the minimum clearance is limited. It indicates that if keeping an appropriately high bearing speed, it will be beneficial to the operational stability of bearing.

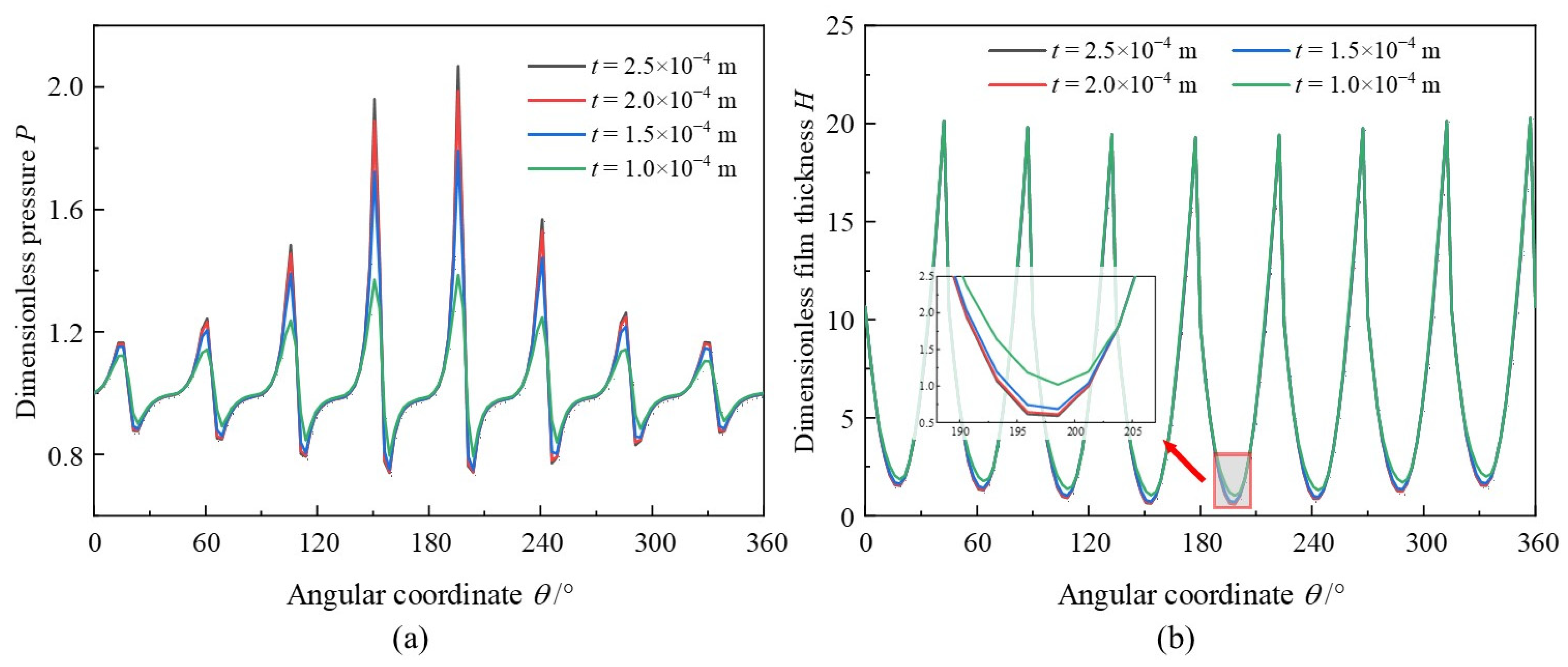
3.3. Foil Thickness

The three-dimensional and two-dimensional distributions of lubrication gas film pressure and thickness under different foil thicknesses are illustrated in Figure 13. With the increase in foil thickness, the maximum pressure around the minimum film clearance is obviously increased at a declining extent, whereas the minimum film pressure is slightly decreased. Additionally, as depicted in Figure 14, with the foil thickness increasing from t = 1.0 × 10⁻⁴ m to t = 2.5 × 10⁻⁴ m, the maximum pressure peak is rapidly escalated; in contrast, the minimum pressure peak is slightly decreased. As seen from Figure 15, the bearing capacity, friction torque, and azimuth angle all vary with the change in foil thicknesses under different eccentricity ratios. As the foil thickness is increased, both the bearing capacity and friction torque are promoted, whereas the azimuth angle is decreased and the variations are more pronounced at larger eccentricity ratio. It is noteworthy that, as illustrated in Figure 15a, within the scope of parameters investigated in current research, the influence of increased foil thickness on the growth amplitude of the bearing capacity is reducing because, at larger foil thickness, the overall stiffness matrix composed by top and bump foils located on the foil’s backside will be strengthened. However, when it exceeds a certain threshold of foil thickness, the deformation resistance becomes more challenging, and the variation scope of the gas film thickness and pressure caused by foil deformation will be constrained. Hence, the increasing rate of bearing capacity tapers off. It indicates that the increase in foil thickness may not always be beneficial, and an optimal value of the foil thickness may exist for the promotion of bearing load capacity, which also confirms the observed phenomenon and conclusion by Li et al. [32]. As shown in Figure 15b, the friction torque is magnified at larger foil thickness and gradually increased with the rise in eccentricity ratio. It can be attributed to the relationships among clearance size, eccentricity ratio, and foil thickness because, at lower eccentricity ratios, the clearance is relatively large, resulting in the minor changes in friction torque. Whereas, at larger eccentricity ratio, the minimum clearance will be decreased and the friction torque is intensified. Additionally, the minimum clearance will also be reduced under increased foil thickness, which contributes to the growth of friction torque. Nevertheless, if the foil thickness exceeds a certain value, the decrease in film thickness will be quite limited, and the increase amplitude of friction torque will be reduced. Additionally, as depicted in Figure 15c, a decreasing trend of azimuth angle with the rise in foil thickness and eccentricity ratio is exhibited. Notably, the descend range is diminished as the foil thickness is increased. It reflects that within the parametric boundaries of this investigation, the overall stiffness of the bearing could be effectively bolstered by the increase in foil thickness, and the operational stability is strengthened. However, it is noteworthy that when the foil thickness surpasses a certain threshold value, this beneficial effect will be impaired.

The variation in the bearing capacity, friction torque, and azimuth angle versus foil thicknesses under different bearing numbers is depicted in Figure 16. As seen from Figure 16, both the bearing capacity and friction torque exhibit approximately linear increase with the rise in bearing numbers. Furthermore, the bearing capacity and friction torque are elevated at higher foil thickness with diminishing increasing amplitude because the bearing overall stiffness is enhanced with the increase in foil thickness. Additionally, compared with the bearing numbers, the impact of increased foil thickness on the minimum film thickness is less obvious; hence, the enhancement on friction torque is limited. As illustrated in Figure 16c, the azimuth angle decreased rapidly with the rise in bearing numbers and foil thickness. When the bearing numbers and the foil thickness surpass a certain threshold, such as Λ = 30 and t = 2.0 × 10⁻⁴ m, respectively, the azimuth angle will not be further decreased distinctly. It could be attributed to the limited bearing clearance size and gas compressibility. Therefore, if the foil thickness and the bearing number are increased within a certain range, the bearing operational stability could be enhanced. Nevertheless, if the specific range is surpassed, the benefits of increased foil thickness will be diminished.

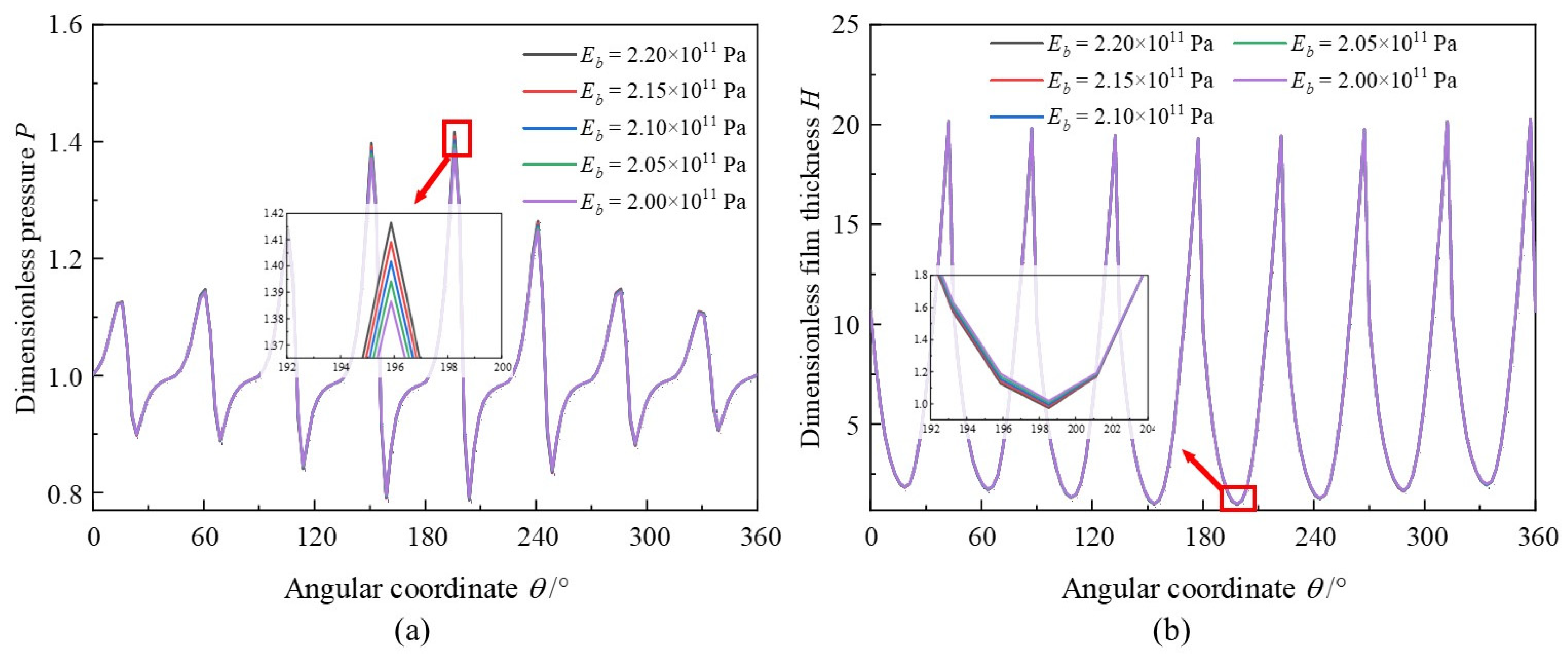
3.4. Foil Elastic Modulus

This section concerns the influence of foil Young’s elasticity modulus on the gas film pressure and thickness, bearing capacity, friction torque, and azimuth angle. As depicted in Figure 17, when the foil elastic modulus is increasing from E_b = 2.00 × 10¹¹ Pa to E_b = 2.20 × 10¹¹ Pa, the maximum peak pressure is slightly increased, and the minimum pressure peak undergoes a marginal decrease. Additionally, the variation in gas film thickness remains inconspicuous. It is revealed in Figure 18a that the bearing capacity is rapidly ascended with the enhancement of bearing numbers and moderately increased with the elevation of foil elastic modulus. Nevertheless, the influence of the latter factor is relatively minor. It can be attributed to the fact that as the foil elastic modulus is increasing, the stiffness coefficient of the bearing will be larger, and the bearing capacity will be improved. However, if compared to other factors, the influence is comparatively limited. As illustrated in Figure 18b, the friction torque is approximately linearly increased with the rise in bearing numbers, and a slight uptick is exhibited as the foil elastic modulus increases. Nevertheless, the overall influence remains unobvious. As seen from Figure 18c, the azimuth angle will be diminished with the rise in bearing numbers and slightly declined with the increase in the foil elastic modulus, respectively. It suggests that through enhancing the foil elastic modulus, the bearing capacity, friction torque, and operational stability can be improved to some extent. However, given the very limited effect degree, this factor can be disregarded when considering the major influencing factors on the bearing static characteristics.

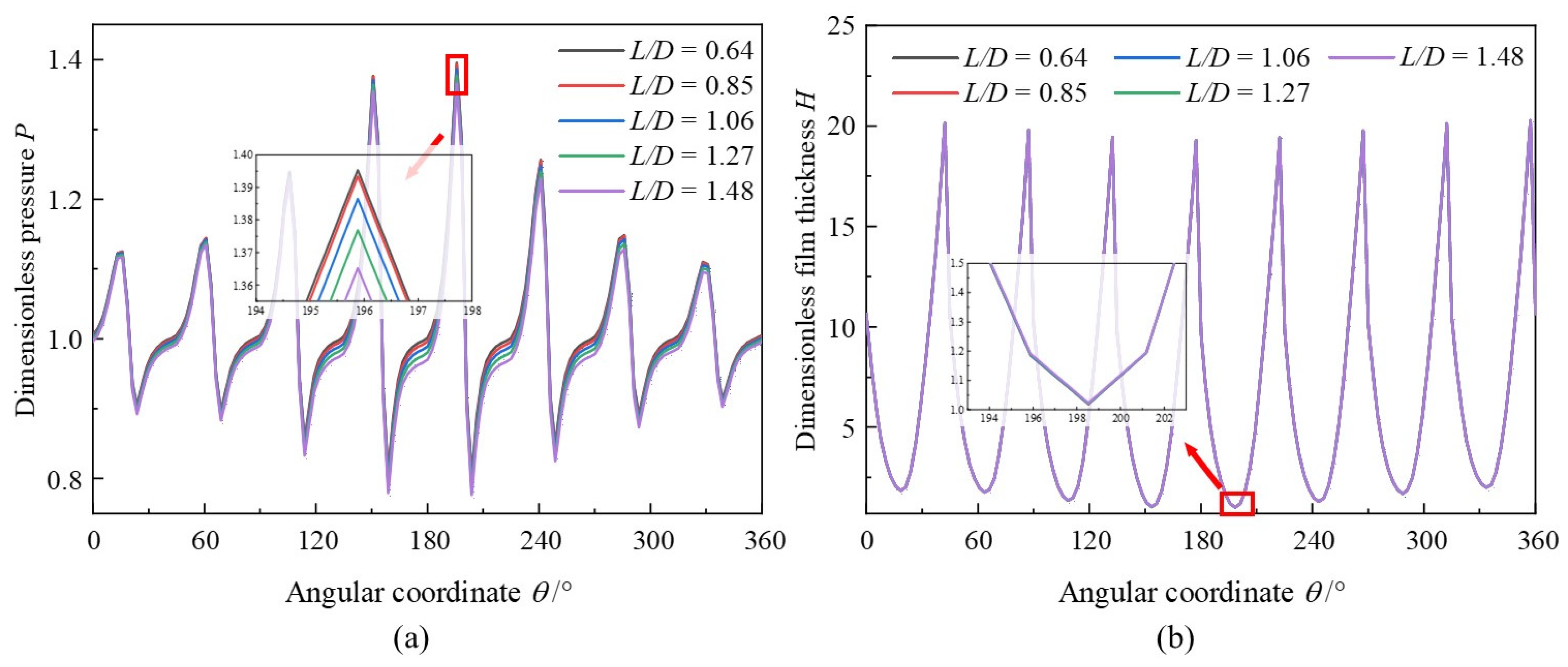
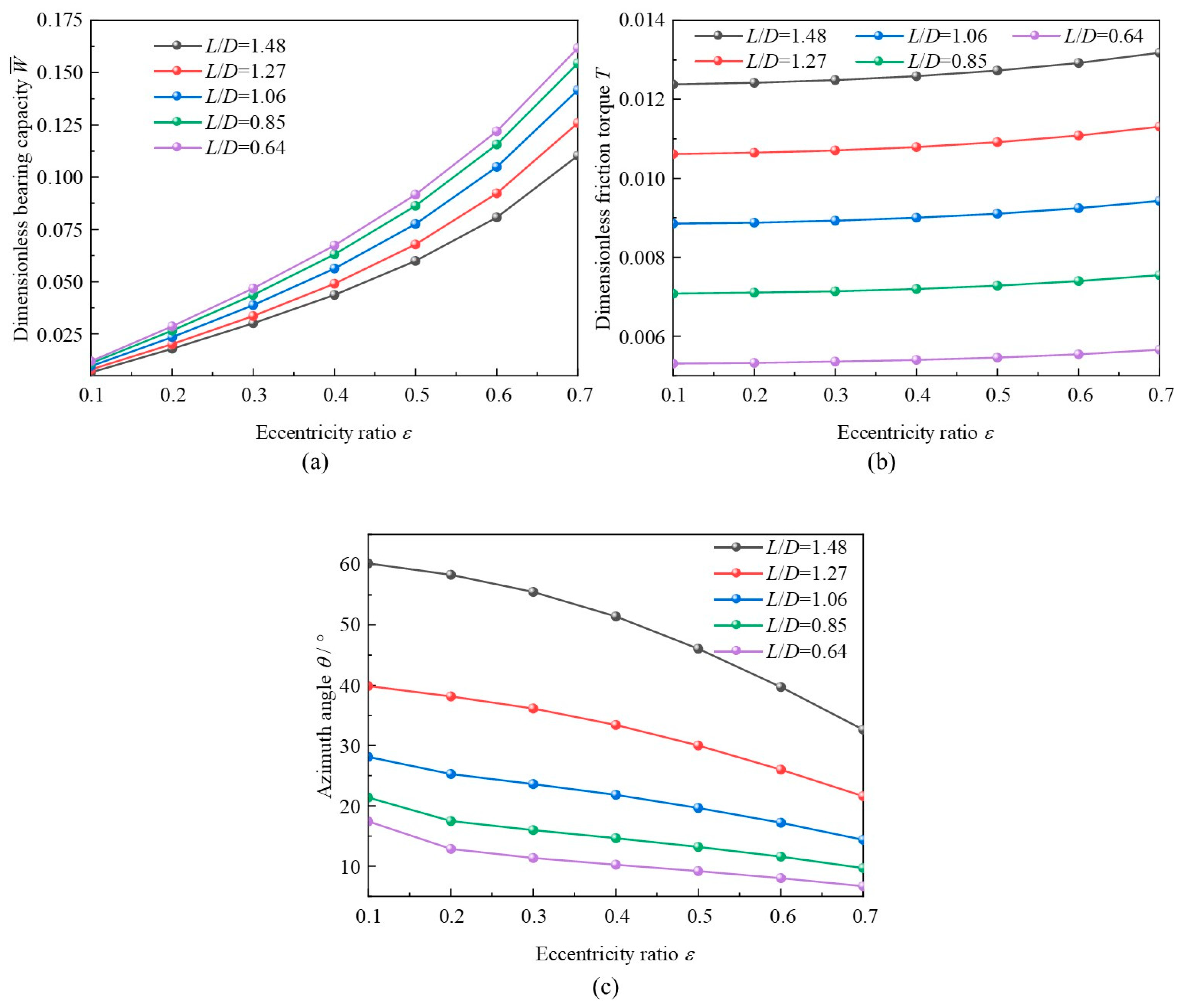
3.5. Length-to-Diameter Ratio

The focus of this section is the influence of length-to-diameter ratio on the gas film pressure and thickness, bearing capacity, friction torque, and azimuth angle. As observed in Figure 19, as the length-to-diameter ratio (L/D) increases from 0.64 to 1.48, the maximum peak pressure is slightly decreased with an increasing amplitude, and the peak area is reduced, whereas the effect on minimum pressure peak is marginal. Additionally, as depicted in Figure 20a, the bearing capacity is increased with the rise in eccentricity ratio and decreased at larger length-to-diameter ratio. It is revealed in Figure 20b that the influence of eccentricity ratio on friction torque is weak, whereas the friction torque is increased with the rise in length-to-diameter ratio. As illustrated in Figure 20c, the azimuth angle will be increased at larger eccentricity ratio or L/D, and this tendency is reinforced at increased L/D. It can be attributed to the fact that as the L/D rises, the maximum gas pressure peak is lifted, and the high-pressure zone is extended. Hence, the effective loading area is expanded, and the bearing capacity and friction torque will be increased. Nevertheless, considering the simultaneously increasing azimuth angle, the bearing operational stability declined to a certain extent. It suggests that it is critical to choose a suitable L/D for the balance relationships among the bearing capacity, friction torque, and azimuth angle, that is, to satisfy the engineering practice and ensure operational stability.

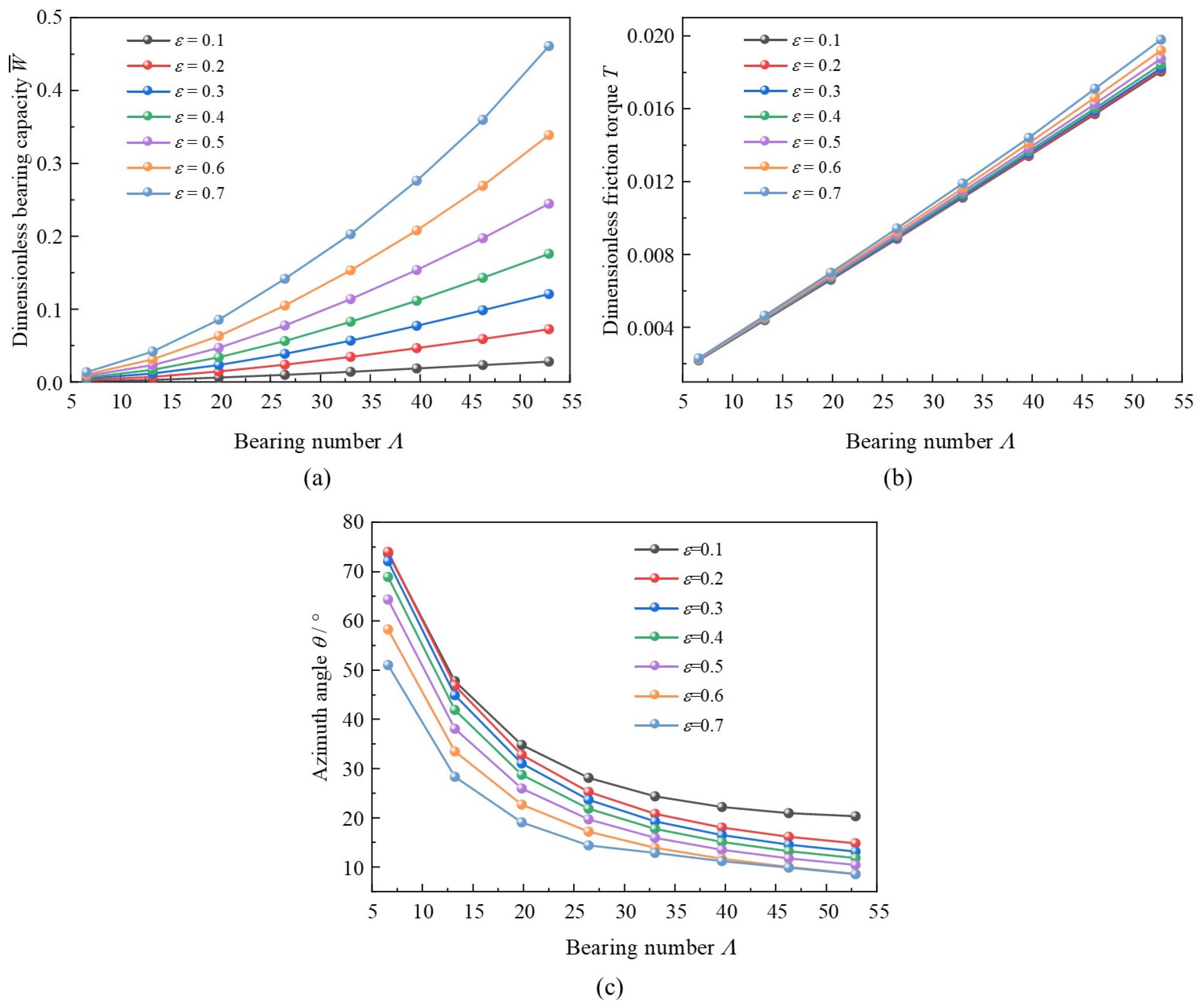
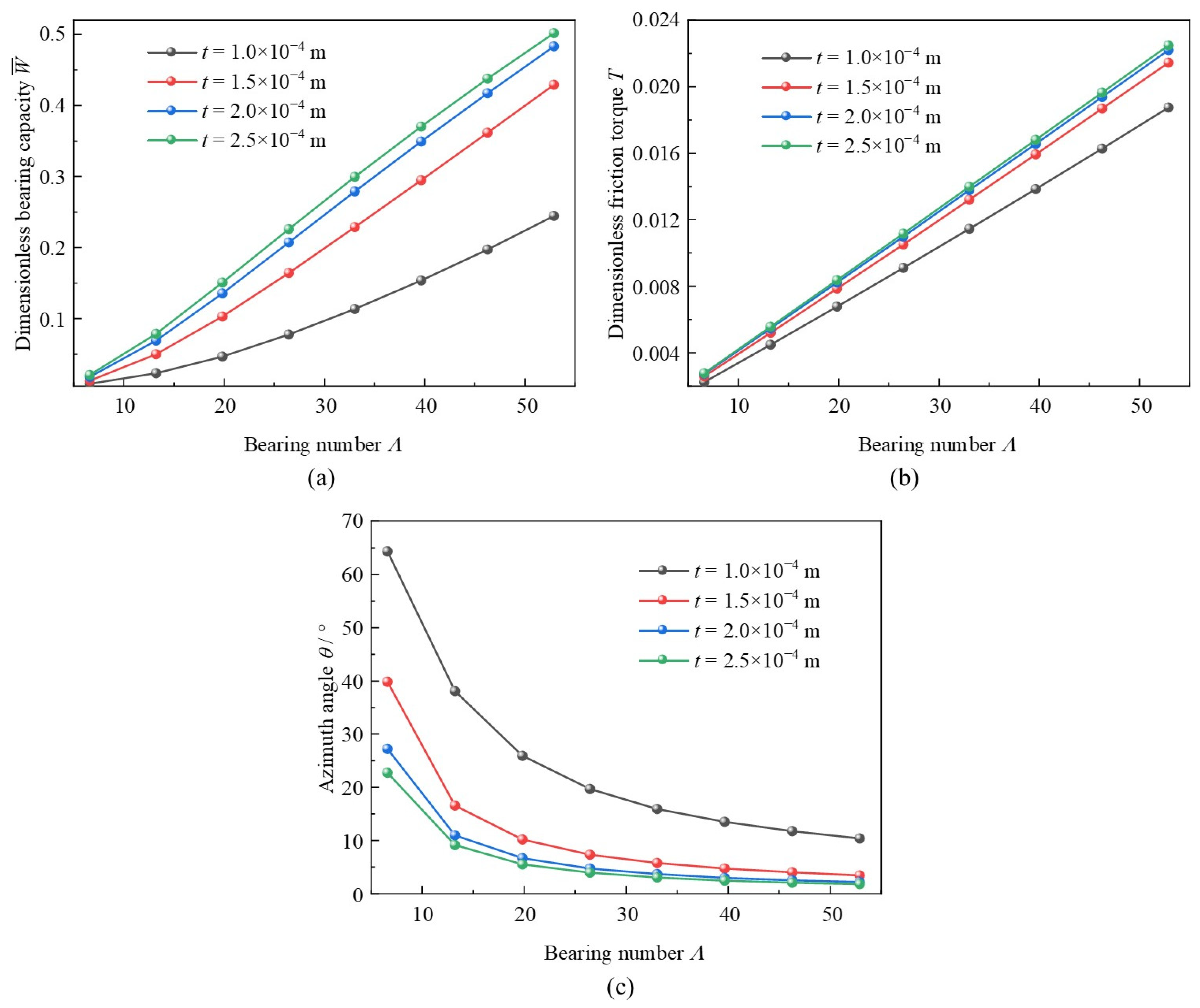
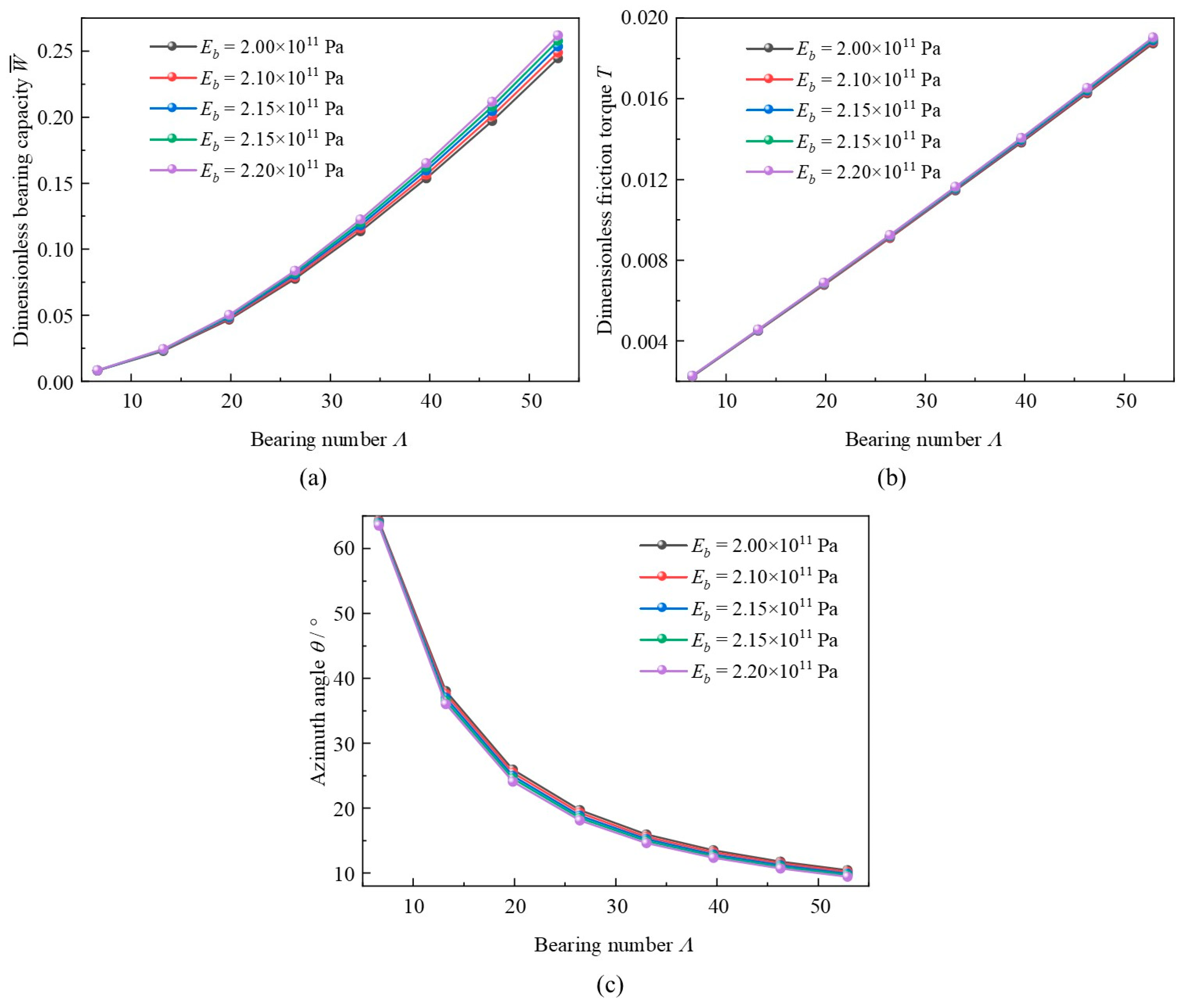
3.6. Bearing Number

In this section, the variation in eccentricity ratio and azimuth angle versus bearing numbers at different vertical bearing loads is discussed. As shown in Figure 21a, the eccentricity ratio is obviously increased with the lift of vertical bearing load. Moreover, the tendency is more distinct at lower bearing numbers. The variation rule is consistent with that of the journal eccentricity ratio versus vertical load at different bearing speeds by Du et al. [12]. It indicates that at the same incremental vertical bearing load, a smaller bearing number signifies a larger variation in eccentricity ratio. It could be explained by the fact that, as the eccentricity ratio increases, a stronger squeezing effect will be exerted on the wedge clearance; hence, more bearing capacity could be supplied at the same bearing number. It indicates that when under the same increasing amplitude of vertical bearing load, the greater variation in eccentricity ratio will occur at a lower bearing number. Correspondingly, the influence of vertical bearing load on the azimuth angle is exhibited in Figure 21b. When it comes to the greater vertical bearing load within limits, the azimuth angle will be decreased. It suggests that the operational stability could be improved to some extent, and the negative coupling effect will be reduced. Additionally, the azimuth angle is generally decreased at larger bearing number, and the operational stability will be improved. It could be explained by the fact that, when under appropriate larger bearing number, the operating position of the bearing shaft is separated from the original orbit of its center, and the more stable operational circumference will be provided. Therefore, if appropriate bearing number and vertical bearing load are selected, the operational stability could be largely improved.

4. Conclusions

In this research, the effective and computationally efficient numerical model for the multi-foil aerodynamic journal bearing with bump-backing foils is established. The foils’ deformation caused by the aeroelastic effect is computed via a one-dimensional beam element model coupled with empirical equations. Simultaneously, the compressible Reynolds equation is solved coupled with the revised gas film thickness equation. Then, the important operational, structural, and geometric parameters’ effects on the static characteristics of bearing are systemically explored and analyzed. Certain conclusions have been reached and are summarized as follows:

(1)

Under larger eccentricity ratio, air film pressure on the foil surface around minimum clearance is significantly higher than that of other foils. The bearing capacity and friction torque could be increased; however, not as prominently as traditional rigid bearings or rolling bearings. The azimuth angle is decreased with the increase in eccentricity ratio and bearing numbers, while at the decreasing declining trend.

(2)

Influenced by the acceleration of bearing speed, the maximum pressure peak and bearing capacity are rapidly increased, which is more evident than the eccentricity ratio. The azimuth angle could be decreased with the increase in bearing speed and eccentricity ratio, while at an overall declining trend. Notably, the decrease could be receding when it surpasses a high eccentricity ratio threshold under large bearing speed.

(3)

Increased foil thickness could lead to friction torque promoting and azimuth angle decreasing at reducing amplitude. However, an optimal value of foil thickness may exist for the improvement of bearing load capacity. Foil thickness affects more obviously than bearing speed on friction torque. Increased bearing number could improve the bearing capacity and friction torque linearly, yet decrease the azimuth angle rapidly. However, the influence of typical elastic modulus is not so obvious.

(4)

Higher L/D could hinder capacity, although magnify friction torque and azimuth angle. At the same incremental vertical bearing load, a smaller bearing number signifies a larger variation in eccentricity ratio. With an appropriate low length-to-diameter ratio, large vertical bearing load, and high bearing number, balance between the suitable static characteristics and the requirements of practical applications could be more easily struck.