Modelling of Static and Dynamic Elastomer Friction in Dry Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Methods
2.1.1. Elastomer Materials and Their Characterization
2.1.2. Surfaces and Their Characterization
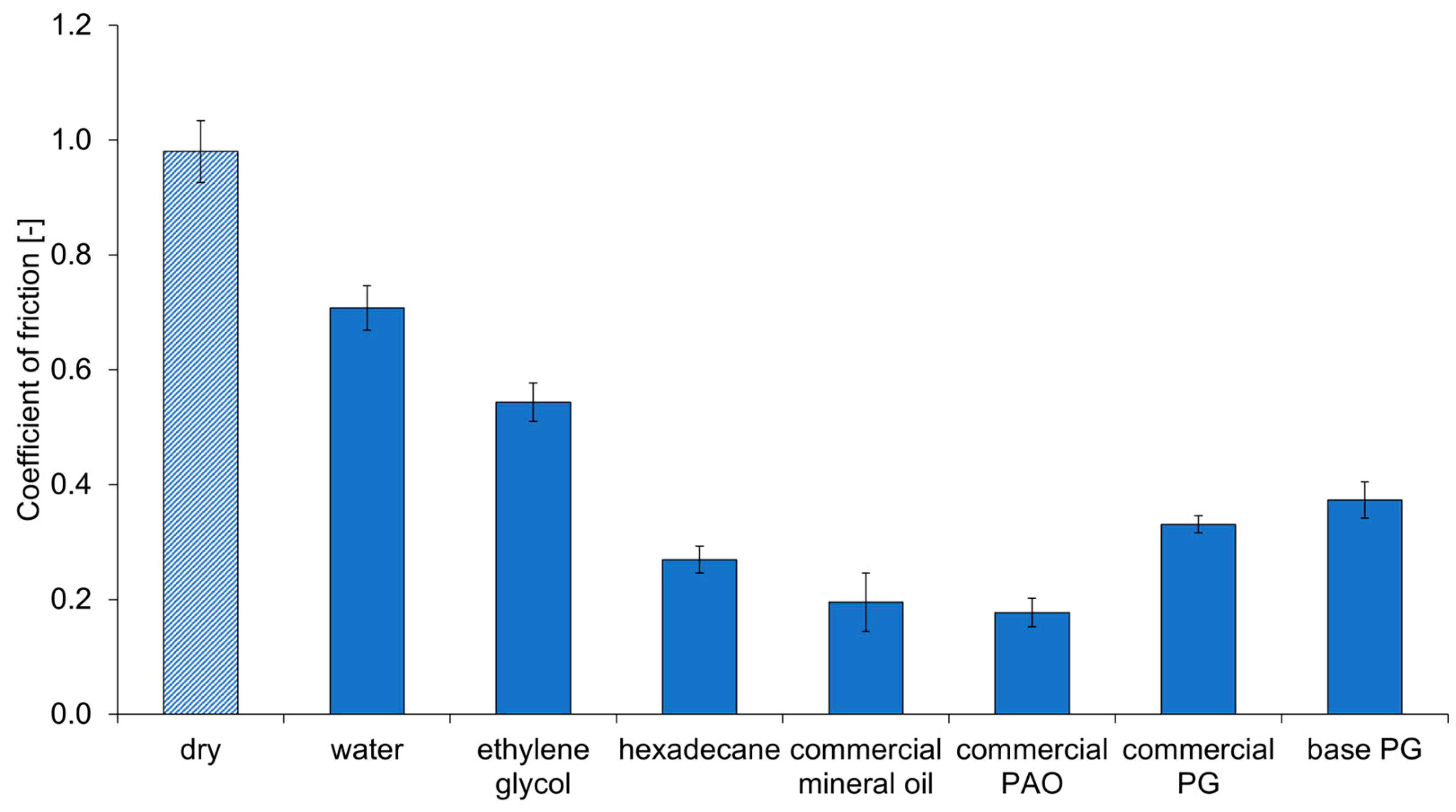
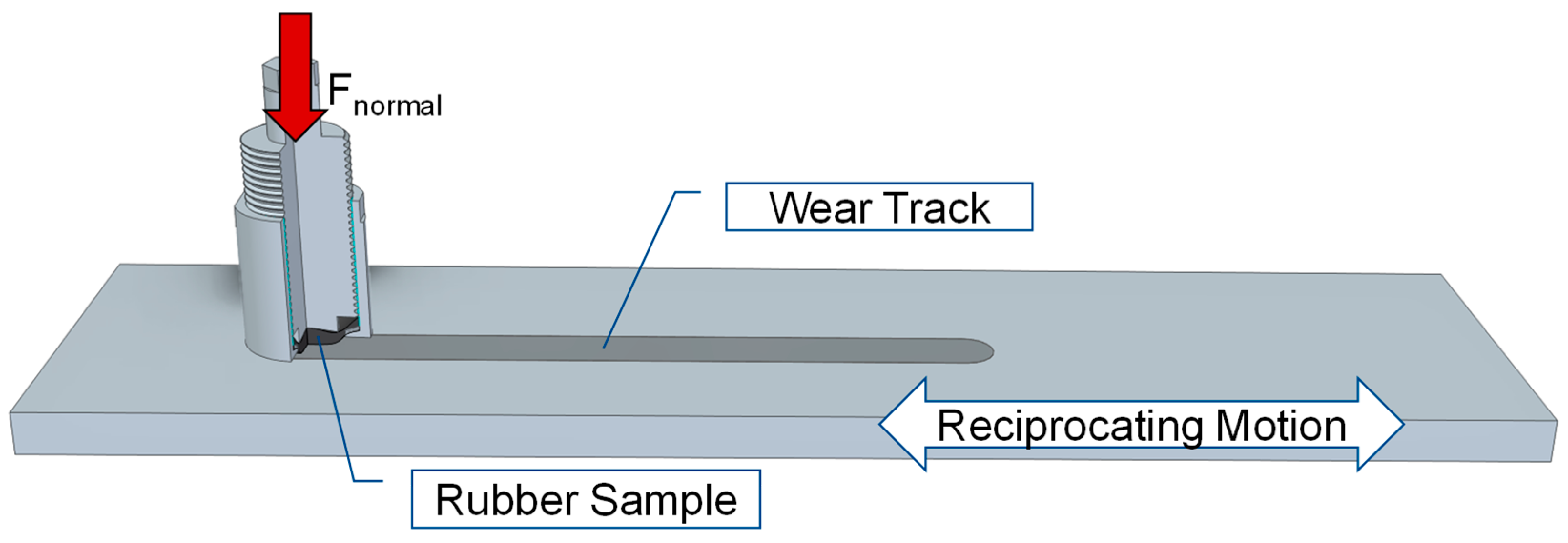
2.1.3. Tribological Testing
2.2. Simulation Methods
2.2.1. Contact Area Calculation
2.2.2. Dynamic Elastomer Friction and Its Contributions
2.2.3. Static Friction Model and Its Contributions
3. Results & Discussion
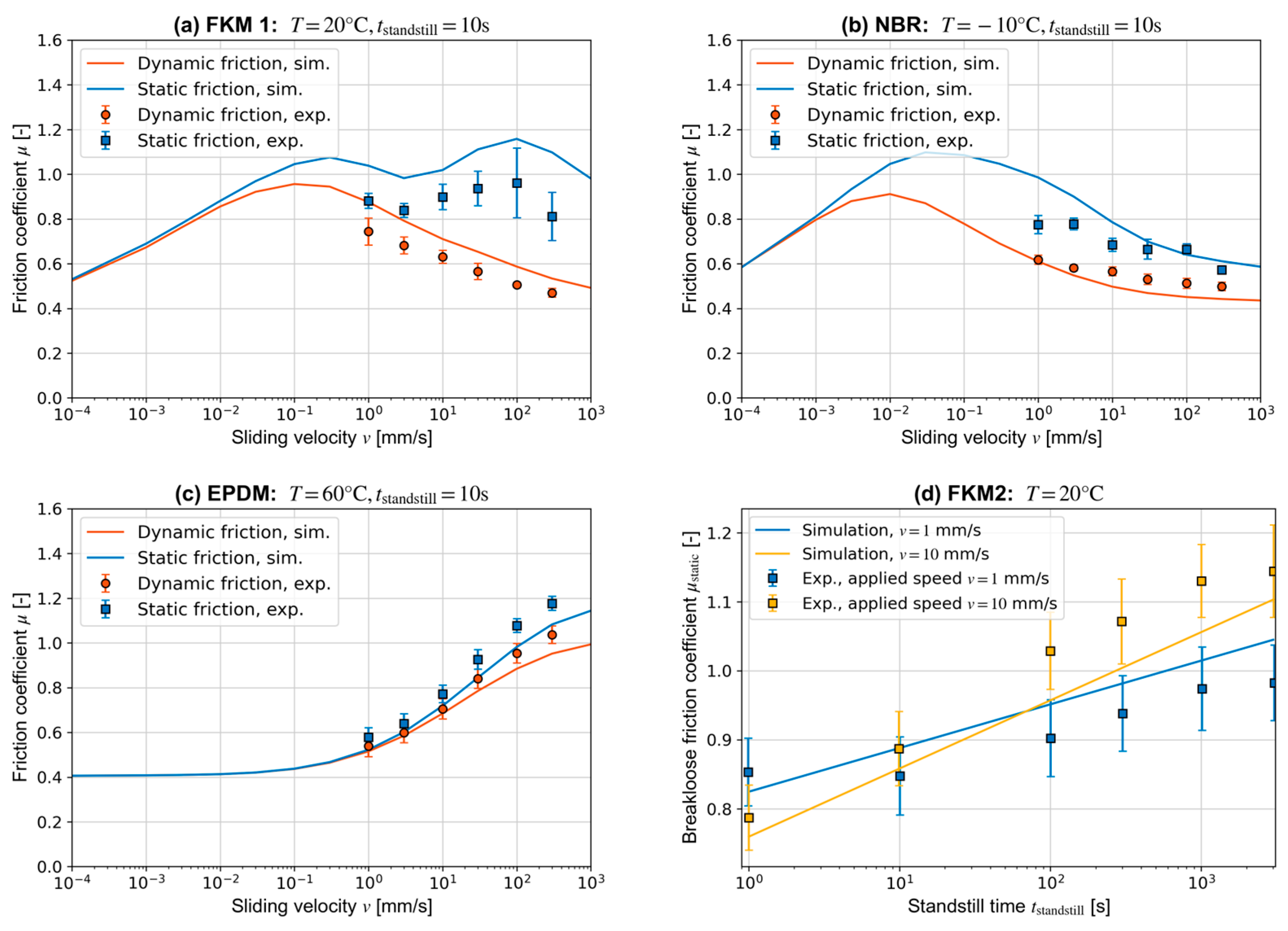
3.1. Model Parametrization and Comparison with Experiments
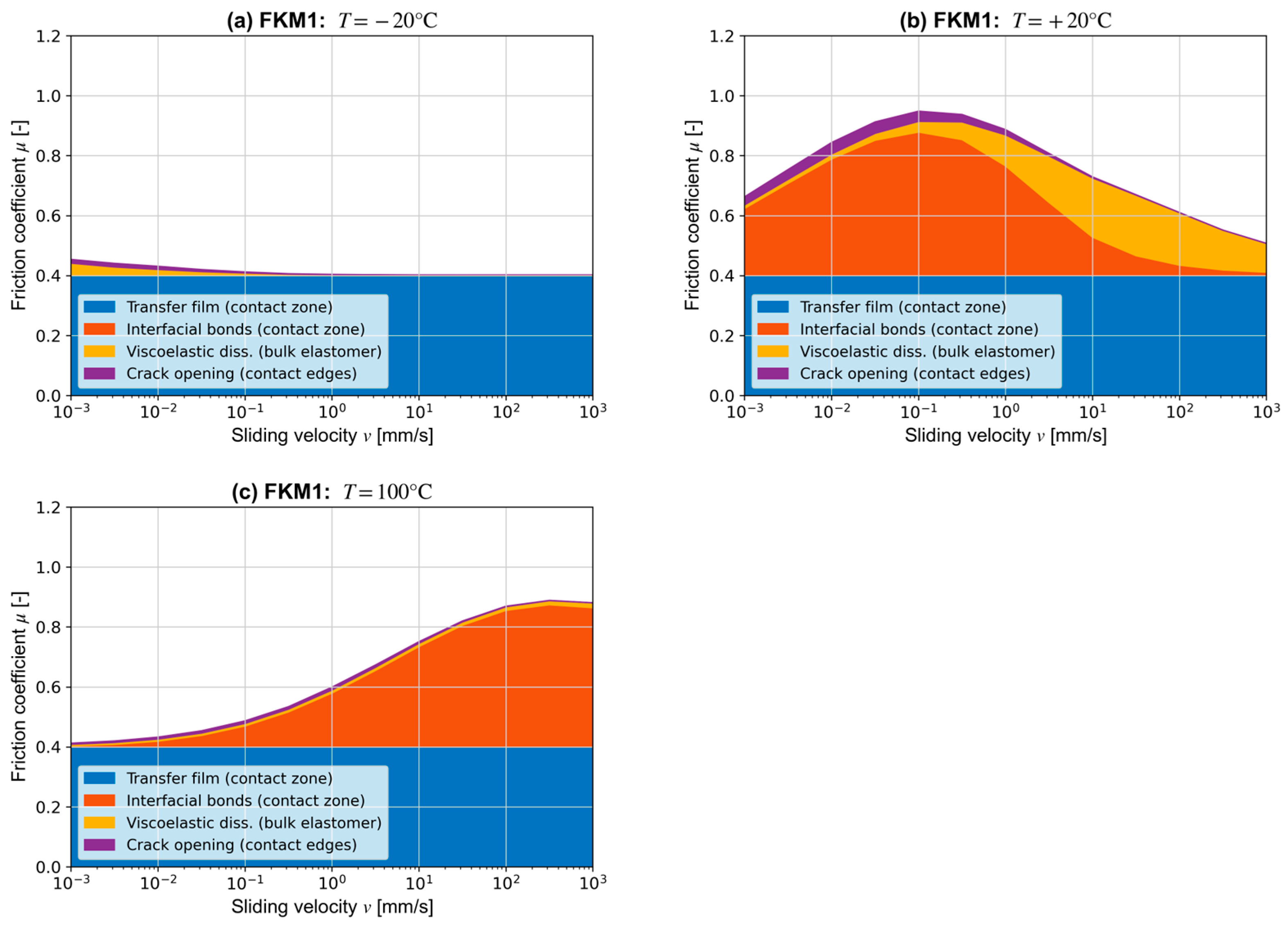
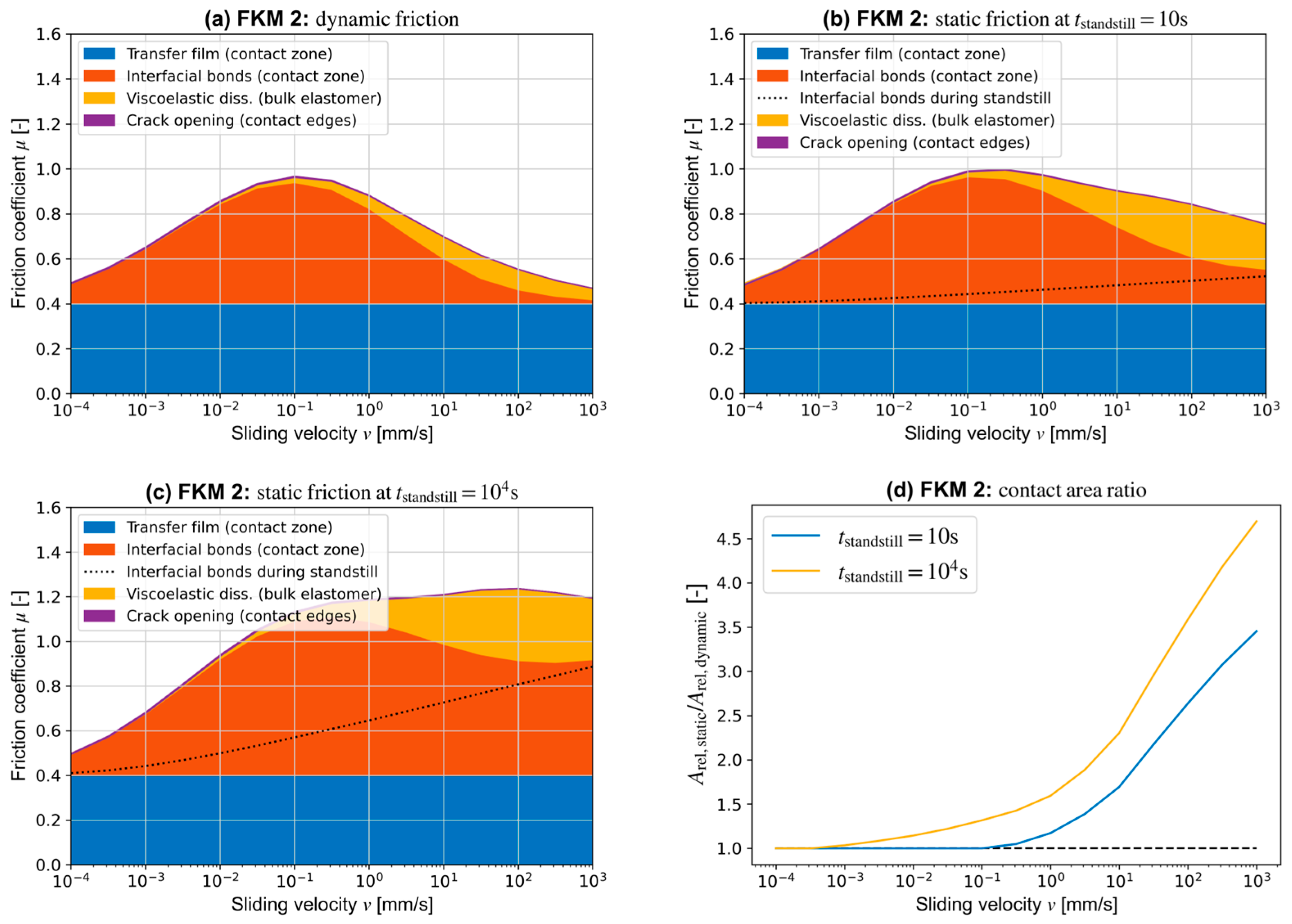
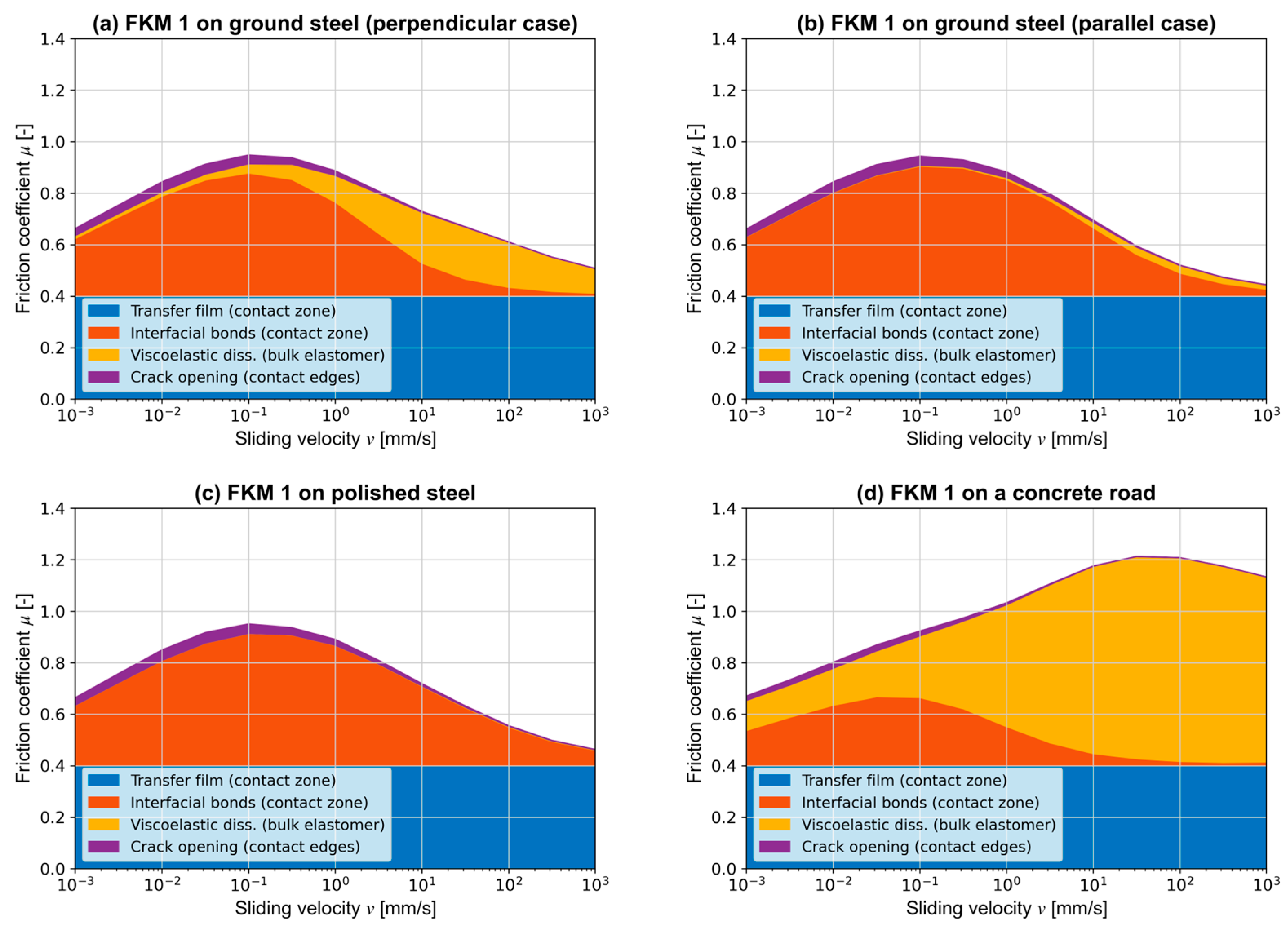
3.2. Relevance of Friction Contributions
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kammüller, M. Zum Abdichtverhalten von Radial-Wellendichtringen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 1986. [Google Scholar]
- Müller, H.K.; Nau, B. Fluid Sealing Technology; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar]
- Persson, B.N.J. Theory of powdery rubber wear. J. Phys. Condens. Matter 2009, 21, 485001. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.J.; Harris, K.; Bennett, A.; Schulze, K.; et al. Meeting the Contact-Mechanics Challenge. Tribol. Lett. 2017, 65, 118. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Scaraggi, M. Theory of adhesion: Role of surface roughness. J. Chem. Phys. 2014, 141, 124701. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J. Contact mechanics for layered materials with randomly rough surfaces. J. Phys. Condens. Matter 2012, 24, 095008. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter 2008, 20, 315011. [Google Scholar] [CrossRef]
- Tiwari, A.; Persson, B.N.J. Physics of suction cups. Soft Matter 2019, 15, 9482–9499. [Google Scholar] [CrossRef]
- Persson, B.N.J. Fluid Leakage in Static Rubber Seals. Tribol. Lett. 2022, 70, 31. [Google Scholar] [CrossRef]
- Fischer, F.J.; Schmitz, K.; Tiwari, A.; Persson, B.N.J. Fluid Leakage in Metallic Seals. Tribol. Lett. 2020, 68, 125. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Larsson, R.; Almqvist, A. Modelling of leakage on metal-to-metal seals. Tribol. Int. 2016, 94, 421–427. [Google Scholar] [CrossRef]
- Jin, L.; Cheng, Y.; Zhang, K.; Xue, Z.; Liu, J. Axisymmetric model of the sealing cylinder in service: Analytical solutions. J. Mech. 2021, 37, 404–414. [Google Scholar] [CrossRef]
- Tiwari, A.; Miyashita, N.; Espallargas, N.; Persson, B.N.J. Rubber friction: The contribution from the area of real contact. J. Chem. Phys. 2018, 148, 224701. [Google Scholar] [CrossRef]
- Tolpekina, T.V.; Persson, B.N.J. Adhesion and Friction for Three Tire Tread Compounds. Lubricants 2019, 7, 20. [Google Scholar] [CrossRef]
- Wohlers, A.; Heipl, O.; Persson, B.N.J.; Scaraggi, M.; Murrenhoff, H. Numerical and Experimental Investigation on O-Ring-Seals in Dynamic Applications. Int. J. Fluid Power 2009, 10, 51–59. [Google Scholar] [CrossRef]
- Dowson, D. History of Tribology; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Almqvist, A. On the Effects of Surface Roughness in Lubrication. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2006. [Google Scholar]
- Persson, B.N.J.; Scaraggi, M. Lubricated sliding dynamics: Flow factors and Stribeck curve. Eur. Phys. J. E 2011, 34, 113. [Google Scholar] [CrossRef] [PubMed]
- Bongaerts, J.H.H.; Foutouni, K.; Stokes, J.R. Soft-tribology: Lubrication in a compliant PDMS–PDMS contact. Tribol. Int. 2007, 40, 1531–1542. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Mugele, F. Squeeze-out and wear: Fundamental principles and applications. J. Phys. Condens. Matter 2004, 16, 295–355. [Google Scholar] [CrossRef]
- Martin, A.; Clain, J.; Burguin, A.; Brochard-Wyart, F. Wetting transitions at soft, sliding interfaces. Phys. Rev. E 2002, 63, 031605. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Jacobs, T.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 13001. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Albohr, O.; Tartaglino, U.; Volokitin, A.I.; Tosatti, E. On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. Condens. Matter 2005, 17, R1. [Google Scholar] [CrossRef]
- Yang, C.; Persson, B.N.J. Contact mechanics: Contact area and interfacial separation from small contact to full contact. J. Phys. Condens. Matter 2008, 20, 215214. [Google Scholar] [CrossRef]
- Wang, A.; Müser, M.H. Gauging Persson Theory on Adhesion. Tribol. Lett. 2017, 65, 103. [Google Scholar] [CrossRef]
- Lorenz, B.; Oh, Y.R.; Nam, S.K.; Jeon, S.H.; Persson, B.N.J. Rubber friction on road surfaces: Experiment and theory for low sliding speeds. J. Chem. Phys. 2015, 142, 194701. [Google Scholar] [CrossRef]
- Singh, A.K.; Juvekar, V.A. Steady dynamic friction at elastomer–hard solid interface: A model based on population balance of bonds. Soft Matter 2011, 7, 10601–10611. [Google Scholar] [CrossRef]
- Fortunato, G.; Ciaravola, V.; Furno, A.; Lorenz, B.; Persson, B.N.J. General Theory of frictional heating with application to rubber friction. J. Phys. Condens. Matter 2015, 27, 175008. [Google Scholar] [CrossRef]
- Persson, B.N.J. Rubber friction: Role of the flash temperature. J. Phys. Condens. Matter 2006, 18, 7789–7823. [Google Scholar] [CrossRef]
- Persson, B.N.J. Crack propagation in finite-sized viscoelastic solids with application to adhesion. Europhys. Lett. 2017, 119, 18002. [Google Scholar] [CrossRef]
- Tiwari, A.; Dorogin, L.; Tahir, M.; Stöckelhuber, K.W.; Heinrich, G.; Espallargas, N.; Persson, B.N.J. Rubber contact mechanics: Adhesion, friction and leakage of seals. Soft Matter 2017, 13, 9103–9121. [Google Scholar] [CrossRef] [PubMed]
- Lengiewicz, J.; de Souza, M.; Lahmar, M.A.; Courbon, C.; Dalmas, D.; Stupkiewicz, S.; Scheibert, J. Finite deformations govern the anisotropic shear-induced area reduction of soft elastic contacts. J. Mech. Phys. Solids 2020, 143, 104056. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J. On the origin of why static or breakloose friction is larger than kinetic friction, and how to reduce it: The role of aging, elasticity and sequential interfacial slip. J. Phys. Condens. Matter 2012, 24, 225008. [Google Scholar] [CrossRef] [PubMed]
- Maegawa, S.; Itoigawa, F.; Nakamura, T. New insight into the mechanism of static friction: A theoretical prediction of the effect of loading history on static friction force based on the static friction model proposed by Lorenz and Persson. Tribol. Int. 2016, 102, 532–539. [Google Scholar] [CrossRef]
- Soni, P.; Singh, A.; Katiyar, J. Experiments and Prediction of Hold Time-Dependent Static Friction of a Wet Granular Layer. Tribol. Lett. 2023, 71, 75. [Google Scholar] [CrossRef]
- Creton, C.; Ciccotti, M. Fracture and adhesion of soft materials: A review. Rep. Prog. Phys. 2016, 79, 046601. [Google Scholar] [CrossRef]
- Müser, M.H.; Persson, B.N.J. Crack and pull-off dynamics of adhesive, viscoelastic solids. Europhys. Lett. 2022, 137, 36004. [Google Scholar] [CrossRef]
- Le Gal, A.; Klüppel, M. Investigation and modelling of rubber stationary friction on rough surfaces. J. Phys. Condens. Matter 2008, 20, 015007. [Google Scholar] [CrossRef]



| Material | Typical Application | Color | Cross-Linker | Fillers | Shore Hardness | (°C) |
|---|---|---|---|---|---|---|
| FKM 1 | Radial shaft seals | Red–brown | Bisphenolic | Mineral | 75 | −8 °C |
| FKM 2 | O-rings | Dark brown | Bisphenolic | Mineral | 90 | −6 °C |
| NBR | Radial shaft seals | Blue | Sulphuric | Mineral | 75 | −20 °C |
| EPDM | O-rings | Black | Peroxidic | Carbon black | 75 | −44 °C |
| Parameters | Conditions |
|---|---|
| Stroke | 50 mm |
| Sliding Speeds | 1–300 mm/s |
| Waiting Times Between Strokes | 1–3600 s |
| Temperatures | −40–100 °C (80 °C for NBR) |
| Normal Load | 40 N (approx. 1.3 MPa nominal contact pressure) |
| Material | k [-] | c [-] | u [-] | [-] | |
|---|---|---|---|---|---|
| FKM 1 | 2.2 | 0.16 | 0.89 | 3.35 × 10−4 | 3.06 |
| FKM 2 | 2.0 | 0.19 | 0.89 | 9.12 × 10−4 | 2.62 |
| NBR | 2.8 | 0.29 | 1.1 | 6.73 × 10−3 | 1.78 |
| EPDM | 1.7 | 0.19 | 0.77 | 9.12 × 10−4 | 2.62 |
| Surface | hrms [µm] | [J/m2] | h’rms [-] |
|---|---|---|---|
| Ground steel (perpendicular case) | 0.47 | 0.25 | 0.28 |
| Ground steel (parallel case) | 0.48 | 0.19 | 0.18 |
| Polished steel | 0.059 | 0.0071 | 0.049 |
| Concrete road | 141 | 247 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaiser, F.; Savio, D.; Bactavatchalou, R. Modelling of Static and Dynamic Elastomer Friction in Dry Conditions. Lubricants 2024, 12, 250. https://doi.org/10.3390/lubricants12070250
Kaiser F, Savio D, Bactavatchalou R. Modelling of Static and Dynamic Elastomer Friction in Dry Conditions. Lubricants. 2024; 12(7):250. https://doi.org/10.3390/lubricants12070250
Chicago/Turabian StyleKaiser, Fabian, Daniele Savio, and Ravindrakumar Bactavatchalou. 2024. "Modelling of Static and Dynamic Elastomer Friction in Dry Conditions" Lubricants 12, no. 7: 250. https://doi.org/10.3390/lubricants12070250
APA StyleKaiser, F., Savio, D., & Bactavatchalou, R. (2024). Modelling of Static and Dynamic Elastomer Friction in Dry Conditions. Lubricants, 12(7), 250. https://doi.org/10.3390/lubricants12070250





