The Generation and Evolution of High-Order Wheel Polygonal Wear from the Effects of Wheelset Rotation
Abstract
1. Introduction
2. Dynamics Modeling of Wheel–Rail Coupled Systems
2.1. Rotor Dynamics Model of Wheel–Rail Coupled System
2.2. Longitudinal Creep Force Model
2.3. Lateral Creep Force Model
2.4. Vertical Force Model
2.5. Lateral Self-Excited Vibration Analysis
2.5.1. The Mechanism of Self-Excitation Vibration
2.5.2. Self-Excited Vibration Stability Condition
3. Wheel Polygonal Wear Model
4. The Numerical Simulation
4.1. Stability Analysis
4.2. Parameter Effects
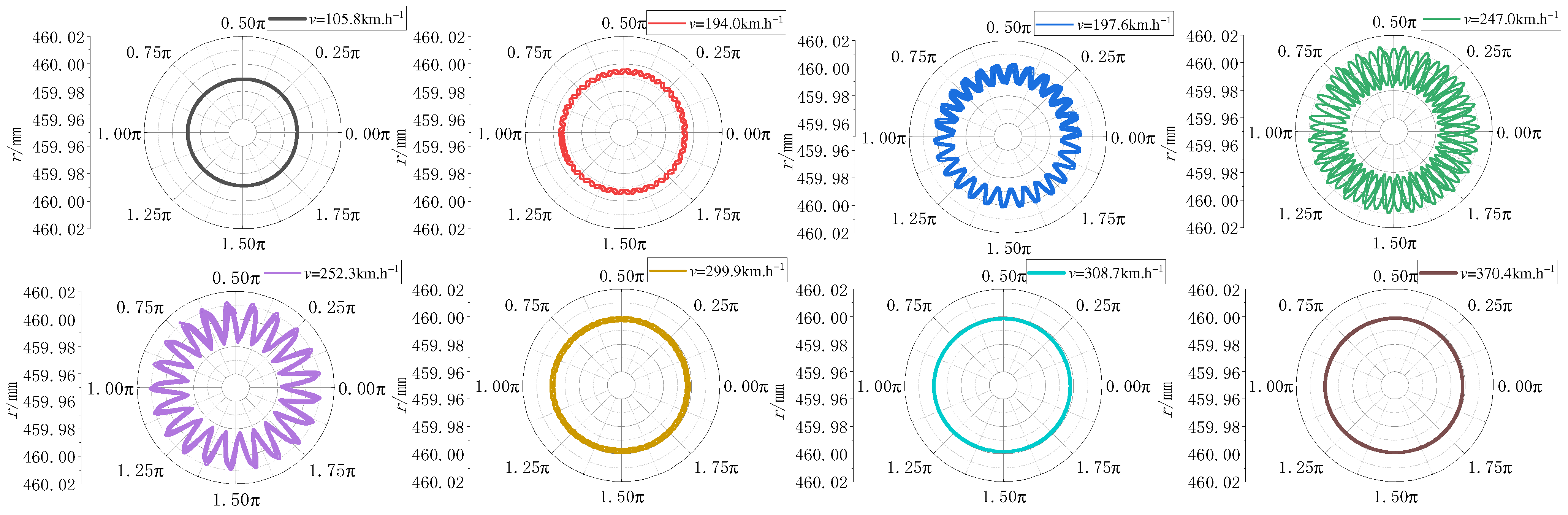
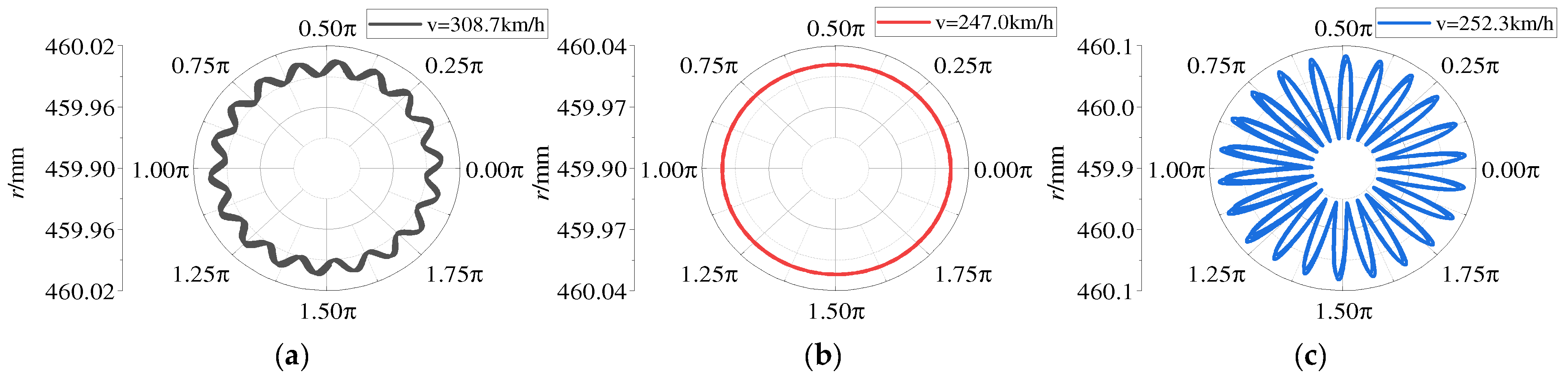
4.2.1. The Effect of the Running Speed
4.2.2. The Effect of the Wheelset Flexibility
4.2.3. The Effect of Primary Suspension Parameters
4.2.4. The Effect of the Rail
5. Analysis of Wheel Polygonal Wear Evolution
5.1. Evolution of Wheel Polygonal Wear at Constant Running Speed
5.2. Evolution of Wheel Polygonal Wear at Variable Running Speed Operations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, J.C.O.; Lunden, R.; Johansson, A. Train-track interaction and mechanisms of irregular wear on wheel and rail surfaces. Veh. Syst. Dyn. 2003, 40, 3–54. [Google Scholar] [CrossRef]
- Tao, G.; Wen, Z.; Jin, X.; Yang, X. Polygonisation of railway wheels: A critical review. Rail. Eng. Sci. 2020, 28, 317–345. [Google Scholar] [CrossRef]
- Jin, X.; Wu, Y.; Liang, S.; Wen, Z.F.; Wu, X.W.; Wang, P. Characteristics, mechanism, influences and countermeasures of polygonal wear of high-speed train wheels. J. Mech. Eng. 2020, 56, 118–136. (In Chinese) [Google Scholar]
- Nielsen, J.C.O.; Johansson, A. Out-of-round railway wheels—A literature survey. Proc. Inst. Mech. Eng. F J. Rail Rapid. Transit. 2000, 214, 79–91. [Google Scholar] [CrossRef]
- Johansson, A.; Nielsen, J.C.O. Out-of-round railway wheels—Wheel-rail contact forces and track response derived from field tests and numerical simulations. Proc. Inst. Mech. Eng. F J. Rail Rapid. Transit. 2003, 217, 135–146. [Google Scholar] [CrossRef]
- Wang, P.; Tao, G.; Yang, X.; Xie, C.; Li, W.; Wen, Z. Analysis of Polygonal Wear Characteristics of Chinese High-Speed Train Wheels. J. Southwest Jiaotong Univ. 2023, 58, 1357–1365. (In Chinese). Available online: http://kns.cnki.net/kcms/detail/51.1277.U.20211124.1532.002.html (accessed on 3 June 2024). (In Chinese).
- Wu, Y.; Wang, J.; Liu, M.; Jin, X.; Hu, X.; Xiao, X.; Wen, Z. Polygonal wear mechanism of high-speed wheels based on full-size wheel-rail roller test rig. Wear 2022, 494–495, 204234. [Google Scholar] [CrossRef]
- Jin, X.; Wu, L.; Fang, J.; Zhong, S.; Ling, L. An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behaviour of a wheel/rail system. Veh. Syst. Dyn. 2012, 50, 1817–1834. [Google Scholar] [CrossRef]
- Tao, G.; Xie, C.; Wang, H.; Yang, X.; Ding, C.; Wen, Z. An investigation into the mechanism of high-order polygonal wear of metro train wheels and its mitigation measures. Veh. Syst. Dyn. 2020, 59, 1557–1572. [Google Scholar] [CrossRef]
- Yang, X.; Tao, G.; Wen, Z. Causes and evolution of asymmetric polygonal wear of metro train wheelsets. Wear 2023, 530–531, 205036. [Google Scholar] [CrossRef]
- Fröhling, R.; Spangenberg, U.; Reitmann, E. Root cause analysis of locomotive wheel tread polygonization. Wear 2019, 432–433, 102911. [Google Scholar] [CrossRef]
- Spangenberg, U. Variable frequency drive harmonics and inter harmonics exciting axle torsional vibration resulting in railway wheel polygonization. Veh. Syst. Dyn. 2019, 58, 404–424. [Google Scholar] [CrossRef]
- Wu, X.; Liang, S.; Chi, M. An investigation of rocking derailment of railway vehicles under the earthquake excitation. Eng. Fail. Anal. 2020, 117, 104913. [Google Scholar] [CrossRef]
- Cai, W.; Chi, M.; Wu, X.; Yang, N.; Huang, H.Z. Effect of wheel initial state on the growth of polygonal wear on high-speed trains. Wear 2023, 526–527, 204894. [Google Scholar] [CrossRef]
- Cai, W.; Chi, M.; Wu, X.; Huang, H.Z. A framework of high-order wheel polygonal wear mitigation for China’s high-speed trains. Mech. Syst. Sig. Proc. 2023, 199, 110487. [Google Scholar] [CrossRef]
- Chen, G.X.; Zhou, Z.R.; Ouyang, H.J.; Jin, X.S.; Zhu, M.H.; Liu, Q.Y. A finite element study on rail corrugation based on saturated creep force-induced self-excited vibration of a wheelset–track system. J. Sound Vib. 2010, 329, 4643–4655. [Google Scholar] [CrossRef]
- Wu, B.; Qiao, Q.; Chen, G.; Lv, J.Z.; Zhu, Q.; Zhao, X.N.; Ouyang, H. Effect of the unstable vibration of the disc brake system of high-speed trains on wheel polygonalization. Proc. Inst. Mech. Eng. F J. Rail Rapid. Transit. 2020, 234, 80–95. [Google Scholar] [CrossRef]
- Meinke, P.; Meinke, S. Polygonalization of wheel treads caused by static and dynamic imbalances. J. Sound Vib. 1999, 227, 979–986. [Google Scholar] [CrossRef]
- Brommundt, E. A simple mechanism for the polygonalization of railway wheels by wear. Mech. Res. Commun. 1997, 24, 435–442. [Google Scholar] [CrossRef]
- Torstensson, P.; Nielsen, J.; Baeza, L. Dynamic train–track interaction at high vehicle speeds-Modelling of wheelset dynamics and wheel rotation. J. Sound Vib. 2011, 330, 5309–5321. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, S. The mechanism of wheel polygonal wear based on rotor dynamics. Veh. Syst. Dyn. 2024, 62, 411–427. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, S. The comprehensive effect of friction self-excited and modal vibration on polygonal wear of high-speed train wheels. Proc. Inst. Mech. Eng. F J. Rail Rapid. Transit. 2023, 237, 763–774. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, S. Polygonal Wear Mechanism of High-Speed Train Wheels Based on Lateral Friction Self-Excited Vibration. Machines 2022, 10, 608. [Google Scholar] [CrossRef]
- Polach, O. A fast wheel-rail forces calculation computer code. Veh. Syst. Dyn. 2000, 33, 728–739. [Google Scholar] [CrossRef]
- Liu, W.; Ma, W.; Luo, S.; Tian, Y. The mechanism of wheelset longitudinal vibration and its influence on periodical wheel wear. Proceedings of the Institution of Mechanical Engineers. Proc. Inst. Mech. Eng. F J. Rail Rapid. Transit. 2016, 232, 396–407. [Google Scholar] [CrossRef]
- Sun, L.; Yao, J.; Hou, F.; Zhao, X. Study on self-excited vibration mechanism of wheel-rail lateral contact system. Appl. Mech. Mater. 2013, 427, 257–261. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Kawamura, A. Maximum adhesive force control in super high speed train. In Proceedings of the Power Conversion Conference—PCC ‘97, Nagaoka, Japan, 6 August 1997. [Google Scholar]
- Kinkaid, N.M.; O’Reilly, O.M.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Morys, B. Enlargement of out-of-round wheel profiles on high speed trains. J. Sound Vib. 1999, 227, 965–978. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. App. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Krause, H.; Poll, G. Wear of wheel-rail surfaces. Wear 1986, 113, 103–122. [Google Scholar] [CrossRef]
- Enblom, R.; Berg, M. Simulation of railway wheel profile development due to wear influence of disc braking and contact environment. Wear 2005, 258, 1055–1063. [Google Scholar] [CrossRef]
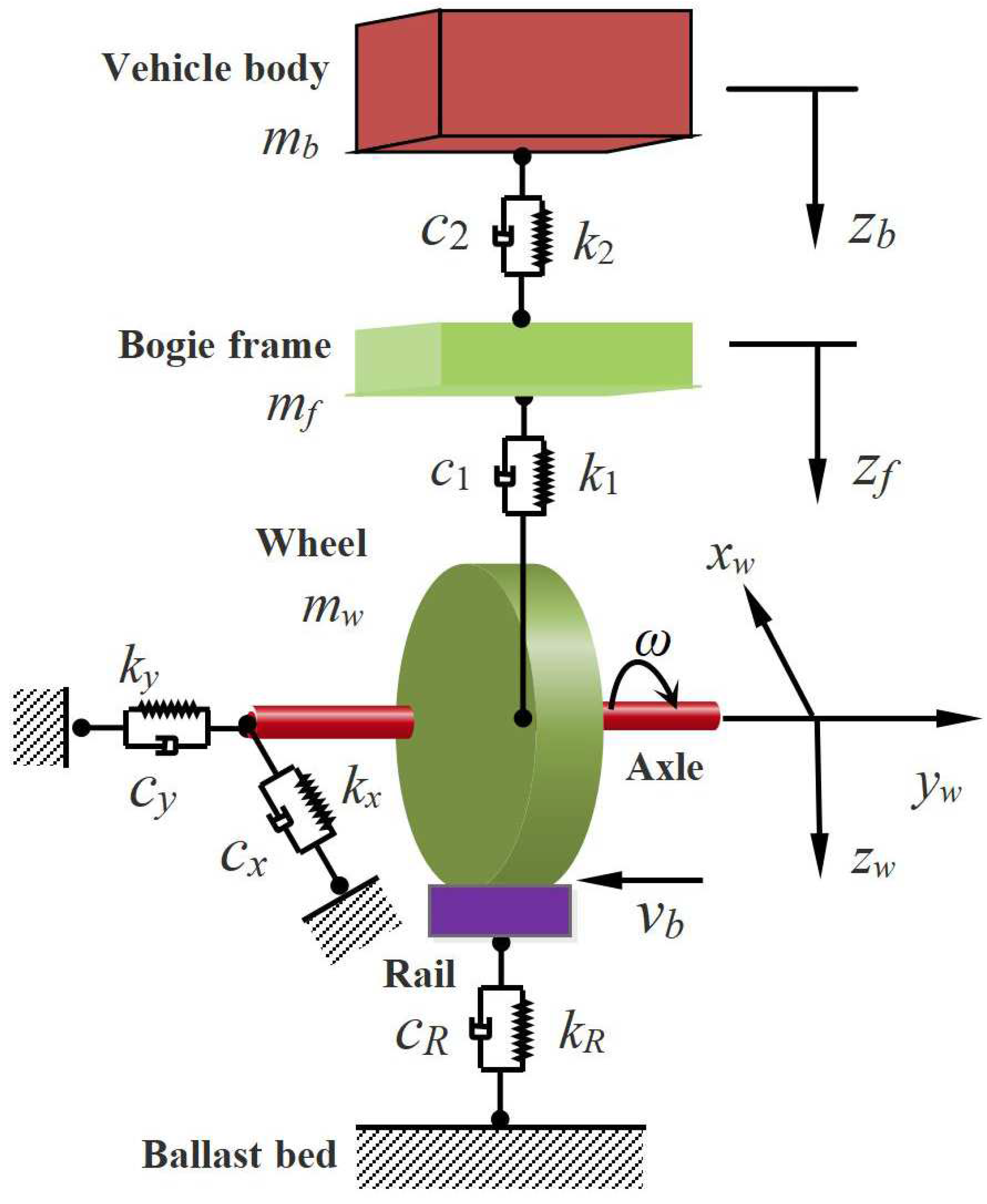
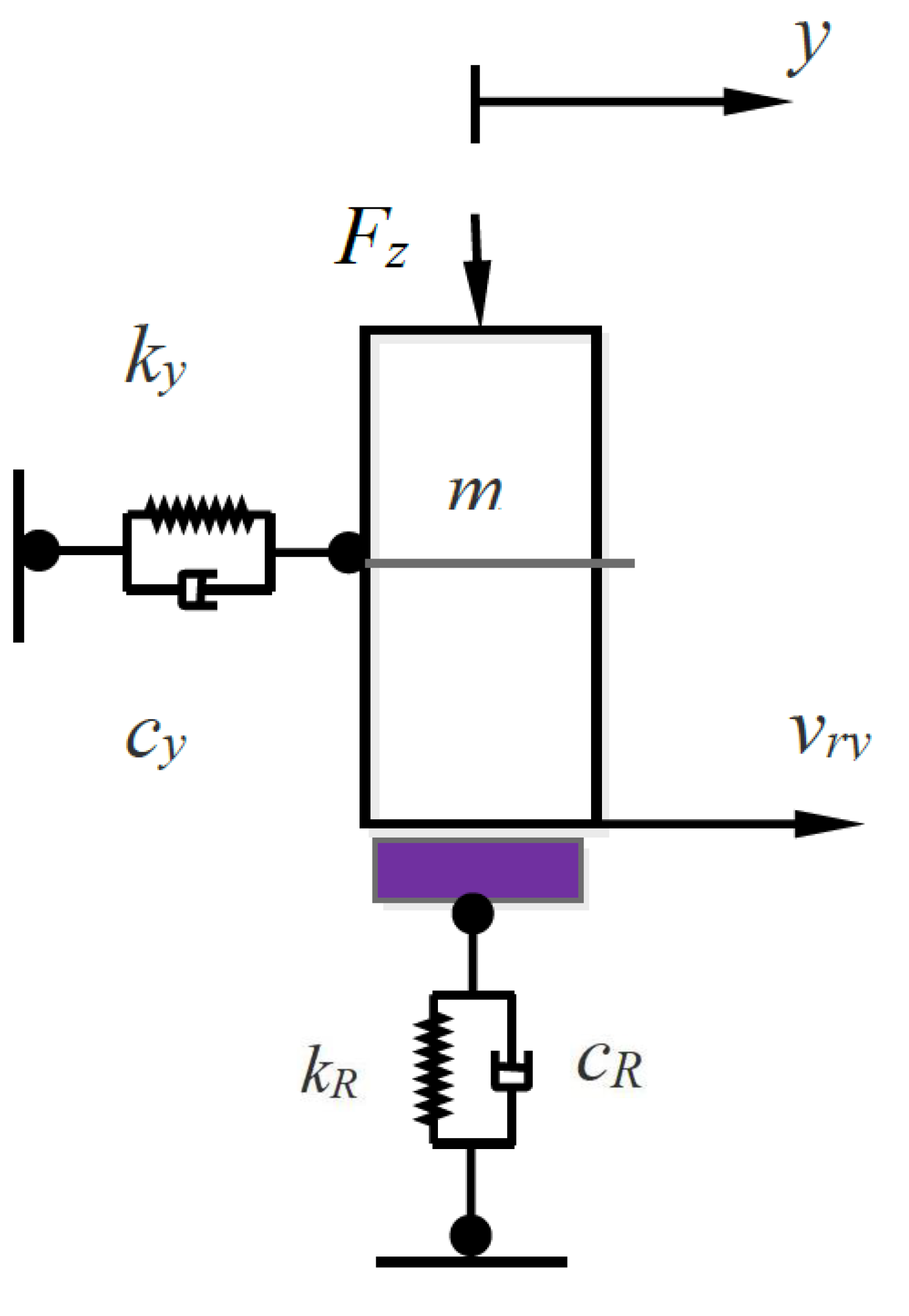
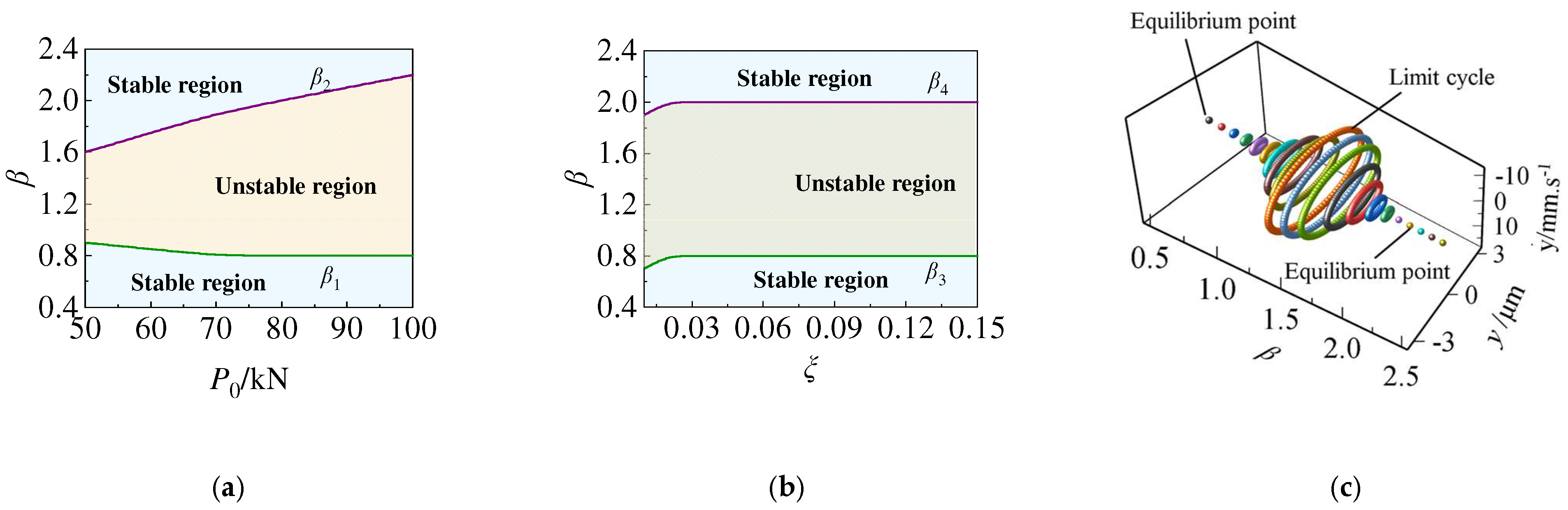


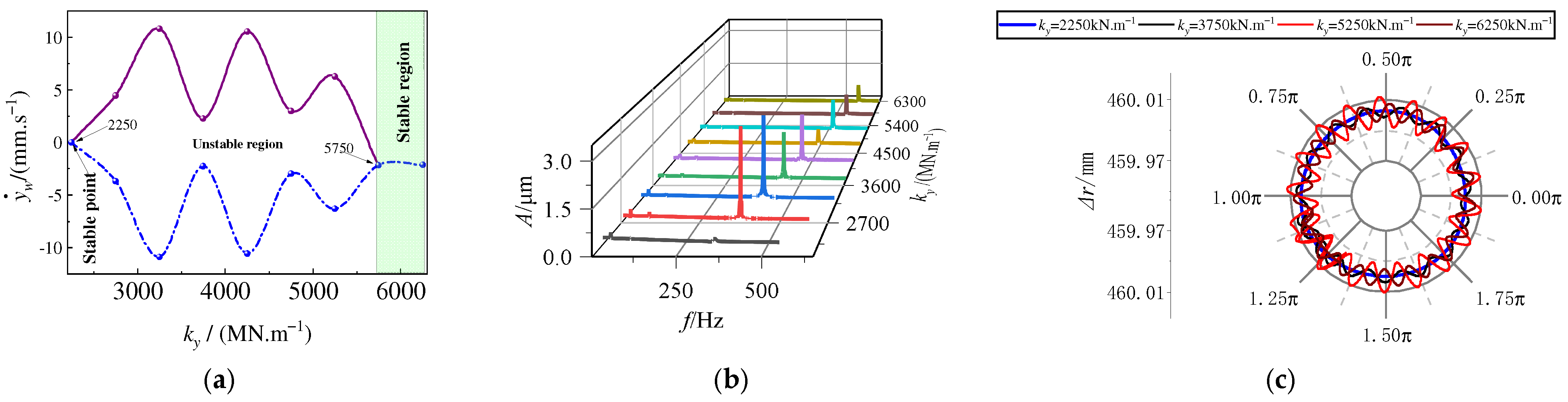


| The Parameter Name | Parameter Values |
|---|---|
| Mass of car body mb/kg | 40,384 |
| Mass of bogie frame mf/kg | 2056 |
| Mass of wheelset mw/kg | 1627 |
| Secondary stiffness k2/(MN·m−1) | 0.80 |
| Secondary damping c2/(kN·s·m−1) | 30 |
| Primary stiffness k1/(MN·m−1) | 2.08 |
| Primary damping c1/(kN·s·m−1) | 20 |
| Wheel diameter D/mm | 920 |
| Wheel load P0/kN | 80 |
| Fastener stiffness kR/(MN·m−1) | 25 |
| Fastener damping cR/(kN·s·m−1) | 15 |
| Eccentricity of wheelset mass ew/(μm) | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Cao, S. The Generation and Evolution of High-Order Wheel Polygonal Wear from the Effects of Wheelset Rotation. Lubricants 2024, 12, 313. https://doi.org/10.3390/lubricants12090313
Dong Y, Cao S. The Generation and Evolution of High-Order Wheel Polygonal Wear from the Effects of Wheelset Rotation. Lubricants. 2024; 12(9):313. https://doi.org/10.3390/lubricants12090313
Chicago/Turabian StyleDong, Yahong, and Shuqian Cao. 2024. "The Generation and Evolution of High-Order Wheel Polygonal Wear from the Effects of Wheelset Rotation" Lubricants 12, no. 9: 313. https://doi.org/10.3390/lubricants12090313
APA StyleDong, Y., & Cao, S. (2024). The Generation and Evolution of High-Order Wheel Polygonal Wear from the Effects of Wheelset Rotation. Lubricants, 12(9), 313. https://doi.org/10.3390/lubricants12090313





