An Analytical Model for Aerostatic Thrust Bearings Based on the Average Pressure of the Area Surrounded by Orifice
Abstract
:1. Introduction
2. Model and Solution
2.1. Geometric Model
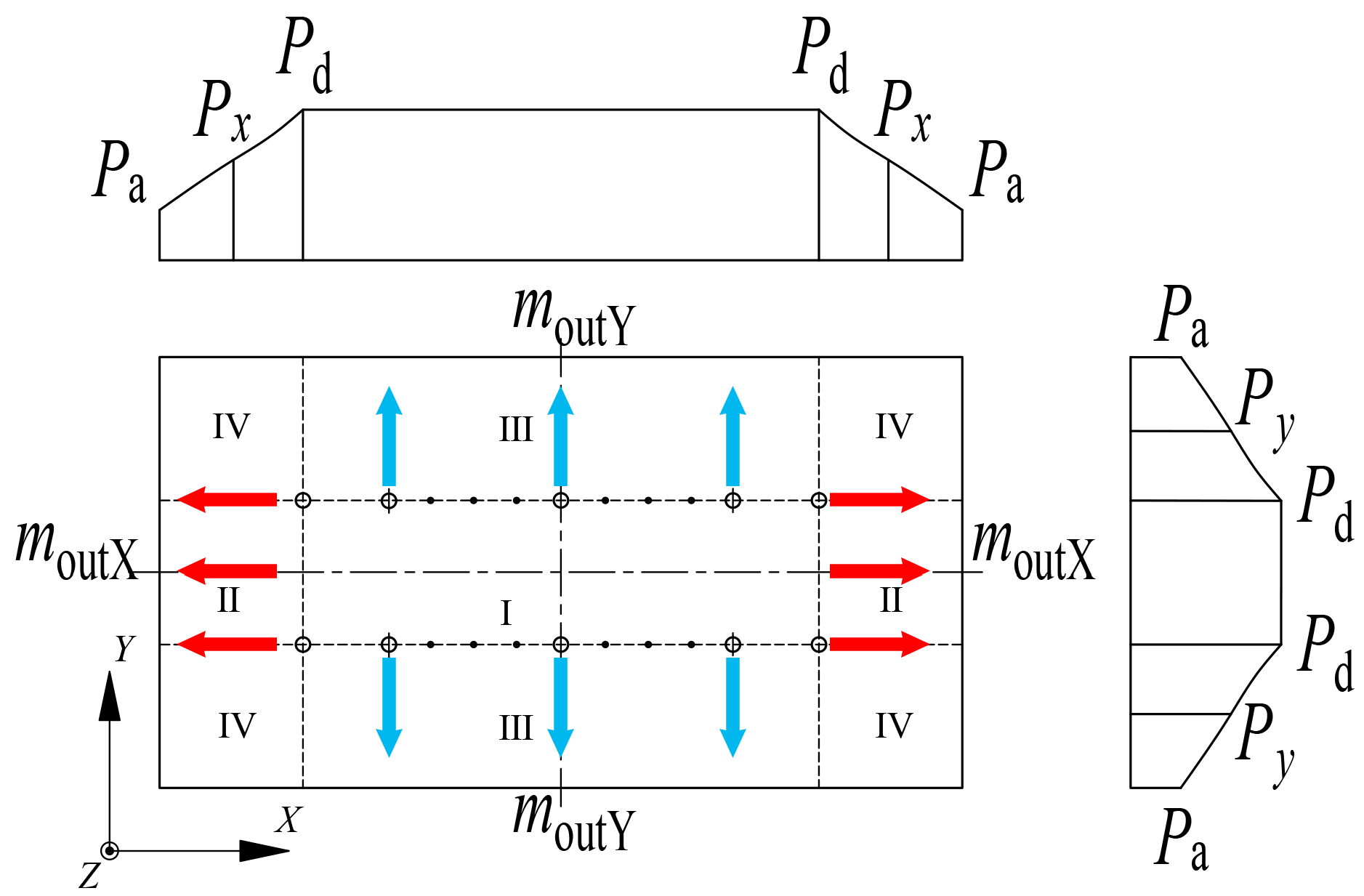
2.2. Analytical Model
2.3. Numerical Model
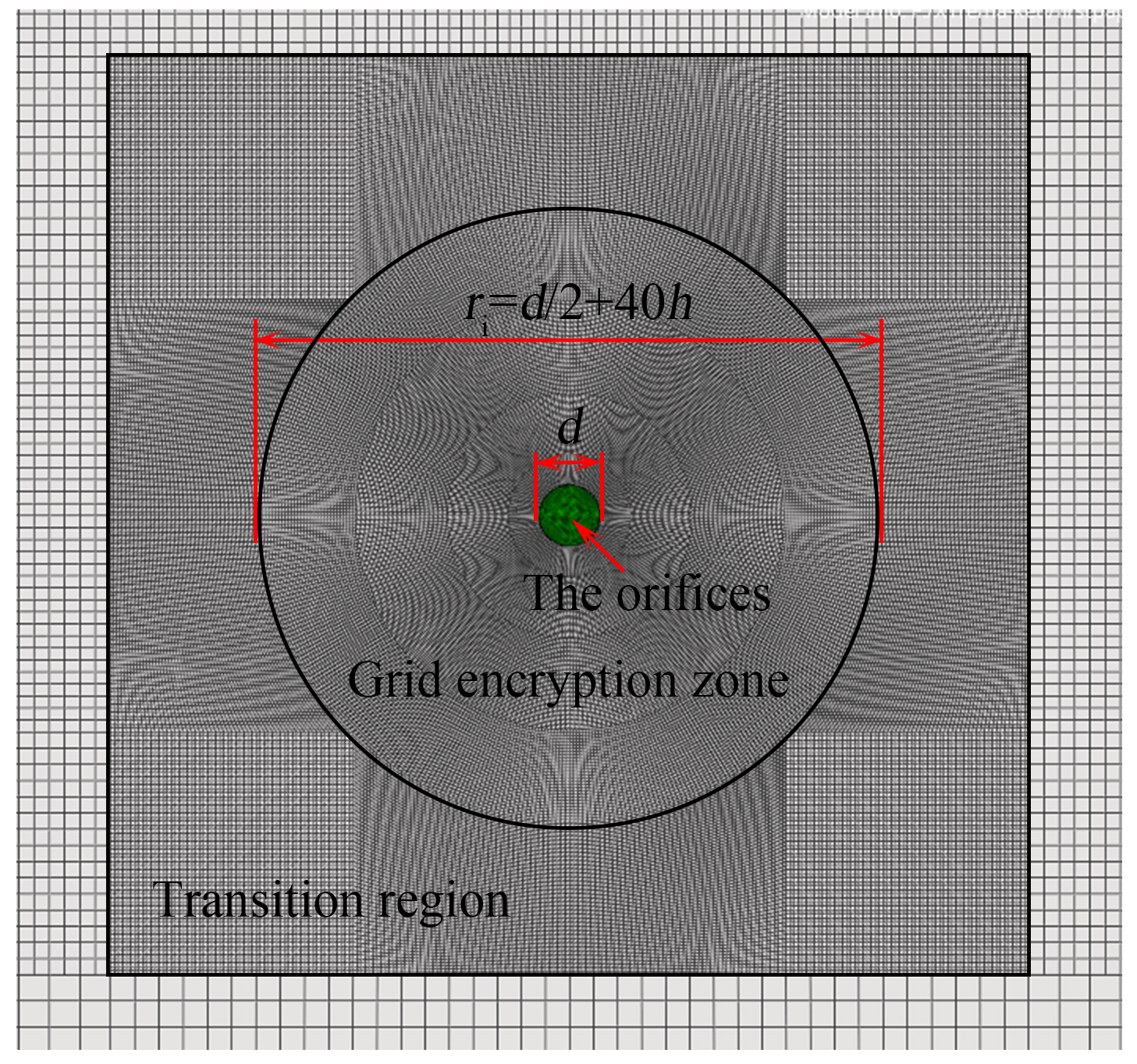
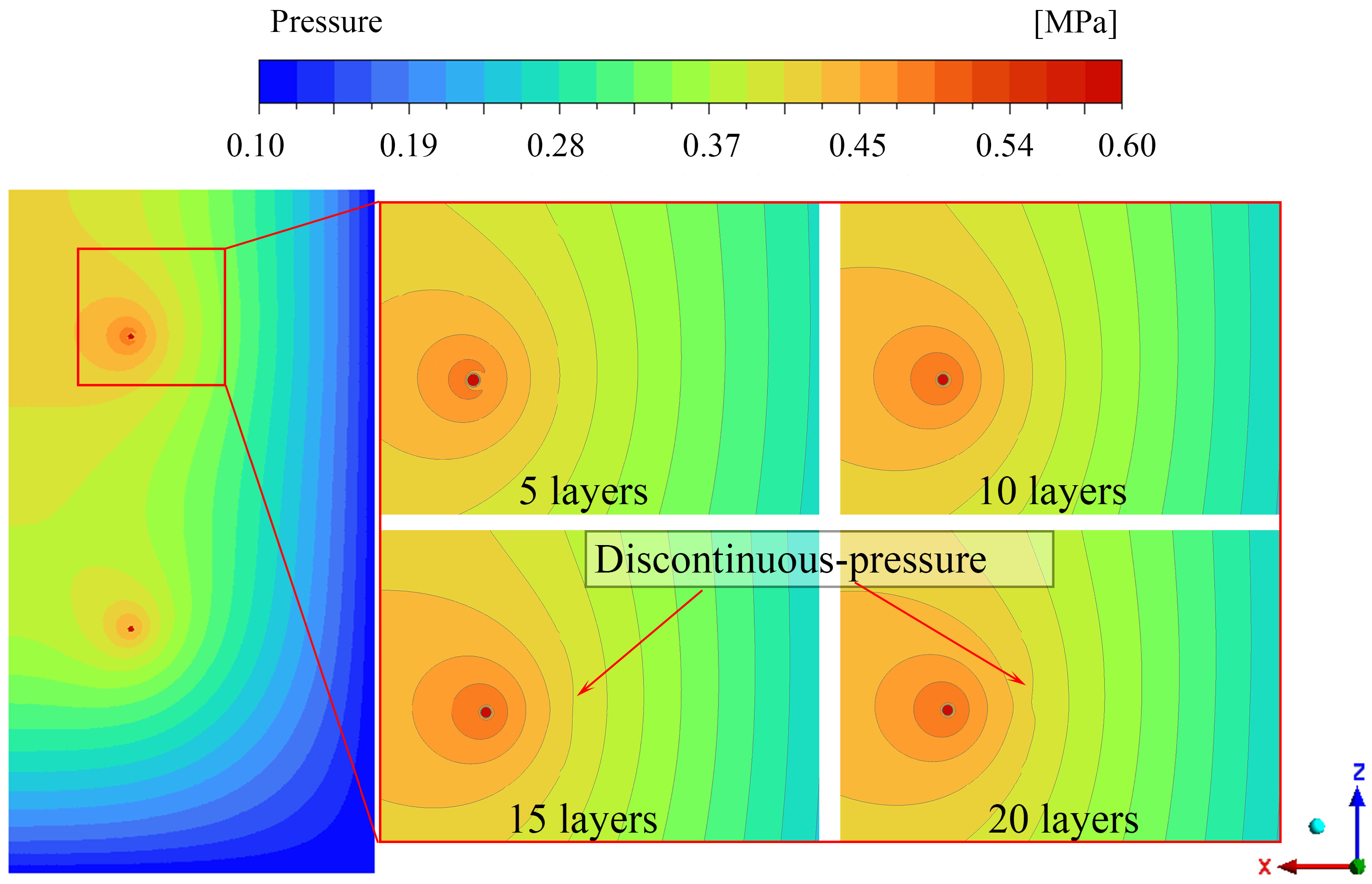
2.3.1. Meshing
2.3.2. Numerical Methods and Control Equations
2.4. Experimental Setup
3. Results
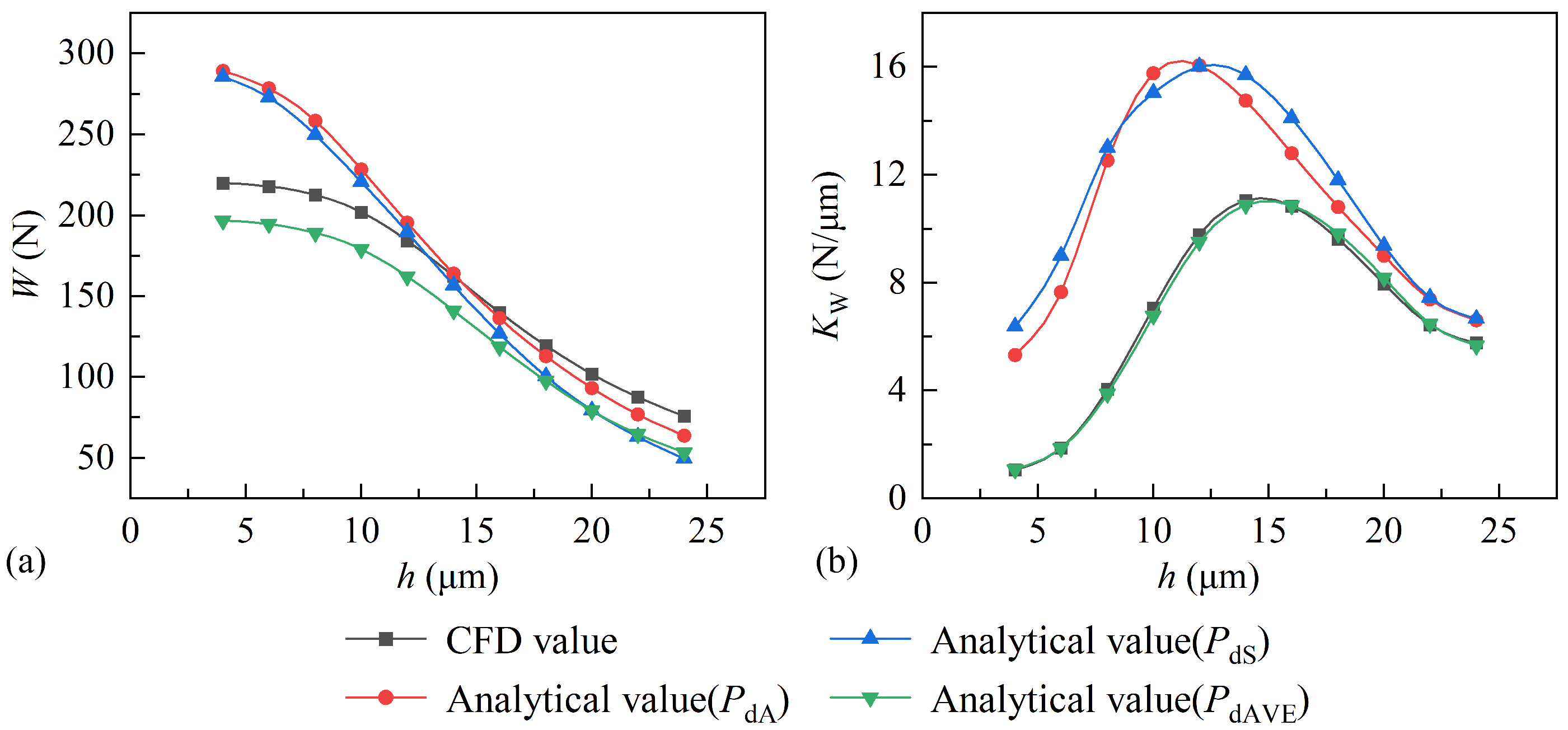
3.1. The Difference Between the Average Pressure PdAVE and the Pressure Pd Behind the Orifice
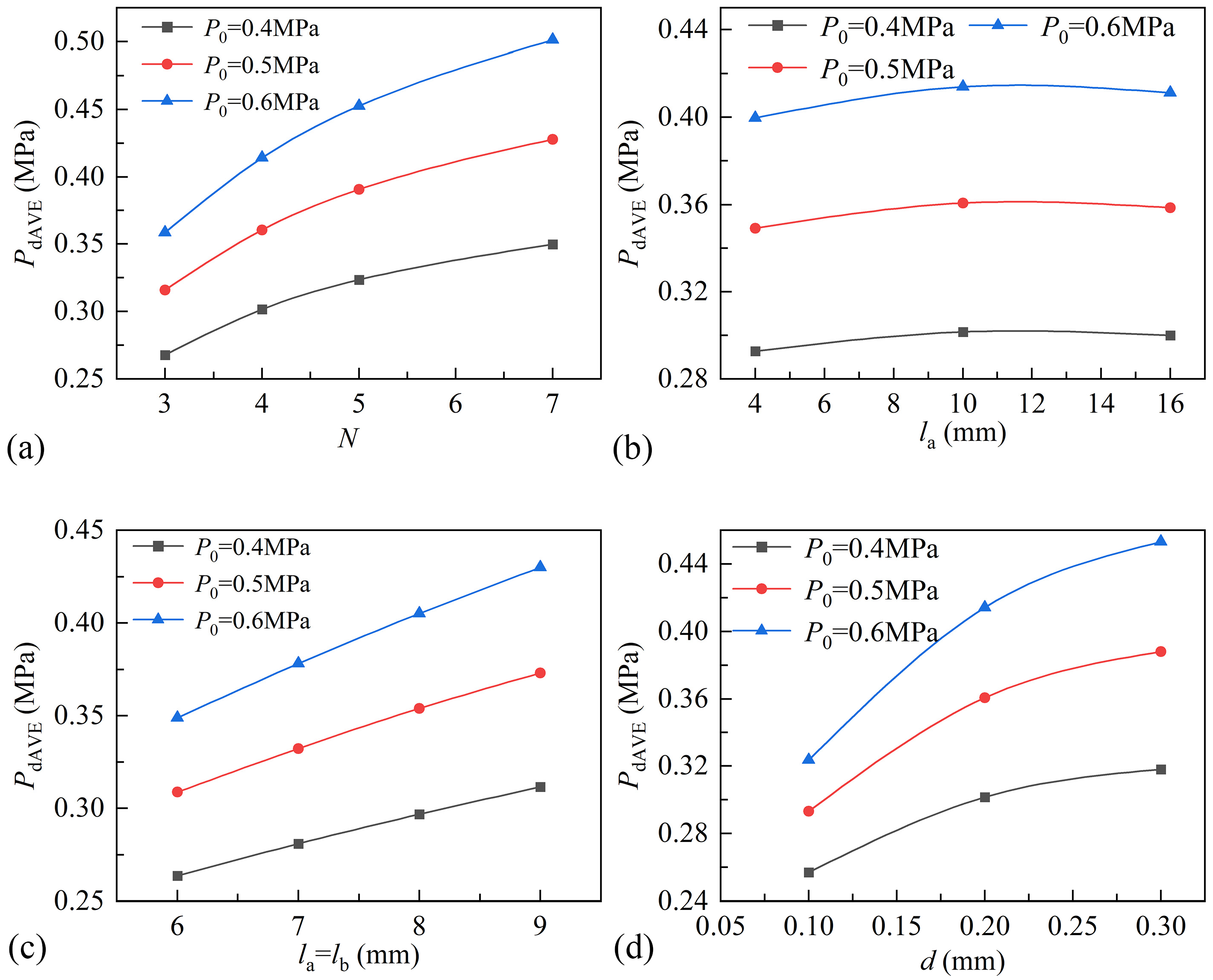
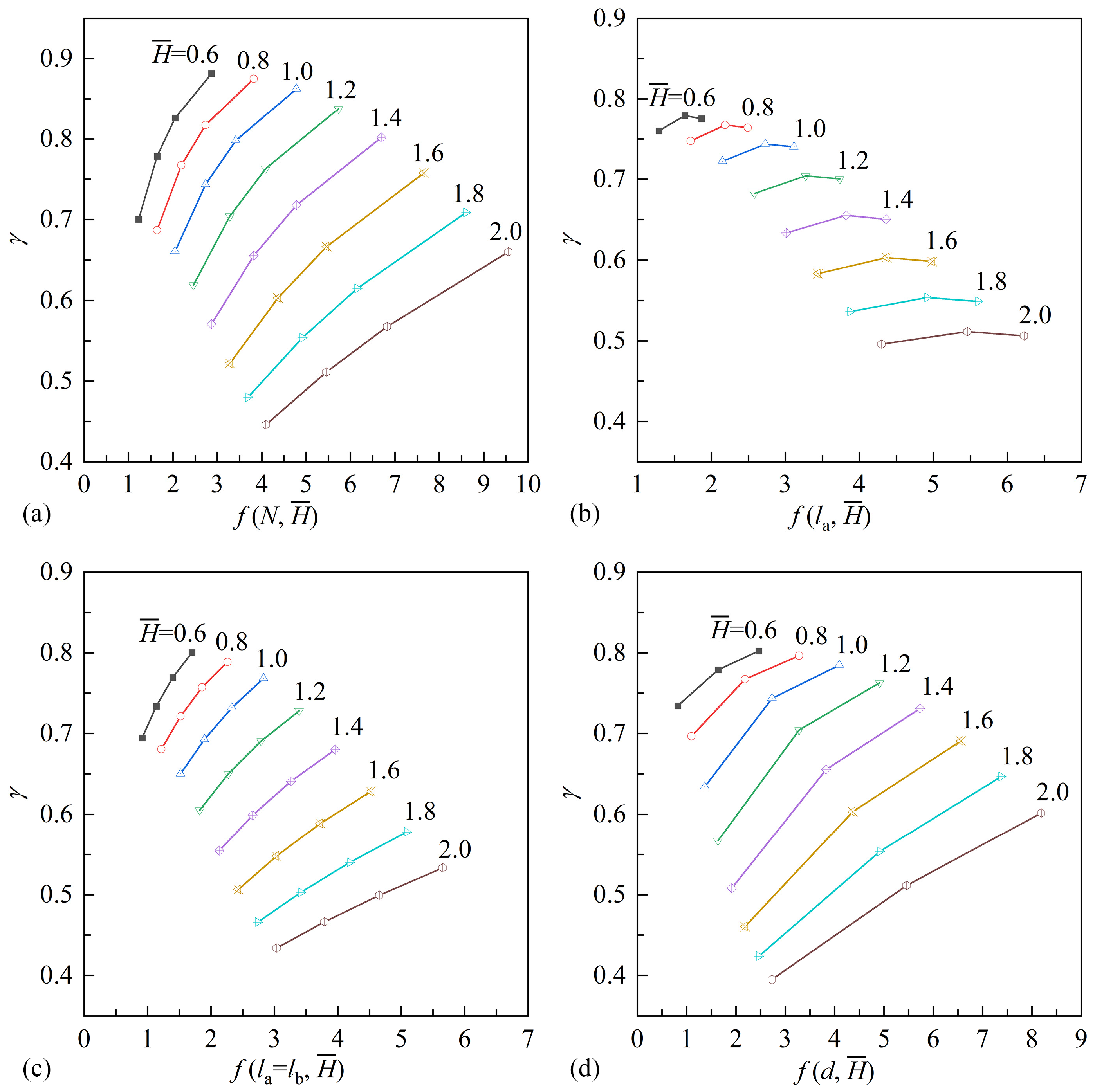
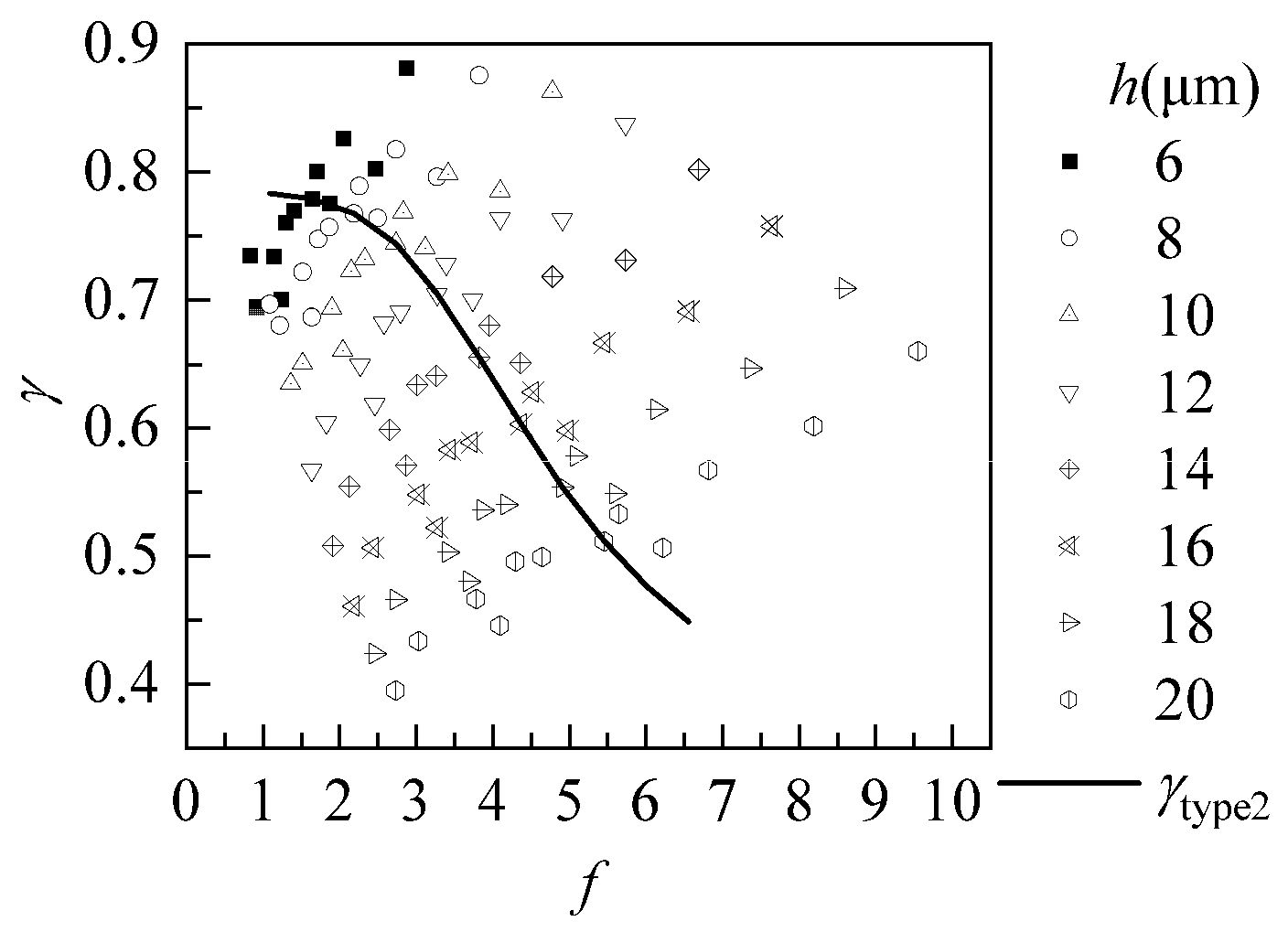
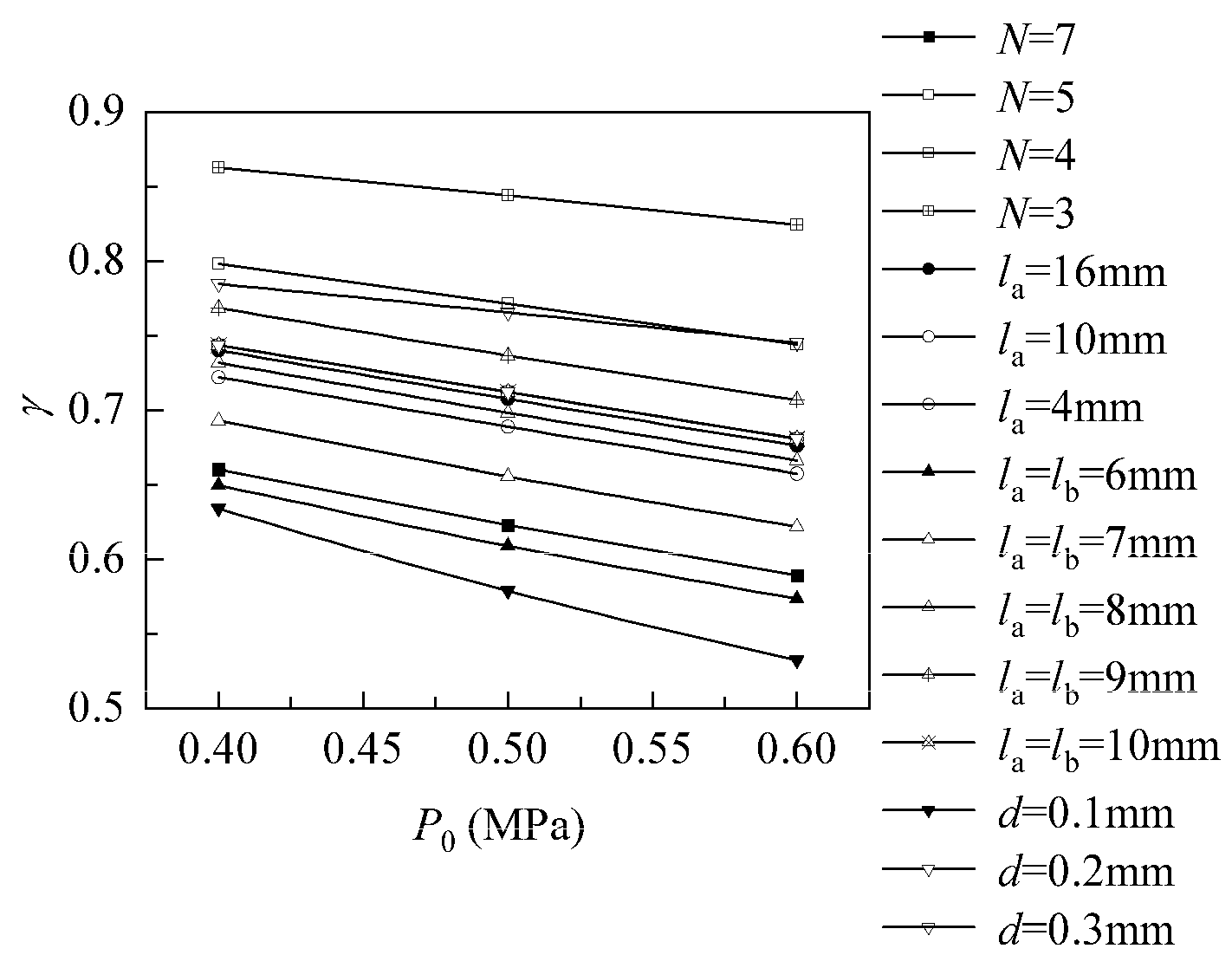
3.2. Influence of Structural Parameters and Supply Pressure on Average Pressure
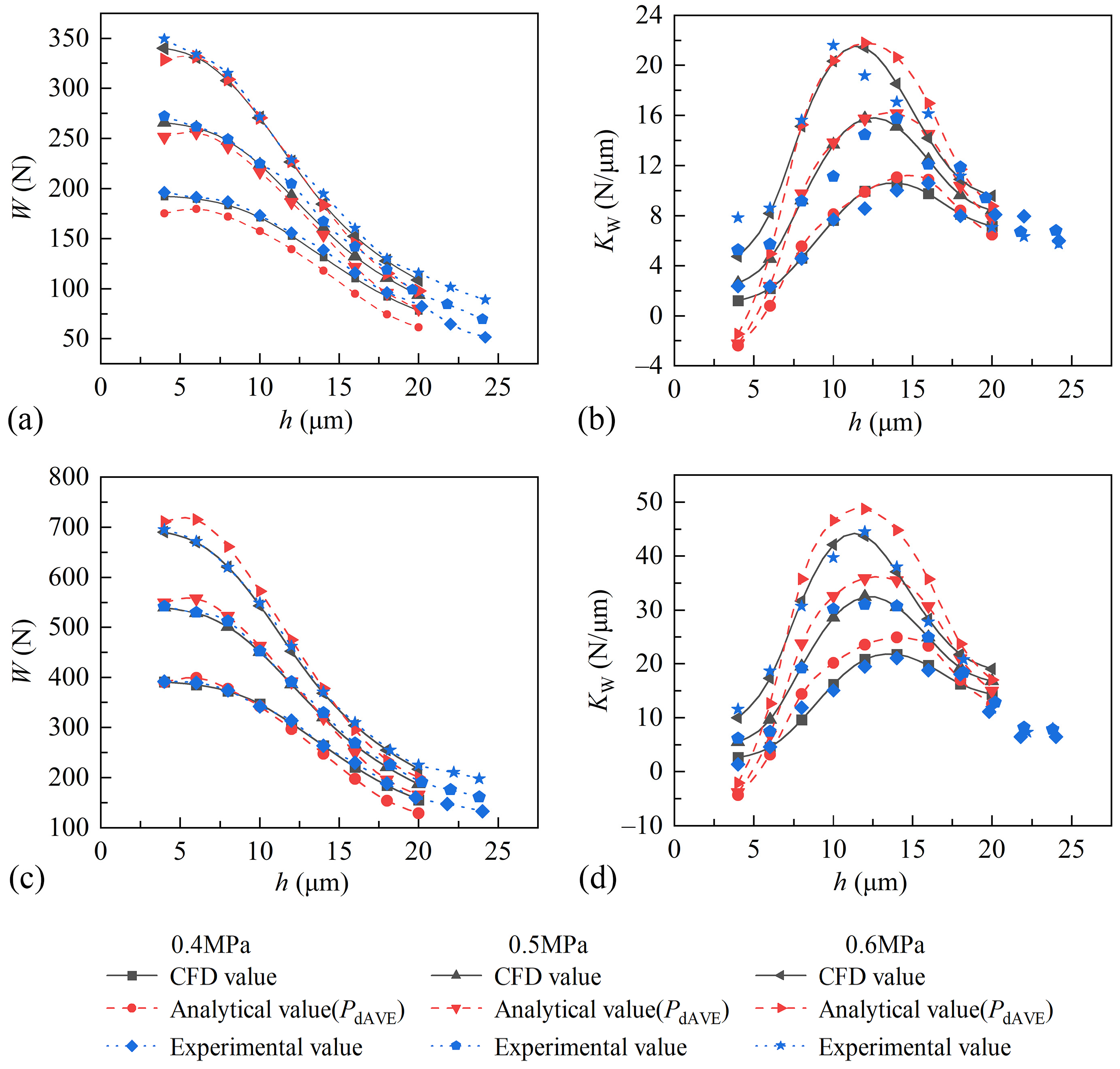
3.3. Comparison and Verification Between Experiments and CFD Simulations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | |||
| CFD | computational fluid dynamics | ||
| EWT | enhanced wall treatment | ||
| ASO | area surrounded by orifice | ||
| Nomenclature | |||
| h | gas film thickness | μ | air viscosity |
| P0 | gas supply pressure | R | gas constant, 287 J/(kg K) |
| Pa | standard atmospheric pressure | T | absolute temperature, 293 K |
| ρ | density | κ | gas specific heat ratio, 1.4 |
| A | single throttling area | λ | thermal conductivity |
| Cd | discharge constant | f | dimensionless geometric parameter |
| PdAVE | average pressure in the ASO | γ | PdAVE/P0, the average pressure coefficient |
| Asup | the area surrounded by orifice | Γ | scaling factor of gas supply pressure |
| Ai | single grid area | W | bearing capacity |
| Pd | orifice downstream pressure | KW | bearing stiffness |
Appendix A
References
- Wen, Z.; Chi, Y.; Gu, H.; Qu, H.; Shi, Z. CFD Research for Air Bearing with Gradient-Depth Recesses. Appl. Sci. 2024, 14, 7710. [Google Scholar] [CrossRef]
- Yu, P.; Lu, J.; Luo, Q.; Li, G.; Yin, X. Optimization design of aerostatic bearings with square micro-hole arrayed restrictor for the improvement of stability: Theoretical predictions and experimental measurements. Lubricants 2022, 10, 295. [Google Scholar] [CrossRef]
- Wen, Z.P.; Wu, J.W.; Xing, K.P.; Zhang, Y.; Li, J.A.; Tan, J.B. Design of Microstructure Parameters on a Small Multi-Throttle air bearing in Photolithography. Engineering 2021, 7, 226–237. [Google Scholar] [CrossRef]
- Powell, J.W. Design of Aero Bearings; Ding, W.G., Lin, X.Q., Eds.; The Machinery Publishing Co., Ltd.: London, UK; National Defense Industry Press: Beijing, China, 1978. [Google Scholar]
- Duran-Castillo, A.; Jauregui-Correa, J.C.; De Santiago, O. Numerical comparison of two methods for predicting the porous gas bearing pressure. Meccanica 2024, 59, 859–874. [Google Scholar] [CrossRef]
- Deb, R.K.; Khan, I.A. Numerical simulation of aerostatic bearing stiffness, damping and critical frequency properties using linear stability analysis. J. Inst. Eng. 2020, 101, 571–578. [Google Scholar] [CrossRef]
- Feng, K.; Wang, G.; An, C.; Chen, R.; Li, W.; Huang, S.; Jiang, J. Design and analysis of biomimetic micro-groove aerostatic bearing inspired by Populus euphratica veins for enhanced load capacity and stiffness. Precis. Eng. 2025, 93, 18–36. [Google Scholar] [CrossRef]
- Cui, H.L.; Wang, Y.; Wang, B.R.; Yang, H.; Xia, H. Numerical simulation and experimental verification of the stiffness and stability of thrust pad aerostatic bearings. Chin. J. Mech. Eng. 2018, 31, 23. [Google Scholar] [CrossRef]
- Wen, Z.; Gu, H.; Shi, Z. Key technologies and design methods of ultra-precision aerostatic bearings. Lubricants 2023, 11, 315. [Google Scholar] [CrossRef]
- Patrick Kwan, Y.B.; Erik, L.L. Nullifying Acceleration Forces in Nano-Positioning Stages for Sub-0.1 mm Lithography Tool for 300 mm Wafers. Proc. SPIC Opt. Microlithogr. 2010, 4346, 544–557. [Google Scholar]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Discharge coefficients of orifice-type restrictor for aerostatic bearings. Tribol. Int. 2007, 40, 512–521. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Comparison between grooved and plane aerostatic thrust bearings: Static performance. Meccanica 2011, 46, 547–555. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Trivella, A.; Viktorov, V.; Visconte, C. CFD analysis of a simple orifice-type feeding system for aerostatic bearings. Tribol. Lett. 2015, 58, 25. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, K.; Deng, Z.; Wu, D.; Su, Z.; Huang, X.; Song, M.; Cao, Y.; Sui, J. Nonlinear Dynamic Analysis of Gas Bearing-Rotor System by the Hybrid Method Which Combines Finite Difference Method and Differential Transform Method. Lubricants 2022, 10, 302. [Google Scholar] [CrossRef]
- Deng, X. A mixed zero-equation and one-equation turbulence model in fluid-film thrust bearings. J. Tribol. 2024, 146, 034101. [Google Scholar] [CrossRef]
- Sahto, M.P.; Wang, W.; Imran, M.; He, L.; Li, H.; Weiwei, G. Modelling and simulation of aerostatic thrust bearings. IEEE Access 2020, 8, 121299–121310. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Study of the static and dynamic performance of rectangular air pads by means of lumped parameters models. Eng. Syst. Des. Anal. ASME 2012, 44878, 531–537. [Google Scholar] [CrossRef]
- Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Lumped parameters models of rectangular pneumatic pads: Static analysis. Precis. Eng. 2015, 42, 283–293. [Google Scholar] [CrossRef]
- Shires, G.L.; Pantall, D. The aerostatic jacking of a vented aerodynamic journal bearing. Inst. Mech. Eng. Lubr. Wear Group Conv. Bournem. 1963, 6, 498. [Google Scholar]
- Mori, A.; Aoyama, K.; Mori, H. Influence of the Gas-film Inertia Forces on the Dynamic Characteristics of Externally Pressurized, Gas Lubricated Journal Bearings: Part l, Proposal of Governing Equations. Bull. JSME 1980, 23, 582–585. [Google Scholar] [CrossRef]
- Mori, A.; Aoyama, K.; Mori, H. Influence of the Gas-film Inertia Forces on the Dynamic Characteristics of Externally Pressurized, Gas Lubricated Journal Bearings: Part II, Analyses of Whirl Instability and Plane Vibration. Bull. JSME 1980, 23, 953–960. [Google Scholar] [CrossRef]
- Mori, H.; Yabe, H. Theoretical Investigation of Externally Pressurized Air-Suspension Conveyer with Multiple Supply Holes. Trans. ASME. J. Lubr. Technol. 1971, 93, 279–286. [Google Scholar] [CrossRef]
- Mondal, N.; Mukhopadhyay, K.; Saha, R.; Sanyal, D. Numerical analysis of aerostatic bearing with central feeding orifice with CFD validation. Mater. Today Proc. 2017, 4, 9860–9864. [Google Scholar] [CrossRef]
- Michalec, M.; Ondra, M.; Svoboda, M.; Chmelík, J.; Zeman, P.; Svoboda, P.; Jackson, R.L. A novel geometry optimization approach for multi-recess hydrostatic bearing pad operating in static and low-speed conditions using CFD simulation. Tribol. Lett. 2023, 71, 52. [Google Scholar] [CrossRef]
- Wen, Z.P.; Wu, J.W.; Tan, J.B. An adaptive modeling method for multi-throttle aerostatic thrust bearing. Tribol. Int. 2020, 149, 105830. [Google Scholar] [CrossRef]
- Bryant, M.R.; Velinsky, S.A.; Beachley, N.H.; Fronczak, F.J. A design methodology for obtaining infinite stiffness in an aerostatic thrust bearing. J. Mech. Trans. Automat. Des. 1986, 108, 448–456. [Google Scholar] [CrossRef]
- Eleshaky, M.E. CFD investigation of pressure depressions in aerostatic circular thrust bearings. Tribol. Int. 2009, 42, 1108–1117. [Google Scholar] [CrossRef]
- Li, W.; Cai, S.; Zhang, P.; Ping, Y.; Feng, K. Numerical and experimental study on the novel active aerostatic bearings with the controllable throttling effect for obtaining high static stiffness. Mech. Syst. Signal Process. 2024, 216, 111469. [Google Scholar] [CrossRef]
- Yoshimoto, S.; Yamamoto, M.; Toda, K. Numerical calculations of pressure distribution in the bearing clearance of circular aerostatic thrust bearings with a single air supply inlet. J. Tribol. ASME 2007, 129, 384–390. [Google Scholar] [CrossRef]
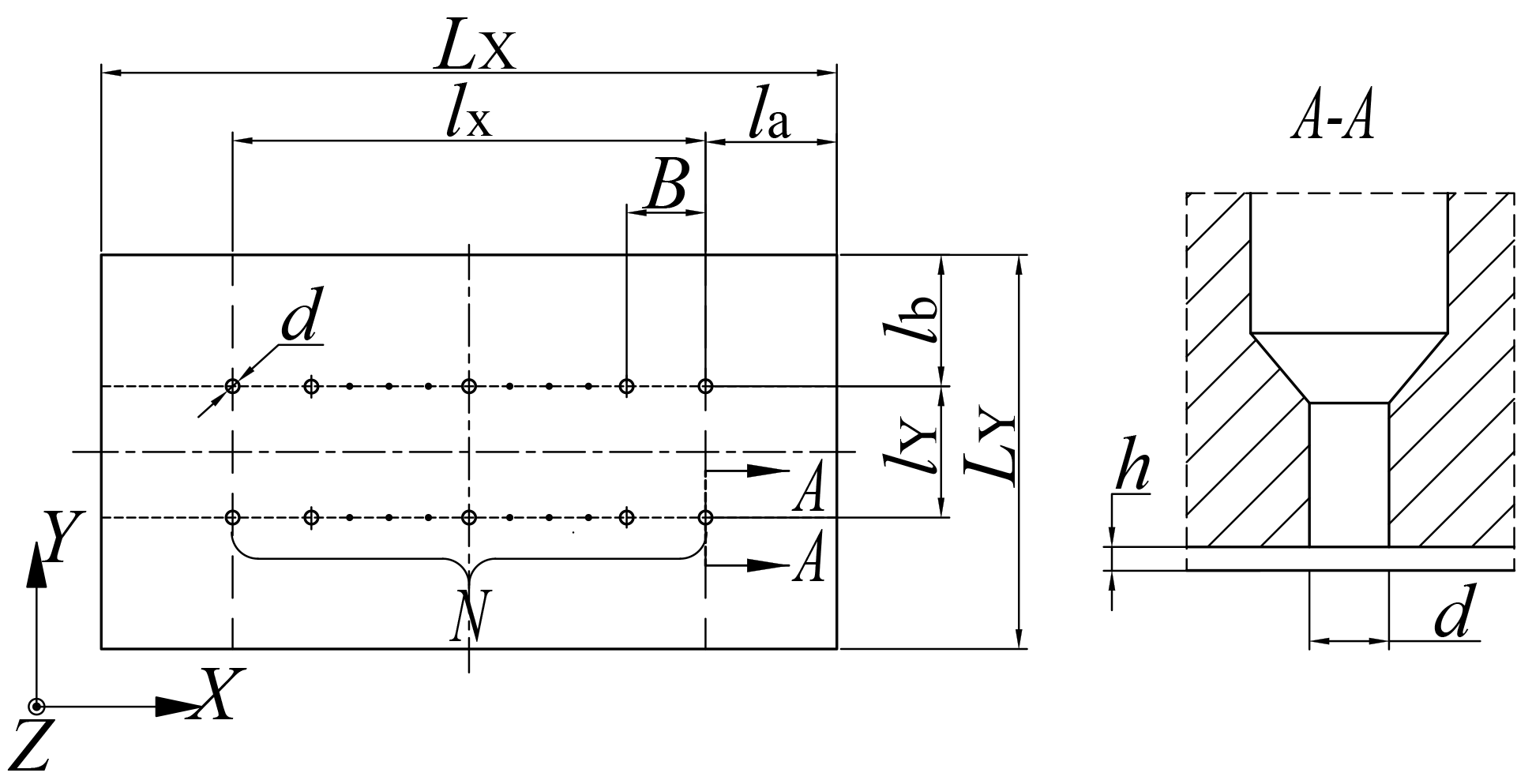






| Type Number | Group | 2 × N | la (mm) | lb (mm) | d (mm) | B (mm) |
|---|---|---|---|---|---|---|
| 1 | Bearing a | 2 × 3 | 10 | 10 | 0.2 | 18 |
| 2 | 2 × 4 | 10 | 10 | 0.2 | 12 | |
| 3 | 2 × 5 | 10 | 10 | 0.2 | 9 | |
| 4 | 2 × 7 | 10 | 10 | 0.2 | 6 | |
| 5 | Bearing b | 2 × 3 | 16 | 10 | 0.2 | 12 |
| 2 | 2 × 4 | 10 | 10 | 0.2 | 12 | |
| 6 | 2 × 5 | 4 | 10 | 0.2 | 12 | |
| 7 | Bearing c | 2 × 5 | 6 | 6 | 0.2 | 11 |
| 8 | 2 × 5 | 7 | 7 | 0.2 | 10.5 | |
| 9 | 2 × 5 | 8 | 8 | 0.2 | 10 | |
| 10 | 2 × 5 | 9 | 9 | 0.2 | 9.5 | |
| 11 | Bearing d | 2 × 4 | 10 | 10 | 0.1 | 12 |
| 2 | 2 × 4 | 10 | 10 | 0.2 | 12 | |
| 12 | 2 × 4 | 10 | 10 | 0.3 | 12 |
| Number of Mesh Layers | Bearing Capacity/N (0.4 MPa) | Bearing Capacity/N (0.5 MPa) | Bearing Capacity/N (0.6 MPa) |
|---|---|---|---|
| 5 | 197.978 | 257.862 | 312.214 |
| 10 | 201.85 | 264.71 | 321.934 |
| 15 | 202.63 | 264.958 | 323.918 |
| 20 | 201.322 | 266.034 | 324.014 |
| P0 (MPa) | PdAVE (MPa) | PdAVE/P0 |
|---|---|---|
| 0.4 | 0.298 | 0.745 |
| 0.5 | 0.356 | 0.712 |
| 0.6 | 0.409 | 0.682 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Wu, J.; Liu, H.; Wang, J.; Zhao, P. An Analytical Model for Aerostatic Thrust Bearings Based on the Average Pressure of the Area Surrounded by Orifice. Lubricants 2025, 13, 110. https://doi.org/10.3390/lubricants13030110
Zheng J, Wu J, Liu H, Wang J, Zhao P. An Analytical Model for Aerostatic Thrust Bearings Based on the Average Pressure of the Area Surrounded by Orifice. Lubricants. 2025; 13(3):110. https://doi.org/10.3390/lubricants13030110
Chicago/Turabian StyleZheng, Jian, Jianwei Wu, Huan Liu, Jiyao Wang, and Pengyue Zhao. 2025. "An Analytical Model for Aerostatic Thrust Bearings Based on the Average Pressure of the Area Surrounded by Orifice" Lubricants 13, no. 3: 110. https://doi.org/10.3390/lubricants13030110
APA StyleZheng, J., Wu, J., Liu, H., Wang, J., & Zhao, P. (2025). An Analytical Model for Aerostatic Thrust Bearings Based on the Average Pressure of the Area Surrounded by Orifice. Lubricants, 13(3), 110. https://doi.org/10.3390/lubricants13030110






