Lubrication and Drag Reduction for Polymer-Coated Interfaces
Abstract
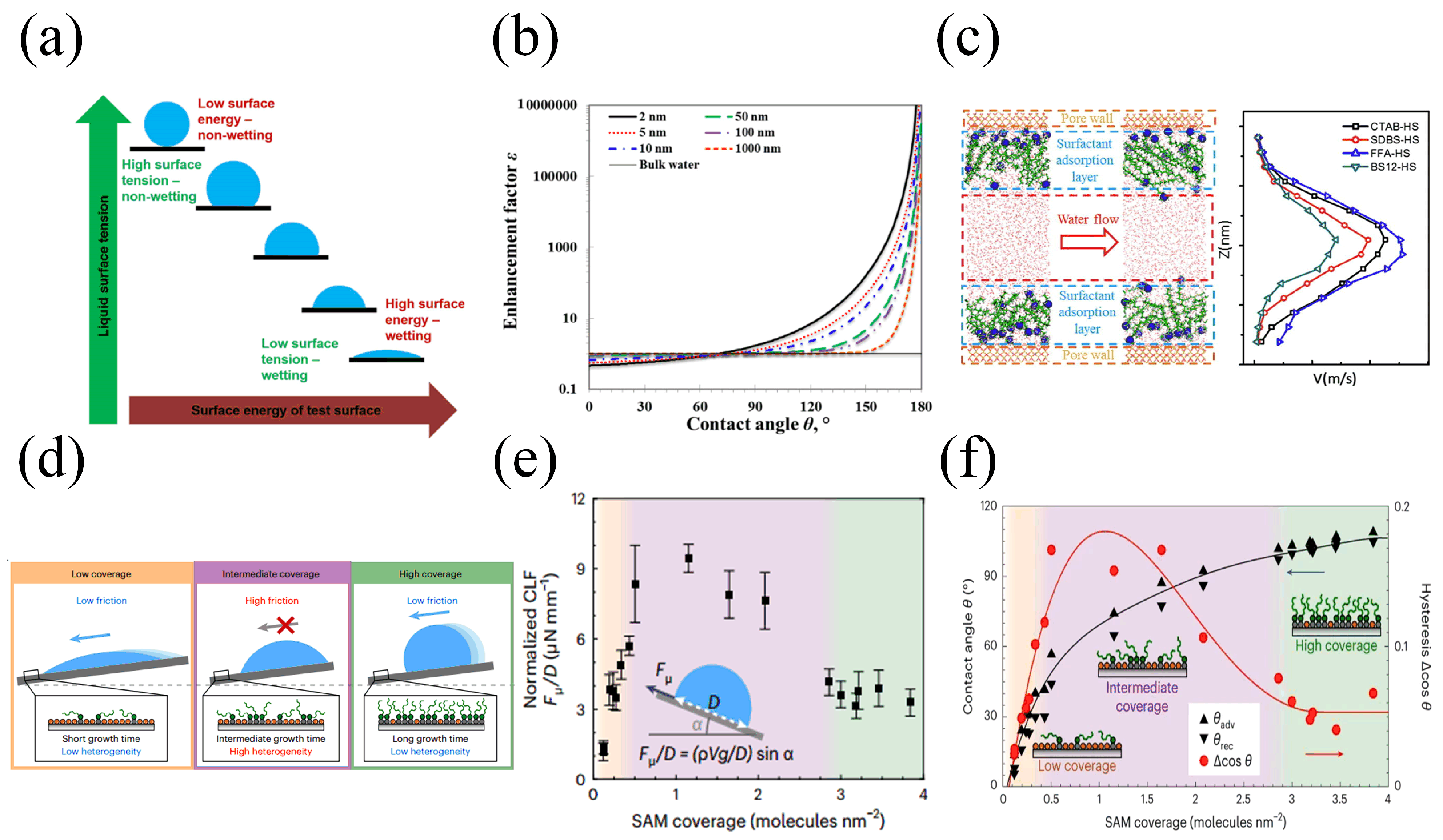
:1. Introduction
2. Experimental and Surface Modification Techniques
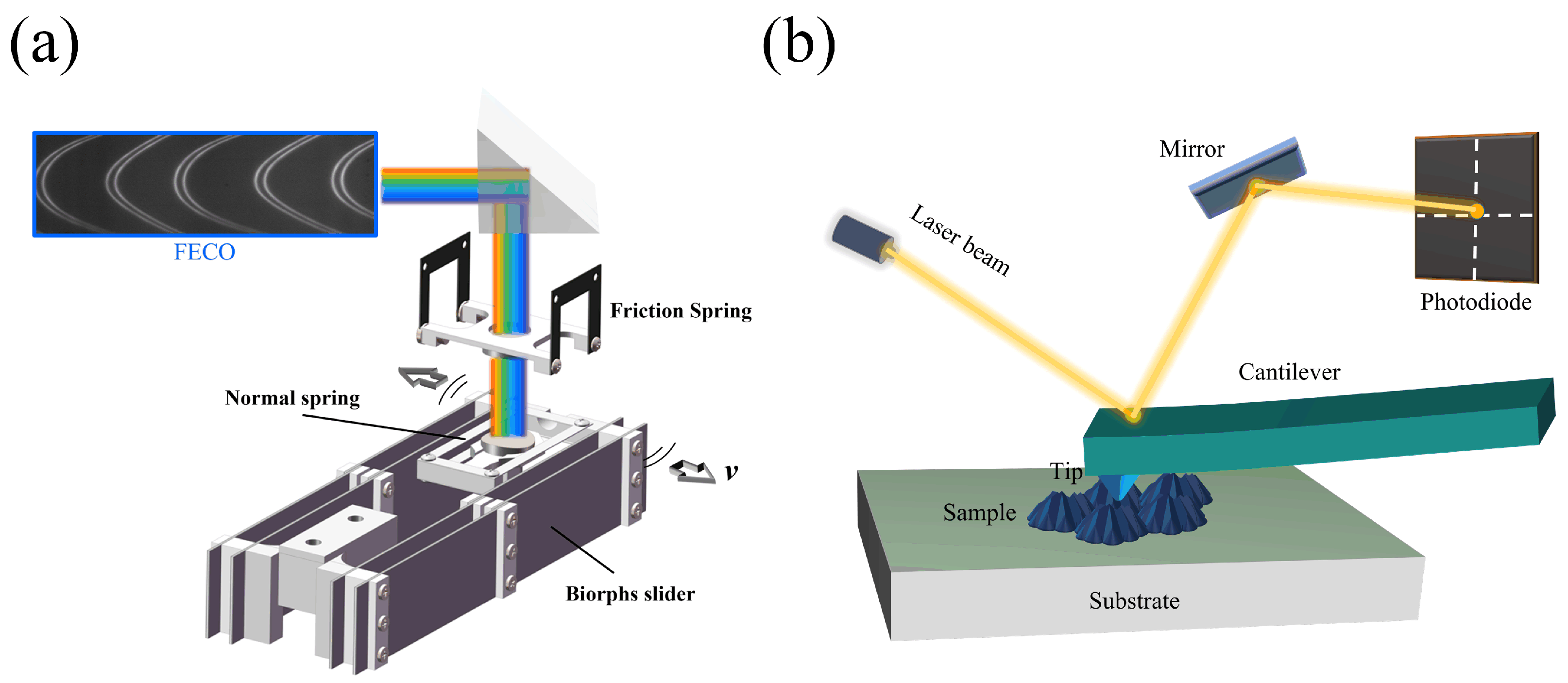
2.1. SFA
2.2. AFM
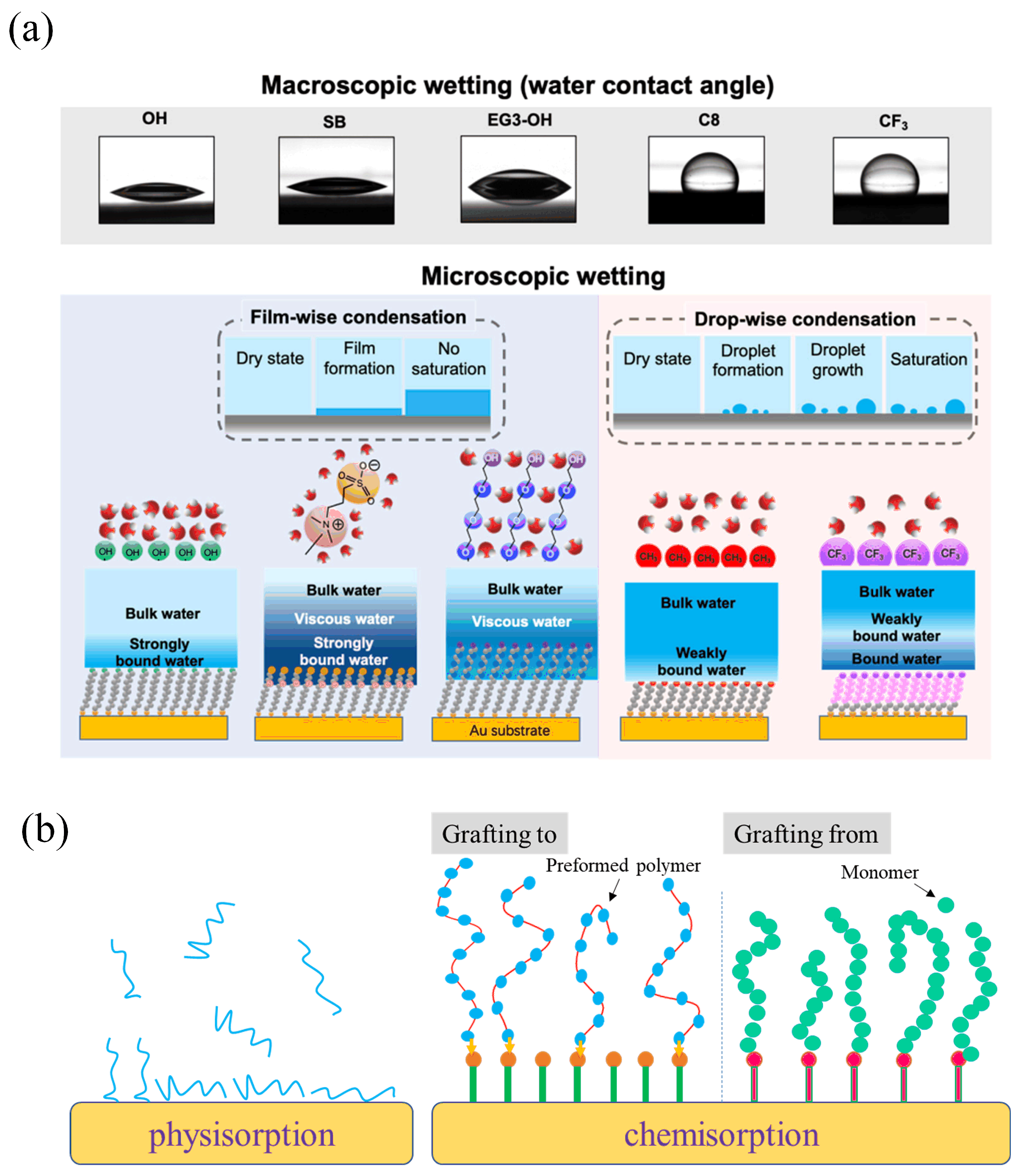
2.3. Interface Modification Methods
3. Fundamentals of the Surface Forces and Hydrodynamic Force
3.1. Hydration Force
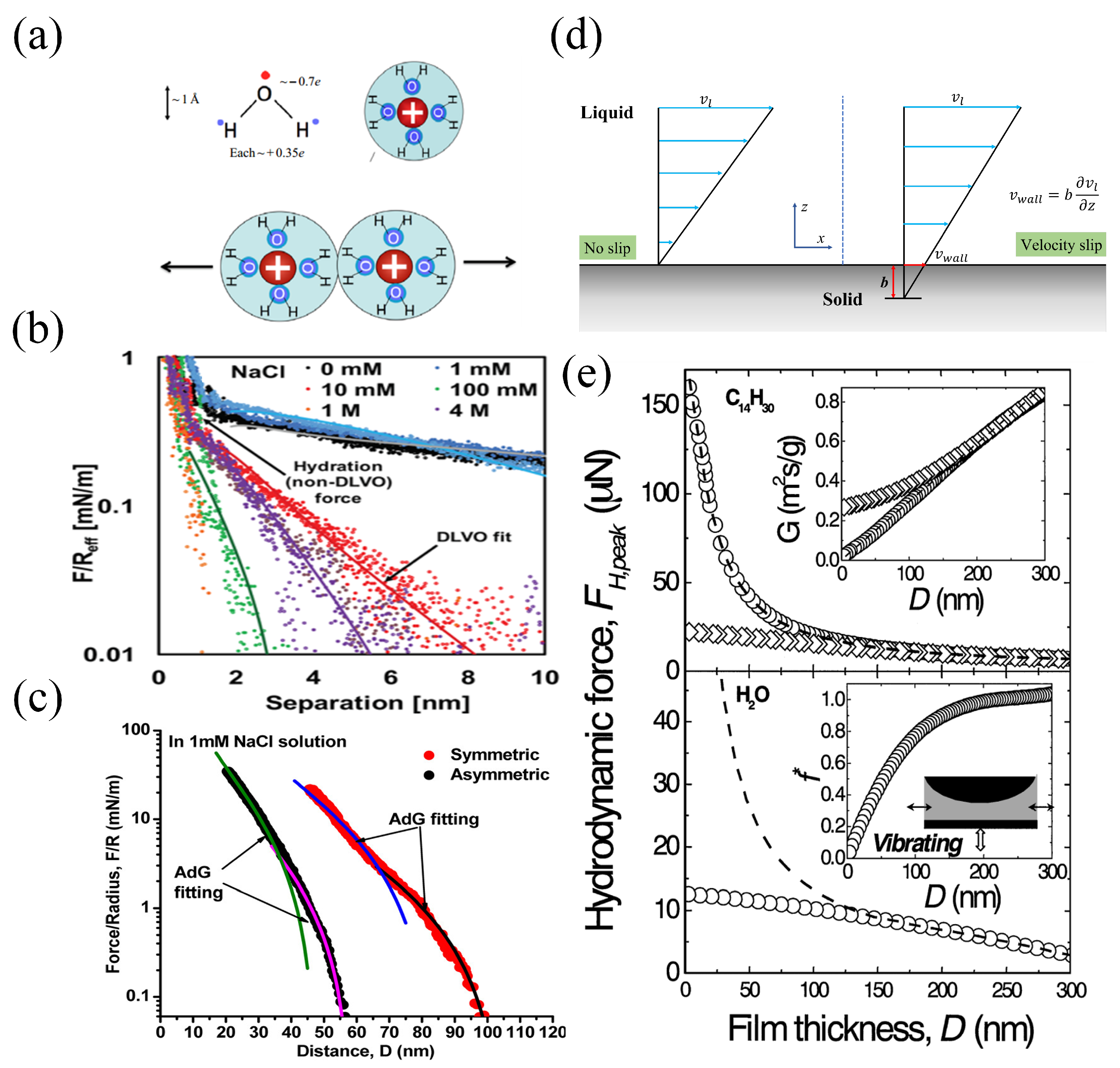
3.2. DLVO Forces
3.3. Repulsive Steric Force
3.4. Hydrodynamic Force
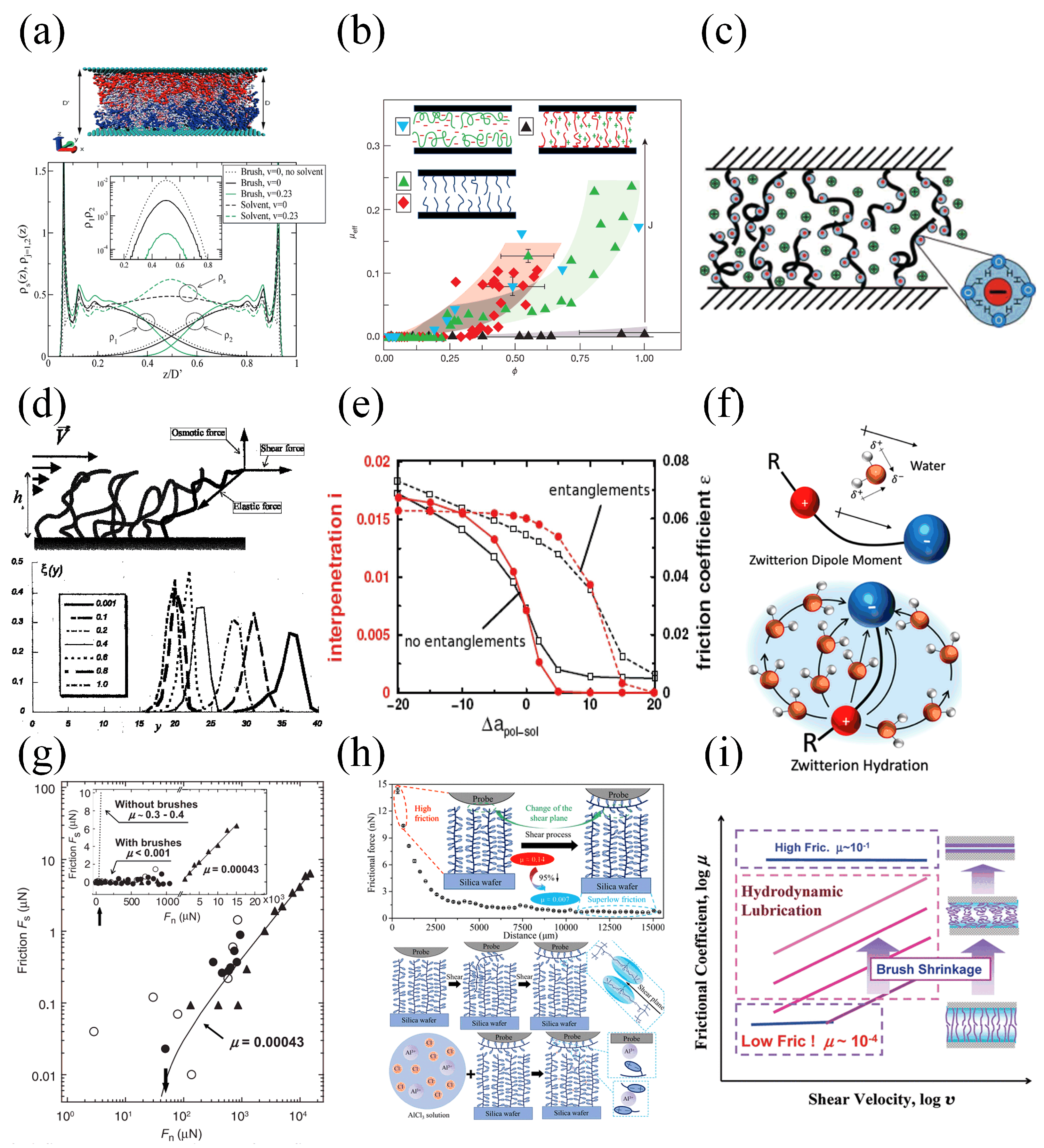
4. Mechanisms Underlying Hydration Lubrication
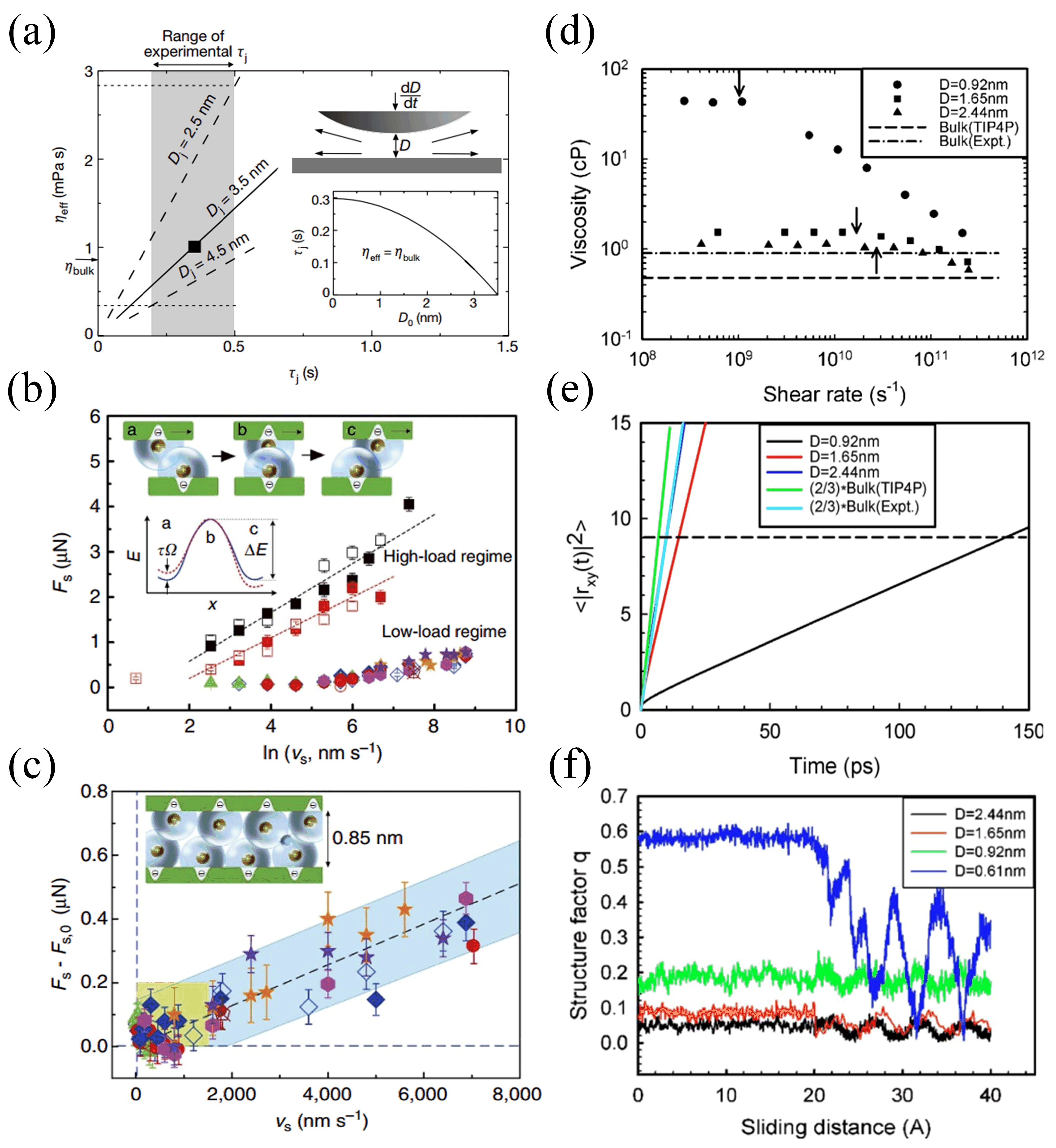
5. Joint Lubrication and Polymer Brush Lubrication
5.1. Mechanisms of Polymers in Joint Lubrication
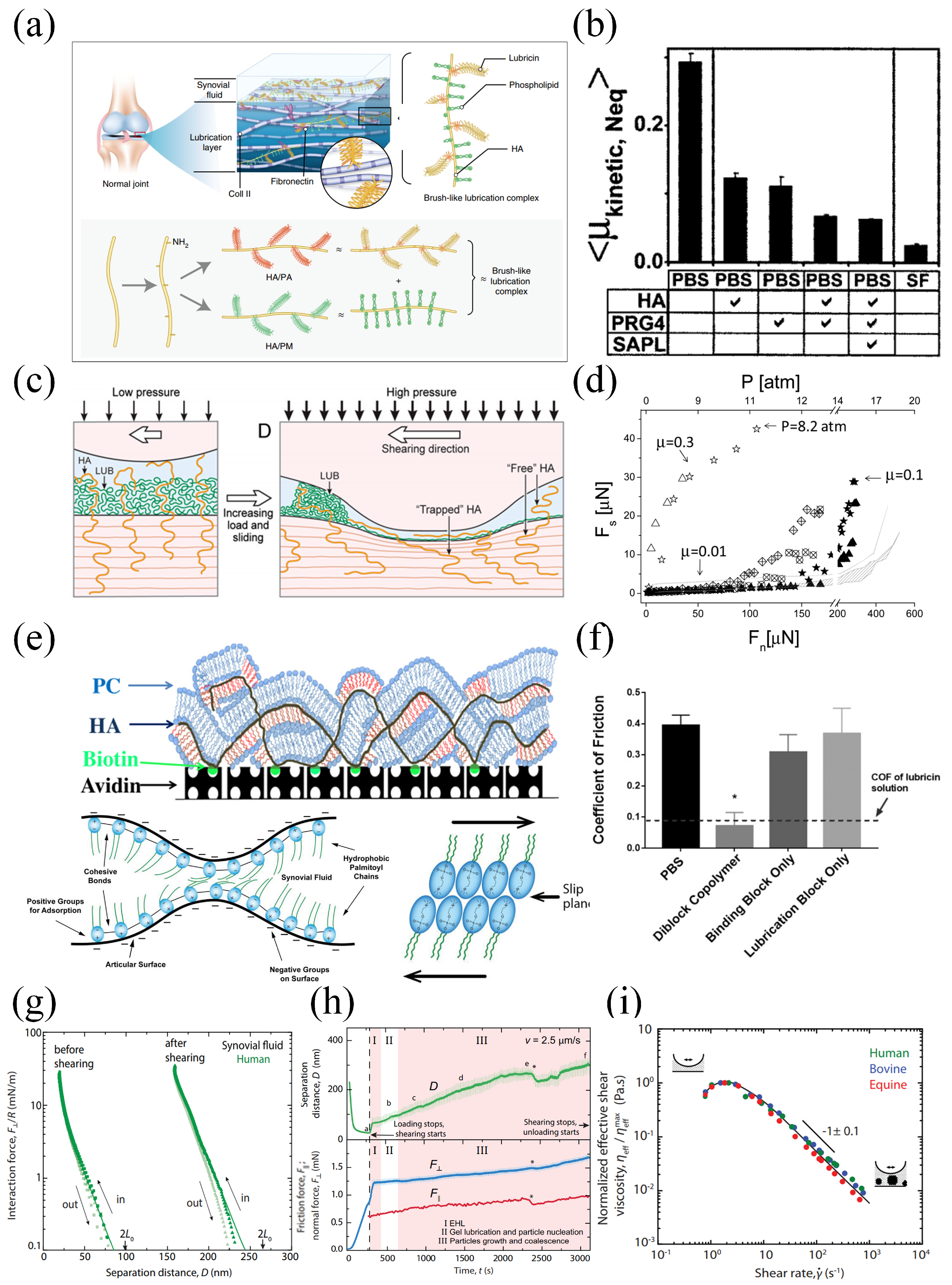
5.2. Polymer Brush Lubrication
6. Friction Tuning and Interfacial Drag Reduction via Polymer Coating Design
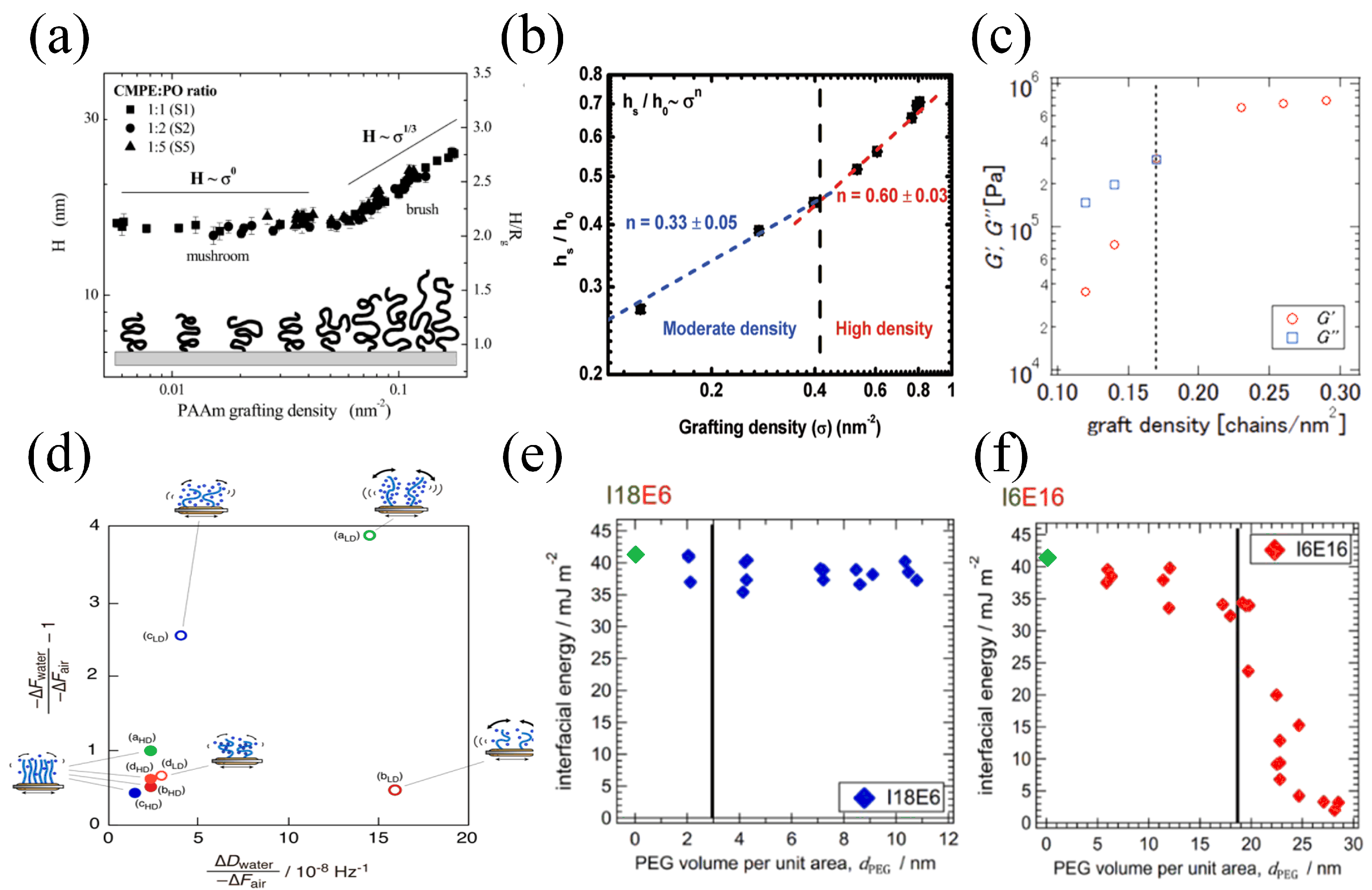
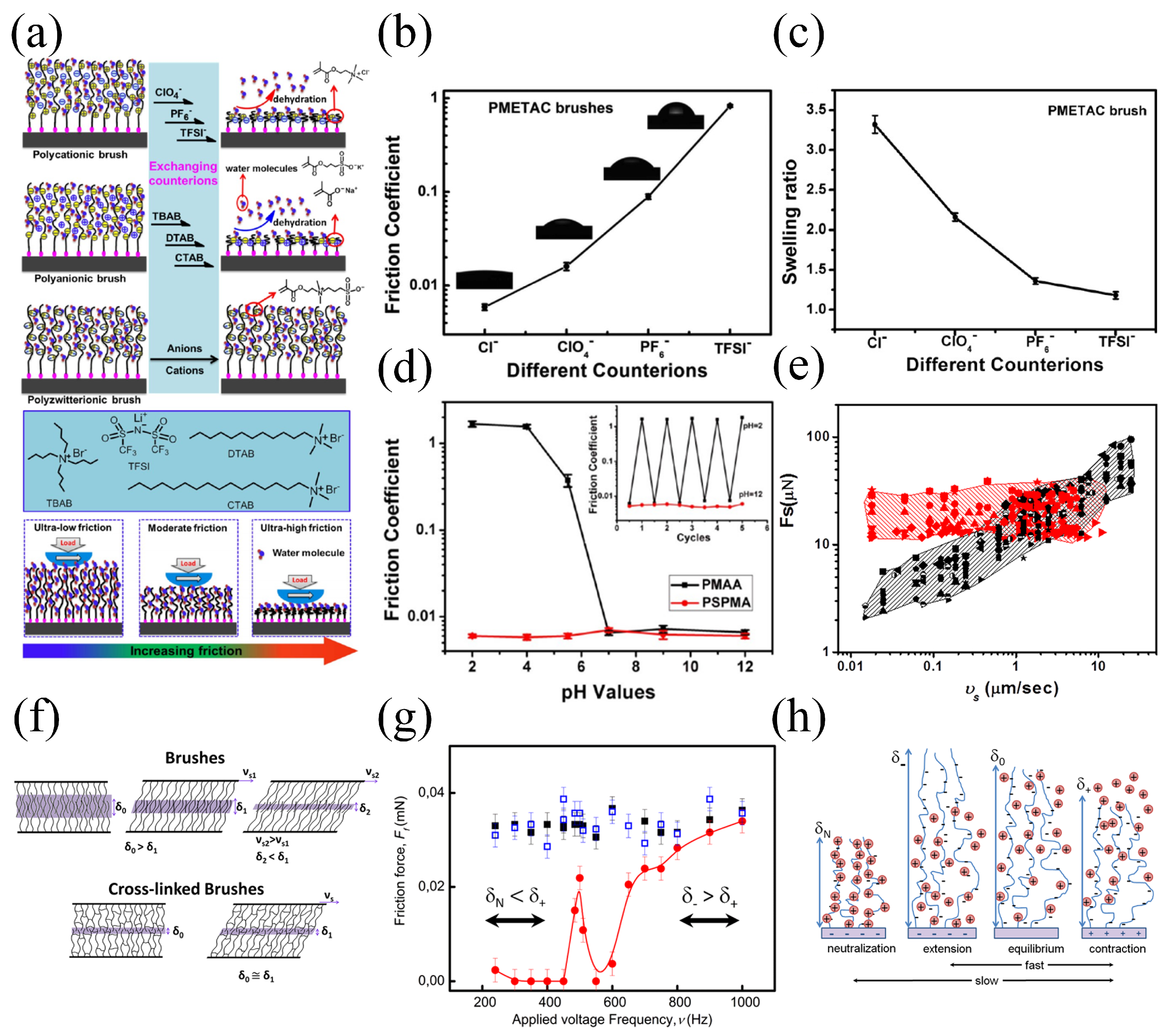
6.1. Friction Control of Polymer Brushes
6.2. Polymer-Based Materials for Drag Reduction
7. Summary and Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBLDR | polymer-based lubrication and drag reduction |
| DLOV | Derjaguin–Landau–Verwey–Overbeek |
| SLI | solid–liquid interfaces |
| NSBC | no-slip boundary condition |
| MD | molecular dynamics |
| SFA | surface forces apparatus |
| SFB | surface force balance |
| QCM | quartz crystal microbalance |
| MBI | multiple beam interferometry |
| AFM | atomic force microscope |
| vdW | van der Waals force |
| DL | double-layer |
| HA | hyaluronic acid |
| PRG4 | proteoglycan 4 |
| SAPL | surface-active phospholipids |
| GAGs | glycosaminoglycans |
| AGG | aggrecan |
| LUB | glycoprotein lubricant |
| LP | link protein |
| PAAM | poly (acrylamide) |
| PMMA | poly(methyl methacrylate) |
| PMPC | poly[2-(methacryloyloxy) ethyl phosphorylcholine] |
| SI-ATRP | surface-initiated atom transfer radical polymerization |
| PSS | polystyrene sulfonate |
| PMETAC | poly[2-(methacryloyloxy)-ethyltrimethylammonium chloride] brush |
| SAMs | self-assembled monolayers |
References
- Prandtl, L. A conceptual model to the kinetic theory of solid bodies. Z. Angew. Math. Mech 1928, 8, 85–106. [Google Scholar] [CrossRef]
- Tomlinson, G. CVI. A molecular theory of friction. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1929, 7, 905–939. [Google Scholar] [CrossRef]
- McFarlane, J.S.; Tabor, D.; Bowden, F.P. Relation between friction and adhesion. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1950, 202, 244–253. [Google Scholar] [CrossRef]
- Yoshizawa, H.; Chen, Y.L.; Israelachvili, J. Fundamental mechanisms of interfacial friction. 1. Relation between adhesion and friction. J. Phys. Chem. 1993, 97, 4128–4140. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. Friction, lubrication and wear: A survey of work during the last decade. Br. J. Appl. Phys. 1966, 17, 1521–1544. [Google Scholar] [CrossRef]
- Tabor, D. Friction as a dissipative process. In Fundamentals of Friction: Macroscopic and Microscopic Processes; Springer: Berlin/Heidelberg, Germany, 1992; pp. 3–24. [Google Scholar]
- Rong, M.; Liu, H.; Scaraggi, M.; Bai, Y.; Bao, L.; Ma, S.; Ma, Z.; Cai, M.; Dini, D.; Zhou, F. High Lubricity Meets Load Capacity: Cartilage Mimicking Bilayer Structure by Brushing Up Stiff Hydrogels from Subsurface. Adv. Funct. Mater. 2020, 30, 2004062. [Google Scholar] [CrossRef]
- Lin, W.; Kluzek, M.; Iuster, N.; Shimoni, E.; Kampf, N.; Goldberg, R.; Klein, J. Cartilage-inspired, lipid-based boundary-lubricated hydrogels. Science 2020, 370, 335–338. [Google Scholar] [CrossRef]
- Briscoe, W.H.; Titmuss, S.; Tiberg, F.; Thomas, R.K.; McGillivray, D.J.; Klein, J. Boundary lubrication under water. Nature 2006, 444, 191–194. [Google Scholar] [CrossRef]
- Raviv, U.; Klein, J. Fluidity of Bound Hydration Layers. Science 2002, 297, 1540–1543. [Google Scholar] [CrossRef]
- Han, T.; Zhang, C.; Luo, J. Macroscale Superlubricity Enabled by Hydrated Alkali Metal Ions. Langmuir 2018, 34, 11281–11291. [Google Scholar] [CrossRef]
- Kim, H.-J.; Kim, D.-E. Water Lubrication of Stainless Steel using Reduced Graphene Oxide Coating. Sci. Rep. 2015, 5, 17034. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Feng, Y.; Zhao, N.; Chen, Z.; Shi, J.; Zhou, F. Polymer-based lubricating materials for functional hydration lubrication. Chem. Eng. J. 2022, 429, 132324. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, X.; Zhang, J.; Ma, S.; Jiang, L.; Wei, Q.; Cai, M.; Zhou, F. Synthesis of charged chitosan nanoparticles as functional biolubricant. Colloids Surf. B Biointerfaces 2021, 206, 111973. [Google Scholar] [CrossRef]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479–3501. [Google Scholar] [CrossRef]
- Klein, J.; Perahia, D.; Warburg, S. Forces between polymer-bearing surfaces undergoing shear. Nature 1991, 352, 143–145. [Google Scholar] [CrossRef]
- Xie, R.; Yao, H.; Mao, A.S.; Zhu, Y.; Qi, D.; Jia, Y.; Gao, M.; Chen, Y.; Wang, L.; Wang, D.-A.; et al. Biomimetic cartilage-lubricating polymers regenerate cartilage in rats with early osteoarthritis. Nat. Biomed. Eng. 2021, 5, 1189–1201. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, R.; Jansson, U.; Nedfors, N. A near-wearless and extremely long lifetime amorphous carbon film under high vacuum. Sci. Rep. 2015, 5, 11119. [Google Scholar] [CrossRef]
- Chhowalla, M.; Amaratunga, G.A.J. Thin films of fullerene-like MoS2 nanoparticles with ultra-low friction and wear. Nature 2000, 407, 164–167. [Google Scholar] [CrossRef]
- Rasheed, T.; Sorour, A.A. Unveiling the power of MXenes: Solid lubrication perspectives and future directions. Adv. Colloid Interface Sci. 2024, 329, 103186. [Google Scholar] [CrossRef]
- Baart, P.; Lugt, P.M.; Prakash, B. Review of the lubrication, sealing, and pumping mechanisms in oil- and grease-lubricated radial lip seals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 347–358. [Google Scholar] [CrossRef]
- Raviv, U.; Laurat, P.; Klein, J. Fluidity of water confined to subnanometre films. Nature 2001, 413, 51–54. [Google Scholar] [CrossRef] [PubMed]
- Raviv, U.; Giasson, S.; Frey, J.; Klein, J. Viscosity of ultra-thin water films confined between hydrophobic or hydrophilic surfaces. J. Phys. Condens. Matter 2002, 14, 9275. [Google Scholar] [CrossRef]
- Banquy, X.; Burdyńska, J.; Lee, D.W.; Matyjaszewski, K.; Israelachvili, J. Bioinspired Bottle-Brush Polymer Exhibits Low Friction and Amontons-like Behavior. J. Am. Chem. Soc. 2014, 136, 6199–6202. [Google Scholar] [CrossRef] [PubMed]
- Seror, J.; Merkher, Y.; Kampf, N.; Collinson, L.; Day, A.J.; Maroudas, A.; Klein, J. Articular Cartilage Proteoglycans As Boundary Lubricants: Structure and Frictional Interaction of Surface-Attached Hyaluronan and Hyaluronan–Aggrecan Complexes. Biomacromolecules 2011, 12, 3432–3443. [Google Scholar] [CrossRef]
- Jahn, S.; Seror, J.; Klein, J. Lubrication of Articular Cartilage. Annu. Rev. Biomed. Eng. 2016, 18, 235–258. [Google Scholar] [CrossRef]
- Lin, W.; Klein, J. Recent Progress in Cartilage Lubrication. Adv. Mater. 2021, 33, 2005513. [Google Scholar] [CrossRef]
- Dowson, D. Bio-tribology. Faraday Discuss. 2012, 156, 9–30. [Google Scholar] [CrossRef]
- Singh, A.; Corvelli, M.; Unterman, S.A.; Wepasnick, K.A.; McDonnell, P.; Elisseeff, J.H. Enhanced lubrication on tissue and biomaterial surfaces through peptide-mediated binding of hyaluronic acid. Nat. Mater. 2014, 13, 988–995. [Google Scholar] [CrossRef]
- Yu, J.; Banquy, X.; Greene, G.W.; Lowrey, D.D.; Israelachvili, J.N. The Boundary Lubrication of Chemically Grafted and Cross-Linked Hyaluronic Acid in Phosphate Buffered Saline and Lipid Solutions Measured by the Surface Forces Apparatus. Langmuir 2012, 28, 2244–2250. [Google Scholar] [CrossRef]
- Chawla, K.; Ham, H.O.; Nguyen, T.; Messersmith, P.B. Molecular resurfacing of cartilage with proteoglycan 4. Acta Biomater. 2010, 6, 3388–3394. [Google Scholar] [CrossRef]
- Das, S.; Banquy, X.; Zappone, B.; Greene, G.W.; Jay, G.D.; Israelachvili, J.N. Synergistic Interactions between Grafted Hyaluronic Acid and Lubricin Provide Enhanced Wear Protection and Lubrication. Biomacromolecules 2013, 14, 1669–1677. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, T.A.; Gastelum, N.S.; Nguyen, Q.T.; Schumacher, B.L.; Sah, R.L. Boundary lubrication of articular cartilage: Role of synovial fluid constituents. Arthritis Rheum. 2007, 56, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Hills, B.A.; Butler, B.D. Surfactants identified in synovial fluid and their ability to act as boundary lubricants. Ann. Rheum. Dis. 1984, 43, 641. [Google Scholar] [CrossRef]
- Giasson, S.; Lagleize, J.-M.; Rodríguez-Hernández, J.; Drummond, C. Boundary Lubricant Polymer Films: Effect of Cross-Linking. Langmuir 2013, 29, 12936–12949. [Google Scholar] [CrossRef]
- Klein, J.; Kumacheva, E.; Perahia, D.; Fetters, L.J. Shear forces between sliding surfaces coated with polymer brushes: The high friction regime. Acta Polym. 1998, 49, 617–625. [Google Scholar] [CrossRef]
- Iuster, N.; Tairy, O.; Driver, M.J.; Armes, S.P.; Klein, J. Cross-Linking Highly Lubricious Phosphocholinated Polymer Brushes: Effect on Surface Interactions and Frictional Behavior. Macromolecules 2017, 50, 7361–7371. [Google Scholar] [CrossRef]
- Yu, J.; Jackson, N.E.; Xu, X.; Morgenstern, Y.; Kaufman, Y.; Ruths, M.; de Pablo, J.J.; Tirrell, M. Multivalent counterions diminish the lubricity of polyelectrolyte brushes. Science 2018, 360, 1434–1438. [Google Scholar] [CrossRef]
- Raviv, U.; Giasson, S.; Kampf, N.; Gohy, J.-F.; Jérôme, R.; Klein, J. Lubrication by charged polymers. Nature 2003, 425, 163–165. [Google Scholar] [CrossRef]
- Léger, L.; Raphaël, E.; Hervet, H. Surface-Anchored Polymer Chains: Their Role in Adhesion and Friction. In Polymers in Confined Environments; Granick, S., Binder, K., de Gennes, P.G., Giannelis, E.P., Grest, G.S., Hervet, H., Krishnamoorti, R., Léger, L., Manias, E., Raphaël, E., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 185–225. [Google Scholar]
- Claesson, P.M.; Ninham, B.W. pH-dependent interactions between adsorbed chitosan layers. Langmuir 1992, 8, 1406–1412. [Google Scholar] [CrossRef]
- Lowack, K.; Helm, C.A. Molecular Mechanisms Controlling the Self-Assembly Process of Polyelectrolyte Multilayers. Macromolecules 1998, 31, 823–833. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Yu, B.; Zhou, F. Brushing up functional materials. NPG Asia Mater. 2019, 11, 24. [Google Scholar] [CrossRef]
- Ali, A.; Ahmed, S. A review on chitosan and its nanocomposites in drug delivery. Int. J. Biol. Macromol. 2018, 109, 273–286. [Google Scholar] [CrossRef] [PubMed]
- Bajpai, A.K.; Shukla, S.K.; Bhanu, S.; Kankane, S. Responsive polymers in controlled drug delivery. Prog. Polym. Sci. 2008, 33, 1088–1118. [Google Scholar] [CrossRef]
- Song, X.; Man, J.; Qiu, Y.; Wang, J.; Liu, J.; Li, R.; Zhang, Y.; Li, J.; Li, J.; Chen, Y. Design, preparation, and characterization of lubricating polymer brushes for biomedical applications. Acta Biomater. 2024, 175, 76–105. [Google Scholar] [CrossRef]
- Sterner, O.; Karageorgaki, C.; Zürcher, M.; Zürcher, S.; Scales, C.W.; Fadli, Z.; Spencer, N.D.; Tosatti, S.G.P. Reducing Friction in the Eye: A Comparative Study of Lubrication by Surface-Anchored Synthetic and Natural Ocular Mucin Analogues. ACS Appl. Mater. Interfaces 2017, 9, 20150–20160. [Google Scholar] [CrossRef]
- Klein, J. Repair or Replacement—A Joint Perspective. Science 2009, 323, 47–48. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, G.; Song, X.; Li, J.; Li, J.; Du, J.; Chen, Y.; Li, R.; Man, J. Lubricating Copolymer Brushes Achieving Excellent Antiadhesion and Antibacterial Performance through Hydration and Electrostatic Repulsion Effects. ACS Appl. Mater. Interfaces 2025, 17, 7406–7423. [Google Scholar] [CrossRef]
- Tardy, B.L.; Mattos, B.D.; Otoni, C.G.; Beaumont, M.; Majoinen, J.; Kämäräinen, T.; Rojas, O.J. Deconstruction and Reassembly of Renewable Polymers and Biocolloids into Next Generation Structured Materials. Chem. Rev. 2021, 121, 14088–14188. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, J.; Wang, W.; Wei, Z.; Chen, Y.; Zeng, H. Targeted Repair of Super-Lubricating Surfaces via Pairing Click Chemistry. Adv. Funct. Mater. 2023, 33, 2301593. [Google Scholar] [CrossRef]
- Zang, X.; Ni, Y.; Wang, Q.; Cheng, Y.; Huang, J.; Cao, X.; Carmalt, C.J.; Lai, Y.; Ha Kim, D.; Liu, Y.; et al. Non-toxic evolution: Advances in multifunctional antifouling coatings. Mater. Today 2024, 75, 210–243. [Google Scholar] [CrossRef]
- Priezjev, N.V. Relationship between induced fluid structure and boundary slip in nanoscale polymer films. Phys. Rev. E 2010, 82, 051603. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Young, D.; Chiu, H.-C.; Kim, S.; Voïtchovsky, K.; Riedo, E. The interplay between apparent viscosity and wettability in nanoconfined water. Nat. Commun. 2013, 4, 2482. [Google Scholar] [CrossRef] [PubMed]
- Warwaruk, L.; Ghaemi, S. Near-wall lubricating layer in drag-reduced flows of rigid polymers. Phys. Rev. Fluids 2022, 7, 064605. [Google Scholar] [CrossRef]
- Pit, R.; Hervet, H.; Léger, L. Friction and slip of a simple liquid at a solid surface. Tribol. Lett. 1999, 7, 147–152. [Google Scholar] [CrossRef]
- Craig, V.S.J.; Neto, C.; Williams, D.R.M. Shear-Dependent Boundary Slip in an Aqueous Newtonian Liquid. Phys. Rev. Lett. 2001, 87, 054504. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Rate-Dependent Slip of Newtonian Liquid at Smooth Surfaces. Phys. Rev. Lett. 2001, 87, 096105. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.-J.; Craig, V.S.J. Boundary slip in Newtonian liquids: A review of experimental studies. Rep. Prog. Phys. 2005, 68, 2859–2897. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Limits of the Hydrodynamic No-Slip Boundary Condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef]
- Huang, D.M.; Sendner, C.; Horinek, D.; Netz, R.R.; Bocquet, L. Water Slippage Versus Contact Angle: A Quasiuniversal Relationship. Phys. Rev. Lett. 2008, 101, 226101. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Enhanced flow in carbon nanotubes. Nature 2005, 438, 44. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.A.; McGaughey, A.J.H. Reassessing Fast Water Transport Through Carbon Nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Wang, D.; Yang, J.; Guo, J.; Duan, Z.; Wang, D.; Xia, F.; Deng, F.; Deng, X. Liquid-like polymer lubricating surfaces: Mechanism and applications. Nano Res. 2024, 17, 476–491. [Google Scholar] [CrossRef]
- Meng, J.; Wang, J.; Wang, L.; Lyu, C.; Lyu, Y.; Nie, B. Effects of polymer-surfactant interactions on drag reduction performance and mechanisms: Molecular dynamics simulations and experimentation. Colloids Surf. A Physicochem. Eng. Asp. 2024, 684, 133126. [Google Scholar] [CrossRef]
- Cu, Y.; Saltzman, W.M. Stealth particles give mucus the slip. Nat. Mater. 2009, 8, 11–13. [Google Scholar] [CrossRef]
- Secchi, E.; Marbach, S.; Niguès, A.; Stein, D.; Siria, A.; Bocquet, L. Massive radius-dependent flow slippage in carbon nanotubes. Nature 2016, 537, 210–213. [Google Scholar] [CrossRef]
- Li, C.; Kim, B.; Yoon, J.; Sett, S.; Oh, J. Advances in Directional Wetting Surfaces for Enhanced Fluid Control: A Comprehensive Review. Adv. Funct. Mater. 2024, 34, 2308265. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Adams, G.E. Measurement of forces between two mica surfaces in aqueous electrolyte solutions in the range 0–100 nm. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1978, 74, 975–1001. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Pashley, R.M. Molecular layering of water at surfaces and origin of repulsive hydration forces. Nature 1983, 306, 249–250. [Google Scholar] [CrossRef]
- Pashley, R.M.; Israelachvili, J.N. Molecular layering of water in thin films between mica surfaces and its relation to hydration forces. J. Colloid Interface Sci. 1984, 101, 511–523. [Google Scholar] [CrossRef]
- Gebbie, M.A.; Wei, W.; Schrader, A.M.; Cristiani, T.R.; Dobbs, H.A.; Idso, M.; Chmelka, B.F.; Waite, J.H.; Israelachvili, J.N. Tuning underwater adhesion with cation–π interactions. Nat. Chem. 2017, 9, 473. [Google Scholar] [CrossRef] [PubMed]
- Kan, Y.; Yang, Q.; Tan, Q.; Wei, Z.; Chen, Y. Diminishing Cohesion of Chitosan Films in Acidic Solution by Multivalent Metal Cations. Langmuir 2020, 36, 4964–4974. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xiang, L.; Yan, B.; Zeng, H. Nanomechanics of Anion−π Interaction in Aqueous Solution. J. Am. Chem. Soc. 2020, 142, 1710–1714. [Google Scholar] [CrossRef]
- Israelachvili, J.; Min, Y.; Akbulut, M.; Alig, A.; Carver, G.; Greene, W.; Kristiansen, K.; Meyer, E.; Pesika, N.; Rosenberg, K.; et al. Recent advances in the surface forces apparatus (SFA) technique. Rep. Prog. Phys. 2010, 73, 036601. [Google Scholar] [CrossRef]
- Yang, Q.; Yong, G.; Kan, Y.; Xiang, L.; Tao, Y.; Chen, Y. Tribological Behavior of Medium Molecular Weight Chitosan in Acid Aqueous Solution. In Proceedings of the 2023 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Chengdu, China, 31 July–4 August 2023; pp. 348–353. [Google Scholar] [CrossRef]
- Israelachvili, J.N. 11—Contrasts between Intermolecular, Interparticle, and Intersurface Forces. In Intermolecular and Surface Forces, 3rd ed.; Israelachvili, J.N., Ed.; Academic Press: Cambridge, MA, USA, 2011; pp. 205–222. [Google Scholar]
- Lim, C.; Lee, D.W.; Israelachvili, J.N.; Jho, Y.; Hwang, D.S. Contact time- and pH-dependent adhesion and cohesion of low molecular weight chitosan coated surfaces. Carbohydr. Polym. 2015, 117, 887–894. [Google Scholar] [CrossRef]
- Goldberg, R.; Schroeder, A.; Silbert, G.; Turjeman, K.; Barenholz, Y.; Klein, J. Boundary Lubricants with Exceptionally Low Friction Coefficients Based on 2D Close-Packed Phosphatidylcholine Liposomes. Adv. Mater. 2011, 23, 3517–3521. [Google Scholar] [CrossRef]
- Jahn, S.; Klein, J. Hydration Lubrication: The Macromolecular Domain. Macromolecules 2015, 48, 5059–5075. [Google Scholar] [CrossRef]
- Angayarkanni, S.A.; Kampf, N.; Klein, J. Surface Interactions between Boundary Layers of Poly(ethylene oxide)–Liposome Complexes: Lubrication, Bridging, and Selective Ligation. Langmuir 2019, 35, 15469–15480. [Google Scholar] [CrossRef]
- Song, W.; Su, X.; Gregory, D.A.; Li, W.; Cai, Z.; Zhao, X. Magnetic Alginate/Chitosan Nanoparticles for Targeted Delivery of Curcumin into Human Breast Cancer Cells. Nanomaterials 2018, 8, 907. [Google Scholar] [CrossRef]
- Kusrini, E.; Arbianti, R.; Sofyan, N.; Abdullah, M.A.A.; Andriani, F. Modification of chitosan by using samarium for potential use in drug delivery system. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 120, 77–83. [Google Scholar] [CrossRef]
- Bernkop-Schnürch, A.; Dünnhaupt, S. Chitosan-based drug delivery systems. Eur. J. Pharm. Biopharm. 2012, 81, 463–469. [Google Scholar] [CrossRef] [PubMed]
- Mitra, D.; Kang, E.-T.; Neoh, K.G. Polymer-Based Coatings with Integrated Antifouling and Bactericidal Properties for Targeted Biomedical Applications. ACS Appl. Polym. Mater. 2021, 3, 2233–2263. [Google Scholar] [CrossRef]
- Maan, A.M.C.; Hofman, A.H.; de Vos, W.M.; Kamperman, M. Recent Developments and Practical Feasibility of Polymer-Based Antifouling Coatings. Adv. Funct. Mater. 2020, 30, 2000936. [Google Scholar] [CrossRef]
- Kanematsu, H.; Oizumi, A.; Sato, T.; Kamijo, T.; Honma, S.; Barry, D.M.; Hirai, N.; Ogawa, A.; Kogo, T.; Kuroda, D.; et al. Biofilm Formation of a Polymer Brush Coating with Ionic Liquids Compared to a Polymer Brush Coating with a Non-Ionic Liquid. Coatings 2018, 8, 398. [Google Scholar] [CrossRef]
- Song, S.; Latag, G.V.; Mondarte, E.A.Q.; Chang, R.; Hayashi, T. Experimental Characterization of Water Condensation Processes on Self-Assembled Monolayers Using a Quartz Crystal Microbalance with Energy Dissipation Monitoring. Micro 2022, 2, 513–523. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Barbey, R.; Lavanant, L.; Paripovic, D.; Schüwer, N.; Sugnaux, C.; Tugulu, S.; Klok, H.-A. Polymer Brushes via Surface-Initiated Controlled Radical Polymerization: Synthesis, Characterization, Properties, and Applications. Chem. Rev. 2009, 109, 5437–5527. [Google Scholar] [CrossRef]
- Cai, W.; Bullerjahn, J.T.; Lallemang, M.; Kroy, K.; Balzer, B.N.; Hugel, T. Angle-dependent strength of a single chemical bond by stereographic force spectroscopy. Chem. Sci. 2022, 13, 5734–5740. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Adams, G.E. Direct measurement of long range forces between two mica surfaces in aqueous KNO3 solutions. Nature 1976, 262, 774–776. [Google Scholar] [CrossRef]
- Pashley, R.M. Hydration forces between mica surfaces in aqueous electrolyte solutions. J. Colloid Interface Sci. 1981, 80, 153–162. [Google Scholar] [CrossRef]
- Pashley, R.M. DLVO and hydration forces between mica surfaces in Li+, Na+, K+, and Cs+ electrolyte solutions: A correlation of double-layer and hydration forces with surface cation exchange properties. J. Colloid Interface Sci. 1981, 83, 531–546. [Google Scholar] [CrossRef]
- Attard, P.; Batchelor, M.T. A mechanism for the hydration force demonstrated in a model system. Chem. Phys. Lett. 1988, 149, 206–211. [Google Scholar] [CrossRef]
- Klein, J. Hydration lubrication. Friction 2013, 1, 1–23. [Google Scholar] [CrossRef]
- Diao, Y.; Han, M.; Lopez-Berganza, J.A.; Valentino, L.; Marinas, B.; Espinosa-Marzal, R.M. Reconciling DLVO and non-DLVO Forces and Their Implications for Ion Rejection by a Polyamide Membrane. Langmuir 2017, 33, 8982–8992. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, H.; Liu, Q. Probing Molecular and Surface Interactions of Comb-Type Polymer Polystyrene-graft-poly(ethylene oxide) (PS-g-PEO) with an SFA. J. Phys. Chem. C 2012, 116, 17554–17562. [Google Scholar] [CrossRef]
- Grabbe, A.; Horn, R.G. Double-Layer and Hydration Forces Measured between Silica Sheets Subjected to Various Surface Treatments. J. Colloid Interface Sci. 1993, 157, 375–383. [Google Scholar] [CrossRef]
- Borkovec, M.; Behrens, S.H. Electrostatic Double Layer Forces in the Case of Extreme Charge Regulation. J. Phys. Chem. B 2008, 112, 10795–10799. [Google Scholar] [CrossRef]
- Wu, J. Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics. Chem. Rev. 2022, 122, 10821–10859. [Google Scholar] [CrossRef]
- Kampf, N.; Ben-Yaakov, D.; Andelman, D.; Safran, S.A.; Klein, J. Direct Measurement of Sub-Debye-Length Attraction between Oppositely Charged Surfaces. Phys. Rev. Lett. 2009, 103, 118304. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Xu, H.; Tian, H.; Deng, J.; Zhuo, Q.; Cui, J.; Wang, J.; Yin, Y.; Yu, P. Review of influence of steric effect on aggregation behavior of fine particles. Miner. Eng. 2023, 203, 108304. [Google Scholar] [CrossRef]
- Schrader, A.M.; Donaldson, S.H.; Song, J.; Cheng, C.-Y.; Lee, D.W.; Han, S.; Israelachvili, J.N. Correlating steric hydration forces with water dynamics through surface force and diffusion NMR measurements in a lipid–DMSO–H2O system. Proc. Natl. Acad. Sci. USA 2015, 112, 10708–10713. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Jackson, N.E.; Xu, X.; Brettmann, B.K.; Ruths, M.; de Pablo, J.J.; Tirrell, M. Multivalent ions induce lateral structural inhomogeneities in polyelectrolyte brushes. Sci. Adv. 2017, 3, eaao1497. [Google Scholar] [CrossRef] [PubMed]
- Luckham, P.F.; Klein, J. Forces between mica surfaces bearing adsorbed homopolymers in good solvents. The effect of bridging and dangling tails. J. Chem. Soc. Faraday Trans. 1990, 86, 1363–1368. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Chapter 16—Steric (Polymer-Mediated) and Thermal Fluctuation Forces. In Intermolecular and Surface Forces, 3rd ed.; Israelachvili, J.N., Ed.; Academic Press: Cambridge, MA, USA, 2011; pp. 381–413. [Google Scholar]
- Faghihnejad, A.; Zeng, H. Fundamentals of Surface Adhesion, Friction, and Lubrication. In Polymer Adhesion, Friction, and Lubrication; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 1–57. [Google Scholar]
- Huang, J.; Yan, B.; Faghihnejad, A.; Xu, H.; Zeng, H. Understanding nanorheology and surface forces of confined thin films. Korea-Aust. Rheol. J. 2014, 26, 3–14. [Google Scholar] [CrossRef]
- Neto, C.; Craig, V.S.J.; Williams, D.R.M. Evidence of shear-dependent boundary slip in newtonian liquids. Eur. Phys. J. E 2003, 12, 71–74. [Google Scholar] [CrossRef]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- Thompson, P.A.; Robbins, M.O. Shear flow near solids: Epitaxial order and flow boundary conditions. Phys. Rev. A 1990, 41, 6830–6837. [Google Scholar] [CrossRef]
- Lallemang, M.; Yu, L.; Cai, W.; Rischka, K.; Hartwig, A.; Haag, R.; Hugel, T.; Balzer, B.N. Multivalent non-covalent interactions lead to strongest polymer adhesion. Nanoscale 2022, 14, 3768–3776. [Google Scholar] [CrossRef]
- Qiao, C.; Sun, Y.; Han, Y.; Zhao, Z.; Ma, L.; Zeng, H. Surface forces dominating tribological phenomena in nanoconfined liquids: A review. Friction 2025, 13, 9440983. [Google Scholar] [CrossRef]
- Cai, W.; Trefs, J.L.; Hugel, T.; Balzer, B.N. Anisotropy of π–π Stacking as Basis for Superlubricity. ACS Mater. Lett. 2023, 5, 172–179. [Google Scholar] [CrossRef]
- Donose, B.C.; Vakarelski, I.U.; Higashitani, K. Silica Surfaces Lubrication by Hydrated Cations Adsorption from Electrolyte Solutions. Langmuir 2005, 21, 1834–1839. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Cummings, P.T. Fluidity of Hydration Layers Nanoconfined between Mica Surfaces. Phys. Rev. Lett. 2005, 94, 026101. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Gaisinskaya-Kipnis, A.; Kampf, N.; Klein, J. Origins of hydration lubrication. Nat. Commun. 2015, 6, 6060. [Google Scholar] [CrossRef]
- Han, T.; Cao, W.; Xu, Z.; Adibnia, V.; Olgiati, M.; Valtiner, M.; Ma, L.; Zhang, C.; Ma, M.; Luo, J.; et al. Hydration layer structure modulates superlubrication by trivalent La3+ electrolytes. Sci. Adv. 2023, 9, eadf3902. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y.; Espinosa-Marzal, R.M. The role of water in fault lubrication. Nat. Commun. 2018, 9, 2309. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Cummings, P.T. Shear dynamics of hydration layers. J. Chem. Phys. 2006, 125, 104701. [Google Scholar] [CrossRef]
- Richetti, P.; Drummond, C.; Israelachvili, J.; In, M.; Zana, R. Inverted stick-slip friction. Europhys. Lett. (EPL) 2001, 55, 653–659. [Google Scholar] [CrossRef]
- Seror, J.; Merkher, Y.; Kampf, N.; Collinson, L.; Day, A.J.; Maroudas, A.; Klein, J. Normal and Shear Interactions between Hyaluronan–Aggrecan Complexes Mimicking Possible Boundary Lubricants in Articular Cartilage in Synovial Joints. Biomacromolecules 2012, 13, 3823–3832. [Google Scholar] [CrossRef]
- Banquy, X.; Lee, D.W.; Das, S.; Hogan, J.; Israelachvili, J.N. Shear-Induced Aggregation of Mammalian Synovial Fluid Components under Boundary Lubrication Conditions. Adv. Funct. Mater. 2014, 24, 3152–3161. [Google Scholar] [CrossRef]
- Klein, J. Molecular mechanisms of synovial joint lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 691–710. [Google Scholar] [CrossRef]
- Lee, D.W.; Banquy, X.; Israelachvili, J.N. Stick-slip friction and wear of articular joints. Proc. Natl. Acad. Sci. USA 2013, 110, E567–E574. [Google Scholar] [CrossRef]
- Radin, E.L.; Swann, D.A.; Weisser, P.A. Separation of a Hyaluronate-free Lubricating Fraction from Synovial Fluid. Nature 1970, 228, 377–378. [Google Scholar] [CrossRef] [PubMed]
- Murakami, T.; Yarimitsu, S.; Nakashima, K.; Sawae, Y.; Sakai, N. Influence of synovia constituents on tribological behaviors of articular cartilage. Friction 2013, 1, 150–162. [Google Scholar] [CrossRef]
- Greene, G.W.; Banquy, X.; Lee, D.W.; Lowrey, D.D.; Yu, J.; Israelachvili, J.N. Adaptive mechanically controlled lubrication mechanism found in articular joints. Proc. Natl. Acad. Sci. USA 2011, 108, 5255–5259. [Google Scholar] [CrossRef]
- Sun, Z.; Feeney, E.; Guan, Y.; Cook, S.G.; Gourdon, D.; Bonassar, L.J.; Putnam, D. Boundary mode lubrication of articular cartilage with a biomimetic diblock copolymer. Proc. Natl. Acad. Sci. USA 2019, 116, 12437–12441. [Google Scholar] [CrossRef]
- Laurent, T.C.; Fraser, J.R.E. Hyaluronan1. FASEB J. 1992, 6, 2397–2404. [Google Scholar] [CrossRef]
- Laurent, T.C.; Laurent, U.B.; Fraser, J.R.E. The structure and function of hyaluronan: An overview. Immunol. Cell Biol. 1996, 74, a1–a7. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, W.; Fan, Y.; Kampf, N.; Wang, Y.; Klein, J. Effects of Hyaluronan Molecular Weight on the Lubrication of Cartilage-Emulating Boundary Layers. Biomacromolecules 2020, 21, 4345–4354. [Google Scholar] [CrossRef]
- Liu, C.; Wang, M.; An, J.; Thormann, E.; Dėdinaitė, A. Hyaluronan and phospholipids in boundary lubrication. Soft Matter 2012, 8, 10241–10244. [Google Scholar] [CrossRef]
- Mabuchi, K.; Obara, T.; Ikegami, K.; Yamaguchi, T.; Kanayama, T. Molecular weight independence of the effect of additive hyaluronic acid on the lubricating characteristics in synovial joints with experimental deterioration. Clin. Biomech. 1999, 14, 352–356. [Google Scholar] [CrossRef]
- Benz, M.; Chen, N.; Israelachvili, J. Lubrication and wear properties of grafted polyelectrolytes, hyaluronan and hylan, measured in the surface forces apparatus. J. Biomed. Mater. Res. Part A 2004, 71A, 6–15. [Google Scholar] [CrossRef]
- Jay, G.D.; Torres, J.R.; Warman, M.L.; Laderer, M.C.; Breuer, K.S. The role of lubricin in the mechanical behavior of synovial fluid. Proc. Natl. Acad. Sci. USA 2007, 104, 6194–6199. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Seror, J.; Day, A.J.; Kampf, N.; Klein, J. Ultra-low friction between boundary layers of hyaluronan-phosphatidylcholine complexes. Acta Biomater. 2017, 59, 283–292. [Google Scholar] [CrossRef] [PubMed]
- Krylov, S.Y.; Frenken, J.W.M. The physics of atomic-scale friction: Basic considerations and open questions. Phys. Status Solidi 2014, 251, 711–736. [Google Scholar] [CrossRef]
- Cieplak, M.; Smith, E.D.; Robbins, M.O. Molecular Origins of Friction: The Force on Adsorbed Layers. Science 1994, 265, 1209–1212. [Google Scholar] [CrossRef]
- Alexander, S. Adsorption of chain molecules with a polar head a scaling description. J. Phys. 1977, 38, 983–987. [Google Scholar] [CrossRef]
- Milner, S.T. Polymer Brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef]
- Bhat, R.R.; Tomlinson, M.R.; Wu, T.; Genzer, J. Surface-Grafted Polymer Gradients: Formation, Characterization, and Applications. In Surface-Initiated Polymerization II; Jordan, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 51–124. [Google Scholar]
- Modica, K.J.; Martin, T.B.; Jayaraman, A. Effect of Polymer Architecture on the Structure and Interactions of Polymer Grafted Particles: Theory and Simulations. Macromolecules 2017, 50, 4854–4866. [Google Scholar] [CrossRef]
- Wu, T.; Efimenko, K.; Vlček, P.; Šubr, V.; Genzer, J. Formation and Properties of Anchored Polymers with a Gradual Variation of Grafting Densities on Flat Substrates. Macromolecules 2003, 36, 2448–2453. [Google Scholar] [CrossRef]
- Moh, L.C.H.; Losego, M.D.; Braun, P.V. Solvent Quality Effects on Scaling Behavior of Poly(methyl methacrylate) Brushes in the Moderate- and High-Density Regimes. Langmuir 2011, 27, 3698–3702. [Google Scholar] [CrossRef]
- Xu, X.; Billing, M.; Ruths, M.; Klok, H.-A.; Yu, J. Structure and Functionality of Polyelectrolyte Brushes: A Surface Force Perspective. Chem. Asian J. 2018, 13, 3411–3436. [Google Scholar] [CrossRef] [PubMed]
- Tanoue, H.; Yamada, N.L.; Ito, K.; Yokoyama, H. Quantitative Analysis of Polymer Brush Formation Kinetics Using Quartz Crystal Microbalance: Viscoelasticity of Polymer Brush. Langmuir 2017, 33, 5166–5172. [Google Scholar] [CrossRef]
- Furusawa, H.; Sekine, T.; Ozeki, T. Hydration and Viscoelastic Properties of High- and Low-Density Polymer Brushes Using a Quartz-Crystal Microbalance Based on Admittance Analysis (QCM-A). Macromolecules 2016, 49, 3463–3470. [Google Scholar] [CrossRef]
- Saito, M.; Yamada, N.L.; Ito, K.; Yokoyama, H. Interfacial Energy Measurement on the Reconstructive Polymer Surface: Dynamic Polymer Brush by Segregation of Amphiphilic Block Copolymers. Langmuir 2020, 36, 6465–6472. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Kumacheva, E.; Mahalu, D.; Perahia, D.; Fetters, L.J. Reduction of frictional forces between solid surfaces bearing polymer brushes. Nature 1994, 370, 634–636. [Google Scholar] [CrossRef]
- Galuschko, A.; Spirin, L.; Kreer, T.; Johner, A.; Pastorino, C.; Wittmer, J.; Baschnagel, J. Frictional Forces between Strongly Compressed, Nonentangled Polymer Brushes: Molecular Dynamics Simulations and Scaling Theory. Langmuir 2010, 26, 6418–6429. [Google Scholar] [CrossRef]
- Klein, J.; Kumacheva, E.; Perahia, D.; Mahalu, D.; Warburg, S. Interfacial sliding of polymer-bearing surfaces. Faraday Discuss. 1994, 98, 173–188. [Google Scholar] [CrossRef]
- Grest, G.S. Interfacial Sliding of Polymer Brushes: A Molecular Dynamics Simulation. Phys. Rev. Lett. 1996, 76, 4979–4982. [Google Scholar] [CrossRef]
- Farina, R.; Laugel, N.; Yu, J.; Tirrell, M. Reversible Adhesion with Polyelectrolyte Brushes Tailored via the Uptake and Release of Trivalent Lanthanum Ions. J. Phys. Chem. C 2015, 119, 14805–14814. [Google Scholar] [CrossRef]
- Klein, J. Shear, Friction, and Lubrication Forces Between Polymer-Bearing Surfaces. Annu. Rev. Mater. Sci. 1996, 26, 581–612. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Y.; Yao, L.; Wang, J.; Chen, H. Antifouling Polymer Coatings for Bioactive Surfaces. Langmuir 2025. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Lan, X.; Hu, Q.; Li, H.; Li, L.; Mao, J. Antifouling strategies based on super-phobic polymer materials. Prog. Org. Coat. 2021, 157, 106285. [Google Scholar] [CrossRef]
- Zhao, P.; Klein, J. Lubricating Polymer Gels/Coatings: Syntheses and Measurement Strategies. Gels 2024, 10, 407. [Google Scholar] [CrossRef]
- Saphiannikova, M.G.; Pryamitsyn, V.A.; Cosgrove, T. Self-Consistent Brownian Dynamics Simulation of Polymer Brushes under Shear. Macromolecules 1998, 31, 6662–6668. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic Simulation of Entangled Polymer Brushes under Shear: Compression and Rheological Properties. Macromolecules 2009, 42, 4310–4318. [Google Scholar] [CrossRef]
- Erfani, A.; Seaberg, J.; Aichele, C.P.; Ramsey, J.D. Interactions Between Biomolecules and Zwitterionic Moieties: A Review. Biomacromolecules 2020, 21, 2557–2573. [Google Scholar] [CrossRef]
- Chen, M.; Briscoe, W.H.; Armes, S.P.; Klein, J. Lubrication at Physiological Pressures by Polyzwitterionic Brushes. Science 2009, 323, 1698–1701. [Google Scholar] [CrossRef]
- Feng, S.; Liu, Y.; Li, J.; Wen, S. Superlubricity Achieved with Zwitterionic Brushes in Diverse Conditions Induced by Shear Actions. Macromolecules 2021, 54, 5719–5727. [Google Scholar] [CrossRef]
- Nomura, A.; Okayasu, K.; Ohno, K.; Fukuda, T.; Tsujii, Y. Lubrication Mechanism of Concentrated Polymer Brushes in Solvents: Effect of Solvent Quality and Thereby Swelling State. Macromolecules 2011, 44, 5013–5019. [Google Scholar] [CrossRef]
- Raviv, U.; Perkin, S.; Laurat, P.; Klein, J. Fluidity of Water Confined Down to Subnanometer Films. Langmuir 2004, 20, 5322–5332. [Google Scholar] [CrossRef]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. The kinetic friction coefficient of neutral and charged polymer brushes. Soft Matter 2013, 9, 2966–2972. [Google Scholar] [CrossRef]
- Ou, Y.; Sokoloff, J.B.; Stevens, M.J. Comparison of the kinetic friction of planar neutral and polyelectrolyte polymer brushes using molecular dynamics simulations. Phys. Rev. E 2012, 85, 011801. [Google Scholar] [CrossRef] [PubMed]
- Tadmor, R.; Janik, J.; Klein, J.; Fetters, L.J. Sliding Friction with Polymer Brushes. Phys. Rev. Lett. 2003, 91, 115503. [Google Scholar] [CrossRef] [PubMed]
- Qu, K.; Yuan, Z.; Wang, Y.; Song, Z.; Gong, X.; Zhao, Y.; Mu, Q.; Zhan, Q.; Xu, W.; Wang, L. Structures, properties, and applications of zwitterionic polymers. ChemPhysMater 2022, 1, 294–309. [Google Scholar] [CrossRef]
- Gong, L.; Xiang, L.; Zhang, J.; Han, L.; Wang, J.; Wang, X.; Liu, J.; Yan, B.; Zeng, H. Interaction Mechanisms of Zwitterions with Opposite Dipoles in Aqueous Solutions. Langmuir 2019, 35, 2842–2853. [Google Scholar] [CrossRef]
- Morozova, S.; Hu, G.; Emrick, T.; Muthukumar, M. Influence of Dipole Orientation on Solution Properties of Polyzwitterions. ACS Macro Lett. 2016, 5, 118–122. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wu, J.-G.; Lin, H.-H.; Luo, S.-C. Electrified Interactions of Polyzwitterions with Charged Surfaces: Role of Dipole Orientation and Surface Potentials. Langmuir 2024, 40, 7653–7660. [Google Scholar] [CrossRef]
- Sarker, P.; Lu, T.; Liu, D.; Wu, G.; Chen, H.; Jahan Sajib, M.S.; Jiang, S.; Chen, Z.; Wei, T. Hydration behaviors of nonfouling zwitterionic materials. Chem. Sci. 2023, 14, 7500–7511. [Google Scholar] [CrossRef]
- Yaseen, M.; Lu, J.R.; Webster, J.R.P.; Penfold, J. The Structure of Zwitterionic Phosphocholine Surfactant Monolayers. Langmuir 2006, 22, 5825–5832. [Google Scholar] [CrossRef]
- Drummond, C.; Israelachvili, J.; Richetti, P. Friction between two weakly adhering boundary lubricated surfaces in water. Phys. Rev. E 2003, 67, 066110. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, J.; Gong, L.; Zeng, H. Surface forces and interaction mechanisms of soft thin films under confinement: A short review. Soft Matter 2020, 16, 6697–6719. [Google Scholar] [CrossRef]
- Israelachvili, J.N. 18—Friction and Lubrication Forces. In Intermolecular and Surface Forces, 3rd ed.; Israelachvili, J.N., Ed.; Academic Press: Cambridge, MA, USA, 2011; pp. 469–499. [Google Scholar]
- Stevens, M.J.; Plimpton, S.J. The effect of added salt on polyelectrolyte structure. Eur. Phys. J. B Condens. Matter Complex Syst. 1998, 2, 341–345. [Google Scholar] [CrossRef]
- Yu, J.; Mao, J.; Yuan, G.; Satija, S.; Jiang, Z.; Chen, W.; Tirrell, M. Structure of Polyelectrolyte Brushes in the Presence of Multivalent Counterions. Macromolecules 2016, 49, 5609–5617. [Google Scholar] [CrossRef]
- Mei, Y.; Ballauff, M. Effect of counterions on the swelling of spherical polyelectrolyte brushes. Eur. Phys. J. E 2005, 16, 341–349. [Google Scholar] [CrossRef]
- Salomäki, M.; Tervasmäki, P.; Areva, S.; Kankare, J. The Hofmeister Anion Effect and the Growth of Polyelectrolyte Multilayers. Langmuir 2004, 20, 3679–3683. [Google Scholar] [CrossRef]
- Yu, J.; Mao, J.; Yuan, G.; Satija, S.; Chen, W.; Tirrell, M. The effect of multivalent counterions to the structure of highly dense polystyrene sulfonate brushes. Polymer 2016, 98, 448–453. [Google Scholar] [CrossRef]
- Wang, T.; Long, Y.; Liu, L.; Wang, X.; Craig, V.S.J.; Zhang, G.; Liu, G. Cation-Specific Conformational Behavior of Polyelectrolyte Brushes: From Aqueous to Nonaqueous Solvent. Langmuir 2014, 30, 12850–12859. [Google Scholar] [CrossRef]
- Konradi, R.; Rühe, J. Interaction of Poly(methacrylic acid) Brushes with Metal Ions: Swelling Properties. Macromolecules 2005, 38, 4345–4354. [Google Scholar] [CrossRef]
- Yu, Y.; Kieviet, B.D.; Liu, F.; Siretanu, I.; Kutnyánszky, E.; Vancso, G.J.; de Beer, S. Stretching of collapsed polymers causes an enhanced dissipative response of PNIPAM brushes near their LCST. Soft Matter 2015, 11, 8508–8516. [Google Scholar] [CrossRef]
- Lee, H.-S.; Yee, M.Q.; Eckmann, Y.Y.; Hickok, N.J.; Eckmann, D.M.; Composto, R.J. Reversible swelling of chitosan and quaternary ammonium modified chitosan brush layers: Effects of pH and counter anion size and functionality. J. Mater. Chem. 2012, 22, 19605–19616. [Google Scholar] [CrossRef]
- Dunderdale, G.J.; Fairclough, J.P.A. Coupling pH-Responsive Polymer Brushes to Electricity: Switching Thickness and Creating Waves of Swelling or Collapse. Langmuir 2013, 29, 3628–3635. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Poisson–Boltzmann Theory of pH-Sensitive (Annealing) Polyelectrolyte Brush. Langmuir 2011, 27, 10615–10633. [Google Scholar] [CrossRef]
- Ramezani Bajgiran, S.; Safi Samghabadi, F.; Li, S.; Conrad, J.C.; Marciel, A.B. Effects of the Ionizable Monomer Fraction on the Swelling Behavior of Weak Polyelectrolyte Brushes. Macromolecules 2023, 56, 9218–9228. [Google Scholar] [CrossRef]
- Brettmann, B.K.; Laugel, N.; Hoffmann, N.; Pincus, P.; Tirrell, M. Bridging contributions to polyelectrolyte brush collapse in multivalent salt solutions. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 284–291. [Google Scholar] [CrossRef]
- Jackson, N.E.; Brettmann, B.K.; Vishwanath, V.; Tirrell, M.; de Pablo, J.J. Comparing Solvophobic and Multivalent Induced Collapse in Polyelectrolyte Brushes. ACS Macro Lett. 2017, 6, 155–160. [Google Scholar] [CrossRef]
- Adibnia, V.; Olszewski, M.; De Crescenzo, G.; Matyjaszewski, K.; Banquy, X. Superlubricity of Zwitterionic Bottlebrush Polymers in the Presence of Multivalent Ions. J. Am. Chem. Soc. 2020, 142, 14843–14847. [Google Scholar] [CrossRef]
- Song, X.; Man, J.; Zhang, X.; Wang, J.; Zhang, Y.; Li, J.; Du, J.; Chen, Y.; Li, J.; Chen, Y. Atomistic Insights into the Ionic Response and Mechanism of Antifouling Zwitterionic Polymer Brushes (Small 6/2025). Small 2025, 21, 2570043. [Google Scholar] [CrossRef]
- Wei, Q.; Cai, M.; Zhou, F.; Liu, W. Dramatically Tuning Friction Using Responsive Polyelectrolyte Brushes. Macromolecules 2013, 46, 9368–9379. [Google Scholar] [CrossRef]
- Motornov, M.; Minko, S.; Eichhorn, K.-J.; Nitschke, M.; Simon, F.; Stamm, M. Reversible Tuning of Wetting Behavior of Polymer Surface with Responsive Polymer Brushes. Langmuir 2003, 19, 8077–8085. [Google Scholar] [CrossRef]
- Inutsuka, M.; Tanoue, H.; Yamada, N.L.; Ito, K.; Yokoyama, H. Dynamic contact angle on a reconstructive polymer surface by segregation. RSC Adv. 2017, 7, 17202–17207. [Google Scholar] [CrossRef]
- Drummond, C. Electric-Field-Induced Friction Reduction and Control. Phys. Rev. Lett. 2012, 109, 154302. [Google Scholar] [CrossRef]
- Nordgren, N.; Rutland, M.W. Tunable Nanolubrication Between Dual-Responsive Polyionic Grafts. Nano Lett. 2009, 9, 2984–2990. [Google Scholar] [CrossRef]
- Lizée, M.; Coquinot, B.; Mariette, G.; Siria, A.; Bocquet, L. Anomalous friction of supercooled glycerol on mica. Nat. Commun. 2024, 15, 6129. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Z.; Zhao, Y.; Cui, P.; Wu, H. Role of Carbon Nanotube Wetting Transparency in Rapid Water Transport for a Nanopore Membrane. Nano Lett. 2024, 24, 3484–3489. [Google Scholar] [CrossRef]
- Jothi Prakash, C.G.; Prasanth, R. Approaches to design a surface with tunable wettability: A review on surface properties. J. Mater. Sci. 2021, 56, 108–135. [Google Scholar] [CrossRef]
- Zhou, P.; Hou, J.; Yan, Y.; Wang, J. The effect of surfactant adsorption on surface wettability and flow resistance in slit nanopore: A molecular dynamics study. J. Colloid Interface Sci. 2018, 513, 379–388. [Google Scholar] [CrossRef]
- Lepikko, S.; Jaques, Y.M.; Junaid, M.; Backholm, M.; Lahtinen, J.; Julin, J.; Jokinen, V.; Sajavaara, T.; Sammalkorpi, M.; Foster, A.S.; et al. Droplet slipperiness despite surface heterogeneity at molecular scale. Nat. Chem. 2024, 16, 506–513. [Google Scholar] [CrossRef]
- Payam, A.F.; Kim, B.; Lee, D.; Bhalla, N. Unraveling the liquid gliding on vibrating solid liquid interfaces with dynamic nanoslip enactment. Nat. Commun. 2022, 13, 6608. [Google Scholar] [CrossRef]
- Codrignani, A.; Peeters, S.; Holey, H.; Stief, F.; Savio, D.; Pastewka, L.; Moras, G.; Falk, K.; Moseler, M. Toward a continuum description of lubrication in highly pressurized nanometer-wide constrictions: The importance of accurate slip laws. Sci. Adv. 2023, 9, eadi2649. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Ben, X.; Lin, J.; Zhang, Y.; Xiang, L.; Wei, Z.; Kan, Y. Lubrication and Drag Reduction for Polymer-Coated Interfaces. Lubricants 2025, 13, 119. https://doi.org/10.3390/lubricants13030119
Yang Q, Ben X, Lin J, Zhang Y, Xiang L, Wei Z, Kan Y. Lubrication and Drag Reduction for Polymer-Coated Interfaces. Lubricants. 2025; 13(3):119. https://doi.org/10.3390/lubricants13030119
Chicago/Turabian StyleYang, Qiang, Xiang Ben, Jingkai Lin, Yuhao Zhang, Li Xiang, Zhiyong Wei, and Yajing Kan. 2025. "Lubrication and Drag Reduction for Polymer-Coated Interfaces" Lubricants 13, no. 3: 119. https://doi.org/10.3390/lubricants13030119
APA StyleYang, Q., Ben, X., Lin, J., Zhang, Y., Xiang, L., Wei, Z., & Kan, Y. (2025). Lubrication and Drag Reduction for Polymer-Coated Interfaces. Lubricants, 13(3), 119. https://doi.org/10.3390/lubricants13030119





