Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings
Abstract
:1. Introduction
2. Time-Varying Stiffness Model of Four-Point Contact Ball Bearing
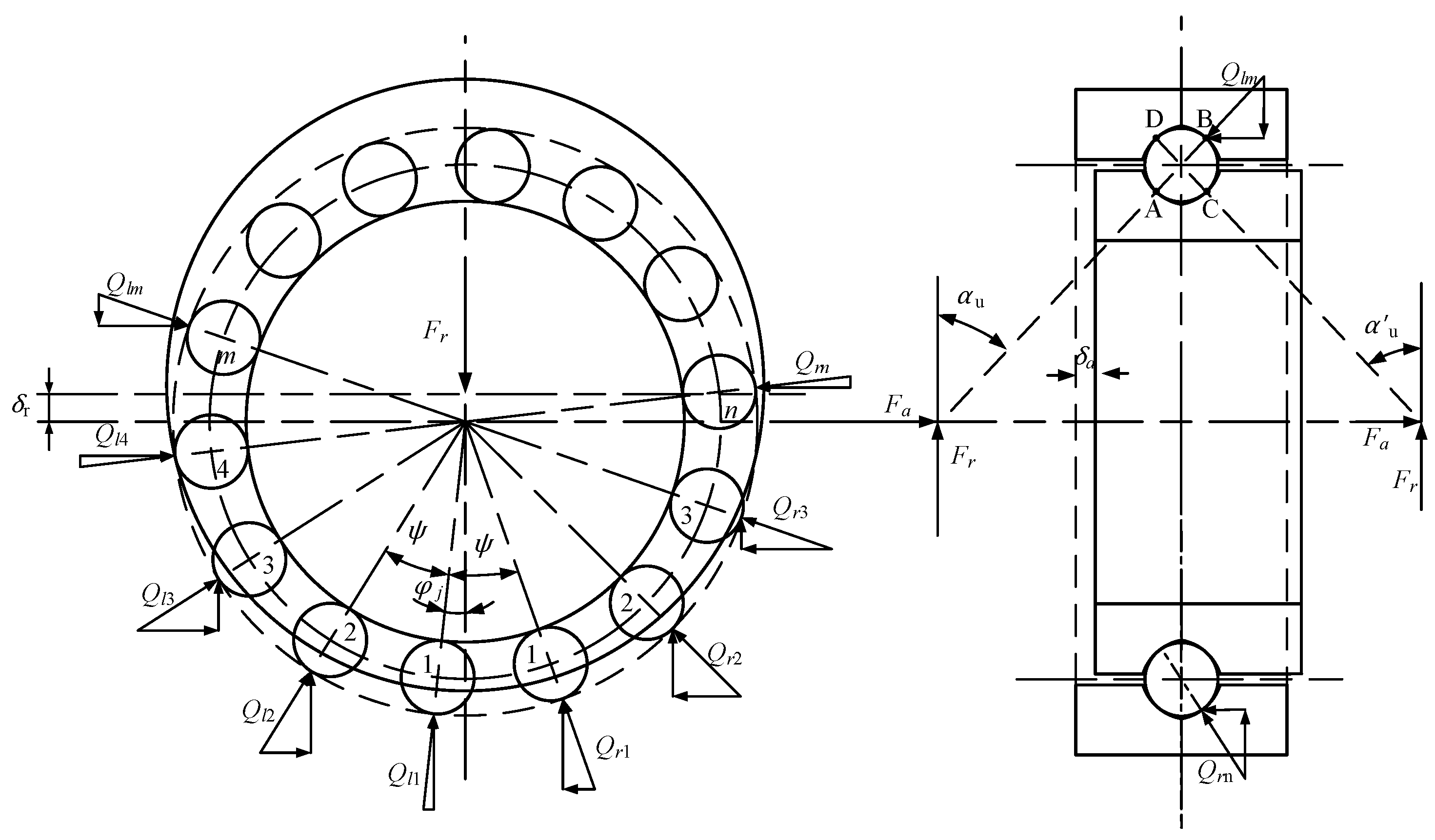
2.1. Load Distribution of Rolling Element Under Combined Load
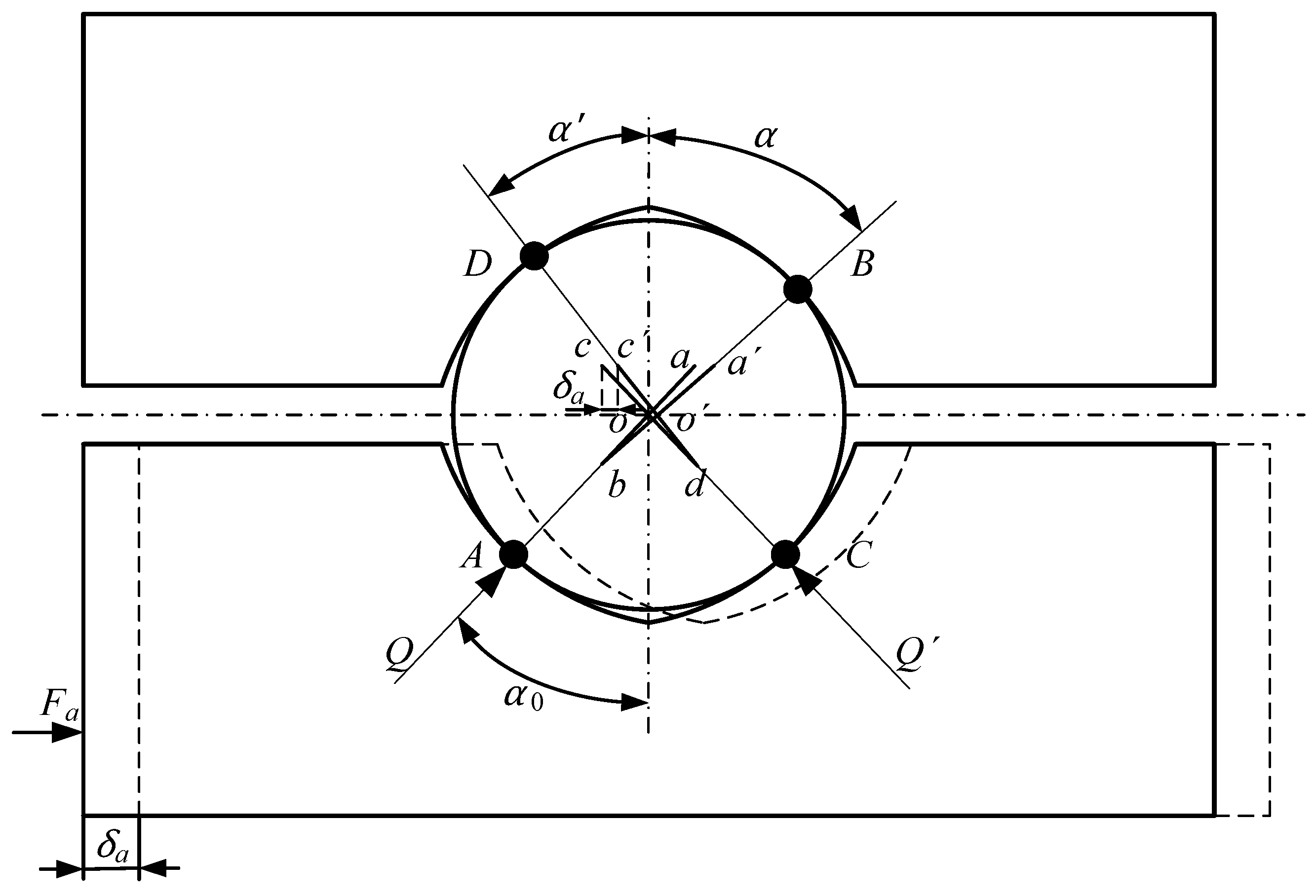
2.2. Stiffness Model and Verification
2.2.1. Time-Varying Stiffness Model Solution
2.2.2. Time-Varying Stiffness Model Verification
2.3. Characterization Parameters of Time-Varying Stiffness
3. Analysis of Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings
3.1. The Structural Parameters and Working Conditions of the Case Bearing
3.2. The Stiffness Variations of the Bearing in a Complete Period
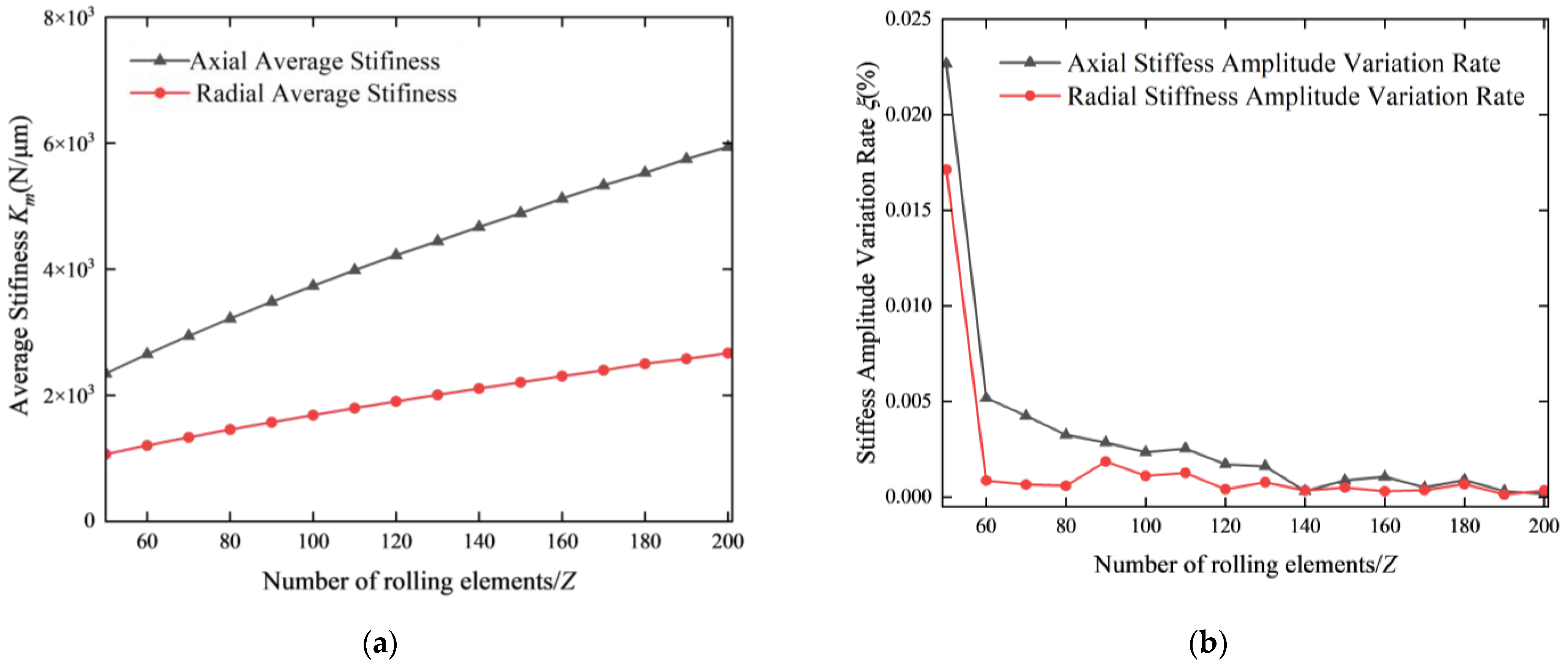
3.3. The Influence of the Number of Rolling Elements on the Time-Varying Characteristics of Stiffness
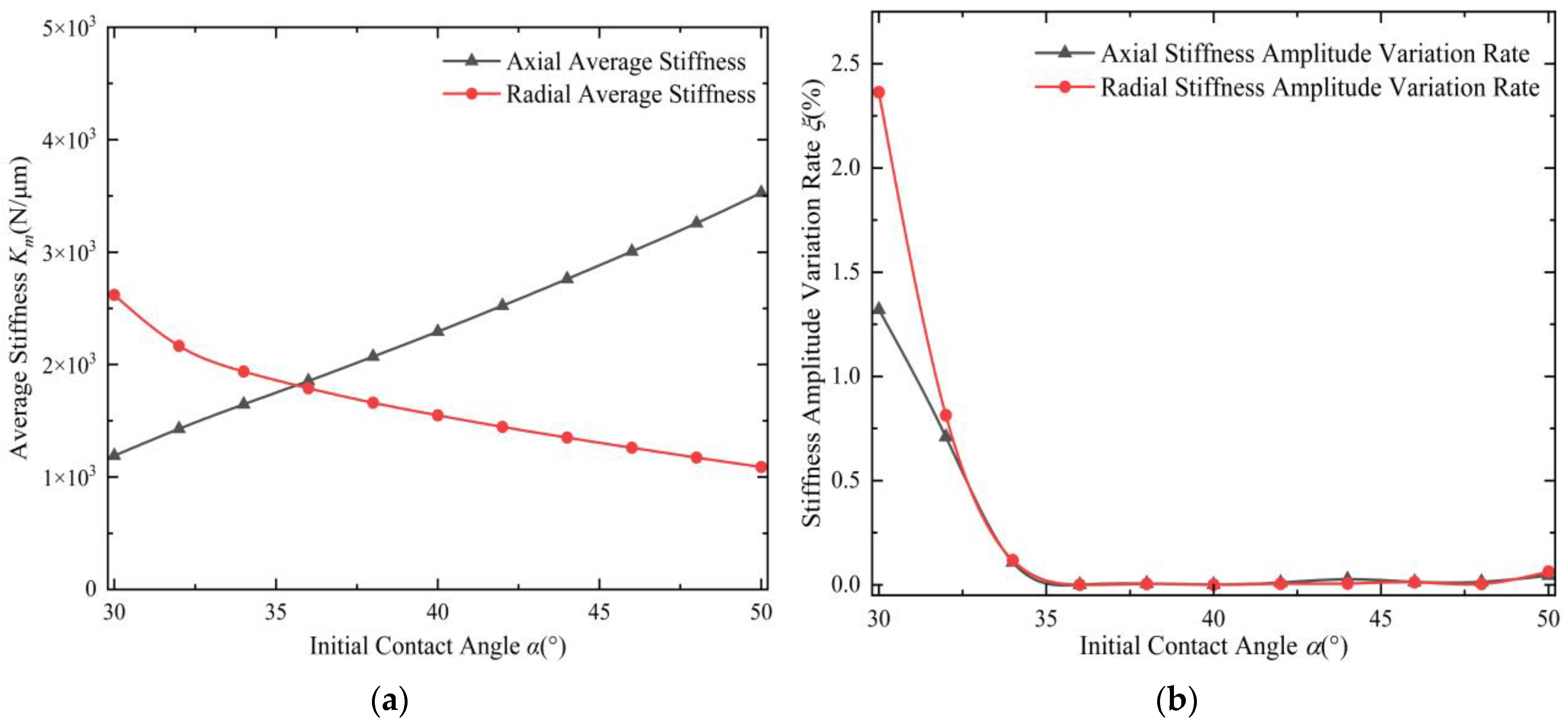
3.4. The Influence of Initial Contact Angle on the Time-Varying Characteristics of Stiffness
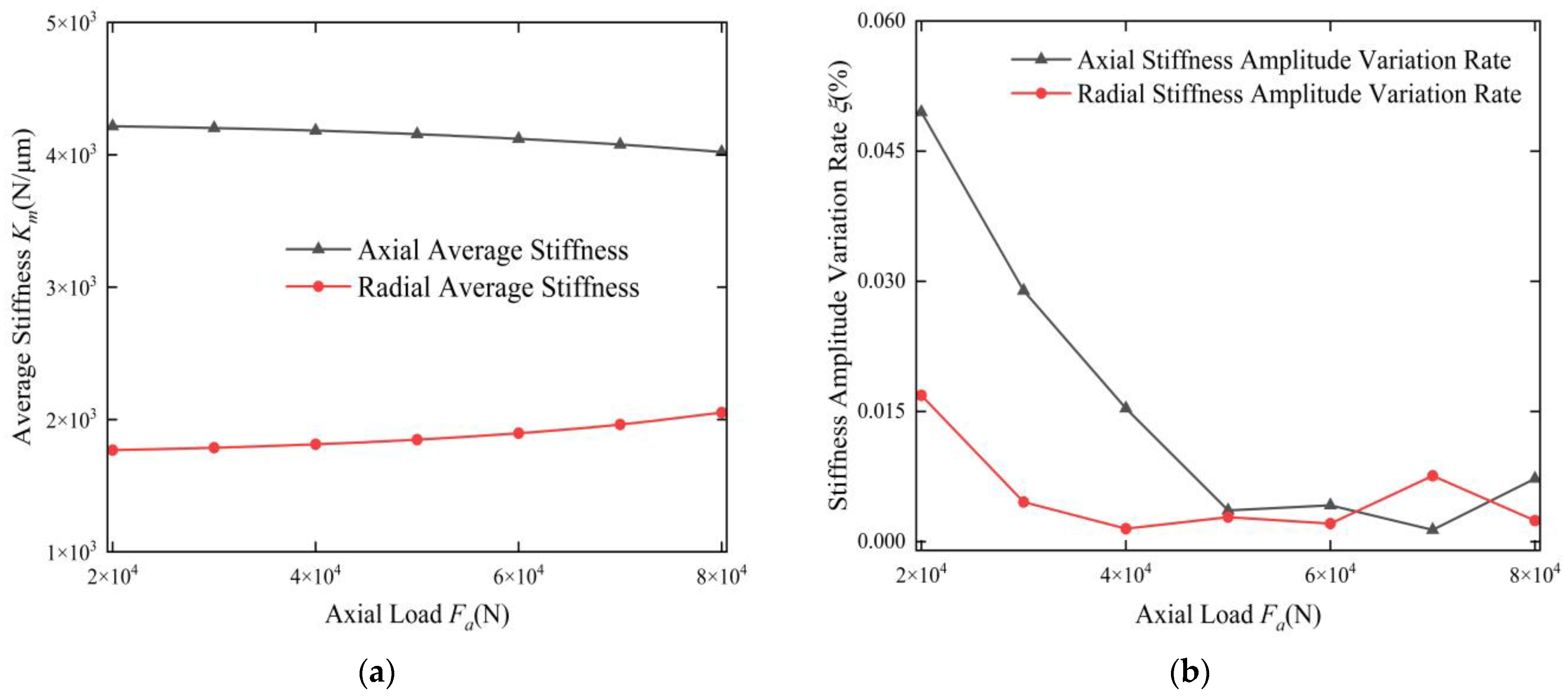
3.5. The Influence of Axial Load on the Time-Varying Characteristics of Stiffness
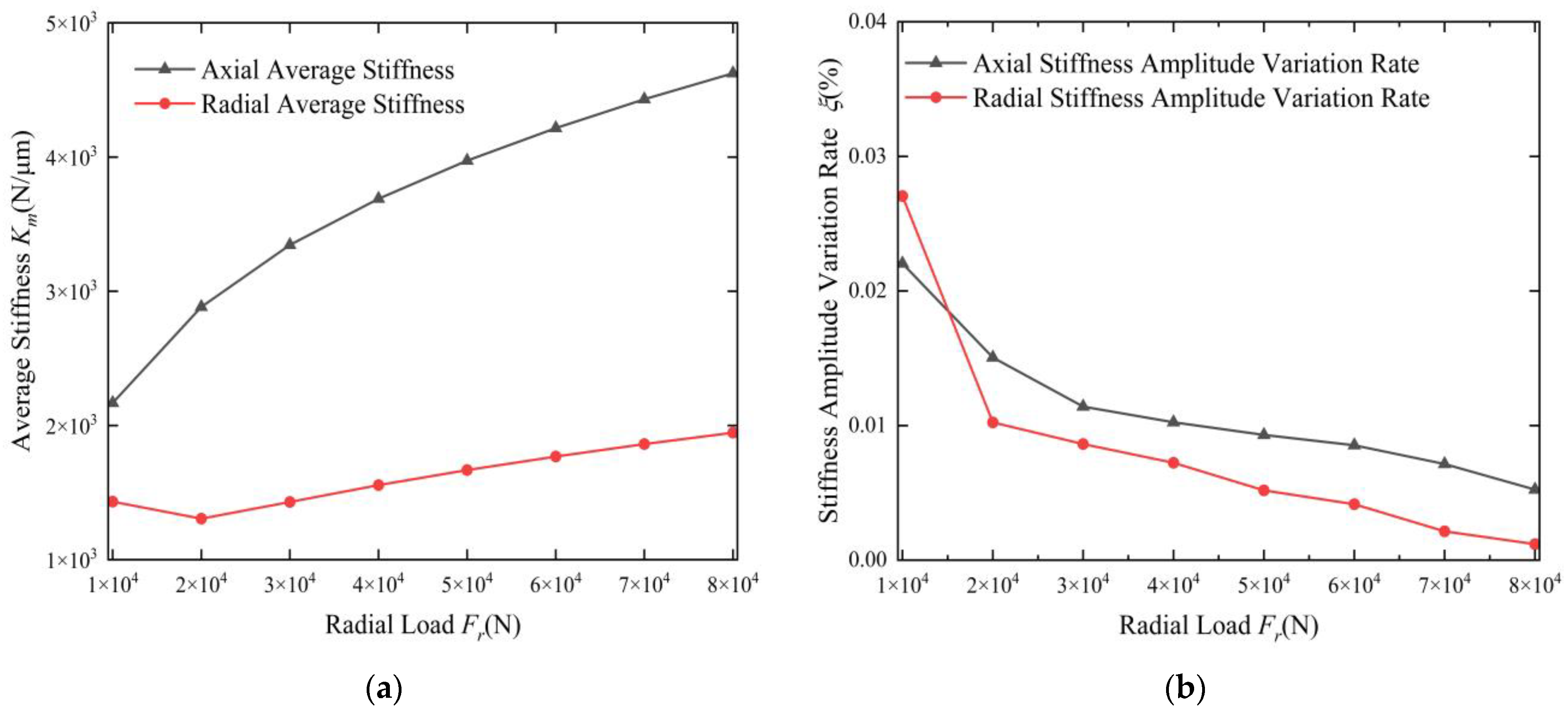
3.6. The Influence of Radial Load on the Time-Varying Characteristics of Stiffness
4. Four-Point Contact Ball Bearing Stiffness Test
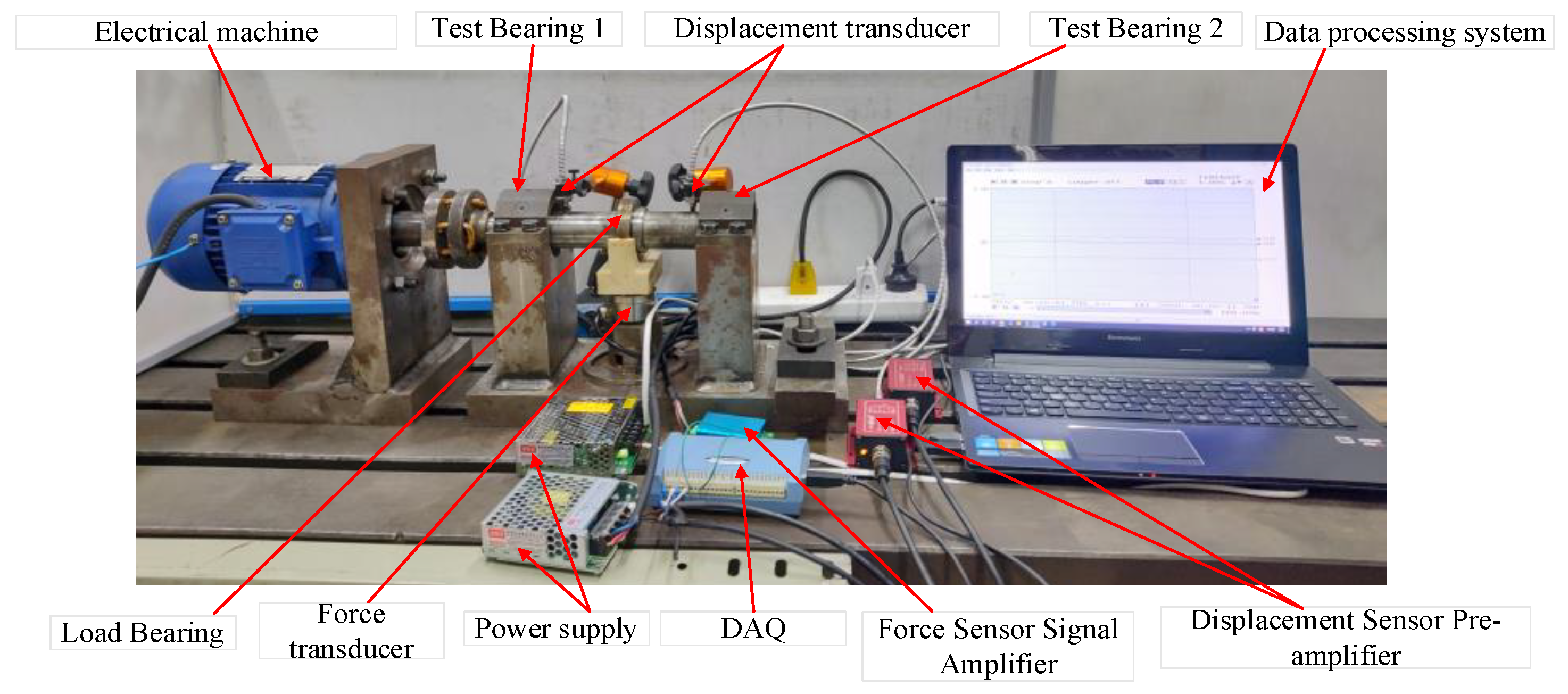
4.1. Test Bench and Test Scheme
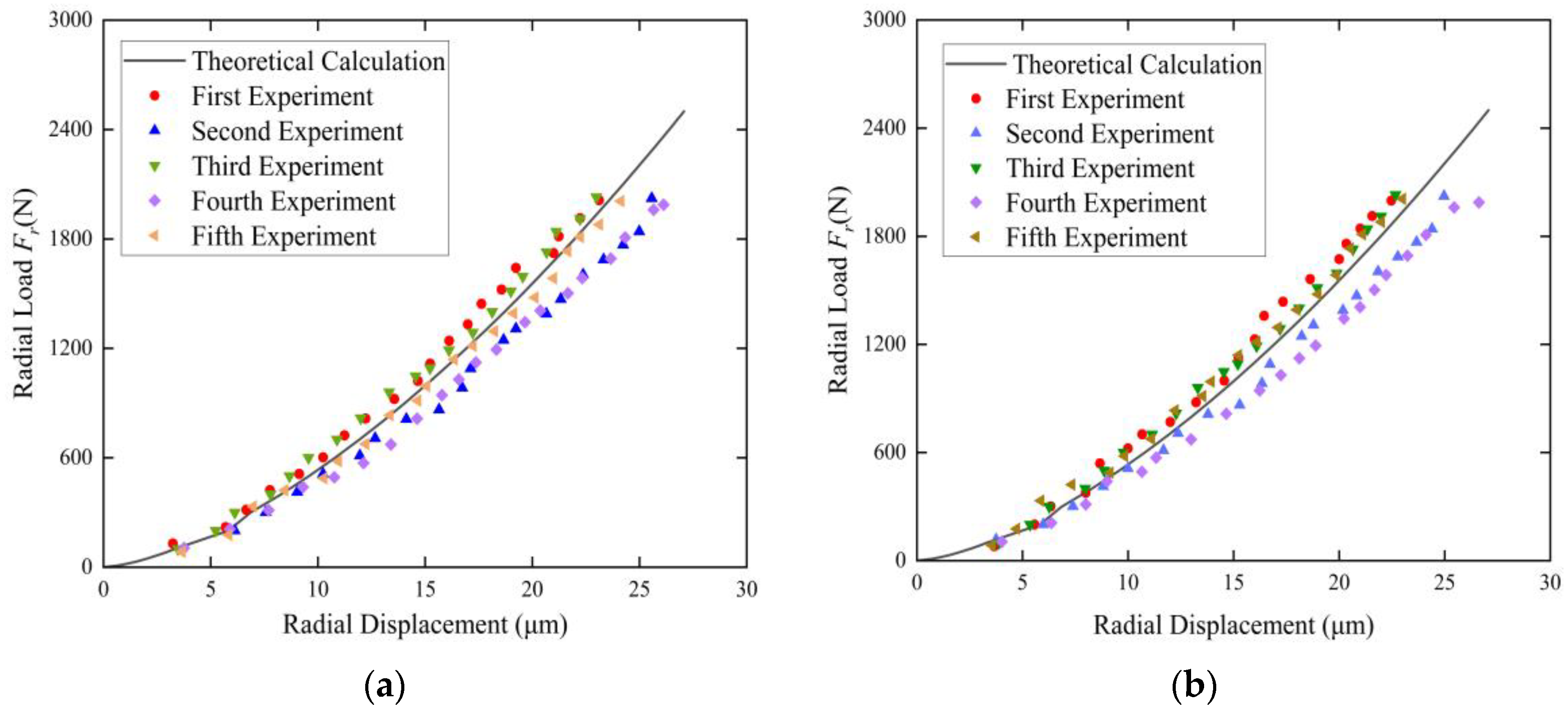
4.2. Experiment Results and Analyses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, H.; Li, Y. Trends and Challenges of Wind Turbine Bearings: A Review. Renew. Sustain. Energy Rev. 2023, 168, 112943. [Google Scholar]
- Wang, Y.; Zhang, H. Research on the Dynamics of Wind Turbine Gearbox Bearings: Modeling and Simulation. Wind Energy Sci. 2022, 7, 373–384. [Google Scholar]
- Liu, X.; Yu, D. Experimental Study on Bearing Lubrication for Offshore Wind Turbines. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104506. [Google Scholar]
- Liu, Z.; Chen, Y. Performance Optimization of Bearings in Wind Turbine Drivetrain. Renew. Energy 2023, 182, 1162–1174. [Google Scholar]
- Zhang, W.; Yang, L. Fault Diagnosis of Wind Turbine Bearings Based on Vibration Analysis and Machine Learning. Mech. Syst. Signal Process. 2021, 147, 107013. [Google Scholar]
- Xu, W.; Li, P. Development and Trends of Wind Power Generation: A Focus on Offshore Wind Turbines and Bearings. Energy Rep. 2024, 10, 455–468. [Google Scholar]
- Li, X.B.; Xu, Y.J.; Liu, J.; Liu, J.Y.; Pan, G.; Shi, Z.F. A dynamic model for a shell-propulsion shaft system considering the shell and shaft flexibilities. Mech. Syst. Signal Process. 2025, 22, 111928. [Google Scholar] [CrossRef]
- Jones, A.B. A General Theory for Elastically Constrained Ball and Radial Roller Bearings Under Arbitrary Load and Speed Conditions. J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Harris, T.A. Closure to “Discussion of ‘An Analytical Method to Predict Skidding in Thrust-Loaded, Angular-Contact Ball Bearings’”. J. Tribol. 1971, 93, 23–24. [Google Scholar]
- He, Z.S.; Shi, Z.P.; Qin, D.C.; Wen, J.B.; Shao, J.G.; Liu, X.H.; Xie, X.H. Study on Comprehensive Performance of Four-Point Contact Ball Slewing Bearings Based on a Bearing Support Bolt-Integrated Model. Machines 2024, 12, 814. [Google Scholar] [CrossRef]
- Chen, R.L.; Zhao, S.D.; Zhang, M.H.; Zhang, Y.C.; Cui, Y.H. Time-Varying Stiffness Model and Load Characteristics Analysis of Angular Contact Ball Bearings. Mech. Des. Res. 2022, 38, 114–119. [Google Scholar]
- Su, Y.; Zhang, J.Q.; Zhang, W. Theoretical and experimental approaches for flexible cage dynamic characteristics of four-point contact ball bearing considering multi-point contact behaviors. Mech. Syst. Signal Process. 2025, 22, 111929. [Google Scholar] [CrossRef]
- Escanciano, I.; Heras, I.; Schleich, F.; Aguirrebeitia, J. Methodology for the assessment of the friction torque of ball slewing bearings considering preload scatter. Friction 2024, 12, 1838–1857. [Google Scholar] [CrossRef]
- Liu, R.; Wang, H.; Pang, B.T.; Gao, X.H.; Zong, H.Y. Load Distribution Calculation of a four-Point-Contact Slewing Bearing and its Experimental Verification. Exp. Tech. 2018, 42, 243–252. [Google Scholar] [CrossRef]
- Yao, T.; Wang, L.; Liu, X.; Huang, Y. Multibody dynamics simulation of thin-walled four-point contact ball bearing with interactions of balls, ring raceways and crown-type cage. Multibody Syst. Dyn. 2019, 48, 337–372. [Google Scholar] [CrossRef]
- He, P.; Wang, Y.; Liu, H.; Guo, E.; Wang, H. Optimization design of structural parameters of single-row four-point contact ball slewing bearing. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 291. [Google Scholar] [CrossRef]
- Han, K.B.; Jong, H.K. Finite Element Analysis of Slewing Bearings for Wind Turbines Using Spring Elements. J. Korea Convergence Soc. 2020, 11, 239–247. [Google Scholar]
- Li, K.Y.; Tang, W.C. Load-displacement relationship model and measurement of deep groove ball bearing and 4-point contact ball bearing. J. Mech. Sci. Technol. 2019, 35, 2045–3058. [Google Scholar] [CrossRef]
- Halpin, J.D.; Tran, A.N. An Analytical Model of Four-Point Contact Rolling Element Ball Bearings. J. Tribol.-Trans. ASME 2016, 138, 031404. [Google Scholar] [CrossRef]
- Mireia, O.; Xabier, S.; Jorge, D. Design of Four Contact-Point Slewing Bearing With a New Load Distribution Procedure to Account for Structural Stiffness. J. Mech. Des. 2010, 132, 021006. [Google Scholar]
- Wang, Y.; Yuan, Q.; Cao, J.; Li, P.; Li, Y. Research on the Load Capacity of Extra-Large Double-Row Four-Point Contact Ball Bearings. J. Mech. Eng. 2014, 50, 65–70. [Google Scholar] [CrossRef]
- Heras, I.; Aguirrebeitia, J.; Abasolo, M.; Coria, I.; Escanciano, I. Load distribution and friction torque in four-point contact slewing bearings considering manufacturing errors and ring flexibility. Mech. Mach. Theory 2019, 137, 23–36. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, D. Dynamic Carrying Capacity Analysis of Double-Row Four-Point Contact Ball Slewing Bearing. Math. Probl. Eng. 2015, 2015, 850908. [Google Scholar] [CrossRef]
- Ma, S.; Li, W.; Yan, K.; Li, Y.; Zhu, Y.; Hong, J. A study on the dynamic contact feature of four-contact-point ball bearing. Mech. Syst. Signal Process. 2022, 174, 109111. [Google Scholar] [CrossRef]
- Rivera, G.; Tong, V.C.; Hong, S.W. Contact Load and Stiffness of Four-Point Contact Ball Bearings Under Loading. Int. J. Precis. Eng. Manuf. 2022, 23, 677–687. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, M.; Zhang, J.; Wang, H. Analysis of the Causes of Multi-Point Contact Between Balls and Raceways in Four-Point Contact Ball Bearings. China Mech. Eng. 2023, 34, 2794–2804. [Google Scholar]
- Gunduz, A.; Singh, R. Stiffness Matrix Formulation for Double Row Angular Contact Ball Bearings: Analytical Development and Validation. J. Sound Vib. 2013, 332, 5898–5916. [Google Scholar] [CrossRef]
- Wang, H.; Li, T.; Wang, L.; Li, F. Research and Application on the Skidding Analysis of the Large Size Ball Bearing. J. Mech. Eng. 2015, 51, 41–47. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Ji, Y.; Wang, Y. Static Stiffness Calculation of Four-Point Contact Slewing Bearings. J. Henan Univ. Sci. Technol. (Nat. Sci. Ed.) 2013, 34, 22–25. [Google Scholar]
- Qin, H. Study on the Dynamic Characteristics of Rolling Bearing-Rotor Systems with Time-Varying Stiffness and Raceway Defect. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Cao, H.; Li, Y.; He, Z.; Zhu, Y. Analysis of Time-Varying Bearing Stiffness and Vibration Response in High-Speed Rolling Bearing-Rotor System. J. Mech. Eng. 2014, 50, 73–81. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Zhai, W.; Lei, Y. Investigation on Skidding Behavior of a Lubricated Rolling Bearing with Fluid–solid-Heat Coupling Effect. Mech. Syst. Signal Process. 2024, 206, 110922. [Google Scholar] [CrossRef]
- Liu, K.; Wang, D.; Li, W.; Shi, X.; Zhang, Q. Dynamic Characteristics Investigation of a Dual Rotor-Casing System Considering the Comprehensive Stiffness of the Intermediate Bearing. J. Sound Vib. 2024, 578, 118355. [Google Scholar] [CrossRef]




| Bearing Parameter | Numerical Value |
|---|---|
| Ball diameter, Dw/mm | 50.8 |
| Bearing pitch circle diameter, dm/mm | 1300 |
| Number of rolling elements, Z | 70 |
| Inner ring curvature coefficient, fi | 0.525 |
| Curvature coefficient of outer ring, fo | 0.525 |
| Initial contact angle, α/(°) | 45 |
| Axial Load/(N) | Reference [30] Results/(N/μm) | Calculation Results of This Paper/(N/μm) | Error (%) |
|---|---|---|---|
| 20,000 | 2000.00 | 2028.486 | 1.424 |
| 40,000 | 2500.00 | 2560.449 | 2.418 |
| 60,000 | 3000.00 | 2935.465 | 2.151 |
| 80,000 | 3200.00 | 3235.258 | 1.101 |
| Axial Load/(N) | Reference [30] Results/(N/μm) | Calculation Results of This Paper/(N/μm) | Error (%) |
|---|---|---|---|
| 20,000 | 1176.47 | 1208.815 | 2.749 |
| 40,000 | 1538.46 | 1528.777 | 0.629 |
| 60,000 | 1714.28 | 1755.507 | 2.405 |
| 80,000 | 1904.76 | 1937.528 | 1.720 |
| Structural Parameter of Bearing | Numerical Value |
|---|---|
| Ball diameter/mm | 53.7 |
| Bearing outside diameter/mm | 2376 |
| Bearing width/mm | 235 |
| Bearing pitch circle diameter/mm | 2174 |
| Number of rolling elements | 68 |
| Inner ring curvature coefficient | 0.525 |
| initial contact angle/° | 45 |
| axial load/N | 20,000 |
| radial load/N | 20,000 |
| Structural Parameter | Numerical Value |
|---|---|
| Bearing outside diameter/mm | 62 |
| Bearing bore diameter/mm | 30 |
| Bearing pitch circle diameter/mm | 46 |
| Ball diameter/mm | 9.525 |
| Number of rolling elements | 9 |
| Initial contact angle/° | 45 |
| Stiffness | Theoretical Stiffness | Test Bearing 1 Test Stiffness | Test Bearing 2 Test Stiffness | Test Bearing 1 Error | Test Bearing 2 Error | |
|---|---|---|---|---|---|---|
| N/μm Load/N | ||||||
| 1000 | 66.478 | 60.351 | 58.017 | 10.15% | 14.58% | |
| 1200 | 70.904 | 65.479 | 63.537 | 8.29% | 11.59% | |
| 1400 | 74.902 | 68.742 | 66.712 | 8.96% | 12.28% | |
| 1600 | 78.568 | 71.663 | 71.999 | 9.64% | 9.12% | |
| 1800 | 81.967 | 73.993 | 74.651 | 10.78% | 9.80% | |
| 2000 | 85.146 | 76.560 | 75.125 | 11.21% | 13.34% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Li, J.; Wang, Y.; Deng, R.; Chen, W.; Li, W. Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings. Lubricants 2025, 13, 118. https://doi.org/10.3390/lubricants13030118
Chen R, Li J, Wang Y, Deng R, Chen W, Li W. Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings. Lubricants. 2025; 13(3):118. https://doi.org/10.3390/lubricants13030118
Chicago/Turabian StyleChen, Runlin, Jiakai Li, Yimo Wang, Rushen Deng, Weihao Chen, and Wenhui Li. 2025. "Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings" Lubricants 13, no. 3: 118. https://doi.org/10.3390/lubricants13030118
APA StyleChen, R., Li, J., Wang, Y., Deng, R., Chen, W., & Li, W. (2025). Study on the Time-Varying Stiffness Characteristics of Four-Point Contact Ball Bearings. Lubricants, 13(3), 118. https://doi.org/10.3390/lubricants13030118





