Research on the Static Thermal Degradation Law of Lubricating Grease for Wind Power Bearings
Abstract
1. Introduction
2. Static Thermal Deterioration Test of Lubricating Grease
2.1. Test Sample
2.2. Test Equipment and Test Methods
2.2.1. Blast-Type Constant-Temperature Drying Oven
2.2.2. HD269 Penetration Tester
2.2.3. Silver-Mesh Oil Separator
2.2.4. FA2004B Electronic Balance
2.3. Thermal Degradation Test Conditions
2.4. Test Procedures
3. Test Results and Analysis
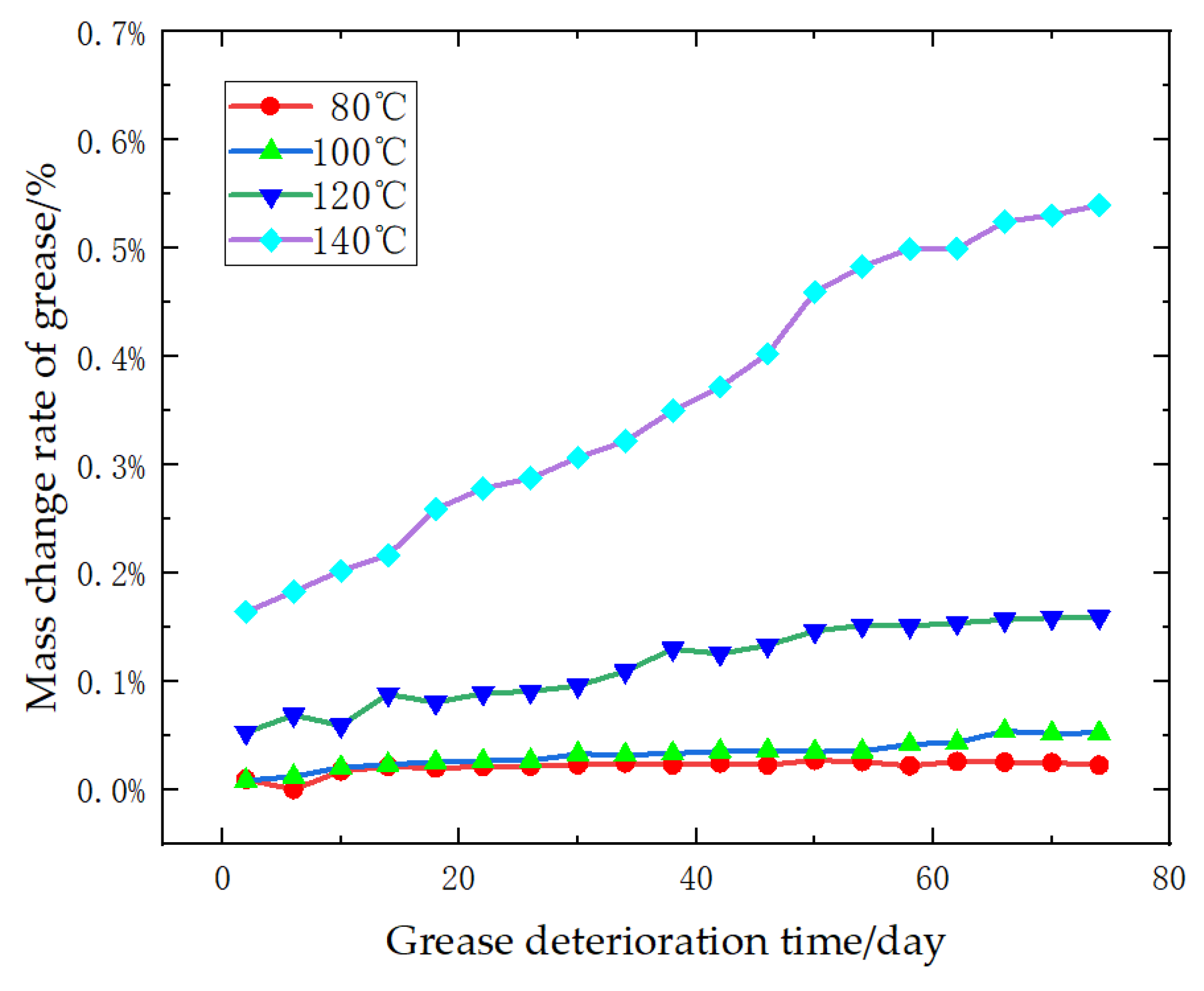
3.1. Mass Change Rate of Grease
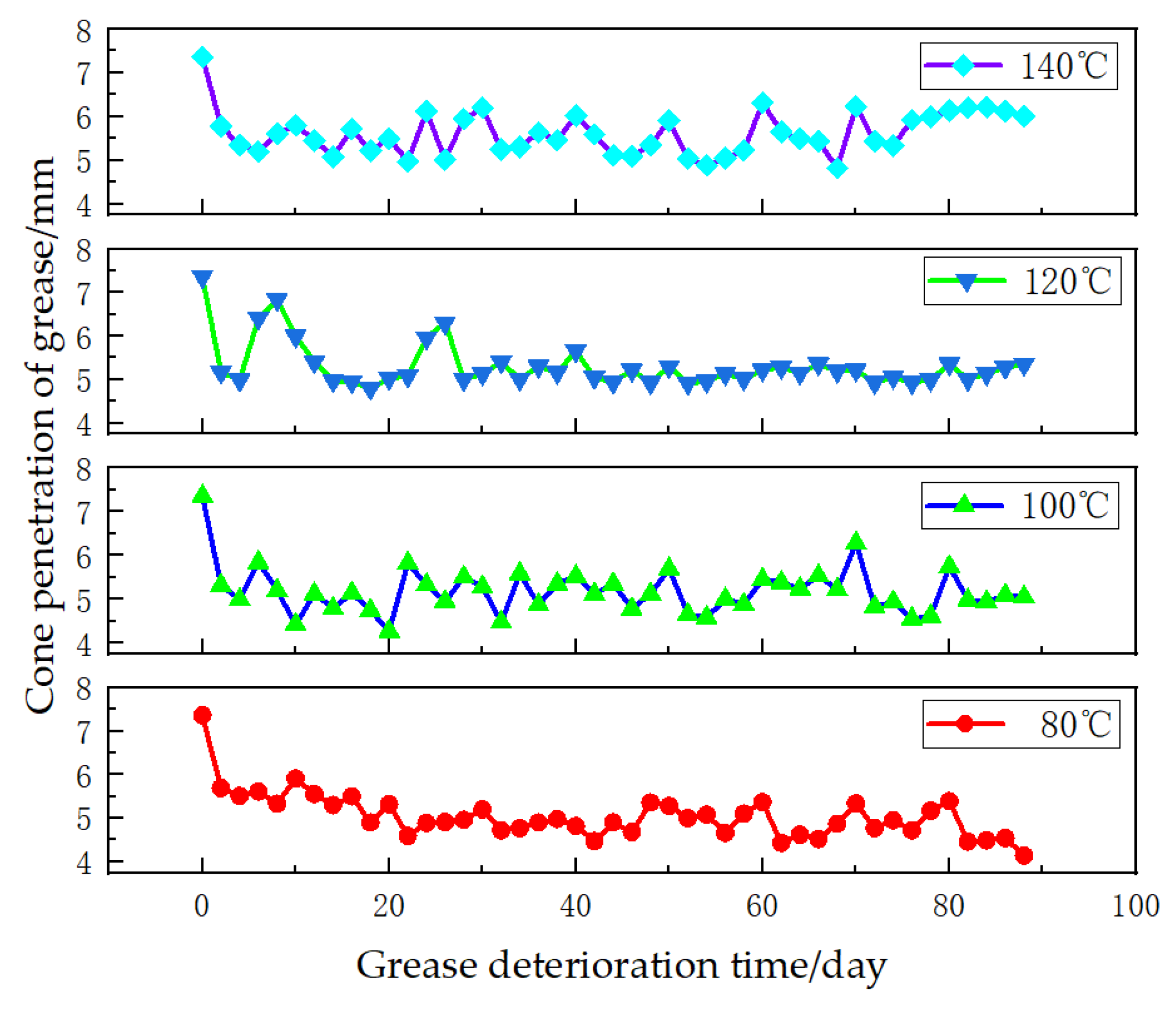
3.2. Change Rule of Grease Cone Penetration
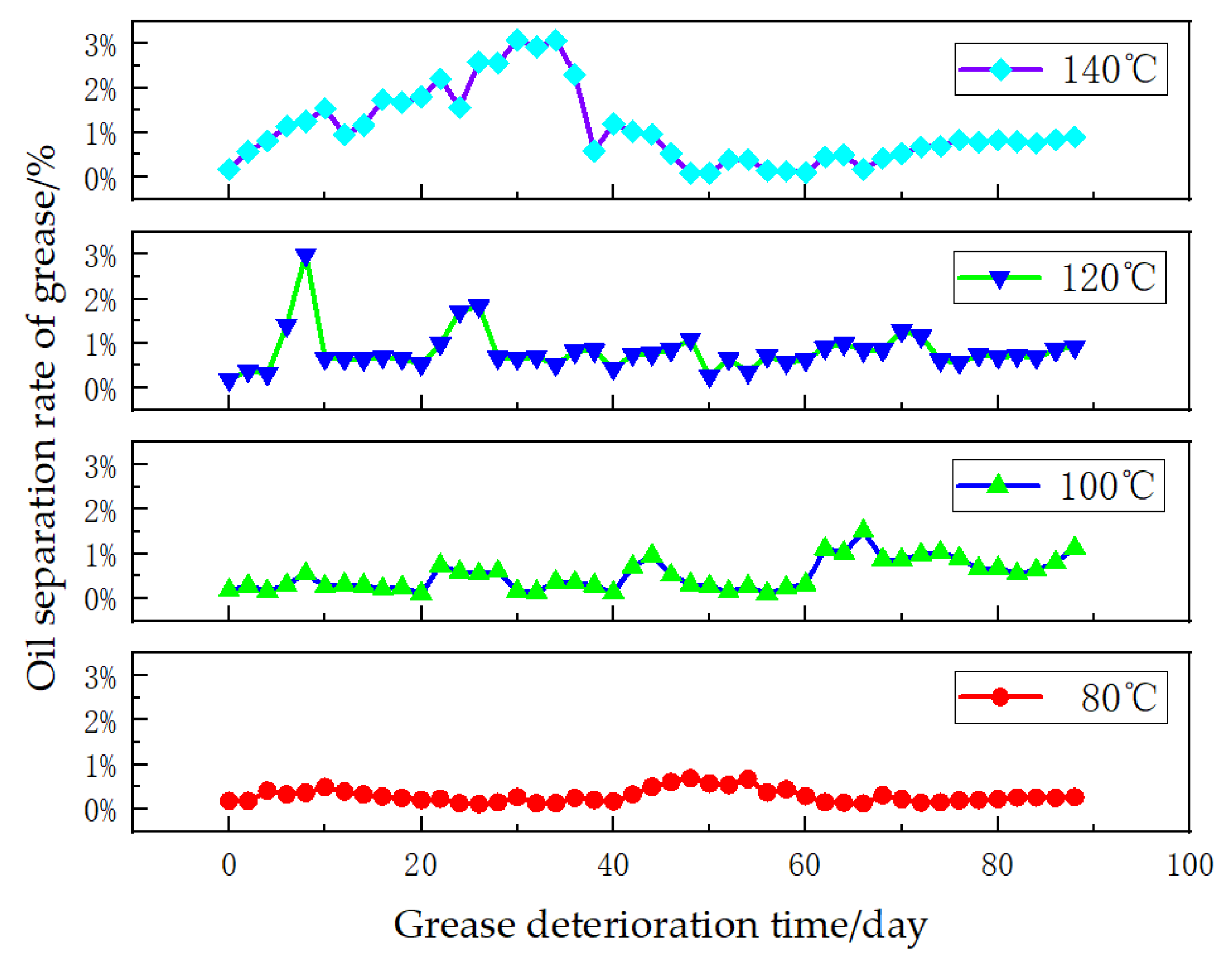
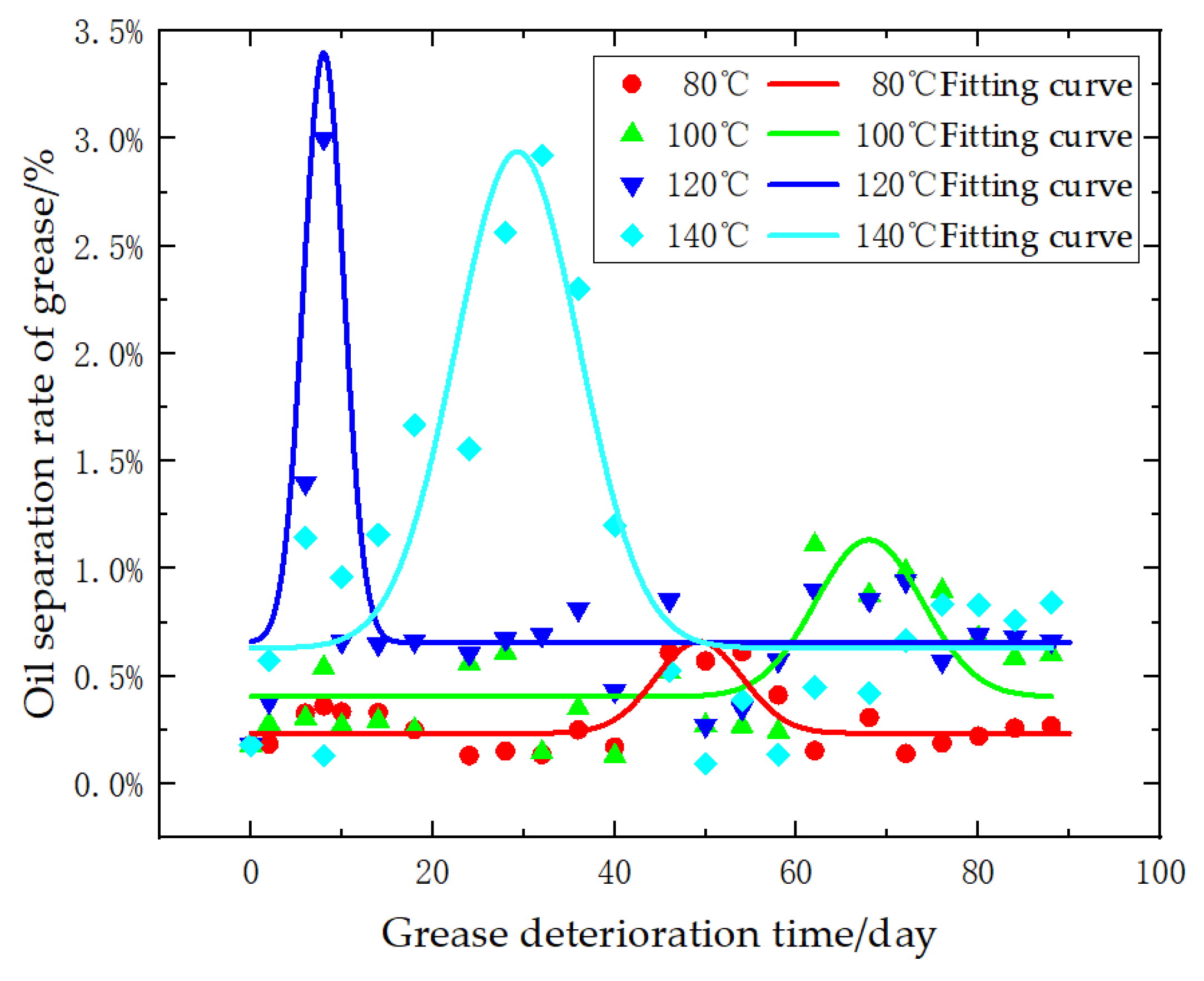
3.3. Variation Rule of Oil Separation Rate of Grease
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gbashi, S.M.; Madushele, N.; Olatunji, O.O.; Adedeii, P.A.; Jen, T.C. Wind turbine main bearing: A mini review of its failure modes and condition monitoring techniques. In Proceedings of the 2022 IEEE 13th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 25–27 May 2022; IEEE: New York, NY, USA, 2022; pp. 127–134. [Google Scholar]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Shangguan, L.; Fan, Y. Review of Tribological Failure Analysis and Lubrication Technology Research of Wind Power Bearings. Polymers 2022, 14, 3041. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Zhao, D.; Shangguan, L.; Li, S.; Cheng, R. Review of Wind Power Bearing Wear Analysis and Intelligent Lubrication Method Research. Coatings 2023, 14, 30. [Google Scholar] [CrossRef]
- Liu, F.; Sommer, F.; Mittemeijer, E.J. An analytical model for isothermal and isochronal transformation kinetics. J. Mater. Sci. 2004, 39, 1621–1634. [Google Scholar] [CrossRef]
- Peng, H.; Li, S.; Shangguan, L.; Zhang, H.; Zhao, D. Research on the rheological characteristics of wind power grease based on rheological parameters. Lubricants 2023, 11, 299. [Google Scholar] [CrossRef]
- Pan, J.; Cao, S.; Wang, J. Colloidal physicochemical properties and variation mechanisms of lithium complex grease under limited operating temperature. J. Test. Eval. 2021, 49, 2518–2530. [Google Scholar] [CrossRef]
- Horng, J.H.; Ta, T.N.; Jheng, R.Y.; Huang, M.W.; Zhang, K.S.; Torkaya, E. Effect of liquid contaminants on tribological performance of greases. Wear 2023, 530, 205054. [Google Scholar] [CrossRef]
- Schwack, F.; Bader, N.; Leckner, J.; Demaille, C.; Poll, G. A study of grease lubricants under wind turbine pitch bearing conditions. Wear 2020, 454, 203335. [Google Scholar] [CrossRef]
- Dhanola, A.; Garg, H.C. Tribological challenges and advancements in wind turbine bearings: A review. Eng. Fail. Anal. 2020, 118, 104885. [Google Scholar] [CrossRef]
- de Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A review of wind turbine bearing condition monitoring: State of the art and challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Frolov, M.M.; Kilyakova, A.Y.; Drangai, L.; Dorr, N. Improvement of Tribotechnical Properties of Polyurea Greases in Various Dispersion Media with Different Fillers. Chem. Technol. Fuels Oils 2020, 55, 697–703. [Google Scholar]
- Yan, F.; Wang, Z.; Du, Y.; Li, Q. Research on rheological and flow behavior of lubricating grease in extremely cold weather. Ind. Lubr. Tribol. 2017, 69, 1066–1073. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, L.; Wang, C.; Zhang, W.; Chen, J.; Wang, C.; Wang, J. A Study on the Effects of Temperature Changes on the Rheological Properties of Lithium Lubricating Grease and Data Processing. In Proceedings of the International Conference in Communications, Signal Processing, and Systems, Changbaishan, China, 24–25 July 2021; Springer Singapore: Singapore, 2021; pp. 1056–1063. [Google Scholar]
- Hodapp, A.; Conrad, A.; Hochstein, B.; Jacob, K.H.; Willenbacher, N. Using Rheological Characteristics for Assessing the Suitability of Lubricating Greases at Low Temperatures. Chem. Ing. Tech. 2022, 94, 402–409. [Google Scholar]
- Paszkowski, M.; Stelmaszek, P.A.; Krzak, J. Effects of contamination on selected rheological and tribological properties of lubricating greases working in underground mines. Lubricants 2023, 11, 425. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y. Study on Rheological Properties of Different Brands of Grease. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; p. 012113. [Google Scholar]
- Garshin, M.V.; Porfiryev, Y.V.; Zaychenko, V.A.; Shuvalov, S.A.; Kolybelsky, D.S.; Gushchin, P.A.; Vinokurov, V.A. Effect of base oil composition on the low-temperature properties of polyurea greases. Pet. Chem. 2017, 57, 1177–1181. [Google Scholar]
- Wang, Y.; Zhang, P.; Lin, J.; Gao, X. Rheological and Tribological Properties of Lithium Grease and Polyurea Grease with Different Consistencies. Coatings 2022, 12, 527. [Google Scholar] [CrossRef]
- Japar, N.S.A.; Aziz, M.A.A.; Hamid, N. Synthesis and properties evaluation of sodium grease formulated from used transformer oil as base oil. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kuantan, Malaysia, 1–2 October 2019; IOP Publishing: Bristol, UK, 2020; p. 012058. [Google Scholar]
- Johnson, B. Determining Possible Impact of In-Service Grease Mixtures With a Stress Rheometer as an Element of a Predictive Maintenance Program. In Symposium on Viscosity and Rheology of In-Service Fluids as They Pertain to Condition Monitoring; ASTM International: West Conshohocken, PA, USA, 2013; pp. 1–19. [Google Scholar]
- Lin, C.L.; Meehan, P.A. Microstructure Characterization of Degraded Grease in Axle Roller Bearings. Tribol. Trans. 2019, 62, 667–687. [Google Scholar]
- Li, L.; Liu, J.J.; Tian, Z.Y.; Zhang, G.Z.; Fu, Z.Y.; Li, T. Ageing Evaluation of No. 2 Lithium Lubricating Grease. Adv. Mater. Res. 2013, 763, 121–124. [Google Scholar]
- Osara, J.A.; Bryant, M.D. Thermodynamics of grease degradation. Tribol. Int. 2019, 137, 433–445. [Google Scholar]
- Camousseigt, L.; Galfré, A.; Couenne, F.; Oumahi, C.; Muller, S.; Tayakout-Fayolle, M. Oil-bleeding dynamic model to predict permeability characteristics of lubricating grease. Tribol. Int. 2023, 183, 108418. [Google Scholar]
- Shetty, P.; Meijer, R.J.; Lugt, P.M. An evaporation model for base oil from grease-lubricated rolling bearings including breathing. Tribol. Trans. 2021, 64, 891–902. [Google Scholar] [CrossRef]
- Rezasoltani, A.; Khonsari, M.M. An engineering model to estimate consistency reduction of lubricating grease subjected to mechanical degradation under shear. Tribol. Int. 2016, 103, 465–474. [Google Scholar] [CrossRef]
- Yin, C.; Li, Y.; Wang, Y.; Dong, Y. Physics-guided degradation trajectory modeling for remaining useful life prediction of rolling bearings. Mech. Syst. Signal Process. 2025, 224, 112192. [Google Scholar] [CrossRef]
- Bupp, E.; Wurzbach, R. Grease Working and Its Role in Consistency Trending. In Symposium on Viscosity and Rheology of In-Service Fluids as They Pertain to Condition Monitoring; ASTM International: West Conshohocken, PA, USA, 2013; pp. 1–5. [Google Scholar]
- Lugt, P.M. A review on grease lubrication in rolling bearings. Tribol. Lubr. Technol. 2010, 66, 44. [Google Scholar] [CrossRef]
- Rawat, S.S.; Harsha, A.P. The lubrication effect of different vegetable oil-based greases on steel-steel tribo-pair. Biomass Convers. Biorefinery 2024, 14, 1993–2005. [Google Scholar] [CrossRef]
- De Laurentis, N.; Cann, P.; Lugt, P.M.; Kadiric, A. The influence of base oil properties on the friction behaviour of lithium greases in rolling/sliding concentrated contacts. Tribol. Lett. 2017, 65, 128. [Google Scholar] [CrossRef]
- GB/T 269-2023; Determination of Cone Penetration of Lubricating Greases and Petrolatum. Standards Press of China: Beijing, China, 2023.
- GB/T 11144-2007; Standard Test Method for Measurement of Extreme-Pressure Properties of Lubricating Fluids (Timken method). Standards Press of China: Beijing, China, 2007.
- SH/T 0202-1992; Method for Determining EP Properties of Greases (Four-Ball Machine Method). China Petrochemical Press: Beijing, China, 1992.
- SH/T 0109-2004; Petroleum Products and Lubricants—Determination of Water Washout Characteristics of Lubricating Greases. China Petrochemical Press: Beijing, China, 2004.







| NLGI Rating | 1.5 |
|---|---|
| Thickener type | Composite lithium base |
| Color, visual | red (color) |
| Penetration, 25 °C, GB/T 269-2023 [33] | 305 |
| melting point (of lubricating oil), °C | 255 |
| Viscosity, cSt @ 40 °C | 460 |
| Timken OK load bearing, GB/T 11144-2007 [34] | 55 |
| Four-ball sintering, SH/T 0202-1992 [35], load bearing, kgf | 250 |
| water abrasion, SH/T 0109-2004 [36], 79 °C loss. %wt | 10 |
| Rust resistance, Distilled water | 0.0 |
| Time/Day | 2 | 4 | 6 | 8 | … | 80 | … | 88 | |
|---|---|---|---|---|---|---|---|---|---|
| Temperature/°C | |||||||||
| 80 °C | √ | √ | √ | √ | √ | √ | √ | √ | |
| 100 °C | √ | √ | √ | √ | √ | √ | √ | √ | |
| 120 °C | √ | √ | √ | √ | √ | √ | √ | √ | |
| 140 °C | √ | √ | √ | √ | √ | √ | √ | √ | |
| τ/Day | Mass Change Rate of Grease (Y1%) | |||
|---|---|---|---|---|
| 80 °C | 100 °C | 120 °C | 140 °C | |
| 2 | 0.0095 | 0.0083 | 0.0528 | 0.1642 |
| 6 | 0.00015 | 0.0122 | 0.0688 | 0.1828 |
| 10 | 0.017 | 0.0204 | 0.0590 | 0.2021 |
| 14 | 0.0213 | 0.0233 | 0.0882 | 0.2165 |
| 18 | 0.0198 | 0.0256 | 0.0803 | 0.2593 |
| 22 | 0.0212 | 0.0267 | 0.0891 | 0.2781 |
| 26 | 0.0216 | 0.0268 | 0.0906 | 0.2876 |
| 30 | 0.0231 | 0.0329 | 0.0961 | 0.3068 |
| 34 | 0.0244 | 0.0321 | 0.1094 | 0.3219 |
| 38 | 0.0228 | 0.0335 | 0.13 | 0.35 |
| 42 | 0.0244 | 0.0355 | 0.1256 | 0.3720 |
| 46 | 0.0228 | 0.0363 | 0.1334 | 0.4025 |
| 50 | 0.0271 | 0.0351 | 0.1466 | 0.4597 |
| 54 | 0.0257 | 0.0356 | 0.1516 | 0.4828 |
| 58 | 0.0220 | 0.0419 | 0.1512 | 0.4995 |
| 62 | 0.0259 | 0.0436 | 0.1539 | 0.4996 |
| 66 | 0.0254 | 0.0539 | 0.1569 | 0.5245 |
| 70 | 0.0250 | 0.0518 | 0.1588 | 0.5305 |
| 74 | 0.0225 | 0.0524 | 0.1592 | 0.5399 |
| Test Temperature | Fitted Equation | R2 | p-Values |
|---|---|---|---|
| 80 °C | 0.7615 | 1.044 × 10−5 | |
| 100 °C | 0.9319 | 5.119 × 10−10 | |
| 120 °C | 0.9632 | 2.584 × 10−12 | |
| 140 °C | 0.9855 | 7.548 × 10−16 |
| Parameter | Parameter Values in Fitting Formula | R2 | p-Values | |
|---|---|---|---|---|
| A | A0 | 1.46 × 10−12 | 0.9999 | 0.00728 |
| A1 | 0.2146 | |||
| B | B0 | −2830 | 0.9759 | 0.04845 |
| B1 | −0.1307 | |||
| C | C0 | −2.058 × 10−72 | 0.9999 | 0.01489 |
| C1 | 1.199 | |||
| C2 | 0.85 | |||
| τ/Day | Cone Penetration of Grease/mm | τ/Day | Cone Penetration of Grease/mm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 80 °C | 100 °C | 120 °C | 140 °C | 80 °C | 100 °C | 120 °C | 140 °C | ||
| 0 | 7.36 | 7.36 | 7.36 | 7.36 | 46 | 4.68 | 4.78 | 5.215 | 5.095 |
| 2 | 5.69 | 5.32 | 5.17 | 5.79 | 48 | 5.36 | 5.12 | 4.93 | 5.355 |
| 4 | 5.51 | 4.99 | 4.99 | 5.345 | 50 | 5.28 | 5.69 | 5.3 | 5.91 |
| 6 | 5.61 | 5.84 | 6.41 | 5.2 | 52 | 5 | 4.65 | 4.915 | 5.04 |
| 8 | 5.33 | 5.2 | 6.835 | 5.615 | 54 | 5.08 | 4.58 | 4.96 | 4.885 |
| 10 | 5.91 | 4.42 | 6 | 5.81 | 56 | 4.66 | 5 | 5.135 | 5.045 |
| 12 | 5.55 | 5.12 | 5.405 | 5.46 | 58 | 5.1 | 4.88 | 5.015 | 5.23 |
| 14 | 5.3 | 4.79 | 4.975 | 5.08 | 60 | 5.37 | 5.45 | 5.22 | 6.32 |
| 16 | 5.5 | 5.14 | 4.95 | 5.72 | 62 | 4.43 | 5.38 | 5.28 | 5.65 |
| 18 | 4.9 | 4.74 | 4.805 | 5.22 | 64 | 4.62 | 5.24 | 5.15 | 5.5 |
| 20 | 5.32 | 4.27 | 5.03 | 5.5 | 66 | 4.52 | 5.53 | 5.36 | 5.435 |
| 22 | 4.59 | 5.82 | 5.08 | 4.97 | 68 | 4.87 | 5.22 | 5.19 | 4.82 |
| 24 | 4.89 | 5.33 | 5.96 | 6.12 | 70 | 5.34 | 6.28 | 5.22 | 6.23 |
| 26 | 4.91 | 4.95 | 6.305 | 5.02 | 72 | 4.77 | 4.82 | 4.935 | 5.435 |
| 28 | 4.96 | 5.5 | 5.005 | 5.94 | 74 | 4.95 | 4.94 | 5.055 | 5.335 |
| 30 | 5.2 | 5.28 | 5.13 | 6.2 | 76 | 4.72 | 4.55 | 4.935 | 5.92 |
| 32 | 4.72 | 4.47 | 5.405 | 5.255 | 78 | 5.17 | 4.61 | 5 | 6 |
| 34 | 4.77 | 5.58 | 5.01 | 5.315 | 80 | 5.39 | 5.74 | 5.36 | 6.13 |
| 36 | 4.9 | 4.87 | 5.305 | 5.64 | 82 | 4.46 | 4.98 | 5.005 | 6.2 |
| 38 | 4.98 | 5.35 | 5.16 | 5.465 | 84 | 4.49 | 4.94 | 5.135 | 6.22 |
| 40 | 4.82 | 5.52 | 5.66 | 6.02 | 86 | 4.54 | 5.09 | 5.28 | 6.13 |
| 42 | 4.47 | 5.12 | 5.05 | 5.595 | 88 | 4.14 | 5.05 | 5.355 | 6 |
| 44 | 4.9 | 5.35 | 4.94 | 5.11 | |||||
| Test Temperature | Fitted Equation | R2 | p-Values |
|---|---|---|---|
| 80 °C | 0.5936 | 3.92 × 10−9 | |
| 100 °C | 0.3934 | 2.147 × 10−5 | |
| 120 °C | 0.3360 | 1.501 × 10−4 | |
| 140 °C | 0.3437 | 3.346 × 10−4 |
| Parameter | Parameter Values in Fitting Formula | R2 | p-Values | |
|---|---|---|---|---|
| D | D0 | −0.5039 | 0.9998 | 0.01135 |
| D1 | 0.2099 | |||
| D2 | −1.167 | |||
| D3 | −1.824 | |||
| E | E0 | −0.5775 | 0.9882 | 0.00005362 |
| E1 | 0.1371 | |||
| E2 | 6.732 | |||
| E3 | −0.6532 | |||
| F | F0 | −1.24877 | 0.9998 | 2.79 × 10−4 |
| F1 | 0.25699 | |||
| τ/Day | Oil Separation Rate of Grease% | τ/Day | Oil Separation Rate of Grease% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 80 °C | 100 °C | 120 °C | 140 °C | 80 °C | 100 °C | 120 °C | 140 °C | ||
| 0 | 0.18% | 0.18% | 0.18% | 0.18% | 46 | 0.61% | 0.52% | 0.85% | 0.52% |
| 2 | 0.18% | 0.28% | 0.38% | 0.57% | 48 | 0.69% | 0.32% | 1.09% | 0.08% |
| 4 | 0.41% | 0.17% | 0.31% | 0.81% | 50 | 0.57% | 0.27% | 0.27% | 0.09% |
| 6 | 0.33% | 0.30% | 1.40% | 1.14% | 52 | 0.54% | 0.15% | 0.65% | 0.39% |
| 8 | 0.36% | 0.55% | 2.99% | 1.25% | 54 | 0.61% | 0.27% | 0.35% | 0.39% |
| 10 | 0.334% | 0.27% | 0.66% | 0.96% | 56 | 0.37% | 0.11% | 0.71% | 0.14% |
| 12 | 0.39% | 0.32% | 0.65% | 0.96% | 58 | 0.41% | 0.24% | 0.57% | 0.13% |
| 14 | 0.33% | 0.29% | 0.65% | 1.16% | 60 | 0.29% | 0.32% | 0.63% | 0.10% |
| 16 | 0.28% | 0.21% | 0.69% | 1.74% | 62 | 0.15% | 1.11% | 0.90% | 0.45% |
| 18 | 0.25% | 0.25% | 0.66% | 1.67% | 64 | 0.14% | 1.02% | 0.99% | 0.50% |
| 20 | 0.20% | 0.11% | 0.53% | 1.80% | 66 | 0.12% | 1.51% | 0.84% | 0.17% |
| 22 | 0.23% | 0.74% | 0.58% | 2.21% | 68 | 0.31% | 0.88% | 0.85% | 0.42% |
| 24 | 0.13% | 0.56% | 0.61% | 1.56% | 70 | 0.22% | 0.87% | 1.28% | 0.53% |
| 26 | 0.11% | 0.55% | 0.71% | 2.58% | 72 | 0.14% | 0.99% | 0.943% | 0.67% |
| 28 | 0.15% | 0.61% | 0.67% | 2.56% | 74 | 0.15% | 1.03% | 0.62% | 0.69% |
| 30 | 0.27% | 0.17% | 0.66% | 3.08% | 76 | 0.19% | 0.90% | 0.57% | 0.83% |
| 32 | 0.13% | 0.14% | 0.69% | 2.92% | 78 | 0.20% | 0.67% | 0.73% | 0.79% |
| 34 | 0.13% | 0.37% | 0.52% | 3.07% | 80 | 0.22% | 0.68% | 0.69% | 0.83% |
| 36 | 0.25% | 0.35% | 0.81% | 2.30% | 82 | 0.26% | 0.55% | 0.72% | 0.8% |
| 38 | 0.20% | 0.29% | 0.84% | 0.59% | 84 | 0.26% | 0.58% | 0.68% | 0.76% |
| 40 | 0.17% | 0.13% | 0.43% | 1.20% | 86 | 0.25% | 0.81% | 0.85% | 0.83% |
| 42 | 0.33% | 0.71% | 0.75% | 1.02% | 88 | 0.27% | 0.61% | 0.92% | 0.84% |
| 44 | 0.50% | 0.96% | 0.76% | 0.96% | |||||
| Test Temperature | Fitted Equation | R2 | p-Values |
|---|---|---|---|
| 80 °C | 0.7002 | 6.425 × 10−10 | |
| 100 °C | 0.524 | 1.159 × 10−5 | |
| 120 °C | 0.749 | 3.489 × 10−4 | |
| 140 °C | 0.7979 | 7.766 × 10−12 |
| Parameter | Parameter Values in Fitting Formula | R2 | p-Values | |
|---|---|---|---|---|
| G | G0 | −0.4375 | 0.99 | 0.00263 |
| G1 | −6.274 | |||
| G2 | 3.09 | |||
| 0.09993 | ||||
| H | H0 | 58.59 | 0.99 | 0.00356 |
| H1 | 75.38 | |||
| H2 | 38.56 | |||
| 0.1416 | ||||
| I | I0 | 38.71 | 0.99 | 0.000632 |
| I1 | −33.66 | |||
| I2 | 18.84 | |||
| 0.09537 | ||||
| J | J0 | 0.545 | 0.99 | 0.000283 |
| J1 | 0.2276 | |||
| J2 | 0.09431 | |||
| 0.7873 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Liu, Y.; Fan, Y.; Wang, G.; Wang, Z. Research on the Static Thermal Degradation Law of Lubricating Grease for Wind Power Bearings. Lubricants 2025, 13, 134. https://doi.org/10.3390/lubricants13030134
Tian H, Liu Y, Fan Y, Wang G, Wang Z. Research on the Static Thermal Degradation Law of Lubricating Grease for Wind Power Bearings. Lubricants. 2025; 13(3):134. https://doi.org/10.3390/lubricants13030134
Chicago/Turabian StyleTian, Heng, Yan Liu, Yuqing Fan, Gaofeng Wang, and Zhiwei Wang. 2025. "Research on the Static Thermal Degradation Law of Lubricating Grease for Wind Power Bearings" Lubricants 13, no. 3: 134. https://doi.org/10.3390/lubricants13030134
APA StyleTian, H., Liu, Y., Fan, Y., Wang, G., & Wang, Z. (2025). Research on the Static Thermal Degradation Law of Lubricating Grease for Wind Power Bearings. Lubricants, 13(3), 134. https://doi.org/10.3390/lubricants13030134





