Atomic Simulation of Wear and Slip Behavior Between Monocrystalline Silicon and 6H-SiC Friction Pair
Abstract
1. Introduction
2. Simulation Method
3. Result and Discussion
3.1. Analysis of Substrate Surface Wear
3.2. Analysis of Sliding and Friction
4. Conclusions
- (1)
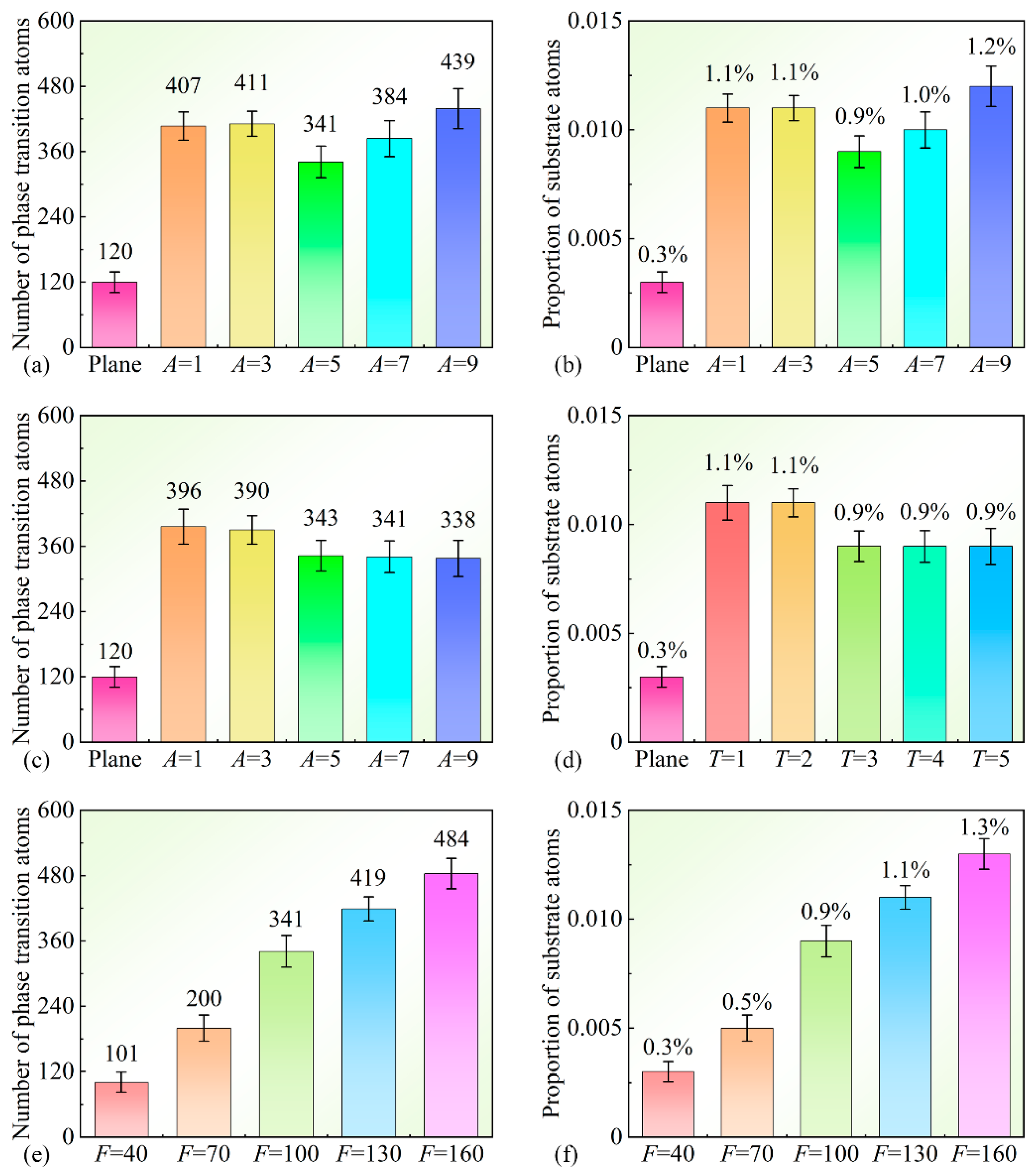
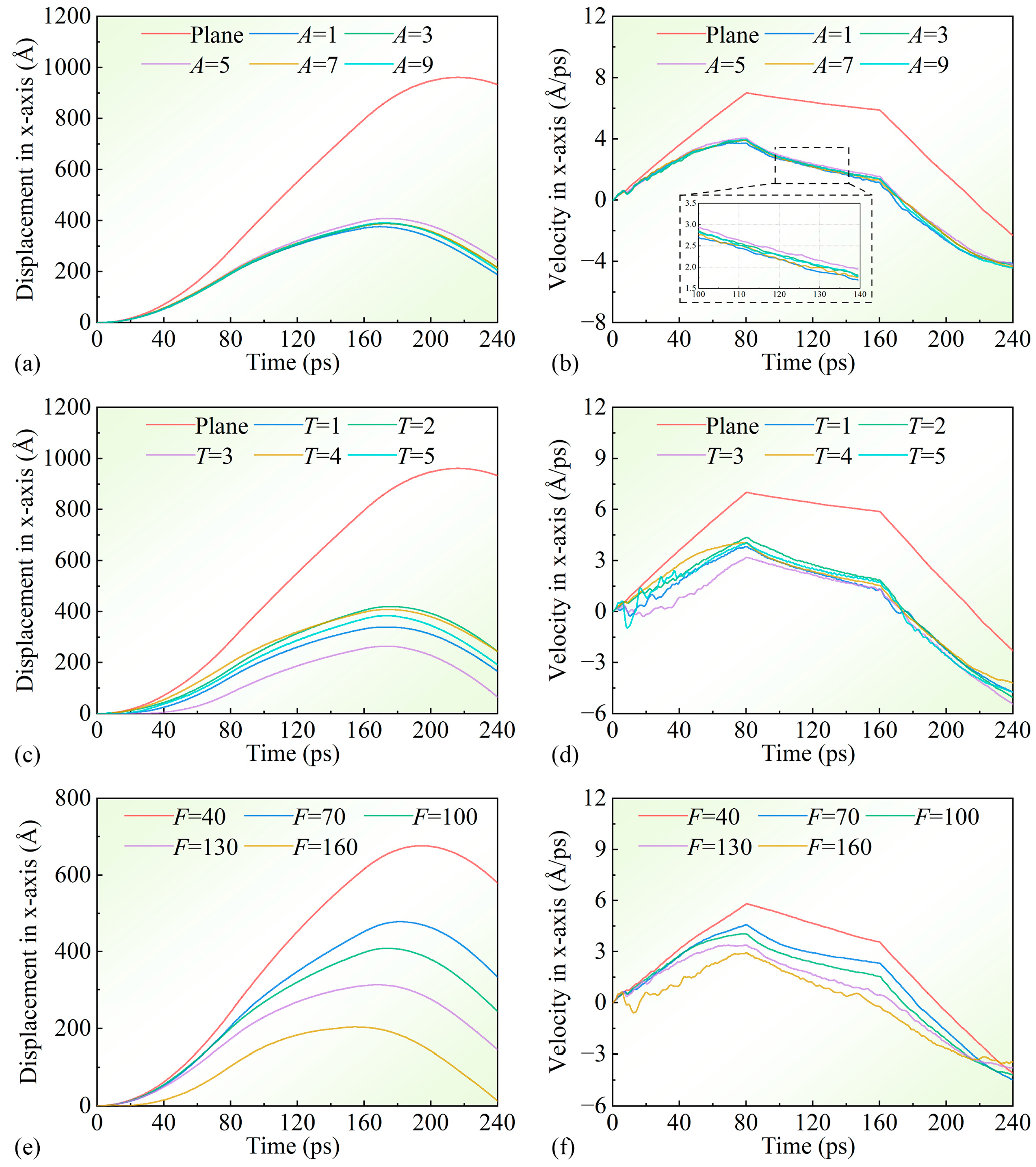
- Analysis of temperature and stress distributions reveals that the actual contact area is smaller than the nominal contact area. The centers of plane sliders and some sinusoidal sliders fail to effectively contact the substrate.
- (2)
- Examination of substrate atomic phase transitions indicates that within the elastic deformation regime, sliders with different amplitudes cause comparable damage levels to the substrate, while lower-period sliders inflict slightly greater damage than longer-period ones. Higher normal loads exacerbate atomic destruction on the substrate surface.
- (3)
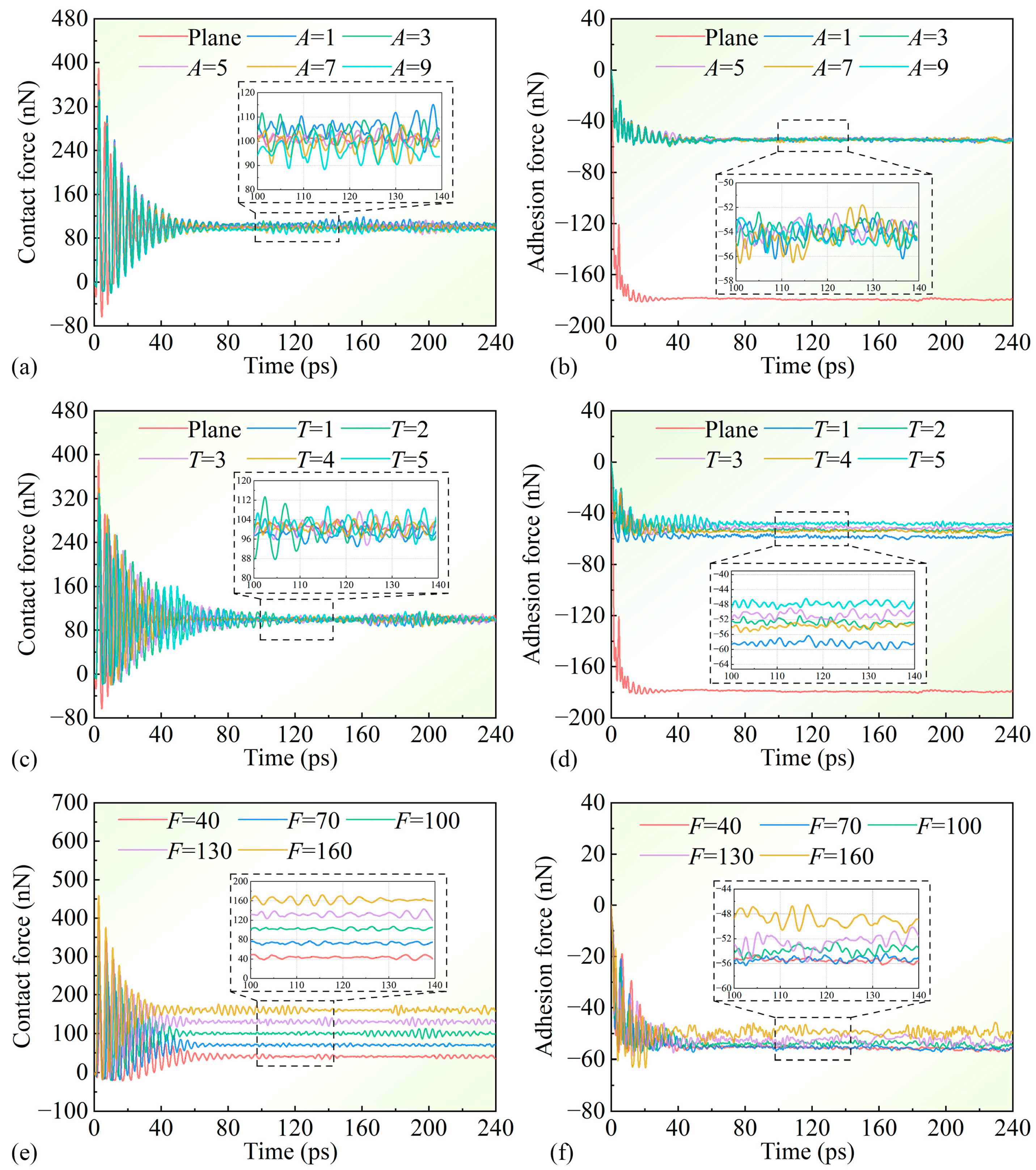
- Plane sliders experience adhesive forces exceeding threefold those of sinusoidal sliders, demonstrating that smoother contact surfaces generate stronger adhesion. Amplitude exertion has minimal influence on adhesion. Reducing the period or normal load increases adhesion.
- (4)
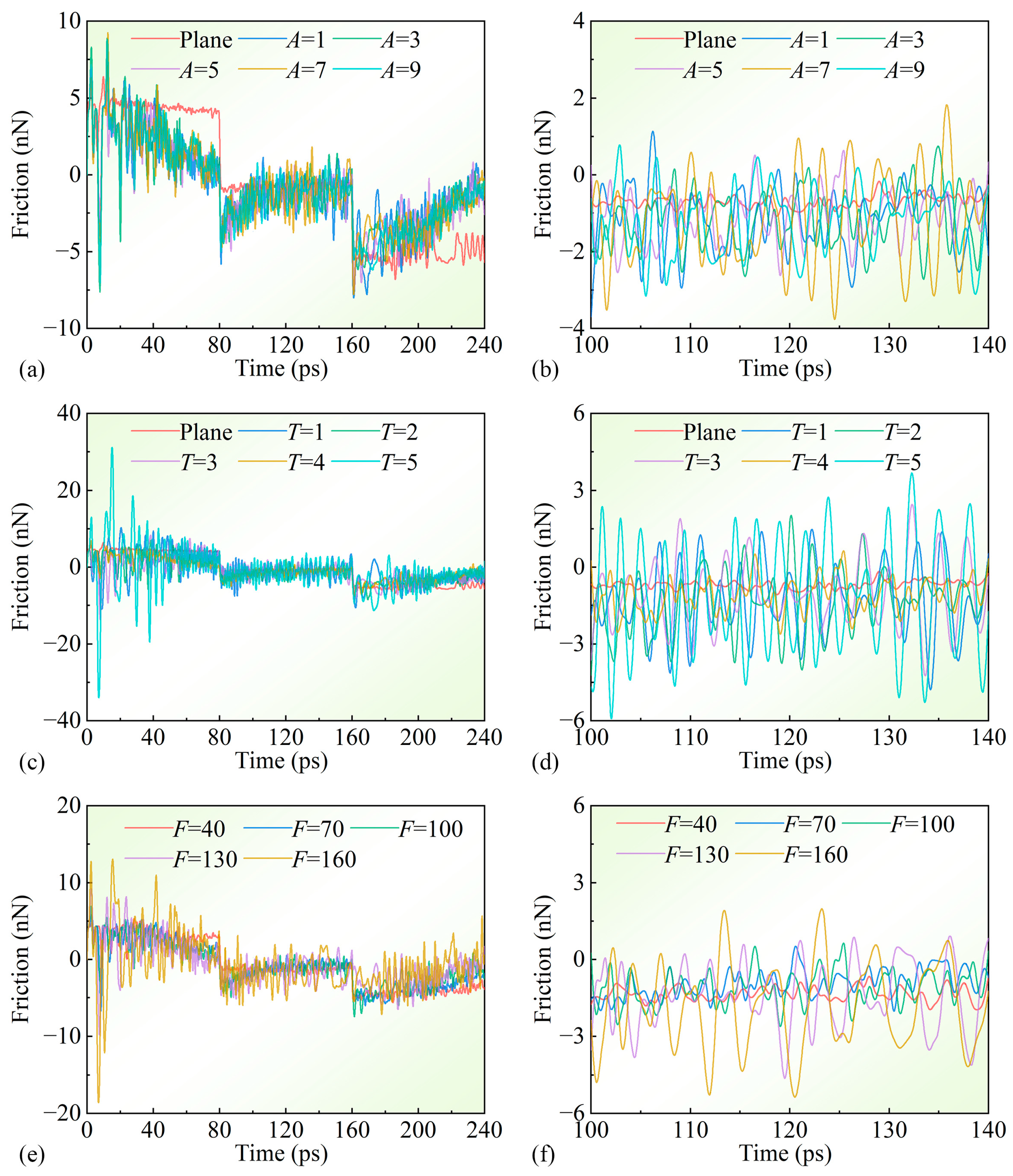
- Under identical normal loads, amplitude variations in surface parameters negligibly affect friction. Lower-period sliders exhibit significantly higher COFs than their longer-period counterparts. At ultra-low normal loads, adhesion-dominated damping surpasses elastic ploughing-induced damping under moderate loads.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, H.; Zhang, L.; Wei, Y.; Liu, S. Influence of the vibration of extreme ultraviolet lithographic tool stages on imaging. Opt. Express 2023, 31, 22358–22371. [Google Scholar] [CrossRef] [PubMed]
- Sharma, E.; Rathi, R.; Misharwal, J.; Sinhmar, B.; Kumari, S.; Dalal, J.; Kumar, A. Evolution in lithography techniques: Microlithography to nanolithography. Nanomaterials 2022, 12, 2754. [Google Scholar] [CrossRef] [PubMed]
- Naaijkens, G.; Rosielle, P.; Steinbuch, M. Mask side wall clamping. Opt. Microlithogr. XXVI 2013, 8683, 736–745. [Google Scholar]
- Amin-Shahidi, D.; Trumper, D.L. Design and control of a piezoelectric driven reticle assist device for prevention of reticle slip in lithography systems. Mechatronics 2014, 24, 562–571. [Google Scholar]
- Hermans, J.V.; Laidler, D.; Foubert, P.; D’havé, K.; Cheng, S.; Dusa, M.; Hendrickx, E. Progress in EUV Lithography Towards Manufacturing from an Exposure Tool Perspective. Extreme Ultrav. (EUV) Lithogr. III 2012, 8322, 832202. [Google Scholar]
- Li, A.S.; Wang, H.Y.; Hu, S.C.; Zhou, Y.; Du, J.G.; Ji, L.Q.; Ming, W.Y. A Systematic Review of Modeling and Simulation for Precision Diamond Wire Sawing of Monocrystalline Silicon. Micromachines 2024, 15, 1041. [Google Scholar] [CrossRef]
- Ma, G.L.; Li, S.J.; Liu, F.L.; Zhang, C.; Jia, Z.; Yin, X.C. A Review on Precision Polishing Technology of Single-Crystal SiC. Crystals 2022, 12, 101. [Google Scholar] [CrossRef]
- Dong, B.; Yu, C.; Deng, C.J.; Zhu, H.X.; Ding, J.; Tang, H. Research progress in thermal conductivity of SiCceramics. Cailiao Gongcheng 2023, 15, 64–75. [Google Scholar]
- Celler, G.K.; Cristoloveanu, S. Frontiers of silicon-on-insulator. J. Appl. Phys. 2003, 93, 4955–4978. [Google Scholar]
- Pan, J.; Yan, Q.; Li, W.; Zhang, X. A nanomechanical analysis of deformation characteristics of 6H-SiC using an indenter and abrasives in different fixed methods. Micromachines 2019, 10, 332. [Google Scholar] [CrossRef]
- Gnecco, E.; Bennewitz, R.; Gyalog, T.; Meyer, E. Friction experiments on the nanometre scale. J. Phys. Condens. Matter 2001, 13, R619. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, H.; Feng, X.; Liao, D.; Wu, N. Molecular dynamics analysis of 6H-SiC subsurface damage by nanofriction. ACS Omega 2022, 7, 18168–18178. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Zhang, L.; Yang, S.; Wu, C.; Xu, K.; Zheng, D. Effects of temperature on the deformation of 6H-SiC during nanoscratching. Wear 2023, 523, 204843. [Google Scholar] [CrossRef]
- Piroozan, N.; Naserifar, S.; Sahimi, M. Sliding friction between two silicon-carbide surfaces. J. Appl. Phys. 2019, 125, 124301. [Google Scholar] [CrossRef]
- Bhushan, B.; Cai, S. Dry and wet contact modeling of multilayered rough solid surfaces. Appl. Mech. Rev. 2008, 61, 050803. [Google Scholar] [CrossRef]
- Ghaednia, H.; Wang, X.; Saha, S.; Xu, Y.; Sharma, A.; Jackson, R.L. A review of elastic plastic contact mechanics. Appl. Mech. Rev. 2017, 69, 060804. [Google Scholar] [CrossRef]
- Chen, Z.T.; Xiong, W.; Xu, G.; Li, Y.M.; Mei, H.P.; Ding, T.; Xiao, S.F. Study on molecular dynamics of the effect of defects on the friction properties of single-crystal metals. Ferroelectrics 2019, 546, 98–108. [Google Scholar]
- Liu, H.; Guo, Y.; Zhao, P.; Li, D.; Sun, S. Anisotropy origins of coefficient of friction and scratch hardness in nano scratching monocrystalline copper. Tribol. Int. 2023, 188, 108808. [Google Scholar] [CrossRef]
- Chen, M.Y.; Hong, Z.H.; Fang, T.H.; Kang, S.H.; Kuo, L.M. Atomistic scale simulation of textured surfaces on dry sliding friction. Trans. Can. Soc. Mech. Eng. 2013, 37, 927936. [Google Scholar] [CrossRef]
- He, X.; Bai, Q.; Shen, R.; Zhang, F.; Guo, Y. The evolution of configuration and final state of graphene on rough iron surface. Appl. Surf. Sci. 2020, 530, 147084. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Salonitis, K. Fractal roughness effects on nanoscale grinding. Appl. Surf. Sci. 2019, 467, 309–319. [Google Scholar] [CrossRef]
- Huang, J.X.; Sun, C.; Chen, J.B. Modeling and characterization of contact behavior of asperities with irregular shapes. Theor. Appl. Mech. Lett. 2025, 15, 100535. [Google Scholar] [CrossRef]
- Moshkovich, A.; Lapsker, I.; Rapoport, L.S. The effect of plastic deformation on the flattening of friction surfaces. Lubricants 2024, 12, 276. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with Ovito the open visualization tool. Modell. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Spreiter, Q.; Walter, M. Classical molecular dynamics simulation with the velocity verlet algorithm at strong external magnetic fields. J. Comput. Phys. 1999, 152, 102–119. [Google Scholar] [CrossRef]
- Fu, C.H.; Lu, H.L.; Sun, S.R. Density functional theory study for adsorption of Oxygen and water molecules on 6H-SiC (0001) surface. Chin. J. Chem. Phys. 2019, 32, 451–456. [Google Scholar] [CrossRef]
- Prasad, K.E.; Ramesh, K. Hardness and mechanical anisotropy of hexagonal SiC single-crystal polytypes. J. Alloys Compd. 2019, 770, 158–165. [Google Scholar] [CrossRef]
- Zhou, L.; Yao, Y.X.; Liu, Q. Experimental research on the influence of indenter tip radius to indentation hardness. Appl. Mech. Mater. 2008, 10, 327–330. [Google Scholar] [CrossRef]
- Goel, S.; Faisal, N.H.; Luo, X.C.; Yan, J.W.; Agrawal, A. Nanoindentation of polysilicon and single crystal silicon molecular dynamics simulation and experimental validation. J. Phys. D Appl. Phys. 2014, 47, 275304. [Google Scholar]
- Qi, Y.; Liu, J.; Zhang, J.; Dong, Y.; Li, Q. Wear resistance limited by step edge failure: The rise and fall of graphene as an atomically thin lubricating material. ACS Appl. Mater. Interfaces 2017, 9, 1099–1106. [Google Scholar] [PubMed]
- Li, S.; Li, Q.; Carpick, R.W.; Gumbsch, P.; Liu, X.Z.; Ding, X.; Sun, J.; Li, J. The evolving quality of frictional contact with graphene. Nature 2016, 539, 541–545. [Google Scholar]
- Kristiansen, K.; Banquy, X.; Zeng, H.; Charrault, E.; Giasson, S.; Israelachvili, J. Measurements of anisotropic (off-axis) friction-induced motion. Adv. Mater. 2012, 38, 5236–5241. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, T.; Hori, D.; Kangawa, Y.; Kakimoto, K.; Yoshimura, M.; Mori, Y. Thermal conductivity of SiC calculated by molecular dynamics. Jpn. J. Appl. Phys. 2008, 47, 8898. [Google Scholar]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W., III; Skiff, W.M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar]
- Cao, A.; Shen, B.; Lin, Q.; Chen, S.; Huang, Z.; Ji, Z.; Zhang, Z. Influence of Stone-Wales defect on graphene friction: Pinning effect and wrinkle modification. Comput. Mater. Sci. 2020, 173, 109423. [Google Scholar]
- Liu, Y.; Ji, Y.; Dong, L.; Xie, H.; Song, J.; Li, J. Effect of grinding depths on SiC nanogrinding behavior based on molecular dynamics. Appl. Phys. A-Mater. Sci. Process 2022, 128, 34. [Google Scholar]
- Zhao, P.Y.; Zhao, B.; Pan, J.S.; Wu, J.W. Nano-grinding process of single-crystal silicon using molecular dynamics simulation: Nano-grinding parameters effect. Mat. Sci. Semicon Proc. 2022, 143, 106351. [Google Scholar]
- Wu, X.H.; Zhang, F.L.; Xia, H.X.; Zhang, L.; Liu, J.H.; Zhang, X.R.; Ao, X.H.; Luo, J.C. Effects of asperity shapes and normal loads on adhesive wear mechanisms. Tribol. Lett. 2025, 73, 42. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, C. Friction and wear of diamond-silicon nano-systems: Effect of moisture and surface roughness. Wear 2013, 302, 929–936. [Google Scholar] [CrossRef]
- Bai, L.; Srikanth, N.; Korznikova, E.A.; Baimova, J.A.; Dmitriev, S.V.; Zhou, K. Wear and friction between smooth or rough diamond-like carbon films and diamond tips. Wear 2017, 372, 12–20. [Google Scholar] [CrossRef]
- Wu, C.; Jia, J.; Che, H.; Mu, J.; Zhao, S.; Zhang, X. Frictional behaviors of three kinds of nanotextured surfaces. Surf. Interface Anal. 2016, 48, 1056–1061. [Google Scholar] [CrossRef]
- Bowden, P.; Tabor, D. Ploughing Friction. Proc. R. Soc. Lond. A Mat. 1967, 295, 221–235. [Google Scholar]
- Wang, X.Z.; Xu, Y.; Jackson, R.L. Elastic–plastic sinusoidal waviness contact under combined normal and tangential loading. Tribol. Lett. 2017, 65, 45. [Google Scholar] [CrossRef]
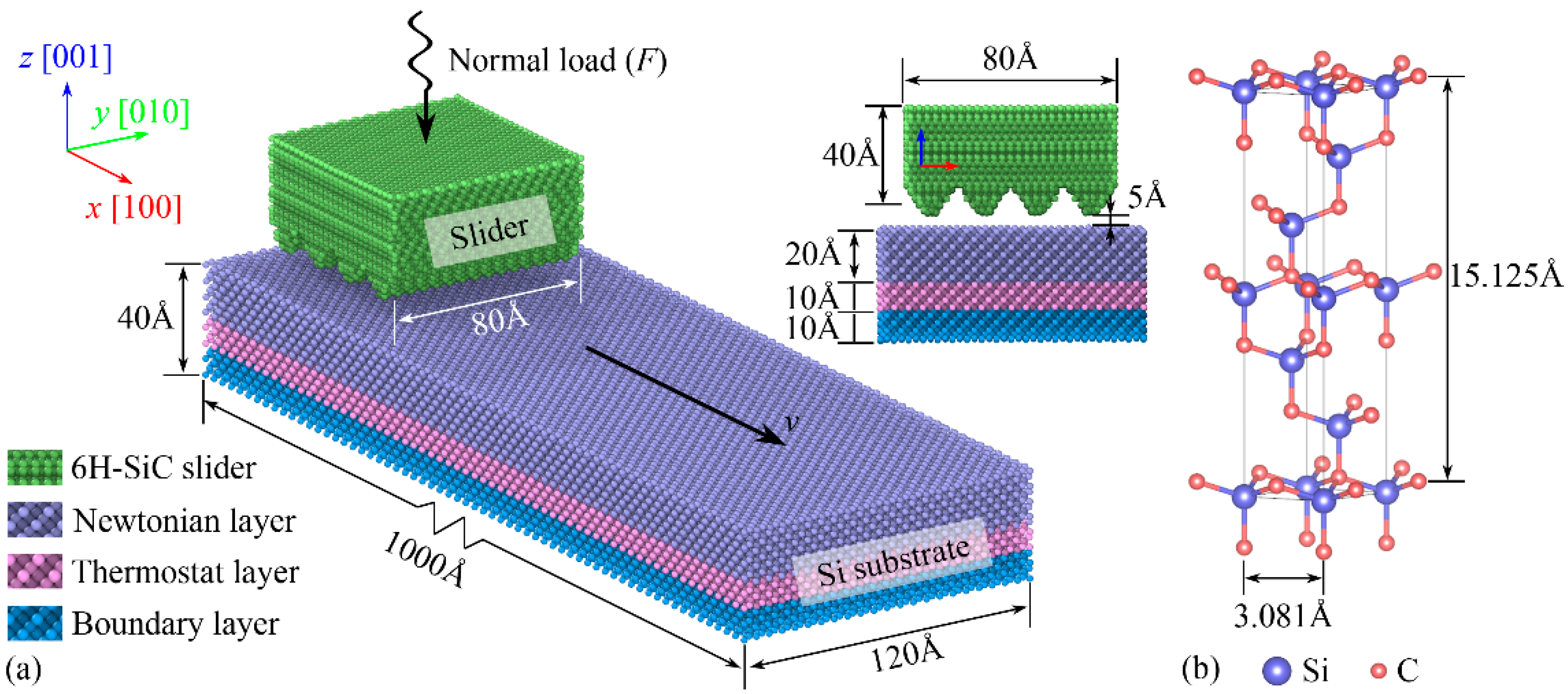
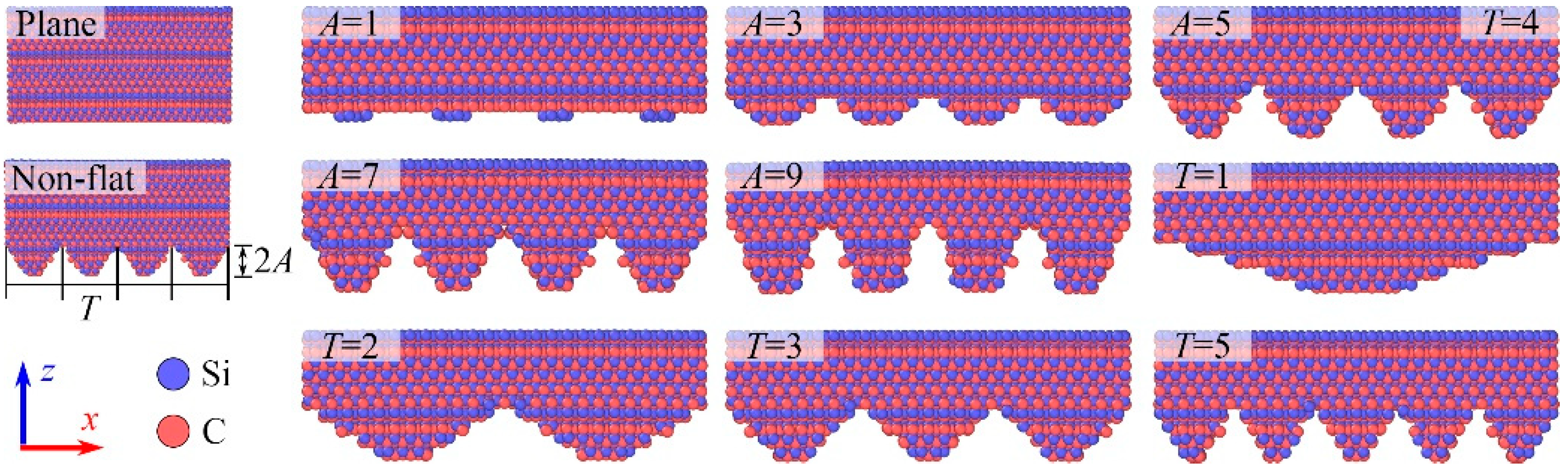

| Simulation Parameters | Value |
|---|---|
| Material of substrate | Si |
| Lattice constant of the substrate (Å) | 5.428 |
| Material of sliders | SiC |
| Lower surface amplitudes (A) of the sliders (Å) | 1, 3, 5, 7, 9 |
| Lower surface periods (T) of the sliders | 1, 2, 3, 4, 5 |
| Normal force (F) on sliders (nN) | 40, 70, 100, 130, 160 |
| Duration of each force field (ps) | 80 |
| Timestep (fs) | 1 |
| Potential function | Tersoff, L-J |
| Initial temperature (K) | 300 |
| Parameters | Average Friction Force | Standard Deviation | COF | Standard Deviation |
|---|---|---|---|---|
| Plane | 0.69 | 0.23 | 0.0068 | 0.0023 |
| A = 1 | 1.15 | 1.14 | 0.0111 | 0.0110 |
| A = 3 | 1.17 | 1.07 | 0.0112 | 0.0103 |
| A = 5 | 1.11 | 1.07 | 0.0108 | 0.0105 |
| A = 7 | 1.14 | 1.50 | 0.0113 | 0.0150 |
| A = 9 | 1.18 | 1.13 | 0.0112 | 0.0117 |
| T = 1 | 1.31 | 1.79 | 0.0132 | 0.0184 |
| T = 2 | 1.36 | 1.70 | 0.0135 | 0.0172 |
| T = 3 | 1.10 | 1.63 | 0.0107 | 0.0162 |
| T = 4 | 1.11 | 1.07 | 0.0108 | 0.0105 |
| T = 5 | 1.21 | 3.00 | 0.0120 | 0.0297 |
| F = 40 | 1.36 | 0.37 | 0.0330 | 0.0085 |
| F = 70 | 0.94 | 0.81 | 0.0133 | 0.0113 |
| F = 100 | 1.11 | 1.07 | 0.0108 | 0.0105 |
| F = 130 | 1.44 | 1.55 | 0.0107 | 0.0118 |
| F = 160 | 1.82 | 1.89 | 0.0112 | 0.0116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Wu, J.; Lei, D.; Liu, H.; Zhao, P.; Zhao, B.; Liu, J.; Yang, Q. Atomic Simulation of Wear and Slip Behavior Between Monocrystalline Silicon and 6H-SiC Friction Pair. Lubricants 2025, 13, 147. https://doi.org/10.3390/lubricants13040147
Pan J, Wu J, Lei D, Liu H, Zhao P, Zhao B, Liu J, Yang Q. Atomic Simulation of Wear and Slip Behavior Between Monocrystalline Silicon and 6H-SiC Friction Pair. Lubricants. 2025; 13(4):147. https://doi.org/10.3390/lubricants13040147
Chicago/Turabian StylePan, Jiansheng, Jianwei Wu, Daiyi Lei, Huan Liu, Pengyue Zhao, Bo Zhao, Jiang Liu, and Qingshan Yang. 2025. "Atomic Simulation of Wear and Slip Behavior Between Monocrystalline Silicon and 6H-SiC Friction Pair" Lubricants 13, no. 4: 147. https://doi.org/10.3390/lubricants13040147
APA StylePan, J., Wu, J., Lei, D., Liu, H., Zhao, P., Zhao, B., Liu, J., & Yang, Q. (2025). Atomic Simulation of Wear and Slip Behavior Between Monocrystalline Silicon and 6H-SiC Friction Pair. Lubricants, 13(4), 147. https://doi.org/10.3390/lubricants13040147






