Unbalance Response of a Hydrogen Fuel Cell Vehicle Air Compressor Rotor Supported by Gas Foil Bearings: Experimental Study and Analysis
Abstract
:1. Introduction
- Test Rig Design: Development of a dedicated test rig. The rig is built around a commercial HFCVAC rotor architecture, providing a realistic platform for investigating GFB-rotor dynamics.
- Experimental Unbalance Response Characterization: An experimental investigation of the rotor’s vibration response to intentional unbalance.
- Vibration Analysis via ODS: Application of Operating Deflection Shape (ODS) analysis on the measured vibration data to visualize the rotor’s deformation pattern.
2. Test Rig and Experimental Setup
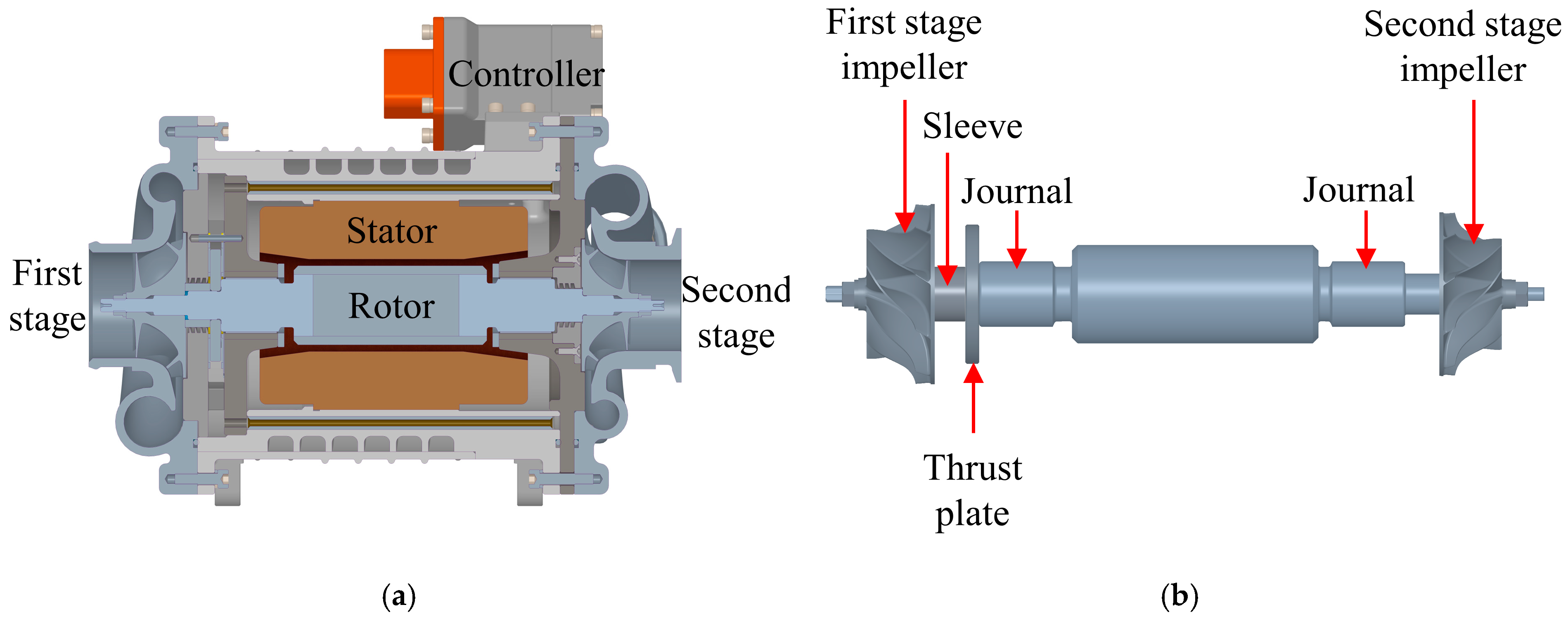
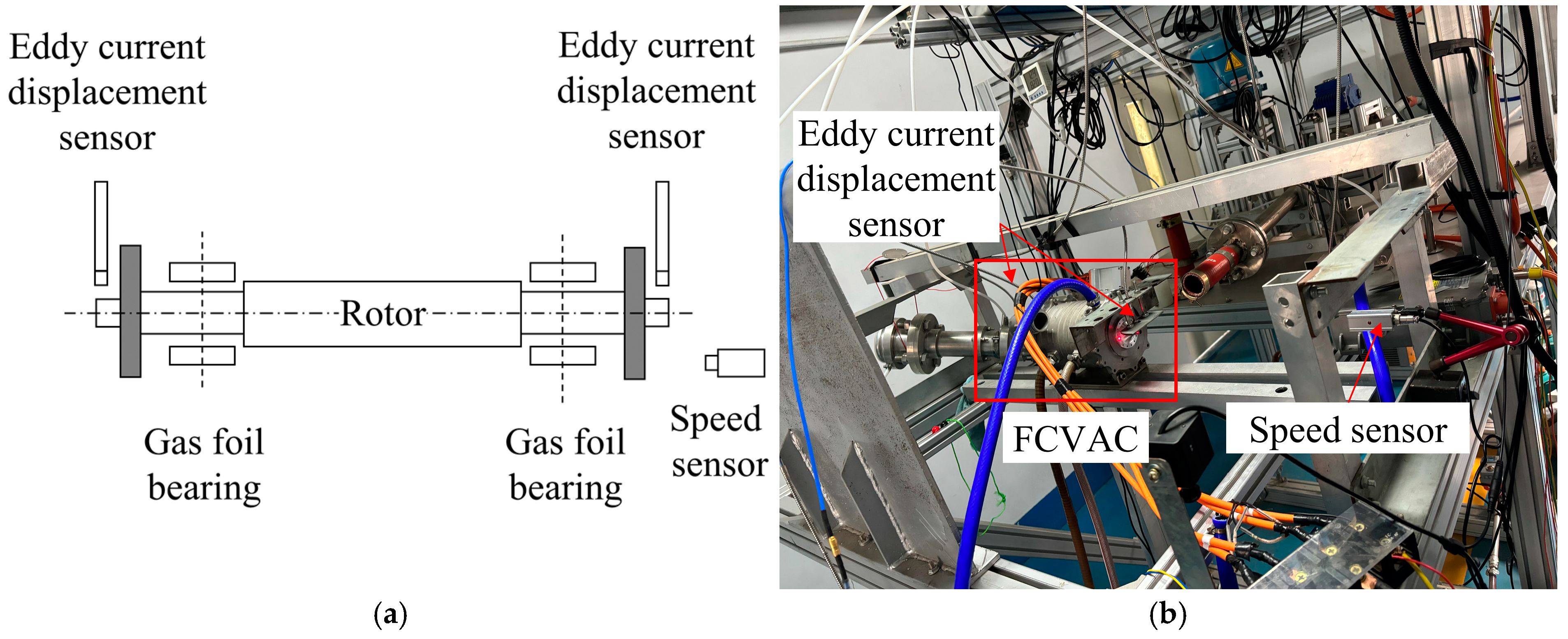
2.1. Test Rig Description
2.2. Specifications of Gas Foil Bearings
2.3. Experimental Procedure
- (1)
- Unilateral Unbalanced Mass Experiments
- (2)
- Bilateral Unbalanced Mass Experiments
3. Theoretical Modeling of the GFB-Rotor System
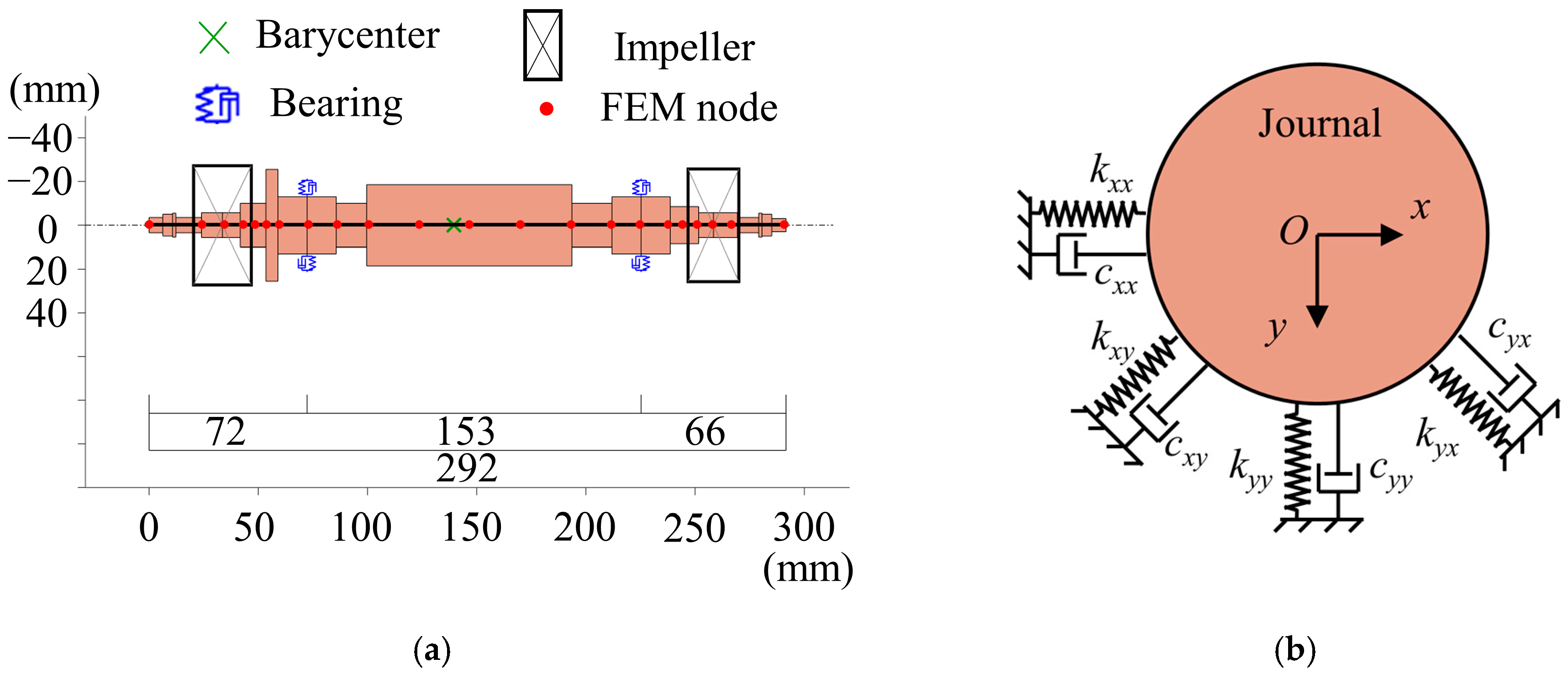
3.1. Rotor Dynamics Model
3.2. Reynolds Equation
3.3. Foil Structure Modeling
4. Results and Discussion
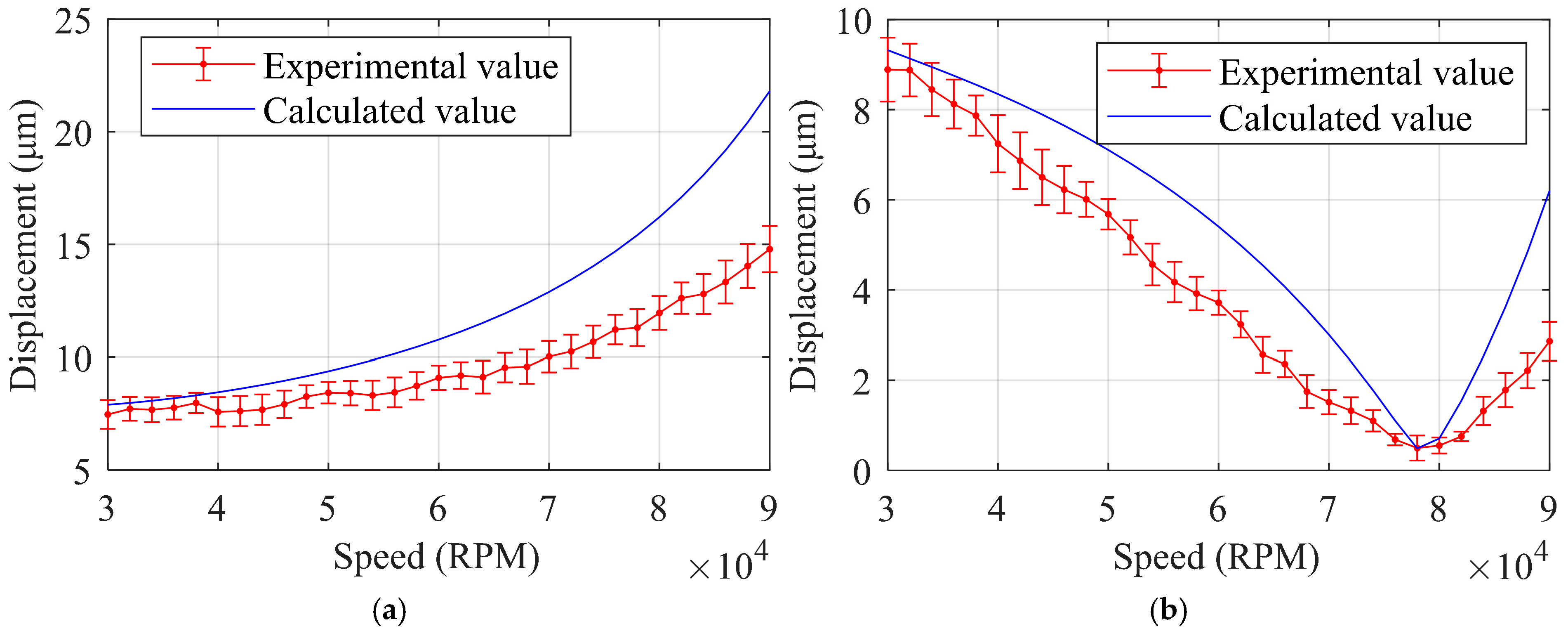
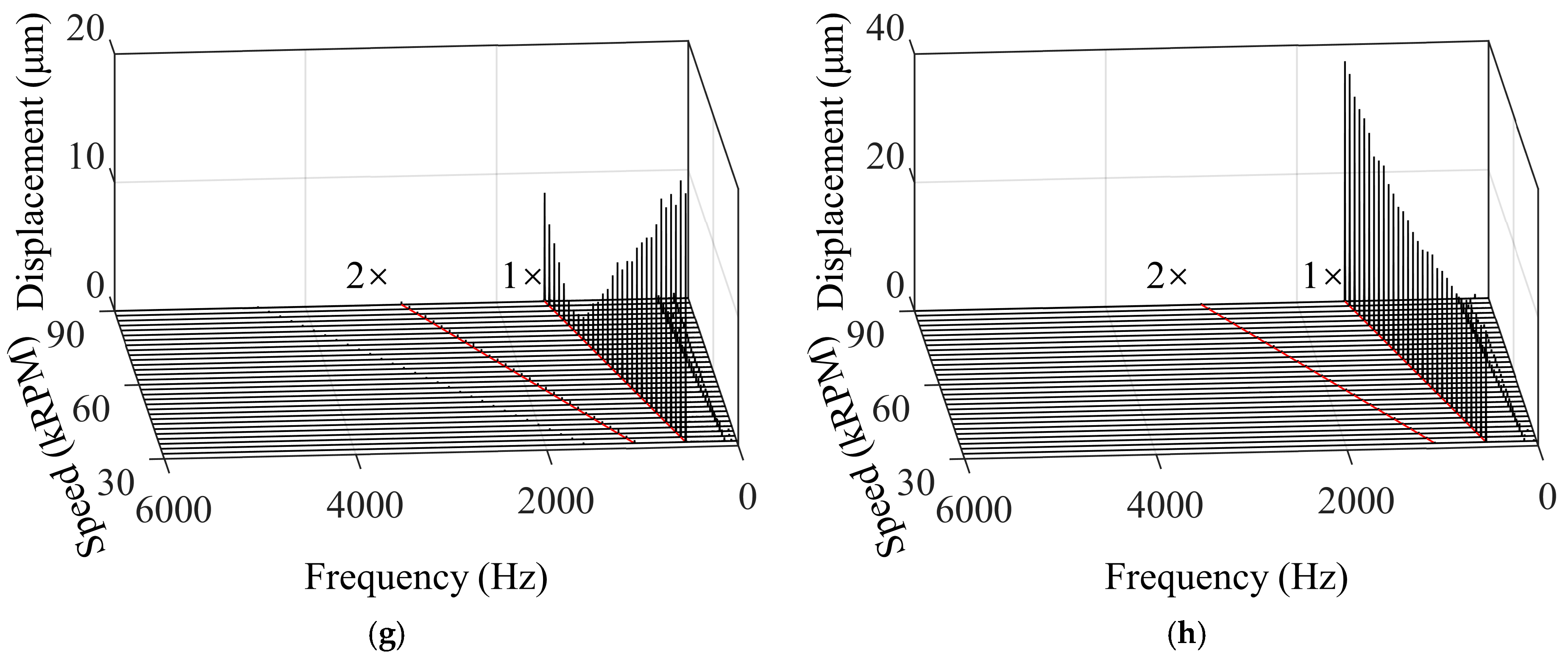
4.1. Model Validation
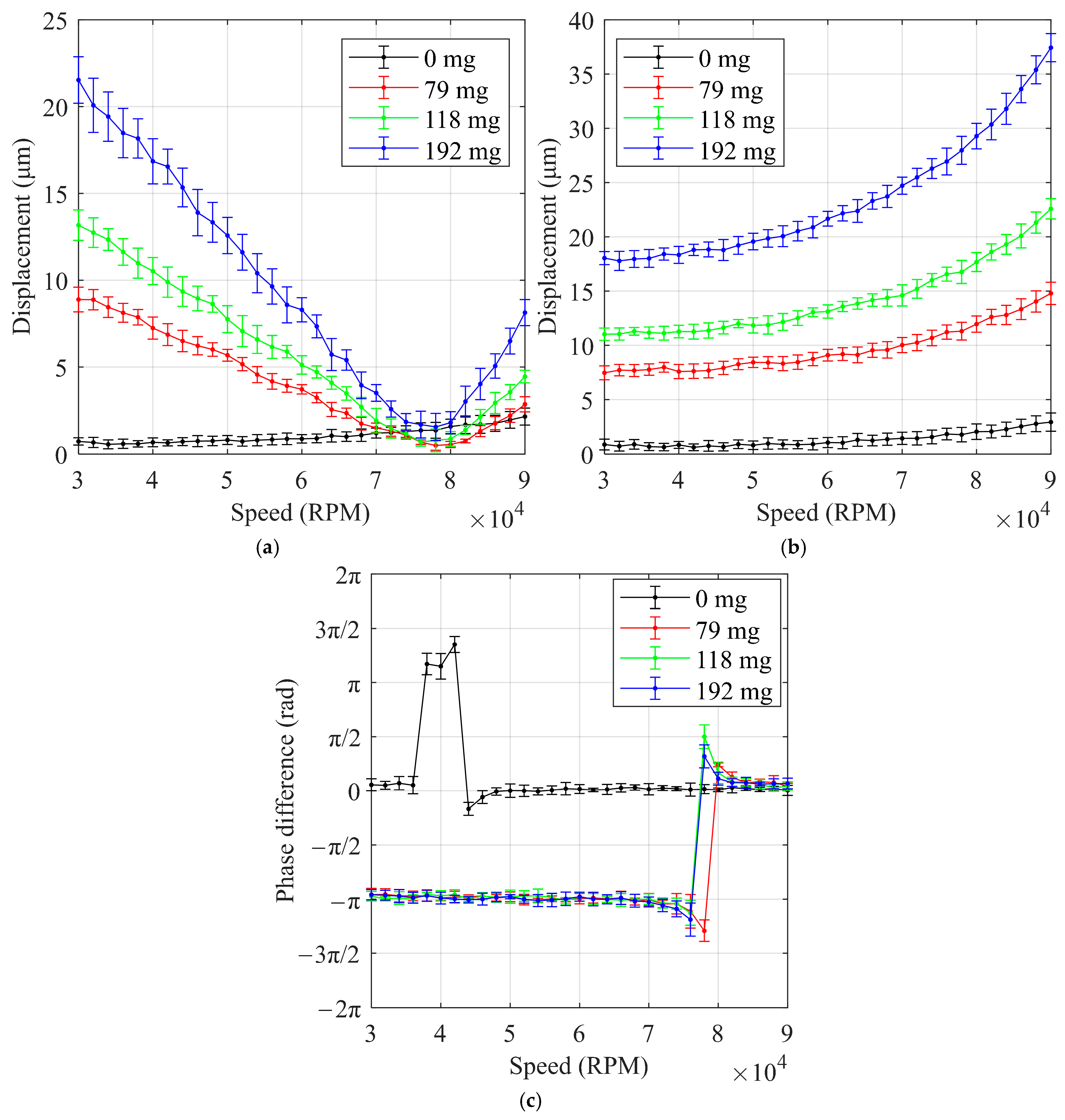
4.2. Unilateral Unbalanced
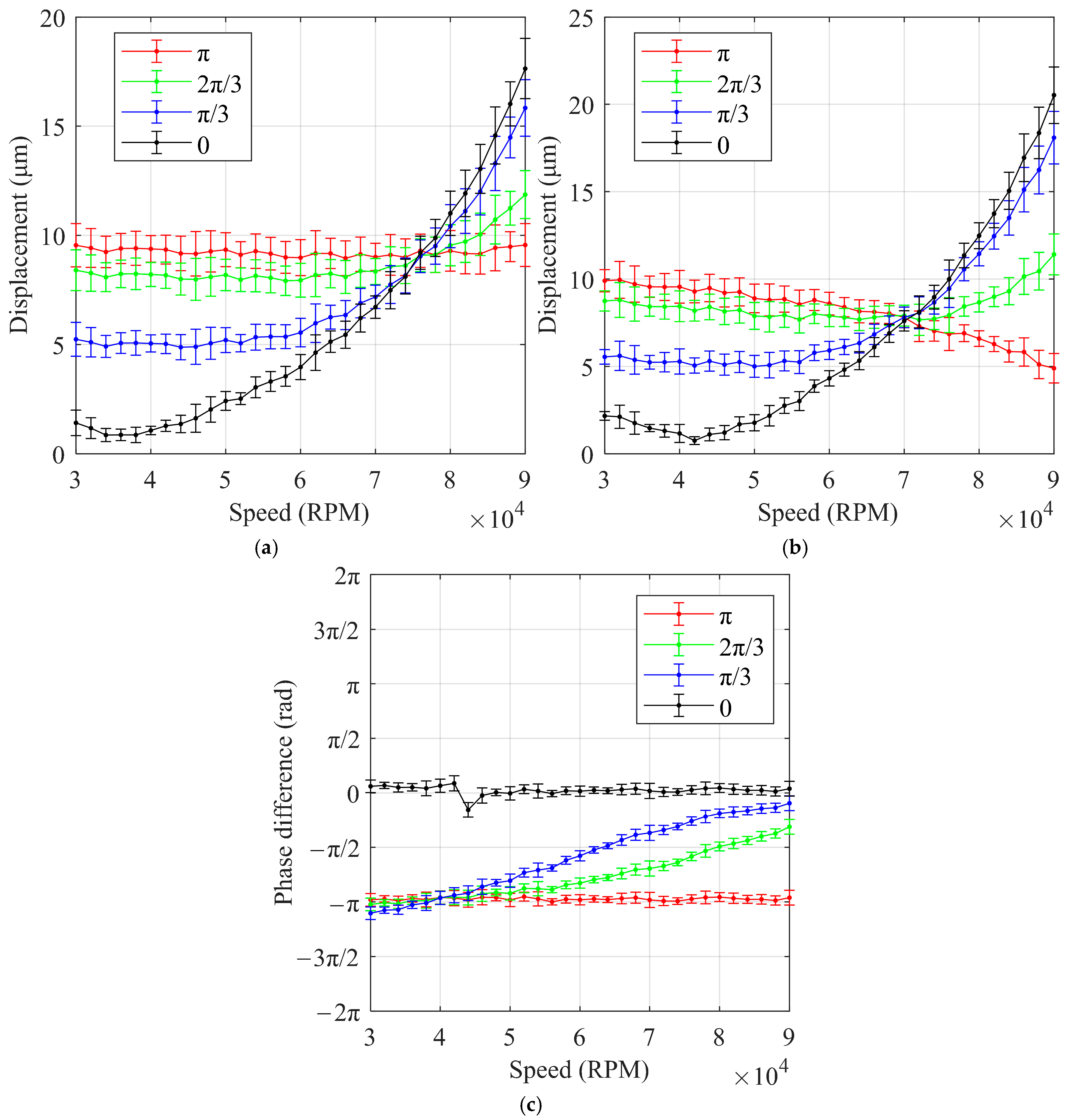
4.3. Bilateral Unbalanced
5. Conclusions
- (1)
- For the HFCVAC studied, the influence of unbalanced mass on subsynchronous vibration is relatively small. Adding unilateral unbalanced mass causes the synchronous vibration on that side of the rotor to decrease and then increase with speed. In contrast, synchronous vibration on the opposite side continuously increases with speed. When bilateral equal unbalanced masses are added, synchronous vibration on each side increases at low speeds with the phase difference of the unbalanced mass, while the opposite trend is observed at high speeds.
- (2)
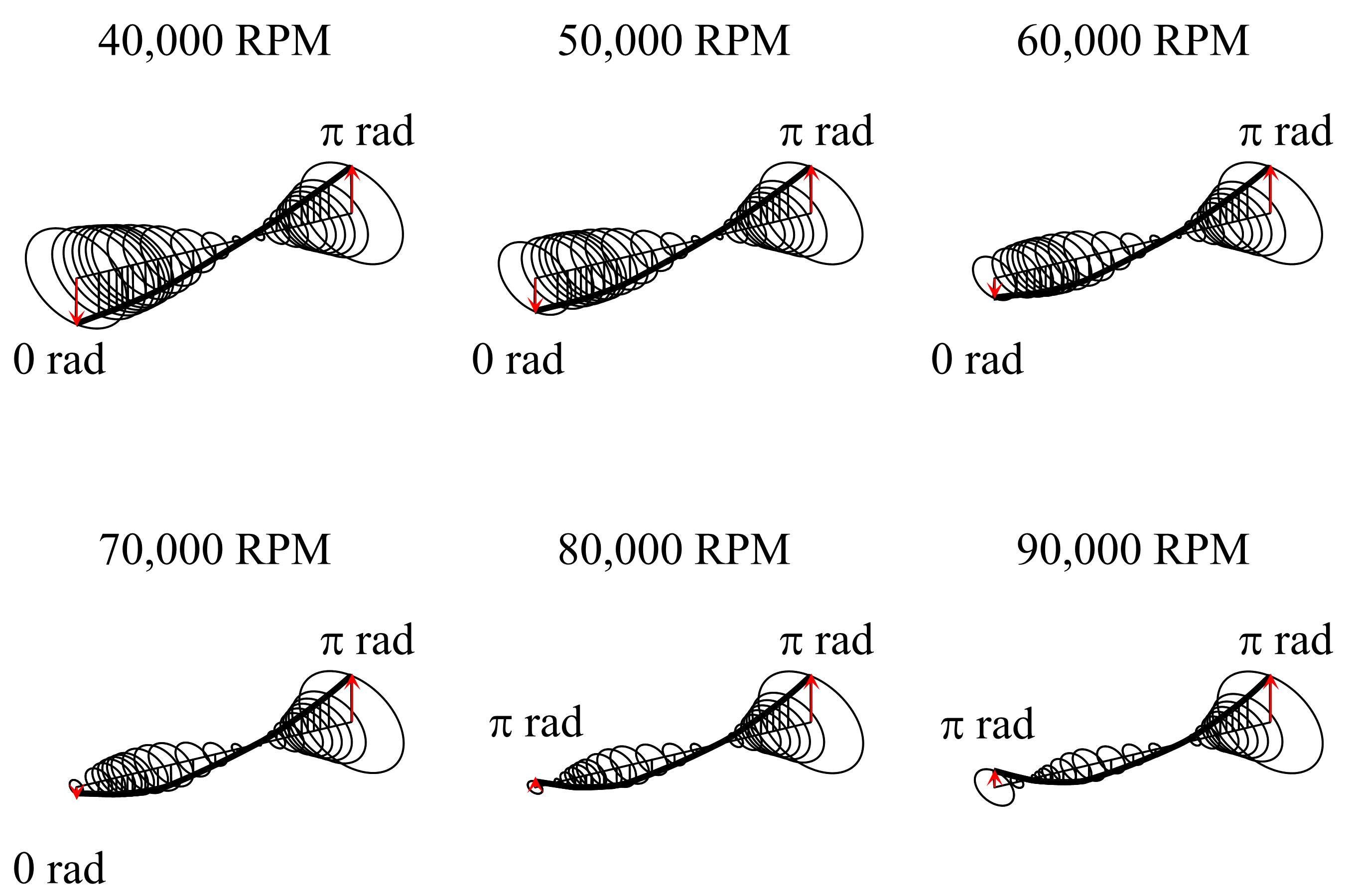
- For high-speed compressors, rotor bending mode significantly affects vibration. This bending causes the rotor’s vibration amplitude to change nonlinearly with speed, even though the rated speed still maintains a sufficient separation margin from the first bending critical speed.
- (3)
- With double-face dynamic balancing of the compressor rotor, the phase of the unbalanced mass needs to be reasonably distributed according to the operating speed. Different optimal phase differences of unbalanced mass distribution exist for low-speed and high-speed compressors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HFCVAC | Hydrogen Fuel Cell Vehicle Air Compressor |
| GFB | Gas Foil Bearing |
| FEM | Finite Element Method |
| ODS | Operational Deflection Shape |
References
- Pramuanjaroenkij, A.; Kakaç, S. The fuel cell electric vehicles: The highlight review. Int. J. Hydrogen Energy 2023, 48, 9401–9425. [Google Scholar] [CrossRef]
- Pattnayak, M.R.; Ganai, P.; Pandey, R.K.; Dutt, J.K.; Fillon, M. An overview and assessment on aerodynamic journal bearings with important findings and scope for explorations. Tribol. Int. 2022, 174, 107778. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, H.; Fu, J.; Wang, X.; Liu, J. Review of recent developments in fuel cell centrifugal air compressor: Comprehensive performance and testing techniques. Int. J. Hydrogen Energy 2023, 48, 32039–32055. [Google Scholar] [CrossRef]
- Larsen, J.S.; Santos, I.F. On the nonlinear steady-state response of rigid rotors supported by air foil bearings—Theory and experiments. J. Sound Vib. 2015, 346, 284–297. [Google Scholar] [CrossRef]
- von Osmanski, S.; Larsen, J.S.; Santos, I.F. A fully coupled air foil bearing model considering friction—Theory & experiment. J. Sound Vib. 2017, 400, 660–679. [Google Scholar] [CrossRef]
- Guo, Z.; Cao, Y.; Feng, K.; Guan, H.; Zhang, T. Effects of Static and Imbalance Loads on Nonlinear Response of Rigid Rotor Supported on Gas Foil Bearings. Mech. Syst. Signal Process. 2019, 133, 106271. [Google Scholar] [CrossRef]
- Baum, C.; Leister, T.; Seemann, W. Stability and bifurcation analysis of a rotor in rigid and foil air bearings utilized for the identification of the air whirl effect. J. Sound Vib. 2022, 536, 117067. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Wei, K.; Zou, H. Rotordynamics of a rotor radially and axially supported by active bump-type foil bearings and bump-type thrust foil bearings. Mech. Syst. Signal Process. 2024, 208, 110995. [Google Scholar] [CrossRef]
- Hu, B.; Yang, X.; Hou, A.; Wang, R.; Wu, Z.; Ni, Q.; Li, Z. Nonlinear Dynamic Responses of Rigid Rotor Supported by Thick Top Foil Bearings. Lubricants 2023, 11, 453. [Google Scholar] [CrossRef]
- Kumar, P. Dynamic analysis and identification in a cracked and unbalanced rigid rotor with two offset discs and one middle disc mounted on foil bearings. Int. J. Dynam. Control 2024, 12, 2648–2673. [Google Scholar] [CrossRef]
- Xu, H.; Shao, C.; Yang, B.; An, Q. Numerical investigation on the rotordynamics of a high-speed air compressor supported by gas foil bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 5580–5596. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Xu, H. Theoretical and experimental study on the effect of adjustable journal bearings on the vibration response of rigid and slender rotor systems. Mech. Syst. Signal Process. 2025, 224, 111951. [Google Scholar] [CrossRef]
- Heshmat, H. Operation of foil bearings beyond the bending critical mode. J. Tribol.-Trans. ASME 2000, 122, 192–198. [Google Scholar] [CrossRef]
- Ying, M.; Liu, X.; Zhang, Y.; Zhang, C. Impact of Gas Foil Bearings, Labyrinth Seals, and Impellers on the Critical Speed of Centrifugal Compressors for Fuel Cell Vehicles: A Comprehensive Investigation. Lubricants 2023, 11, 532. [Google Scholar] [CrossRef]
- Chen, S.; Zuo, S.; Wu, Z.; Liu, C. Comprehensive vibro-acoustic characteristics and mathematical modeling of electric high-speed centrifugal compressor surge for fuel cell vehicles at various compressor speeds. Mech. Syst. Signal Process. 2022, 178, 109311. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Q.; Peng, X.; Feng, J.; Guo, Y. Multi-objective optimization of the oil-free centrifugal air compressor in hydrogen fuel cell vehicles based on grey relational analysis. Int. J. Hydrogen Energy 2023, 48, 26341–26355. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Liu, G.; Yang, Q.; Li, L.; Gao, Z. Air and hydrogen supply systems and equipment for PEM fuel cells: A review. Int. J. Green Energy 2022, 19, 331–348. [Google Scholar] [CrossRef]
- Ying, M.; Liu, X.; Zhang, C.; Wang, X.; Liu, Y.; Zhang, Y. The Two-Pad: A Novel Gas Foil Bearing for Fuel Cell Vehicles. Int. J. Energy Res. 2023, 2023, 5521171. [Google Scholar] [CrossRef]
- ISO 1940-1; Mechanical Vibration—Balance Quality Requirements for Rotors in a Constant (Rigid) State—Part 1: Specification and Verification of Balance Tolerances. ISO: Geneva, Switzerland, 2003.
- Hoffmann, R.; Pronobis, T.; Liebich, R. Non-linear stability analysis of a modified gas foil bearing structure. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1259–1276. [Google Scholar]
- Gu, Y.; Ren, G.; Zhou, M. A Novel Method for Calculating the Dynamic Force Coefficients of Gas Foil Bearings and Its Application in the Rotordynamic Analysis. J. Sound Vib. 2021, 515, 116466. [Google Scholar] [CrossRef]
- Friswell, M.I.; Penny, J.E.T.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Lund, J.W. Calculation of Stiffness and Damping Properties of Gas Bearings. J. Lubr. Technol. 1968, 90, 793–803. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of Gas Lubricated Compliant Thrust Bearings. J. Lubr. Technol. 1983, 105, 638–646. [Google Scholar] [CrossRef]
- Zywica, G.; Baginski, P.; Bogulicz, M.; Martowicz, A.; Roemer, J.; Kantor, S. Numerical identification of the dynamic characteristics of a nonlinear foil bearing structure: Effect of the excitation force amplitude and the assembly preload. J. Sound Vib. 2022, 520, 116663. [Google Scholar] [CrossRef]
- ANSI/HI 9.6.8; Rotodynamic Pumps—Guideline for Dynamics of Pumping Machinery. American National Standards Institute, Hydraulic Institute: Parsippany, NJ, USA, 2014.







| Parameters | Values |
|---|---|
| Rated power | 30 kW |
| Rated speed | 90 kRPM |
| Idle speed | 30 kRPM |
| Rotor mass | 1443 g |
| Thrust plate mass | 122 g |
| Sleeve mass | 17 g |
| Total rotor length | 292 mm |
| Journal bearing center span | 153 mm |
| First-stage impeller mass | 79 g |
| First-stage impeller radial moment of inertia | 18.4 kg·mm2 |
| Second-stage impeller mass | 56 g |
| Second-stage impeller radial moment of inertia | 11.2 kg·mm2 |
| Parameters | Values |
|---|---|
| Bearing diameter | 25 mm |
| Bearing width | 25 mm |
| Nominal clearance | 30 μm |
| Preload | 30 μm |
| Top foil thickness | 0.1 mm |
| Bump foil thickness | 0.1 mm |
| Bump pitch | 3.17 mm |
| Bump half length | 1.27 mm |
| Poisson’s ratio | 0.29 |
| Modulus of elasticity | 214 GPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, M.; Liu, X. Unbalance Response of a Hydrogen Fuel Cell Vehicle Air Compressor Rotor Supported by Gas Foil Bearings: Experimental Study and Analysis. Lubricants 2025, 13, 181. https://doi.org/10.3390/lubricants13040181
Ying M, Liu X. Unbalance Response of a Hydrogen Fuel Cell Vehicle Air Compressor Rotor Supported by Gas Foil Bearings: Experimental Study and Analysis. Lubricants. 2025; 13(4):181. https://doi.org/10.3390/lubricants13040181
Chicago/Turabian StyleYing, Ming, and Xinghua Liu. 2025. "Unbalance Response of a Hydrogen Fuel Cell Vehicle Air Compressor Rotor Supported by Gas Foil Bearings: Experimental Study and Analysis" Lubricants 13, no. 4: 181. https://doi.org/10.3390/lubricants13040181
APA StyleYing, M., & Liu, X. (2025). Unbalance Response of a Hydrogen Fuel Cell Vehicle Air Compressor Rotor Supported by Gas Foil Bearings: Experimental Study and Analysis. Lubricants, 13(4), 181. https://doi.org/10.3390/lubricants13040181





