Contact Load Calculation Models for Finite Line Contact Rollers in Bearing Dynamic Simulation Under Dry and Lubricated Conditions
Abstract
1. Introduction
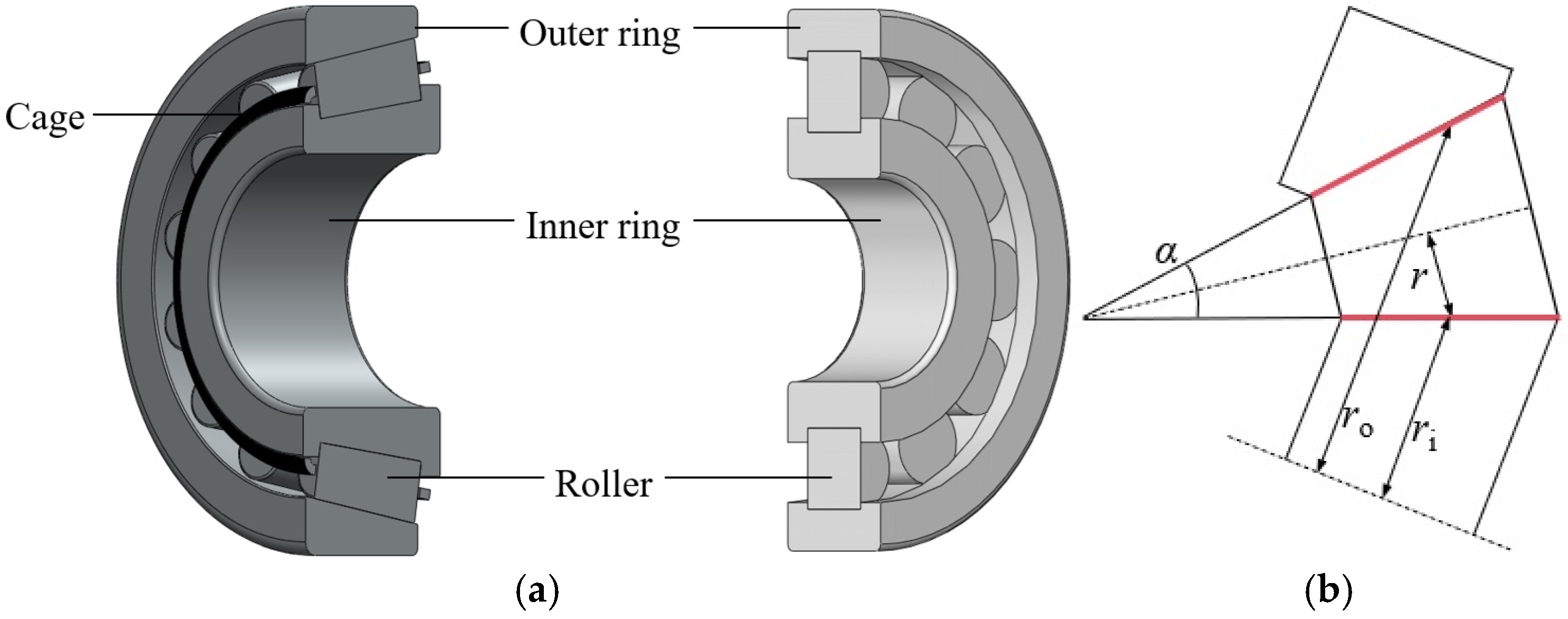
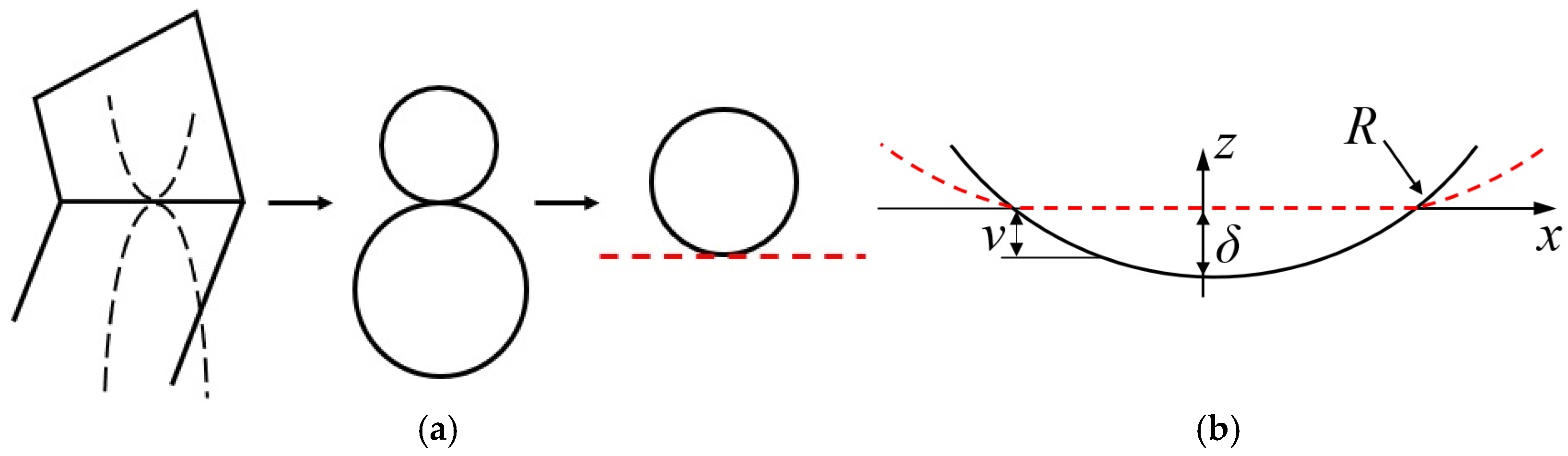
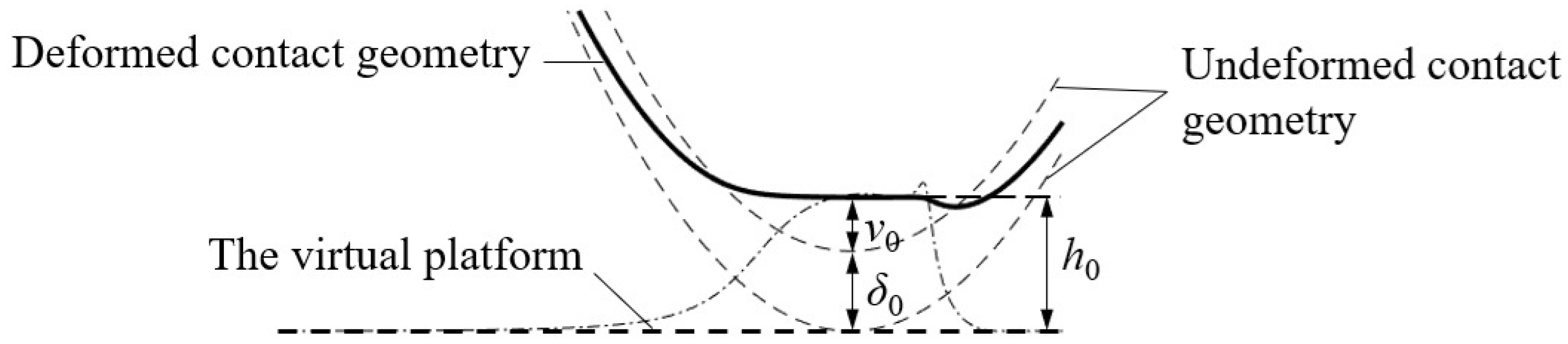
2. Contact Geometry Between Roller and Raceway
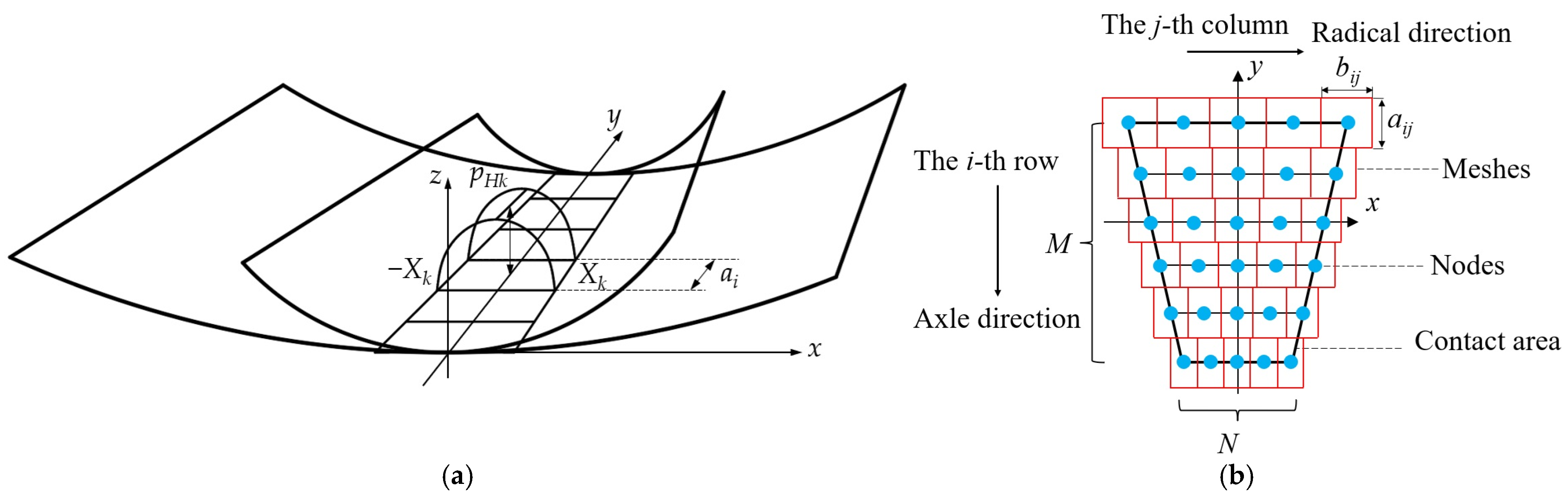
3. Contact Load Calculation Model Based on the Half-Space Theory
| Algorithm 1 The Contact Load Calculating Model Based on the Half-Space Theory | |
| Require: Parameters: Radius of roller R; Contact line length L; Mutual approach δ; Mesh numbers M, N; Composite modulus of elasticity E Tolerance: e Ensure: Half width of contact area for each roller slice bi | |
| 1: //Initialize | |
| 2: | ▷ Contact width of the i-th roller slice |
| 3: | ▷ Length of mesh of the i-th roller slice |
| 4: | ▷ Current difference, initialized to e + 1 |
| 5: | ▷ Initial contact width |
| 6: while do | |
| 7: // Influence coefficient matrix construction | |
| 8: Matrix matrix_construction (M, N, ai, bi) | |
| 9: // Contact load update | |
| 10: W Matrix-1 × δ | |
| 11: Wi W[i] | ▷ Extract the i-th contact load |
| 12: // Contact width update | |
| 13: | |
| 14: //Calculate error | |
| 15: | |
| 16: | |
| 17: end while | |
| 18: return Wi | |
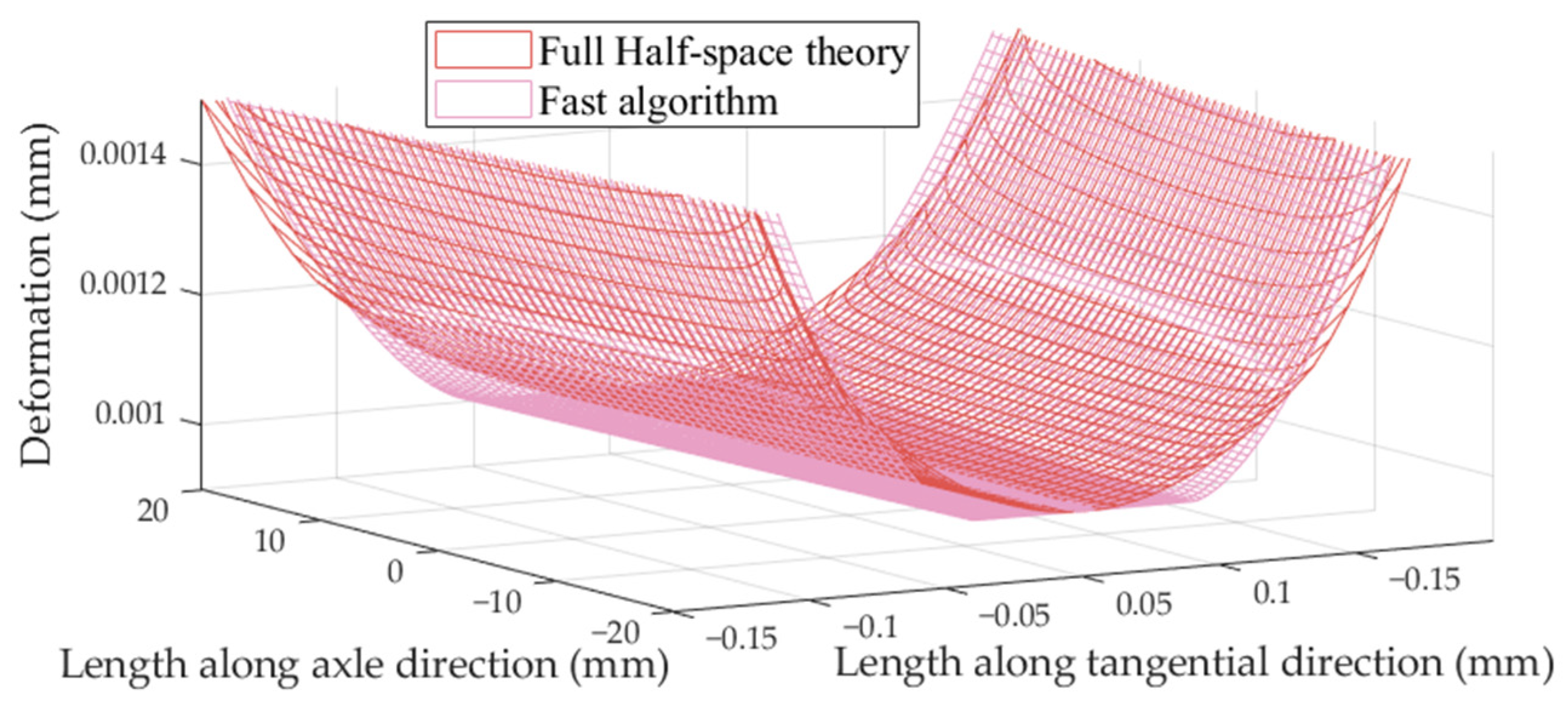
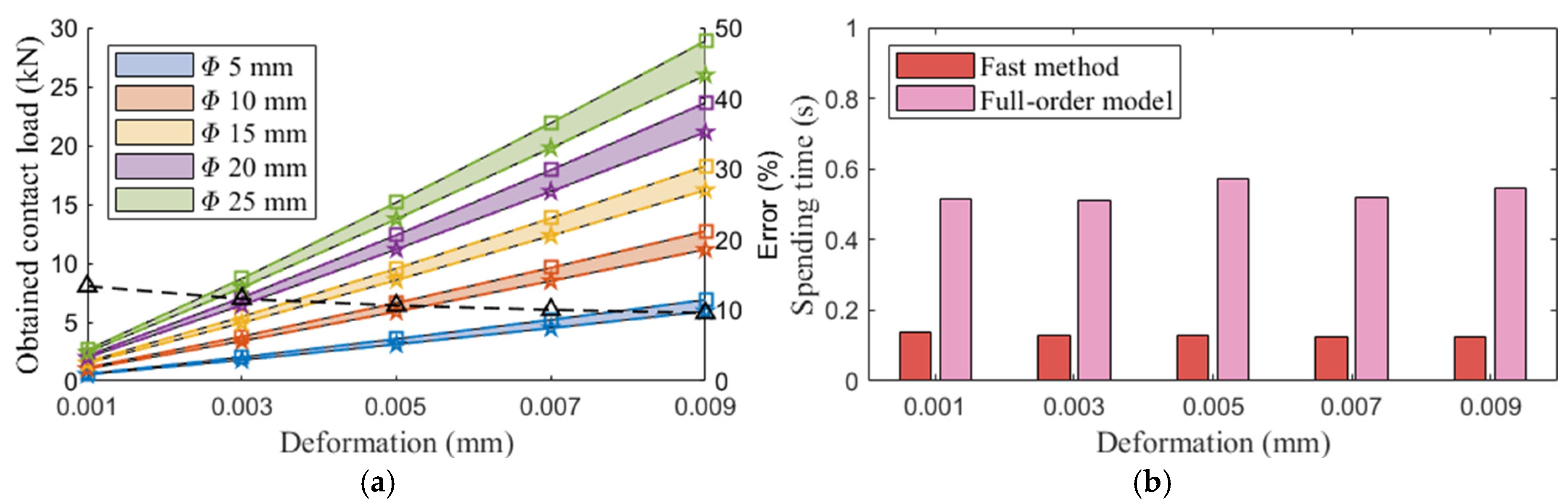
4. Fast Method for the Contact Load Calculation Model
5. Contact Load Calculation Under Lubricated Condition
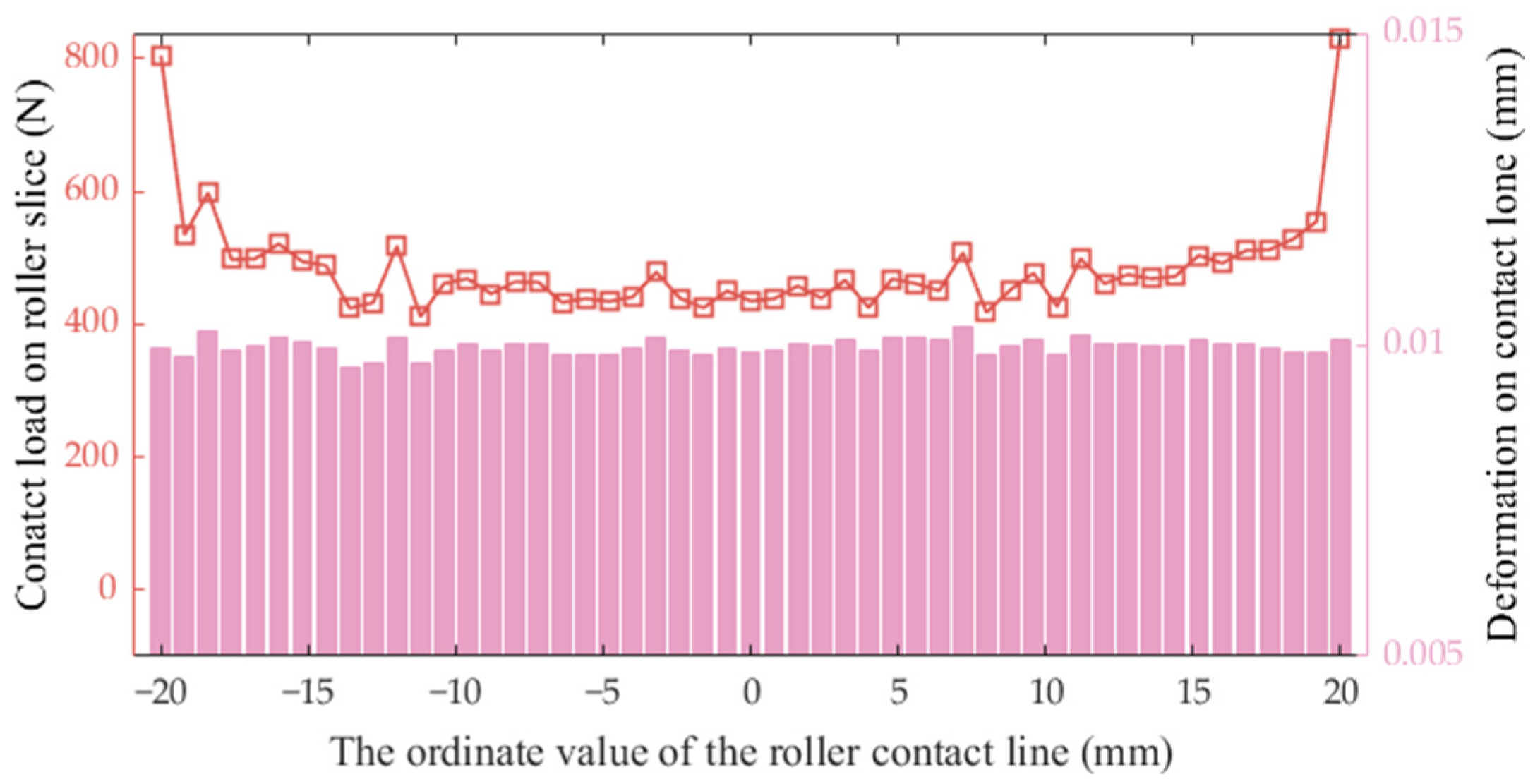
6. Comparison of the Proposed Model with Other Models
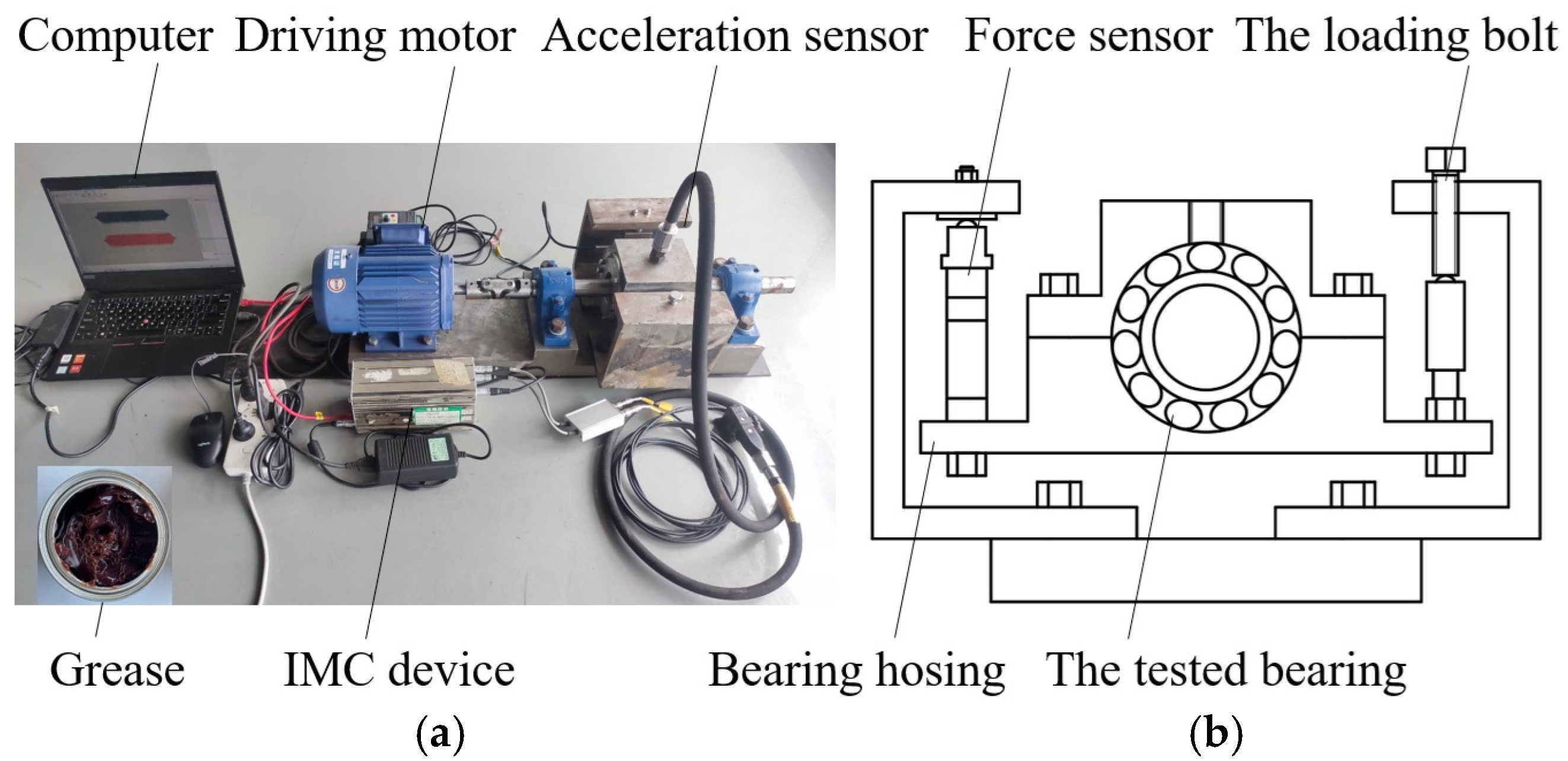
7. Dynamic Simulation and Experimental Validation
8. Conclusions
- (1)
- An algorithm for calculating contact load of finite line contact roller based on the half-space theory was developed, in which the iterative procedure was used to determine the contact half-width of each roller slice, and the influence coefficient matrix was constructed to solve for the contact load of each roller slice.
- (2)
- A fast algorithm for calculating rolling contact load was developed, and the disparity in contact load calculation results between the full half-space theory and the fast method were compared. The results indicated that the errors of the fast method relative to the full-order model decreased with increasing the contact load applied on the roller, and the fast method reduced the calculation time by approximately 77% compared to the iterative procedure.
- (3)
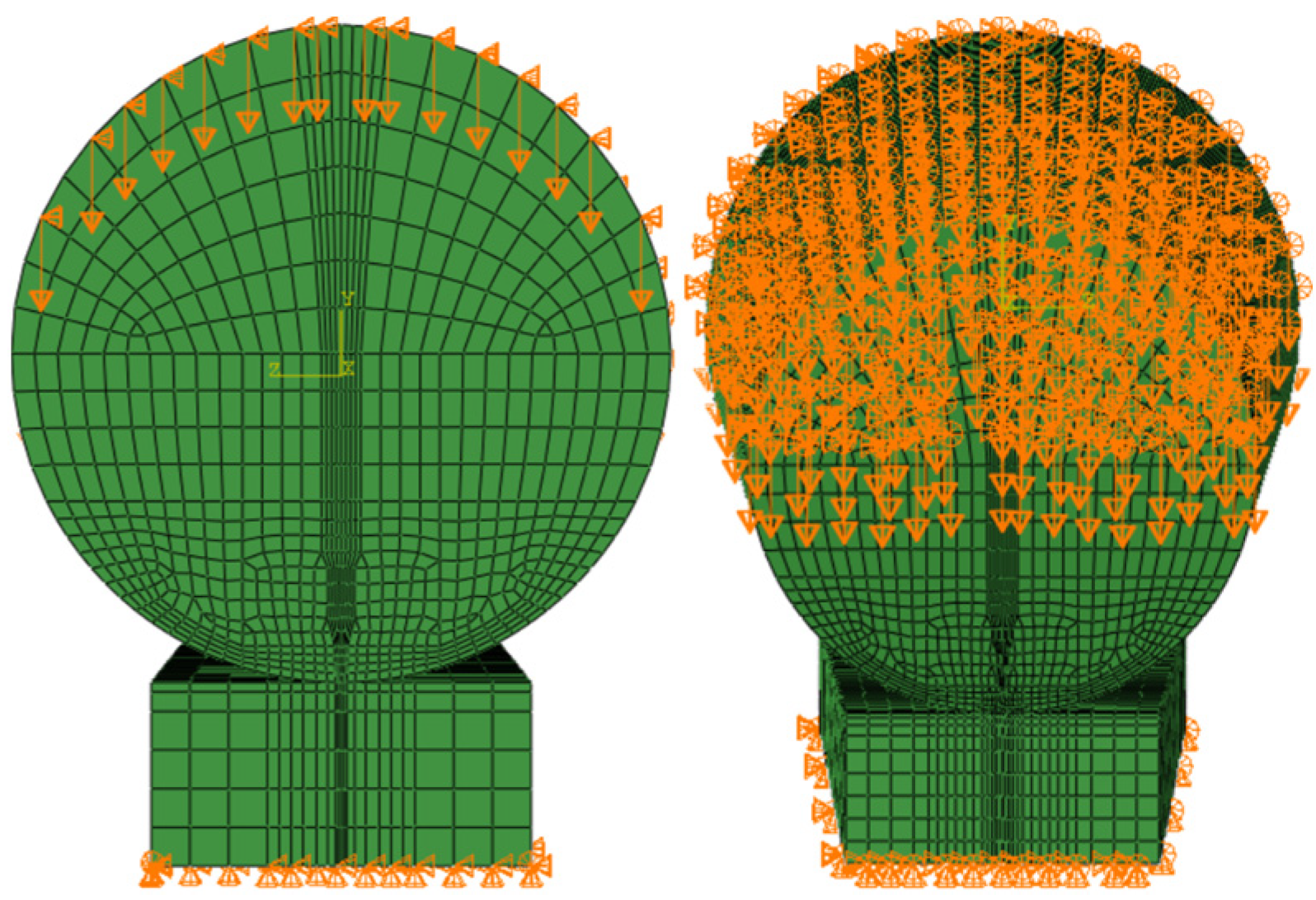
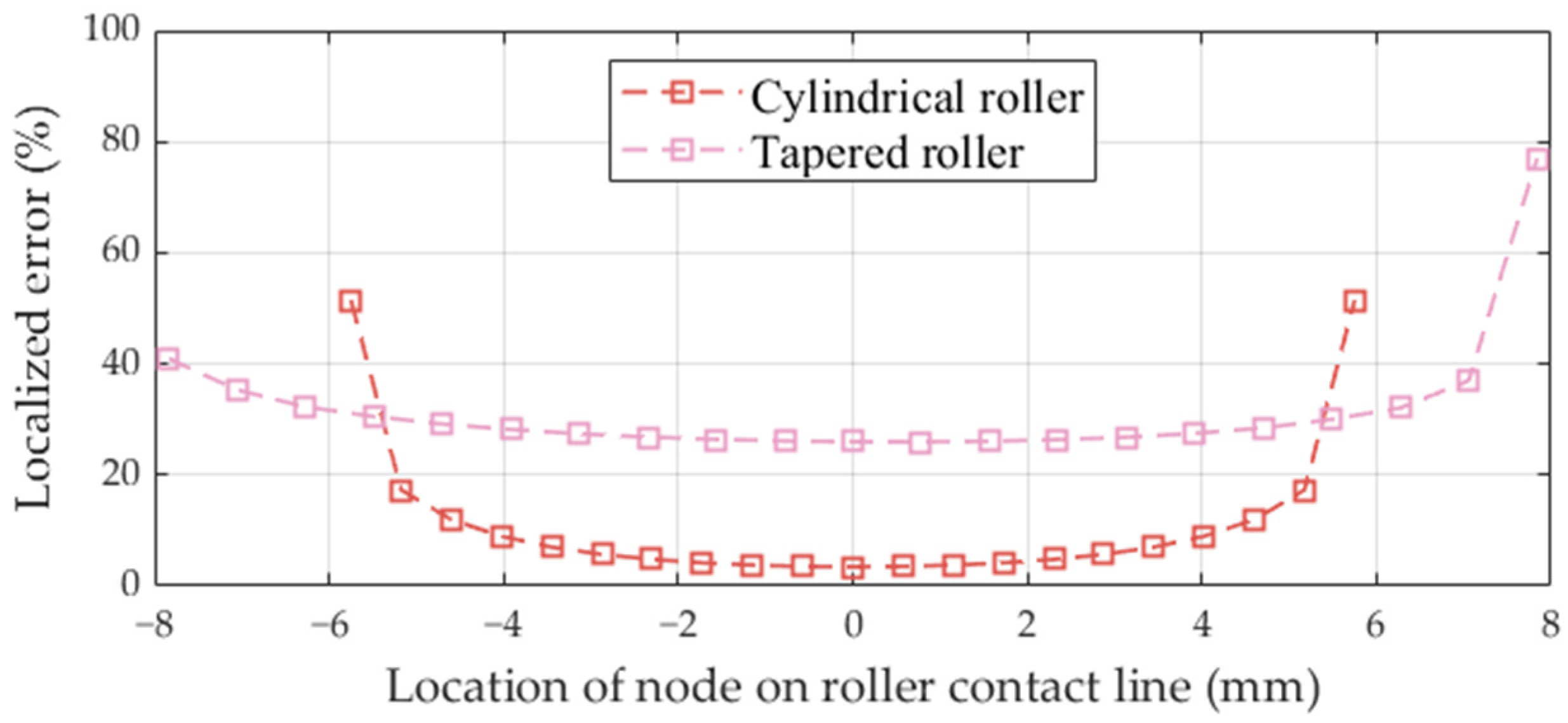
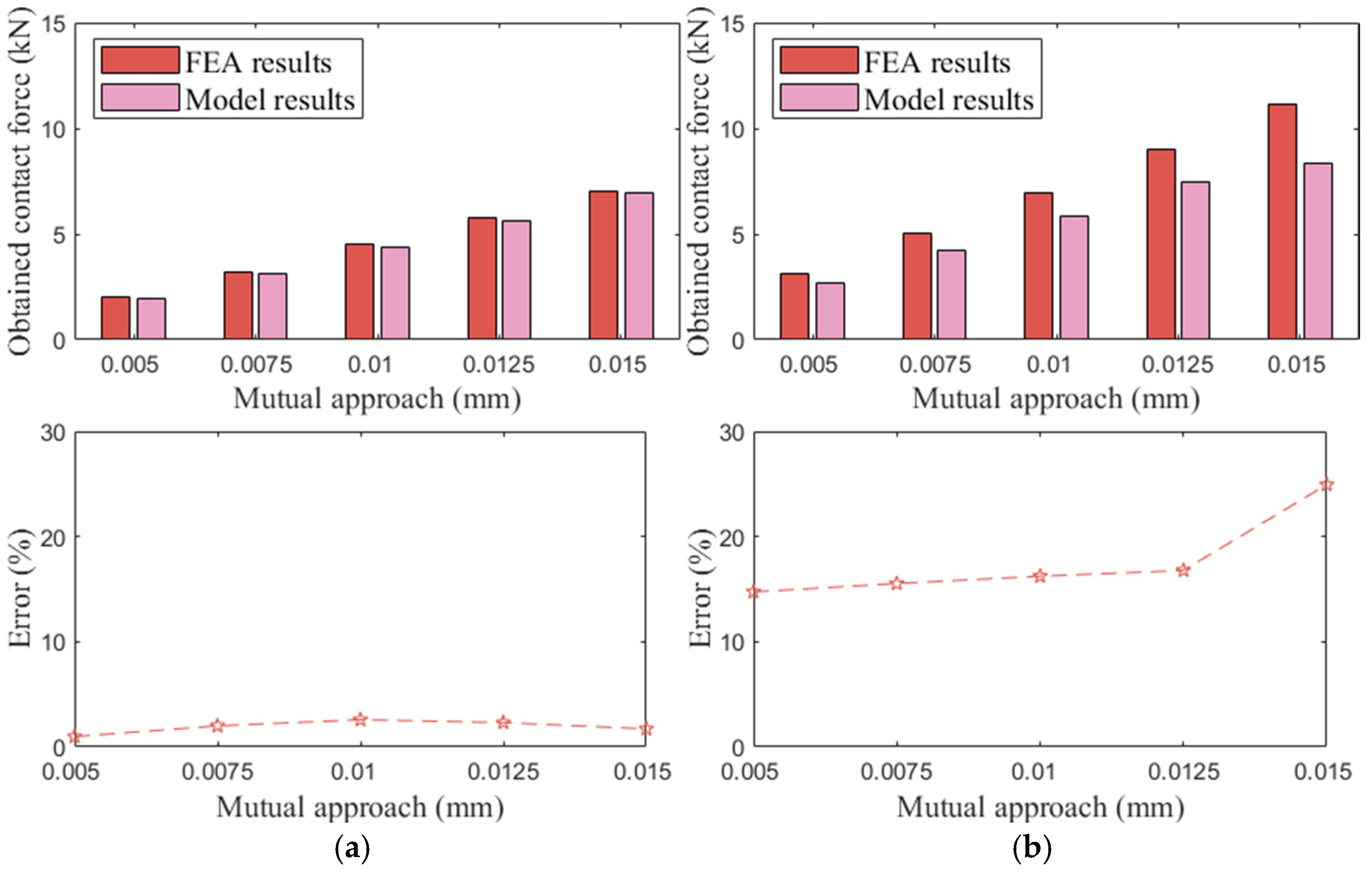
- A cylindrical roller and a tapered roller were utilized to compare stresses and contact loads obtained by the proposed model and FEA. The stress calculation results indicated that the localized errors of the stress near the ends of the rollers were much greater than those near the middle region, and the errors for the tapered roller were more significant compared with those for the cylindrical roller. Nevertheless, the differences between the contact loads obtained by the proposed model and FEA for the cylindrical roller were smaller than those for the tapered roller.
- (4)
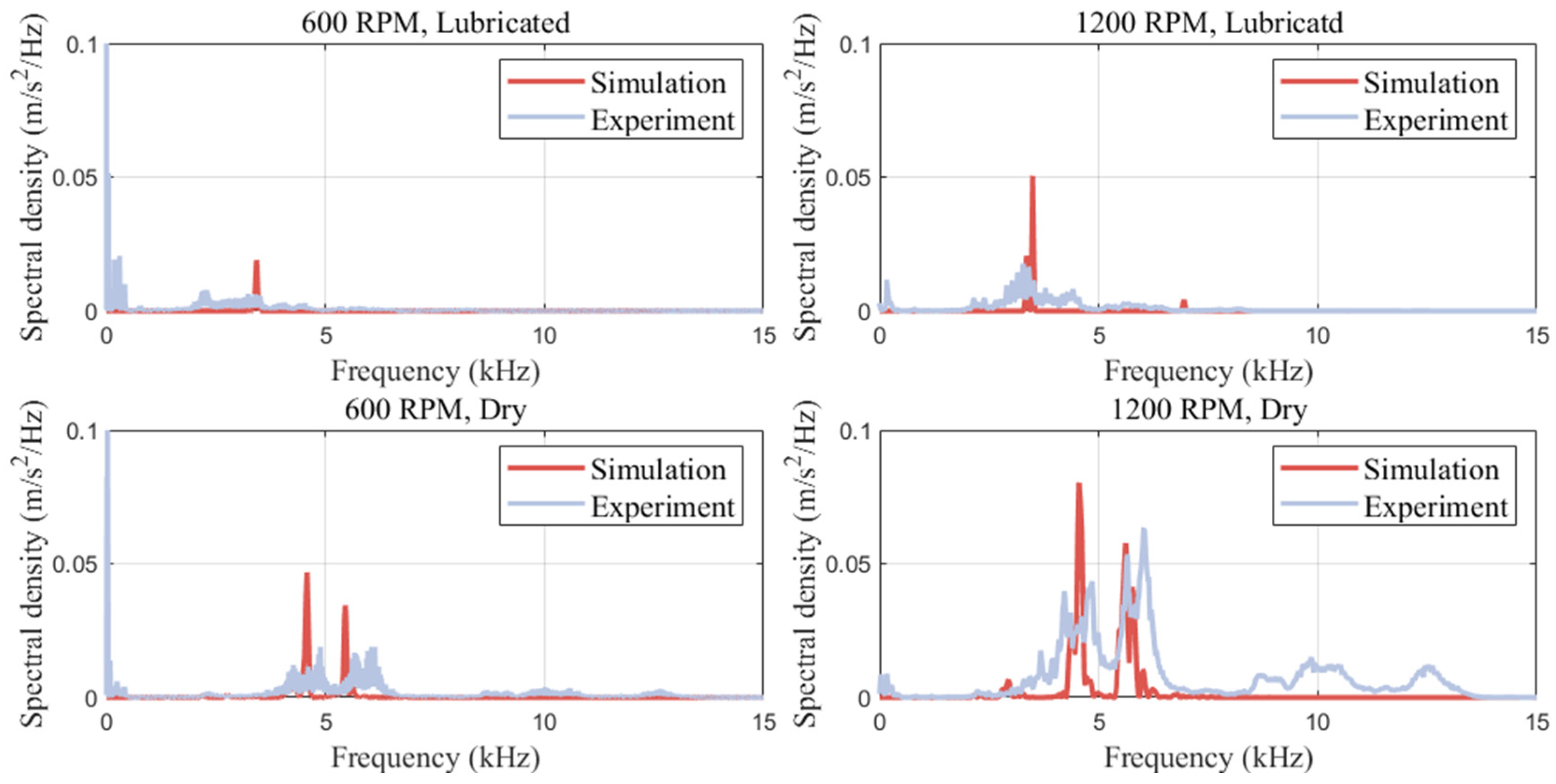
- Dynamic simulations and experiments were conducted to verify applicability of the proposed model, and the results indicated that the contact stiffness between the roller and raceway predicted by the proposed model was higher under the dry contact conditions than that under the lubricated conditions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moazen Ahmadi, A.; Petersen, D.; Howard, C. A nonlinear dynamic vibration model of defective bearings—The importance of modelling the finite size of rolling elements. Mech. Syst. Signal Process. 2015, 52–53, 309–326. [Google Scholar] [CrossRef]
- Yan, P.; Yan, C.; Wang, K.; Wang, F.; Wu, L. 5-DOF Dynamic Modeling of Rolling Bearing with Local Defect considering Comprehensive Stiffness under Isothermal Elastohydrodynamic Lubrication. Shock Vib. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Zhang, F.; Zhang, J.; Lee, S. Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis. J. Sound Vib. 2016, 364, 67–76. [Google Scholar] [CrossRef]
- Petersen, D.; Howard, C.; Prime, Z. Varying stiffness and load distributions in defective ball bearings: Analytical formulation and application to defect size estimation. J. Sound Vib. 2015, 337, 284–300. [Google Scholar] [CrossRef]
- Kabus, S.; Hansen, M.R.; Mouritsen, O. A new quasi-static cylindrical roller bearing model to accurately consider non-hertzian contact pressure in time domain simulations. J. Tribol. 2012, 134, 041401. [Google Scholar] [CrossRef]
- Wang, J.; Cui, L.; Xu, Y. Quantitative and localization fault diagnosis method of rolling bearing based on quantitative mapping model. Entropy 2018, 20, 510. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Fang, B.; Hong, J.; Zhu, Y. Effect of preload on ball-raceway contact state and fatigue life of angular contact ball bearing. Tribol. Int. 2017, 114, 365–372. [Google Scholar] [CrossRef]
- Li, X.; Yu, K.; Ma, H.; Cao, L.; Luo, Z.; Li, H.; Che, L. Analysis of varying contact angles and load distributions in defective angular contact ball bearing. Eng. Fail. Anal. 2018, 91, 449–464. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, J. An improved planar dynamic model for vibration analysis of a cylindrical roller bearing. Mech. Mach. Theory 2020, 153, 103994. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, W.; Luo, J.; Wang, W. An improved dynamic model of defective bearings considering the three-dimensional geometric relationship between the rolling element and defect area. Mech. Syst. Signal Process. 2019, 129, 694–716. [Google Scholar] [CrossRef]
- Andreason, S. Load distribution in a taper roller bearing arrangement. Tribology 1973, 6, 84–92. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Cavalca, K.L. Stiffness and damping of elastohydrodynamic line contact applied to cylindrical roller bearing dynamic model. J. Sound Vib. 2020, 481, 115444. [Google Scholar] [CrossRef]
- Liu, C.S.; Zhang, K.; Yang, R. The FEM analysis and approximate model for cylindrical joints with clearances. Mech. Mach. Theory 2007, 42, 183–197. [Google Scholar] [CrossRef]
- Gudehus, G. Sliding friction, Physical Principles and Applications by Bo N. J. Persson, Springer, Berlin, 1998. Mech. Cohesive-Frict. Mater. 1998, 3, 365. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Pereira, C.M.; Ramalho, A.L.; Ambrósio, J.A. A critical overview of internal and external cylinder contact force models. Nonlinear Dyn. 2011, 63, 681–697. [Google Scholar] [CrossRef]
- Dubowsky, S.; Freudenstein, F. Dynamic Analysis of Mechanical Systems with Clearances—Part 2: Dynamic Response. J. Eng. Ind. 1971, 93, 310–316. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A Contact Force Model with Hysteresis Damping for Impact Analysis of Multibody Systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Pereira, C.; Ramalho, A.; Ambrosio, J. An enhanced cylindrical contact force model. Multibody Syst. Dyn. 2015, 35, 277–298. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Xia, M. A dynamic model for the planetary bearings in a double planetary gear set. Mech. Syst. Signal Process. 2023, 194, 110257. [Google Scholar] [CrossRef]
- Liu, J.; Tang, C.; Shao, Y. An innovative dynamic model for vibration analysis of a flexible roller bearing. Mech. Mach. Theory 2019, 135, 27–39. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Wang, K.; Zhai, W. Non-uniform roller-race contact performance of bearings along width in the rotor-bearing system under dynamic loads. J. Sound Vib. 2022, 538, 117251. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z. A simulation investigation of lubricating characteristics for a cylindrical roller bearing of a high-power gearbox. Tribol. Int. 2022, 167, 107373. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Yin, Z.; Cheng, Y.; Huang, G.; Zou, H. Effect of vehicle vibration environment of high-speed train on dynamic performance of axle box bearing. Veh. Syst. Dyn. 2019, 57, 543–563. [Google Scholar] [CrossRef]
- Niu, L.; Cao, H.; Hou, H.; Wu, B.; Lan, Y.; Xiong, X. Experimental observations and dynamic modeling of vibration characteristics of a cylindrical roller bearing with roller defects. Mech. Syst. Signal Process. 2020, 138, 106553. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L. Dynamic modelling of combination imperfects of a cylindrical roller bearing. Eng. Fail. Anal. 2022, 135, 106102. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Shi, Z. Dynamic modelling of the defect extension and appearance in a cylindrical roller bearing. Mech. Syst. Signal Process. 2022, 173, 109040. [Google Scholar] [CrossRef]
- Zhang, F.; Lv, H.; Han, Q.; Li, M. The Effects Analysis of Contact Stiffness of Double-Row Tapered Roller Bearing under Composite Loads. Sensors 2023, 23, 4967. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, G.; He, C.; Rao, M.; Tu, W. A new instantaneous contact based dynamic model of rolling element bearings with local defects. Mech. Syst. Signal Process. 2023, 200, 110600. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, C.; Jin, Y.; Wang, J. Nonlinear vibration characteristics of a rotor bearing system with irregular raceway defect. Nonlinear Dyn. 2024, 113, 11259–11281. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; He, D.; Tian, D. Nonlinear Dynamic Characteristics of Rolling Bearings with Multiple Defects. J. Vib. Eng. Technol. 2023, 11, 4303–4321. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, S.; Chen, X.; Wang, Z. Lubrication and loading characteristics of cylindrical roller bearings with misalignment and roller modifications. Tribol. Int. 2022, 165, 107291. [Google Scholar] [CrossRef]
- Cui, L.; He, Y. A new logarithmic profile model and optimization design of cylindrical roller bearing. Ind. Lubr. Tribol. 2015, 67, 498–508. [Google Scholar] [CrossRef]
- Zheng, Z.; Song, D.; Zhang, W.; Xu, X.; Ma, C.; Cui, W. Dynamic response analysis of high-speed train axle box bearing by considering time-varying dynamic parameters. Mech. Syst. Signal Process. 2025, 224, 112119. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Zhai, W.; Lei, Y. Investigation on skidding behavior of a lubricated rolling bearing with fluid–solid-heat coupling effect. Mech. Syst. Signal Process. 2024, 206, 110922. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, J.; Xiao, G. Analysis of cage slip and impact force in a cylindrical roller bearing with race defects. Tribol. Int. 2023, 180, 108208. [Google Scholar] [CrossRef]
- Meymand, S.Z.; Keylin, A.; Ahmadian, M. A survey of wheel-rail contact models for rail vehicles. Veh. Syst. Dyn. 2016, 54, 386–428. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Hou, Y. A Fast Calculation Approach for Elastohydrodynamic Finite Line Contacts Applicable to Online Calculations of Rolling Bearing Models. J. Tribol. 2024, 146, 1–14. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Wang, M.; Wen, B. Dynamic Modeling and Behavior of Cylindrical Roller Bearings Considering Roller Skew and the Influence of Eccentric Load. Lubricants 2024, 12, 317. [Google Scholar] [CrossRef]






| Cylincal Roller | Tapered Roller | |
|---|---|---|
| Length of roller | 11.5 mm | 15.5 mm |
| Diameter of roller at the small end | 8.5 mm | 6.68 mm |
| Diameter of roller at the big end | 8.5 mm | 10.85 mm |
| Cone angle of roller | 0° | 7.64° |
| Parameter | Value |
|---|---|
| Elasticity modulus of materials | 206 GPa |
| Poisson’s ratio of materials | 0.3 |
| Length of roller | 15.68 mm |
| Diameter of roller at the small end | 6.68 mm |
| Diameter of roller at the big end | 10.85 mm |
| Diameter of outer ring at the small end | 70.0 mm |
| Diameter of outer ring at the big end | 82.0 mm |
| Diameter of inner ring at the small end | 56.66 mm |
| Diameter of inner ring at the big end | 60.90 mm |
| Cone angle of outer ring | 22.3° |
| Cone angle of inner ring | 7° |
| Viscosity | 0.1 Pa·s |
| Number of nodes | 31 (M) × 51 (N) |
| Surface roughness | 0.001 mm |
| x | y | z | ϕ | β | ψ | |
|---|---|---|---|---|---|---|
| Inner ring | xi | yi | zi | ϕi | βi | ψi |
| Outer ring | xo | yo | zo | ϕo | βo | ψo |
| Roller | ----- | yr | zr | ϕr | βr | ----- |
| Cage | ----- | ----- | ----- | ----- | βc | ----- |
| No. | Contact Condition | Rotational Speed | Applied Load |
|---|---|---|---|
| 1 | Lubricated | 600 RPM | 1000 N |
| 2 | Lubricated | 1200 RPM | 1000 N |
| 3 | Dry | 600 RPM | 1000 N |
| 4 | Dry | 1200 RPM | 1000 N |
| No. | Condition | Speed (RPM) | Simulation (m/s2) | Epxeriment (m/s2) | Error (%) |
|---|---|---|---|---|---|
| 1 | Lubricated | 600 | 2.442 | 1.767 | 38.2 |
| 2 | Lubricated | 1200 | 5.681 | 4.057 | 40.0 |
| 3 | Dry | 600 | 3.447 | 2.734 | 26.1 |
| 4 | Dry | 1200 | 10.121 | 10.714 | 5.5 |
| No. | Condition | Speed (RPM) | Simulation (Hz) | Epxeriment (Hz) | Error (%) |
|---|---|---|---|---|---|
| 1 | Lubricated | 600 | 3450 | 3075 | 12.2 |
| 2 | Lubricated | 1200 | 3662 | 3756 | 2.3 |
| 3 | Dry | 600 | 4843 | 5948 | 18.6 |
| 4 | Dry | 1200 | 5061 | 6792 | 25.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; He, L.; Luo, Y.; Tan, A.C.; Yi, C. Contact Load Calculation Models for Finite Line Contact Rollers in Bearing Dynamic Simulation Under Dry and Lubricated Conditions. Lubricants 2025, 13, 183. https://doi.org/10.3390/lubricants13040183
Hu Y, He L, Luo Y, Tan AC, Yi C. Contact Load Calculation Models for Finite Line Contact Rollers in Bearing Dynamic Simulation Under Dry and Lubricated Conditions. Lubricants. 2025; 13(4):183. https://doi.org/10.3390/lubricants13040183
Chicago/Turabian StyleHu, Yongxu, Liu He, Yan Luo, Andy Chit Tan, and Cai Yi. 2025. "Contact Load Calculation Models for Finite Line Contact Rollers in Bearing Dynamic Simulation Under Dry and Lubricated Conditions" Lubricants 13, no. 4: 183. https://doi.org/10.3390/lubricants13040183
APA StyleHu, Y., He, L., Luo, Y., Tan, A. C., & Yi, C. (2025). Contact Load Calculation Models for Finite Line Contact Rollers in Bearing Dynamic Simulation Under Dry and Lubricated Conditions. Lubricants, 13(4), 183. https://doi.org/10.3390/lubricants13040183





