Pin-on-Disc Experimental Study of Thermomechanical Processes Related to Squeal Occurrence
Abstract
1. Introduction
2. Experimental Tests
2.1. Materials
2.2. Experimental Setup
2.3. Instrumentation and Measurements
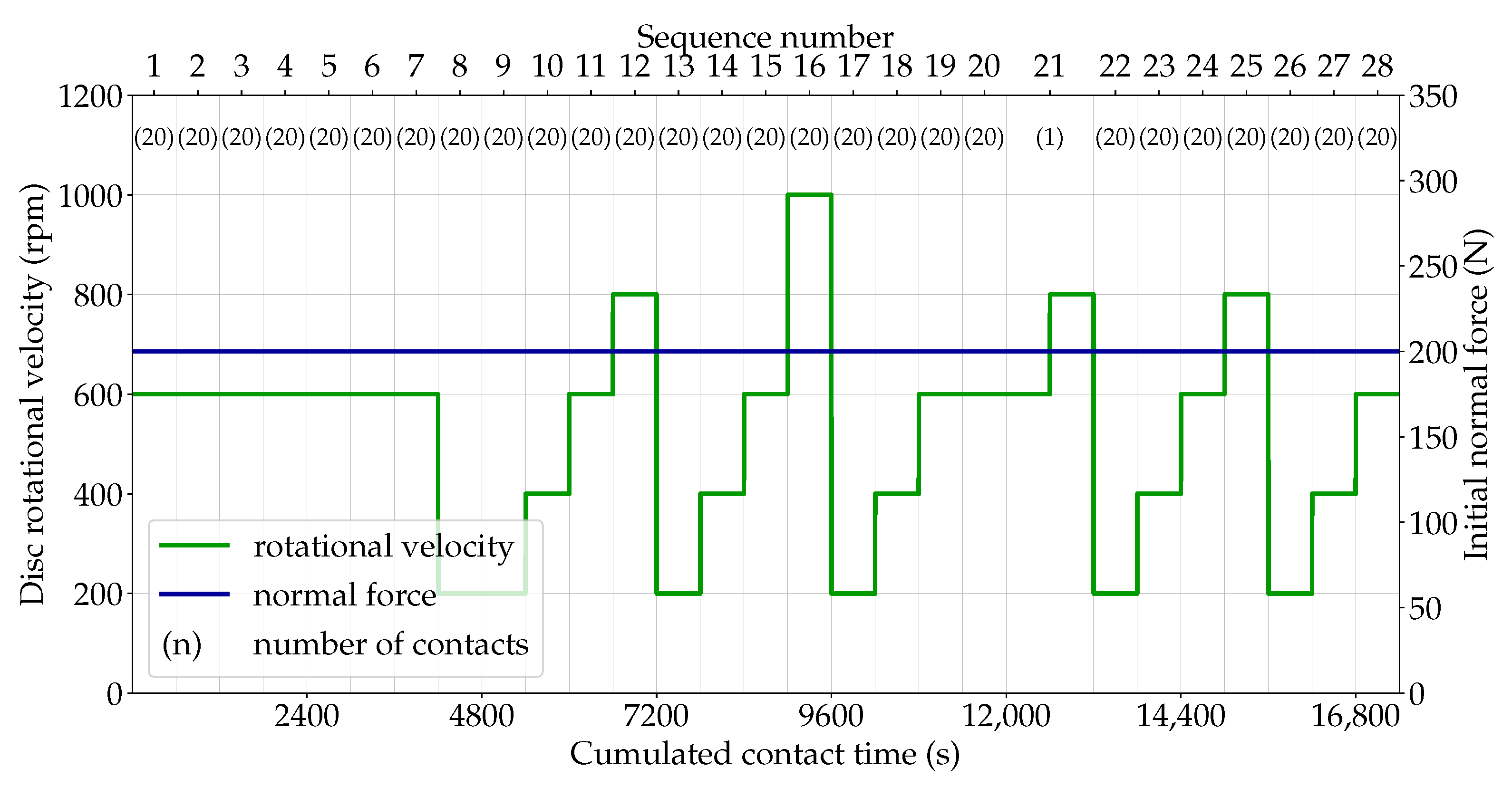
2.4. Test Campaign
3. Global Results Analysis
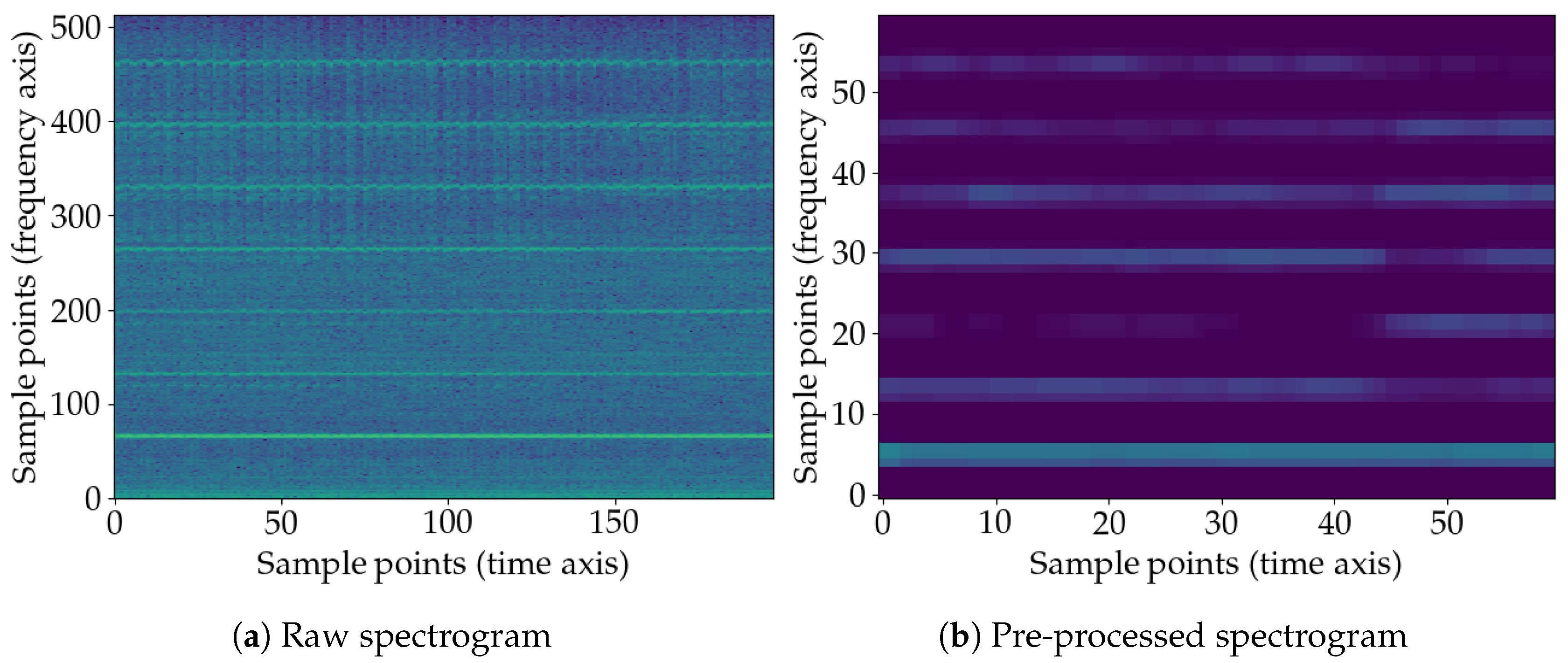
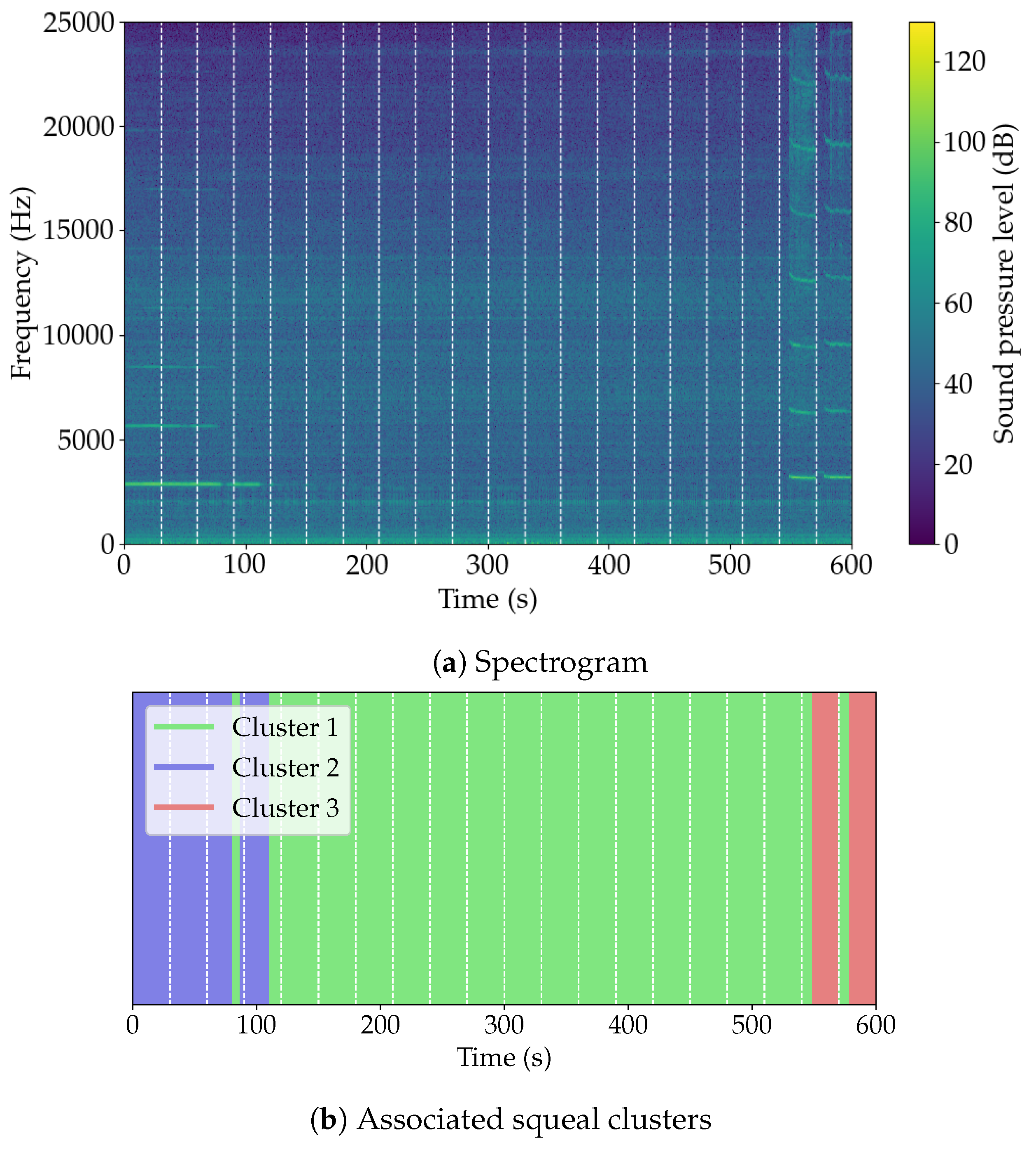
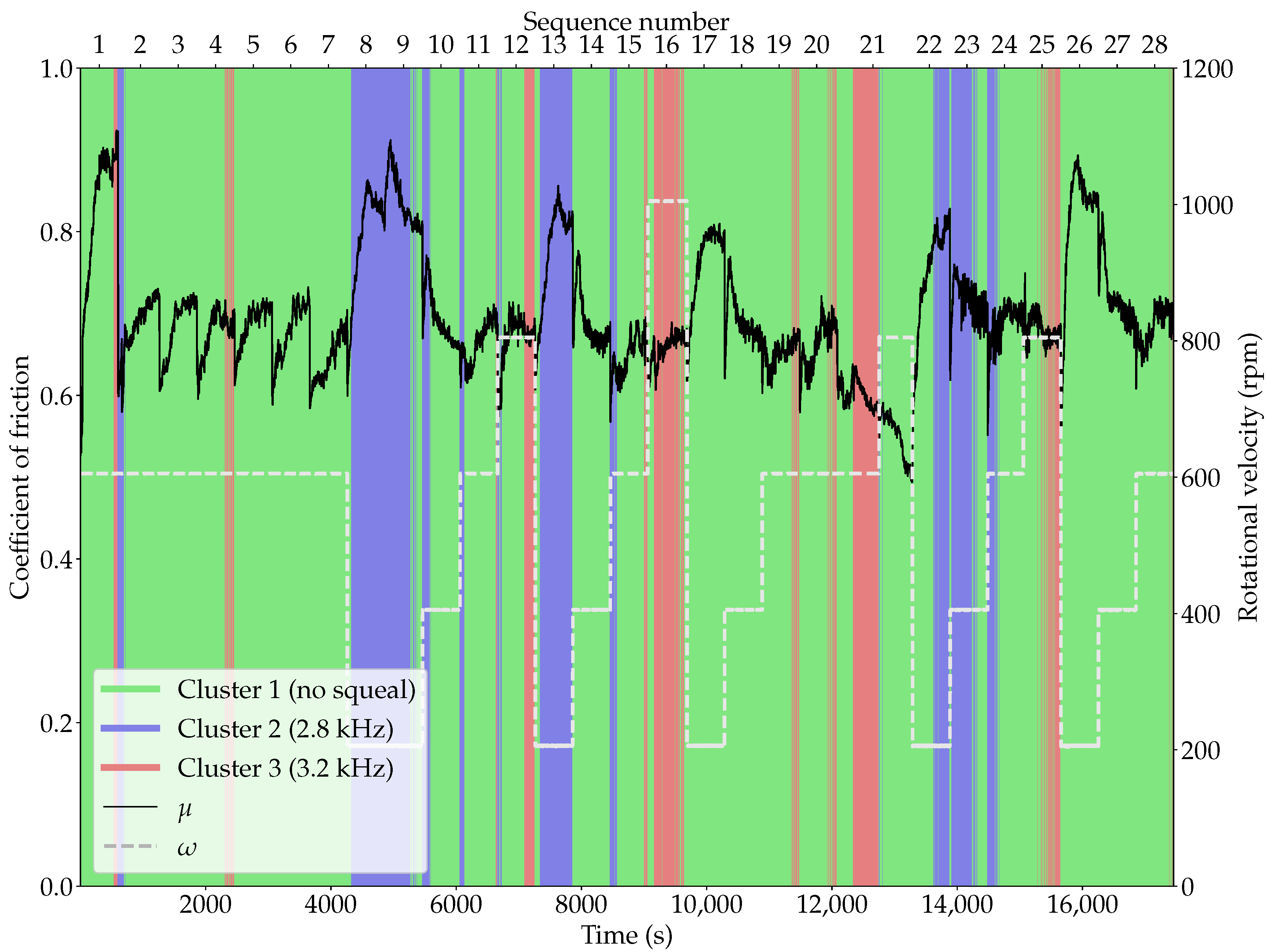
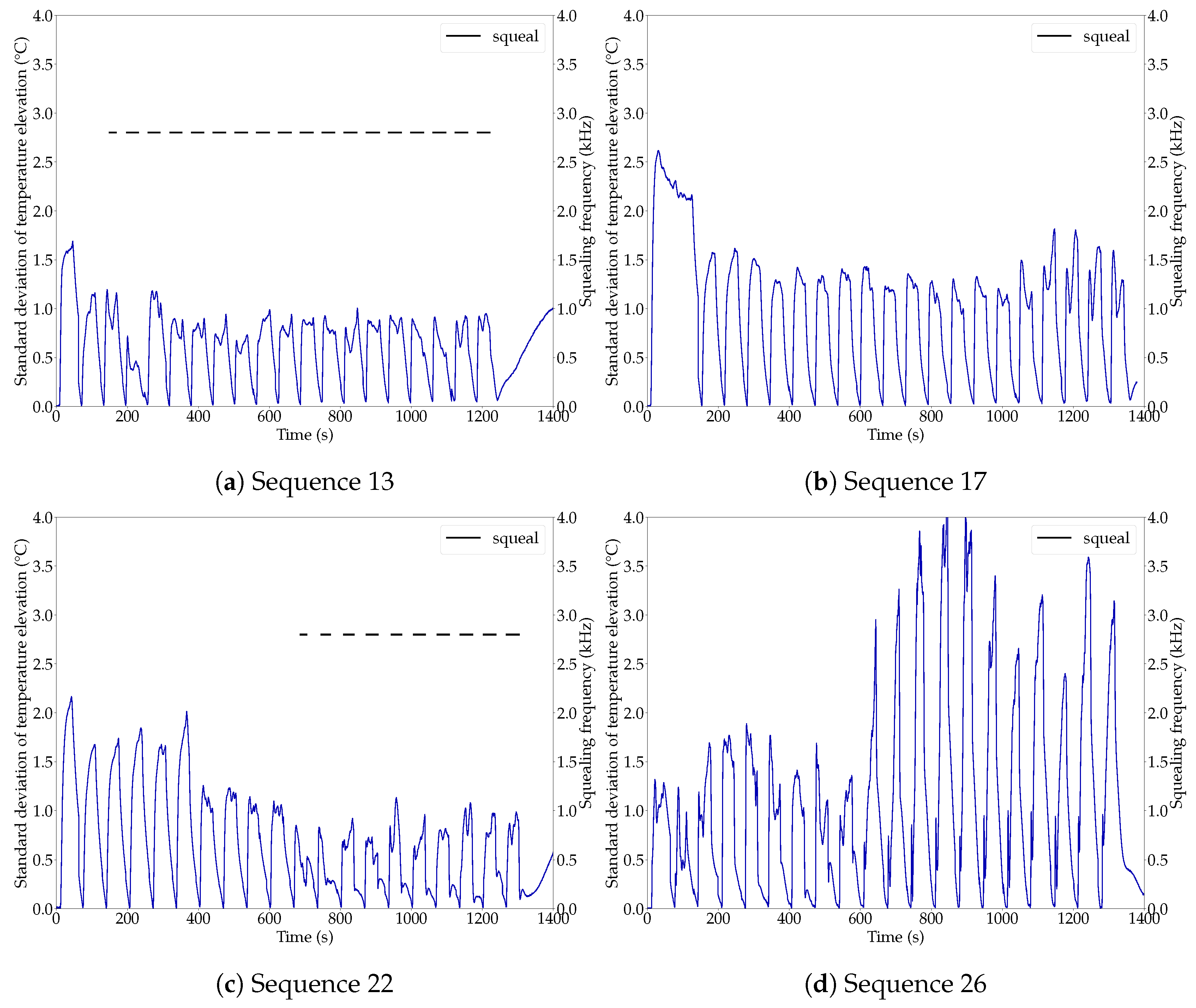
3.1. Analysis of Squeal Events
3.2. Relation Between Squeal and Loading
3.3. Relation Between Squeal and Friction
3.4. Relation Between Squeal and Temperature
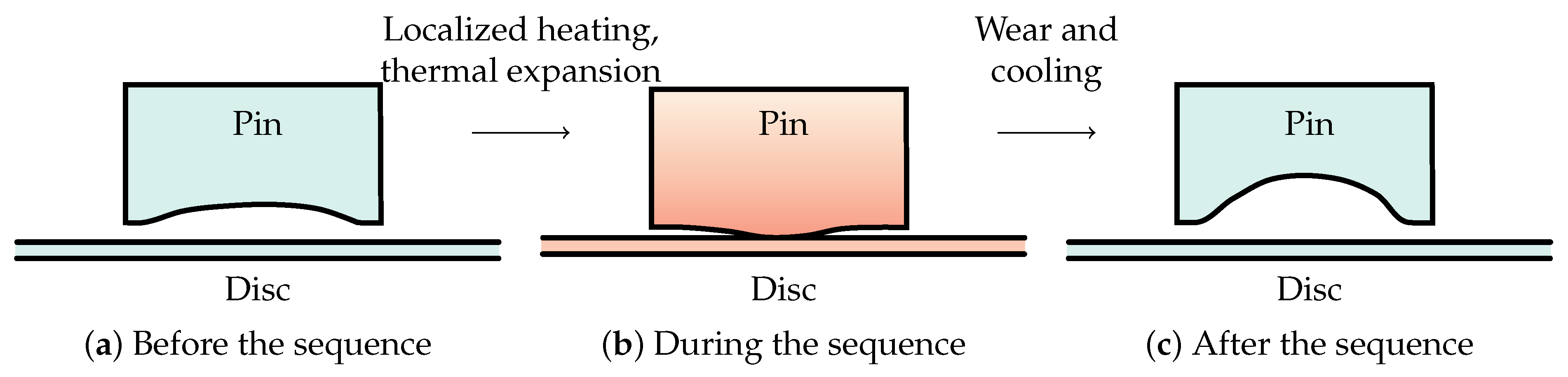
3.5. Surface Evolution
3.6. Postmortem Surface Analysis
4. Focus on Squeal at Low Temperature
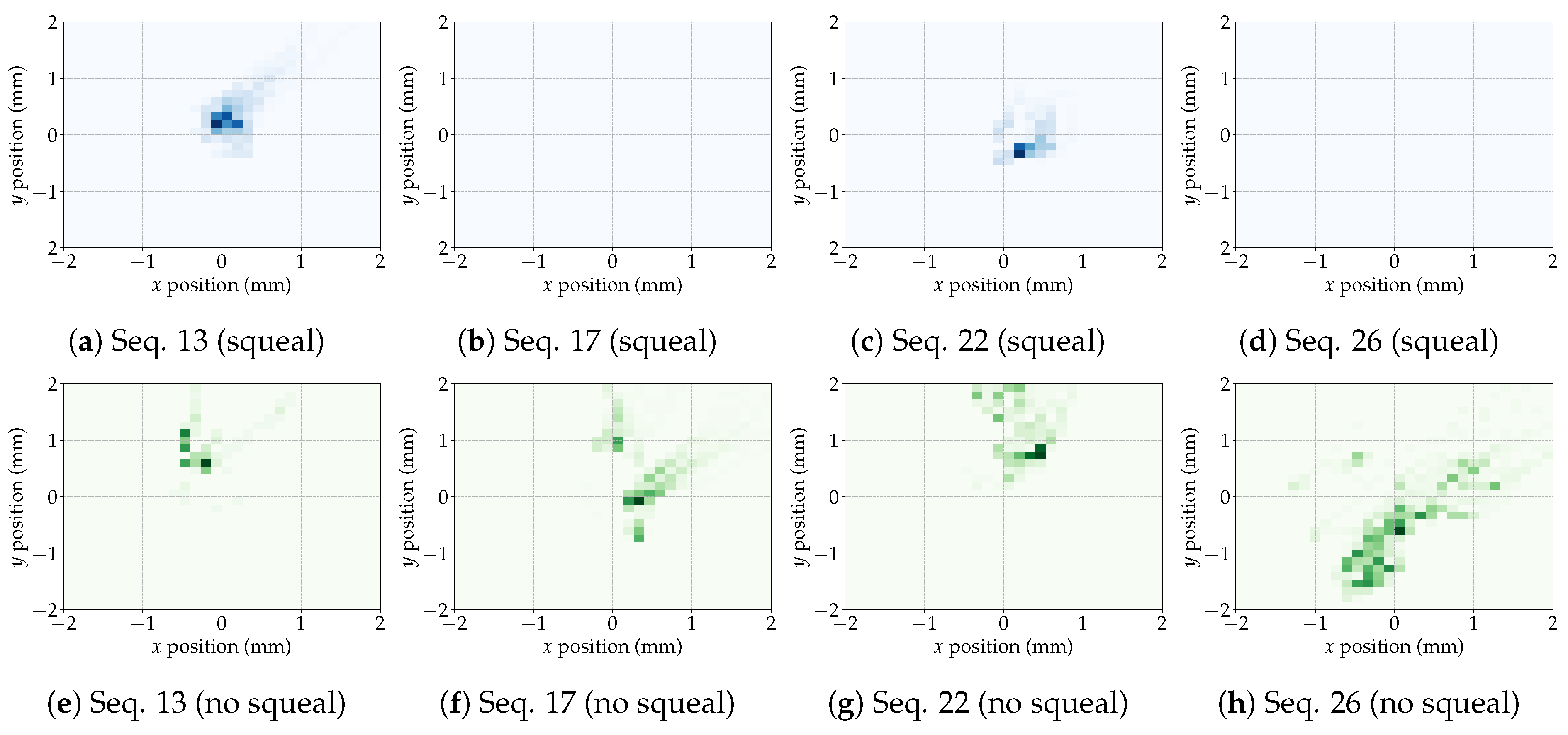
4.1. Detailed Surface Analysis
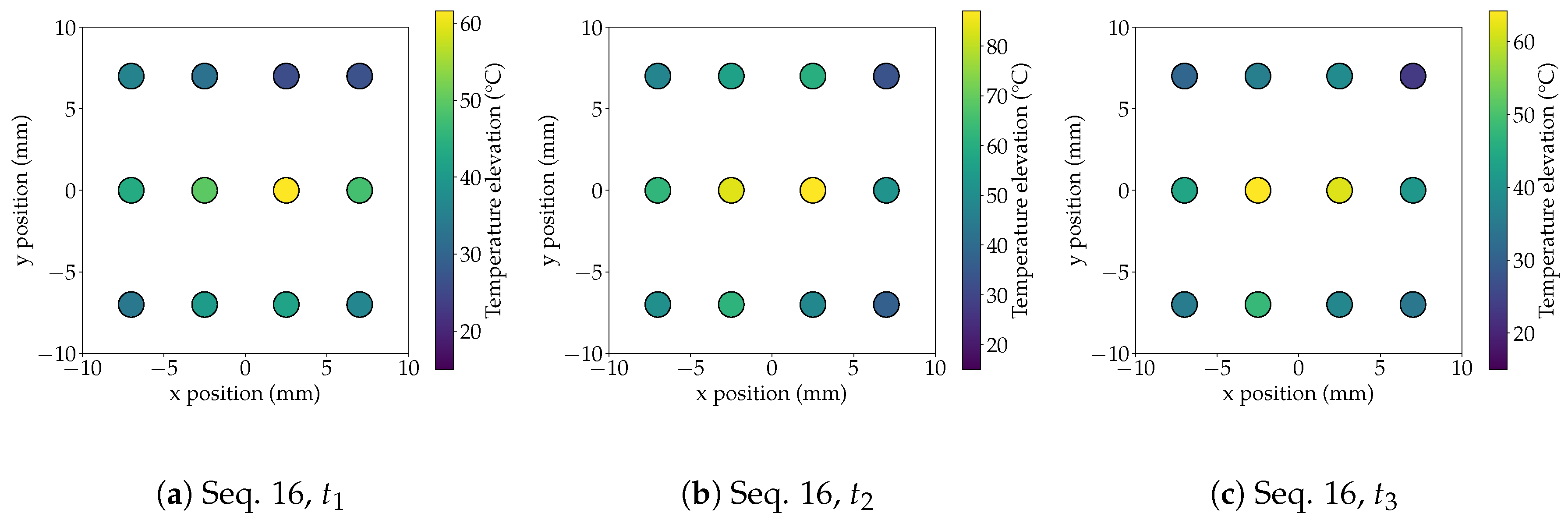
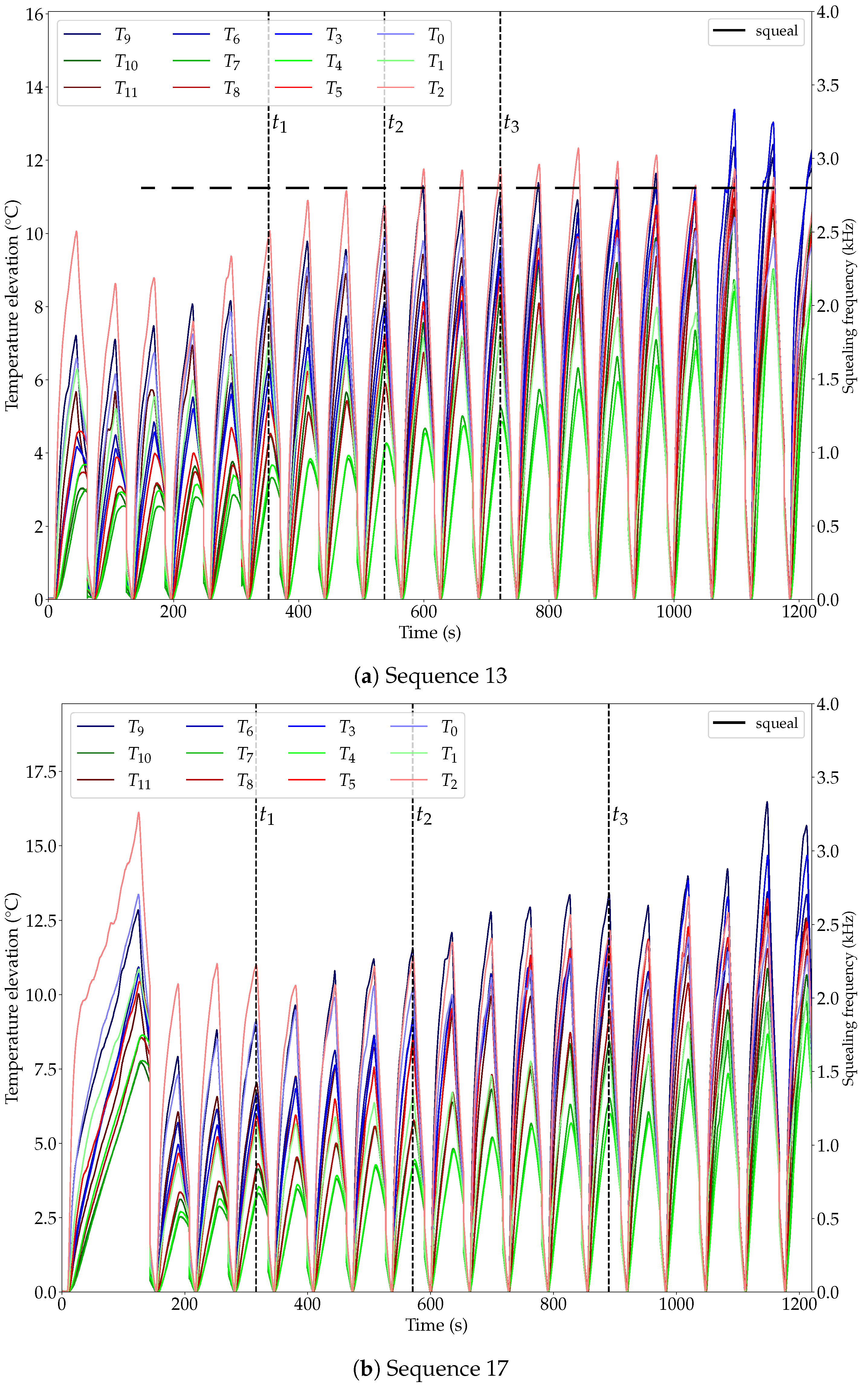
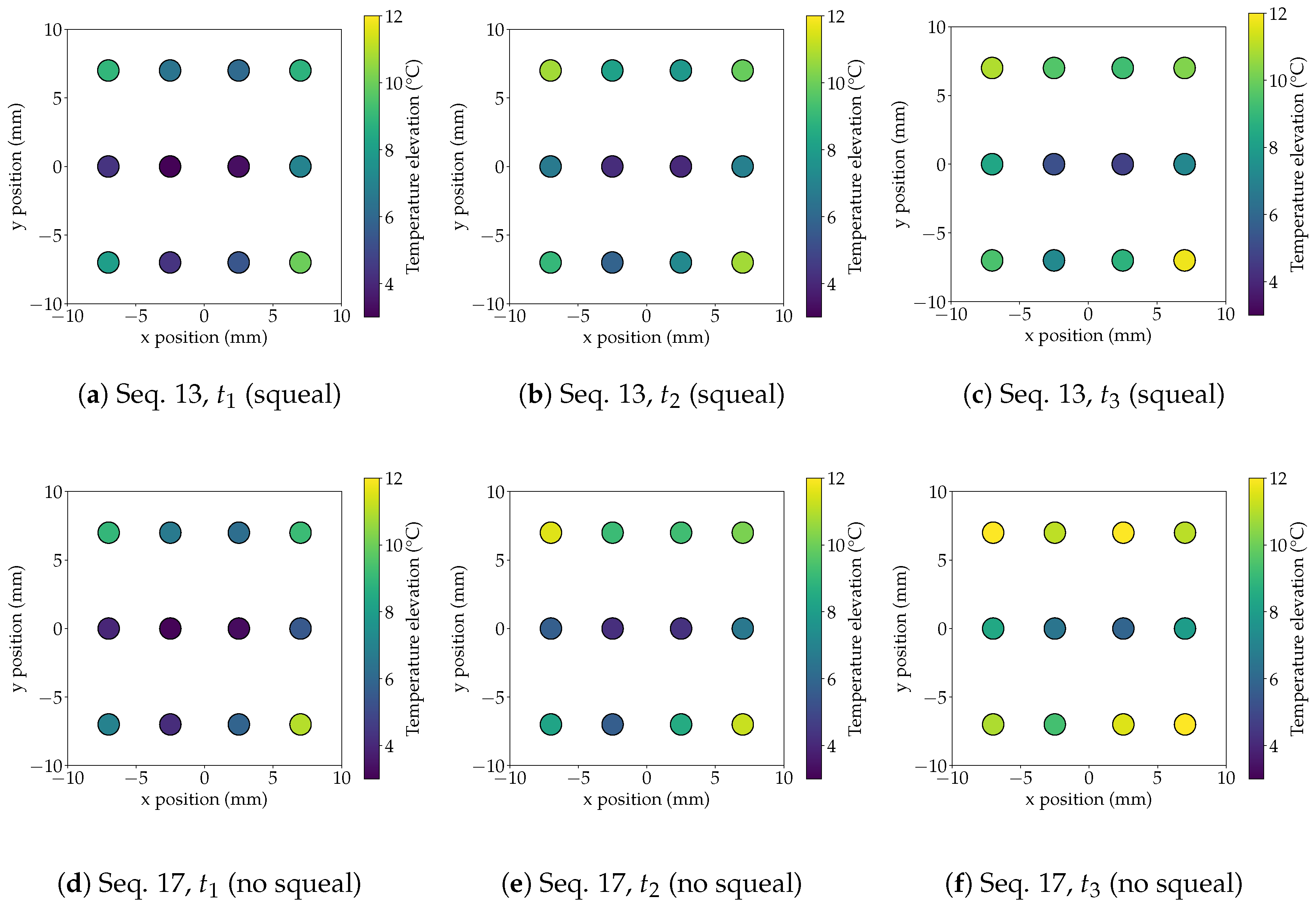
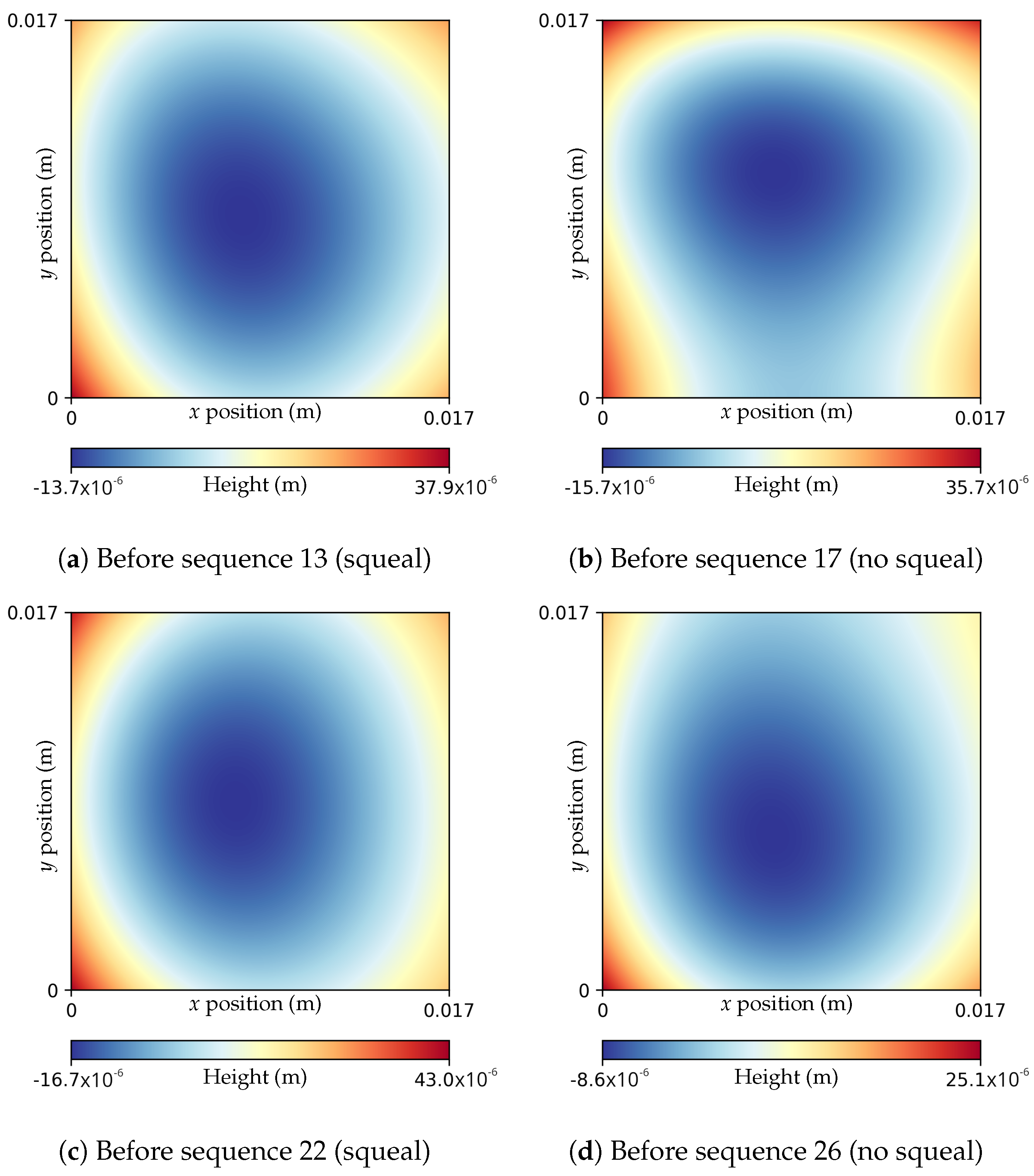
4.2. Evolution of Local Temperature Elevation
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oesterle, W.; Doerfel, I.; Prietzel, C.; Rooch, H.; Cristol-Bulthe, A.L.; Degallaix, G.; Desplanques, Y. A comprehensive microscopic study of third body formation at the interface between a brake pad and brake disc during the final stage of a pin-on-disc test. Wear 2009, 267, 781–788. [Google Scholar] [CrossRef]
- Candeo, S.; Leonardi, M.; Gialanella, S.; Straffelini, S. Influence of contact pressure and velocity on the brake behaviour and particulate matter emissions. Wear 2023, 514, 204579. [Google Scholar] [CrossRef]
- Kinkaid, N.; O’Reilly, O.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- Akay, A. Acoustics of friction. J. Acoust. Soc. Am. 2002, 111, 1525–1548. [Google Scholar] [CrossRef]
- Hoffmann, N.; Fischer, M.; Allgaier, R.; Gaul, L. A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations. Mech. Res. Commun. 2002, 29, 197–205. [Google Scholar] [CrossRef]
- Sinou, J.J.; Jezequel, L. Mode coupling instability in friction-induced vibrations and its dependency on system parameters including damping. Eur. J. Mech. A-Solids 2007, 26, 106–122. [Google Scholar] [CrossRef]
- von Wagner, U.; Hochlenert, D.; Hagedorn, P. Minimal models for disk brake squeal. J. Sound Vib. 2007, 302, 527–539. [Google Scholar] [CrossRef]
- Stender, M.; Tiedemann, M.; Spieler, D.; Schoepflin, D.; Hoffmann, N.; Oberst, S. Deep learning for brake squeal: Brake noise detection, characterization and prediction. Mech. Syst. Signal Process. 2021, 149, 107181. [Google Scholar] [CrossRef]
- Eriksson, M.; Jacobson, S. Friction behaviour and squeal generation of disc brakes at low speeds. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2001, 215, 1245–1256. [Google Scholar] [CrossRef]
- Sinou, J.J.; Lenoir, D.; Besset, S.; GilIot, F. Squeal analysis based on the laboratory experimental bench “Friction-Induced Vibration and noisE at Ecole Centrale de Lyon” (FIVE@ECL). Mech. Syst. Signal Process. 2019, 119, 561–588. [Google Scholar] [CrossRef]
- Bergman, F.; Eriksson, M.; Jacobson, S. The effect of reduced contact area on the occurrence of disc brake squeals for an automotive brake pad. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2000, 214, 561–568. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, Z.; Kapsa, P.; Vincent, L. Effect of surface topography on formation of squeal under reciprocating sliding. Wear 2002, 253, 411–423. [Google Scholar]
- Hetzler, H.; Willner, K. On the influence of contact tribology on brake squeal. Tribol. Int. 2012, 46, 237–246. [Google Scholar] [CrossRef]
- Kennedy, F.E.; Ling, F.F. A Thermal, Thermoelastic, and Wear Simulation of a High-Energy Sliding Contact Problem. J. Lubr. Technol. 1974, 96, 497–505. [Google Scholar] [CrossRef]
- Eriksson, M.; Bergman, F.; Jacobson, S. On the nature of tribological contact in automotive brakes. Wear 2002, 252, 26–36. [Google Scholar] [CrossRef]
- Massi, F.; Berthier, Y.; Baillet, L. Contact surface topography and system dynamics of brake squeal. Wear 2008, 265, 1784–1792. [Google Scholar] [CrossRef]
- Godet, M. The third-body approach: A mechanical view of wear. Wear 1984, 100, 437–452. [Google Scholar] [CrossRef]
- Berthier, Y. Maurice Godet’s Third Body. In The Third Body Concept Interpretation of Tribological Phenomena; Dowson, D., Taylor, C.M., Childs, T.H.C., Dalmaz, G., Berthier, Y., Flamand, L., Georges, J.M., Lubrecht, A.A., Eds.; Tribology Series; Elsevier: Amsterdam, The Netherlands, 1996; Volume 31, pp. 21–30. [Google Scholar]
- Wu, Y.K.; Tang, B.; Xiang, Z.Y.; Qian, H.H.; Mo, J.L.; Zhou, Z.R. Brake squeal of a high-speed train for different friction block configurations. Appl. Acoust. 2021, 171, 107540. [Google Scholar] [CrossRef]
- Ciprari, S.; Tonazzi, D.; Ripard, V.; Saulot, A.; Massi, F. Experimental investigation on brake squeal unpredictability: Role of the friction noise. Tribol. Int. 2024, 195, 109590. [Google Scholar] [CrossRef]
- Ouyang, H.; Nack, W.; Yuan, Y.; Chen, F. Numerical analysis of automotive disc brake squeal: A review. Int. J. Veh. Noise Vib. 2005, 1, 207–231. [Google Scholar] [CrossRef]
- Massi, F.; Baillet, L.; Giannini, O.; Sestieri, A. Brake squeal: Linear and nonlinear numerical approaches. Mech. Syst. Signal Process. 2007, 21, 2374–2393. [Google Scholar] [CrossRef]
- Sinou, J.J. Transient non-linear dynamic analysis of automotive disc brake squeal—On the need to consider both stability and non-linear analysis. Mech. Res. Commun. 2010, 37, 96–105. [Google Scholar] [CrossRef]
- Lai, V.V.; Paszkiewicz, I.; Brunel, J.F.; Dufrénoy, P. Multi-Scale Contact Localization and Dynamic Instability Related to Brake Squeal. Lubricants 2020, 8, 43. [Google Scholar] [CrossRef]
- Hubert, C.; El Attaoui, Y.; Leconte, N.; Massa, F. A coupled finite element-discrete element method for the modelling of brake squeal instabilities. Eur. J. Mech. A/Solids 2024, 108, 105427. [Google Scholar] [CrossRef]
- Lai, V.V.; Paszkiewicz, I.; Brunel, J.F.; Dufrénoy, P. Squeal occurrence related to the tracking of the bearing surfaces on a pin-on-disc system. Mech. Syst. Signal Process. 2022, 165, 108364. [Google Scholar] [CrossRef]
- Thévenot, M.; Brunel, J.F.; Brunel, F.; Bigerelle, M.; Stender, M.; Hoffmann, N.; Dufrénoy, P. In Situ Operando Indicator of Dry Friction Squeal. Lubricants 2024, 12, 435. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]



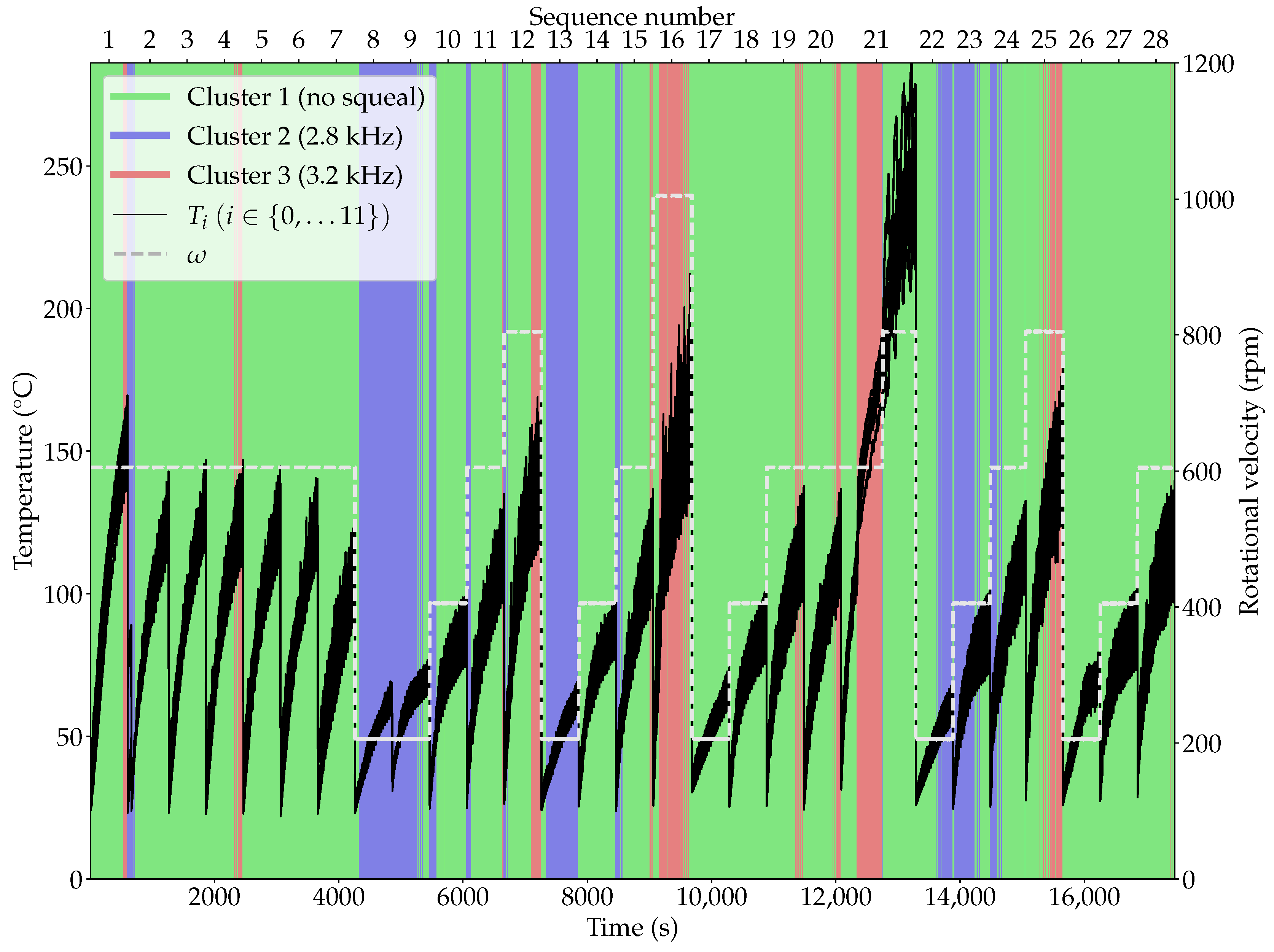




| Cluster | Number of Time Intervals | Corresponding Squeal Mode |
|---|---|---|
| Cluster 1 | 4344 (74.7%) | No squeal |
| Cluster 2 | 922 (15.8%) | 2.8 kHz |
| Cluster 3 | 552 (9.49%) | 3.2 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caradec, Q.; Durain, S.; Thévenot, M.; Briatte, M.; Stender, M.; Brunel, J.-F.; Dufrénoy, P. Pin-on-Disc Experimental Study of Thermomechanical Processes Related to Squeal Occurrence. Lubricants 2025, 13, 186. https://doi.org/10.3390/lubricants13040186
Caradec Q, Durain S, Thévenot M, Briatte M, Stender M, Brunel J-F, Dufrénoy P. Pin-on-Disc Experimental Study of Thermomechanical Processes Related to Squeal Occurrence. Lubricants. 2025; 13(4):186. https://doi.org/10.3390/lubricants13040186
Chicago/Turabian StyleCaradec, Quentin, Sacha Durain, Maël Thévenot, Mathis Briatte, Merten Stender, Jean-François Brunel, and Philippe Dufrénoy. 2025. "Pin-on-Disc Experimental Study of Thermomechanical Processes Related to Squeal Occurrence" Lubricants 13, no. 4: 186. https://doi.org/10.3390/lubricants13040186
APA StyleCaradec, Q., Durain, S., Thévenot, M., Briatte, M., Stender, M., Brunel, J.-F., & Dufrénoy, P. (2025). Pin-on-Disc Experimental Study of Thermomechanical Processes Related to Squeal Occurrence. Lubricants, 13(4), 186. https://doi.org/10.3390/lubricants13040186





