Study on the Tribological Behaviors of a Wave Glider’s Wing’s Rotating Shaft Using Fractal and Chaotic Analysis
Abstract
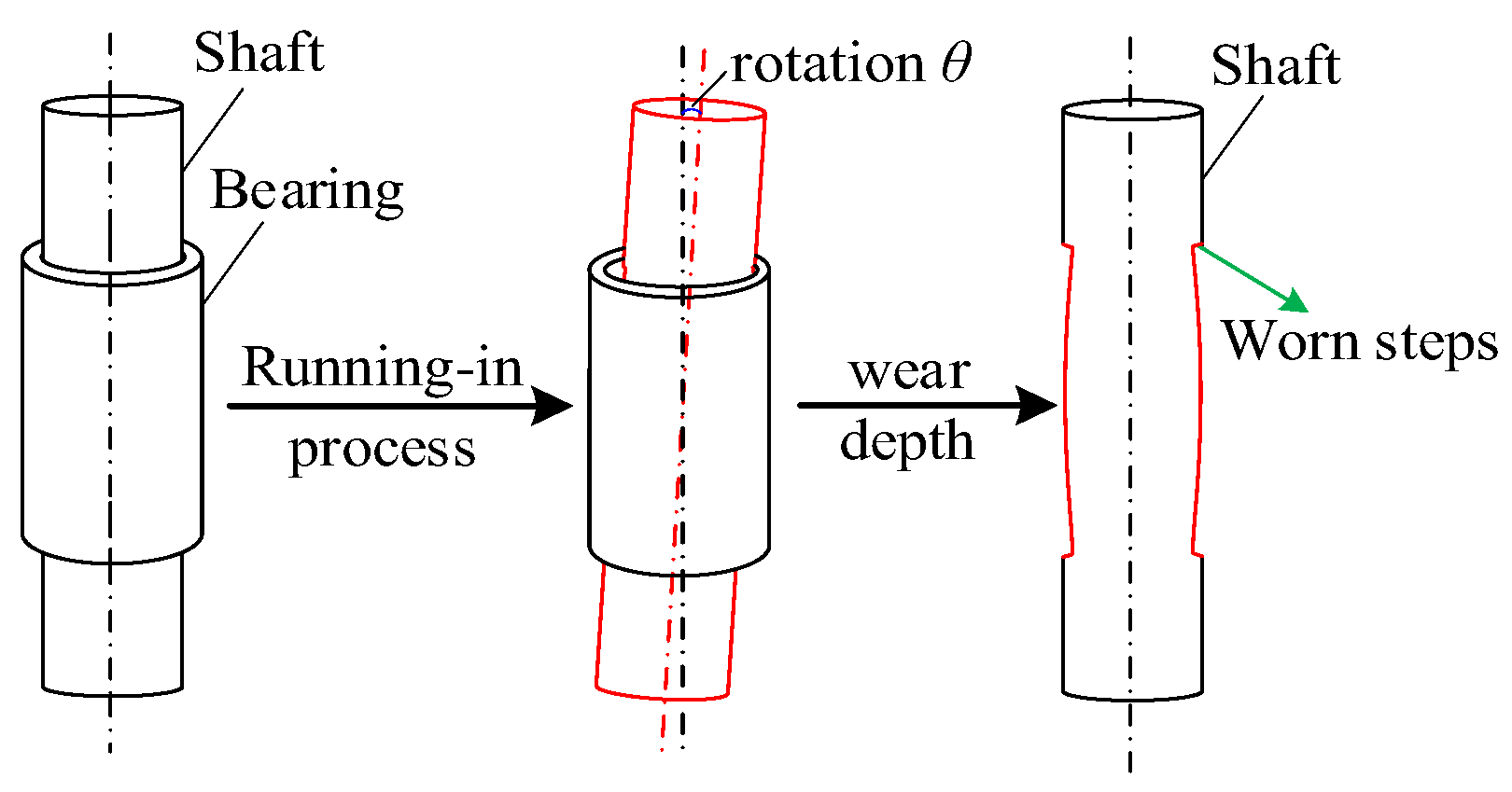
1. Introduction
2. Wear Test and Result Analysis
2.1. Test Equipment and Specimens
2.2. Test Method
2.3. Test Results and Analysis
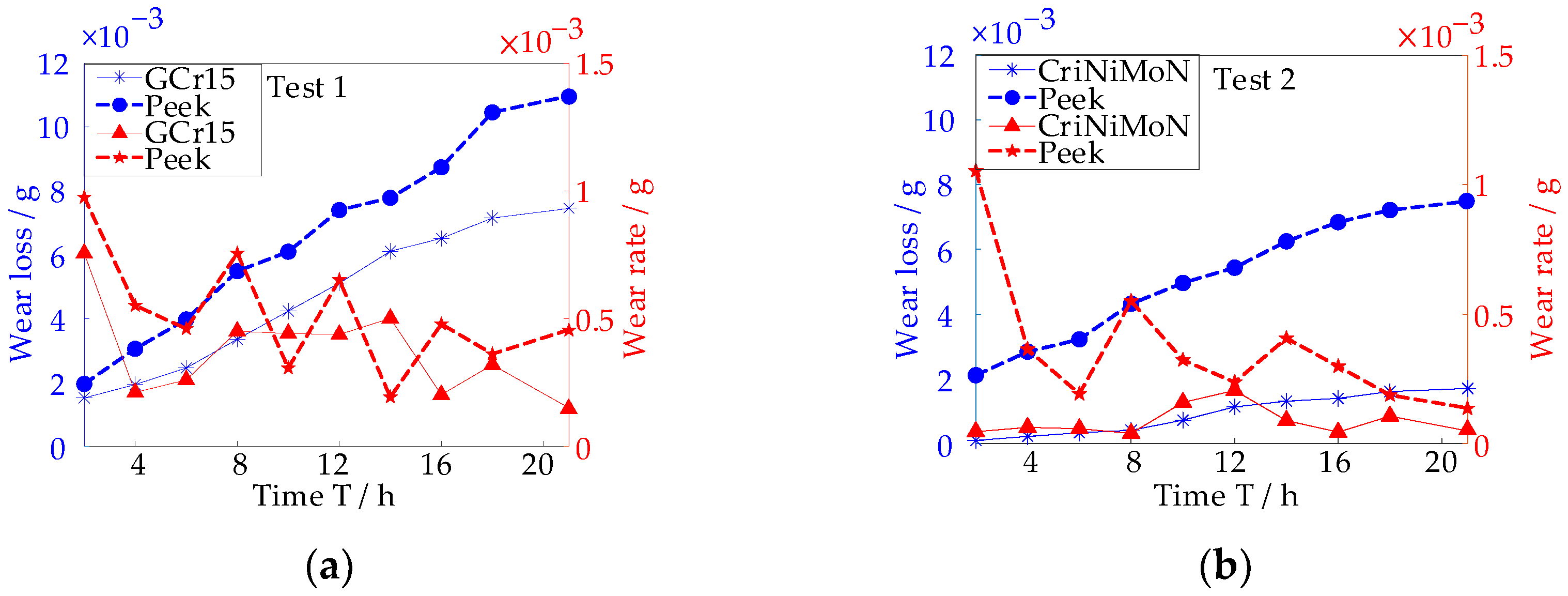
2.3.1. Wear Amount and Wear Rate
2.3.2. Wear Surface Morphology
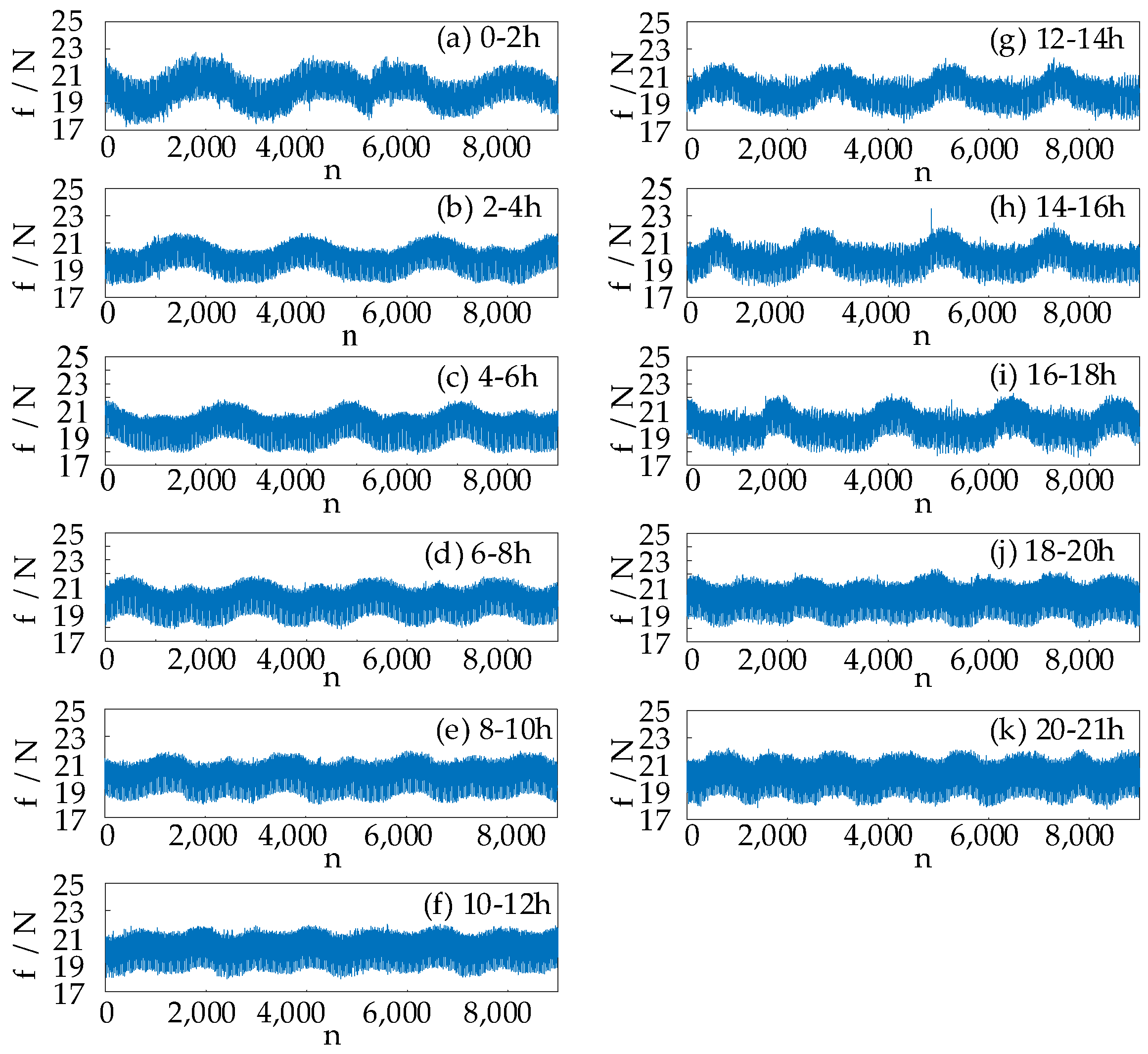
2.3.3. Friction Force Signals
3. Results
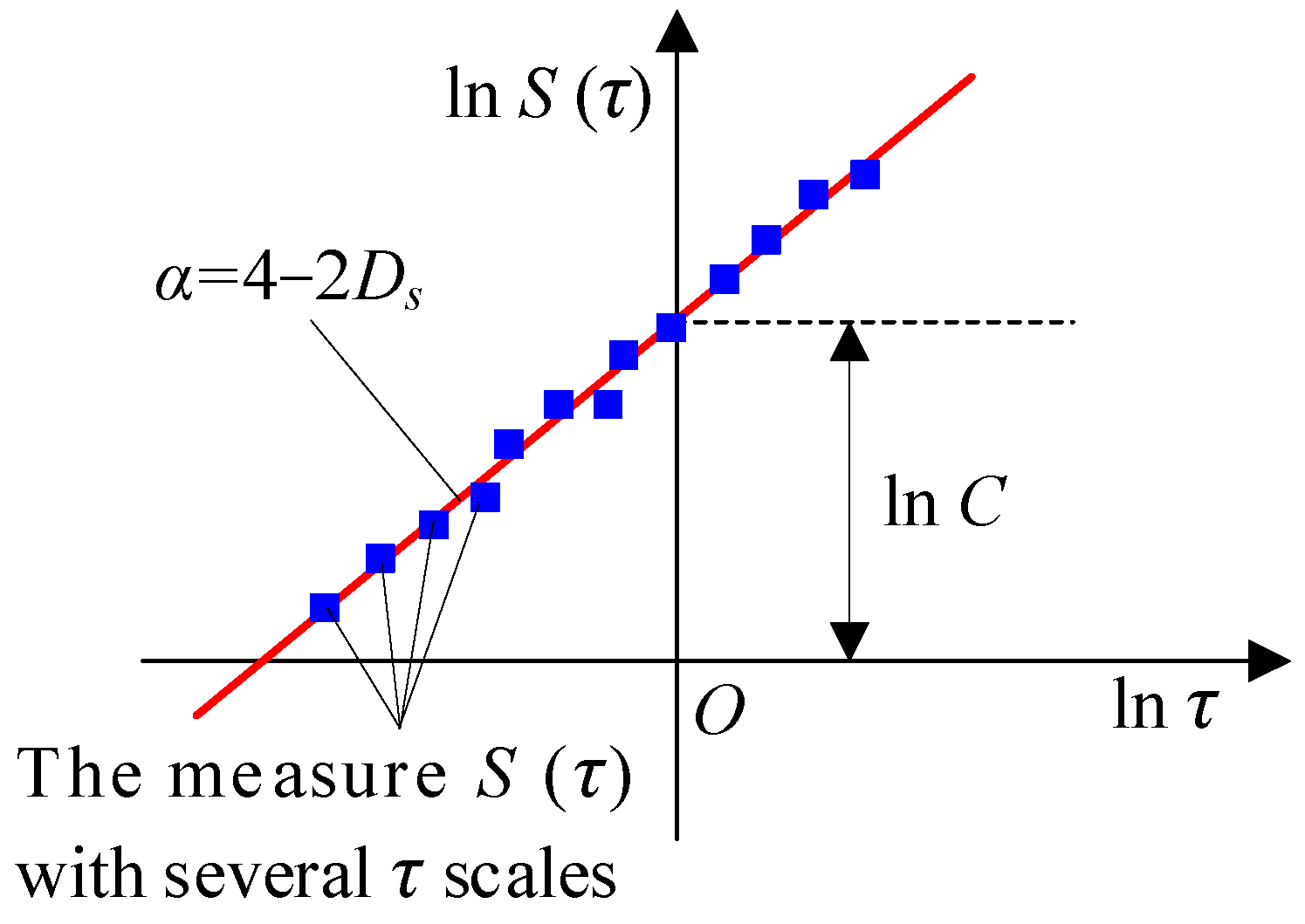
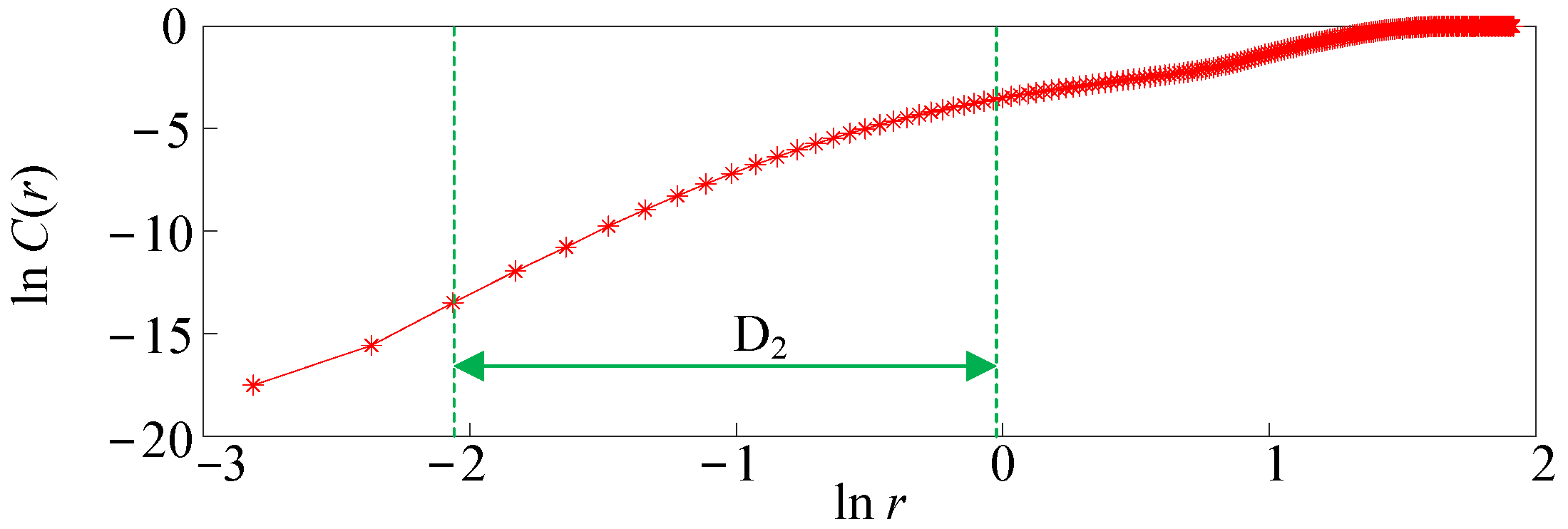
3.1. Fractal Characterization Method for Worn Surfaces
3.2. Chaos Characterization Method for Friction Signals
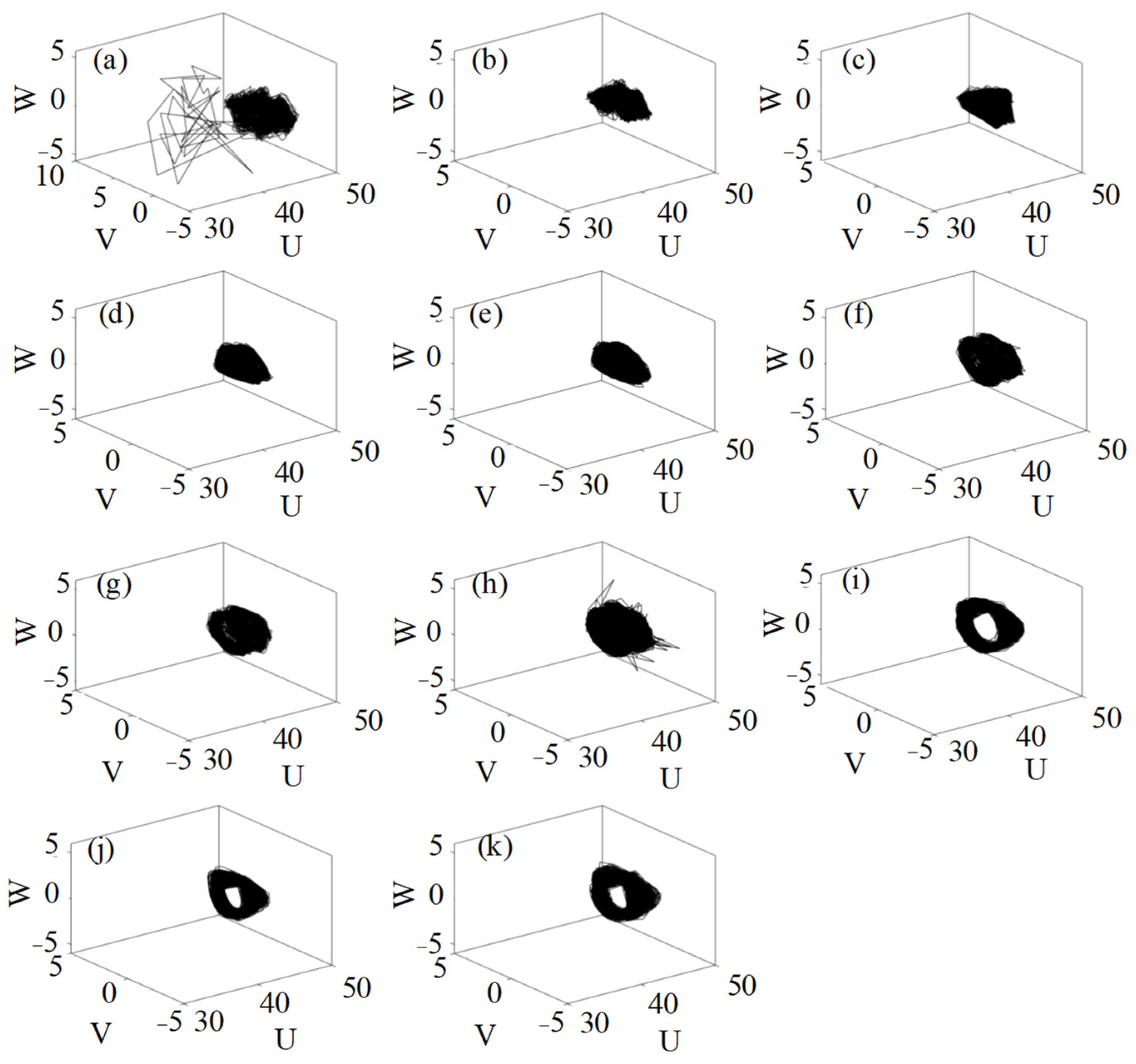
3.2.1. Phase Trajectory Method
3.2.2. Correlation Dimension Method
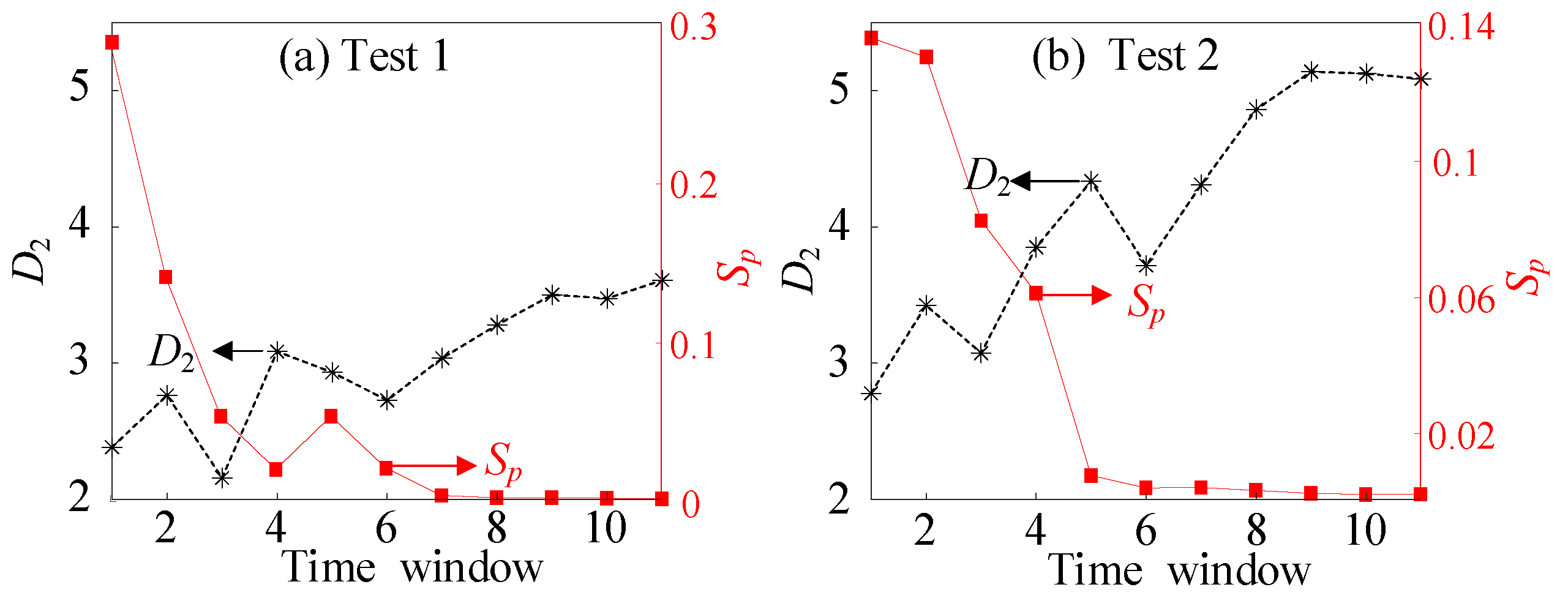
3.2.3. Phase-Point Saturation Method
3.3. Fractal and Chaos Characterization Method for Friction Signals
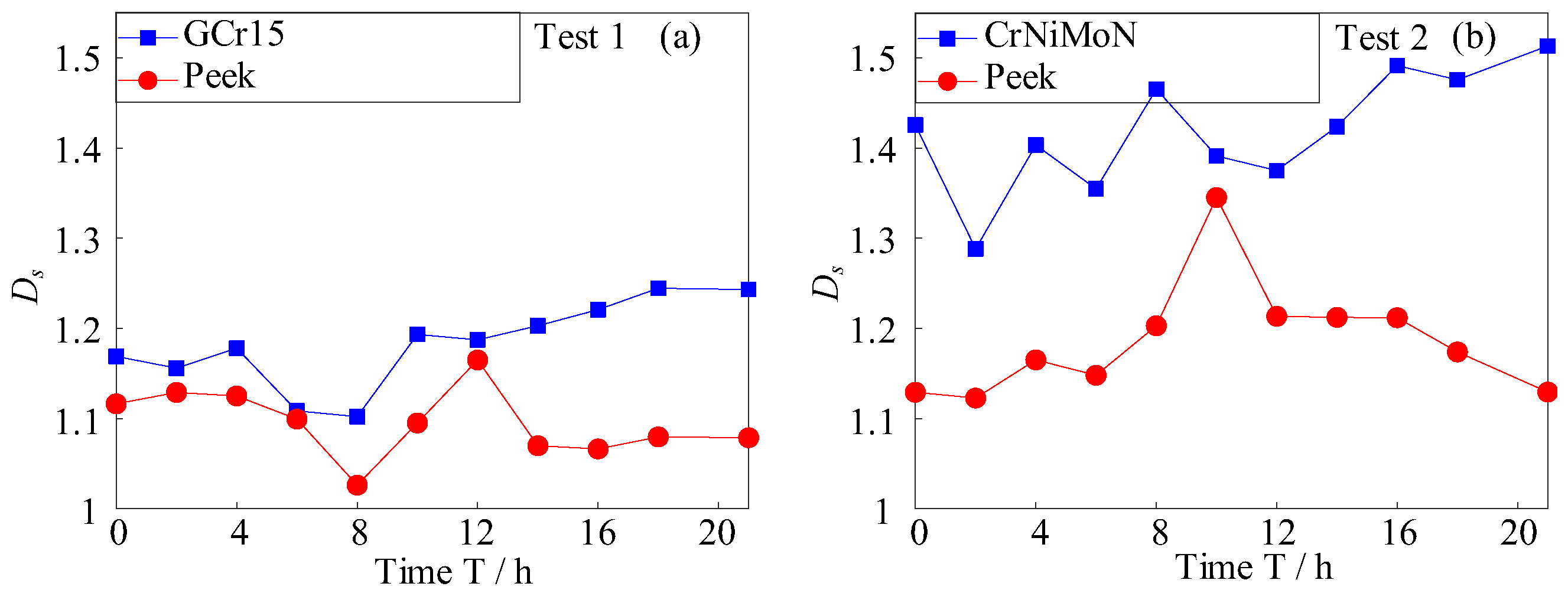
3.3.1. Fractal Characterization Results and Analysis of Worn Surfaces
3.3.2. Chaos Characterization Results and Analysis of Wear Process
4. Discussion
5. Conclusions
- (1)
- During the wear process of the rotating shaft and bearing specimen of the wave glider wing, the wear amount, surface morphology, and evolution law of friction force signals are consistent. The wear amount increases, the wear rate decreases, the worn surface morphology changes from rough to smooth, and the friction force signal first decreases and then increases. These friction and wear information indicate that the wear process of the bearing pair consists of changing from an unstable state in the initial wear stage to a stable convergence state. The result indicates that CrNiMoN has better wear resistance than CGr15.
- (2)
- By introducing the fractal and chaos theory, the fractal dimension of surface morphology, correlation dimension, and phase-point saturation of friction force signals are calculated, and the phase trajectory is constructed. The obtained results show that the range of phase trajectory motion follows an evolutionary law of significantly decreasing and then maintaining a finite phase space. The surface fractal dimension and correlation dimension first increase then gradually stabilize around large values, whereas phase-point saturation is the opposite, revealing the dynamic evolution process of the wear changing from an unstable divergent state to a stable convergent state in time and space. These results indicate that CrNiMoN has better wear resistance and quality than GCr15.
- (3)
- Therefore, the use of fractal and chaotic characterization methods can objectively describe friction systems of high complexity, irregularity, and nonlinear characteristics, without being affected by the device resolution and sampling length. This provides new ideas and methods for the identification of the wear state and the characterization of the wear characteristics of wave glider wing rotation shafts. CrNiMoN is more suited to the be used in the wing bearing of a wave glider compared with GCr15. Thus, the method can be used to make a selection for different material designs based on the worn surface and friction force signals in other industrial friction pairs with a multi-factor coupling effect.
- (4)
- The quality evaluation and state characterization of the wear process can be applied to other complex friction systems. The stronger and more complex the nonlinearity of the system, the more advantageous the characterization results will be. By identifying and monitoring the state of the wear process, timely measures can be taken to extend the service life of the shaft, increase the reliability and operational efficiency of the wave glider, and provide a certain theoretical basis and practical guidance for future studies in this field.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Chang, Z.; Lu, G.; Zheng, Z.; Zhang, Z. Analysis of the dynamic system of wave glider with a towed body. J. Ocean Univ. China 2020, 19, 519–524. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Zhang, X.; Guo, X.; Li, X.; Tian, X. Path following control of the wave glider in waves and currents. Ocean Eng. 2019, 193, 106578. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Zhang, X.; Li, X.; Peng, T.; Lu, H.; Tian, X. Numerical and experimental study on the maneuverability of an active propeller control based on wave glider. Appl. Ocean Res. 2020, 104, 102369. [Google Scholar] [CrossRef]
- Kowalski, S.; Pexa, M.; Aleš, Z.; Čedík, J. Failure Analysis and the Evaluation of Forced-in Joint Reliability for Selected Operation Conditions. Coatings 2021, 11, 1305. [Google Scholar] [CrossRef]
- Xu, C.; Li, B.; Wu, T. Wear characterization under sliding–rolling contact using friction-induced vibration features. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 634–647. [Google Scholar] [CrossRef]
- Savchenko, N.L.; Filippov, A.V.; Tarasov, S.Y.; Dmitriev, A.I.; Shilko, E.V.; Grigoriev, A.S. Acoustic emission characterization of sliding wear under condition of direct and inverse transformations in low temperature degradation aged Y-TZP and Y-TZP-Al2O3. Friction 2018, 6, 323–340. [Google Scholar] [CrossRef]
- Lychagin, D.V.; Filippov, A.V.; Kolubaev, E.A.; Novitskaia, O.S.; Chumlyakov, Y.I.; Kolubaev, A.V. Dry sliding of had field steel single crystal oriented to deformation by slip and twinning: Deformation, wear, and acoustic emission characterization. Tribol. Int. 2018, 119, 1–18. [Google Scholar] [CrossRef]
- Li, G.; Yang, S.; Xing, P.; Liu, T.; Gao, H.; Song, Y.; Zhang, H. Experimental Investigation of Triboelectrification Behaviour in the Friction Process. Lubricants 2022, 10, 180. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Z.; Zuo, X. Multi-Objective Optimization of Three-Stage Running-In Process for Main Bearing of Marine Diesel Engine. J. Tribol. 2023, 145, 081701. [Google Scholar] [CrossRef]
- Zuo, X.; Xie, W.; Zhou, Y. Influence of Electric Current on the Wear Topography of Electrical Contact Surfaces. J. Tribol. 2022, 144, 071702. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.; Xing, P.; He, W.; Feng, Z.; Zhang, H. Investigation on alignment state evolution of ship propulsion shafting based on chaotic characteristics of vibration signals. Ocean Eng. 2025, 322, 120521. [Google Scholar] [CrossRef]
- Sun, D.; Li, G.; Wei, H.; Liao, H. Experimental study on the chaotic attractor evolvement of the friction vibration in a running-in process. Tribol. Int. 2015, 88, 290–297. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Zuo, X. Tribological effect of ZBUP additive on the running-in quality of sliding bearing by fractal analysis. Ind. Lubr. Tribol. 2022, 74, 1165–1173. [Google Scholar] [CrossRef]
- Xing, P.; Li, G.; Gao, H.; Gao, H.; Lu, L.; Yang, S.; Zhang, H. Experimental investigation on the scroll attractor evolvement of friction-induced vibration under the different friction conditions. Mech. Syst. Signal Process. 2022, 168, 108725. [Google Scholar] [CrossRef]
- Peng, M.; Zhou, Y.; Zuo, X. Application of recurrence dynamic analysis to running-in state recognition. Ind. Lubr. Tribol. 2021, 73, 756–764. [Google Scholar] [CrossRef]
- Mevel, B.; Guyader, J. Experiments on routes to chaos in ball bearings. J. Sound Vib. 2008, 318, 549–564. [Google Scholar] [CrossRef]
- Ye, L.; Xia, X.; Chang, Z. Evaluation of dynamic uncertainty of rolling bearing vibration performance. Math. Probl. Eng. 2019, 2019, 2896046. [Google Scholar] [CrossRef]
- Xia, X.; Chen, L.; Fu, L.; Li, J. Information mining for friction torque of rolling bearing for space applications using chaotic theory. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 5223–5229. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, X.; Zuo, X. Prediction model of fractal dimensions in steady state through a multi-stage running in of Sn11Sb6Cu and AISI 1045 steel. Wear 2021, 477, 203770. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, H.; Zuo, X. The Behavior of intrinsic randomness and dynamic abrupt changes of friction force signal during the friction process. J. Tribol. 2016, 138, 031605. [Google Scholar] [CrossRef]
- Ding, C.; Feng, S.; Qiao, Z.; Zhu, H.; Zhou, Z.; Piao, Z. Experimental prediction model for the running-in state of a friction system based on chaotic characteristics and BP neural network. Tribol. Int. 2023, 188, 108846. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Sun, G.; Zhu, H.; Ding, C.; Jiang, Y.; Wei, C. On the boundedness of running-in attractors based on recurrence plot and recurrence qualification analysis. Friction 2019, 7, 432–443. [Google Scholar] [CrossRef]
- Kennel, M.B.; Abarbanel, H.D. False neighbors and false strands: A reliable minimum embedding dimension algorithm. Phys. Rev. E 2002, 66, 026209. [Google Scholar] [CrossRef]
- Goudarzi, S.; Anisi, M.H.; Kama, N.; Doctor, F.; Soleymani, S.A.; Sangaiah, A.K. Predictive modelling of building energy consumption based on a hybrid nature-inspired optimization algorithm. Energy Build. 2019, 196, 83–93. [Google Scholar] [CrossRef]
- Tsonis, A.; Elsner, J.B. The weather attractor over very short timescales. Nature 1988, 333, 545–547. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Principal component analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractor. Phys. Rev. Lett. 1983, 50, 346. [Google Scholar] [CrossRef]
- Lang, S.; Zhu, H.; Wei, C.; Zhou, W.; Li, Y. Study on characterization method of phase-point saturation based on the capacity dimension. Fractals 2022, 30, 2250035. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Z.; Zuo, X.; Zhao, H. Identification of wear mechanisms of main bearings of marine diesel engine using recurrence plot based on CNN model. Wear 2023, 520, 204656. [Google Scholar] [CrossRef]
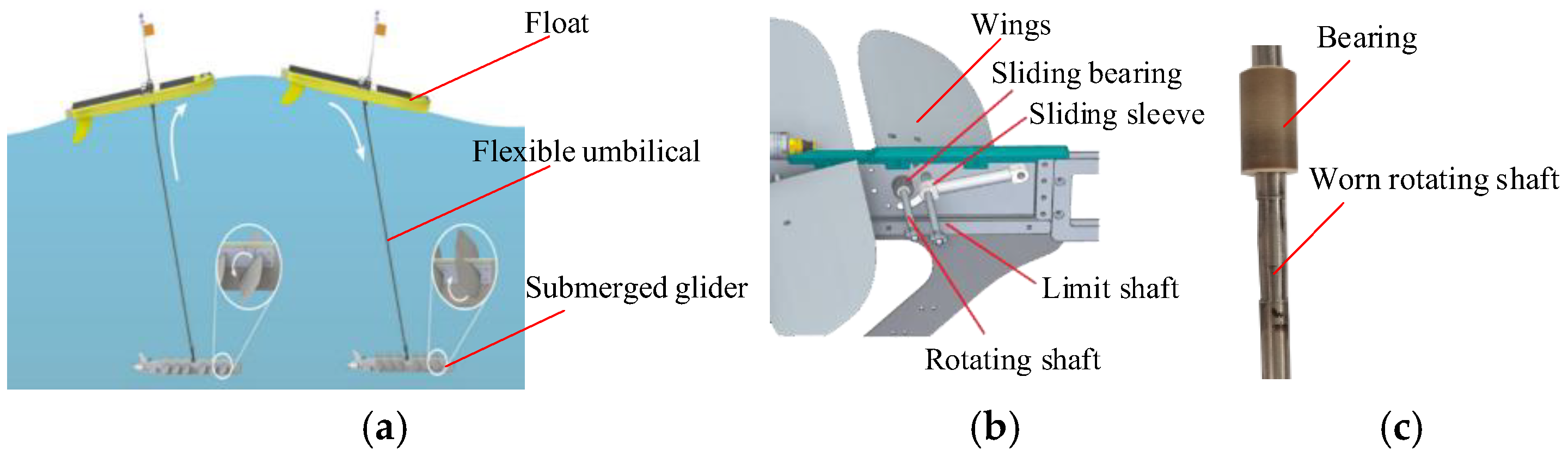




| Number | 1 | 2 |
|---|---|---|
| Upper specimen material | GCr15 | CrNiMoN |
| Lower specimen material | Peek | Peek |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, S.; Zhu, H.; Lian, X. Study on the Tribological Behaviors of a Wave Glider’s Wing’s Rotating Shaft Using Fractal and Chaotic Analysis. Lubricants 2025, 13, 185. https://doi.org/10.3390/lubricants13040185
Lang S, Zhu H, Lian X. Study on the Tribological Behaviors of a Wave Glider’s Wing’s Rotating Shaft Using Fractal and Chaotic Analysis. Lubricants. 2025; 13(4):185. https://doi.org/10.3390/lubricants13040185
Chicago/Turabian StyleLang, Shihui, Hua Zhu, and Xuehai Lian. 2025. "Study on the Tribological Behaviors of a Wave Glider’s Wing’s Rotating Shaft Using Fractal and Chaotic Analysis" Lubricants 13, no. 4: 185. https://doi.org/10.3390/lubricants13040185
APA StyleLang, S., Zhu, H., & Lian, X. (2025). Study on the Tribological Behaviors of a Wave Glider’s Wing’s Rotating Shaft Using Fractal and Chaotic Analysis. Lubricants, 13(4), 185. https://doi.org/10.3390/lubricants13040185




