Wear Analysis of a Heterogeneous Annular Cylinder
Abstract
:1. Introduction
2. Model of Heterogeneous Cylinder
3. Calculation of the Wear Process Using the MDR
3.1. Method of Dimensionality Reduction
3.2. Simulation Procedure
3.2.1. Defining Initial State (0)–(1)
3.2.2. Change of Profile Due to Wear: Steps (2)–(3)
3.2.3. Stress Distribution of the Updated Profile: Steps (4)–(6)
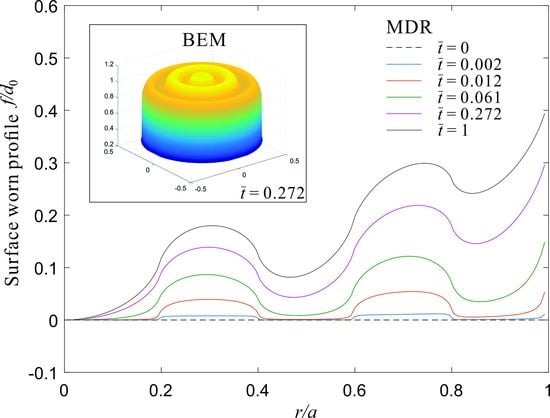
3.3. Numerical Results
4. Limiting Profile and Surface Gradient
4.1. Calculation of the Limiting Profile by Direct Integration
4.2. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
List of Symbols
| Normal stiffness | , , | One-dimensional profile | |
| Spring force | , | Widths of rings | |
| Normalized deformation | The index of rings | ||
| Material loss in volume | , , | Wear coefficients | |
| Spring distance | Number of rings | ||
| , | Surface gradient | , , , | Pressure distribution |
| Elliptic integral | Linear force density | ||
| Hardness | Polar coordinate | ||
| Poisson’s ratio | Radius of rings | ||
| Radius of cylinder | Sliding distance | ||
| , , | Indentation depth | , | Time |
| Elastic modulus | Normalized time | ||
| Effective elastic modulus | , , , | Vertical deformation | |
| , , , | Three-dimensional profile | Sliding velocity | |
| Normal load | Coordinate |
References
- Wallman, C.G.; Åström, H. Friction Measurement Methods and the Correlation between Road Friction and Traffic Safety—A Literature Review Report of the Swedish National Road and Traffic Institute, VTI Meddelande 911A; Swedish National Road and Transport research Institute: Linköping, Sweden, 2001. [Google Scholar]
- Sarang, G.; Lekha, B.M.; Geethu, J.S.; Shankar, A.U.R. Laboratory performance of stone matrix asphalt mixtures with two aggregate gradations. J. Mod. Transp. 2015, 23, 130–136. [Google Scholar] [CrossRef]
- Kogbara, R.B.; Masad, E.A.; Kassem, E.; Scarpas, A.; Anupam, K.A. State-of-the-art review of parameters influencing measurement and modeling of skid resistance of asphalt pavements. Constr. Build. Mater. 2016, 114, 602–617. [Google Scholar] [CrossRef]
- Do, M.T.; Tang, Z.; Kane, M.; De Larrard, F. Pavement polishing–Development of a dedicated laboratory test and its correlation with road results. Wear 2007, 263, 36–42. [Google Scholar] [CrossRef]
- Kane, M.; Artamendi, I.; Scarpas, T. Long-term skid resistance of asphalt surfacings: Correlation between Wehner–Schulze friction values and the mineralogical composition of the aggregates. Wear 2013, 303, 235–243. [Google Scholar] [CrossRef]
- Li, Q.; Popov, M.; Dimaki, A.; Filippov, A.E.; Kürschner, S.; Popov, V.L. Friction Between a Viscoelastic Body and a Rigid Surface with Random Self-Affine Roughness. Phys. Rev. Lett. 2013, 111, 034301. [Google Scholar] [CrossRef] [PubMed]
- Popov, V.L. Contact Mechanics and Friction, Physical Principles and Applications, 2nd ed.; Springer-Verlag: Berlin, Germany, 2017; pp. 283–289. [Google Scholar]
- Archard, J.F.; Hirst, W. The Wear of Metals under Unlubricated Conditions. Proc. R. Soc. Lond. A 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Popov, V.L.; Hess, M. Method of Dimensionality Reduction in Contact Mechanics and Friction; Springer-Verlag: Berlin, Germany, 2015; pp. 65–86. [Google Scholar]
- Popov, V.L. Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 2014, 4, 3749. [Google Scholar] [CrossRef] [PubMed]
- Dimaki, A.V.; Dmitriev, A.I.; Chai, Y.S.; Popov, V.L. Rapid Simulation Procedure for Fretting Wear on the basis of the method of dimensionality reduction. Int. J. Solids Struct. 2014, 51, 4215–4220. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Voll, L.B.; Psakhie, S.G.; Popov, V.L. Universal limiting shape of worn profile under multiple-mode fretting conditions: theory and experimental evidence. Sci. Rep. 2016, 6, 23231. [Google Scholar] [CrossRef] [PubMed]
- Dimaki, A.V.; Dmitriev, A.I.; Menga, N.; Papangelo, A.; Ciavarella, M.; Popov, V.L. Fast High-Resolution Simulation of the Gross Slip Wear of Axially Symmetric Contacts. Tribol. Trans. 2016, 59, 189–194. [Google Scholar] [CrossRef]
- Popov, V.L.; Hess, M. Method of Dimensionality Reduction in contact mechanics and friction: A user’s handbook. FU Mech. Eng. 2014, 12, 1–14. [Google Scholar]
- Pohrt, R.; Li, Q. Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 2014, 17, 334–340. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Forsbach, F.; Schuster, M.; Pielsticker, D.; Popov, V.L. Wear Analysis of a Heterogeneous Annular Cylinder. Lubricants 2018, 6, 28. https://doi.org/10.3390/lubricants6010028
Li Q, Forsbach F, Schuster M, Pielsticker D, Popov VL. Wear Analysis of a Heterogeneous Annular Cylinder. Lubricants. 2018; 6(1):28. https://doi.org/10.3390/lubricants6010028
Chicago/Turabian StyleLi, Qiang, Fabian Forsbach, Maximilian Schuster, Daniel Pielsticker, and Valentin L. Popov. 2018. "Wear Analysis of a Heterogeneous Annular Cylinder" Lubricants 6, no. 1: 28. https://doi.org/10.3390/lubricants6010028
APA StyleLi, Q., Forsbach, F., Schuster, M., Pielsticker, D., & Popov, V. L. (2018). Wear Analysis of a Heterogeneous Annular Cylinder. Lubricants, 6(1), 28. https://doi.org/10.3390/lubricants6010028