Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis
Abstract
:1. Introduction
2. Material and Methods
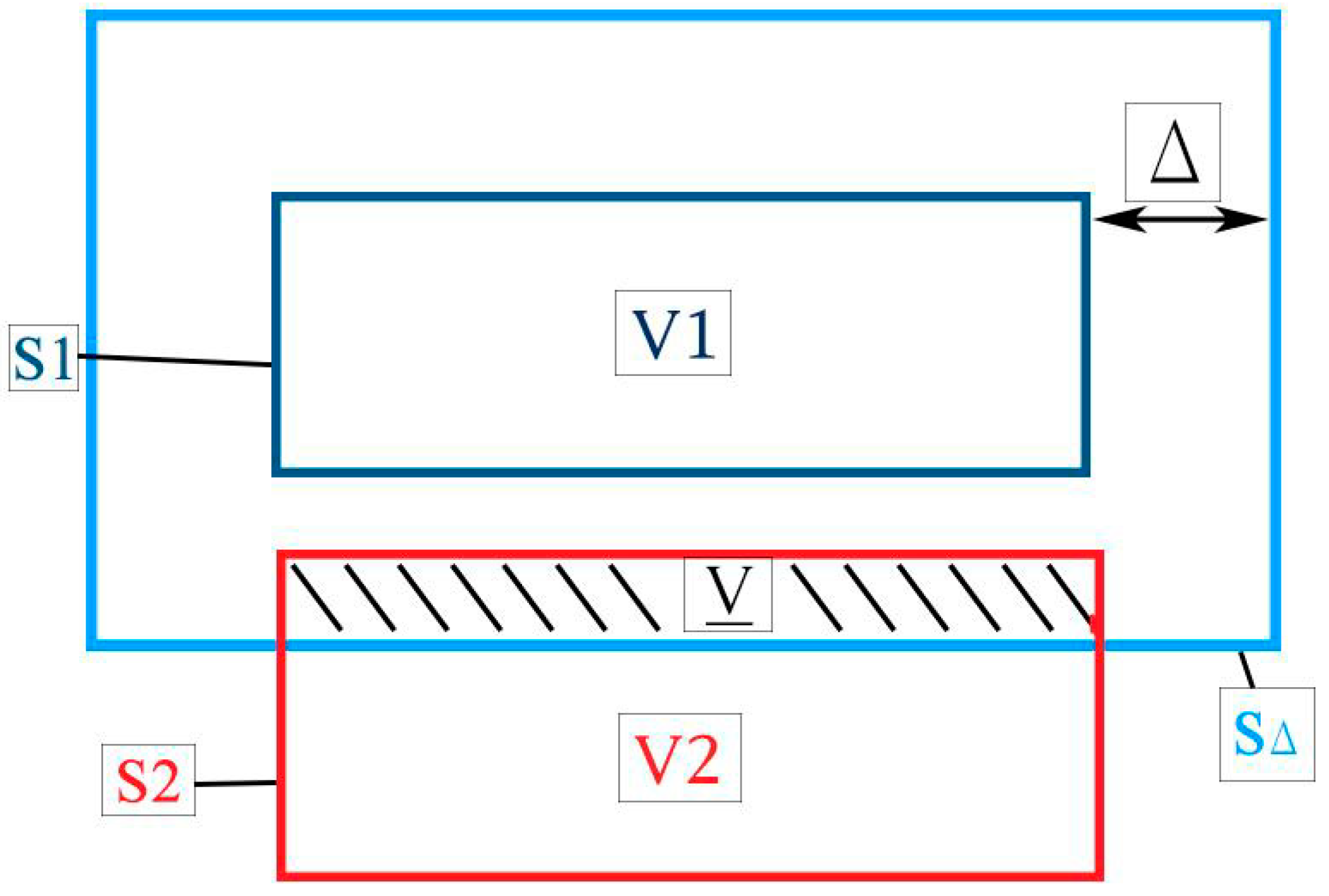
2.1. Joint Congruence and Contact Model
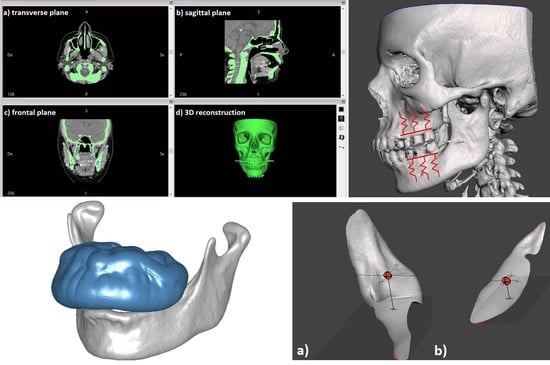
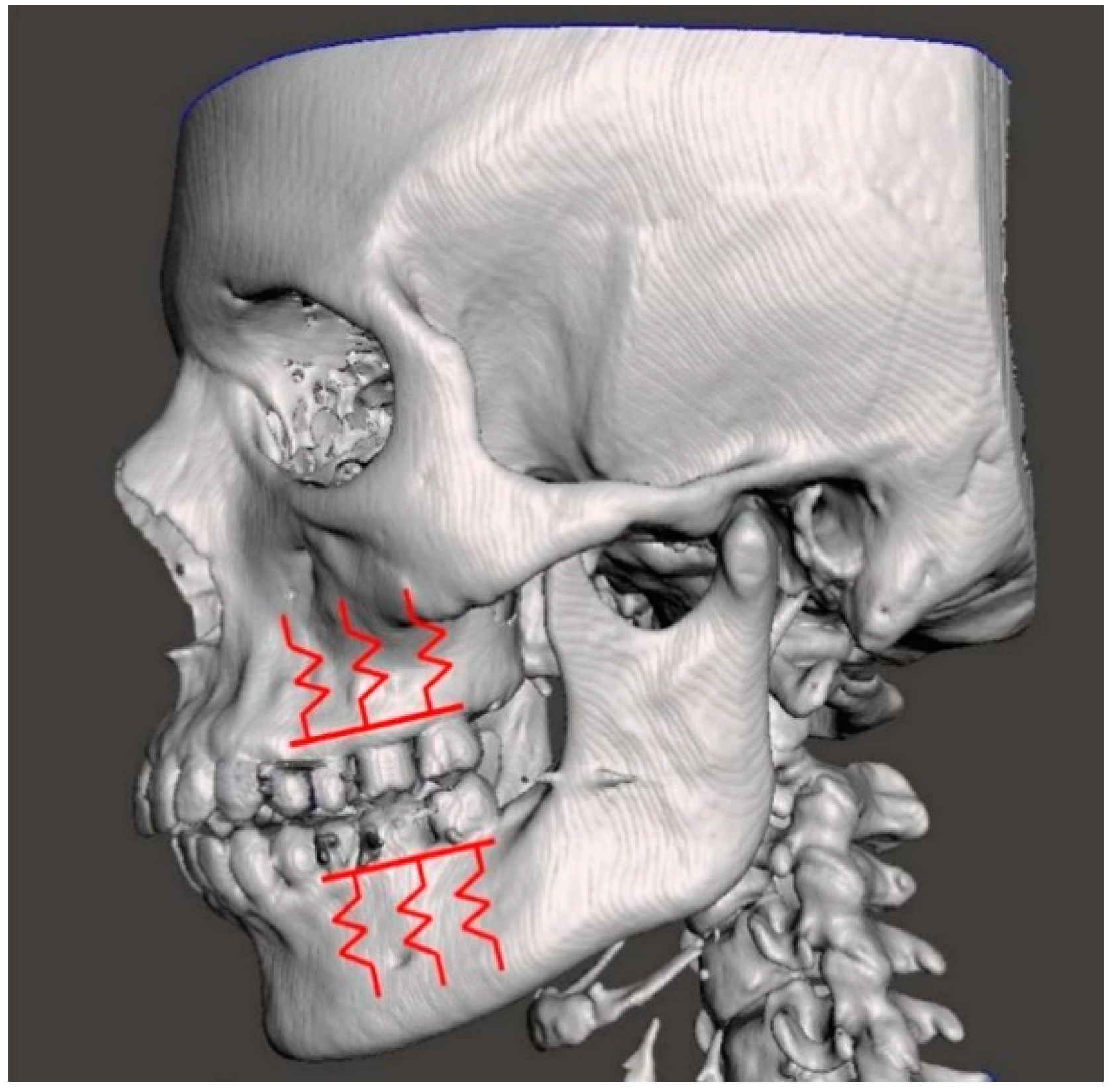
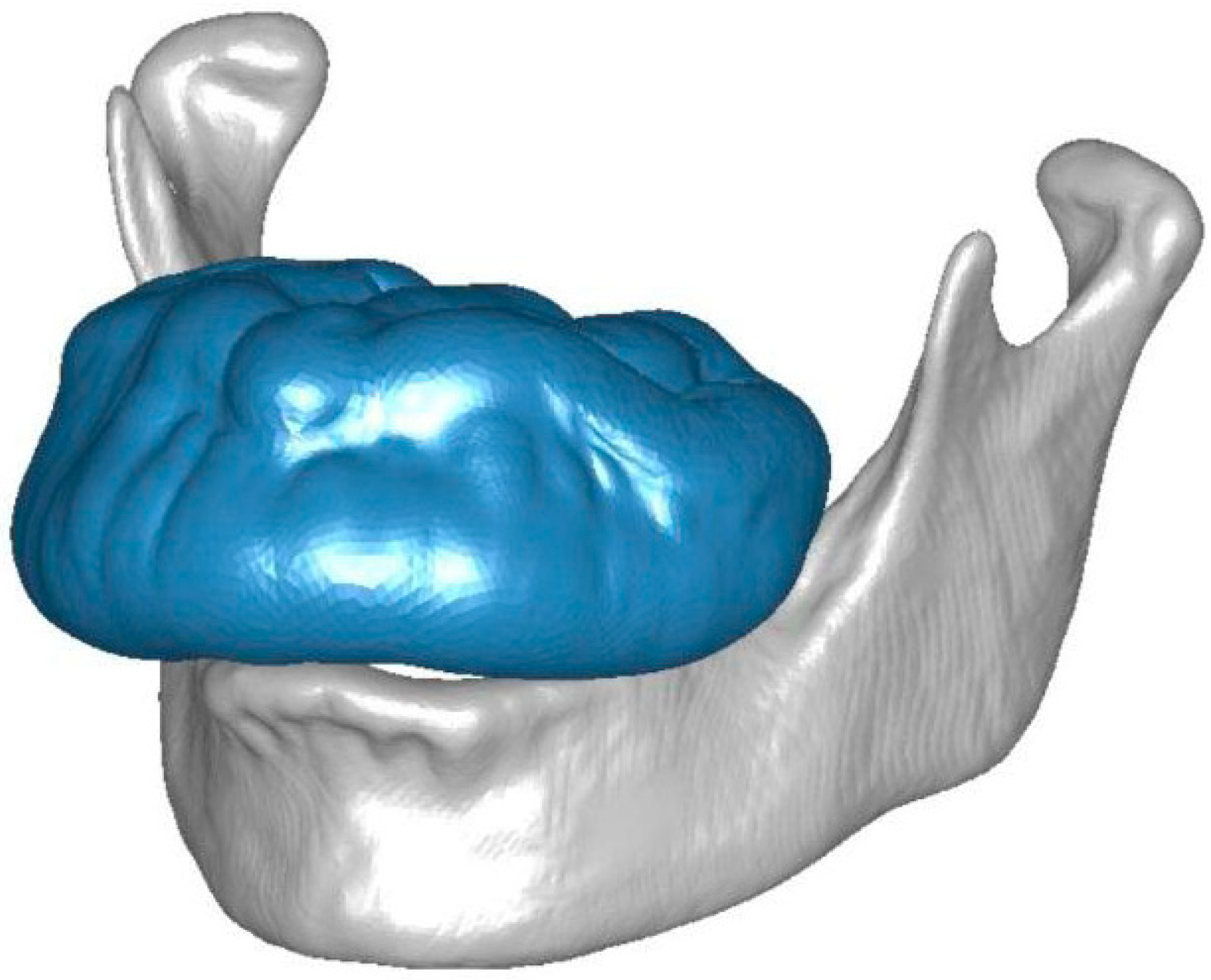
2.2. Case Study of a Maxillary Exostosis: Congruence and Contact Evaluation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sierra, A.C.; Jackson, I.T. A torus palatinus with a family history. Eur. J. Plast. Surg. 1992, 15, 98–99. [Google Scholar] [CrossRef]
- Castellano, L.; Carini, F.; Minenna, L.; Lomartire, G.; Amosso, E. Exostoses of oral cavity: Classification and clinical aspects. Ital. Oral Surg. 2010, 9, 233–247. [Google Scholar] [CrossRef]
- Regezi, J.A.; Sciubba, J.J. Oral Pathology: Clinico-Pathologic Correlations; WB Saunders Co.: Philadelphia, PA, USA, 1989; pp. 386–387. [Google Scholar]
- Suzuki, M.; Sakai, T. A familial study of torus palatinus and torus mandibularis. Am. J. Phys. Anthropol. 1969, 18, 263–272. [Google Scholar] [CrossRef]
- Reichart, P.A.; Neuhaus, F.; Sookasem, M. Prevalence of torus palatinus and torus mandibularis in Germans and Thais. Community Dent. Oral Epidemiol. 1988, 16, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Eggen, S. Torus mandibularis: An estimation of the degree of genetic determination. Acta Odontol. Scand. 1989, 47, 409–415. [Google Scholar] [CrossRef] [PubMed]
- Gorsky, M.; Bukai, A.; Shohat, M. Genetic influence on the prevalence of torus palatinus. Am. J. Med. Genet. 1998, 75, 138–140. [Google Scholar] [CrossRef]
- Bayer, I.S. Advances in Tribology of Lubricin and Lubricin-Like Synthetic Polymer Nanostructures. Lubricants 2018, 6, 30. [Google Scholar] [CrossRef]
- Moss, M.L. The functional matrix hypothesis revisited. 1. The role of mechanotransduction. Am. J. Orthod. Dentofac. Orthop. 1997, 112, 8–11. [Google Scholar] [CrossRef]
- Moss, M.L. The functional matrix hypothesis revisited. 2. The role of an osseous connected cellular network. Am. J. Orthod. Dentofac. Orthop. 1997, 112, 221–226. [Google Scholar] [CrossRef]
- Moss, M.L. The functional matrix hypothesis revisited. 3. The genomic thesis. Am. J. Orthod. Dentofac. Orthop. 1997, 112, 338–342. [Google Scholar] [CrossRef]
- Moss, M.L. The functional matrix hypothesis revisited. 4. The epigenetic antithesis and the resolving synthesis. Am. J. Orthod. Dentofac. Orthop. 1997, 112, 410–417. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Singh, G.D. On the etiology and significance of palatal and mandibular tori. Cranio J. Craniomandib. Pract. 2010, 28, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Pearson, O.M.; Lieberman, D.E. The Aging of Wolff’s “Law”: Ontogeny and Responses to Mechanical Loading in Cortical Bone. Yearb. Phys. Anthropol. 2004, 47, 63–99. [Google Scholar] [CrossRef] [PubMed]
- Conconi, M.; Leardini, A.; Parenti-Castelli, V. Joint kinematics from functional adaptation: A validation on the tibio-talar articulation. J. Biomech. 2015, 48, 2960–2967. [Google Scholar] [CrossRef] [PubMed]
- Conconi, M.; Parenti-Castelli, V. A sound and efficient measure of joint congruence. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 935–941. [Google Scholar] [CrossRef] [PubMed]
- Conconi, M.; Halilaj, E.; Parenti-Castelli, V.; Crisco, J.J. Is early osteoarthritis associated with differences in joint congruence? J. Biomech. 2014, 47, 3787–3793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazilu, T.; Gheti, M. On the vertical interaction between a three-axle bogie and track. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2017. [Google Scholar]
- Li, D.; Smith, S.; Ma, X. End condition effect on initial buckling performance of thin plates resting on tensionless elastic or rigid foundations. Int. J. Mech. Sci. 2016, 105, 83–89. [Google Scholar] [CrossRef]
- Voss, R.; Seeholzer, L.; Kuster, F.; Wegener, K. Analytical force model for orthogonal machining of unidirectional carbon fibre reinforced polymers (CFRP) as a function of the fibre orientation. J. Mater. Process. Technol. 2019, 263, 440–469. [Google Scholar] [CrossRef]
- Valigi, M.C.; Papini, S. Analysis of chattering phenomenon in industrial S6-high rolling mill. Diagnostyka 2013, 14, 3–8. [Google Scholar]
- Papini, S.; Valigi, M.C. Analysis of chattering phenomenon in industrial S6-high rolling mill. Part II: Experimental study. Diagnostyka 2016, 17, 27–32. [Google Scholar]
- Valigi, M.C.; Cervo, S.; Petrucci, A. Chatter marks and vibration analysis in a S6-high cold rolling mill. Lect. Notes Mech. Eng. 2014, 5, 567–575. [Google Scholar]
- Argatov, I.; Mishuris, G. Contact Mechanics of Articular Cartilage Layers: Asymptotic Models; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valigi, M.C.; Logozzo, S. Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis. Lubricants 2019, 7, 15. https://doi.org/10.3390/lubricants7020015
Valigi MC, Logozzo S. Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis. Lubricants. 2019; 7(2):15. https://doi.org/10.3390/lubricants7020015
Chicago/Turabian StyleValigi, Maria Cristina, and Silvia Logozzo. 2019. "Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis" Lubricants 7, no. 2: 15. https://doi.org/10.3390/lubricants7020015
APA StyleValigi, M. C., & Logozzo, S. (2019). Do Exostoses Correlate with Contact Disfunctions? A Case Study of a Maxillary Exostosis. Lubricants, 7(2), 15. https://doi.org/10.3390/lubricants7020015