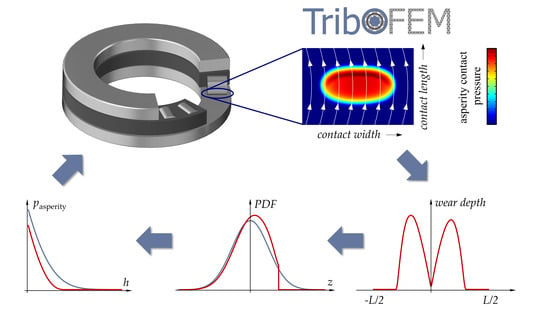
Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication
Abstract
:1. Introduction
2. Numerical Modeling
2.1. Load Cases, Material and Lubricant Properties
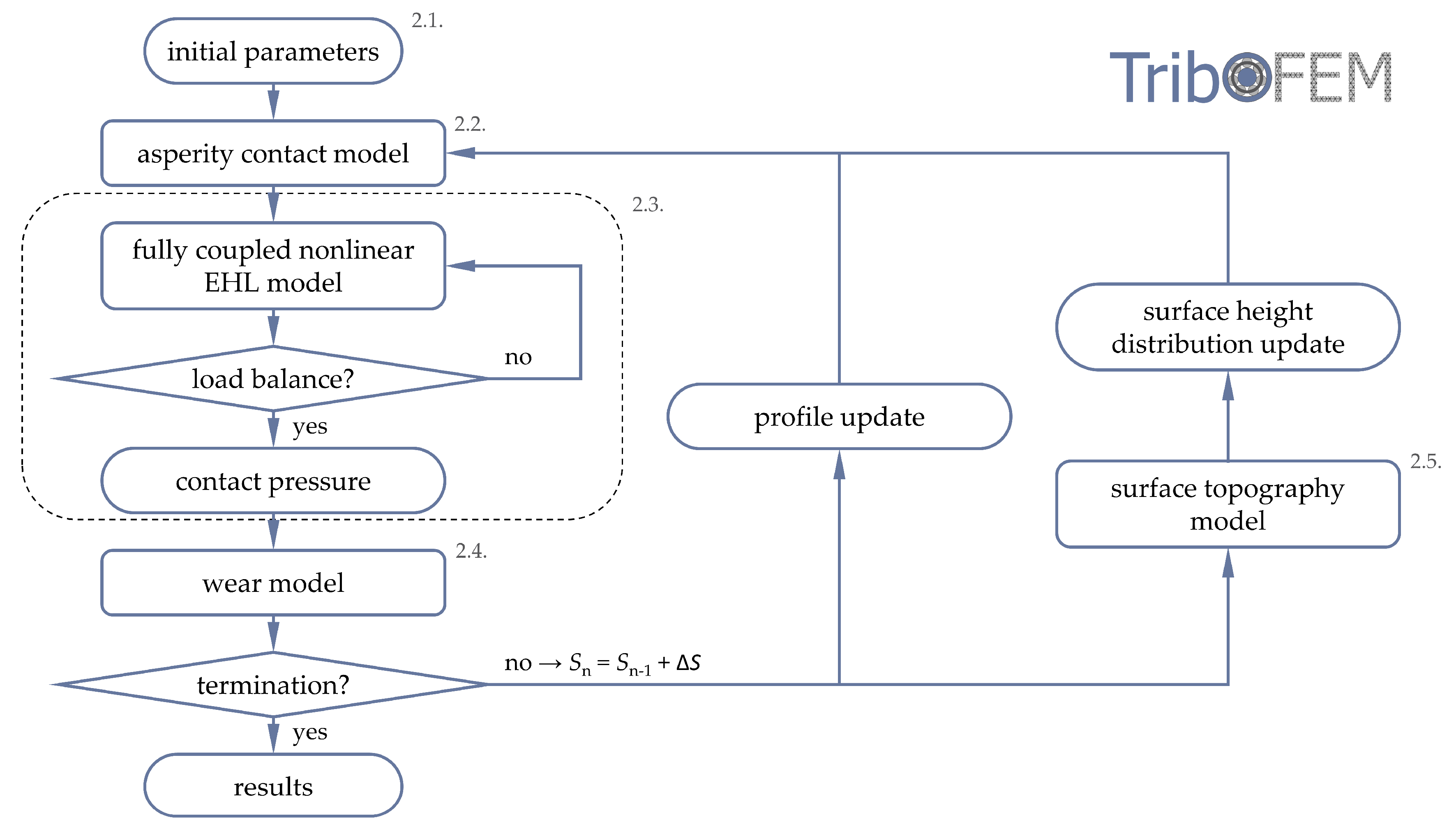
2.2. Asperity Contact Model
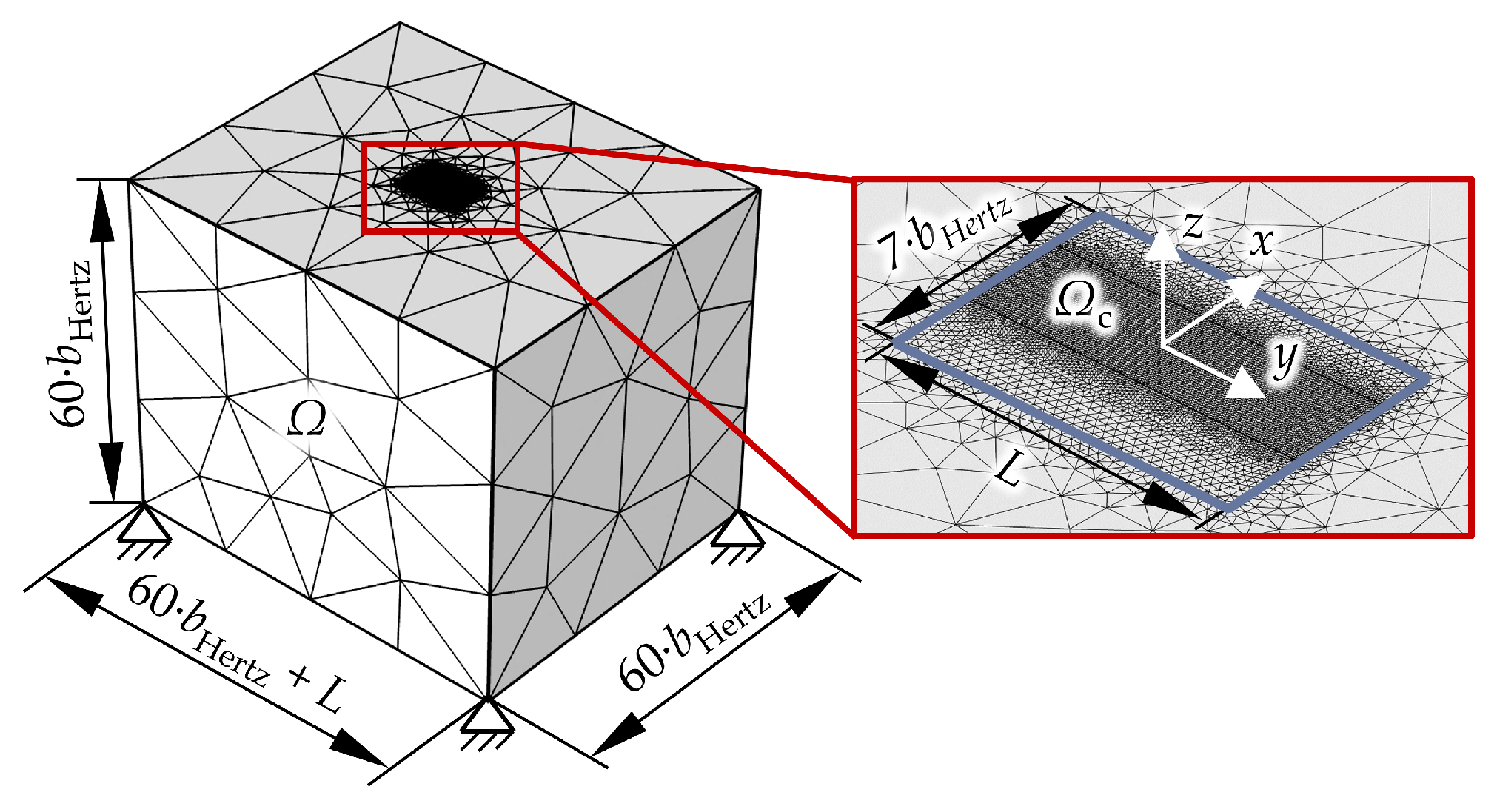
2.3. EHL Modeling
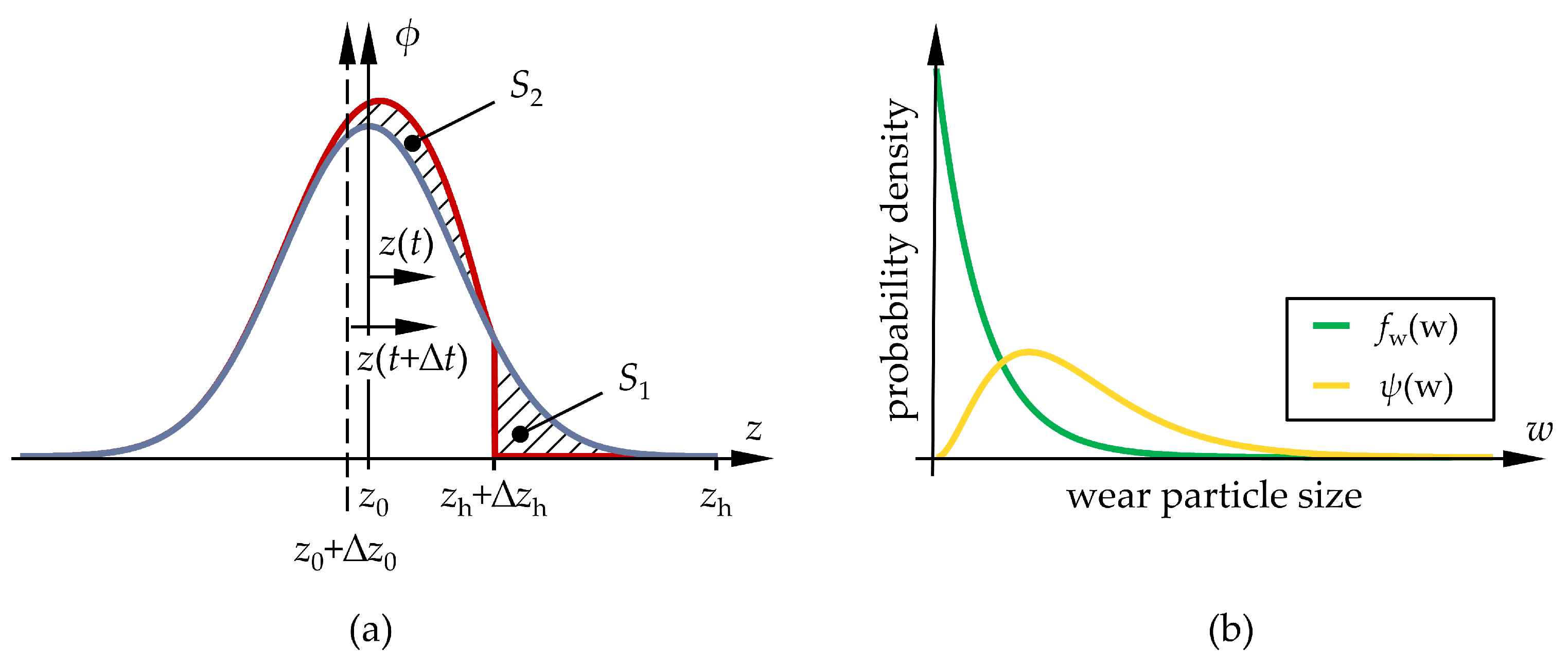
2.4. Wear Modeling
2.5. Surface Topography Model
2.6. Overall Numerical Procedure
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| bHertz | Hertzian contact half-width |
| C | compliance matrix |
| d | separation based on asperity heights |
| D | diameter of roller |
| E’ | reduced Young’s modulus |
| E1, E2 | Young’ modulus of washer/roller |
| Eeq | equivalent Young’s modulus |
| f | probability density function of the wear particle size |
| fw | marginal density function of the wear particle density function |
| F | bearing load |
| FN | normal contact force |
| h | lubricant gap |
| h0 | film thickness constant parameter |
| hliq | lubricant film thickness |
| hw | local wear depth |
| H | dimensionless lubricant gap |
| k | global wear coefficient |
| local wear coefficient | |
| L | length of roller |
| m0,2,4 | zeroth, second and fourth spectral moment of a surface profile |
| n | rotational speed |
| pa | asperity contact pressure |
| ph | fluid pressure |
| pHertz | Hertzian contact pressure |
| ptotal | total pressure |
| P | dimensionless pressure |
| Rx | radius of curvature in x direction |
| s | sliding distance |
| s0 | geometry-function of the roller |
| SRR | slide-to-roll ratio |
| t | test duration |
| u, v, w | size of cuboid shaped wear particle |
| u1,u2 | relative velocity of the washer/roller in x direction |
| U | displacement tensor |
| Uz | displacement in z direction |
| v1,v2 | relative velocity of the washer/roller in y direction |
| vslip | slip velocity |
| Vw | wear volume |
| mean height loss | |
| W | mean wear depth |
| x,y | coordinates in and perpendicular to the rolling direction |
| X, Y | dimensionless coordinates in and perpendicular to the rolling direction |
| ys | distance between the mean height of asperities and the mean height of surface |
| z | profile coordinate based on mean height of surface |
| zs | profile coordinate based on mean height of asperities |
| z0 | ordinate of the mean line of the composite profile |
| Δz0 | descending quantity of mean line |
| zh | highest point of composite profile |
| Δzh | moving distance of highest point |
| α | bandwidth parameter |
| αp | pressure-viscosity coefficient |
| β | mean summit radius |
| γ | penalty function |
| elastic deformation in z direction | |
| dimensionless elastic deformation in z direction | |
| ε | strain tensor |
| ν1, ν2 | Poisson’s ratio of washer/roller |
| νeq | equivalent Poisson’s ratio |
| lubricant density | |
| dimensionless lubricant density | |
| lubricant density at reference state (40 °C) | |
| η | lubricant viscosity |
| dimensionless lubricant viscosity | |
| η0 | lubricant viscosity at reference state (40 °C) |
| ηs | area density of asperities |
| θ | fractional film content |
| σ | standard deviation of surface heights |
| σelastic | stress tensor of the equivalent body |
| σs | standard deviation of asperity heights |
| ϕ | probability density function of surface heights |
| ϕs | probability density function of asperity heights |
| ψ | height-loss probability density function |
| ω | angular velocity |
| Ωc | contact domain |
References
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Simulating sliding wear with finite element method. Tribol. Int. 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Wear simulation with the Winkler surface model. Wear 1997, 207, 79–85. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Winkler, E. Die Lehre von der Elasticitaet und Festigkeit: Mit Besonderer Rücksicht auf Ihre Anwendung in der Technik für Polytechnische Schulen, Bauakademien, Ingenieue, Maschinenbauer, Architecten, etc; Dominicus: Prague, Austria-Hungary, 1868. [Google Scholar]
- Hegadekatte, V.; Huber, N.; Kraft, O. Modeling and simulation of wear in a pin on disc tribometer. Tribol. Lett. 2006, 24, 51–60. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Kurzenhäuser, S.; Huber, N.; Kraft, O. A predictive modeling scheme for wear in tribometers. Tribol. Int. 2008, 41, 1020–1031. [Google Scholar] [CrossRef] [Green Version]
- Andersson, J.; Almqvist, A.; Larsson, R. Numerical simulation of a wear experiment. Wear 2011, 271, 2947–2952. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q.; Liu, G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Ahmed, R.; Ali, O.; Faisal, N.H.; El-Sherik, A.M.; Goosen, M.F.A. Finite Element Modeling of Sliding Wear in a Composite Alloy Using a Free-Mesh. J. Tribol. Trans. ASME 2015, 137, 27. [Google Scholar] [CrossRef]
- Sfantos, G.; Aliabadi, M. A boundary element formulation for three-dimensional sliding wear simulation. Wear 2007, 262, 672–683. [Google Scholar] [CrossRef]
- Terwey, J.T.; Berninger, S.; Burghardt, G.; Jacobs, G.; Poll, G. Numerical Calculation of Local Adhesive Wear in Machine Elements Under Boundary Lubrication Considering the Surface Roughness. In Proceedings of the 7th International Conference on Fracture Fatigue and Wear; Abdel Wahab, M., Ed.; Springer: Singapore, 2019; pp. 796–807. ISBN 978-981-13-0410-1. [Google Scholar]
- Terwey, J.T.; Fourati, M.A.; Pape, F.; Poll, G. Energy-Based Modelling of Adhesive Wear in the Mixed Lubrication Regime. Lubricants 2020, 8, 16. [Google Scholar] [CrossRef] [Green Version]
- Zhu, N.; Martini, A.; Wang, W.; Hu, Y.; Lisowsky, B.; Wang, Q.J. Simulation of Sliding Wear in Mixed Lubrication. J. Tribol. 2007, 129, 544–552. [Google Scholar] [CrossRef]
- Zhu, N.; Hu, Y.-Z. A Computer Program Package for the Prediction of EHL and Mixed Lubrication Characteristics, Friction, Subsurface Stresses and Flash Temperatures Based on Measured 3-D Surface Roughness. Tribol. Trans. 2001, 44, 383–390. [Google Scholar] [CrossRef]
- Hu, Y.-Z.; Zhu, N. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 1999, 122, 1–9. [Google Scholar] [CrossRef]
- Lorentz, B.; Albers, A. A numerical model for mixed lubrication taking into account surface topography, tangential adhesion effects and plastic deformations. Tribol. Int. 2013, 59, 259–266. [Google Scholar] [CrossRef]
- Reichert, S.; Lorentz, B.; Heldmaier, S.; Albers, A. Wear simulation in non-lubricated and mixed lubricated contacts taking into account the microscale roughness. Tribol. Int. 2016, 100, 272–279. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. A Thermodynamic Approach for Prediction of Wear Coefficient Under Unlubricated Sliding Condition. Tribol. Lett. 2010, 38, 347–354. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Thermoelastohydrodynamic Analysis of Spur Gears with Consideration of Surface Roughness. Tribol. Lett. 2008, 32, 129–141. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
- Hao, L.; Meng, Y. Numerical Prediction of Wear Process of an Initial Line Contact in Mixed Lubrication Conditions. Tribol. Lett. 2015, 60, 443. [Google Scholar] [CrossRef]
- Chang, W.-R.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Zhang, Y.; Kovalev, A.; Hayashi, N.; Nishiura, K.; Meng, Y. Numerical Prediction of Surface Wear and Roughness Parameters During Running-In for Line Contacts Under Mixed Lubrication. J. Tribol. Trans. ASME 2018, 140, 061501. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Static Friction Model for Elastic-Plastic Contacting Rough Surfaces. J. Tribol. 2004, 126, 34–40. [Google Scholar] [CrossRef]
- Sugimura, J.; Kimura, Y. Characterization of topographical changes during lubricated wear. Wear 1984, 98, 101–116. [Google Scholar] [CrossRef]
- Sugimura, J.; Kimura, Y.; Amino, K. Analysis of the topographical changes due to wear—Geometry of the running-in process. J. Jpn. Soc. Lubr. Eng. 1986, 31, 813–820. [Google Scholar]
- Kimura, Y.; Sugimura, J. Microgeometry of sliding surfaces and wear particles in lubricated contact. Wear 1984, 100, 33–45. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, H.; Kovalev, A.; Meng, Y. Numerical Running-In Method for Modifying Cylindrical Roller Profile Under Mixed Lubrication of Finite Line Contacts. J. Tribol. 2019, 141, 041401. [Google Scholar] [CrossRef]
- Evans, H.; Snidle, B. Analysis of micro-elastohydrodynamic lubrication for engineering contacts. Tribol. Int. 1996, 29, 659–667. [Google Scholar] [CrossRef]
- Johnson, K.; Greenwood, J.A.; Poon, S. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Roelands, C.J.A.; Winer, W.O.; Wright, W.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils (Dr In dissertation at Technical University of Delft, 1966). J. Lubr. Technol. 1971, 93, 209–210. [Google Scholar] [CrossRef] [Green Version]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Elastic Contact of Rough Spheres. J. Appl. Mech. 1967, 34, 153–159. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Thomas, T. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- McCool, J.I. Comparison of models for the contact of rough surfaces. Wear 1986, 107, 37–60. [Google Scholar] [CrossRef]
- Halling, J.; Nuri, K. Elastic/plastic contact of surfaces considering ellipsoidal asperities of work-hardening multi-phase materials. Tribol. Int. 1991, 24, 311–319. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An Asperity Microcontact Model Incorporating the Transition From Elastic Deformation to Fully Plastic Flow. J. Tribol. 2000, 122, 86. [Google Scholar] [CrossRef]
- Jamari, J.; Schipper, D.J. An elastic–plastic contact model of ellipsoid bodies. Tribol. Lett. 2006, 21, 262–271. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A Finite Element Study of Elasto-Plastic Hemispherical Contact Against a Rigid Flat. J. Tribol. 2005, 127, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.L.; Green, I. A statistical model of elasto-plastic asperity contact between rough surfaces. Tribol. Int. 2006, 39, 906–914. [Google Scholar] [CrossRef]
- Nayak, P.R. Random Process Model of Rough Surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Bush, A.; Gibson, R.; Keogh, G. The limit of elastic deformation in the contact of rough surfaces. Mech. Res. Commun. 1976, 3, 169–174. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. Asperity micro-contact models as applied to the deformation of rough line contact. Tribol. Int. 2012, 52, 61–74. [Google Scholar] [CrossRef]
- Hartinger, M.; Dumont, M.-L.; Ioannides, S.; Gosman, D.; Spikes, H. CFD Modeling of a Thermal and Shear-Thinning Elastohydrodynamic Line Contact. J. Tribol. 2008, 130, 041503. [Google Scholar] [CrossRef]
- Hartinger, M.; Gosman, D.; Ioannides, S.; Spikes, H. Two-and Three-Dimensional CFD Modelling of Elastohydrodynamic Lubrication. In Proceedings of the 34th Leeds–Lyon Symposium on Tribology, Lyon, France, 4–7 September 2007. [Google Scholar]
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- Venner, C.H.; Lubrecht, A.A. Multilevel Methods in Lubrication; 1. Auflage; Elsevier: Amsterdam, The Netherlands, 2000; ISBN 0-444-50503-2. [Google Scholar]
- Habchi, W.; Demirci, I.; Eyheramendy, D.; Morales-Espejel, G.; Vergne, P. A finite element approach of thin film lubrication in circular EHD contacts. Tribol. Int. 2007, 40, 1466–1473. [Google Scholar] [CrossRef]
- Marian, M.; Weschta, M.; Tremmel, S.; Wartzack, S. Simulation of Microtextured Surfaces in Starved EHL Contacts Using Commercial FE Software. Mater. Perform. Charact. 2017, 6, 165–181. [Google Scholar] [CrossRef]
- Brooks, A.N.; Hughes, T.J. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics; 7. Aufl.; Elsevier Butterworth-Heinemann: Oxford, UK, 2014; ISBN 1306160901. [Google Scholar]
- Marian, M.; Grützmacher, P.G.; Rosenkranz, A.; Tremmel, S.; Mücklich, F.; Wartzack, S. Designing surface textures for EHL point-contacts—Transient 3D simulations, meta-modeling and experimental validation. Tribol. Int. 2019, 137, 152–163. [Google Scholar] [CrossRef]
- Kragelsky, I.V.; Alisin, V.V. Friction Wear Lubrication: Tribology Handbook; Elsevier Science & Technology, ProQuest: Kent, UK; Ann Arbor, MI, USA, 2016; ISBN 9781483165950. [Google Scholar]
- Fleischer, G.; Gröger, H.; Thum, H. Verschleiß und Zuverlässigkeit; Verl. Technik: Berlin, Germany, 1980. [Google Scholar]
- Archard, J.F.; Hirst, W. The wear of metals under unlubricated conditions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts: Theory and Application, Fourth Completely Rewritten ed.; Springer: Berlin/Heidelberg, Germany, 1967; ISBN 978-3-662-06688-1. [Google Scholar]
- Wriggers, P.; Laursen, T.A. Computational Contact Mechanics; Springer: Wien, Austria; New York, NY, USA, 2007; ISBN 978-3-540-32609-0. [Google Scholar]
- Bhushan, B. Modern Tribology Handbook; CRC Press: Boca Raton, FL, USA, 2001; ISBN 9780849384035. [Google Scholar]
- Czichos, H.; Habig, K.-H. Tribologie-Handbuchb. Tribometrie, Tribomaterialien, Tribotechnik; 4, vollst. überarb. u. erw. Aufl. 2015; Springer: Wiesbaden, Germany, 2015; ISBN 978-3-8348-2236-9. [Google Scholar]
- Habchi, W. Finite Element Modeling of Elastohydrodynamic Lubrication Problems; John Wiley & Sons Incorporated: Newark, NJ, USA, 2018; ISBN 978-1119225126. [Google Scholar]



| Operating Parameters | Load Case 1 | Load Case 2 | Load Case 3 | Load Case 4 |
|---|---|---|---|---|
| load F | 7.5 kN | 7.5 kN | 15.0 kN | 15.0 kN |
| initial Hertzian pressure pHertz | 0.5 GPa | 0.5 GPa | 0.7 GPa | 0.7 GPa |
| rotational speed n | 250 min−1 | 500 min−1 | 250 min−1 | 500 min−1 |
| test duration t | 20 h | 10 h | 20 h | 10 h |
| Lubricant Properties | FVA 1 | FVA 2 |
|---|---|---|
| base density ρ0 | 843 kg/m³ | 852 kg/m³ |
| base viscosity η0 | 0.014 Pa∙s | 0.026 Pa∙s |
| pressure-viscosity coefficient αp | 16.7 GPa−1 | 17.7 GPa−1 |
| Lubricant | Load Case 1 | Load Case 2 | Load Case 3 | Load Case 4 |
|---|---|---|---|---|
| FVA 1 | 5.1 mg | 3.6 mg | 10.8 mg | 7.2 mg |
| FVA 2 | 3.7 mg | 2.0 mg | 7.4 mg | 3.4 mg |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkler, A.; Marian, M.; Tremmel, S.; Wartzack, S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants 2020, 8, 58. https://doi.org/10.3390/lubricants8050058
Winkler A, Marian M, Tremmel S, Wartzack S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants. 2020; 8(5):58. https://doi.org/10.3390/lubricants8050058
Chicago/Turabian StyleWinkler, Andreas, Max Marian, Stephan Tremmel, and Sandro Wartzack. 2020. "Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication" Lubricants 8, no. 5: 58. https://doi.org/10.3390/lubricants8050058
APA StyleWinkler, A., Marian, M., Tremmel, S., & Wartzack, S. (2020). Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants, 8(5), 58. https://doi.org/10.3390/lubricants8050058