CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface
Abstract
:1. Introduction
2. Theory
2.1. Governing Equations
2.2. Cavitation Modeling
2.3. Roughness Modeling
3. Simulation Method
3.1. Model
3.2. Meshing
3.3. Assumption and Boundary Condition
3.4. Solution Setup
4. Results and Discussion
4.1. Validation
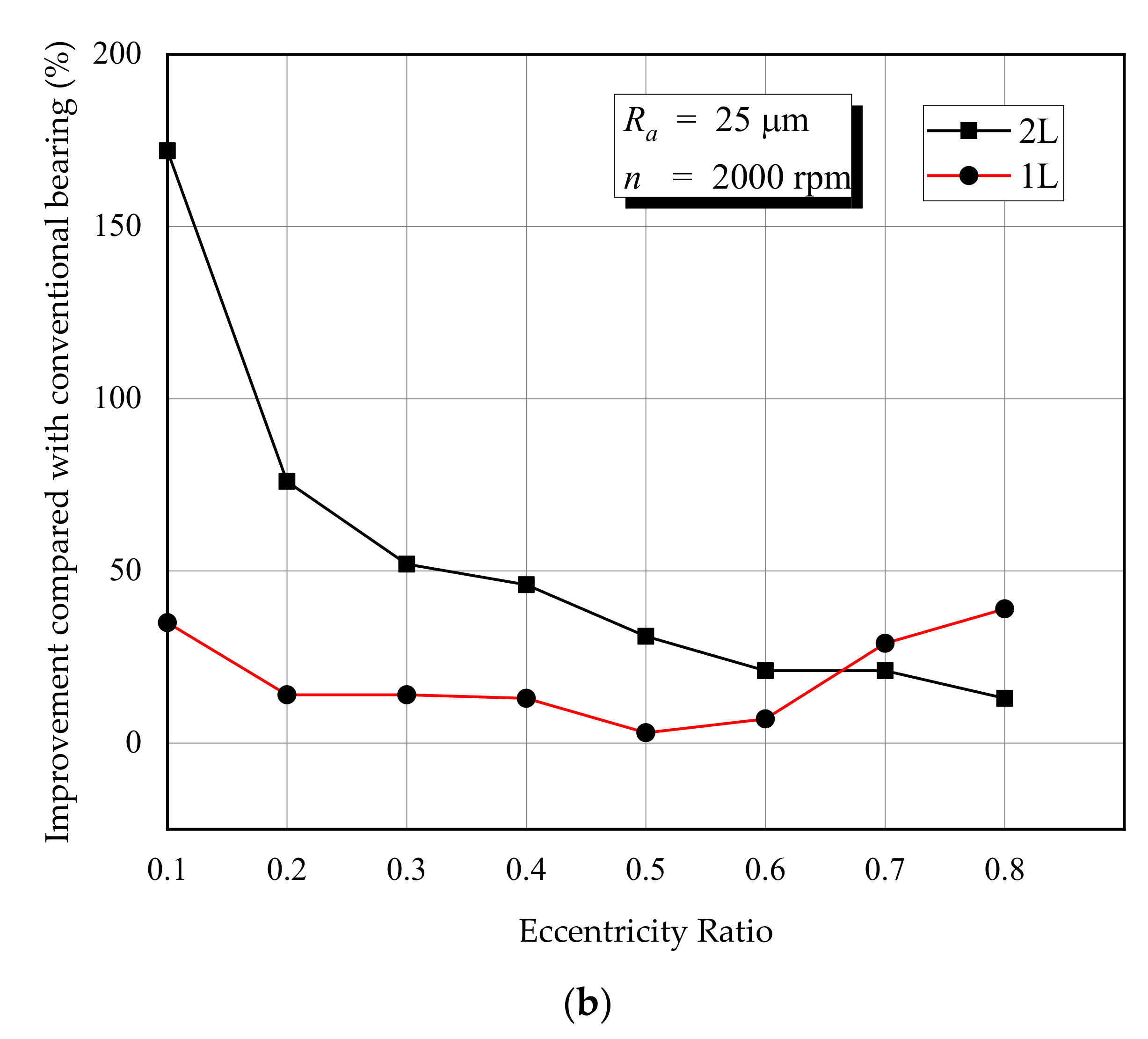
4.2. At Varied Eccentricity Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Local speed of the sound | |
| B | Bearing width |
| c | Radial clearance |
| Cs | Roughness constant |
| D | Bearing diameter |
| E | Empirical constant |
| fr | Roughness function |
| Fevap | Evaporation coefficient |
| Fcond | Condensation coefficient |
| hmin | Minimum film thickness |
| hmax | Maximum film thickness |
| Ks | Roughness height |
| k | Turbulent kinetic energy |
| l | Length scale |
| Lθ | Circumferential length of the bearing |
| n | Rotational speed |
| p | Hydrodynamic pressure |
| PA | Acoustic power level |
| psat | Saturation pressure |
| W | Load-carrying capacity |
| r | Shaft radius |
| R | Bearing radius |
| Ra | Arithmetic average of the roughness profile |
| RB | Bubble radius |
| Rec | Critical Reynolds number |
| Rer | Real Reynolds number |
| Rg, Rc | Mass transfer between the liquid and vapor phase |
| up | Mean velocity of the fluid at the near-wall node P |
| u* | dimensionless velocity |
| yp | Distance from point P to the wall |
| αnuc | Nucleation site volume fraction |
| αv | Vapor volume fraction |
| ε | Eccentricity ratio |
| εd | Turbulent dissipation rate |
| von Karman constant | |
| Circumferential angle | |
| µ | Lubricant viscosity |
| µv | Vapor viscosity |
| ρ | Lubricant density |
| ρv | Vapor density |
| Attitude angle |
References
- Malcolm, E.; Leader, P.E. Understanding Journal Bearings; Applied Machinery Dynamics, Co.: Durango, CO, USA, 2001. [Google Scholar]
- Tala-Ighil, N.; Fillon, M.; Maspeyrot, P. Effect of textured area on the performances of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 211–219. [Google Scholar] [CrossRef]
- Brizmer, V.; Kligerman, Y. A laser surface textured journal bearing. J. Tribol. 2012, 134, 031702. [Google Scholar] [CrossRef]
- Ji, J.; Fu, Y.; Bi, Q. Influence of geometric shapes on the hydrodynamic lubrication of a partially textured slider with micro-grooves. J. Tribol. 2014, 136, 041702. [Google Scholar] [CrossRef]
- Meng, F.M.; Zhang, L.; Liu, Y.; Li, T.T. Effect of compound dimple on tribological performances of journal bearing. Tribol. Int. 2015, 91, 99–110. [Google Scholar] [CrossRef]
- Meng, F.M.; Wei, Z.; Minggang, D.; Gao, G. Study of acoustic performance of textured journal bearing. Proc. Ins. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 156–169. [Google Scholar] [CrossRef]
- Meng, F.M.; Zhang, W. Effects of compound groove texture on noise of journal bearing. J. Tribol. 2017, 140, 031703. [Google Scholar] [CrossRef]
- Meng, F.; Yu, H.; Gui, C.; Chen, L. Experimental study of compound texture effect on acoustic performance for lubricated textured surfaces. Tribol. Int. 2019, 133, 47–54. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Lin, J.; Ma, L. Study on lubrication performance of journal bearing with multiple texture distributions. Appl. Sci. 2018, 8, 244. [Google Scholar] [CrossRef] [Green Version]
- Manser, B.; Belaidi, I.; Khelladi, S.; Chikh, M.A.A.; Deligant, M.; Bakir, F. Computational investigation on the performance of hydrodynamic micro-textured journal bearing lubricated with micropolar fluid using mass-conserving numerical approach. Proc. Ins. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1310–1331. [Google Scholar] [CrossRef]
- Saleh, A.M.; Crosby, W.; El Fahham, I.M.; Elhadary, M. The effect of liner surface texture on journal bearing performance under thermo-hydrodynamic conditions. Ind. Lub. Tribol. 2020, 72, 405–414. [Google Scholar] [CrossRef]
- Javorova, J. EHD lubrication of journal bearings with rough surfaces. In Proceedings of the International Conference “Mechanical Engineering in XXI Century”, Nis, Serbia, 25–26 November 2010. [Google Scholar]
- Hsu, T.C.; Chen, J.H.; Chiang, H.L.; Chou, T.L. Lubrication performance of short journal bearings considering the effects of surface roughness and magnetic field. Tribol. Int. 2013, 61, 169–175. [Google Scholar] [CrossRef]
- Kalavathi, G.K.; Dinesh, P.A.; Gururajan, K. Influence of roughness on porous finite journal bearing with heterogeneous slip/no-slip surface. Tribo. Int. 2016, 102, 174–181. [Google Scholar] [CrossRef]
- Cui, S.; Gu, L.; Fillon, M.; Wang, L.; Zhang, C. The effects of surface roughness on the transient characteristics of hydrodynamic cylindrical bearings during startup. Tribol. Int. 2018, 128, 421–428. [Google Scholar] [CrossRef]
- Abd Al-Samieh, M.F. Surface roughness effects for Newtonian and non-Newtonian lubricants. Tribol. Ind. 2019, 41, 56–63. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Ichsan, B.C.; Jamari, M. Influence of roughness on the behavior of three-dimensional journal bearing based on fluid-structure interaction approach. J. Mech. Sci. Technol. 2019, 33, 4783–4790. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Wang, S.; Ding, X. Study on the mutual influence of surface roughness and texture features of rough-textured surfaces on the tribological properties. Proc. Ins. Mech. Eng. Part J. J. Eng. Tribol. 2021, 235, 256–273. [Google Scholar] [CrossRef]
- Fortier, A.E.; Salant, R.F. Numerical analysis of a journal bearing with a heterogeneous slip/no-slip surface. J. Tribol. 2005, 127, 820–825. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Wei, Z.; Zhang, Y.; Wang, N. Effects of the slip surface on the tribological performances of high-speed hybrid journal bearings. Proc. Ins. Mech. Eng. Part. J J. Eng. Tribol. 2016, 230, 1149–1156. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Dutt, J.K.; Pandey, R.K. Influence of hydrodynamic journal bearings with multiple slip zones on rotordynamic behavior. J. Tribol. 2017, 139, 061701. [Google Scholar] [CrossRef]
- Wu, Z.; Ding, X.; Zeng, L.; Chen, X.; Chen, K. Optimization of hydrodynamic lubrication performance based on a heterogeneous slip/no-slip surface. Ind. Lubr. Tribol. 2019, 71, 772–778. [Google Scholar] [CrossRef]
- Cui, S.; Zhang, C.; Fillon, M.; Gu, L. Optimization performance of plain journal bearings with partial wall slip. Tribol. Int. 2020, 145, 106–137. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Afif, M.F.; Paryanto, P.; Jamari, J.; Caesarendra, W. Investigation of the tribological performance of heterogeneous slip/no-slip journal bearing considering thermo-hydrodynamic effects. Fluids 2021, 6, 48. [Google Scholar] [CrossRef]
- Dhande, D.Y.; Pande, D.W. Multiphase flow analysis of hydrodynamic journal bearing using CFD coupled fluid structure interaction considering cavitation. J. King Saud Univ. Eng. Sci. 2018, 30, 345–354. [Google Scholar] [CrossRef] [Green Version]
- Morris, N.J.; Shahmohamadi, H.; Rahmani, R.; Rahnejat, H.; Garner, C.P. Combined experimental and multiphase computational fluid dynamics analysis of surface textured journal bearings in mixed regime of lubrication. Lubr. Sci. 2018, 30, 161–173. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Li, S.; Fei, C.; Ai, Y.; Liem, R.P. Investigation of the effect of cavitation and journal whirl on static and dynamic characteristics of journal bearing. J. Mech. Sci. Technol. 2019, 33, 77–86. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Wibowo, B.S.; Fauzan, H.M.; Muchammad, M. Multiphase computational fluid dynamics analysis of hydrodynamic journal bearing under the combined influence of texture and slip. Lubricants 2019, 7, 97. [Google Scholar] [CrossRef] [Green Version]
- ANSYS. ANSYS Fluent, Version 16.0: User Manual; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Zwart, P.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamic. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May 2004. [Google Scholar]
- Adams, T.; Grant, C.; Watson, H. A Simple algorithm to relate measured surface roughness to equivalent sand-grain roughness. Int. J. Mech. Eng. Mechatron. 2012, 1, 66–71. [Google Scholar] [CrossRef]
- Gao, G.; Yin, Z.; Jiang, D.; Zhang, X.; Wang, Y. Analysis on design parameters of water-lubricated journal bearings under hydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1019–1029. [Google Scholar] [CrossRef]
- Japanese Industrial Standard/Japanese Standards Association. JIS B 0601:2013 Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters (Foreign Standard); Japanese Industrial Standard/Japanese Standards Association: Tokyo, Japan, January 2013. [Google Scholar]
- Patankar, N.A. On the modeling of hydrophobic contact angles on rough surfaces. Langmuir 2003, 19, 1249–1253. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Contact angle, adhesion and friction properties of micro and nanopatterned polymers for superhydrophobicity. Nanotechnology 2006, 17, 4970–4980. [Google Scholar] [CrossRef]

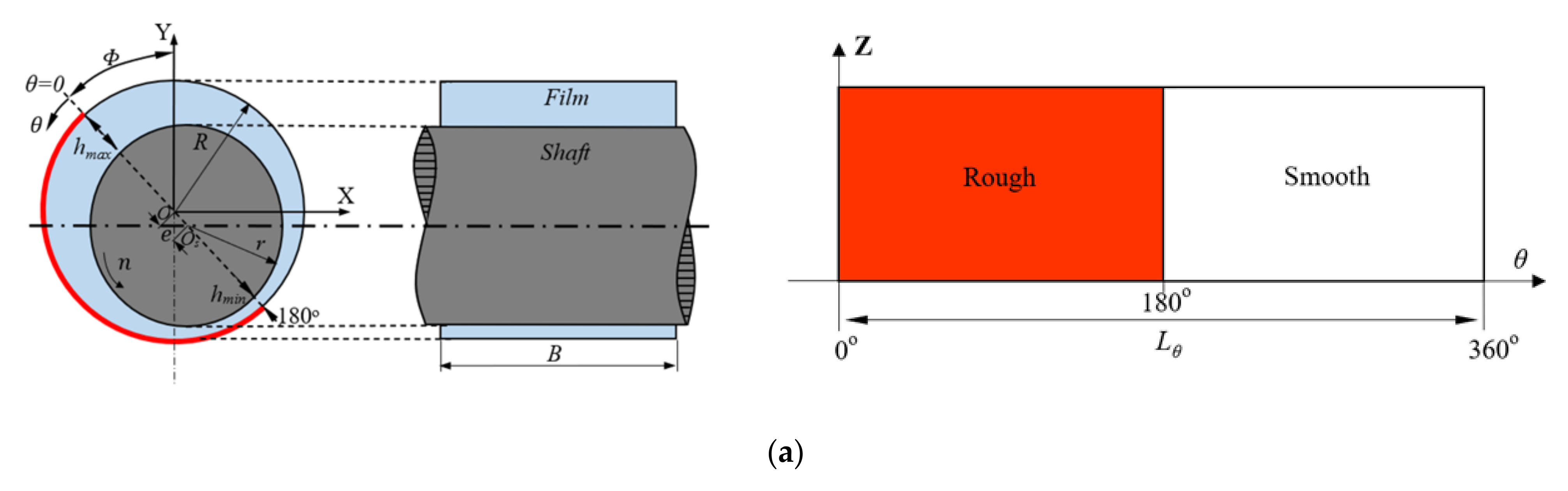
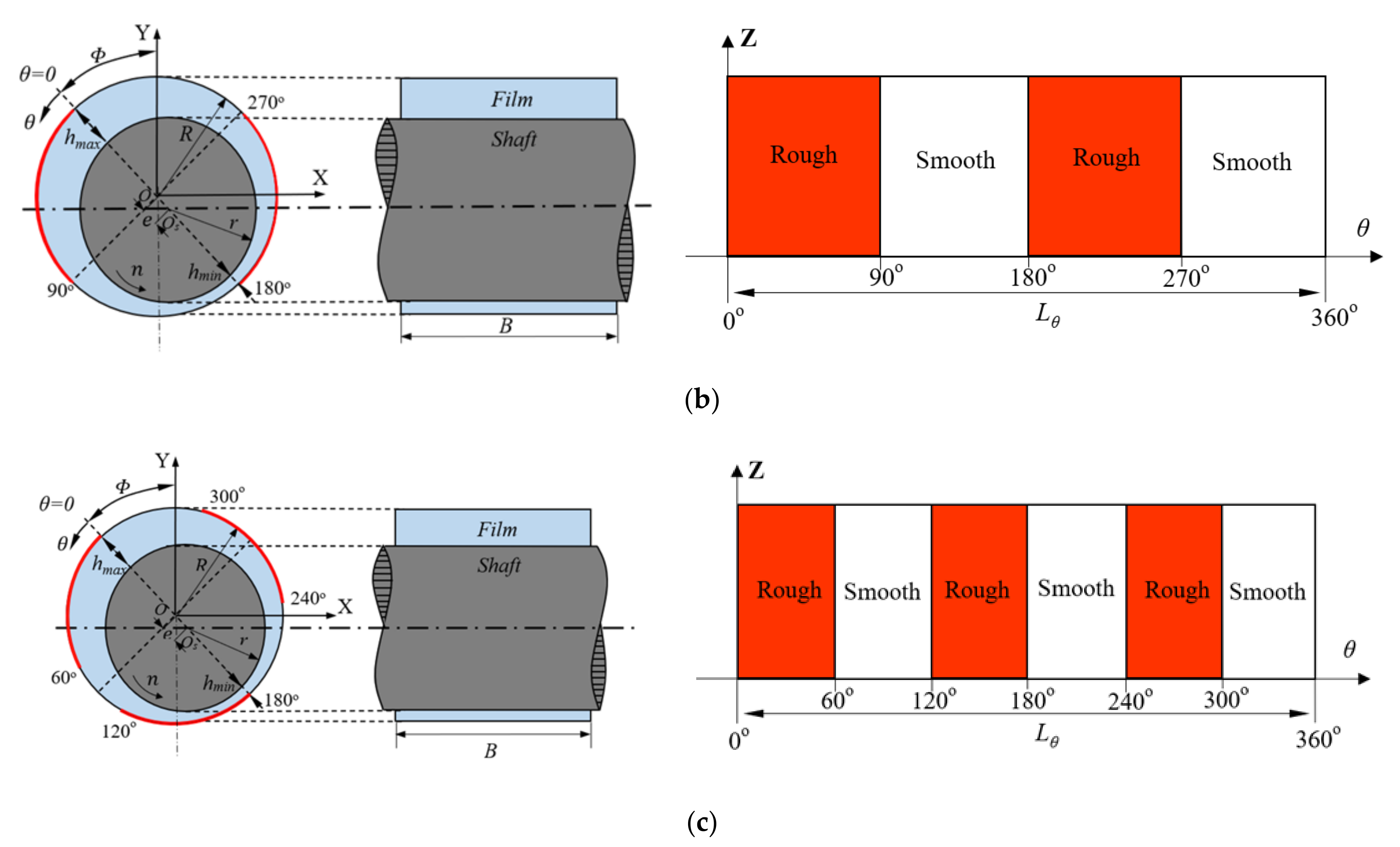
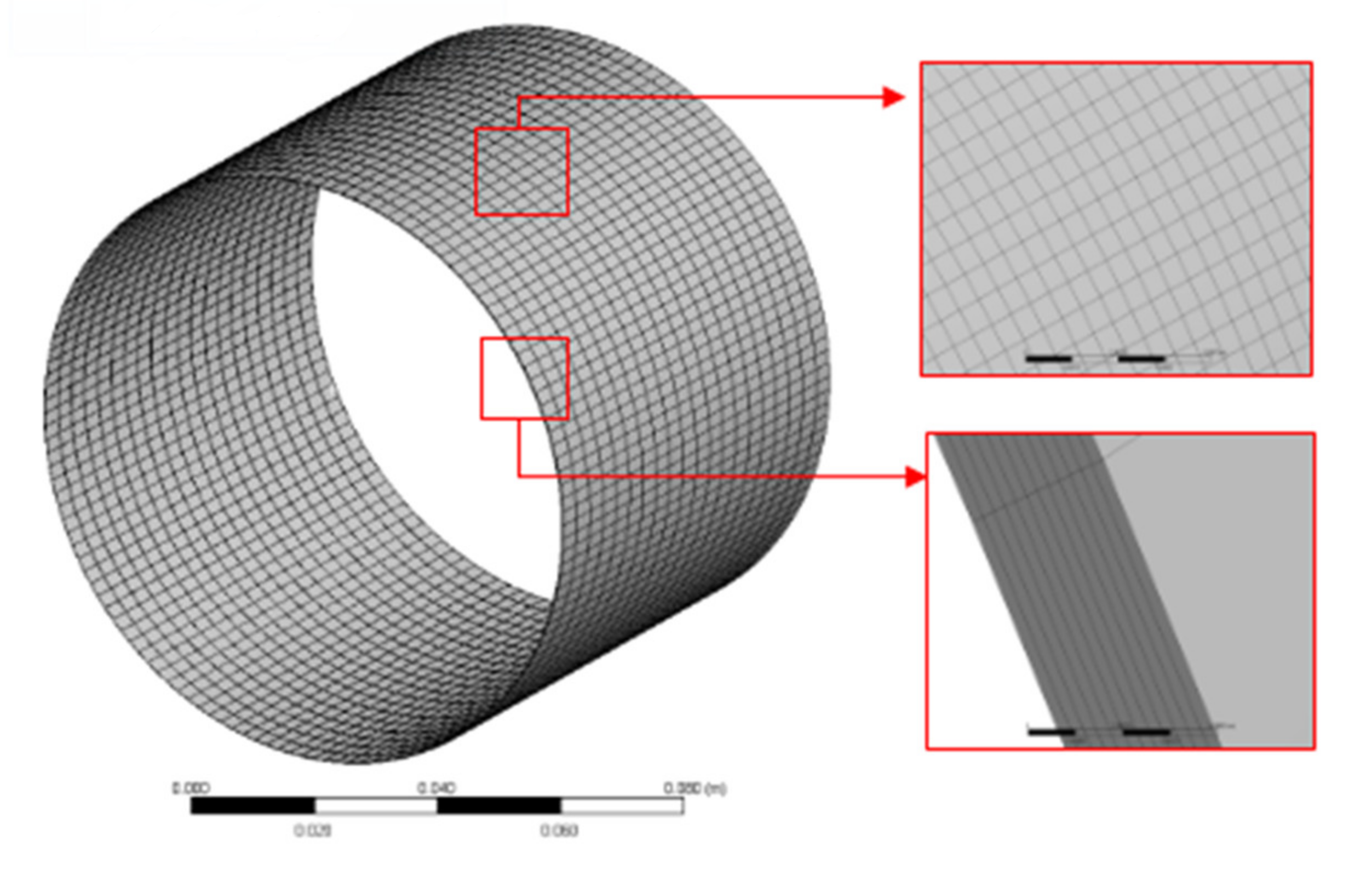











| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Bearing radius | R | 50 | mm |
| Width-diameter ratio | B/D | 0.8 | [[–] |
| Radial clearance | 0.152 | mm | |
| Eccentricity ratio | 0; 0.1; 0.2; 0.3; 0.4; 0.5; 0.6; 0.7; 0.8 | [[–] | |
| Attitude angle | 54 | Deg | |
| Fluid density | 998.2 | kg/m3 | |
| Fluid viscosity | 0.001005 | Pa.s | |
| Rotational speed | 2000 | rpm | |
| Saturation pressure | psat | 2340 | Pa |
| Vapor density | 0.5542 | kg/m3 | |
| Vapor viscosity | 1.34 × 10−5 | Pa.s | |
| Roughness level | Ra | 25 | μm |
| Mesh Criteria | Value |
|---|---|
| Edge sizing 1 | 400 division |
| Edge sizing 2 | 60 division |
| Face Meshing | 12-layers of division |
| Method | Sweep |
| Element number | 288,000 |
| For case ε = 0 | |
| Maximum skewness | 9.137 × 10−2 |
| Minimum skewness | 7.194 × 10−3 |
| Average skewness | 5.703 × 10−2 |
| For case ε > 0 | |
| Maximum skewness | 0.155 |
| Minimum skewness | 5.019 × 10−3 |
| Average skewness | 5.604 × 10−2 |
| Boundary Condition | Setup |
|---|---|
| Inlet | Pressure inlet (0 Pa) |
| Outlet | Pressure outlet (0 Pa) |
| Stationary wall | No-slip |
| Moving wall | No slip, n = 2000 rpm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tauviqirrahman, M.; Jamari, J.; Wicaksono, A.A.; Muchammad, M.; Susilowati, S.; Ngatilah, Y.; Pujiastuti, C. CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface. Lubricants 2021, 9, 88. https://doi.org/10.3390/lubricants9090088
Tauviqirrahman M, Jamari J, Wicaksono AA, Muchammad M, Susilowati S, Ngatilah Y, Pujiastuti C. CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface. Lubricants. 2021; 9(9):88. https://doi.org/10.3390/lubricants9090088
Chicago/Turabian StyleTauviqirrahman, Mohammad, J. Jamari, Arjuno Aryo Wicaksono, M. Muchammad, S. Susilowati, Yustina Ngatilah, and Caecilia Pujiastuti. 2021. "CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface" Lubricants 9, no. 9: 88. https://doi.org/10.3390/lubricants9090088
APA StyleTauviqirrahman, M., Jamari, J., Wicaksono, A. A., Muchammad, M., Susilowati, S., Ngatilah, Y., & Pujiastuti, C. (2021). CFD Analysis of Journal Bearing with a Heterogeneous Rough/Smooth Surface. Lubricants, 9(9), 88. https://doi.org/10.3390/lubricants9090088






