Comparison of Static and Dynamic Assays When Quantifying Thermal Plasticity of Drosophilids
Abstract
:Simple Summary
Abstract
1. Introduction
2. Methods and Materials:
2.1. Animal Husbandry
2.2. Experimental Protocol
2.3. Data Analysis
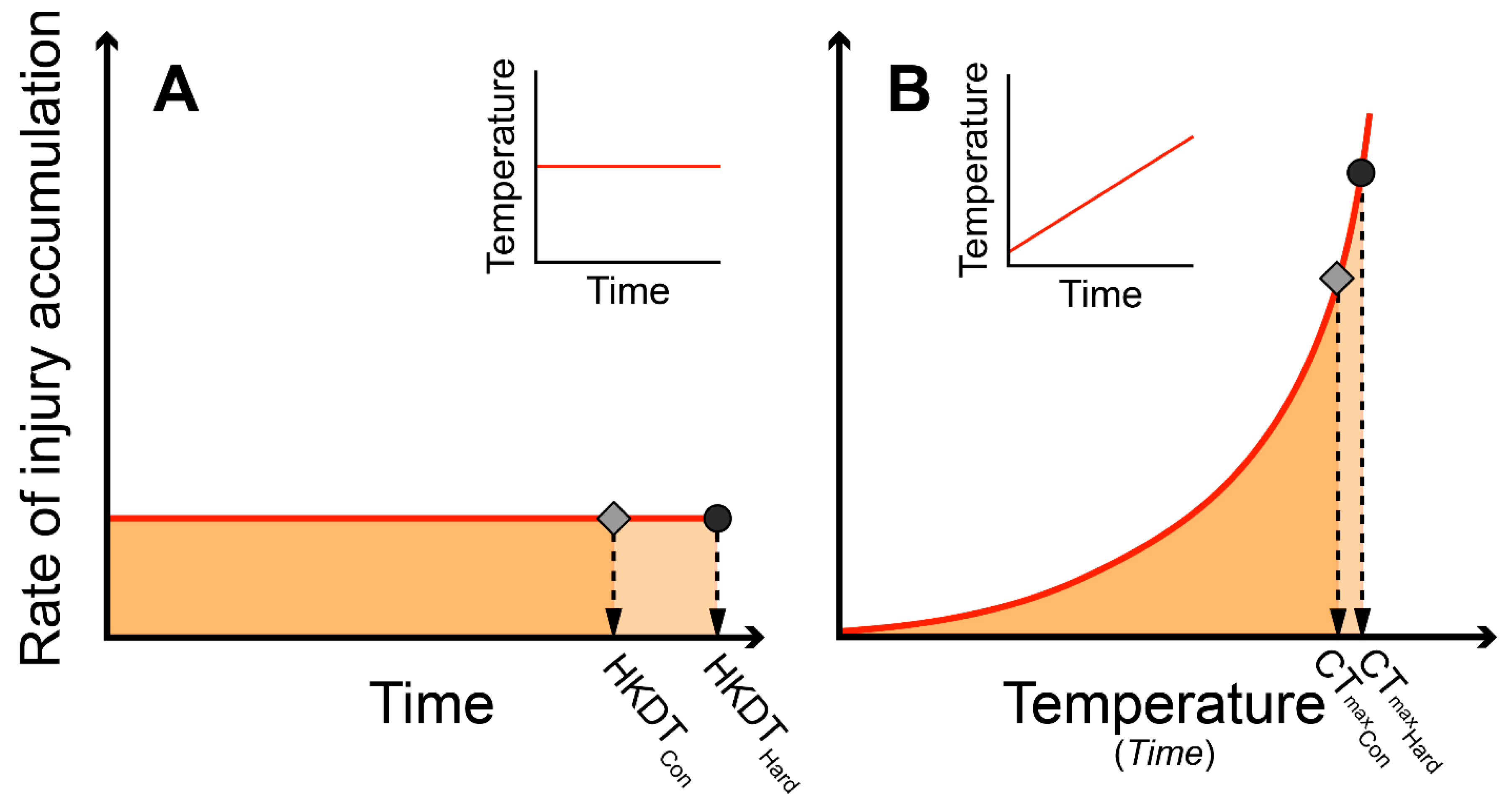
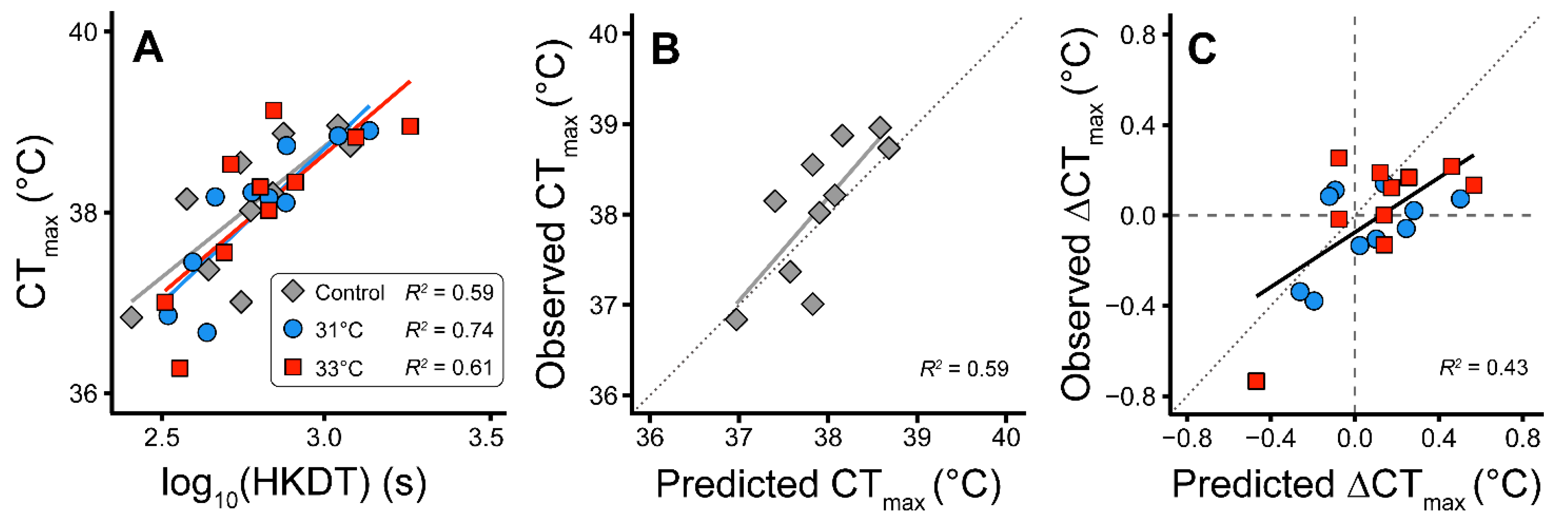
2.4. Predicting CTmax from HKDT (Heat Knockdown Time)
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rezende, E.L.; Tejedo, M.; Santos, M. Estimating the adaptive potential of critical thermal limits: Methodological problems and evolutionary implications. Funct. Ecol. 2011, 25, 111–121. [Google Scholar] [CrossRef] [Green Version]
- Santos, M.; Castañeda, L.E.; Rezende, E.L. Making sense of heat tolerance estimates in ectotherms: Lessons from Drosophila. Funct. Ecol. 2011, 25, 1169–1180. [Google Scholar] [CrossRef]
- Terblanche, J.S.; Hoffmann, A.A.; Mitchell, K.A.; Rako, L.; le Roux, P.C.; Chown, S.L. Ecologically relevant measures of tolerance to potentially lethal temperatures. J. Exp. Biol. 2011, 214, 3713–3725. [Google Scholar] [CrossRef] [Green Version]
- Kristensen, T.N.; Hoffmann, A.A.; Overgaard, J.; Sørensen, J.G.; Hallas, R.; Loeschcke, V. Costs and benefits of cold acclimation in field-released Drosophila. Proc. Natl. Acad. Sci. USA 2008, 105, 216–221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinclair, B.J.; Alvarado, L.E.C.; Ferguson, L.V. An invitation to measure insect cold tolerance: Methods, approaches, and workflow. J. Therm. Boil. 2015, 53, 180–197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovacevic, A.; Latombe, G.; Chown, S.L. Rate dynamics of ectotherm responses to thermal stress. Proc. R. Soc. B Biol. Sci. 2019, 286, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoffmann, A.A.; Sørensen, J.G.; Loeschcke, V. Adaptation of Drosophila to temperature extremes: Bringing together quantitative and molecular approaches. J. Therm. Biol. 2003, 28, 175–216. [Google Scholar] [CrossRef]
- Lutterschmidt, W.I.; Hutchison, V.H. The critical thermal maximum: History and critique. Can. J. Zool. 1997, 75, 1561–1574. [Google Scholar] [CrossRef]
- Jørgensen, L.B.; Malte, H.; Overgaard, J. How to assess Drosophila heat tolerance: Unifying static and dynamic tolerance assays to predict heat distribution limits. Funct. Ecol. 2019, 33, 629–642. [Google Scholar] [CrossRef]
- Rezende, E.L.; Castañeda, L.E.; Santos, M. Tolerance landscapes in thermal ecology. Funct. Ecol. 2014, 28, 799–809. [Google Scholar] [CrossRef]
- Lanciani, C.A.; Lipp, K.E.; Giesel, J.T. The effect of photoperiod on cold tolerance in Drosophila melanogaster. J. Therm. Biol. 1992, 17, 147–148. [Google Scholar] [CrossRef]
- Moghadam, N.N.; Kurbalija Novicic, Z.; Pertoldi, C.; Kristensen, T.N.; Bahrndorff, S. Effects of photoperiod on life-history and thermal stress resistance traits across populations of Drosophila subobscura. Ecol. Evol. 2019, 9, 2743–2754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hollingsworth, M.J.; Bowler, K. The decline in ability to withstand high temperature with increase in age in Drosophila subobscura. Exp. Gerontol. 1966, 1, 251–257. [Google Scholar] [CrossRef]
- Bowler, K.; Terblanche, J.S. Insect thermal tolerance: What is the role of ontogeny, ageing and senescence? Biol. Rev. 2008, 83, 339–355. [Google Scholar] [CrossRef]
- Sinclair, B.J.; Klok, C.J.; Scott, M.B.; Terblanche, J.S.; Chown, S.L. Diurnal variation in supercooling points of three species of Collembola from Cape Hallett, Antarctica. J. Insect Physiol. 2003, 49, 1049–1061. [Google Scholar] [CrossRef]
- McMillan, D.M.; Fearnley, S.L.; Rank, N.E.; Dahlhoff, E.P. Natural temperature variation affects larval survival, development and Hsp70 expression in a leaf beetle. Funct. Ecol. 2005, 19, 844–852. [Google Scholar] [CrossRef]
- Kelty, J. Rapid cold-hardening of Drosophila melanogaster in a field setting. Physiol. Entomol. 2007, 32, 343–350. [Google Scholar] [CrossRef]
- Terblanche, J.S.; Sinclair, B.J.; Klok, C.J.; McFarlane, M.L.; Chown, S.L. The effects of acclimation on thermal tolerance, desiccation resistance and metabolic rate in Chirodica chalcoptera (Coleoptera: Chrysomelidae). J. Insect Physiol. 2005, 51, 1013–1023. [Google Scholar] [CrossRef]
- Bahrndorff, S.; Gertsen, S.; Pertoldi, C.; Kristensen, T.N. Investigating thermal acclimation effects before and after a cold shock in Drosophila melanogaster using behavioural assays. Biol. J. Linn. Soc. 2016, 117, 241–251. [Google Scholar] [CrossRef] [Green Version]
- MacLean, H.J.; Kristensen, T.N.; Overgaard, J.; Sørensen, J.G.; Bahrndorff, S. Acclimation responses to short-term temperature treatments during early life stages causes long lasting changes in spontaneous activity of adult Drosophila melanogaster. Physiol. Entomol. 2017, 42, 404–411. [Google Scholar] [CrossRef]
- Schou, M.F.; Kristensen, T.N.; Pedersen, A.; Karlsson, B.G.; Loeschcke, V.; Malmendal, A. Metabolic and functional characterization of effects of developmental temperature in Drosophila melanogaster. Am. J. Physiol. Integr. Comp. Physiol. 2017, 312, R211–R222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kelty, J.D.; Lee, R.E. Rapid cold-hardening of Drosophila melanogaster (Diptera: Drosophiladae) during ecologically based thermoperiodic cycles. J. Exp. Biol. 2001, 204, 1659–1666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowler, K. Acclimation, heat shock and hardening. J. Therm. Biol. 2005, 30, 125–130. [Google Scholar] [CrossRef]
- Bahrndorff, S.; Mariën, J.; Loeschcke, V.; Ellers, J. Dynamics of heat-induced thermal stress resistance and hsp70 expression in the springtail, Orchesella cincta. Funct. Ecol. 2009, 23, 233–239. [Google Scholar] [CrossRef]
- Bubli, O.A.; Imasheva, A.G.; Loeschcke, V. Selection for Knockdown Resistance to Heat in Drosophila melanogaster at high and low larval densities. Evolution 2006, 52, 619. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, J.G.; Loeschcke, V. Larval crowding in Drosophila melanogaster induces Hsp70 expression, and leads to increased adult longevity and adult thermal stress resistance. J. Insect Physiol. 2001, 47, 1301–1307. [Google Scholar] [CrossRef]
- Nilson, T.L.; Sinclair, B.J.; Roberts, S.P. The effects of carbon dioxide anesthesia and anoxia on rapid cold-hardening and chill coma recovery in Drosophila melanogaster. J. Insect Physiol. 2006, 52, 1027–1033. [Google Scholar] [CrossRef] [Green Version]
- Milton, C.C.; Partridge, L. Brief carbon dioxide exposure blocks heat hardening but not cold acclimation in Drosophila melanogaster. J. Insect Physiol. 2008, 54, 32–40. [Google Scholar] [CrossRef]
- Rako, L.; Hoffmann, A.A. Complexity of the cold acclimation response in Drosophila melanogaster. J. Insect Physiol. 2006, 52, 94–104. [Google Scholar] [CrossRef]
- Mitchell, K.A.; Hoffmann, A.A. Thermal ramping rate influences evolutionary potential and species differences for upper thermal limits in Drosophila. Funct. Ecol. 2010, 24, 694–700. [Google Scholar] [CrossRef]
- Sgrò, C.M.; Overgaard, J.; Kristensen, T.N.; Mitchell, K.A.; Cockerell, F.E.; Hoffmann, A.A. A comprehensive assessment of geographic variation in heat tolerance and hardening capacity in populations of Drosophila melanogaster from Eastern Australia. J. Evol. Biol. 2010, 23, 2484–2493. [Google Scholar] [CrossRef] [PubMed]
- Overgaard, J.; Sørensen, J.G.; Petersen, S.O.; Loeschcke, V.; Holmstrup, M. Reorganization of membrane lipids during fast and slow cold hardening in Drosophila melanogaster. Physiol. Entomol. 2006, 31, 328–335. [Google Scholar] [CrossRef]
- Sørensen, J.G.; Loeschcke, V.; Kristensen, T.N. Cellular damage as induced by high temperature is dependent on rate of temperature change—Investigating consequences of ramping rates on molecular and organismal phenotypes in Drosophila melanogaster. J. Exp. Biol. 2012, 216, 809–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terblanche, J.S.; Deere, J.A.; Clusella-Trullas, S.; Janion, C.; Chown, S.L. Critical thermal limits depend on methodological context. Proc. R. Soc. B Biol. Sci. 2007, 274, 2935–2942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersen, J.L.; Manenti, T.; Sørensen, J.G.; Macmillan, H.A.; Loeschcke, V.; Overgaard, J. How to assess Drosophila cold tolerance: Chill coma temperature and lower lethal temperature are the best predictors of cold distribution limits. Funct. Ecol. 2015, 29, 55–65. [Google Scholar] [CrossRef]
- Overgaard, J.; Kristensen, T.N.; Sørensen, J.G. Validity of thermal ramping assays used to assess thermal tolerance in arthropods. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [Green Version]
- Cooper, B.S.; Williams, B.H.; Angilletta, M.J. Unifying indices of heat tolerance in ectotherms. J. Therm. Biol. 2008, 33, 320–323. [Google Scholar] [CrossRef]
- Mitchell, K.A.; Boardman, L.; Clusella-Trullas, S.; Terblanche, J.S. Effects of nutrient and water restriction on thermal tolerance: A test of mechanisms and hypotheses. Comp. Biochem. Physiol. Part. A Mol. Integr. Physiol. 2017, 212, 15–23. [Google Scholar] [CrossRef]
- Sørensen, M.H.; Kristensen, T.N.; Lauritzen, J.M.S.; Noer, N.K.; Høye, T.T.; Bahrndorff, S. Rapid induction of the heat hardening response in an Arctic insect. Biol. Lett. 2019, 15, 20190613. [Google Scholar] [CrossRef]
- Taylor, F. Ecology and Evolution of Physiological Time in Insects. Am. Nat. 1981, 117, 1–23. [Google Scholar] [CrossRef]
- Kilgour, D.M.; McCauley, R.W. Reconciling the two methods of measuring upper lethal temperatures in fishes. Environ. Biol. Fishes 1986, 17, 281–290. [Google Scholar] [CrossRef]
- Kellermann, V.; Loeschcke, V.; Hoffmann, A.A.; Kristensen, T.N.; Fløjgaard, C.; David, J.R.; Svenning, J.C.; Overgaard, J. Phylogenetic Constraints In Key Functional Traits Behind Species’ Climate Niches: Patterns Of Desiccation And Cold Resistance Across 95 Drosophila Species. Evolution 2012, 66, 3377–3389. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, T.N.; Henningsen, A.K.; Aastrup, C.; Bech-Hansen, M.; Bjerre, L.B.H.; Carlsen, B.; Hagstrup, M.; Jensen, S.G.; Karlsen, P.; Kristensen, L.; et al. Fitness components of Drosophila melanogaster developed on a standard laboratory diet or a typical natural food source. Insect Sci. 2016, 23, 771–779. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef] [Green Version]
- Zar, J. Biostatistical Analysis, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous Inference in General Parametric Models. Biom. J. 2008, 50, 346–363. [Google Scholar] [CrossRef] [Green Version]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Sunday, J.M.; Bates, A.E.; Dulvy, N.K. Global analysis of thermal tolerance and latitude in ectotherms. Proc. R. Soc. B Biol. Sci. 2011, 278, 1823–1830. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, A.A.; Chown, S.L.; Clusella-Trullas, S. Upper thermal limits in terrestrial ectotherms: How constrained are they? Funct. Ecol. 2013, 27, 934–949. [Google Scholar] [CrossRef]
- Nyamukondiwa, C.; Terblanche, J.S.; Marshall, K.E.; Sinclair, B.J. Basal cold but not heat tolerance constrains plasticity among Drosophila species (Diptera: Drosophilidae). J. Evol. Biol. 2011, 24, 1927–1938. [Google Scholar] [CrossRef]
- Gibert, P.; Huey, R.B. Chill-coma temperature in Drosophila: Effects of developmental temperature, latitude, and phylogeny. Physiol. Biochem. Zool. 2001, 74, 429–434. [Google Scholar] [CrossRef] [Green Version]
- Klok, C.J.; Sinclair, B.J.; Chown, S.L. Upper thermal tolerance and oxygen limitation in terrestrial arthropods. J. Exp. Biol. 2004, 207, 2361–2370. [Google Scholar] [CrossRef] [Green Version]
- Overgaard, J.; Kristensen, T.N.; Mitchell, K.A.; Hoffmann, A.A. Thermal Tolerance in Widespread and Tropical Drosophila Species: Does Phenotypic Plasticity Increase with Latitude? Am. Nat. 2011, 178, S80–S96. [Google Scholar] [CrossRef] [PubMed]
| Species | Collection Location | Year Collected |
|---|---|---|
| D. immigrans | San Diego, USA | 2016 |
| D. yakuba | Liberia | 1983 |
| D. equinoxialis | Honduras | <1984 |
| D. sulfurigaster | Finch Hatton, Australia | 2013 |
| D. rufa | Ehime, Japan | 2016 |
| D. mercatorum | Ehime, Japan | - |
| D. simulans | Ehime, Japan | 2016 |
| D. birchii | Mackay, Australia | 2014 |
| D. lutescens | Ehime, Japan | 2016 |
| D. montana | Finland | 2008 |
| Static | Dynamic | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Control | Hard. 31 °C | Hard. 33 °C | Control | Hard. 31 °C | Hard. 33 °C | ||||
| SPECIES | Obs. HKDT (s) | ∆HKDT[%] | Obs. CTmax (°C) | Pred. CTmax (°C) | Obs. ∆CTmax (°C) | Pred. ∆CTmax (°C) | Obs. ∆CTmax (°C) | Pred. ∆CTmax (°C) | |
| D. equinoxialis | 552.8 | −0.17 | −0.07 | 38.55 | 37.83 | −0.379 | −0.195 | −0.017 | −0.076 |
| D. rufa | 694.1 | 0.10 | 0.17 | 38.21 | 38.08 | −0.105 | 0.101 | 0.122 | 0.174 |
| D. immigrans | 254.5 | 0.30 | 0.27 | 36.84 | 36.98 | 0.021 | 0.281 | 0.168 | 0.257 |
| D. montana | 1206.4 | −0.08 | 0.53 | 38.74 | 38.69 | 0.111 | −0.094 | 0.217 | 0.460 |
| D. mercatorum | 749.6 | 0.02 | −0.07 | 38.87 | 38.17 | −0.134 | 0.023 | 0.253 | −0.076 |
| D. yakuba | 554.6 | −0.22 | −0.35 | 37.01 | 37.83 | −0.337 | −0.261 | −0.734 | −0.469 |
| D.sulfurigaster | 376.9 | 0.59 | 0.69 | 38.15 | 37.40 | 0.073 | 0.503 | 0.133 | 0.566 |
| D.simulans | 1102.1 | 0.25 | 0.14 | 38.96 | 38.58 | −0.058 | 0.244 | −0.131 | 0.140 |
| D. birchii | 593.6 | 0.14 | 0.14 | 38.02 | 37.90 | 0.140 | 0.140 | 0.001 | 0.139 |
| D. lutescens | 440.3 | −0.11 | 0.12 | 37.37 | 37.57 | 0.084 | −0.122 | 0.189 | 0.120 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winther Bak, C.; Bahrndorff, S.; Krog Noer, N.; Bjerregaard Jørgensen, L.; Overgaard, J.; Nygaard Kristensen, T. Comparison of Static and Dynamic Assays When Quantifying Thermal Plasticity of Drosophilids. Insects 2020, 11, 537. https://doi.org/10.3390/insects11080537
Winther Bak C, Bahrndorff S, Krog Noer N, Bjerregaard Jørgensen L, Overgaard J, Nygaard Kristensen T. Comparison of Static and Dynamic Assays When Quantifying Thermal Plasticity of Drosophilids. Insects. 2020; 11(8):537. https://doi.org/10.3390/insects11080537
Chicago/Turabian StyleWinther Bak, Christian, Simon Bahrndorff, Natasja Krog Noer, Lisa Bjerregaard Jørgensen, Johannes Overgaard, and Torsten Nygaard Kristensen. 2020. "Comparison of Static and Dynamic Assays When Quantifying Thermal Plasticity of Drosophilids" Insects 11, no. 8: 537. https://doi.org/10.3390/insects11080537
APA StyleWinther Bak, C., Bahrndorff, S., Krog Noer, N., Bjerregaard Jørgensen, L., Overgaard, J., & Nygaard Kristensen, T. (2020). Comparison of Static and Dynamic Assays When Quantifying Thermal Plasticity of Drosophilids. Insects, 11(8), 537. https://doi.org/10.3390/insects11080537






