Deformation Behavior Causing Excessive Thinning of Outer Diameter of Micro Metal Tubes in Hollow Sinking

Abstract

The deformation behavior of microtubes during hollow sinking was investigated to clarify the mechanism of the excessive thinning of their outer diameters. Stainless-steel, copper, and aluminum alloy tubes were drawn without an inner tool to evaluate the effect of Lankford values on outer diameter reduction. Drawing stress and stress-strain curves were obtained to evaluate the yielding behavior during hollow sinking. The observed yielding behavior indicated that the final outer diameter of the drawn tube was always smaller than the die diameter due to the uniaxial tensile deformation starting from the die approach end even though the drawing stress was in the elastic range. The results of a loading-unloading tensile test demonstrated that the strain remained even after unloading. Therefore, the outer diameter is considered to become smaller than the die diameter during hollow sinking due to microscopic yielding at any Lankford value. Furthermore, the outer diameter becomes smaller than the die diameter as the Lankford value increases, as theorized. As the drawing stress decreases or the apparent elastic modulus of the stress-strain curve increases, the outer diameter seems to approach the die diameter during unloading, which is caused by the elastic recovery outside the microscopic yielding region.

1. Introduction

Micro metal tubes are used in various fields that entail medical devices and heat exchangers [1,2]. Thin tube walls are required to increase the volume flow rate of a liquid from needles during injection [3]. Low surface roughness of the tubes is also required to improve blood flow in injection needles when injecting liquid. Therefore, control over the wall thickness and outer surface quality are requirements of the micro tube fabrication process. A plug or mandrel is generally used to control the wall thickness during tube drawing. However, inserting a plug or mandrel into micro metal tubes is impractical for creating micro metal tubes with a maximum outer diameter of 3 mm [4]. In conventional hollow sinking, where only the drawing speed on the die’s exit side can be controlled, the wall thickness generally increases. Therefore, fabricating thin-walled tubes using conventional hollow sinking is difficult [5]. Tube volume entering the die is equal to that exiting the die over a single unit of time. Therefore, the final wall thickness decreases as the length of the drawn tubes increases. In other words, the final wall thickness decreases as the drawing speed ratio on the die’s entrance and exit sides increases, when the outer diameter of the drawn tube matches the die diameter during the hollow sinking. This theory for controlling wall thickness has not been validated because only the drawing speed on the die’s exit side can be controlled in a conventional drawing machine. However, a contemporary drawing machine that controls both the drawing speeds on the die’s entrance and exit sides has recently been developed [6]. Previously, the authors investigated the conditions for wall thickness reduction by using this machine [7]. The results demonstrated that the wall thickness could be decreased when the drawing speed ratio was larger than a threshold value, which was obtained from the die reduction and the starting dimensions. Therefore, the drawing speed ratio must be set above this threshold to reduce the wall thickness during hollow sinking.

In our previous work, a theory for controlling wall thickness during hollow sinking was established [7]. Furthermore, a high dimension accuracy is required so that the outer diameter of the drawn micro tube matches the die diameter to improve the expansibility of stents [8]. In this study, tubes with a maximum outer diameter of 2 mm, which are required for several applications [5], were defined as the microscale tubes. Generally, the outer diameter of a macroscale drawn tube, such as an outer diameter of about 20 mm, matches the die diameter [9]. However, the authors reported that the outer diameter of the microscale drawn tubes with the outer diameter of about 1.5 mm became smaller than the die diameter starting from the die approach end [10]. Furthermore, the free surface roughening developed on the outer surface of the drawn tube due to the excessive thinning of the outer diameter. We assume that this excessive thinning of the outer diameter is caused by a uniaxial tensile deformation starting from the die approach end. In this study, we focused on the following aspects to clarify the mechanism causing the excessive thinning of the outer diameter: (1) flow stress, (2) friction force, and (3) plastic anisotropy. The details are described in the following paragraphs.

Several studies have reported that the size effect caused by miniaturization influences the deformation behavior of micro tubes [11,12]. For example, flow stress decreases with the grain number across the thickness of a specimen due to miniaturization [13]. The decrease in flow stress can be explained by using a surface layer model [14]. Dislocations pile up not at the free surface grain, but at the grain boundary. Therefore, dislocation movement in the free surface grains is less obstructed than movement at core grains. Furthermore, free surface grains exhibit lesser hardening than inner volume grains [15]. The fraction of grains representing the surface layer increases with miniaturization. Therefore, the flow stress decreases with the number of grains across the thickness. Several papers reported that this size effect appeared when only 10–20 grains exist in the thickness [11,12]. According to the above discussion, we assume that a microscale tube seems to yield more easily than a macroscale tube for a given drawing stress when the tube is stretched from the die approach end. The magnitude of the drawing stress during hollow sinking can be investigated using a finite element method (FEM) [16]. However, investigating complex phenomena such as the size effect by using this method is difficult. Therefore, the yielding behavior due to the size effect should be investigated by evaluating the magnitude of the measured drawing stress against the bulk yield stress.

The size effect on friction should also be considered when verifying the mechanism of the excessive thinning of the outer diameter during microscale hollow sinking. The force required to deform the tube decreases because of miniaturization even though the frictional force does not change. The proportion of the friction force to the drawing force increases with miniaturization. As a result, the micro tube seems to yield more easily during drawing than macroscale tubes because the drawing stress applied to the micro tube increases. The outer diameter of the micro tube seems to become smaller than the die diameter because of both the size effect on the flow stress and the effect of friction.

In addition to considering the size effect, investigating plastic anisotropy is expected to help clarify the mechanism causing the excessive thinning of the outer diameter during microscale hollow sinking. Several studies have reported on the effect of plastic anisotropy on the mechanical property of sheet metal forming by evaluating Lankford values [17]. The outer diameter of tubes decreases as the Lankford value increases in a tensile test. Therefore, the outer diameter is estimated to decrease from the die approach end as the Lankford value increases during hollow sinking. Generally, this value is calculated as the strain ratio of width to sheet thickness obtained via tensile testing. A study reported a method of measuring the Lankford value of tubes by realizing tensile testing on a specimen retaining a tube-shape [18]. The Lankford value of the tube can be calculated as the ratio of the circumferential strain ε_θ to wall thickness strain ε_t. From the above information, a more extreme reduction in the outer diameter due to an increase in the Lankford value should also be considered when verifying the mechanism causing the excessive thinning of the outer diameter during microscale hollow sinking.

We previously reported that the final outer diameter of the microscale copper tubes was smaller than the die diameter during hollow sinking [10]. The mechanism causing this excessive thinning of the outer diameter was not elucidated in our previous work. This mechanism will be clarified by considering the size effect and plastic anisotropy, which have not been considered in conventional macroscale hollow sinking.

This study aims to verify the mechanism causing the excessive thinning of the outer diameter during microscale hollow sinking. In this study, the stainless-steel, copper, and aluminum alloy tubes, which have been reported to have different Lankford values [18], were drawn to investigate the effect of the Lankford value on the outer diameter reduction during hollow sinking. The metals selected were adopted from the face-centered cube (FCC) metals so that the effect of the crystal structure on the deformation behavior could be neglected. A metal’s crystal structure seems to affect the deformation behavior of the drawn micro tube. Furthermore, the micro tubes were drawn at several drawing speed ratios to confirm that they yielded easily due to miniaturization. The measurement results of the outer diameter and the outer surface roughness of copper drawn tubes were already reported in our previous paper [10]. However, additional experiments were conducted to investigate the deformation behavior of the micro tubes in more detail using the stainless-steel and the aluminum alloy tubes. Therefore, the contents in this study were deeper, more detailed, and original.

2. Materials and Methods

2.1. Materials

Stainless-steel (SUS304), commercial purity copper (C1220), and aluminum alloy (A6063) tubes with an outer diameter D₀ of 1.50 mm and a wall thickness t₀ of 0.21 mm were used as starting materials. These materials were provided after drawing with a plug by Nippon Tokushukan MFG. Co., Ltd. (Osaka, Japan). The starting materials were annealed after plug drawing to relieve internal stresses.

Table 1. Chemical composition of the stainless-steel (SUS304) tube used in this study (mass percentage).

C	Si	Mn	P	S	Ni	Cr	Fe
0.05	0.79	1.72	0.035	0.004	8.88	18.22	Bal.

and

Table 2. Chemical composition of the aluminum alloy (A6063) tube used in this study (mass percentage).

Si	Fe	Cu	Mn	Mg	Cr	Zn	Al
0.43	0.18	0.04	0.02	0.52	0.01	0.01	Bal.

show the chemical compositions of the stainless-steel and the aluminum alloy tubes, which fall within the the reference range in accordance with Japanese Industrial Standards JIS-G4305 [19] and JIS-H4080 [20], respectively. The copper tubes used in this study were the same as those used in our previous study [10], which contained 99.96 mass percent copper, 0.02 mass percent phosphorus, and 0.02 mass percent other impurities. This chemical composition was in the reference range stated in Japanese Industrial Standards JIS-H3300 [21].

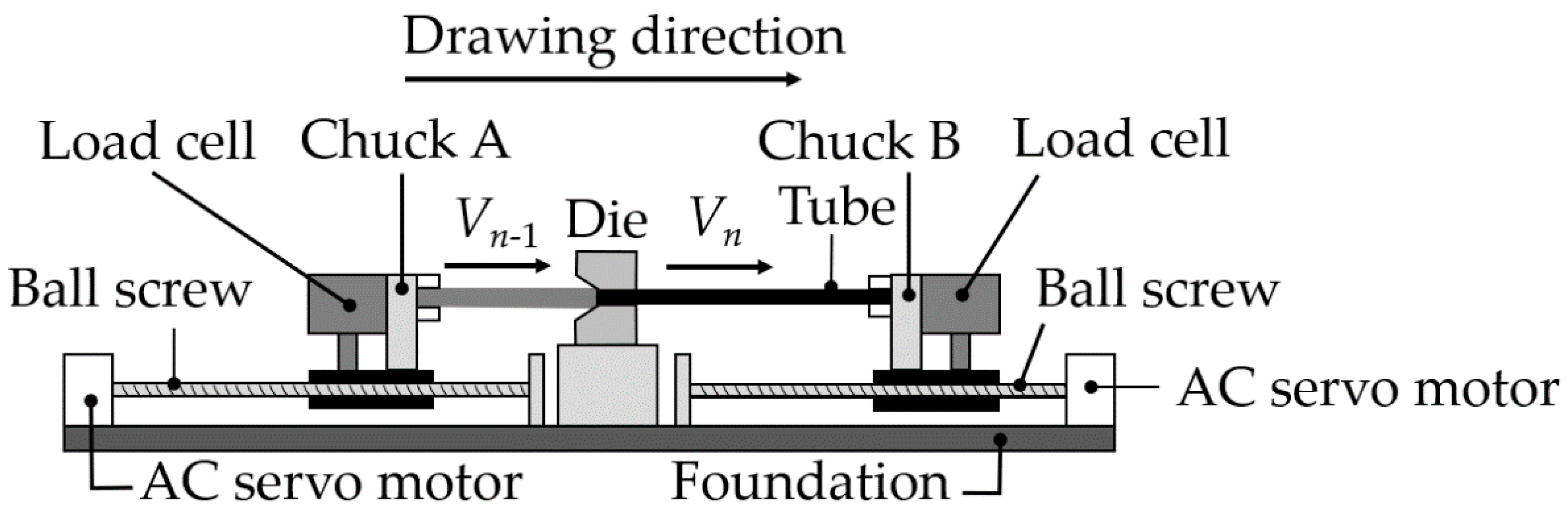
2.2. Hollow Sinking

The starting materials were drawn without an inner tool using a draw-bench machine (Factory-Automation Electronics Inc., Osaka, Japan). A schematic illustration of the draw-bench machine is shown in Figure 1. The detailed drawing procedures and drawing conditions were previously reported [10].

Table 3. Drawing conditions.

Die Reduction Re	Drawing Speed Ratio β (= Vn/Vn−1)		Die Half Angle θ°
	1-chuck *1	2-chuck *2
0.05	1.03	1.05, 1.10, 1.20	4
0.17	1.08	1.10, 1.20, 1.50	4
0.29	1.17	1.20, 1.50	4

*¹: Only the tube on the exit side of the die was chucked.*²: Both the tubes on the entrance and exit sides of the die were chucked.

shows the drawing conditions. The die reduction R_e is defined by the outer diameter of the starting material D₀ and the die diameter D_die, as expressed in Equation (1).

$$R_e=1-\frac{{D_{\mathrm{d}\mathrm{i}\mathrm{e}}}^2}{{D_0}^2}$$

(1)

A load cell (PW6CC3MB 30 kg, Hottinger Brüel & Kjær GmbH, Darmstadt, Germany) was affixed to each chuck of the draw-bench machine. The load cell on the die’s exit side measured the drawing force. The drawing force was calculated as the average load within 3% of the maximum load. The drawing stress was calculated by dividing of the drawing tension by the cross-sectional area of the tube on the die’s exit side. The measurement method of the cross-sectional area is described in Section 2.4.

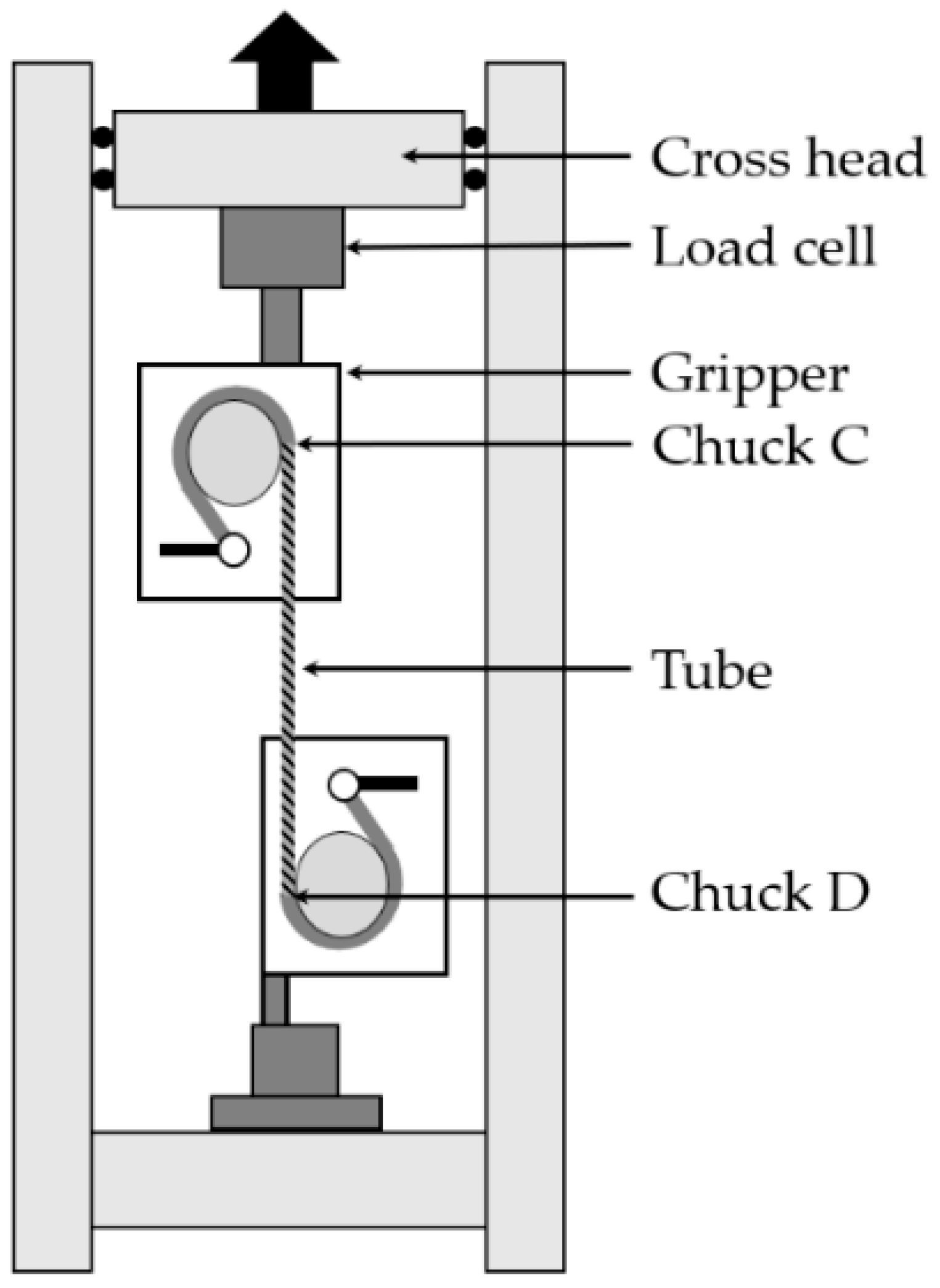
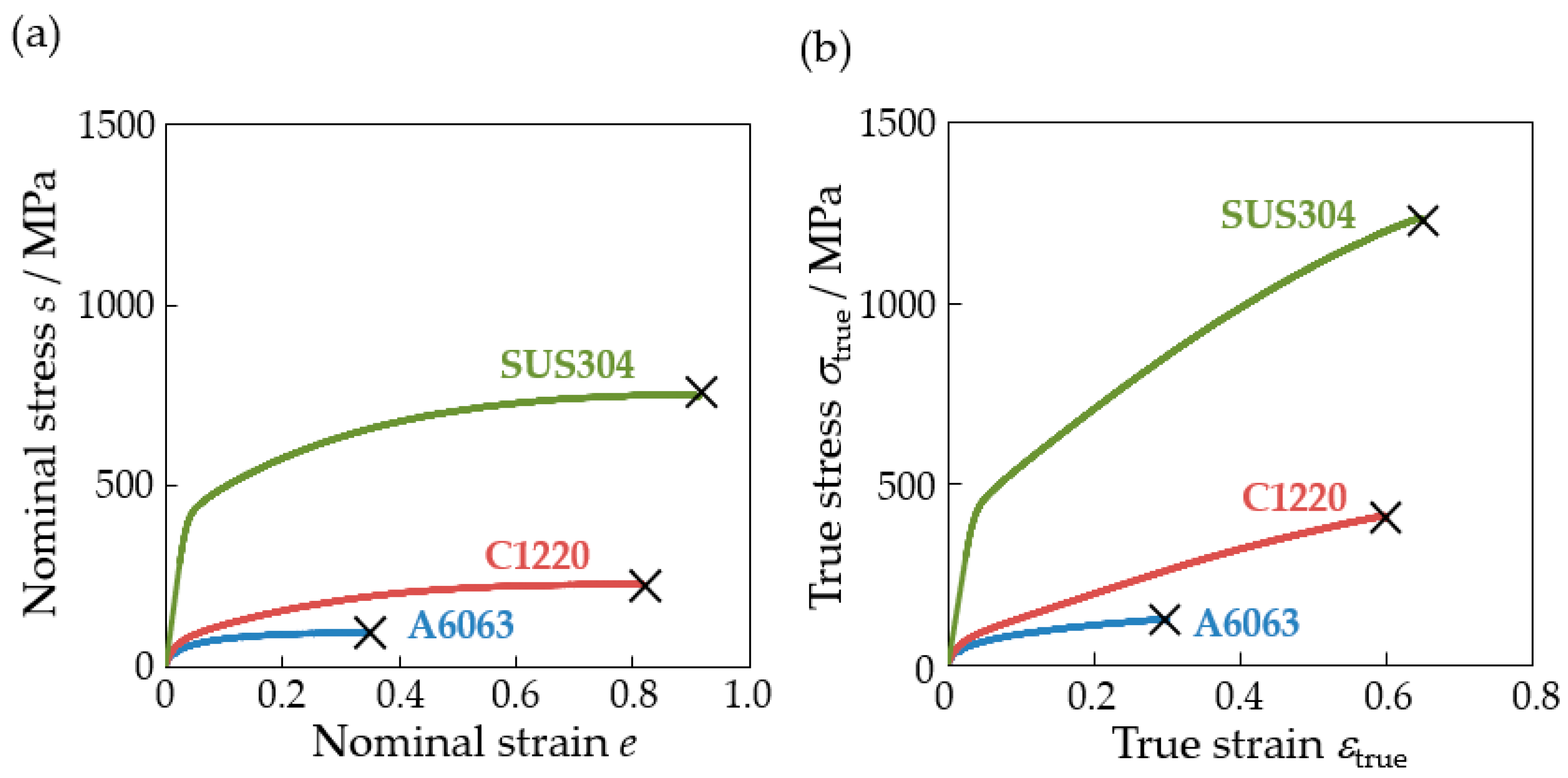
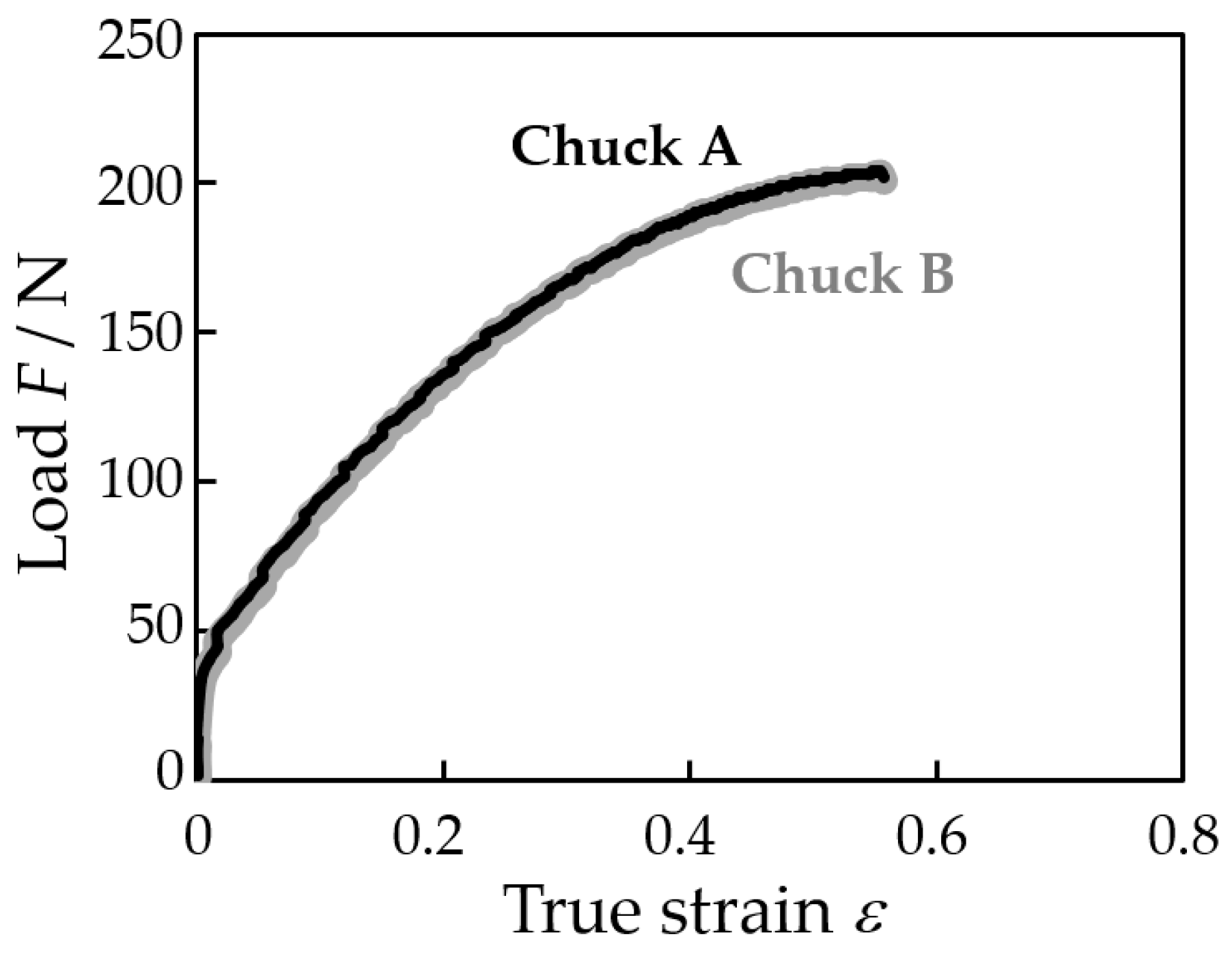
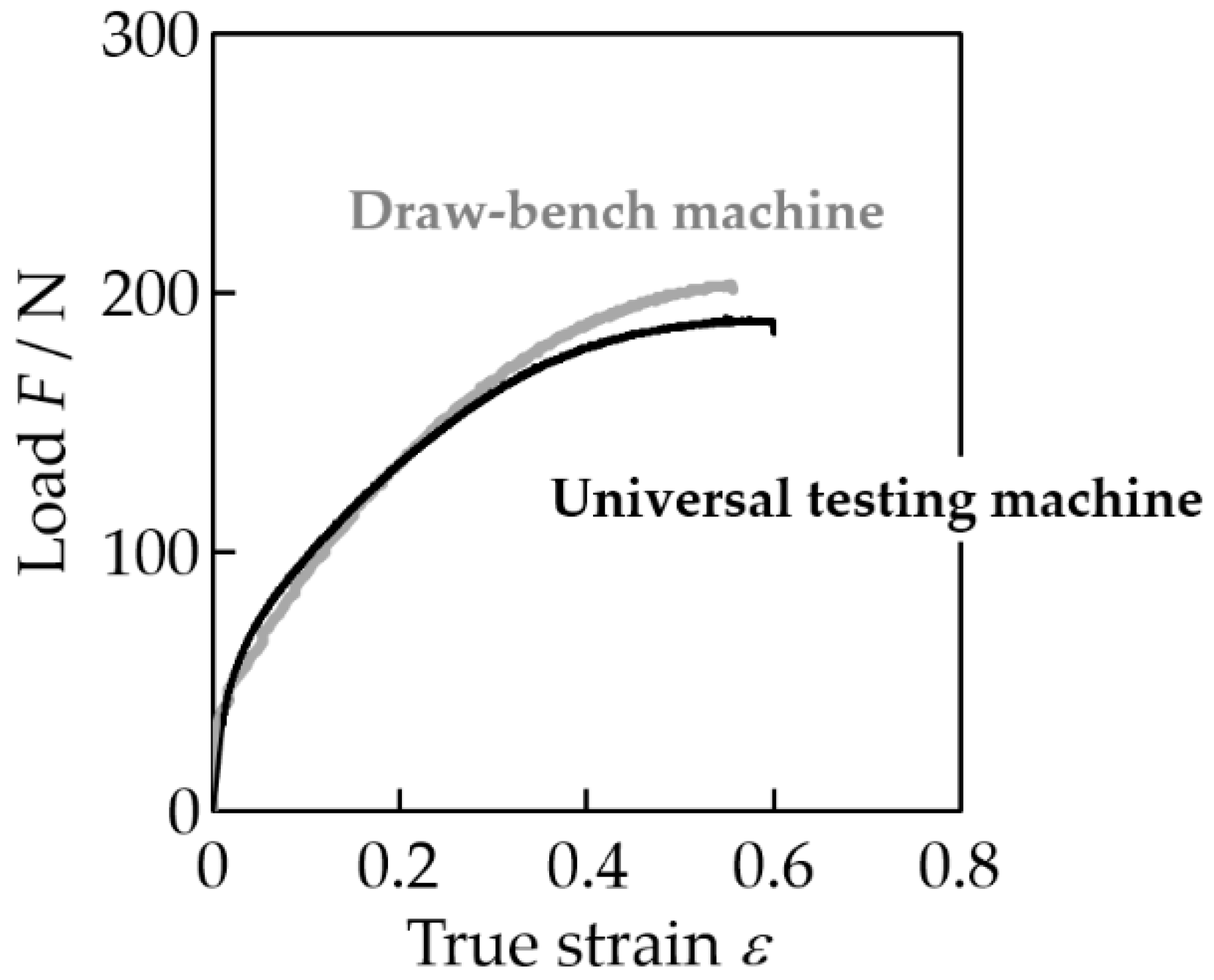
2.3. Tensile Test

Tensile tests of the starting materials and the drawn tubes were performed using a universal testing machine (Autograph AG 25 TB, Shimadzu Co., Kyoto, Japan), as shown in Figure 2. Tensile tests were performed to evaluate the followings: (1) the stress-strain curves of the starting materials and the drawn tubes, (2) the Lankford value of the starting materials at a maximum stroke, and (3) the unloading behavior of the drawn tube after reaching a drawing tension.

The tube was grasped using a 5 kN grips set for fine wire (343-07529-01, Shimadzu Co., Kyoto, Japan). The distance between the chuck C and D was 100 mm before the test. The test speed was 5.0 mm/s. The test load was measured with a 5 kN load cell (SLBL-5kN, Shimadzu Co., Kyoto, Japan) affixed to the cross-head. The tensile test ended at a fracture point to obtain the stress-strain curves of the starting materials and the drawn tubes. The tensile tests of each material were conducted in triplicate. The nominal stress s was calculated by dividing the load by the initial cross-sectional area of the tube. The nominal strain e was calculated by dividing the stroke by the initial chuck distance. The true strain ε_true was calculated by converting the nominal strain to ln(e + 1). The true stress σ_true was calculated by converting the nominal stress to s(e + 1).

The Lankford value during each maximum stroke was evaluated by conducting tensile tests at maximum strokes of 10, 20, 30, 40, and 50 mm. The Lankford value r was calculated using Equation (2). The average values were calculated, and the standard deviations were obtained.

$$r=\frac{\{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$D_{\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{e}}$}\!\left/ \!\raisebox{-1ex}{$D_0$}\right.\right)+\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$d_{\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{e}}$}\!\left/ \!\raisebox{-1ex}{$d_0$}\right.\right)\}/2}{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$t_{\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{e}}$}\!\left/ \!\raisebox{-1ex}{$t_0$}\right.\right)}$$

(2)

The parameters D_tensile and d_tensile are the outer diameter and inner diameter at each maximum stroke, respectively, as shown in Figure 3a. The method of measuring D_tensile and d_tensile is described in Section 2.4.

The loading-unloading tensile test was conducted to evaluate specimen unloading behavior. The drawn copper tube was loaded until reaching a load that corresponded to the drawing tension at a die reduction R_e of 0.17 and drawing speed ratio β of 1.10. The cross-head was moved until the load reached 2 N during unloading. The test speed during loading and unloading was 1.0 mm/s. An equivalent strain was obtained by evaluating the change in chuck distance during loading and unloading using a digital image correlate (DIC) software GOM Correlate^TM (2019, Gesellschaft für Optische Messtechnik GmbH, Braunschweig, Germany).

Tensile test of the copper tube was also conducted using the draw-bench machine without the die to investigate the load measurement accuracy of the load cell affixed to the chuck of the draw-bench machine. The copper tube was chucked without setting the die. The initial chuck distance was 465 mm. The tube was stretched by moving the two chucks. The moving speeds of the chuck A and B were 3.3 mm/s and 5.0 mm/s, respectively. The stroke was calculated as the difference in the distance between the two chucks. The nominal stress was calculated by dividing the load by the initial cross-sectional area of the tube. The nominal strain was calculated by dividing the stroke by the initial chuck distance.

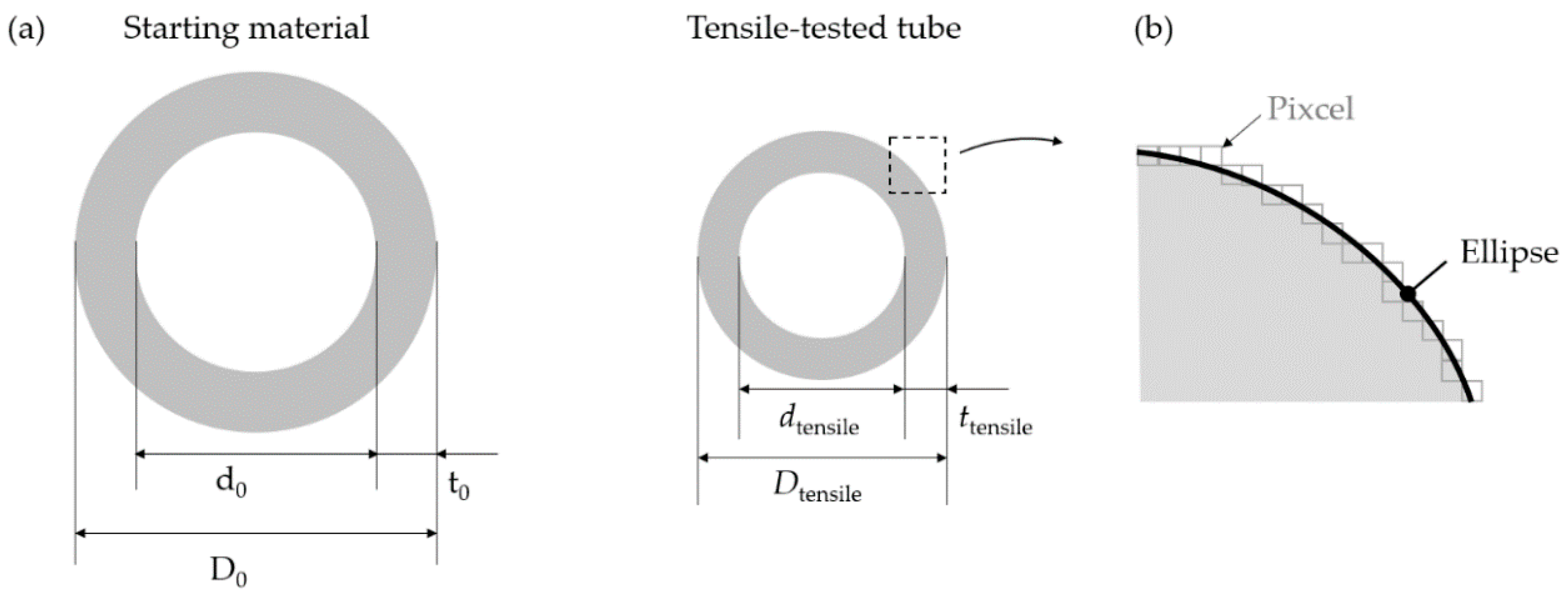
2.4. Dimension and Surface Quality Measurement

Cross sections of the drawn and tensile-tested tubes at each maximum stroke were polished and observed using a three-dimensional microscope (VHX-5000, Keyence, Miyagi, Japan). The outer diameter D and the inner diameter d of the tensile-tested and drawn tubes were measured by an image analysis as the following method. The pixels of the outer and inner circumference of the tube image were read using a proprietary programming language, MATLAB^TM (R2020a, Mathworks, Natick, MA, USA). A tube cross-section outline of the image became elliptical when the tube was cut diagonally. The minor axis of the ellipse was closest to the true diameter of the tubes. Therefore, ellipses were drawn by ellipse approximation of each circumference pixel, as shown in Figure 3b. The outer or inner diameter of the tube was measured as the minor axis of this ellipse. The wall thickness t was calculated as (D − d)/2. The cross-sectional area was calculated as πt(D − t). The outer diameters of the drawn tube on the die’s entrance and exit sides were measured using a micrometer (MDC-25M, Mitutoyo, Kanagawa, Japan) at four points. The average values were calculated, and the standard deviations were obtained.

Maps of the height of the uneven outer surface of the drawn tubes h were obtained using a laser microscope (VK9510, Keyence, Miyagi, Japan). The height from an arbitrary position of the uneven outer surface of the tube H was measured, excepting abnormally high or low value. The average values H_ave of the H were calculated. The height of the outer uneven surface of the tube h was calculated as the difference between the height from the arbitrary position H and the average height H_ave as H − H_ave.

2.5. Microstructural Observation

The number of crystal grains across the wall thickness t₀ of the starting materials was evaluated. The cross sections of the starting materials were mechanically polished after resin filling. Kikuchi patterns of the starting materials were obtained using a field emission scanning electron microscope (FE-SEM) (JSM-6500F, JEOL, Tokyo, Japan) with electron backscatter diffraction (EBSD) (OIM7, TSL, Kanagawa, Japan). The Inverse pole figure (IPF) maps were drawn, and the average grain size g was measured using an OIM Analysis^TM (ver.8, TSL, Kanagawa, Japan). A boundary with an orientation of 15° or more was defined as a grain boundary. The weighted mean of the grain area was calculated, and the average diameter of crystal grains was calculated as the grain size. The grain numbers across the wall thicknesses of the starting materials were calculated by dividing the wall thicknesses by the average grain size as t₀/g.

3. Results

3.1. Grain Number across Wall Thicknesses of Staring Materials

Figure 4 shows the IPF maps of the starting materials. The average grain size g of the stainless-steel, copper, and aluminum alloy tubes were 9 µm, 17 µm, and 71 µm, respectively. Therefore, the grain numbers across the wall thicknesses of starting materials t₀/g of the stainless-steel, copper, and aluminum alloy tubes were 23, 12, and 3, respectively.

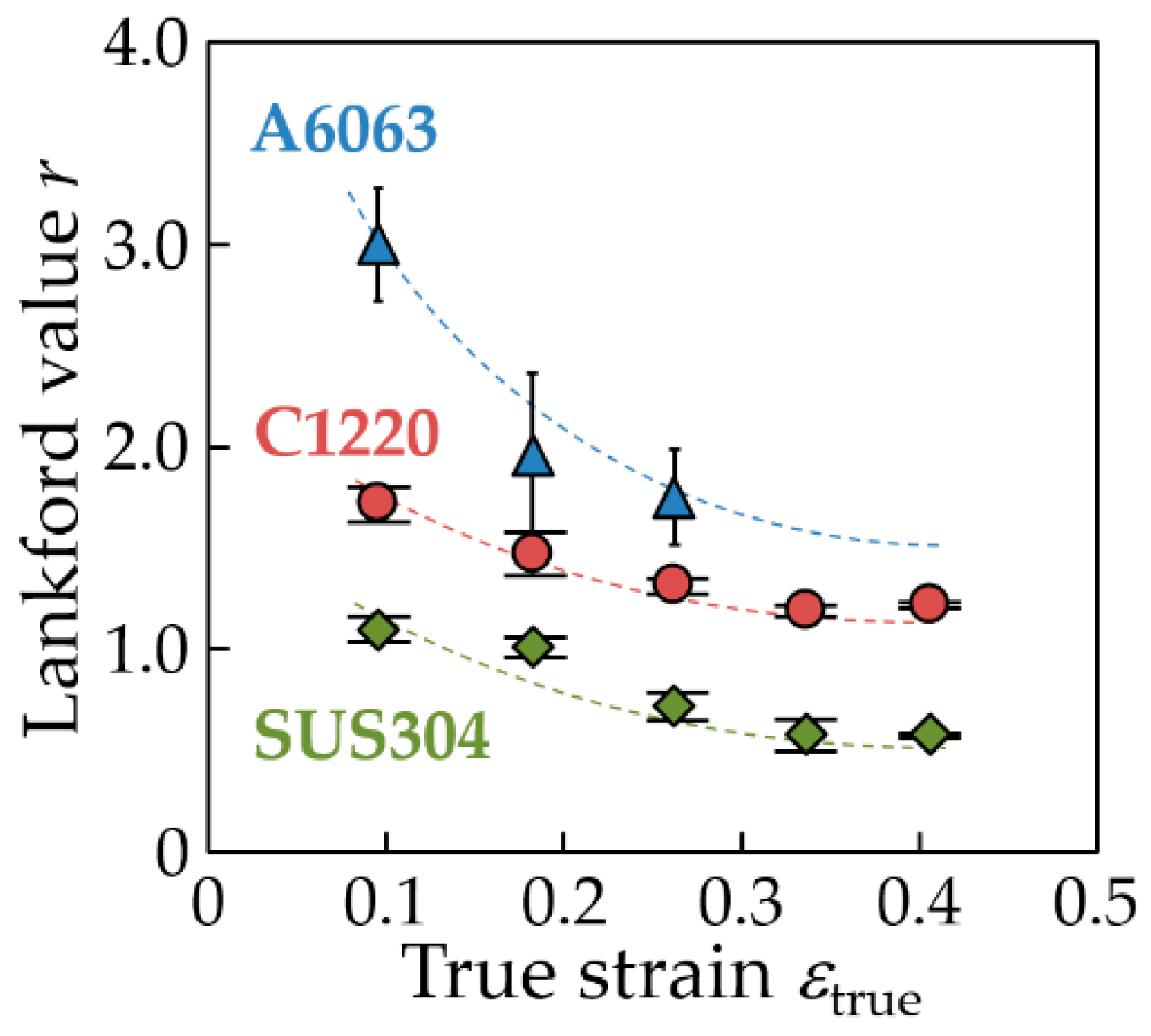
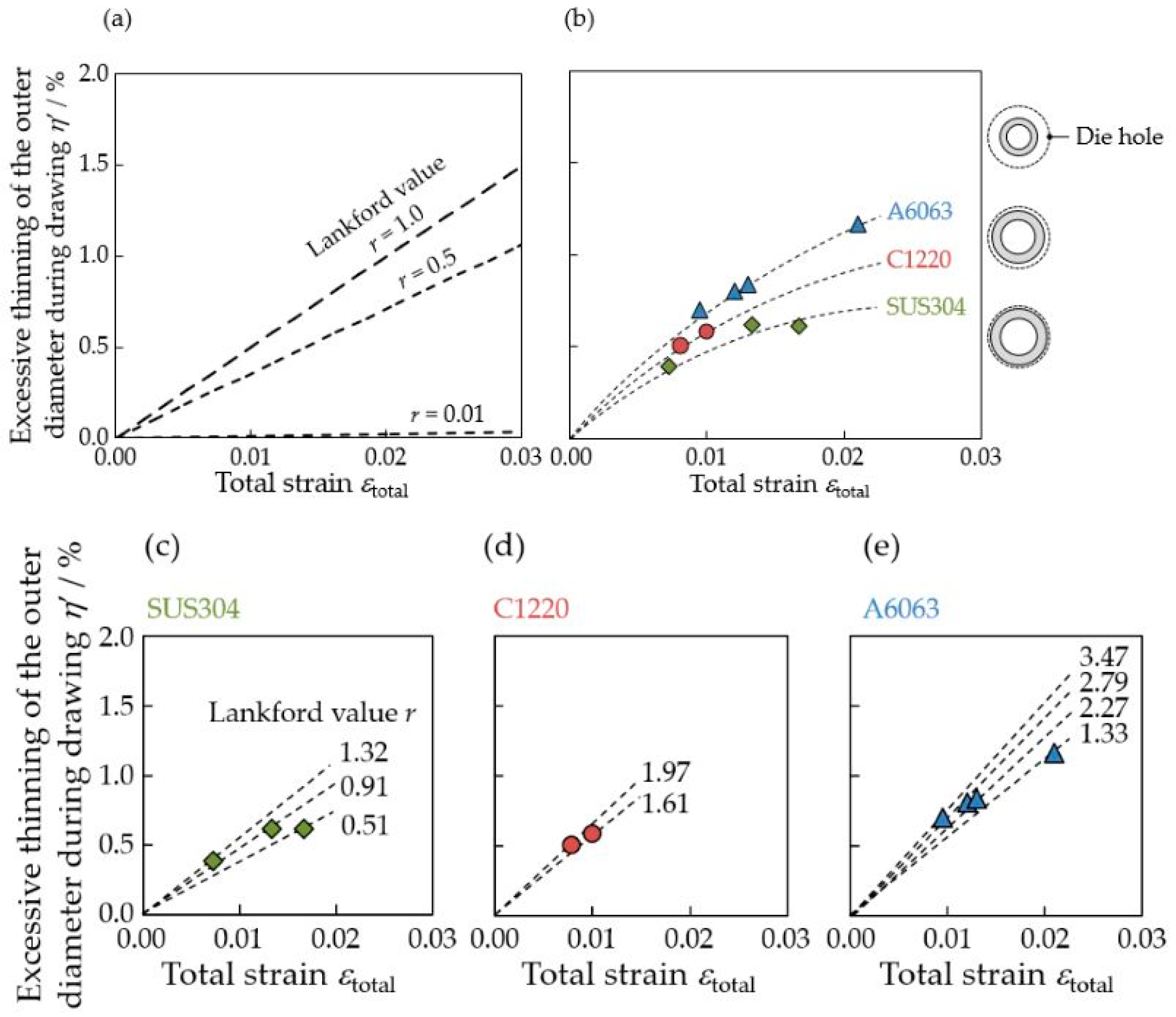
3.2. Lankford Value of Starting Materials

Figure 5 and Figure 6 show the stress-strain curves and Lankford values r of each starting material, respectively. The true strain ε_true in Figure 6 corresponds to that in Figure 5b. A drop in stress due to necking was not observed for all materials, as shown in Figure 5a. Necking was observed only on the fractured surface of the copper tube. It is considered that necking occurred immediately before the fracture. Therefore, the strain from necking to fracture was negligible. The measured fracture strain of the aluminum alloy tube was 0.31. Therefore, the Lankford values r of the aluminum alloy tube at the true strain of 0.34 and 0.41 could not be measured. The Lankford value decreased as the true strain increased for each material. The Lankford values decreased in the order of the aluminum alloy, the copper, and the stainless-steel tube at each true strain.

3.3. Dimension of Drawn Tubes

Figure 7 shows the cross sections of the drawn tubes of the selected materials at a die reduction of 0.17 (die diameter D_die = 1.37 mm). The results observed on the copper tube were already reported in our previous paper [10]. The dotted circles in the image area are equivalent to the die diameter. For each material, all the cross sections were smaller than the die’s exit hole. The cross section became smaller than the die’s exit hole as the drawing speed ratio increased. Figure 8 shows the measurement results of the outer diameter of the drawn tubes on the die’s exit side for each drawing condition. The error bars indicate the standard deviations. The dotted lines indicate the die diameter. The outer diameter was smaller than the die diameter for all drawing conditions. The outer diameter became smaller than the die diameter as the drawing speed increased.

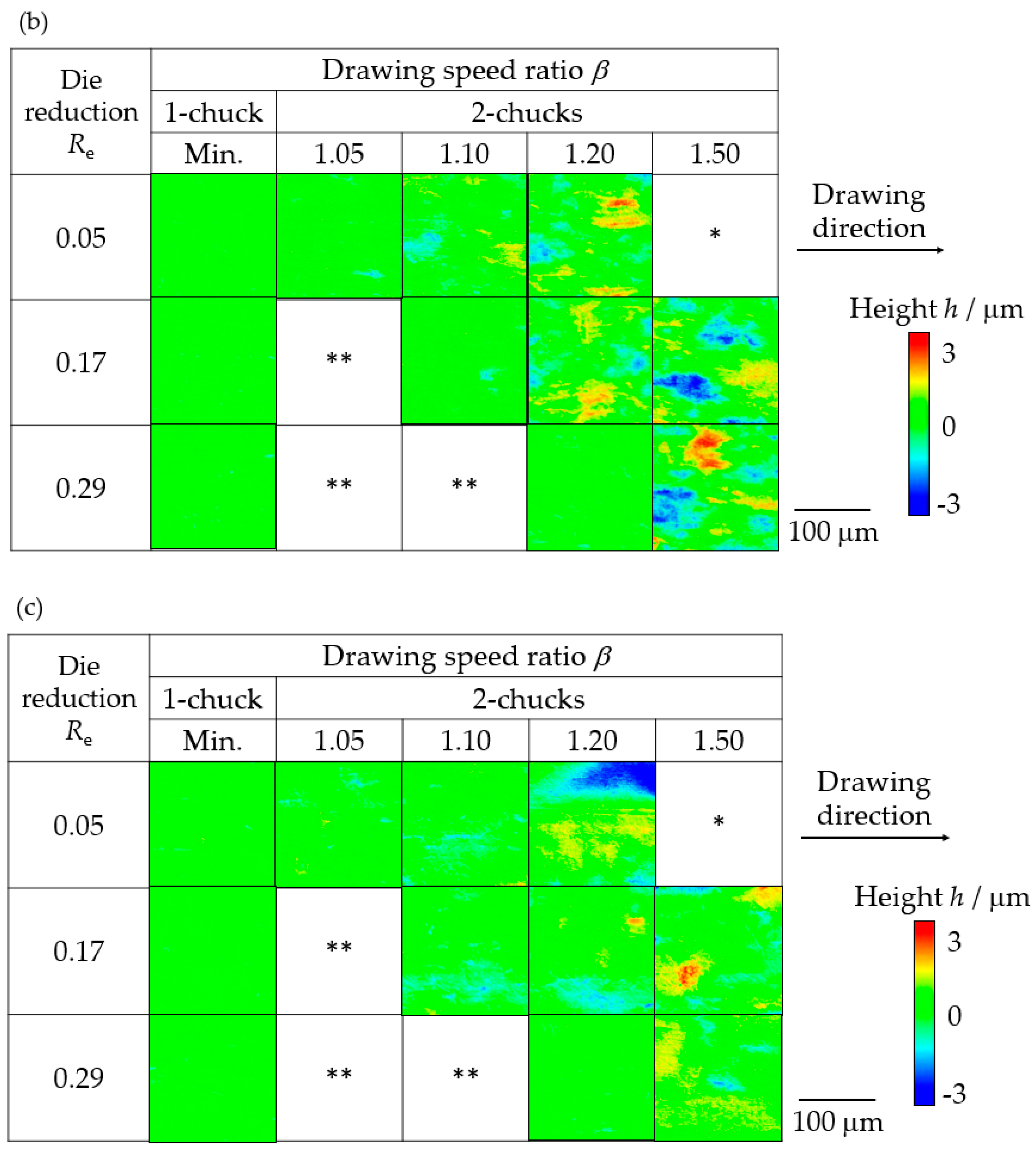
3.4. Outer Surface Quality of Drawn Tubes

Figure 9 shows the height maps of the outer surface of the drawn tubes. Since the outer diameter was estimated to be much smaller than the die diameter before the tube drawing test, tube drawing at a drawing speed ratio of 1.50 was not performed at a die reduction of 0.05. Asterisks indicate that the tube drawing was not performed for this reason. The minimum drawing speed ratio for each die reduction is shown in Table 3. The symbol ** indicates drawing experiments that were impossible to perform because the drawing speed ratio was less than the minimum value. The number of areas with regions of particularly high (red) or low (blue) heights increased as the drawing speed ratio increased for each material. The proportion of low-height and the high-height parts decreased in the order of the copper, the aluminum alloy, and the stainless-steel tube. Therefore, the outer surfaces of the materials were rougher in the order of the copper, the aluminum alloy, and the stainless-steel tube for drawing conditions.

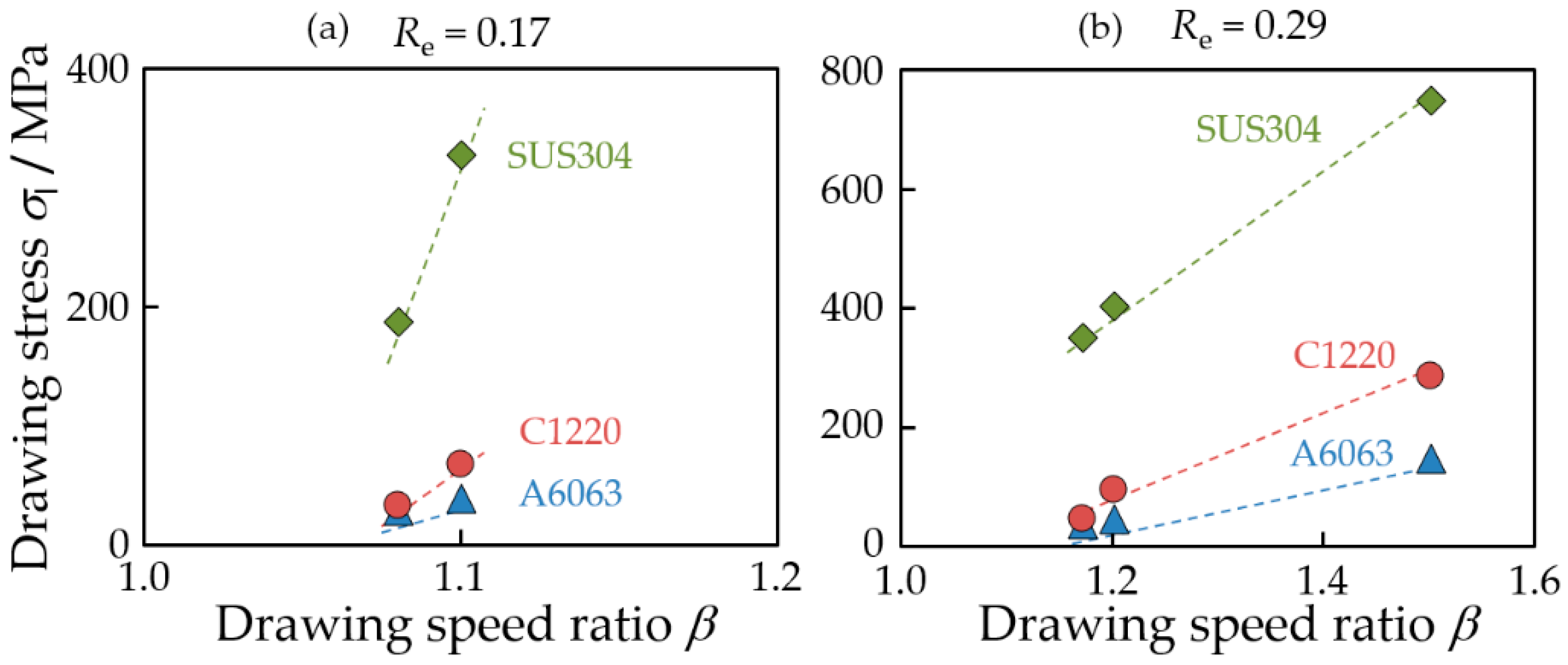
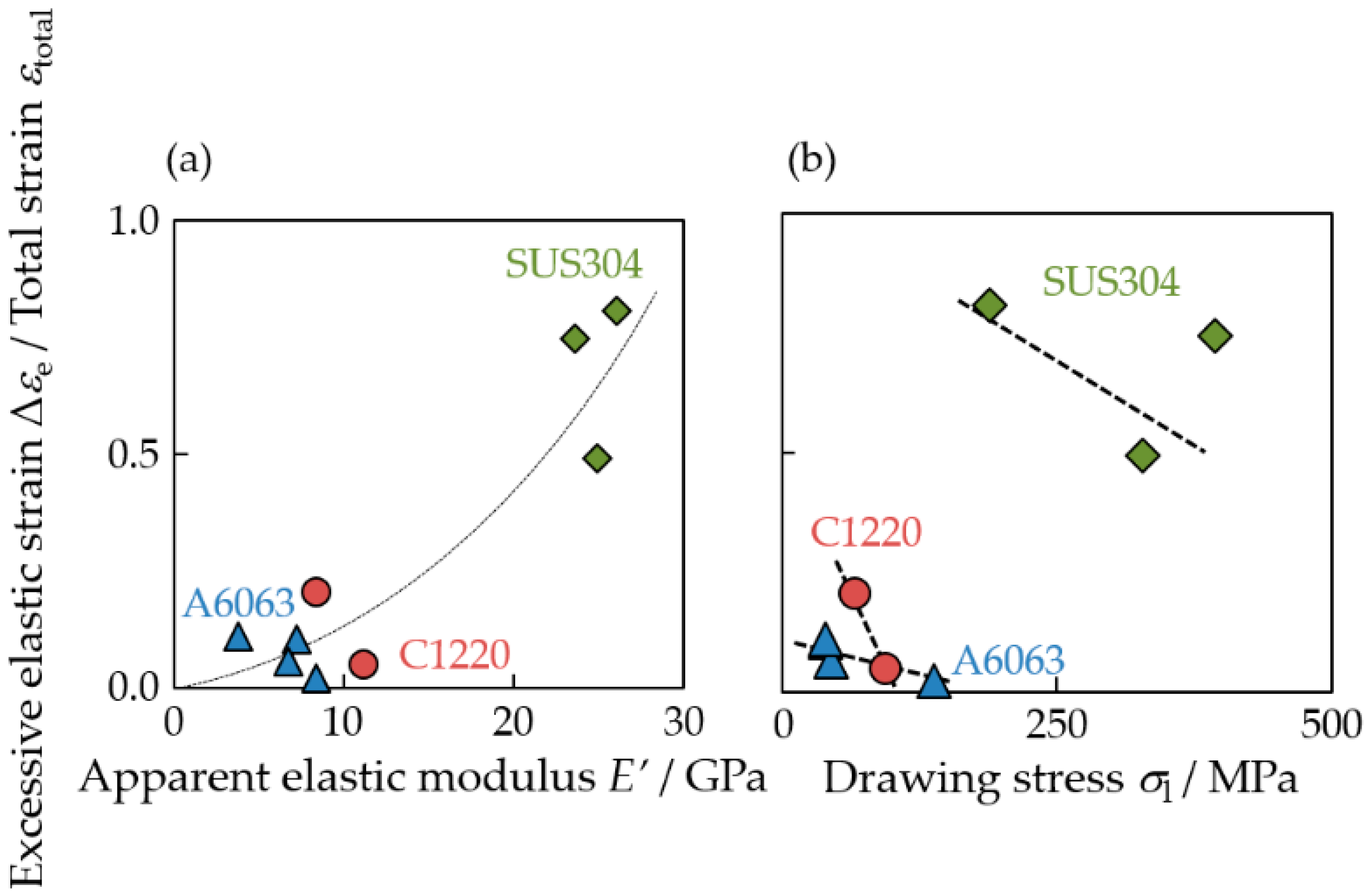
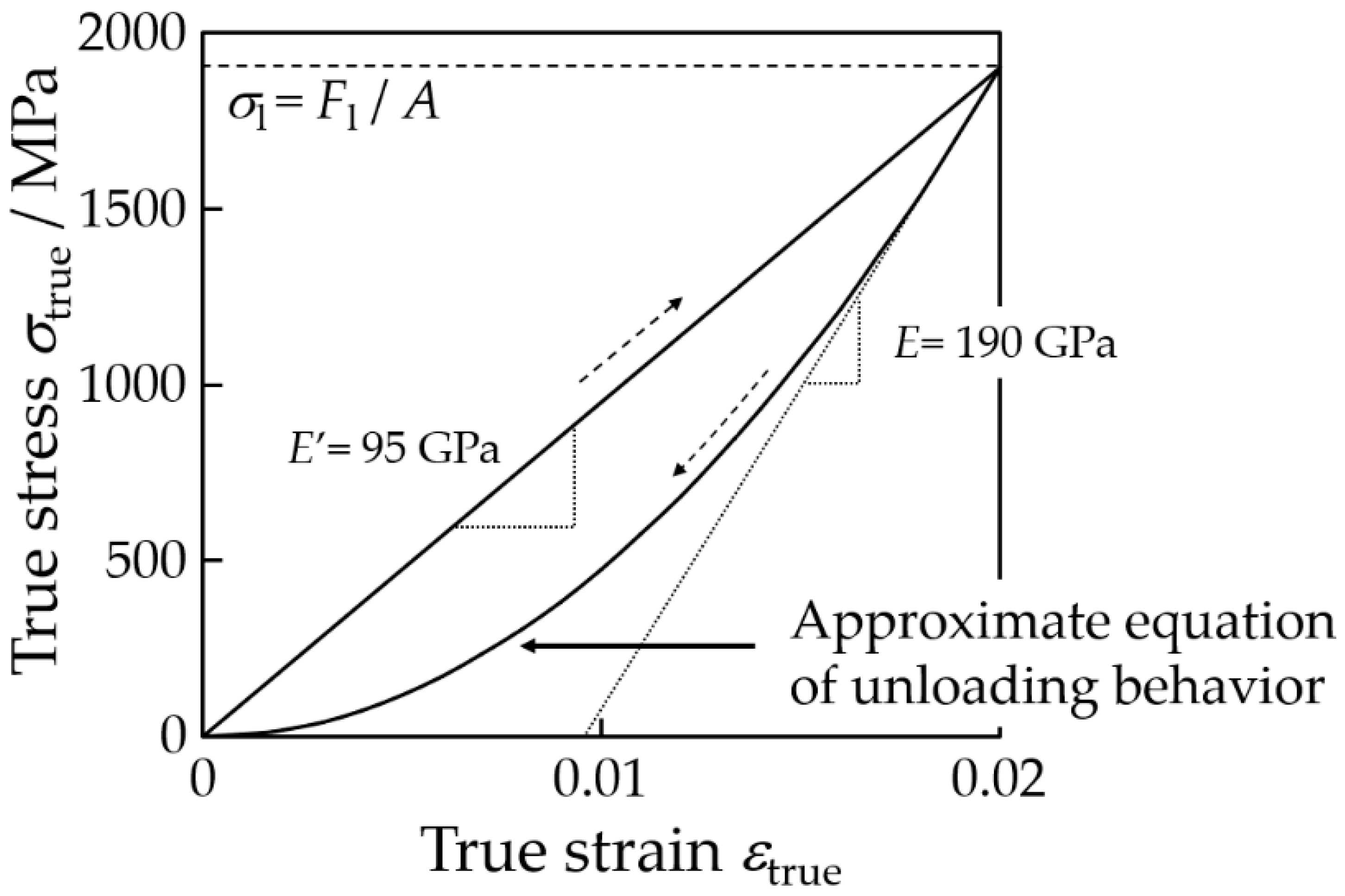
3.5. Drawing Stress during Drawing

The mechanism causing the excessive thinning of the diameter was discussed based on the drawing stress, calculated from the load measured by the load cell affixed to the chucks of the draw-bench machine. Therefore, the load measurement accuracy of the draw-bench machine was investigated. The load measured by each load cell affixed to chucks A and B should match when a tube is simply stretched. It was confirmed that the two load cells affixed to chucks A and B measured an equivalent load, as shown in Figure 10. The load measurement accuracy of the draw-bench machine was evaluated by comparing the load obtained by the universal testing machine and the draw-bench machine. The load of the chuck A was applied for comparison. Figure 11 shows a comparison of the load measured by the universal testing machine and the draw-bench machine. In the true strain range larger than 0.4, the load of the draw-bench machine was up to 2% smaller than that of the universal testing machine. However, the drawing tension under most of the experimental conditions in this study was in a strain range smaller than 0.4. Therefore, the load measurement accuracy of the draw bench was allowed when compared to the universal testing machine.

Figure 12 shows measurement results of the copper tube’s load at the die reduction R_e of 0.17 and the drawing speed ratio of 1.10. The drawing force was calculated as the average load within 3% of the maximum. Figure 13 shows the measured drawing stress at the die reduction of 0.17 and 0.29 for each material. The tubes were drawn without contacting the die during drawing under an increased drawing speed ratio when the die reduction was 0.05. Therefore, the results of the drawing stress at the die reduction R_e of 0.05 are not shown. The drawing stress increased as the drawing speed ratio increased for each material. The drawing stress was large in the order of the stainless-steel, the copper, and the aluminum alloy tubes. This order corresponded to the fracture stress of the stress-strain curves in Figure 5.

4. Discussion

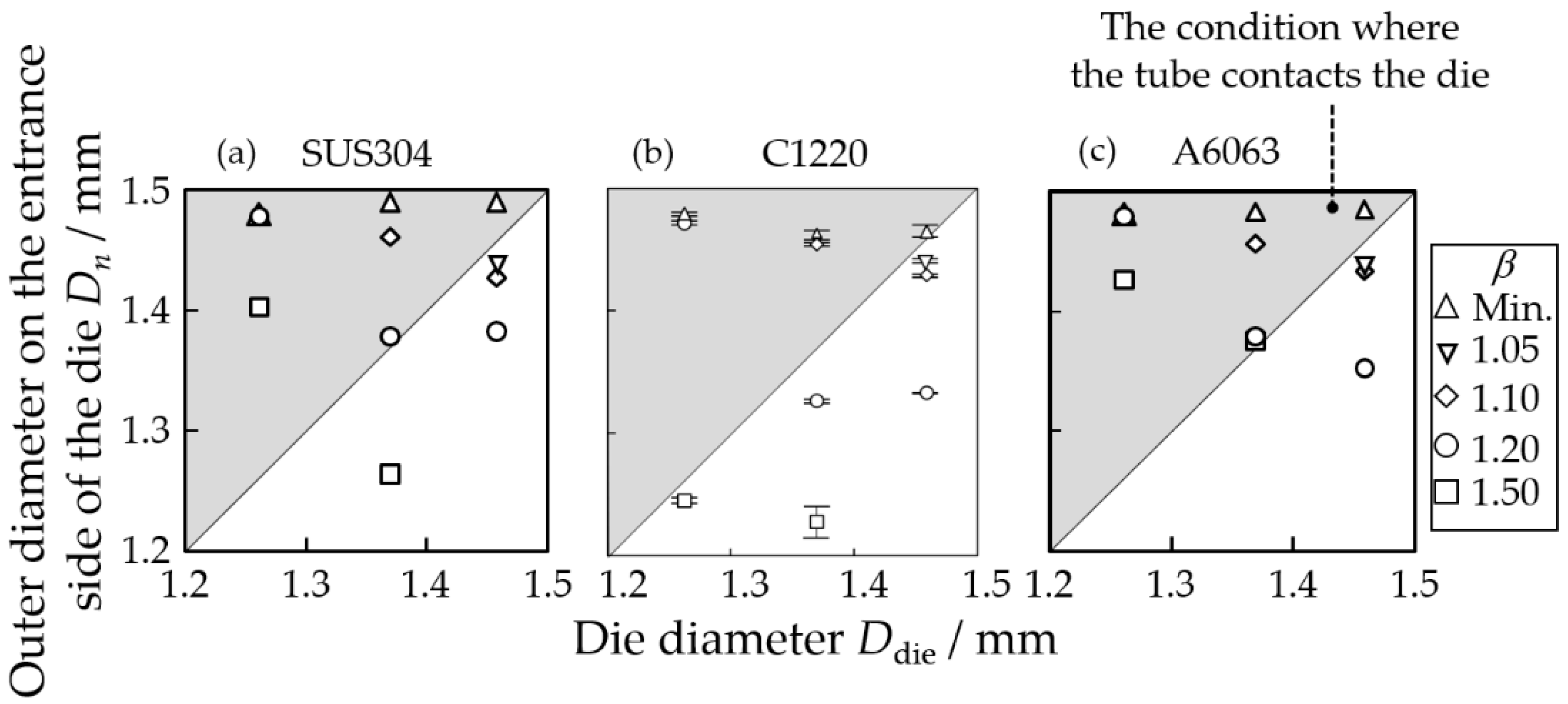
4.1. Conditions to Prevent Non Contact between the Tube and Die

We have previously reported that the copper tubes contacted the die under the conditions where the outer diameter on the die’s entrance side was larger than the die diameter, as shown in the gray area of Figure 14b [10]. Therefore, the drawing speed ratio should be set low so that the die diameter increases, which prevents non contact between the tube and the die. Figure 14a,c show the outer diameter on the die’s entrance side of stainless-steel and aluminum alloy drawn tubes, respectively. Similar to our previous report [10], the tube contacted the die at a small die diameter and a low drawing speed ratio. Only the aluminum tube contacted the die at a die diameter D_die of 1.37 mm and a drawing speed ratio β of 1.50. In the following sections, the excessive thinning of the outer diameter was discussed only under the conditions where the tube contacted the die.

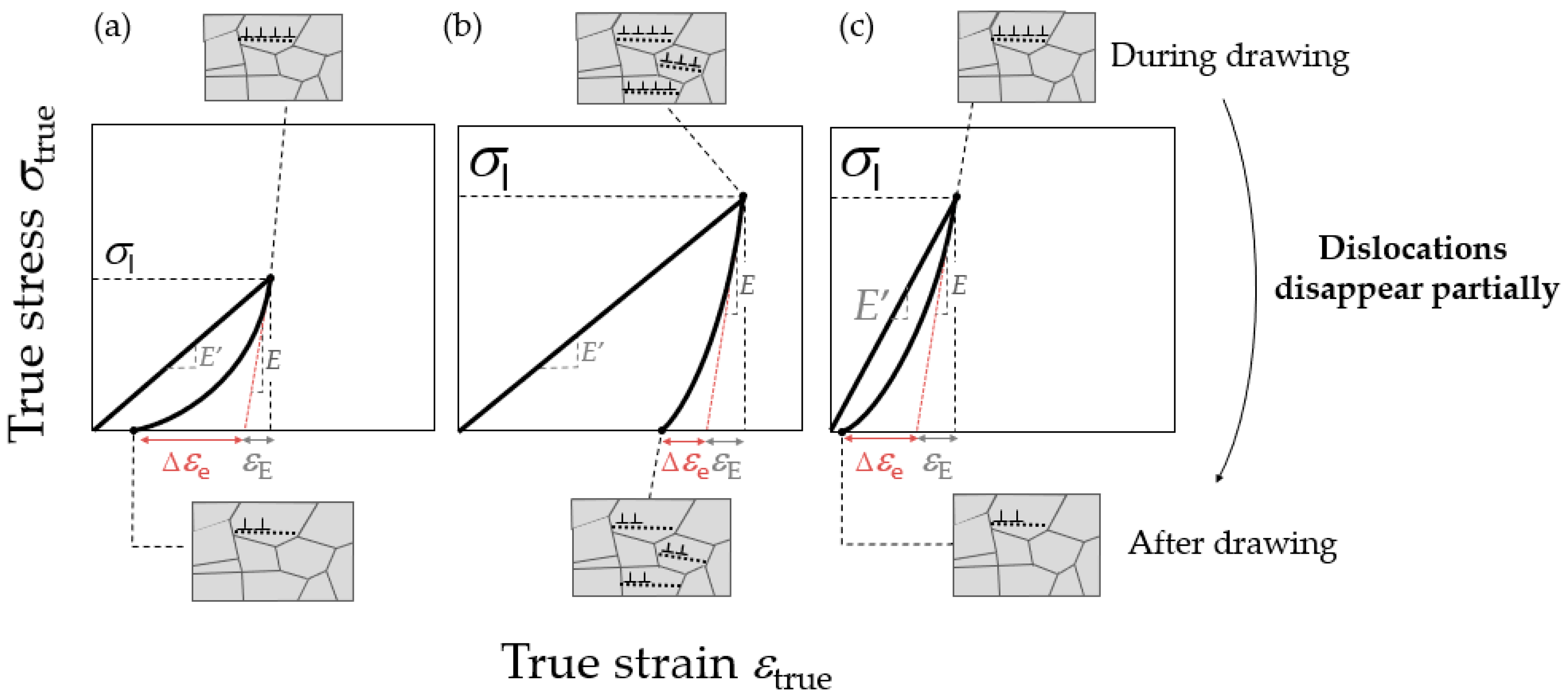
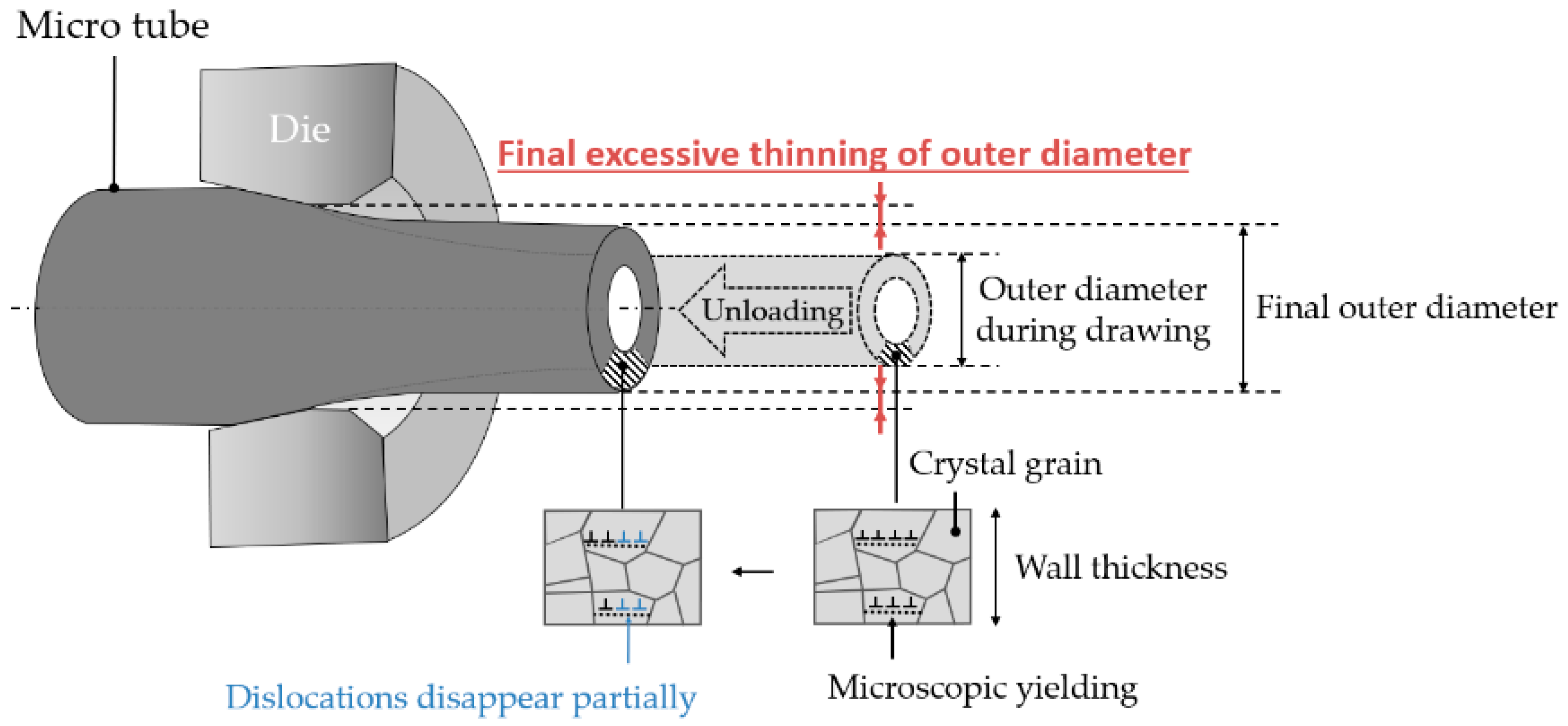
4.2. Mechanism of the Excessive Thinning of the Outer Diameter during and after Drawing

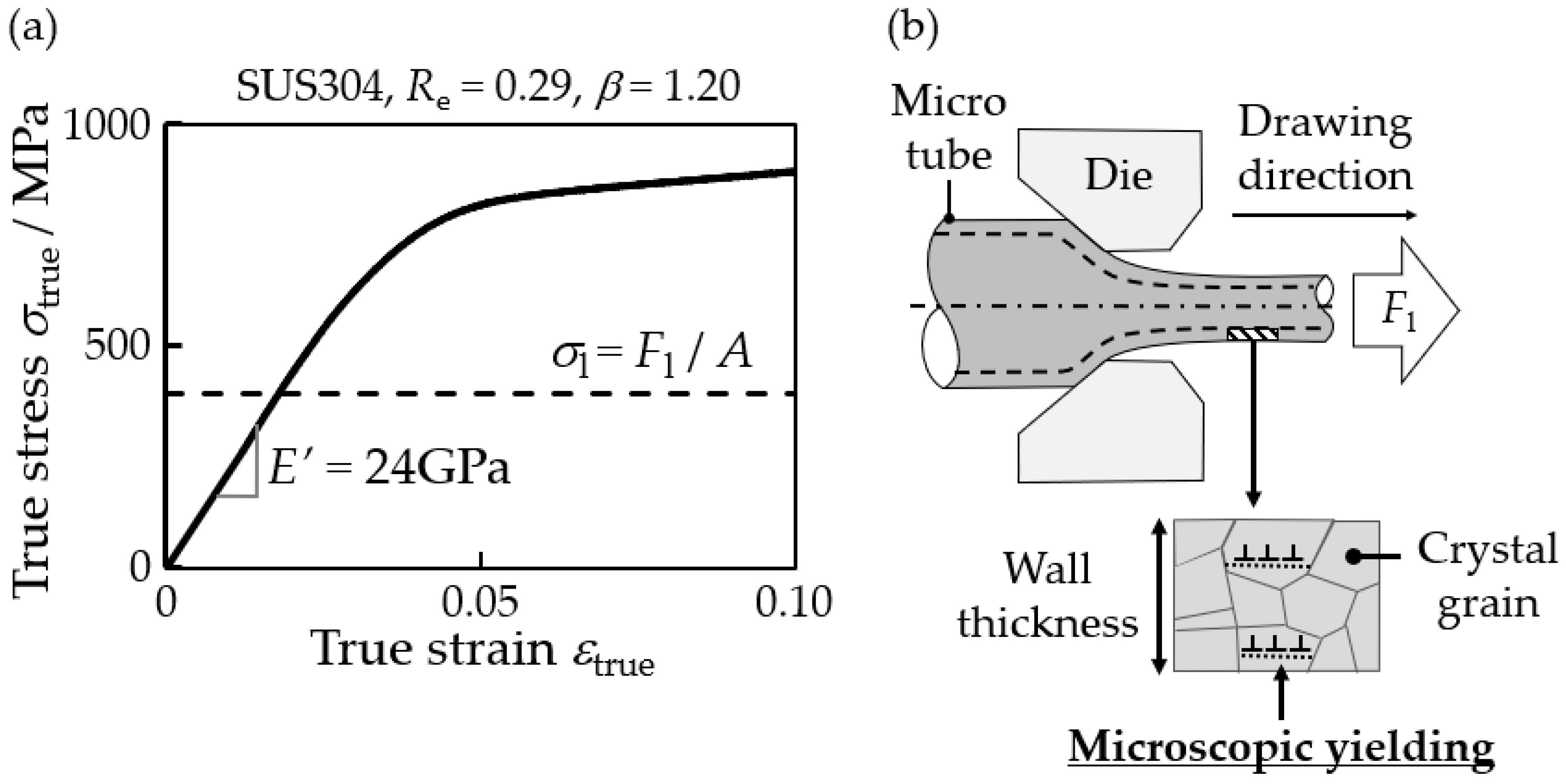
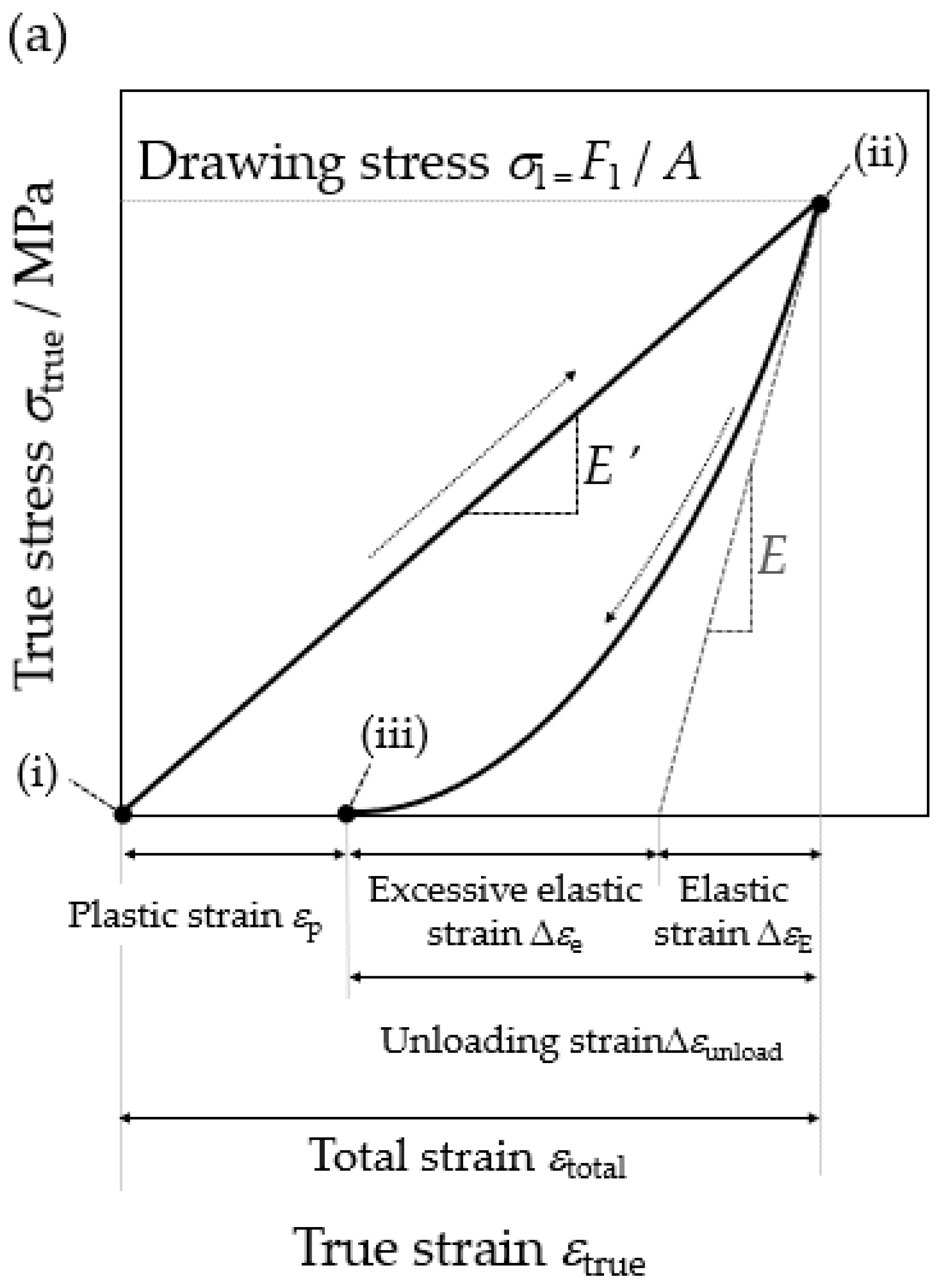
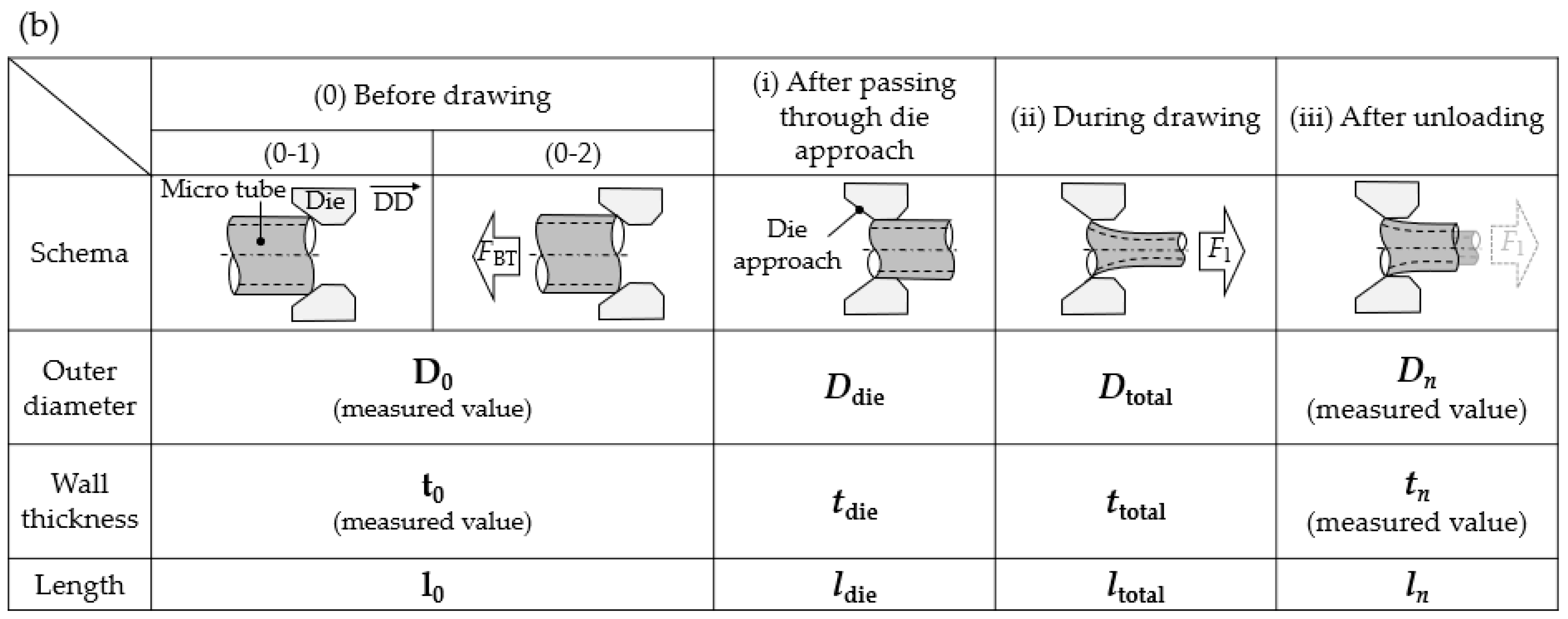
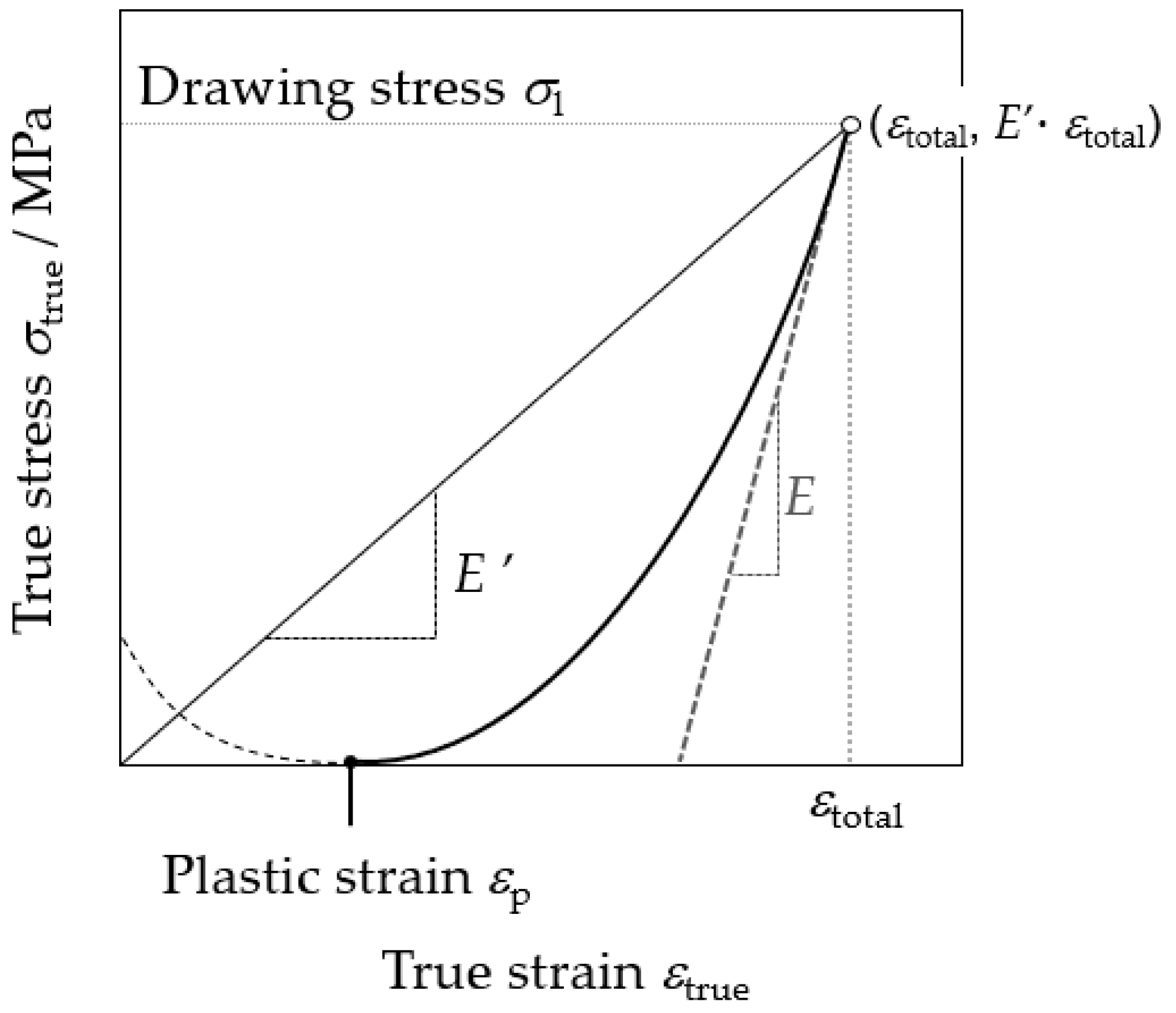
4.2.1. Deformation Behavior of Micro Tube during Drawing and Unloading

We have previously reported that the outer diameter of the micro tube decreased from the die approach end [10]. Therefore, the excessive thinning of the outer diameter was considered as a uniaxial tensile deformation starting from the die approach end. To investigate this deformation behavior, the magnitude of the drawing stress in the stress-strain curve of the drawn tubes was evaluated. Figure 15a shows the stress-strain curve of the drawn stainless-steel tube at a die reduction R_e of 0.29 and a drawing speed ratio β of 1.20. The dotted line indicates the drawing stress σ_l during drawing. The state where the outer diameter matched the die diameter after passing through the die approach corresponds to the origin in Figure 15a. Generally, a bulk metal that has been deformed under a load in the elastic range will recover to its original shape as soon as the load is removed. In this study, the drawing stress σ_l was in the macroscopic elastic region of the stress-strain curve. However, the outer diameter finally decreased excessively from the die approach end as the plastic strain. Therefore, it is considered that the excessive thinning of the outer diameter was caused by microscopic yielding of the micro tube due to the small number of crystal grains across the wall thickness, as shown in Figure 15b. Bulk metal, where many crystal grains exist across the thickness, yields microscopically even under macroscopically elastic deformation behavior [22]. Therefore, it is considered that the micro tube used in this study easily yielded microscopically because of the small number of crystal grains across the wall thickness. Furthermore, the apparent elastic modulus E′ of the micro stainless-steel tube in Figure 15a was 24 GPa, which was much smaller than that of the reference value of bulk stainless-steel (204 GPa [23]). The reason for the decrease in the apparent elastic modulus due to the miniaturization reported elsewhere has not been clarified [24]. However, it is considered that this decrease in the apparent elastic modulus was also caused by microscopic yielding. The slope during loading in the macroscopic elastic range seems to decrease because of easy yielding for a certain drawing stress. The measurement accuracy of the true stress using the universal testing machine was confirmed in Section 3.5. Therefore, the apparent elastic modulus in Figure 5b seems to be appropriate.

Figure 16 shows the result of the loading-unloading tensile test of the drawn copper tube at a die reduction R_e of 0.17 and a drawing speed ratio β of 1.10. Figure 16b shows the equivalent strain distribution during loading. The strain distribution between the chucks was uniform. Therefore, it is considered that the true strain can be evaluated by measuring the change in the chuck distance. The equivalent strain was also obtained using DIC by measuring the chuck distance. The total strain ε_total and the unloading strain Δε_unload obtained using the universal testing machine and the DIC matched with errors of 4.3% and 9.2%, respectively, as shown in Figure 16c. The measurement accuracy of the true strain using the universal testing machine was almost equivalent to that of the DIC in this study. The measurement accuracy of the true stress using the universal testing machine was confirmed in Section 3.5. Therefore, the apparent elastic modulus in Figure 5b seems to be appropriate.

The true stress ε_true increased during loading until reaching the drawing stress σ_l, as shown in Figure 16a. The apparent elastic modulus during loading E′ was 5 GPa, which was much smaller than that of the reference value of the bulk copper (119 GPa [23]). This decrease in the apparent elastic modulus due to miniaturization was also shown in the stress-strain curve of the starting material as shown in Figure 15. This decrease in the apparent elastic modulus was considred to be a result of microscopic yielding. The slope during loading seems to decrease because of easy yielding for a certain drawing stress. The true stress ε_true dropped slightly at a true strain of approximately 0.010 during loading. The reason for this stress drop is unclear. However, the true strain during this dropping was 0.7% against the total strain ε_total. Therefore, it is considered that this stress drop was negligible.

The true strain did not recover completely during unloading. The unloading strain/total strain was 0.31. This result also indicates that the micro tube yielded microscopically during loading. The outer diameter seems to approach the die diameter as the unloading strain Δε_unload increases. It is apparent that the unloading behavior depends on the elastic recovery outside the microscopically yielded region. Therefore, the unloading strain at the initial stage of the unloading behavior seems to depend on the elastic strain Δε_E, which was calculated by dividing the drawing stress σ_l by the bulk elastic modulus E of 119 GPa [23]. However, the unloading strain Δε_unload was significantly larger than the elastic strain Δε_E. Therefore, it is considered that the outer diameter of the micro tube increased more than the linear elastic strain Δε_E during unloading. The difference between the unloading strain and the elastic strain is defined as the excessive elastic strain Δε_e, which is discussed in Section 4.2.3.

According to the above discussion, the following two deformation behaviors should be investigated to clarify the mechanism that causes the excessive thinning of the outer diameter: (1) the excessive thinning of the outer diameter due to the microscopic yielding during drawing and (2) the unloading behavior caused by elastic recovery outside the microscopically yielded region during unloading, which determines the final outer diameter. Therefore, the followings were investigated: (1) the relationship between the total strain ε_total and the outer diameter during drawing D_total and (2) the relationship between the unloading strain Δε_unload and the final outer diameter D_n. The detail procedures are shown in Figure 17. The outer diameter during drawing D_total and the unloading strain Δε_unload could not be measured. Therefore, the outer diameter during drawing D_total was calculated by using the Lankford value, which indicated the plastic anisotropy, and the total strain ε_total. The unloading strain Δε_unload was calculated by using the plastic strain ε_p and the total strain ε_total.

The tensile residual stress, which is generated during drawing [25], seems to hinder the unloading behavior, because the force directions of the unloading behavior and the tensile residual stress are opposing. Tensile residual stress is not generated during uniaxial tensile deformation. Therefore, the difference in the unloading behavior between the tensile test and the drawing test is discussed based on the tensile residual stress in Section 4.2.3.

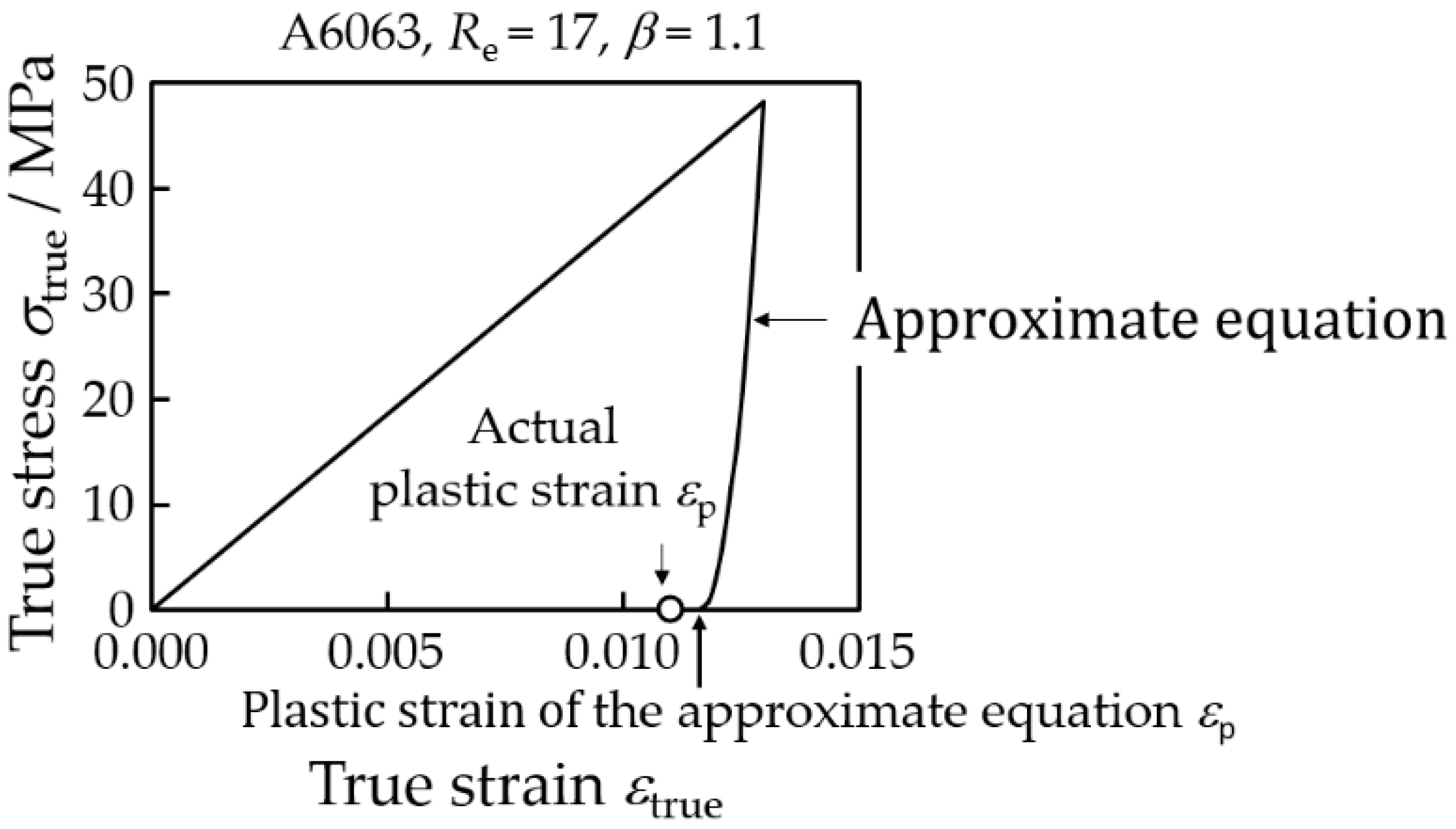
4.2.2. Excessive Thinning of the Outer Diameter during Drawing

The relationship between the total strain ε_total and the outer diameter during drawing D_total was investigated. The deformation of the micro tube on the die’s entrance side due to the back tension (state (0-2) shown in Figure 17) was small when compared to the main deformation (state (0-1)$\to$(ii)). Therefore, this deformation was neglected. It is assumed that the outer diameter decreased during drawing from the state where the outer diameter matched with the die diameter D_die, as (i)$\to$(ii) shown in Figure 17. The outer diameter during drawing D_total was calculated using the die diameter D_die, the wall thickness after passing through the die approach t_die, the Lankford value r in deformation during drawing, and the total strain ε_total. The wall thickness after passing through the die approach t_die and the Lankford value r were calculated using Equations (3) and (4), respectively. The detailed deviations of Equations (3) and (4) are shown in the Appendix A.

$$t_{\mathrm{d}\mathrm{i}\mathrm{e}}=\frac{1}{2}(D_{\mathrm{d}\mathrm{i}\mathrm{e}}+\sqrt{D_{\mathrm{d}\mathrm{i}\mathrm{e}}-\frac{4t_0\left(d_0-t_0\right)}{\beta }})$$

(3)

$$r=\frac{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$D_n$}\!\left/ \!\raisebox{-1ex}{$D_{\mathrm{d}\mathrm{i}\mathrm{e}}$}\right.\right)}{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$t_n$}\!\left/ \!\raisebox{-1ex}{$t_{\mathrm{d}\mathrm{i}\mathrm{e}}$}\right.\right)}$$

(4)

Equation (5) indicates the total strain during drawing. By substituting Equation (4) into Equation (5) to eliminate the wall thickness t_total, Equation (6) is obtained.

$${\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\mathrm{l}\mathrm{n}\frac{l_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{l_{\mathrm{d}\mathrm{i}\mathrm{e}}}=\mathrm{l}\mathrm{n}\frac{t_{\mathrm{d}\mathrm{i}\mathrm{e}}\left(D_{\mathrm{d}\mathrm{i}\mathrm{e}}-t_{\mathrm{d}\mathrm{i}\mathrm{e}}\right)}{t_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(D_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-t_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\right)}$$

(5)

$$r=\frac{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$D_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$}\!\left/ \!\raisebox{-1ex}{$D_{\mathrm{d}\mathrm{i}\mathrm{e}}$}\right.\right)}{\mathrm{l}\mathrm{n}\frac{D_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\pm \sqrt{D_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-\frac{D_{\mathrm{d}\mathrm{i}\mathrm{e}}-t_{\mathrm{d}\mathrm{i}\mathrm{e}}}{\mathrm{e}\mathrm{x}\mathrm{p}\left({\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\right)}}}{2t_{\mathrm{d}\mathrm{i}\mathrm{e}}}}$$

(6)

The outer diameter during drawing D_total was calculated using Equation (6). The excessive thinning of the outer diameter during drawing η’ was calculated using Equation (7). Furthermore, the excessive thinning of the outer diameter after drawing η was calculated using Equation (8). The measurement results of the final outer diameter D_n are already shown in Figure 8.

$${\eta }^{\prime }=\frac{D_{\mathrm{d}\mathrm{i}\mathrm{e}}-D_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{D_{\mathrm{d}\mathrm{i}\mathrm{e}}}\times 100$$

(7)

$$\eta =\frac{D_{\mathrm{d}\mathrm{i}\mathrm{e}}-D_n}{D_{\mathrm{d}\mathrm{i}\mathrm{e}}}\times 100$$

(8)

Figure 18a shows the theoretical relationship between the total strain ε_total and the excessive thinning of the outer diameter during drawing η’. η’ increases as the total strain ε_total increases, and further grows during drawing as the Lankford value r increases. η’ is greater than zero at any Lankford value. Therefore, it is considered that the outer diameter always becomes much smaller than the die diameter during drawing at any Lankford value r. Figure 18b shows η’ in this study. Figure 18c–e show the Lankford value of each η’ in Figure 18a. η’ was obtained by substituting t_die, ε_total, and D_die into Equation (6) for each drawing condition. The theoretical excessive thinning of the outer diameter during drawing η’ was larger in the order of the aluminum alloy, the copper, and the stainless-steel tube corresponding to the order of the Lankford values r in Figure 6. Therefore, the relationship of the magnitude between the theoretical values for each material seems to be appropriate, and the excessive thinning of the outer diameter during drawing η’ increased as the Lankford value grew for each material.

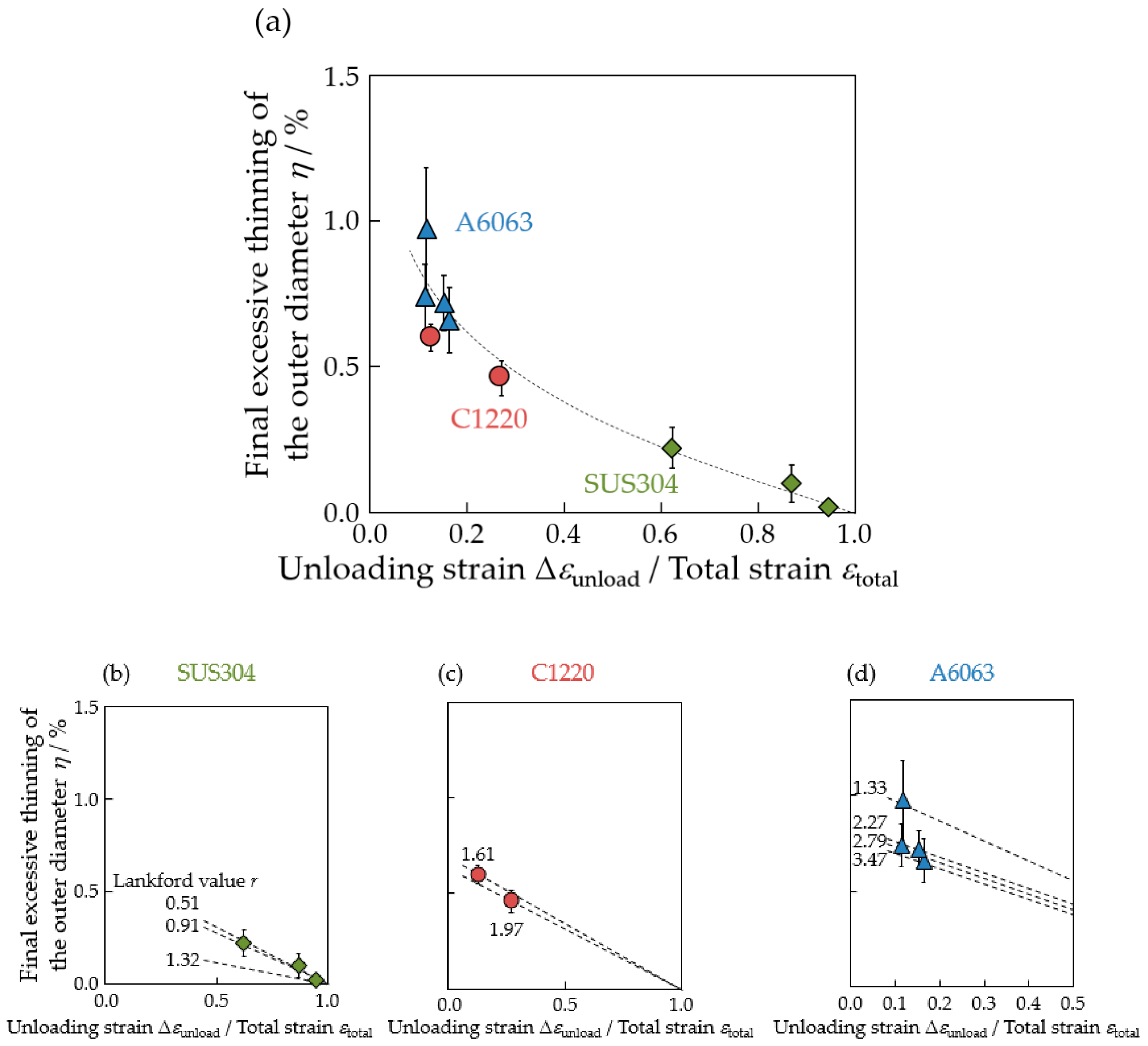
4.2.3. Excessive Thinning of the Outer Diameter after Drawing

The relationship between the unloading strain Δε_unload and the final outer diameter D_n (state(iii) in Figure 17a,b) was investigated. The unloading strain Δε_unload was calculated as the difference between the total strain ε_total and plastic strain ε_p, which is required for deformation to the final dimensions described by Equations (9) and (10).

$${\epsilon }_{\mathrm{p}}=\mathrm{l}\mathrm{n}\frac{l_n}{l_{\mathrm{d}\mathrm{i}\mathrm{e}}}=\mathrm{l}\mathrm{n}\frac{t_{\mathrm{d}\mathrm{i}\mathrm{e}}\left(D_{\mathrm{d}\mathrm{i}\mathrm{e}}-t_{\mathrm{d}\mathrm{i}\mathrm{e}}\right)}{t_n\left(D_n-t_n\right)}$$

(9)

$$\Delta {\epsilon }_{\mathrm{u}\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}={\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-{\epsilon }_{\mathrm{p}}$$

(10)

Figure 19 shows the relationship between the unloading strain Δε_unload and the final excessive thinning of the outer diameter η. The final excessive thinning of the outer diameter η decreased when the unloading strain Δε_unload increased. Therefore, the final excessive thinning of the outer diameter decreased as the drawn tube recovered elastically during unloading.

The physical meaning of the unloading strain Δε_unload is discussed as follows. The elastic strain Δε_E, which depends on the elastic modulus of the bulk metal, was significantly smaller against the unloading strain of the loading-unloading tensile test, as shown in Figure 16. The elastic strain Δε_E in hollow sinking was calculated using Equation (11).

Δε_E = σ_l/E

(11)

The parameter E is the elastic modulus of the bulk metal. The reference value of the elastic modulus of each bulk metal is substituted into Equation (11). The reference values of stainless-steel, copper, and aluminum alloy are 204 GPa [23], 119 GPa [23], and 69 GPa [26], respectively. The elastic strain value in the range of 0.0005 to 0.002 was significantly smaller against the unloading strain of 0.002 to 0.015. Therefore, the outer diameter of the micro tube approached the die diameter due to the unloading strain, which was larger than the elastic strain, during unloading. The excessive elastic strain Δε_e, which was the difference between the unload strain Δε_unload and the elastic strain Δε_E, was calculated using Equation (12).

Δε_e = Δε_unload − Δε_E

(12)

Figure 20a,b show the relationship between the excessive elastic strain Δε_e and the apparent elastic modulus E′, and the drawing stress σ_l. The excessive elastic strain Δε_e grew when the apparent elastic modulus increased, or when the drawing stress decreased. The final outer diameter approached the die diameter as the drawing speed ratio decreased in Figure 8. Furthermore, the final outer diameter D_n fell in the order of the stainless-steel, the copper, and the aluminum alloy tube as shown in Figure 8. Figure 21 schematically shows the physical meaning of the excessive elastic strain. The micro tube recovered elastically to a degree greater than the elastic strain during unloading. Therefore, it is considered that the dislocations generated by microscopic yielding that occurred during drawing, disappeared partially during unloading. This phenomenon seems to be equivalent to the Bauschinger effect. It is considered that the dislocation density remaining after unloading was small under the conditions where few dislocations were generated during drawing such as with a high apparent elastic modulus, or low drawing stress. Therefore, the excessive elastic strain increased when the apparent elastic modulus grew, or the drawing stress decreased.

The unloading strain/total strain during the tensile test of the copper tube in Figure 16 was larger than that of the drawing experiment in Figure 19. Generally, the tensile residual stress is generated in the longitudinal direction during drawing [25]. Since the direction of the forces associated with the unloading behavior and the tensile residual stress are opposite, the tensile residual stress is considered to hinder the unloading behavior after drawing. Therefore, the amount of strain recovery during the tensile test was larger than that of the drawing test. A significant difference in tensile residual stress occurs when the die half angle is changed for the tube drawing process. Tube drawing was performed in this case using only one die half angle. Therefore, the effect of the tensile residual stress on the unloading strain is negligible. Investigation of the effect of the tensile residual stress on the unloading strain remains a subject of future research.

An approximation of the unloading behavior was performed to investigate the effect of the apparent elastic modulus on the unloading behavior. Figure 22 shows the approximation method for the unloading behavior.

The unloading behavior was approximated by a quadratic function, as shown in Equation (13). The parameter a is constant. By considering that the slope at the point (ε_total, E′·ε_total) is E, Equation (14) is obtained.

$${\sigma }_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}=\mathrm{a}{(\epsilon -{\epsilon }_{\mathrm{p}})}^2$$

(13)

$$\mathrm{a}=\frac{E}{2\left({\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-{\epsilon }_{\mathrm{p}}\right)}$$

(14)

The plastic strain ε_p is obtained by substituting ε_total and E′·ε_total into ε and σ_true of Equation (15), respectively, as shown in Equation (15).

$${\epsilon }_{\mathrm{p}}={\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-\frac{2E^{\prime }·{\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{E}$$

(15)

Lastly, substituting the plastic strain into Equation (15), Equation (16) is obtained as follows.

$${\sigma }_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}={\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-\frac{E^2{\left(\epsilon -{\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}+\frac{2E^{\prime }·{\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{E}\right)}^2}{4E^{\prime }·{\epsilon }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}$$

(16)

Figure 23 compares the actual plastic strain calculated by Equation (9) and calculated by Equation (15). The experimental values of the total strain ε_total, the bulk elastic modulus E, and the apparent elastic modulus E′ are substituted into Equation (15). The plastic strain obtained by Equation (15) generally agrees with the value obtained from Equation (9). Therefore, the unloading behavior can be expressed by a quadratic approximation. Figure 24 shows the unloading behavior obtained by Equation (16) at the bulk elastic modulus E and the apparent elastic modulus E′ of 190 GPa and 95 GPa, respectively. The experimental value of the total strain ε_total is substituted into Equation (16). The strain completely recovered after unloading. Therefore, it is considered that the dislocations caused by the microscopic yielding disappear completely during unloading when the apparent elastic modulus is larger than a threshold value.

4.2.4. Summary of Excessive Thinning of Outer Diameter

Figure 25 illustrates the excessive thinning of the outer diameter in the hollow sinking of a micro metal tube. The final outer diameter becomes smaller than the die diameter even when the drawing stress is in the elastic region and at any Lankford value. Furthermore, the outer diameter becomes smaller than the die diameter with an increase in the Lankford value, as shown by a theoretical formula (6). Therefore, it is considered that the micro tube yields microscopically during drawing, even under macroscopically elastic deformation behavior. The outer diameter seems to approach the die diameter during unloading more than the linear elastic strain outside the microscopic yielding region. Therefore, the dislocations generated during drawing are considered to disappear partially during unloading, which is similar to the Bauchinger effect. The unloading strain increases under the condition where few dislocations are generated during drawing, such as low drawing stress or high apparent elastic modulus of the stress-strain curve. Therefore, the final excessive thinning of the outer diameter decreases as the drawing stress decreases, or the apparent elastic modulus increases.

According to the above discussion, it is considered that the excessive thinning of the outer diameter can be suppressed by reducing the die half angle or the frictional force between the micro tube and the die, which results in reduced drawing stress for a particular yield stress. Furthermore, the drawing stress increases due to work hardening. However, since few dislocations are generated during the drawing of the micro tube, the drawing stress is much smaller than the yield stress because of the small size of the tube. Therefore, it is considered that work hardening of the micro tube suppresses the excessive thinning of the outer diameter.

5. Conclusions

The deformation behavior causing the excessive thinning of the outer diameter in the hollow sinking of micro thin-walled tubes can be explained as follows.

(1) At any Lankford value, the micro thin-walled tube yields microscopically during drawing even under a drawing stress lower than the yield stress of the bulk metal. Therefore, the outer diameter always becomes smaller than the die diameter during drawing.

(2) The outer diameter approaches the die diameter due to the unloading strain, which is larger than the linear elastic recovery, during unloading. The unloading strain increases as the drawing stress decreases or the apparent elastic modulus of the stress-strain curve increases. Therefore, the final excessive thinning of the outer diameter decreases as the drawing stress decreases, or the apparent elastic modulus increases. From the approximated unloading behavior, it is considered that the final outer diameter matches the die diameter completely during unloading due to elastic recovery when the apparent elastic modulus is larger than a threshold value.