The Anisotropic Stress-Induced Diffusion and Trapping of Nitrogen in Austenitic Stainless Steel during Nitriding
Abstract
1. Introduction
2. Mass Transport Model—The Coupling Between Nitrogen Stress-Assisted Diffusion and Trapping
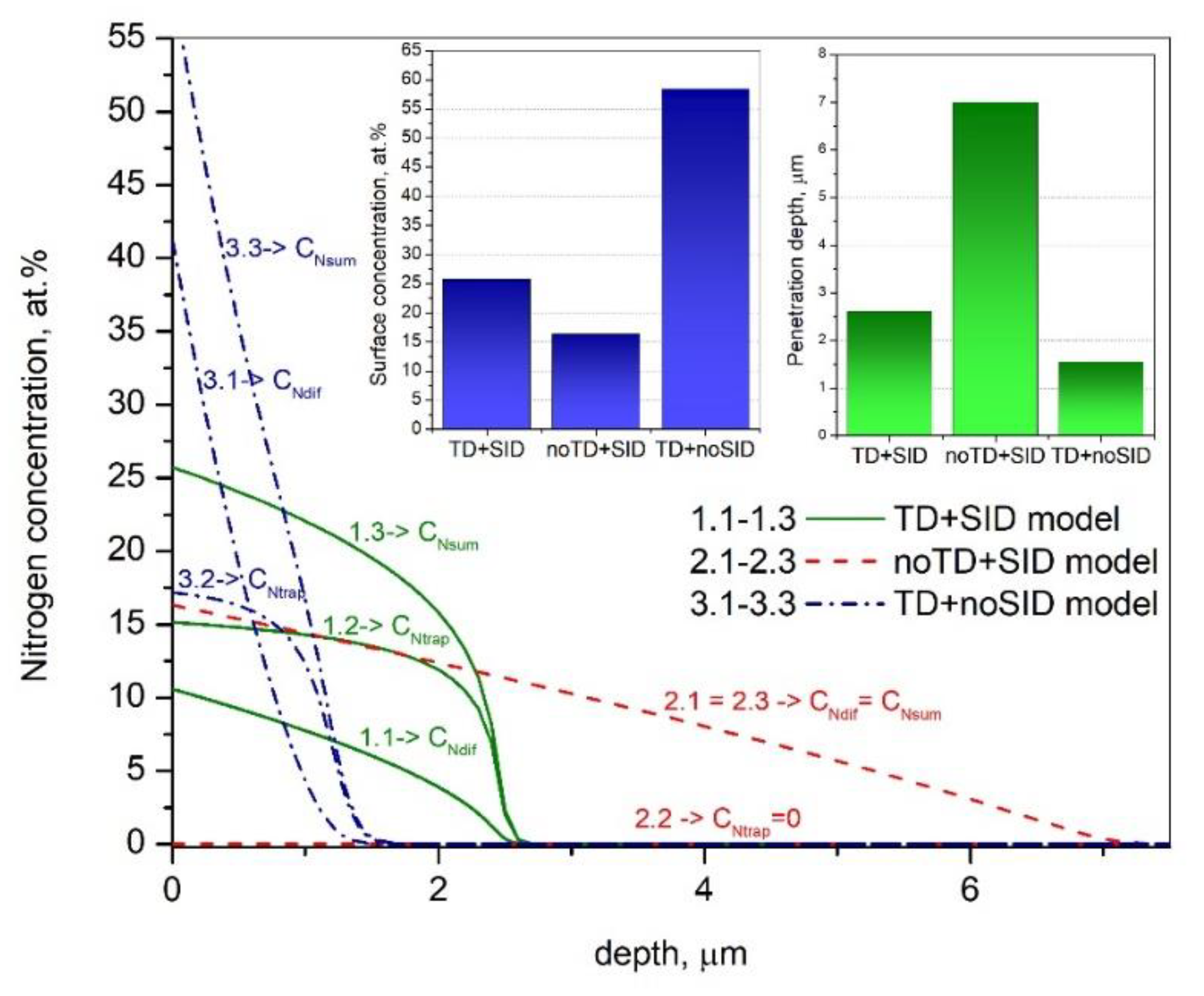
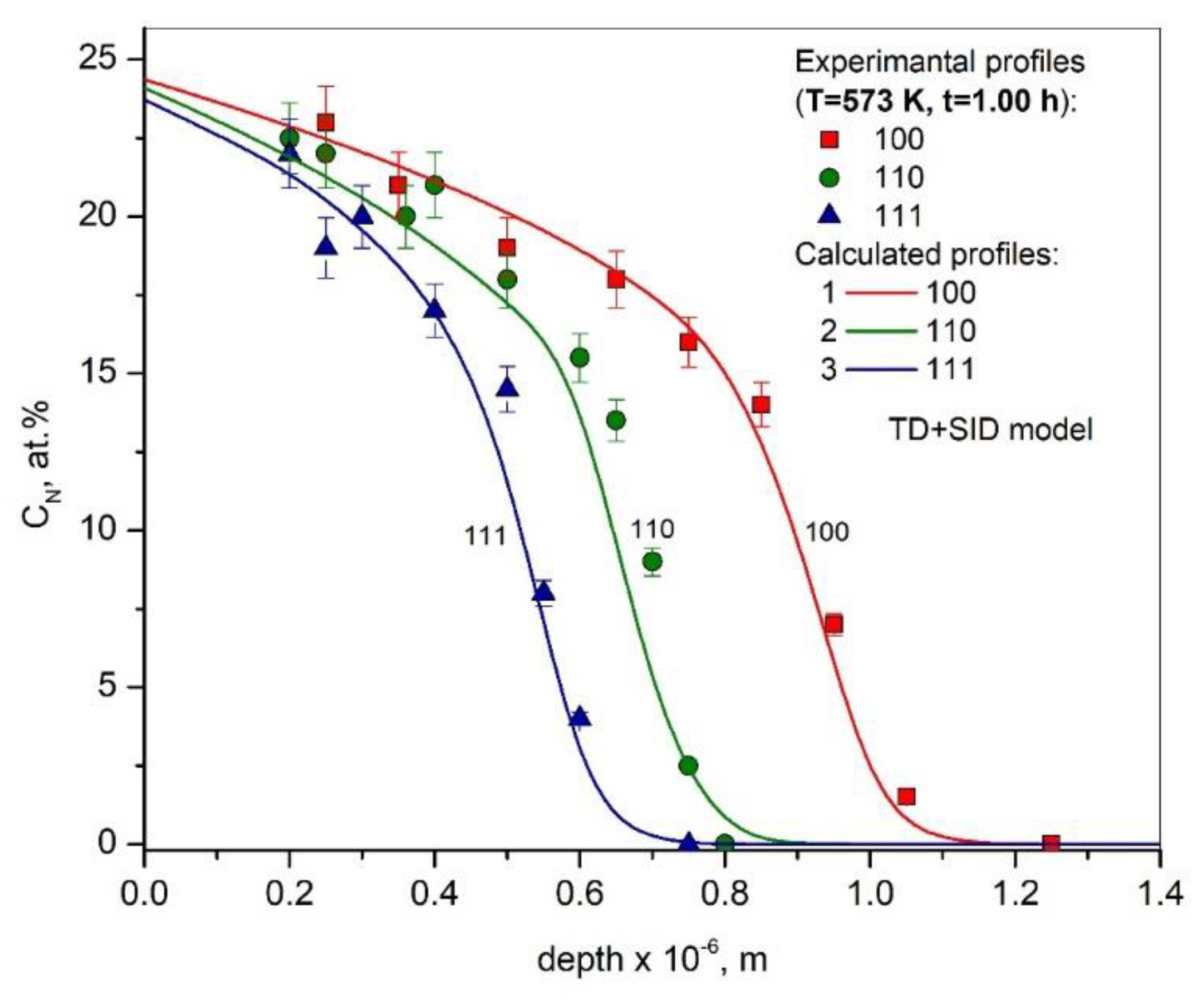
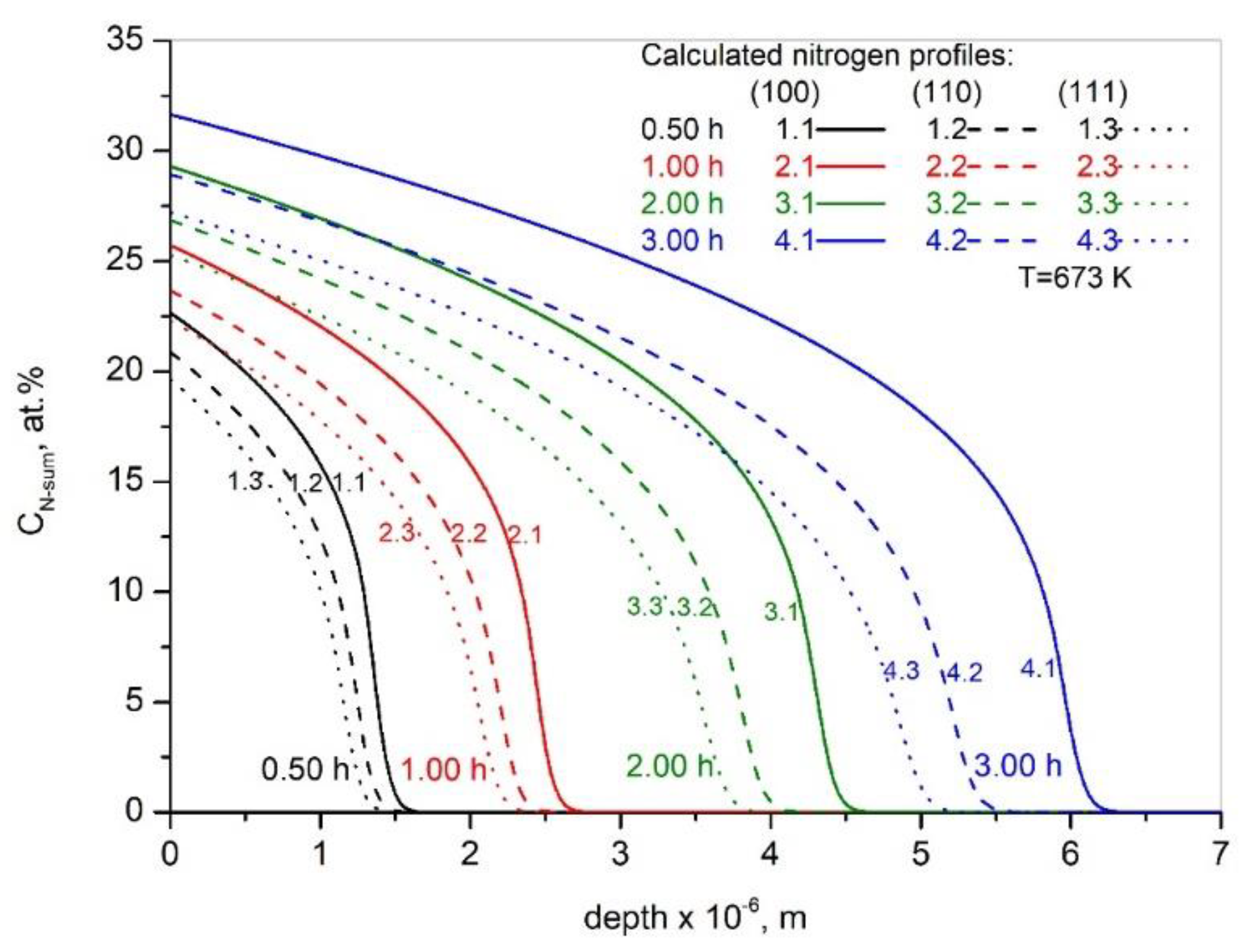
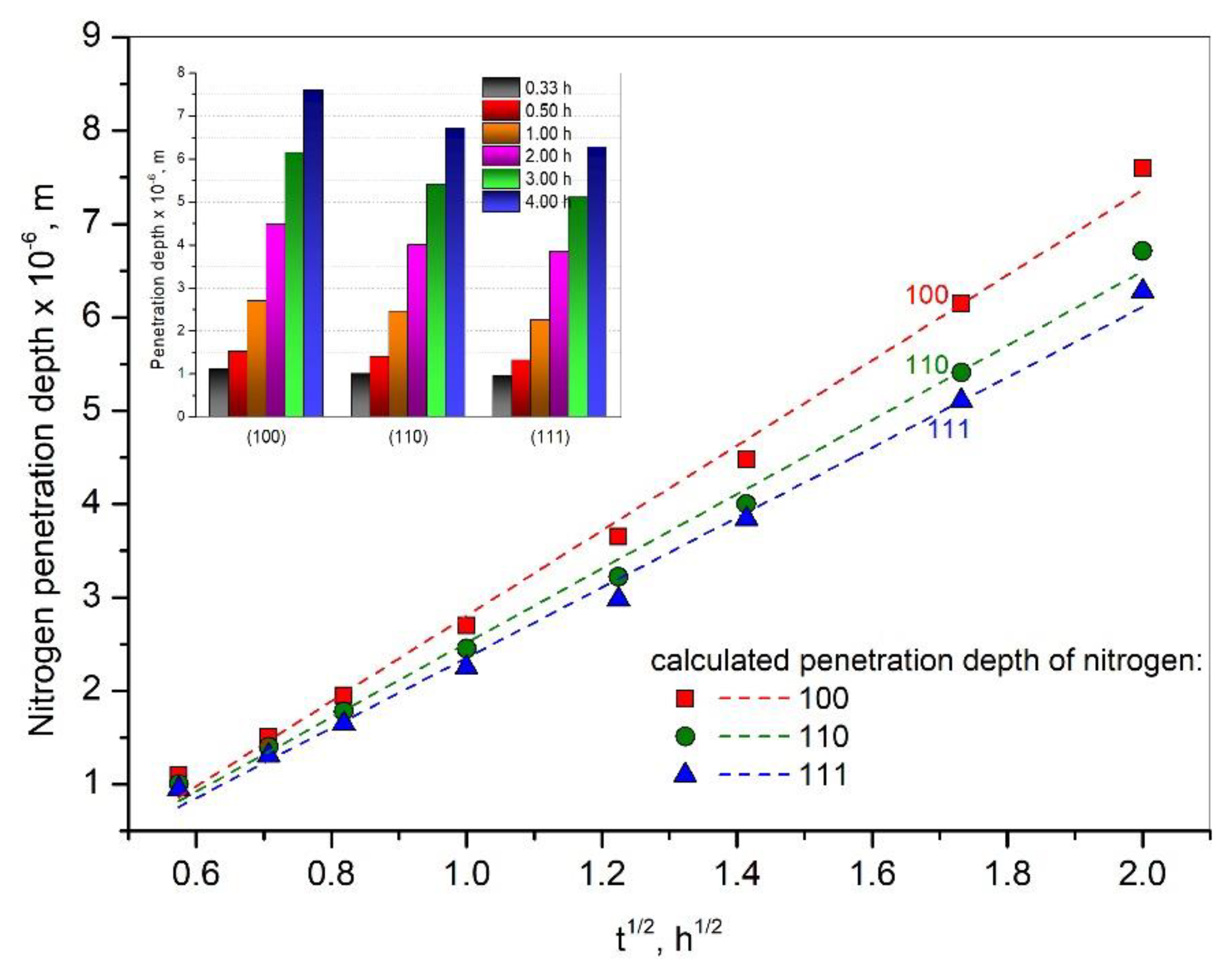
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Menthe, E.; Rie, K.T. Further investigation of the structure and properties of austenitic stainless steel after plasma nitriding. Surf. Coat. Technol. 1999, 116–119, 199–204. [Google Scholar] [CrossRef]
- Menthe, E.; Rie, K.T.; Schultze, J.W.; Simson, S. Structure and properties of plasma-nitrided stainless steel. Surf. Coat. Technol. 1995, 74–75, 412. [Google Scholar] [CrossRef]
- Ozturk, O.; Williamson, D.L. Phase and composition depth distribution analyses of low energy, high flux N implanted stainless steel. J. Appl. Phys. 1995, 77, 3839–3850. [Google Scholar] [CrossRef]
- Dahm, K.L.; Dearnley, P.A. On the nature, properties and wear response of s-phase (nitrogen-alloyed stainless steel) coatings on AISI 316L. Proc. Inst. Mech. Eng. Pt. L J. Mater. Des. Appl. 2000, 214, 181–198. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.Y.; Bell, T. X-ray diffraction characterisation of low temperature plasma nitrided austenitic stainless steels. J. Mater. Sci. 1999, 34, 4793–4802. [Google Scholar] [CrossRef]
- Mingolo, N.; Tschiptschin, A.P.; Pinedo, C.E. On the formation of expanded austenite during plasma nitriding of an AISI 316L austenitic stainless steel. Surf. Coat. Technol. 2006, 201, 4215–4218. [Google Scholar] [CrossRef]
- Mandl, S.; Rauschenbach, B. Nitrogen diffusion in austenitic stainless steel and the formation of expanded austenite. Defects Diffus. Metals III 2001, 125. [Google Scholar] [CrossRef]
- Wu, D.; Kahn, H.; Dalton, J.C.; Michal, G.M.; Ernst, F.; Heuer, A.H. Orientation dependence of nitrogen supersaturation in austenitic stainless steel during low-temperature gas-phase nitriding. Acta Mater. 2014, 79, 339. [Google Scholar] [CrossRef]
- Fewell, M.P.; Mitchell, D.R.G.; Priest, J.M.; Short, K.T.; Collins, G.A. The nature of expanded austenite. Surf. Coat. Technol. 2000, 131, 300–306. [Google Scholar] [CrossRef]
- Keddam, M.; Marcos, G.; Thiriet, T.; Czerwiec, T.; Michel, H. Microstructural characterization of the expanded austenite formed on the plasma nitrided AISI 316 L steel. Mater. Tech. 2013, 101, 204. [Google Scholar] [CrossRef]
- Somers, M.A.J.; Kücükyildiz, Ö.C.; Ormstrup, C.A.; Alimadadi, H.; Hattel, J.H.; Christiansen, T.L.; Winther, G. Residual stress in expanded austenite on stainless steel; origin, measurement, and prediction. Mater. Perform. Charact. 2018, 7, 693–716. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Hummelshøj, T.S.; Somers, M.A.J. Expanded austenite, crystallography and residual stress. Surf. Eng. 2010, 26, 242–247. [Google Scholar] [CrossRef]
- Riviere, J.P.; Pichon, L.; Drouet, M.; Poquillon, D.; Galdikas, A. Silicon based coatings deposited by dynamic ion mixing for oxidation protection of a Ti6242 alloy. Surf. Coat. Technol. 2007, 201, 8343–8347. [Google Scholar] [CrossRef]
- Picard, S.; Memet, J.B.; Sabot, R.; Grosseau-Poussard, J.L.; Rivière, J.P.; Meilland, R. Corrosion behaviour, microhardness and surface characterisation of low energy, high current ion implanted austenitic stainless steel. Mater. Sci. Eng. A 2001, 303, 163–172. [Google Scholar] [CrossRef]
- Stinville, J.C.; Villechaise, P.; Templie, C.; Riviere, J.P.; Drouet, M. Lattice rotation induced by plasma nitriding in a 316L polycrystalline stainless steel. Acta Mater. 2010, 58, 2814–2821. [Google Scholar] [CrossRef]
- Borgioli, F. From austenitic stainless steel to expanded austenite-S phase: Formation, characteristics and properties of an elusive metastable phase. Metals 2020, 10, 187. [Google Scholar] [CrossRef]
- Martinavičius, A.; Abrasonis, G.; Möller, W. Influence of crystal orientation and ion bombardment on the nitrogen diffusivity in single-crystalline austenitic stainless steel. J. Appl. Phys. 2011, 110, 075907. [Google Scholar] [CrossRef]
- Akhlaghi, M.; Jung, M.; Meka, S.R.; Fonović, M.; Leineweber, A.; Mittemeijer, E.J. Dependence of the nitriding rate of ferritic and austenitic substrates on the lattice orientation of surface grains; gaseous nitriding of Fe-Cr and Ni-Ti alloys. Philos. Mag. 2015, 95, 4143–4160. [Google Scholar] [CrossRef]
- Menéndez, E.; Templier, C.; Garcia-Ramirez, P.; Santiso, J.; Vantomme, A.; Temst, K.; Nogués, J. Magnetic properties of single crystalline expanded austenite obtained by plasma nitriding of austenitic stainless steel single crystals. ACS Appl. Mater. Interfaces 2013, 5, 10118–10126. [Google Scholar] [CrossRef]
- Fewell, M.P.; Priest, J.M. High-order diffractometry of expanded austenite using synchrotron radiation. Surf. Coat. Technol. 2008, 202, 802–1815. [Google Scholar] [CrossRef]
- He, H.; Zou, J.X.; Dong, C.; Czerwiec, T.; Michel, H. Stress induced anisotropic diffusion during plasma-assisted nitriding of a Ni-based alloy. Mater. Sci. Forum. 2005, 475–479, 3669–3672. [Google Scholar] [CrossRef]
- Kahn, H.; Michal, G.M.; Ernst, F.; Heuer, A.H. Poisson effects on X-ray diffraction patterns in low-temperature-carburized austenitic stainless steel. Metall. Mater. Trans. A 2009, 40A, 1799–1804. [Google Scholar] [CrossRef]
- Mändl, S.; Rauschenbach, B. Anisotropic strain in nitrided austenitic stainless steel. J. Appl. Phys. 2000, 88, 3323–3329. [Google Scholar] [CrossRef]
- Jespersen, F.N.; Hattel, J.H.; Somers, M.A.J. Modelling the evolution of composition-and stress-depth profiles in austenitic stainless steels during low-temperature nitriding. Model. Simul. Mat. Sci. Eng. 2016, 24, 025003. [Google Scholar] [CrossRef]
- Kücükyildiz, Ö.C.; Sonne, M.R.; Thorborg, J.; Somers, M.A.J.; Hattel, J.H. Thermo-chemical-mechanical simulation of low temperature nitriding of austenitic stainless steel; inverse modelling of surface reaction rates. Surf. Coat. Technol. 2020, 381, 125145. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A. Stress induced nitrogen diffusion in nitrided austenitic stainless steel. Mater. Sci. Medz. 2011, 17, 11–15. [Google Scholar] [CrossRef]
- Galdikas, A.; Moskalioviene, T. Swelling effect on stress induced and concentration dependent diffusion of nitrogen in plasma nitrided austenitic stainless steel. Comput. Mater. Sci. 2013, 72, 140–145. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A. The effect of hydrogen on plasma nitriding of austenitic stainless steel: Kinetic modeling. Metall. Mater. Trans. A 2015, 46, 5588–5595. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A. Kinetic model of anisotropic stress assisted diffusion of nitrogen in nitrided austenitic stainless steel. Surf. Coat. Technol. 2019, 366, 277–285. [Google Scholar] [CrossRef]
- Galdikas, A.; Moskalioviene, T. Stress induced nitrogen diffusion during nitriding of austenitic stainless steel. Comput. Mater. Sci. 2010, 50, 796–799. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A. Lattice orientation dependence of nitrogen mass transport in austenitic stainless steel. Metals 2020, 10, 615. [Google Scholar] [CrossRef]
- Zangwill, A. Physics at Surfaces; Cambridge University Press: New York, NY, USA, 1988. [Google Scholar]
- Czerwiec, T.; Andrieux, A.; Marcos, G.; Michel, H.; Bauer, P. Is “expanded austenite” really a solid solution? Mossbauer observation of an annealed AISI 316L nitrided sample. J. Alloys Compd. 2019, 811, 151972. [Google Scholar] [CrossRef]
- Oddershede, J.; Christiansen, T.L.; Stahl, K.; Somers, M.A.J. Extended X-ray absorption fine structure investigation of nitrogen stabilized expanded austenite. Scr. Mater. 2010, 62, 290–293. [Google Scholar] [CrossRef]
- Tao, X.; Matthews, A.; Leyland, A. On the Nitrogen-Induced Lattice Expansion of a Non-stainless Austenitic Steel, Invar 36®, Under Triode Plasma Nitriding. Metall. Mater. Trans. A 2020, 51, 436–447. [Google Scholar] [CrossRef]
- Parascandola, S.; Moller, W.; Williamson, D.L. The nitrogen transport in austenitic stainless steel at moderate temperatures. Appl. Phys. Lett. 2000, 76, 2194–2196. [Google Scholar] [CrossRef]
- Riviere, J.P.; Cahoreau, M.; Meheust, P. Chemical bonding of nitrogen in low energy high flux implanted austenitic stainless steel. J. Appl. Phys. 2002, 91, 6361. [Google Scholar] [CrossRef]
- Martinavicius, A.; Abrasonis, G.; Möller, W.; Templier, C.; Rivière, J.P.; Declémy, A.; Chumlyakov, Y. Anisotropic ion-enhanced diffusion during ion nitriding of single crystalline austenitic stainless steel. J. Appl. Phys. 2009, 105, 093502. [Google Scholar] [CrossRef]
- Moskalioviene, T.; Galdikas, A.; Riviere, J.P.; Pichon, L. Modeling of nitrogen penetration in polycrystalline AISI 316L austenitic stainless steel during plasma nitriding. Surf. Coat. Technol. 2011, 205, 3301–3306. [Google Scholar] [CrossRef]
- Mändl, S.; Scholze, F.; Neumann, H.; Rauschenbach, B. Nitrogen diffusivity in expanded austenite. Surf. Coat. Technol. 2003, 174–175, 1191–1195. [Google Scholar] [CrossRef]
- Gu, X.; Michal, G.M.; Ernst, F.; Kahn, H.; Heuer, A.H. Numerical Simulations of Carbon and Nitrogen Composition-Depth Profiles in Nitrocarburized Austenitic Stainless Steels. Metall. Mater. Trans. A 2014, 45, 4268–4279. [Google Scholar] [CrossRef]
- Christiansen, T.; Dahl, K.V.; Somers, M.A.J. Nitrogen diffusion and nitrogen depth profiles in expanded austenite: Experimental assessment, numerical simulation and role of stress. Mater. Sci. Technol. 2008, 24, 159–167. [Google Scholar] [CrossRef]
- Fischer, F.D.; Svoboda, J.; Kozeschnik, E. Interstitial diffusion in systems with multiple sorts of traps. Model Simul. Mat. Sci. Eng. 2013, 21, 025008. [Google Scholar] [CrossRef]
- Svoboda, J.; Fischer, F.D.; Fratzl, P. Diffusion and creep in multi-component alloys with non-ideal sources and sinks for vacancies. Acta Mater. 2006, 54, 3043–3053. [Google Scholar] [CrossRef]
- Svoboda, J.; Fischer, F.D. Modelling for hydrogen diffusion in metals with traps revisited. Acta Mater. 2012, 60, 1211–1220. [Google Scholar] [CrossRef]
- Möller, W.; Parascandola, S.; Telbizova, T.; Günzel, R.; Richter, E. Surface processes and diffusion mechanisms of ion nitriding of stainless steel and aluminium. Surf. Coat. Technol. 2001, 136, 73–79. [Google Scholar] [CrossRef]
- Oriani, R. The diffusion and trapping of hydrogen in steel. Acta Metall. 1970, 18, 147–157. [Google Scholar] [CrossRef]
- Sofronis, P.; McMeeking, R.M. Numerical analysis of hydrogen transport near a blunting crack tip. J. Mech. Phys. Solids 1989, 37, 317–350. [Google Scholar] [CrossRef]
- Krom, A.H.M.; Koers, R.W.J.; Bakker, A. Hydrogen transport near a blunting crack tip. J. Mech. Phys. Solids 1999, 47, 971–992. [Google Scholar] [CrossRef]
- Zhang, L.; Barrett, R.; Cloetens, P.; Detlefs, C.; Rio, M.S. Anisotropic elasticity of silicon and its application to the modelling of X-ray optics. J. Synchrotron Radiat. 2014, 21, 507–517. [Google Scholar] [CrossRef]
- He, H.; Czerwiec, T.; Dong, C.; Michel, H. Effect of grain orientation on the nitriding rate of a nickel base alloy studied by electron backscatter diffraction. Surf. Coat. Technol. 2003, 163–164, 331–338. [Google Scholar] [CrossRef]
- Zener, C. Contributions to the Theory of Beta-Phase Alloys. Phys. Rev. 1947, 71, 846–851. [Google Scholar] [CrossRef]
- Templier, C.; Stinville, J.C.; Villechaise, P.; Renault, P.O.; Abrasonis, G.; Riviere, J.P.; Martinavicius, A.; Drouet, M. On lattice plane rotation and crystallographic structure of the expanded austenite in plasma nitrided AISI 316L steel. Surf. Coat. Technol. 2010, 204, 2551–2558. [Google Scholar] [CrossRef]
- Juul, N.Y.; Oddershede, J.; Beaudoin, A.; Chatterjee, K.; Koker, M.K.A.; Dale, D.; Shade, P.; Winther, G. Measured resolved shear stresses and Bishop-Hill stress states in individual grains of austenitic stainless steel. Acta Mater. 2017, 141, 388–404. [Google Scholar] [CrossRef]
- Gressmann, T.; Wohlschlogel, M.; Shang, S.; Welzel, U.; Leineweber, A.; Mittemeijer, E.J.; Liu, Z.K. Elastic anisotropy of γ’-Fe4N and elastic grain interaction in γ’-Fe4N1−y layers on α-Fe: First-principles calculations and diffraction stress measurements. Acta Mater. 2007, 55, 5833–5843. [Google Scholar] [CrossRef]



| Elastic Constants | AISI 316L γ Phase [54] | AISI 316L γN Phase [55] | T, K | 673,573 |
| iN, s−1 | 27.2 × 10−4 | |||
| C11, GPa | 206 | 307.2 | Do, m2s−1 | 17.5 × 10−9 |
| C12, GPa | 133 | 134.1 | EA, eV [39] | 1.1 |
| C44, GPa | 119 | 46 | EB, eV | 0.23 |
| , 1/GPa | 0.00984 | 0.00443 | αN | 0.8 |
| αN-hkl | ||||
| , 1/GPa | −0.00386 | −0.00135 | Xstress, GPa presented in Figure 2 | |
| , 1/GPa | 0.00840 | 0.02174 | N0, m−3 [39] | 7.29 × 1028 |
| Ht, m−3 [39] | 1.31 × 1028 | |||
| Zener ratio | 3.26 | 0.53 | VN, m3/mol | 3.9 × 10−5 |
| Rt, m [39] | 0.38 × 10−9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galdikas, A.; Moskalioviene, T. The Anisotropic Stress-Induced Diffusion and Trapping of Nitrogen in Austenitic Stainless Steel during Nitriding. Metals 2020, 10, 1319. https://doi.org/10.3390/met10101319
Galdikas A, Moskalioviene T. The Anisotropic Stress-Induced Diffusion and Trapping of Nitrogen in Austenitic Stainless Steel during Nitriding. Metals. 2020; 10(10):1319. https://doi.org/10.3390/met10101319
Chicago/Turabian StyleGaldikas, Arvaidas, and Teresa Moskalioviene. 2020. "The Anisotropic Stress-Induced Diffusion and Trapping of Nitrogen in Austenitic Stainless Steel during Nitriding" Metals 10, no. 10: 1319. https://doi.org/10.3390/met10101319
APA StyleGaldikas, A., & Moskalioviene, T. (2020). The Anisotropic Stress-Induced Diffusion and Trapping of Nitrogen in Austenitic Stainless Steel during Nitriding. Metals, 10(10), 1319. https://doi.org/10.3390/met10101319






