On the Zener–Hollomon Parameter, Multi-Layer Perceptron and Multivariate Polynomials in the Struggle for the Peak and Steady-State Description
Abstract
:1. Introduction
2. Materials and Methods
2.1. Acquiring of Experimental Hot Flow Curve Dataset
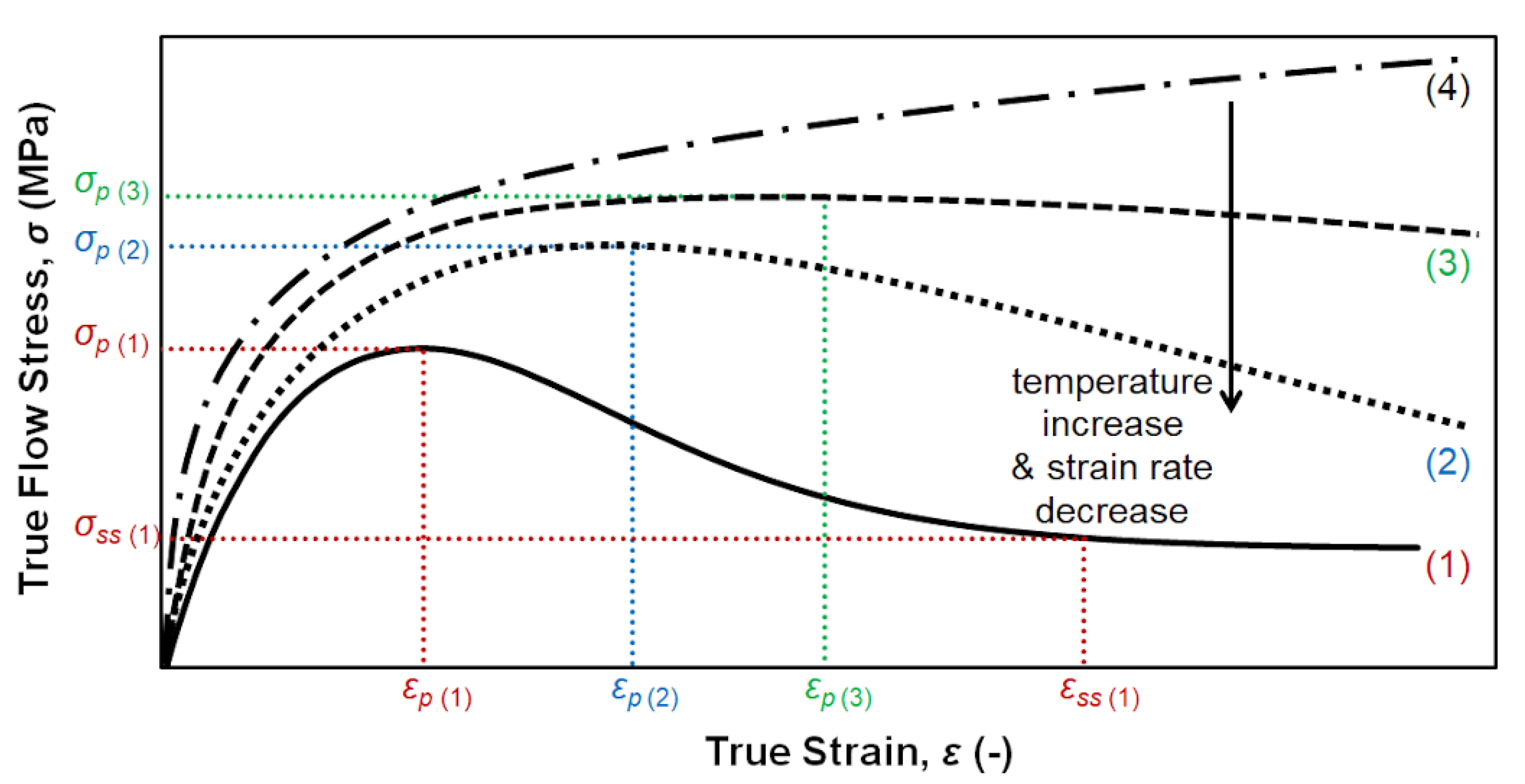
2.2. Flow Curve Description
2.2.1. Peak and Steady-State Description via Zener–Hollomon Parameter
2.2.2. Peak and Steady-State Description via Multi-Layer Perceptron Network
2.2.3. Peak and Steady-State Description via Multivariate Polynomials
3. Results and Discussion
3.1. Experimental Dataset
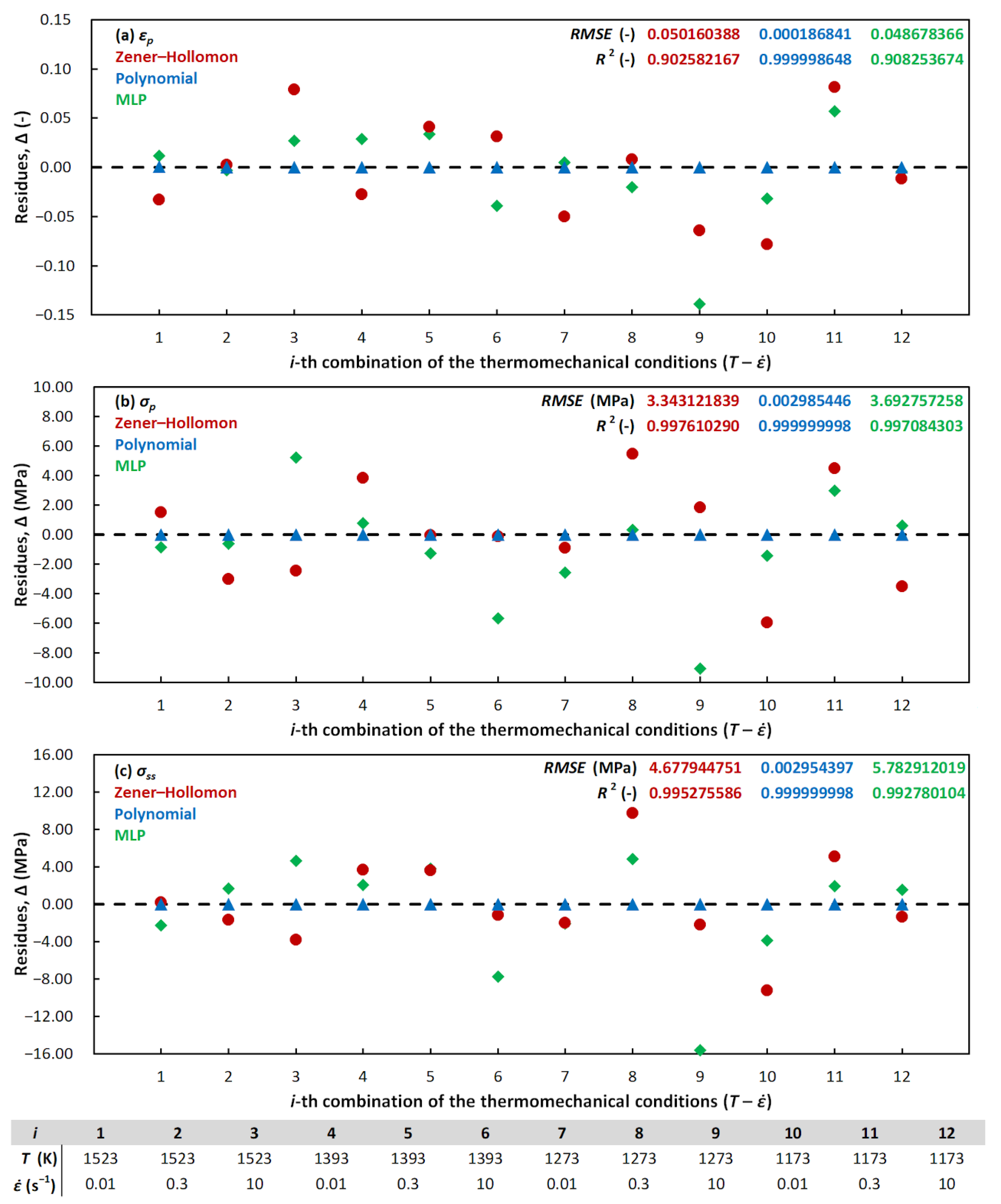
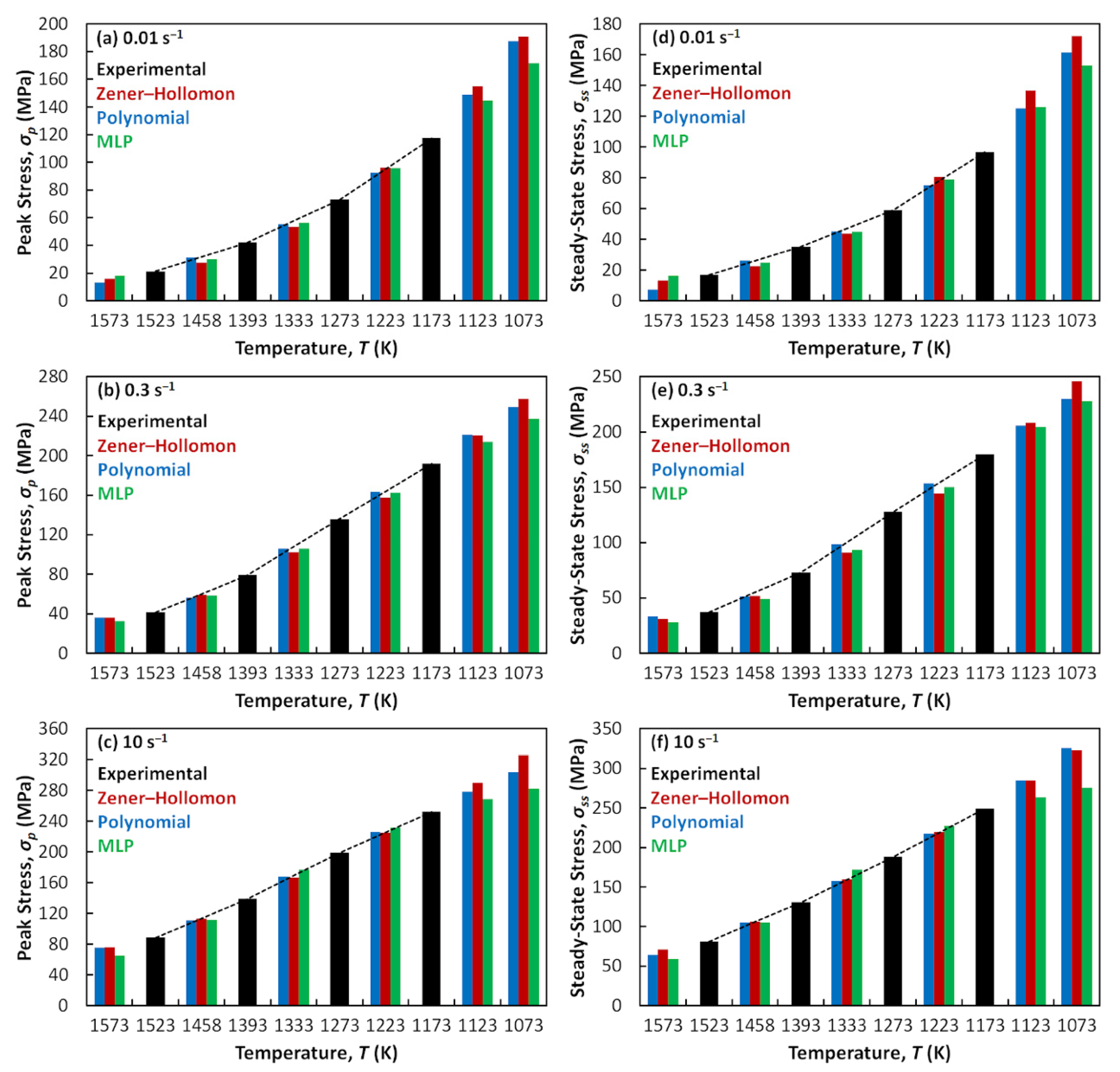
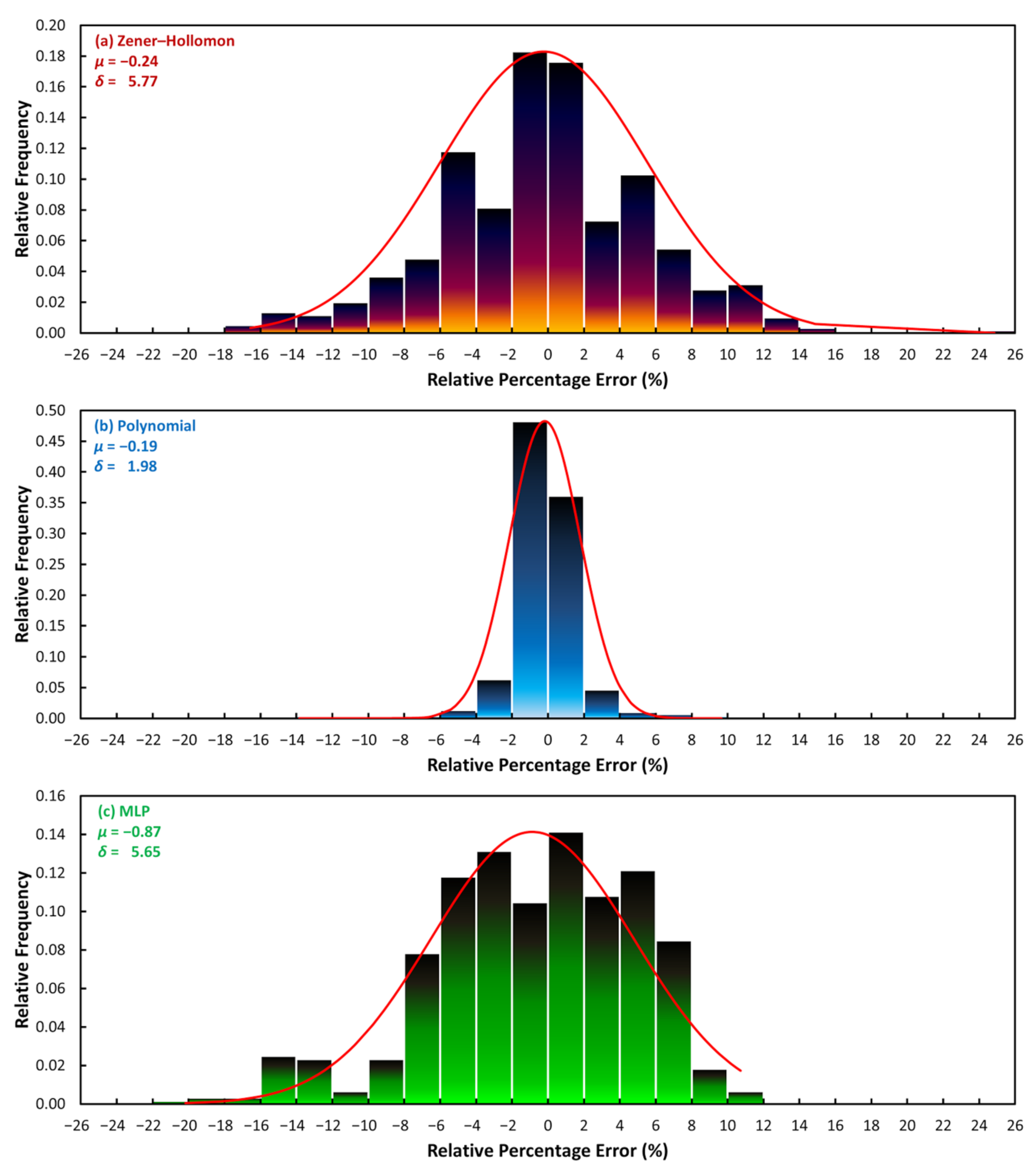
3.2. Evaluation of the Peak and Steady-State Description
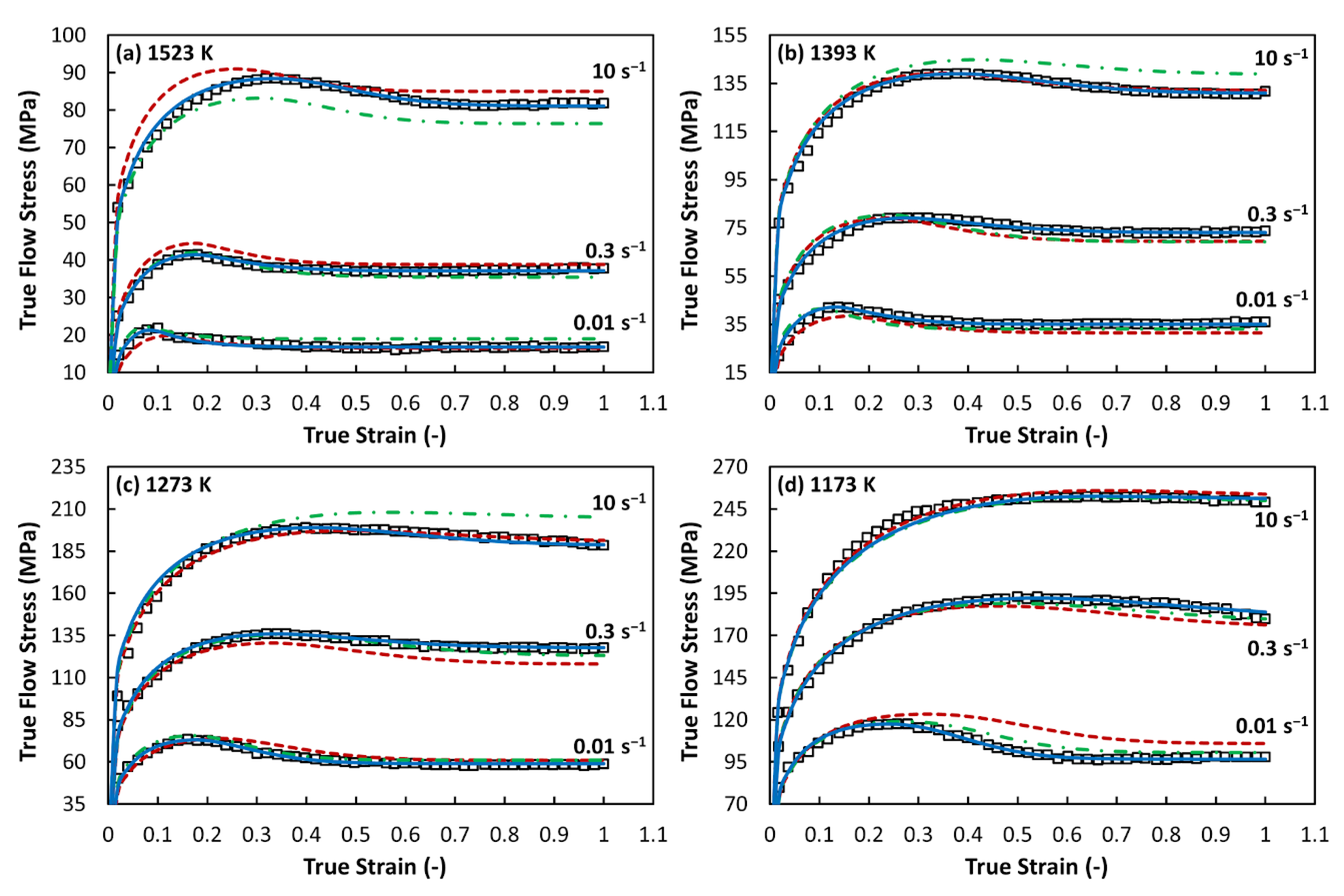
3.3. Evaluation of the Flow Curve Description
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gronostajski, Z. The Constitutive Equations for FEM Analysis. J. Mater. Process. Technol. 2000, 106, 40–44. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Shafiei, E. Mathematical Modeling of Single Peak Dynamic Recrystallization Flow Stress Curves in Metallic Alloys. In Recrystallization; Sztwiertnia, K., Ed.; InTech: Rijeka, Croatia, 2012; pp. 207–225. [Google Scholar] [CrossRef] [Green Version]
- Fields, D.S.; Backofen, W.A. Determination of Strain Hardening Characteristics by Torsion Testing. Proc. ASTM 1957, 57, 1259–1272. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; American Defense Preparedness Association: Arlington, VA, USA, 1983; pp. 541–547. [Google Scholar]
- Cingara, A.; McQueen, H.J. New Formula for Calculating Flow Curves from High Temperature Constitutive Data for 300 Austenitic Steels. J. Mater. Process. Technol. 1992, 36, 31–42. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Zahiri, S.H.; Najafizadeh, A. Mathematical Modelling of the Stress–Strain Curves of Ti-IF Steel at High Temperature. J. Mater. Process. Technol. 2006, 171, 301–305. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.-S.; Zhong, J. Constitutive Modeling for Elevated Temperature Flow Behavior of 42CrMo Steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive Equations to Predict High Temperature Flow Stress in a Ti-Modified Austenitic Stainless Steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K.; Ebrahimi, G.R.; Keshmiri, H. Modeling the Flow Curve Characteristics of 410 Martensitic Stainless Steel under Hot Working Condition. Metall. Mater. Trans. A 2010, 41, 2898–2904. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Flow Stress Prediction at Hot Working Conditions. Mater. Sci. Eng. A 2010, 527, 1160–1164. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Extrapolation of Flow Curves at Hot Working Conditions. Mater. Sci. Eng. A 2010, 527, 1856–1860. [Google Scholar] [CrossRef]
- Shafaat, M.A.; Omidvar, H.; Fallah, B. Prediction of Hot Compression Flow Curves of Ti–6Al–4V Alloy in α + β Phase Region. Mater. Des. 2011, 32, 4689–4695. [Google Scholar] [CrossRef]
- YU, B.-J.; Guan, X.-J.; Wang, L.-J.; Zhao, J.; Liu, Q.-Q.; Cao, Y. Hot Deformation Behavior and Constitutive Relationship of Q420qE Steel. J. Cent. South Univ. Technol. 2011, 18, 36–41. [Google Scholar] [CrossRef]
- Lin, Y.C.; Li, Q.-F.; Xia, Y.-C.; Li, L.-T. A Phenomenological Constitutive Model for High Temperature Flow Stress Prediction of Al–Cu–Mg Alloy. Mater. Sci. Eng. A 2012, 534, 654–662. [Google Scholar] [CrossRef]
- Fereshteh-Saniee, F.; Barati, F.; Badnava, H.; Nejad, K.F. An Exponential Material Model for Prediction of the Flow Curves of Several AZ Series Magnesium Alloys in Tension and Compression. Mater. Des. 2012, 35, 1–11. [Google Scholar] [CrossRef]
- Changizian, P.; Zarei-Hanzaki, A.; Roostaei, A.A. The High Temperature Flow Behavior Modeling of AZ81 Magnesium Alloy Considering Strain Effects. Mater. Des. 2012, 39, 384–389. [Google Scholar] [CrossRef]
- Li, H.-Y.; Wei, D.-D.; Hu, J.-D.; Li, Y.-H.; Chen, S.-L. Constitutive Modeling for Hot Deformation Behavior of T24 Ferritic Steel. Comput. Mater. Sci. 2012, 53, 425–430. [Google Scholar] [CrossRef]
- Nayak, K.C.; Date, P.P. Development of Constitutive Relationship for Thermomechanical Processing of Al-SiC Composite Eliminating Deformation Heating. J. Mater. Eng. Perform. 2019, 28, 5323–5343. [Google Scholar] [CrossRef]
- Sheikhali, A.H.; Morakkabati, M.; Abbasi, S.M. Constitutive Modeling for Hot Working Behavior of SP-700 Titanium Alloy. J. Mater. Eng. Perform. 2019, 28, 6525–6537. [Google Scholar] [CrossRef]
- Schindler, I.; Kawulok, P.; Očenášek, V.; Opěla, P.; Kawulok, R.; Rusz, S. Flow Stress and Hot Deformation Activation Energy of 6082 Aluminium Alloy Influenced by Initial Structural State. Metals 2019, 9, 1248. [Google Scholar] [CrossRef] [Green Version]
- Hensel, A.; Spittel, T. Kraft- und Arbeitsbedarf bildsamer Formgebungsverfahren, 1st ed.; Deutscher Verlag für Grundstoffindustrie: Leipzig, Germany, 1978. [Google Scholar]
- Solhjoo, S. Analysis of Flow Stress up to the Peak at Hot Deformation. Mater. Des. 2009, 30, 3036–3040. [Google Scholar] [CrossRef]
- Solhjoo, S. Determination of Critical Strain for Initiation of Dynamic Recrystallization. Mater. Des. 2010, 31, 1360–1364. [Google Scholar] [CrossRef]
- Solhjoo, S. Determination of Flow Stress under Hot Deformation Conditions. Mater. Sci. Eng. A 2012, 552, 566–568. [Google Scholar] [CrossRef]
- Solhjoo, S. Determination of Flow Stress and the Critical Strain for the Onset of Dynamic Recrystallization Using a Hyperbolic Tangent Function. Mater. Des. 2014, 54, 390–393. [Google Scholar] [CrossRef]
- Solhjoo, S. Determination of Flow Stress and the Critical Strain for the Onset of Dynamic Recrystallization Using a Sine Function. Available online: https://arxiv.org/ftp/arxiv/papers/1405/1405.0196.pdf (accessed on 19 May 2020).
- Solhjoo, S.; Vakis, A.I.; Pei, Y.T. Two Phenomenological Models to Predict the Single Peak Flow Stress Curves up to the Peak during Hot Deformation. Mech. Mater. 2017, 105, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Spigarelli, S.; El Mehtedi, M. A New Constitutive Model for the Plastic Flow of Metals at Elevated Temperatures. J. Mater. Eng. Perform. 2014, 23, 658–665. [Google Scholar] [CrossRef]
- Quan, G.; Tong, Y.; Luo, G.; Zhou, J. A Characterization for the Flow Behavior of 42CrMo Steel. Comput. Mater. Sci. 2010, 50, 167–171. [Google Scholar] [CrossRef]
- Shen, J.; Hu, L.; Sun, Y.; Wan, Z.; Feng, X.; Ning, Y. A Comparative Study on Artificial Neural Network, Phenomenological-Based Constitutive and Modified Fields–Backofen Models to Predict Flow Stress in Ti-4Al-3V-2Mo-2Fe Alloy. J. Mater. Eng. Perform. 2019, 28, 4302–4315. [Google Scholar] [CrossRef]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.-M. A Simple Constitutive Model for Predicting Flow Stress of Medium Carbon Microalloyed Steel during Hot Deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef] [Green Version]
- Mohamadizadeh, A.; Zarei-Hanzaki, A.; Abedi, H.R. Modified Constitutive Analysis and Activation Energy Evolution of a Low-Density Steel Considering the Effects of Deformation Parameters. Mech. Mater. 2016, 95, 60–70. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.-X.; Gong, H.; Wang, K. Modification of Constitutive Model and Evolution of Activation Energy on 2219 Aluminum Alloy during Warm Deformation Process. Trans. Nonferrous Met. Soc. China 2019, 29, 448–459. [Google Scholar] [CrossRef]
- Wang, F.; Shen, J.; Zhang, Y.; Ning, Y. A Modified Constitutive Model for the Description of the Flow Behavior of the Ti-10V-2Fe-3Al Alloy during Hot Plastic Deformation. Metals 2019, 9, 844. [Google Scholar] [CrossRef] [Green Version]
- Anand, L. Constitutive Equations for the Rate-Dependent Deformation of Metals at Elevated Temperatures. J. Eng. Mater. Technol. 1982, 104, 12–17. [Google Scholar] [CrossRef]
- Koric, S.; Thomas, B.G. Thermo-Mechanical Models of Steel Solidification Based on Two Elastic Visco-Plastic Constitutive Laws. J. Mater. Process. Technol. 2008, 197, 408–418. [Google Scholar] [CrossRef]
- Kozlowski, P.F.; Thomas, B.G.; Azzi, J.A.; Wang, H. Simple Constitutive Equations for Steel at High Temperature. Metall. Mater. Trans. A 1992, 23, 903–918. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Zou, Z.-Y.; Wang, T.; Liu, B.; Li, J.-C. Modeling the Hot Deformation Behaviors of As-Extruded 7075 Aluminum Alloy by an Artificial Neural Network with Back-Propagation Algorithm. High. Temp. Mater. Process. 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Lv, J.; Ren, H.; Gao, K. Artificial Neural Network-Based Constitutive Relationship of Inconel 718 Superalloy Construction and its Application in Accuracy Improvement of Numerical Simulation. Appl. Sci. 2017, 7, 124. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Pan, Q.L.; Li, A.D.; Song, W.B. Flow Behavior of Al-6.2Zn-0.70Mg-0.30Mn-0.17Zr Alloy During Hot Compressive Deformation Based on Arrhenius and ANN Models. Trans. Nonferrous Met. Soc. China 2017, 27, 638–647. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liang, Y.J.; Chen, M.S.; Chen, X.M. A Comparative Study on Phenomenon and Deep Belief Network Models for Hot Deformation Behavior of an Al–Zn–Mg–Cu Alloy. Appl. Phys. A Mater. Sci. Process. 2017, 123, 68. [Google Scholar] [CrossRef]
- Opěla, P.; Kawulok, P.; Kawulok, R.; Kotásek, O.; Buček, P.; Ondrejkovič, K. Extension of Experimentally Assembled Processing Maps of 10CrMo9-10 Steel via a Predicted Dataset and the Influence on Overall Informative Possibilities. Metals 2019, 9, 1218. [Google Scholar] [CrossRef] [Green Version]
- Song, S.H. A Comparison Study of Constitutive Equation, Neural Networks, and Support Vector Regression for Modeling Hot Deformation of 316L Stainless Steel. Materials 2020, 13, 3766. [Google Scholar] [CrossRef]
- Mozaffar, M.; Bostanabad, R.; Chen, W.; Ehmann, K.; Cao, J.; Bessa, M.A. Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. USA 2019, 116, 26414–26420. [Google Scholar] [CrossRef] [Green Version]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2020, 136, 102852. [Google Scholar] [CrossRef]
- Wu, S.W.; Zhou, X.G.; Cao, G.M.; Liu, Z.Y.; Wang, G.D. The Improvement on Constitutive Modeling of Nb-Ti Micro Alloyed Steel by Using Intelligent Algorithms. Mater. Des. 2017, 116, 676–685. [Google Scholar] [CrossRef]
- Opěla, P.; Schindler, I.; Kawulok, P.; Kawulok, R.; Rusz, S.; Rodak, K. Hot Flow Curve Description of CuFe2 Alloy via Different Artificial Neural Network Approaches. J. Mater. Eng. Perform. 2019, 28, 4863–4870. [Google Scholar] [CrossRef]
- Pietrzyk, M.; Kusiak, J.; Szeliga, D.; Rauch, Ł.; Sztangret, Ł.; Górecki, G. Application of Metamodels to Identification of Metallic Materials Models. Adv. Mater. Sci. Eng. 2016, 2016, 2357534. [Google Scholar] [CrossRef] [Green Version]
- Sztangret, Ł.; Szeliga, D.; Kusiak, J.; Pietrzyk, M. Application of Inverse Analysis with Metamodelling for Identification of Metal Flow Stress. Can. Metall. Q. 2012, 51, 440–446. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Schindler, I.; Kawulok, P.; Kawulok, R.; Hadasik, E.; Kuc, D. Influence of Calculation Method on Value of Activation Energy in Hot Forming. High Temp. Mater. Processes 2013, 32, 149–155. [Google Scholar] [CrossRef]
- Razali, M.K.; Irani, M.; Joun, M.S. General Modeling of Flow Stress Curves of Alloys at Elevated Temperatures Using Bi-Linearly Interpolated or Closed-Form Functions for Material Parameters. J. Mater. Res. Technol. 2019, 8, 2710–2720. [Google Scholar] [CrossRef]
- GLEEBLE: Gleeble®Thermal-Mechanical Simulators. Available online: https://gleeble.com/ (accessed on 1 October 2019).
- Kolmogorov, A.N. К статистическoй теoрии кристаллизации металлoв [On the statistics of crystallization processes in metals]. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1937, 1, 355–359. [Google Scholar]
- Wei, H.-L.; Liu, G.-Q.; Xiao, X.; Zhang, M.-H. Dynamic Recrystallization Behavior of a Medium Carbon Vanadium Microalloyed Steel. Mater. Sci. Eng. A 2013, 573, 215–221. [Google Scholar] [CrossRef]
- Legendre, A.M. Nouvelles méthodes pour la détermination des orbites des comètes [New Methods for the Determination of the Orbits of Comets]; Firmin-Didot: Mesnil-sur-I’Estrée, France, 1805. [Google Scholar]
- Opěla, P.; Schindler, I.; Kawulok, P.; Vančura, F.; Kawulok, R.; Rusz, S. New Model Predicting Flow Curves in Wide Range of Thermomechanical Conditions of 38MnVS6 Steel. In Proceedings of the Metal 2016: 25th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 25–27 May 2016; Tanger Ltd.: Ostrava, Czech Republic, 2017; pp. 458–463. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Roweis, S. Levenberg-Marquardt Optimization. Available online: https://cs.nyu.edu/~roweis/notes/lm.pdf (accessed on 1 October 2019).
- Garofalo, F. An Empirical Relation Defining the Stress Dependence of Minimum Creep Rate in Metals. Trans. Metall. Soc-AIME 1963, 227, 351–356. [Google Scholar]
- McCulloch, W.S.; Pitts, W.H. A Logical Calculus of Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krenker, A.; Bešter, J.; Kos, A. Introduction to the Artificial Neural Networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; Suzuki, K., Ed.; InTech: Rijeka, Croatia, 2011; pp. 3–18. [Google Scholar]
- Gauss, J.C.F. Theoria Combinationis Observationum Erroribus Minimis Obnoxiae [Theory of the Combination of Observations Least Subject to Errors]; Henricum Dieterich: Göttingen, Germany, 1823; pp. 53–57. [Google Scholar]
- Bayes, T.; Price, R. An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, F.R.S. communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S. Phil. Trans. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- MacKey, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Feldman, J.A., Hayes, P.J., Rumelhart, D.E., Eds.; The MIT Press: Cambridge, USA, 1986; Volume 1: Foundations, pp. 318–362. [Google Scholar]
- Debes, K.; Koenig, A.; Gross, H.M. Transfer Functions in Artificial Neural Networks: A Simulation-Based Tutorial. Available online: https://www.brains-minds-media.org/archive/151/ (accessed on 16 September 2019).
- MathWorks. MATLAB® Math. Graphics. Programming. Available online: https://www.mathworks.com/products/matlab.html (accessed on 18 September 2019).
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network ToolboxTM 7: User’s Guide. Available online: https://www2.cs.siu.edu/~rahimi/cs437/slides/nnet.pdf (accessed on 18 September 2019).
- Descartes, R. Discours de la méthode pour bien conduire sa raison, & chercher la vérité dans les sciences. Plus la dioptrique. Les météores. Et la géométrie. [Discourse on the Method of Rightly Conducting One’s Reason and of Seeking Truth in the Sciences. Plus the Diopter, Meteors and Geometry]; De l’imprimerie de Ian Maire: Leiden, The Netherlands, 1637. [Google Scholar]
- Gnuplot: Portable Command-Line Driven Graphing Utility. Available online: http://www.gnuplot.info/ (accessed on 18 September 2019).
- Wright, S. Correlation and Causation. J. Agric. Res. 1921, 20, 557–585. [Google Scholar]
- Simpson, T. A letter to the Right Honourable George Earl of Macclesfield, President of the Royal Society, On the Advantage of Taking the Mean of a Number of Observations in Practical Astronomy. Philos. Trans. 1755, 49, 82–93. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; Dover Publications: Mineola, NY, USA, 1972; p. 14. [Google Scholar]
- Pearson, K. On the dissection of asymmetrical frequency curves. Phil. Trans. Roy. Soc. Lond. Ser. A 1894, 185, 719–810. [Google Scholar]
- Gauss, J.C.F. Theoria motus corporum coelestium in sectionibus conicis solem ambientium [Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections]; Friedrich Perthes and I. H. Besser: Hamburg, Germany, 1809. [Google Scholar]




| MLP Architecture Feature | εp | σp | σss |
|---|---|---|---|
| Overall number of layers | 4 | 3 | 3 |
| Number of perceptrons in layers | 2—2—2—1 | 2—1—1 | 2—1—1 |
| Hidden layers activation function | tansig 1 | tansig 1 | tansig 1 |
| Summary layer activation function | purelin 2 | purelin 2 | purelin 2 |
| Coordinate | A (s−1) | a (s) | b (-) | n (-) | Q (kJ·mol−1) | α (MPa−1) |
|---|---|---|---|---|---|---|
| σp | 1.565 × 1013 | 4.012 × 100 | 3.735 × 102 | 1.267 × 10−2 | ||
| σss | 3.145 × 1012 | 3.856 × 100 | 3.433 × 102 | 1.181 × 10−2 | ||
| εp | 8.410 × 10−3 | 1.078 × 10−1 |
| wil−1,jl | εp | wil−1,jl | εp | bjl | εp |
|---|---|---|---|---|---|
| w11,12 | −6.229 × 10−1 | w12,23 | −1.059 × 10−3 | b12 | −5.415 × 10−1 |
| w11,22 | 4.530 × 10−3 | w22,13 | −4.050 × 10−1 | b22 | −1.695 × 10−1 |
| w21,12 | 2.927 × 10−1 | w22,23 | 1.450 × 10−3 | b13 | 2.561 × 10−3 |
| w21,22 | −4.224 × 10−1 | w13,14 | 5.994 × 10−1 | b23 | −9.288 × 10−4 |
| w12,13 | 5.390 × 10−1 | w23,14 | −2.022 × 10−3 | b14 | 4.047 × 10−1 |
| wil−1,jl | σp | σss | bjl | σp | σss |
|---|---|---|---|---|---|
| w11,12 | −5.530 × 10−1 | −6.036 × 10−1 | b12 | −4.199 × 10−1 | −5.019 × 10−1 |
| w21,12 | 4.144 × 10−1 | 4.923 × 10−1 | b13 | 1.644 × 102 | 1.588 × 102 |
| w12,13 | 1.571 × 102 | 1.490 × 102 |
| aij | εp | σp | σss | aij | εp | σp | σss |
|---|---|---|---|---|---|---|---|
| a00 | 6.968 × 106 | −1.884 × 107 | −7.455 × 106 | a20 | −6.375 × 100 | −7.559 × 100 | −2.078 × 100 |
| a01 | 4.275 × 106 | −1.156 × 107 | −4.572 × 106 | a21 | −3.910 × 100 | −4.635 × 100 | −1.271 × 100 |
| a02 | −1.914 × 106 | 5.174 × 106 | 2.048 × 106 | a22 | 1.751 × 100 | 2.076 × 100 | 5.703 × 10−1 |
| a03 | −5.458 × 105 | 1.476 × 106 | 5.838 × 105 | a23 | 4.993 × 10−1 | 5.918 × 10−1 | 1.624 × 10−1 |
| a10 | 1.566 × 100 | −1.354 × 101 | −1.363 × 101 | a30 | −3.964 × 100 | −5.850 × 100 | −7.003 × 100 |
| a11 | 1.040 × 100 | −1.072 × 101 | −1.258 × 101 | a31 | −2.432 × 100 | −3.589 × 100 | −4.296 × 100 |
| a12 | −4.671 × 10−1 | 4.483 × 100 | 3.880 × 100 | a32 | 1.089 × 100 | 1.607 × 100 | 1.924 × 100 |
| a13 | −1.342 × 10−1 | 1.434 × 100 | 1.404 × 100 | a33 | 3.105 × 10−1 | 4.583 × 10−1 | 5.486 × 10−1 |
| Parameter | a1 (-) | a2 (-) | a3 (K) | a4 (K−1) | R2 (-) |
|---|---|---|---|---|---|
| c | 7.183 × 10−2 | −4.964 × 10−1 | −5.720 × 102 | −1.090 × 10−3 | 0.8647 |
| n | 3.109 × 100 | 3.701 × 10−1 | 4.623 × 102 | 4.558 × 10−4 | 0.4757 |
| k | 1.205 × 100 | 3.227 × 10−1 | 3.311 × 102 | −2.369 × 10−4 | 0.4375 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opěla, P.; Kawulok, P.; Schindler, I.; Kawulok, R.; Rusz, S.; Navrátil, H. On the Zener–Hollomon Parameter, Multi-Layer Perceptron and Multivariate Polynomials in the Struggle for the Peak and Steady-State Description. Metals 2020, 10, 1413. https://doi.org/10.3390/met10111413
Opěla P, Kawulok P, Schindler I, Kawulok R, Rusz S, Navrátil H. On the Zener–Hollomon Parameter, Multi-Layer Perceptron and Multivariate Polynomials in the Struggle for the Peak and Steady-State Description. Metals. 2020; 10(11):1413. https://doi.org/10.3390/met10111413
Chicago/Turabian StyleOpěla, Petr, Petr Kawulok, Ivo Schindler, Rostislav Kawulok, Stanislav Rusz, and Horymír Navrátil. 2020. "On the Zener–Hollomon Parameter, Multi-Layer Perceptron and Multivariate Polynomials in the Struggle for the Peak and Steady-State Description" Metals 10, no. 11: 1413. https://doi.org/10.3390/met10111413
APA StyleOpěla, P., Kawulok, P., Schindler, I., Kawulok, R., Rusz, S., & Navrátil, H. (2020). On the Zener–Hollomon Parameter, Multi-Layer Perceptron and Multivariate Polynomials in the Struggle for the Peak and Steady-State Description. Metals, 10(11), 1413. https://doi.org/10.3390/met10111413





