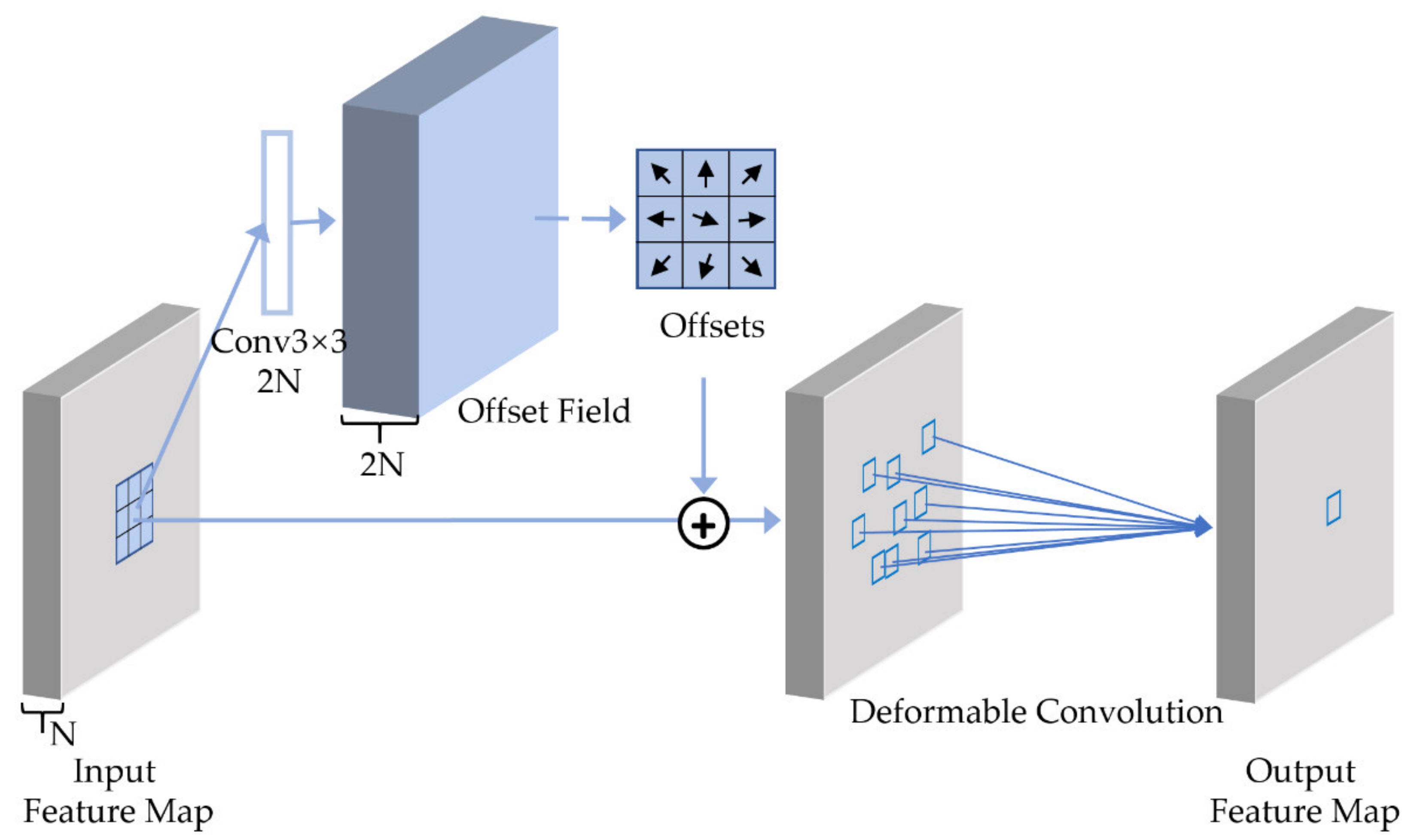
1. Introduction
Steel plates are indispensable materials for the automobile industry, national defense industry, machinery manufacturing, chemical industry, light industry, etc. However, due to the problems of raw materials and technology, various types of defects will be produced in the production process of steel plates—especially cracks, scabs, curling edges, cavities, abrasions, and other defects on the surface [
1]. These have a fatal impact on the corrosion resistance and strength of the steel plate, and affect the economic benefits of the factory. At present, the surface defect detection of strip steel mostly adopts the method of manual detection. This method is easily affected by the subjective factors of the testing personnel. Moreover, the accuracy of the test results is low, and the reliability is poor. Therefore, it is essential to study the algorithm of automatic real-time detection of surface defects on the production line.
In the past decades, researchers have developed a variety of algorithms to detect defects on steel surfaces [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]. One is the traditional methods is based on statistical information and image features. This method requires researchers to manually design some image features and conduct statistical analysis on these features to obtain the detection results. The commonly used methods are Sobel [
15], canny [
16], hog [
17], local binary patterns (LBP) [
18], Fourier transform [
19], wavelet transform [
20], etc. For instance, Shi et al. [
3] propose an improved Sobel algorithm with eight directional templates. It helps to obtain overall edge information, makes edge detection more accurate and faster, and finally makes the algorithm more robust. Liu et al. [
4] present different feature extraction approaches (scale invariant feature transform (SIFT), speeded up robust features (SURF) and LBP) and various classifiers (back propagation (BP) neural network, support vector machine (SVM), and extreme learning machine (ELM)) to find the fastest combination method with satisfactory classification accuracy. The method based on machine learning usually extracts some image features first, and then processes these features by a learning algorithm to detect surface defects. Some commonly used algorithms include SVM, artificial neural networks (ANN) [
17,
18], and Adaboost. Wang et al. [
5] propose a novel computational framework, based on SVM and spreading algorithm. The algorithm first uses the SVM algorithm to get the location and shape of the defect, and then uses a spreading algorithm to classify the detected defects. Finally, the covariance matrix is used to calculate the defect size. Kang et al. [
6] discuss an approach to detect surface defects of steel strips based on a feed-forward neural network (FFN).
In recent years, with the popularity of computer vision methods based on deep learning [
7,
8,
9,
10,
11,
12,
13,
14,
19,
20], more and more researchers have applied deep learning methods to surface defect detection, and replaced the traditional and machine learning methods. This automatic defect detection method is based on deep learning, and can significantly improve product quality and production efficiency, as well as realize end-to-end surface defect detection. This algorithm also can automatically extract the deep and robust features of the image and obtain the results, and complete the task of defect detection efficiently and accurately. At present, the deep learning algorithms used in defect detection mainly include Autoencoder, generative adversarial networks (GAN), and convolutional neural networks (CNN). He et al. [
7] propose a semi-supervised learning approach named CAE-SGAN (convolutional autoencoder (CAE) and semi-supervised generative adversarial networks (SGAN)), based on GAN, which improves the performance with limited samples, and Autoencoder, which is used to extract image features. Thomas et al. [
8] present an anomaly detection based on deep generative adversarial networks (AnoGAN) to learn a manifold of normal anatomical variability, accompanying a novel anomaly scoring scheme based on the mapping from image space to a latent space. The method based on CNN can be divided into three sub-areas: Image classification [
9], image segmentation [
10,
11], and object detection [
12,
13,
14]. Lee et al. [
9] propose a classification method of steel defects based on CNN and class activation maps. It can implement a real-time decision-making process. Tabernik et al. [
10] developed an architecture based on image segmentation, which can train the network with fewer samples. This is more suitable for the industrial environment. Surface defect detection algorithms based on object recognition can be divided into two categories: Single-stage and two-stage. Single-stage object recognition algorithms mainly include ‘you only look once’ (YOLO). For example, Li et al. [
12] have improved the YOLO algorithm, which contains 27 convolution layers and can provide end-to-end solutions. It can predict the location, size, and category of defects at the same time. Two-stage object recognition algorithms mainly include faster region convolutional neural networks (faster R-CNN) [
13]. Firstly, a region proposal is applied to an image to select the region with possible objects, and then the candidate images, which are considered as positive samples in the first step, are taken as sub-image to classify and locate these. Oh et al. [
14] advance an approach based on faster R-CNN. They use Inception-ResNet-V2 and data augmentation to improve the accuracy of the model.
As mentioned above, a variety of algorithms have been proposed with the development of machine learning and computer vision, and they all have their own strengths and weaknesses. Traditional and machine learning based methods are usually sensitive to defect scale and noise and are easily affected. Moreover, the accuracy of this algorithm cannot meet the actual needs of automatic defect detection. Some features need to be designed manually, and the scope of the application is very limited. The classification method based on deep learning can only classify images, but cannot determine the location and size of defects. This has a significant impact on the later data analysis. It is very difficult to train a stable and accurate model based on GAN and reinforcement learning. To realize the automatic detection and location of steel plate surface defects, further improve the accuracy and stability, and reduce the average running time of the algorithm. This paper presents a method combining the classification model with the object recognition model. The main contributions of this paper are summarized below.
The organizational structure of this paper is as follows:
Section 2 introduces the structure of our algorithm, including the overall architecture, classification model, object detection model, etc.
Section 3 analyzes the dataset and guides the improvement of the algorithm.
Section 4 and
Section 5 use the experiment to prove the accuracy and efficiency of the algorithm, and compare our results with other methods. Finally,
Section 5 summarizes the paper and draws a conclusion.
3. Steel Defect Dataset
The dataset used in this paper comes from the Kaggle competition, “Severstal: Steel Defect Detection” [
37], with a total of 12,568 steel sheet grayscale images with the size of 1600 × 256 in the training dataset. Because there is a big gap between the height and width of the original dataset, we divided each image into four images with the size of 400 × 256 in the experiment. Therefore, there are 50,272 samples in our experiment, including 37,080 samples without defects, 12,876 samples with only one type of defect, and 316 samples with two types of defects.
As shown in
Figure 8, there are four types of defects in the dataset: Pitted surface, crazing, scrapes, and patches. First, select two images for each class of defects in the dataset. Then, second, mark the bounding box on the picture. Finally, change all the pictures to 256 × 256 and put them on one picture. The classification model uses all the images with defects as one class, and the images without defects as another class, as shown in
Table 1. It can be clearly seen from
Table 2 that 1306 pictures have pitted surface defects, 214 pictures have inclusion defects, 9980 pictures have scratch defects, 1376 pictures have patch defects, and 316 pictures have two kinds of defects. Images of various defects with bounding box and label used in object detection model are shown in
Table 2.
It can be seen from
Table 1 and
Table 2 that there is a large imbalance in the dataset. In particular, crazing defects only account for 1.6% of the total number of defect samples. Also, the number of no defects samples is too large, accounting for the majority of the total loss, which makes the optimization direction of the model is not what we want. To reduce the impact of imbalanced data sets on the algorithm, firstly, we use the data augmentation method to expand the crazing defect samples to 800 to increase the diversity of samples. Furthermore, the weighted cross entropy loss [
38] function and focal loss [
39] function are introduced in training.
Let me first introduce the standard cross entropy loss function. The cross entropy describes the distance between two probability distributions, and the closer its value is, the closer the two distributions are. The cross entropy loss function is also the cross entropy between the output of the algorithm and the label. The higher the value is, the more the output is the same as the label, and the higher the accuracy is. Formula (1) is used to calculate the cross entropy loss.
where
,
, x is the output of the algorithm and y is the actual label.
The idea of weighted cross entropy is to use a coefficient to describe the importance of samples in loss. For a small number of samples, strengthen its contribution to loss, for a large number of samples reduce its contribution to loss. The formula is as follows.
where
, there is only a little change between this and cross entropy, that is, a coefficient is added to the discrimination of positive samples. In the object detection task, the weight of each defect is represented by a list
. In the classification task, the list is
.
Focal loss is improved, based on cross entropy loss. This new loss function can reduce the weight of samples that are easy to classify, and make the model pay more attention to the learning of difficult samples.
where
,
is the same as in cross entropy loss,
and
are super parameters. Usually,
= 2,
= 0.75.
is called modulating factor. It can adjust the weight of easy to classify samples, which makes the model pay more attention to learning difficult to classify samples in training.
Because training CNN requires a large number of samples, it is difficult to obtain them in the actual production environment. In this paper, data augmentation [
40] is used to increase the diversity of samples and improve the accuracy and robustness of the algorithm. By using data augmentation, which is a regularization method, the model reduces overfitting and improves the generalization ability of the network. The methods used in this paper include an improved cutout, horizontal flip, vertical flip, random cropping, and random contrast and brightness transformation.
Figure 9 shows the results of various data augmentation methods.
The original cutout method [
41] is very simple—that is, randomly delete an area on the image and replace it with zero. In this paper, we study an object detection problem, which includes the label box and class information of four defects. Therefore, we improve the cutout method, randomly delete the label box with a probability of 0.5 and fill it with 0. Only when all the label boxes in a sample are deleted, the label changes to no defect. As shown in
Figure 9a,b, there are two scratch defects in the original image. After random improved cutout data augmentation, only one defect is left, and the other defect area is filled with 0. Horizontal and vertical flipping is used in
Figure 9c,d, with a probability of 0.5. Random cropping is used in
Figure 9e. The top, bottom, left, and right of the image are cropped no more than 15%. After that, the image is resized to 400 × 256. Random contrast and brightness transformation are used in
Figure 9f. The probability of 0.5 is used to decide whether to carry out the contrast or brightness transformation. If the two parameters are changed, the transformation range of the image is limited to 50%.
From
Figure 8a, we can see that the pitted surface defect is usually small in the steel plate surface defect detection task. We can see from
Figure 10 that the defect accounts for a large proportion of the statistical value with a small area. And the area of crazing defect is relatively small. To improve the accuracy of small defect detection, this paper uses SPP and FPN to increase the effect of multi-scale feature extraction.
By counting the aspect ratio of various defects, we find a large aspect ratio for cracking and scratches defects, as shown in
Figure 11a. Scratch defects also account for a large proportion in a very small proportion, as shown in
Figure 11b (b only shows the data in the range of 0–2.4, in more detail). To improve the detection accuracy of these two parts, the anchor setting in faster R-CNN is changed from [0.5, 1, 2.0] to [0.25, 0.5, 1, 2, 5]. By using k-means++ [
42] algorithm to cluster bounding box, it is found that this setting can also meet the needs of most defects. The clustering results are shown in
Table 3.