Pneumatic Experimental Design for Strain Rate Sensitive Forming Limit Evaluation of 7075 Aluminum Alloy Sheets under Biaxial Stretching Modes at Elevated Temperature
Abstract
:1. Introduction
2. Finite Element Modeling
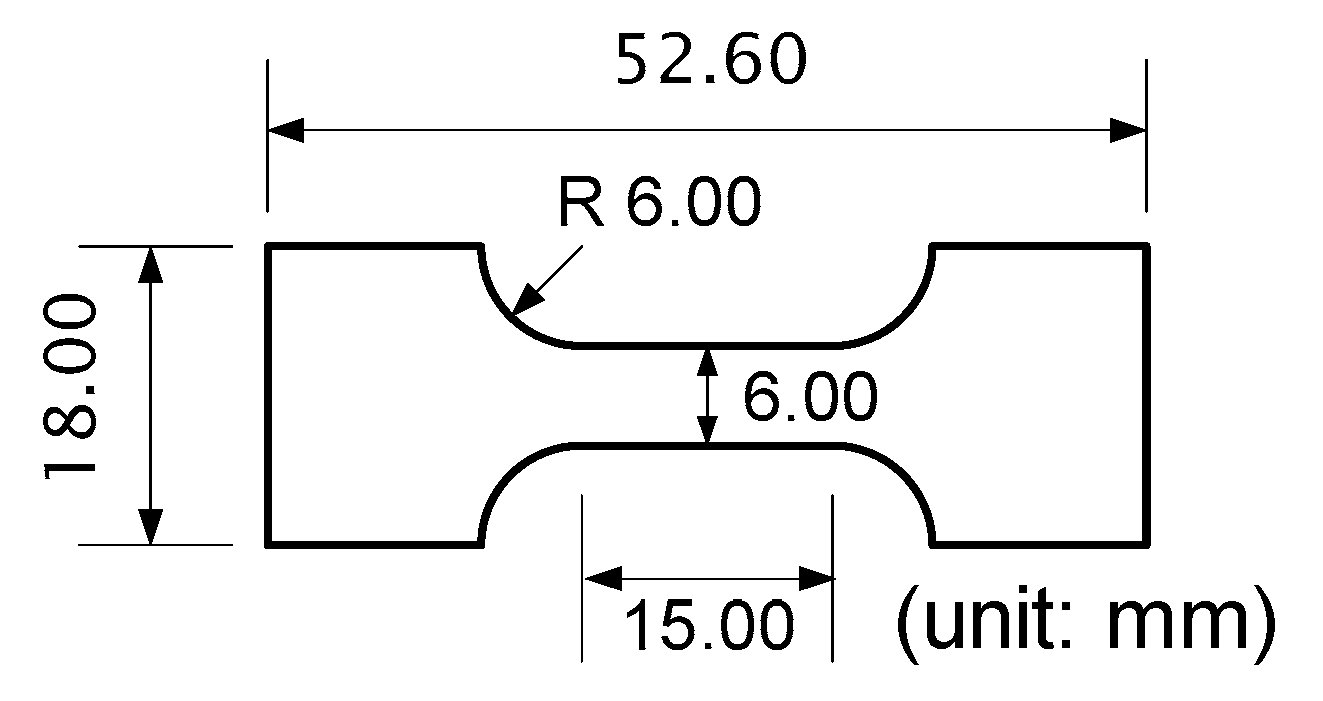
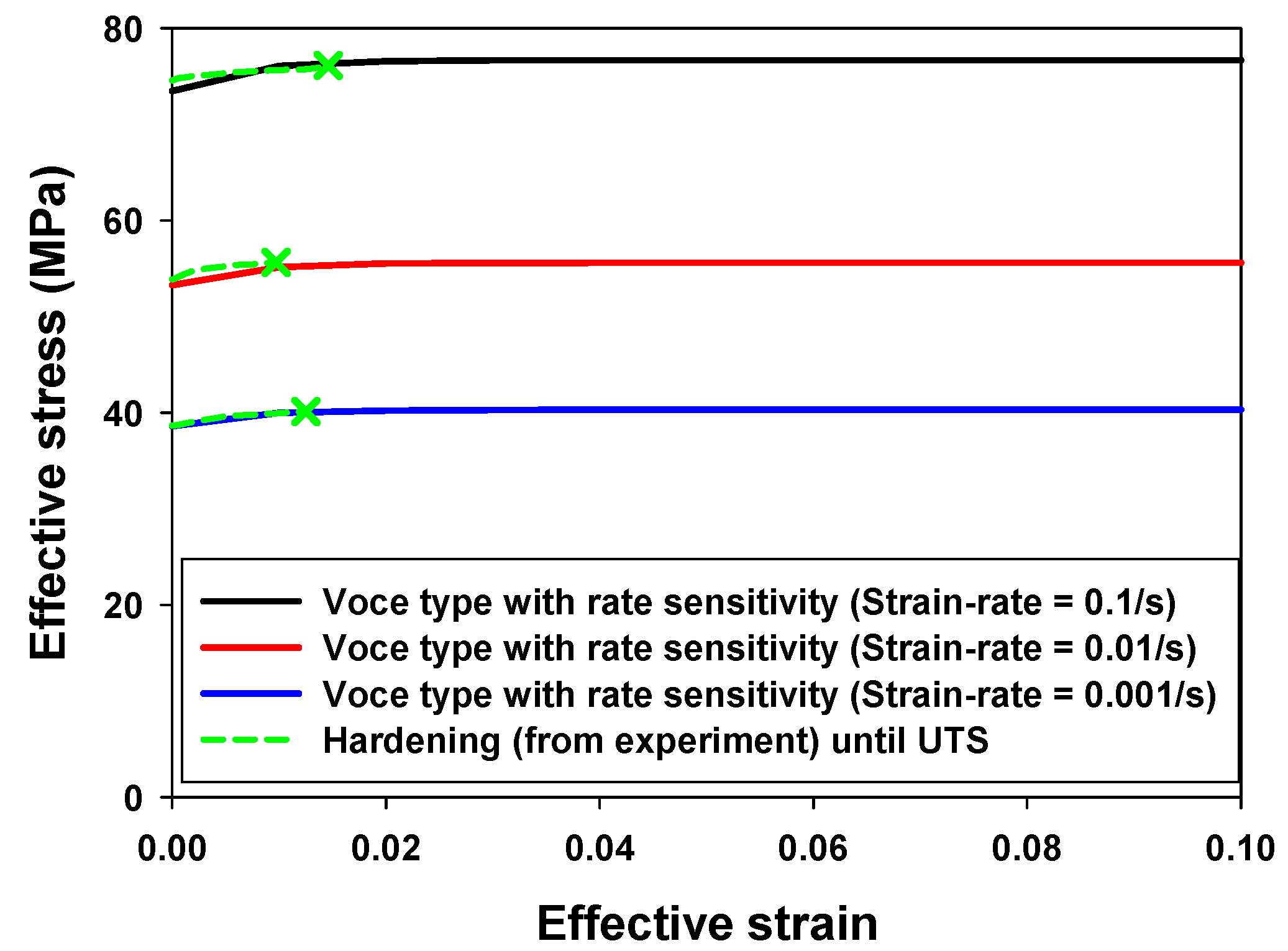
2.1. Materials
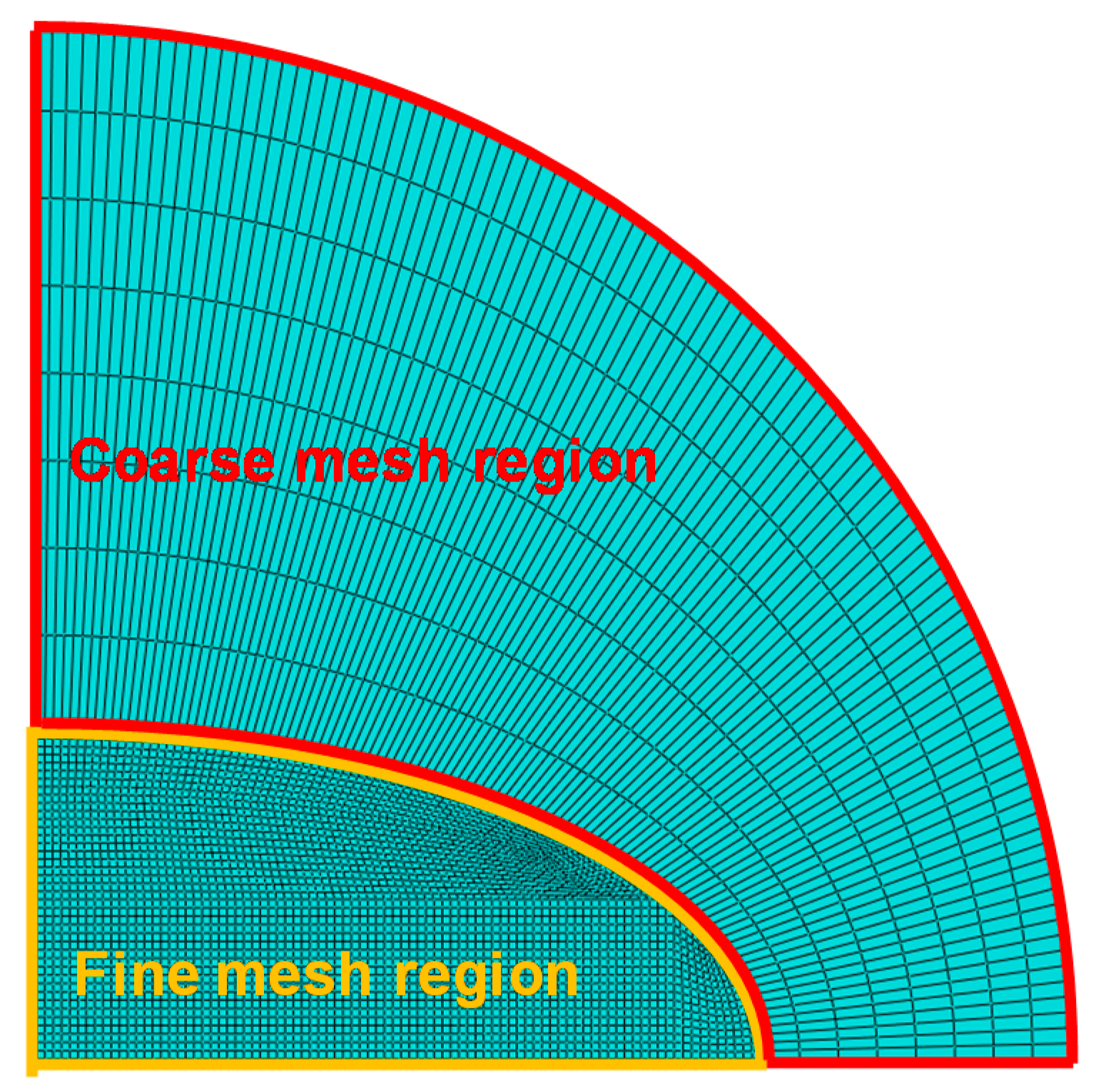
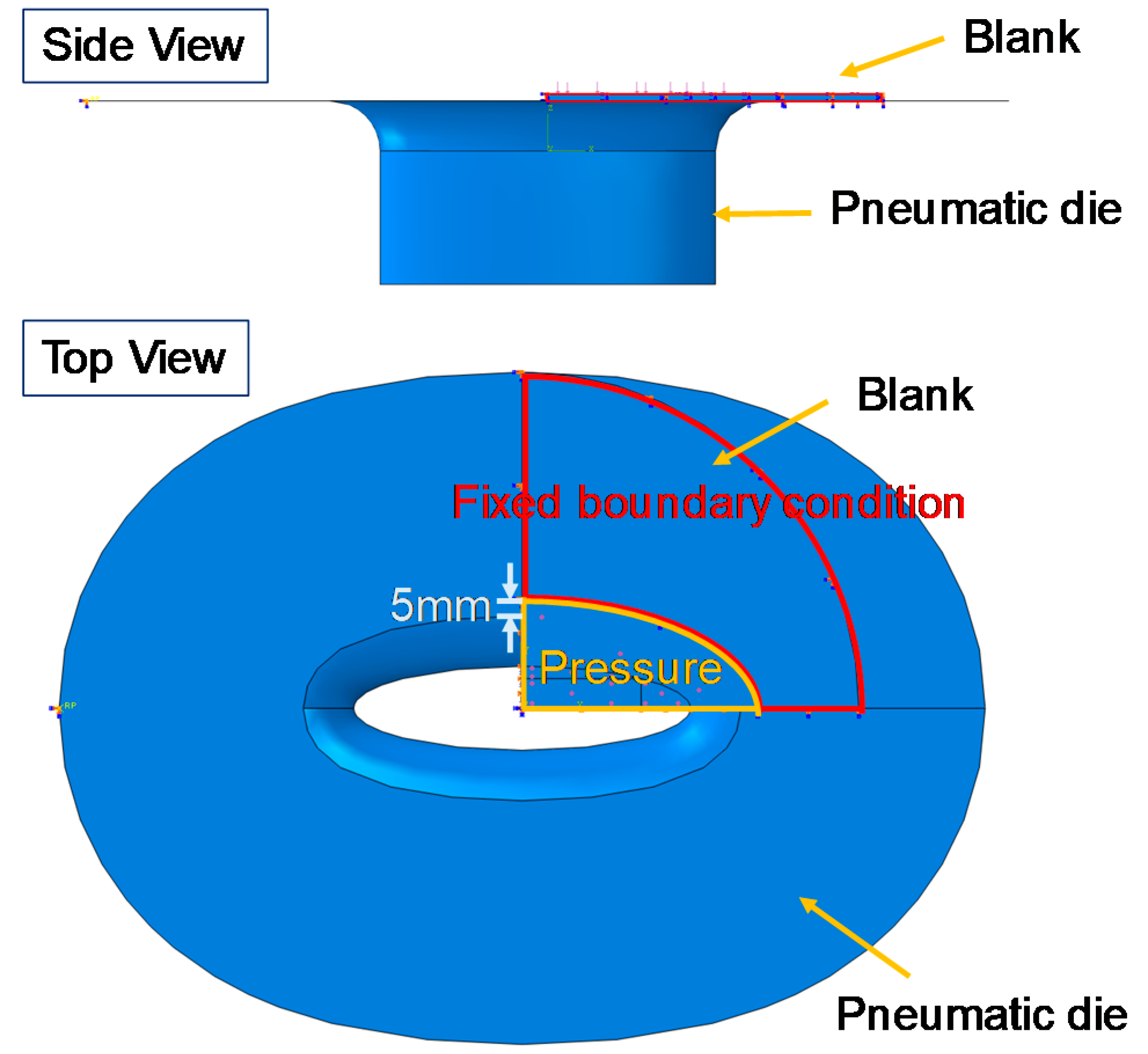
2.2. Numerical Simulation Procedure
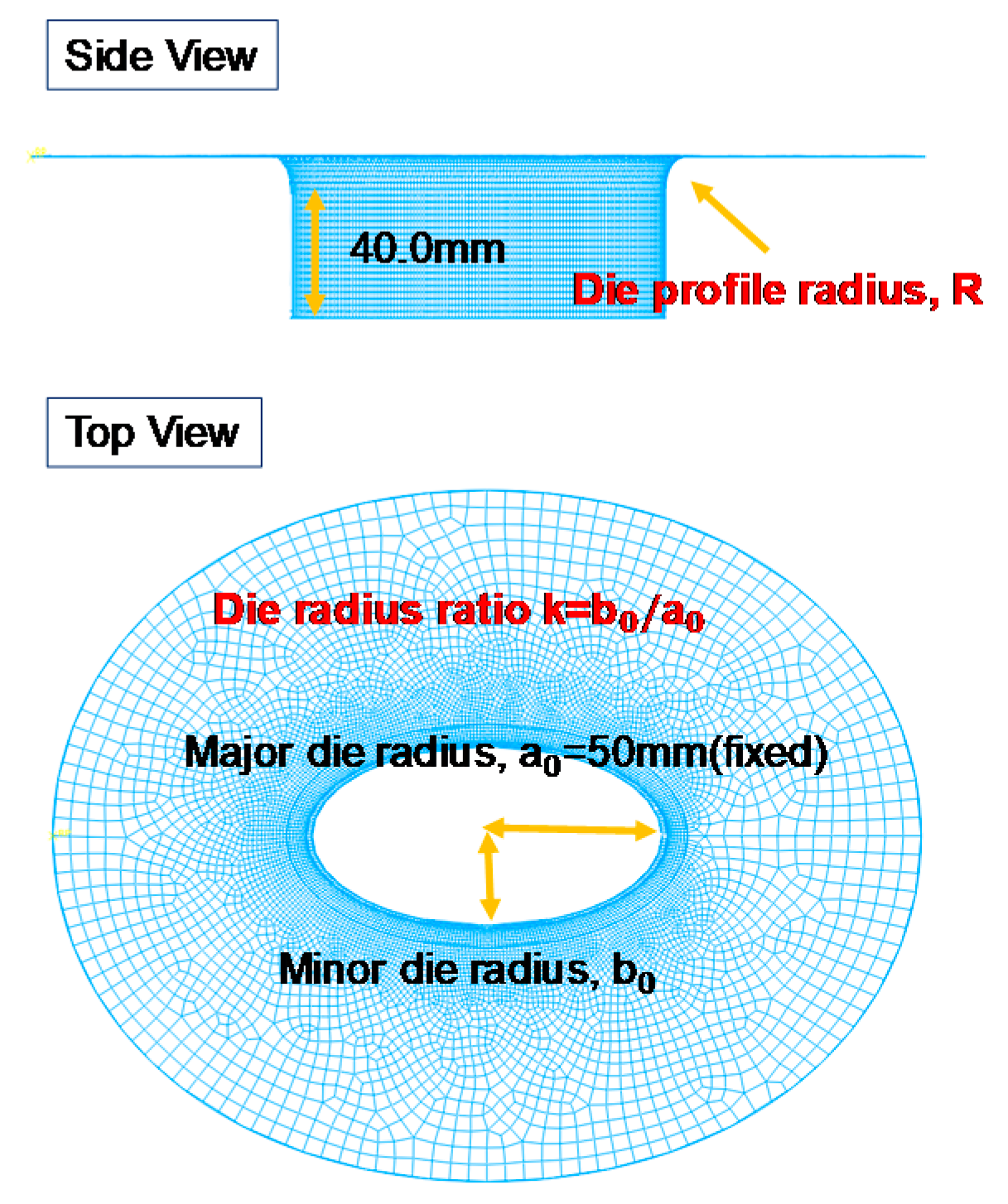
3. Design of Geometric and Process Conditions
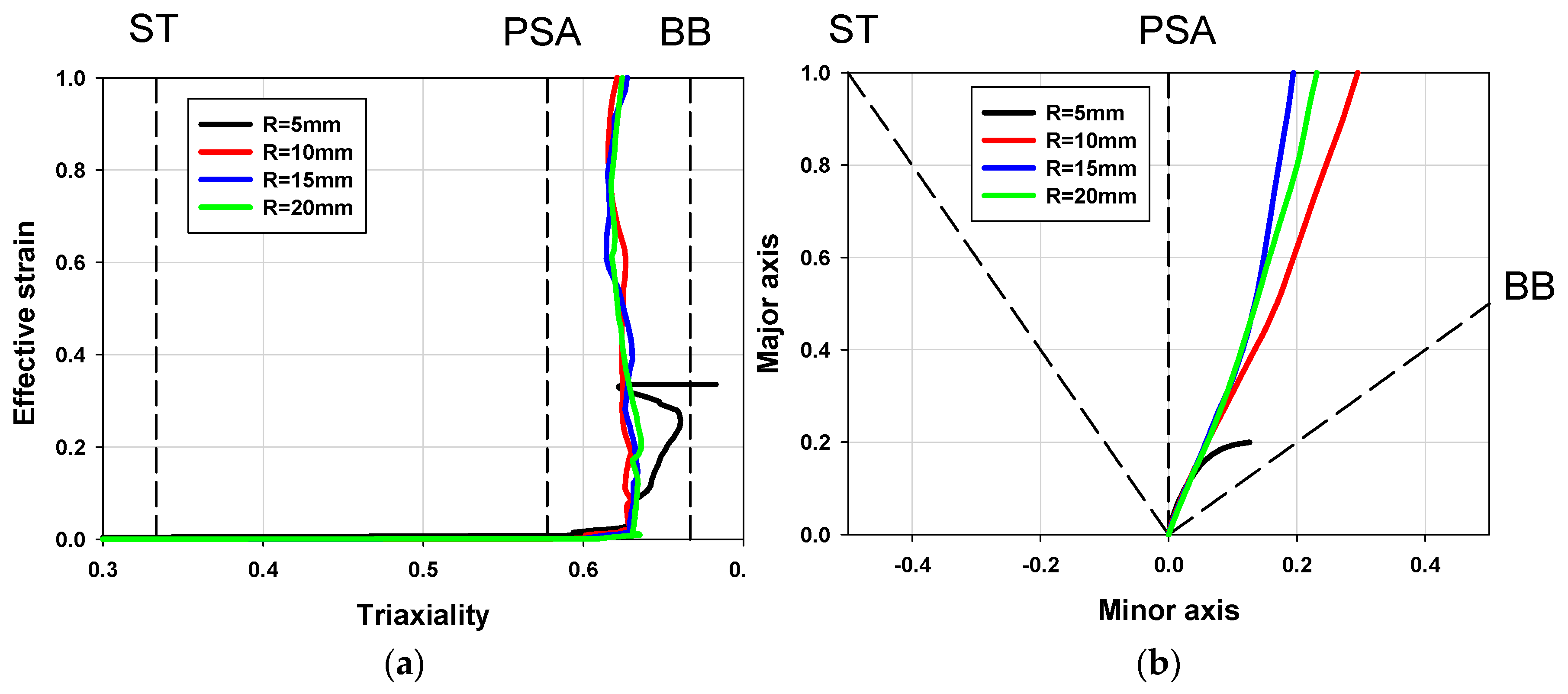
3.1. Geometric Design: The Ratio of Minor to Major Radius (k)
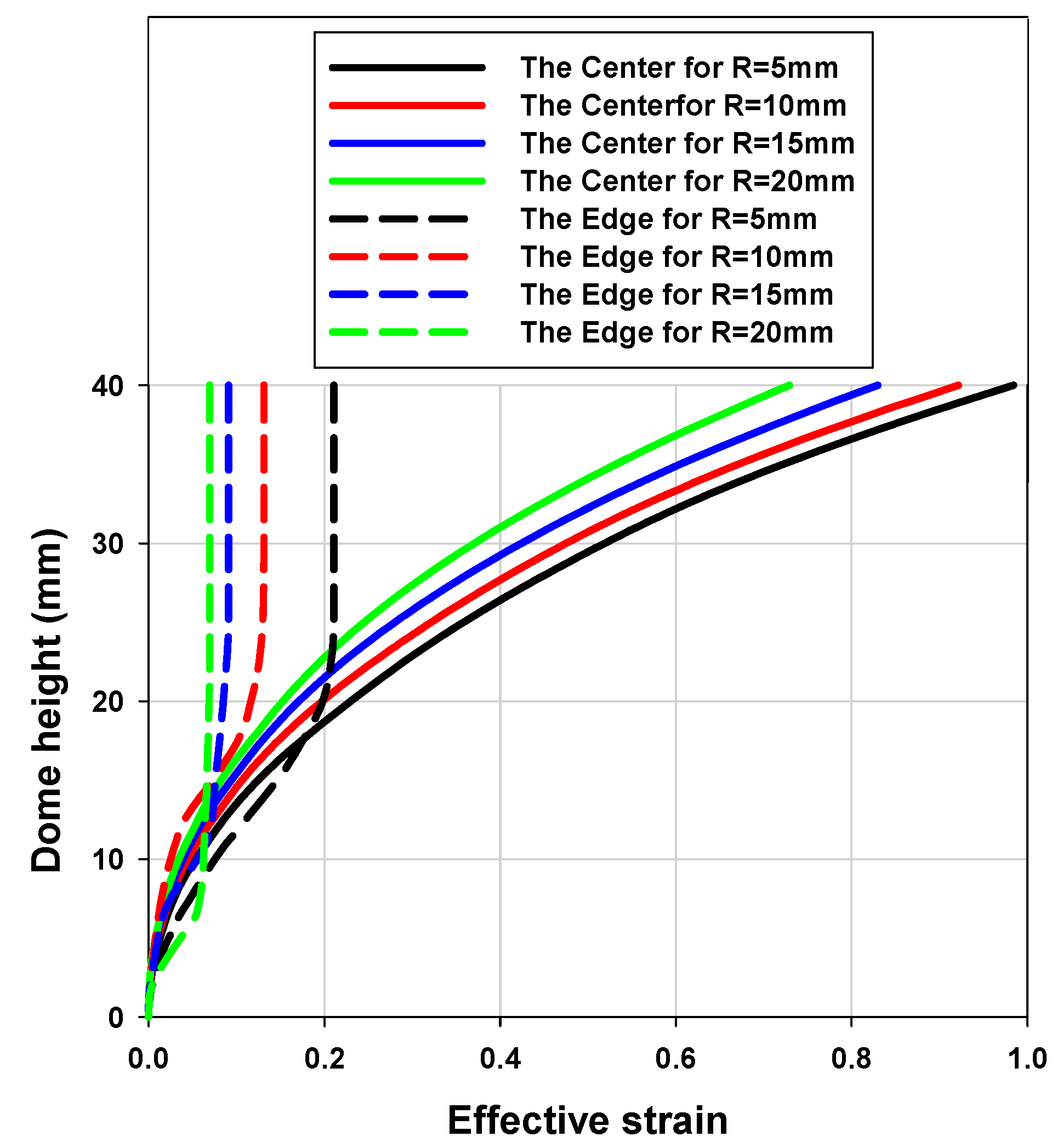
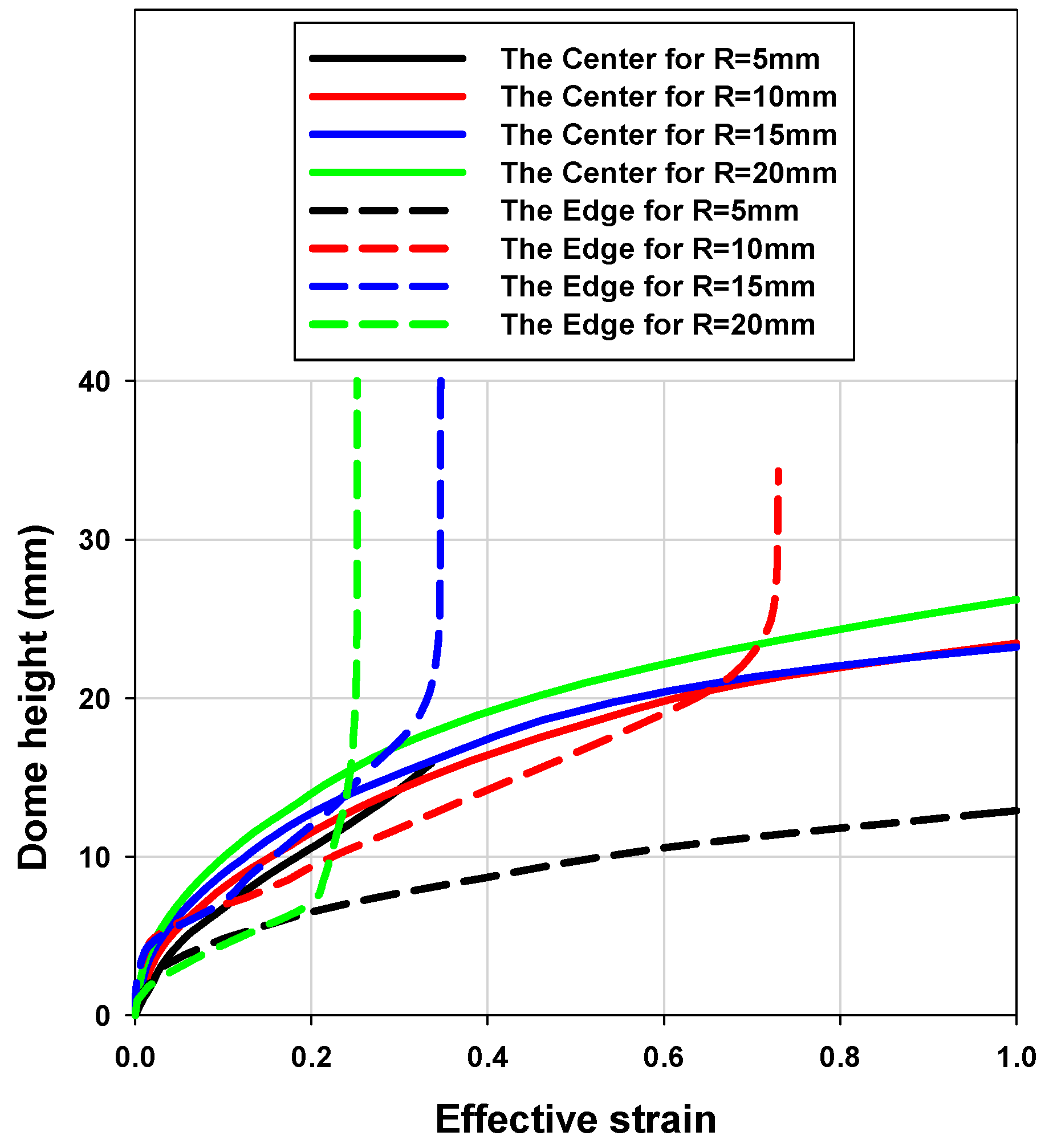
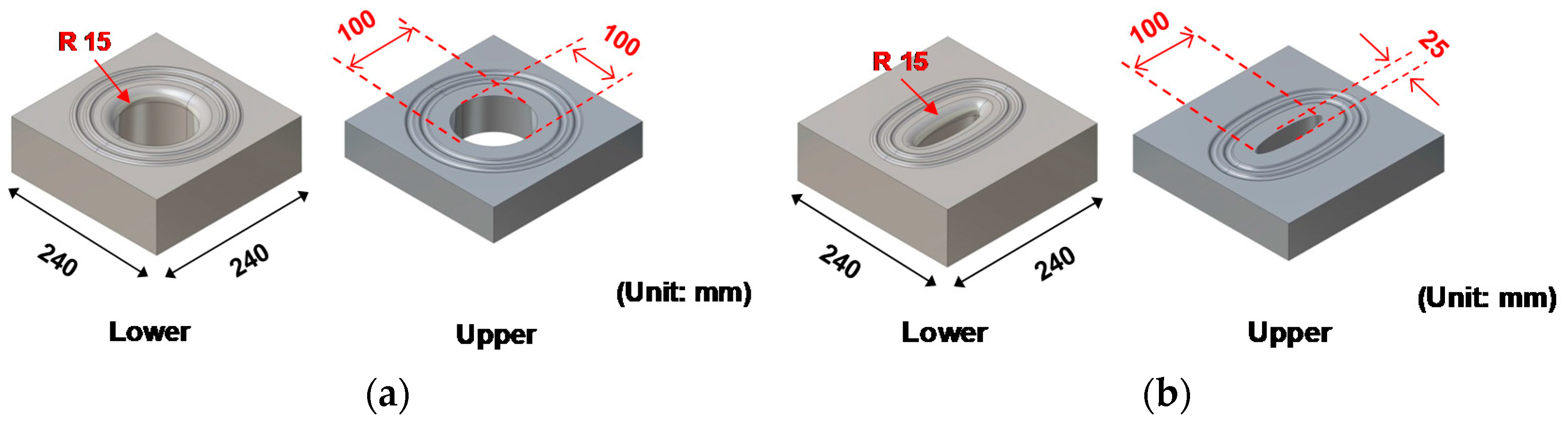
3.2. Geometric Design: The Profile Radius (R)
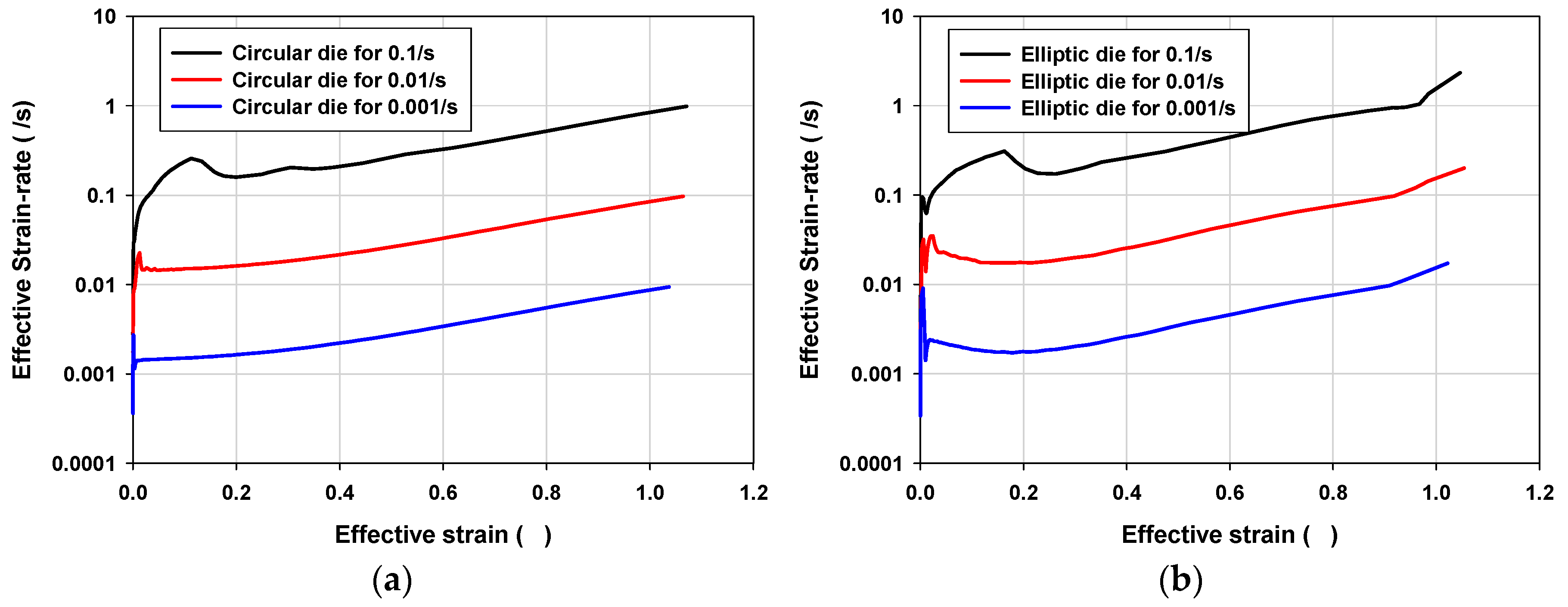
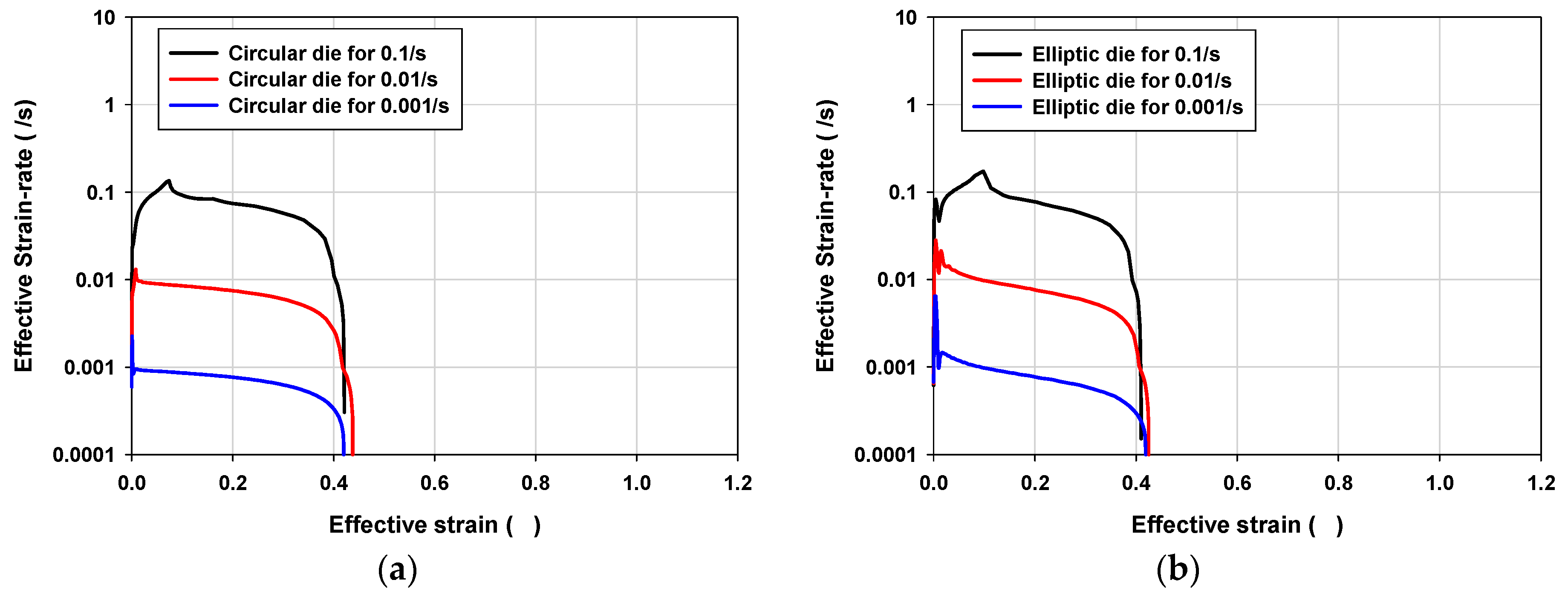
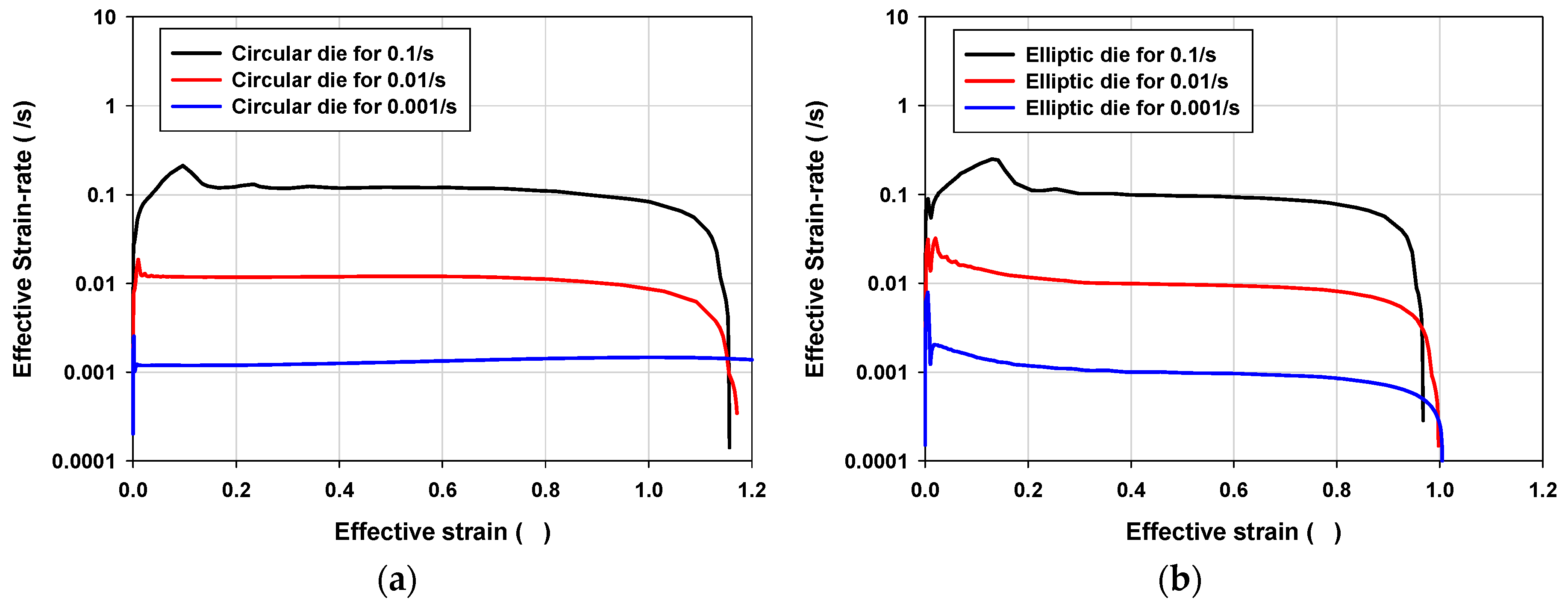
3.3. Process Condition Design
4. Validation
5. Conclusions
- As the ratio of minor to major radius (k) became smaller, more effective strain was likely concentrated on the edge and more pressure was needed to complete the forming process. As the ratio of minor to major radius (k) became smaller, the history of the deformation mode in triaxiality (η) and major/minor domain approached the near plane strain (PSA) mode; however, when the k was too small, it did not show uniform deformation history because of the 3D effect (no more plane strain). As for the ratio of minor to major radius (k) of the die, a circular die with k = 1.0 and elliptic die with k = 0.25 were selected for balanced biaxial mode and near plane strain mode, respectively.
- As the profile radius (R) of the die got larger, deformation was more likely concentrated on the center for both circular and elliptic dies. R = 15, which is safe and small enough for favorable fracture occurrence at the center of the blank, was also chosen as profile radius (R) for both circular and elliptic dies.
- For the process design, a preexisting analytical model was modified with geometrical consideration of the profile radius (R). The modified analytical model induced fracture at the pole with approximately constant targeted strain rate.
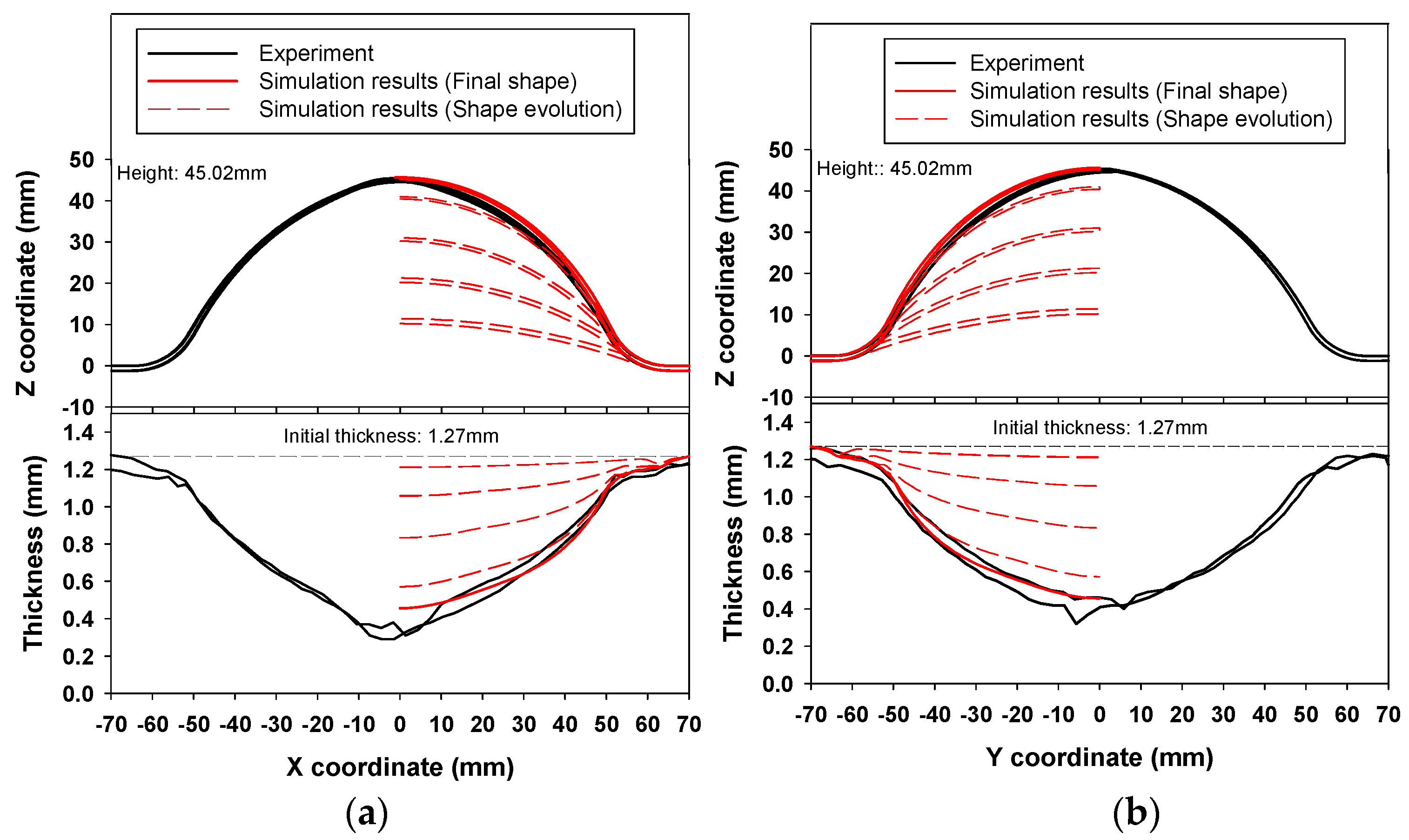
- Finally, the simulation results of the designed geometric and process conditions were compared with the experimental results, and they showed good agreement with regard to shape and thickness distribution.
Author Contributions
Funding
Conflicts of Interest
References
- Barnes, A. Superplastic forming 40 years and still growing. J. Mater. Eng. Perform. 2007, 16, 440–454. [Google Scholar] [CrossRef]
- Friedman, P.A.; Luckey, S.G.; Copple, W.B.; Allor, R.; Miller, C.E.; Young, C. Overview of superplastic forming research at ford motor company. J. Mater. Eng. Perform. 2004, 13, 670–677. [Google Scholar] [CrossRef]
- Abu-Farha, F.; Verma, R.; Hector, L.G. High temperature composite forming limit diagrams of four magnesium AZ31B sheets obtained by pneumatic stretching. J. Mater. Proc. Technol. 2012, 212, 1414–1429. [Google Scholar] [CrossRef]
- Mitukiewicz, G.; Antheshwara, K.; Zhou, G.; Mishra, R.K.; Jain, M.K. A new method of determining forming limit diagram for sheet materials by gas blow forming. J. Mater. Proc. Technol. 2014, 214, 2960–2970. [Google Scholar] [CrossRef]
- Banabic, D.; Vulcan, M.; Siegert, K. Bulge testing under constant and variable strain rates of superplastic aluminium alloys. CIRP Annals 2005, 54, 205–208. [Google Scholar] [CrossRef]
- Hill, R.C. A theory of the plastic bulging of a metal diaphragm by lateral pressure. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1950, 41, 1133–1142. [Google Scholar] [CrossRef]
- Banabic, D.; Bălan, T.; Comşa, D.-S. Closed-form solution for bulging through elliptical dies. J. Mater. Proc. Technol. 2001, 115, 83–86. [Google Scholar] [CrossRef]
- Rong, H.; Hu, P.; Ying, L.; Hou, W.; Zhang, J. Thermal forming limit diagram (TFLD) of AA7075 aluminum alloy based on a modified continuum damage model: Experimental and theoretical investigations. Int. J. Mech. Sci. 2019, 156, 59–73. [Google Scholar] [CrossRef]
- Wang, N.; Ilinich, A.; Chen, M.; Luckey, G.; D’Amours, G. A comparison study on forming limit prediction methods for hot stamping of 7075 aluminum sheet. Int. J. Mech. Sci. 2019, 151, 444–460. [Google Scholar] [CrossRef]
- Shojaei, K.; Sajadifar, S.V.; Yapici, G.G. On the mechanical behavior of cold deformed aluminum 7075 alloy at elevated temperatures. Mater. Sci. Eng. A 2016, 670, 81–89. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Ahn, K.; Yoo, D.; Son, H.; Kim, G.; Chung, K. Inverse characterization method for mechanical properties of strain/strain-rate/temperature/temperature-history dependent steel sheets and its application for hot press forming. Metals Mater. Int. 2015, 21, 874–890. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, J.W.; Chung, K.; Lee, M. A multiplicative plastic hardening model in consideration of strain softening and strain rate: Theoretical derivation and characterization of model parameters with simple tension and creep test. Int. J. Mech. Sci. 2020, 187, 105913. [Google Scholar] [CrossRef]
- Kim, H. Characterization Method for Hardening and Strain-Rate Sensitivity at Elevated Temperature Based on Uniaxial Tension and Creep Tests. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2015. [Google Scholar]








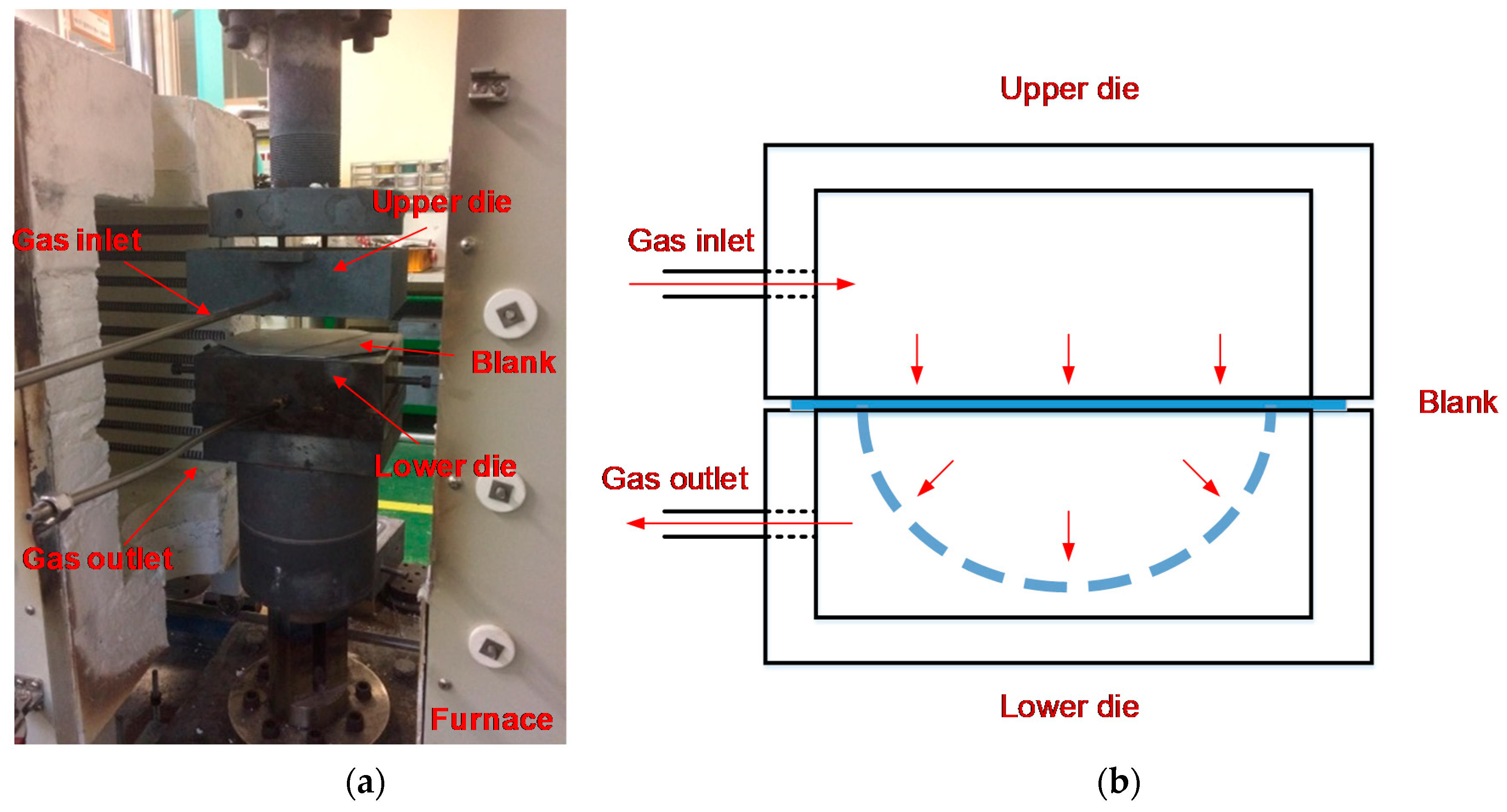


| Temperature (°C) | Crosshead Speed (mm/s) | E (GPa) | Poisson’s Ratio | UTS (MPa) | Elongation (%) | |
|---|---|---|---|---|---|---|
| UTS | Total | |||||
| 400 | 2.0 | 51.82 | 0.35 | 76.15 | 1.48 | 82.36 |
| 0.2 | 55.66 | 0.98 | 65.85 | |||
| 0.02 | 40.14 | 1.25 | 44.85 | |||
| Temperature (°C) | K (MPa) | C (MPa) | p | m | (s−1) |
|---|---|---|---|---|---|
| 400 | 38.63 | 1.68 | 171 | 0.14 | 0.001 |
| Die Insert Radius Ratios (k) | Major Die Radius (a0) | Minor Die Radius (b0) | Die Profile Radius (R) | Pressure Values |
|---|---|---|---|---|
| 1 | 50.0 mm | 50.0 mm | 15.0 mm | 1 MPa |
| 0.75 | 37.5 mm | 2 MPa | ||
| 0.5 | 25.0 mm | 2 MPa | ||
| 0.25 | 12.5 mm | 4 MPa | ||
| 0.1 | 5.0 mm | 6 MPa |
| Die Insert Radius Ratio (k) | Die Profile Radius (R) | Major Die Radius (a0) | Pressure Value |
| 1 (Circular die) | 5.0 mm | 50.0 mm | 1 MPa |
| 10.0 mm | |||
| 15.0 mm | |||
| 20.0 mm | |||
| 0.25 (Elliptic die) | 5.0 mm | 4 MPa | |
| 10.0 mm | |||
| 15.0 mm | |||
| 20.0 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, J.-H.; Yoo, D.; Kwon, Y.N.; Kim, D. Pneumatic Experimental Design for Strain Rate Sensitive Forming Limit Evaluation of 7075 Aluminum Alloy Sheets under Biaxial Stretching Modes at Elevated Temperature. Metals 2020, 10, 1639. https://doi.org/10.3390/met10121639
Hong J-H, Yoo D, Kwon YN, Kim D. Pneumatic Experimental Design for Strain Rate Sensitive Forming Limit Evaluation of 7075 Aluminum Alloy Sheets under Biaxial Stretching Modes at Elevated Temperature. Metals. 2020; 10(12):1639. https://doi.org/10.3390/met10121639
Chicago/Turabian StyleHong, Jong-Hwa, Donghoon Yoo, Yong Nam Kwon, and Daeyong Kim. 2020. "Pneumatic Experimental Design for Strain Rate Sensitive Forming Limit Evaluation of 7075 Aluminum Alloy Sheets under Biaxial Stretching Modes at Elevated Temperature" Metals 10, no. 12: 1639. https://doi.org/10.3390/met10121639
APA StyleHong, J.-H., Yoo, D., Kwon, Y. N., & Kim, D. (2020). Pneumatic Experimental Design for Strain Rate Sensitive Forming Limit Evaluation of 7075 Aluminum Alloy Sheets under Biaxial Stretching Modes at Elevated Temperature. Metals, 10(12), 1639. https://doi.org/10.3390/met10121639





