Multi-Objective Optimization of Intermediate Roll Profile for a 6-High Cold Rolling Mill

Abstract

The multi-objective optimization of the SmartCrown intermediate roll profile for a cold rolling mill was proposed in this paper in order to improve the strip flatness quality. A coupling model of roll profile and strip flatness was established, and the roll gap profile, roll gap crown adjustment range, rolls contact pressure, and strip flatness under different intermediate roll profile parameters were calculated based on the coupling model. The results showed that the roll gap crown adjustment range and rolls contact pressure difference increased with increasing roll profile parameters. The roll profile parameters were multi-optimized based on the non-dominated sorting genetic algorithm II (NSGA-II). The minimum rolls contact pressure difference and maximum roll gap crown adjustment range were taken as the objective function of multi-objective optimization. The optimal roll profile parameters were applied to a six-high five stand tandem cold rolling mills, which improved the flatness quality of the DP780 steel strip.

1. Introduction

Flatness control is an important indicator for measuring the level of cold rolling technology. Strip thickness control accuracy has been very high with the development of automatic gauge control (AGC). Hence, the flatness control problem becomes more and more prominent [1,2]. The flatness of the strip is directly affected by the loaded roll gap profile. Therefore, the original roll profile is a decisive factor in flatness control [3,4]. The contact stress concentration between the rolls is generated by the unreasonable design of the original roll profile and then induces the roll spalling and flatness defects, which are shown in Figure 1.

The rolls have a deflection under the action of rolling force, which can be compensated by designing an original roll profile as a parabola. Li et al. [5] modified the parabola roll profile by a finite element method (FEM) to improve the flatness quality. Wang et al. [6] developed a new type of roll contour configuration for a four-high temper rolling mill, and the flatness of the thin gauge hot strip was improved by 10%. In addition to the parabola roll profile, the taper roll profile has the advantage of controlling the edge drop. He et al. [7] designed a symmetry variable taper (SVT) work roll to decreased edge drop and obtained a more uniform work roll wear. However, the parabola roll profile and the taper roll profile both have the disadvantage that the original roll profile needs to be regrinding according to the thickness and width of the strip, so the adjustment of roll gap profile is not flexible and timely. Bald et al. [8,9] developed a continuously variable crown (CVC) system and applied in cold and hot rolling mill to achieve the purpose of online adjustment of the roll gap profile. The upper and bottom rolls are both ground to an S-shape in the CVC system, and the crown of the roll gap can continuously vary by axial shifting of rolls against each other. Many researches focus on the optimization and improvement of CVC roll profile to achieve the purpose of stable rolling process and improve the strip flatness. He et al. [10] developed a mixed variable crown (MVC) on the basis of the CVC roll profile, and the roll gap adjustment capacity was improved. Lu et al. [11] design a third-order CVC roll profile and the axial force was minimized. Equation (1) describes the third-order CVC roll profile of the upper roll.

$$y_u=a+bx+c{x}^2+d{x}^3$$

(1)

Although the CVC roll profile has a strong ability to adjust the quadratic roll gap crown, the quartic roll gap crown cannot be effectively adjusted [12,13]. Hence, in the early twenty-first century, SVAI developed a new profile and flatness control system, called SmartCrown, to eliminate the quarter buckles. The SmartCrown roll profile is defined as the sum of a sinusoidal and linear function. A continuous, gradual adjustment of roll gap profile is achieved by the continuous axial shifting. SmartCrown roll profile can be described as Equation (2) and Equation (3).

$$y_{su}\left(x\right)=A\sin \left(\frac{2Fai\left(x+C\right)}{L}\right)-B\left(x+C\right)$$

(2)

$$y_{sb}\left(x\right)=-A\sin \left(\frac{2Fai\left(x-C\right)}{L}\right)+B\left(x-C\right)$$

(3)

Li et al. [14] and Yang et al. [15] analyzed the crown control characteristics for SmartCrown work roll, and concluded that the profile parameter Fai was the most key factor for crown control. Yang et al. [16] developed a new flexible shape backup roll (FSR) based on the SmartCrown roll profile. The problem of nonuniform contact pressure between rolls was alleviated. The optimal profile parameters were not determined, although the effect of SmartCrown profile parameters on roll gap control was analyzed in the kinds of literature. Meanwhile, FEM is used as the research method in most of the literature [6,7,14,17,18], so that the calculation takes a long time that is not suitable for the optimization algorithms to determine the optimal profile parameters. Besides, the optimization objective of the roll profile in the literature is relatively single.

A coupling model of roll profile and strip flatness is established in the present paper in order to analyze the effect of roll profile parameters of SmartCrown intermediate roll on roll gap, rolls contact pressure, and strip flatness. The effect of A, B, C, and Fai on roll gap, rolls contact pressure, and strip flatness is analyzed. Subsequently, the multi-optimal roll profile parameters are obtained by non-dominated sorting genetic algorithm II (NSGA-II) optimization. Finally, the optimization results are applied to a 1740mm tandem cold rolling mill, and the flatness quality is significantly improved.

2. Coupling Model of Roll Profile and Strip Flatness

The influence function method has the advantages of fast calculation speed and high calculation accuracy, which is widely used in the online control system of the cold rolling process. In addition, the high calculation speed of the influence function method also provides a foundation for roll profile parameter optimization. Hence, the coupling model of roll profile and strip flatness is established based on the influence function method.

Note that the rolls are abstracted in to double cantilever beam structure. The center of the rolls is the fixed end, and the ends of the rolls are the free end of the cantilever beam. The rolling force is loaded on both necks of the backup roll ends. Figure 2 shows the diagram of loading, deflection, shifting, and discrete of rolls.

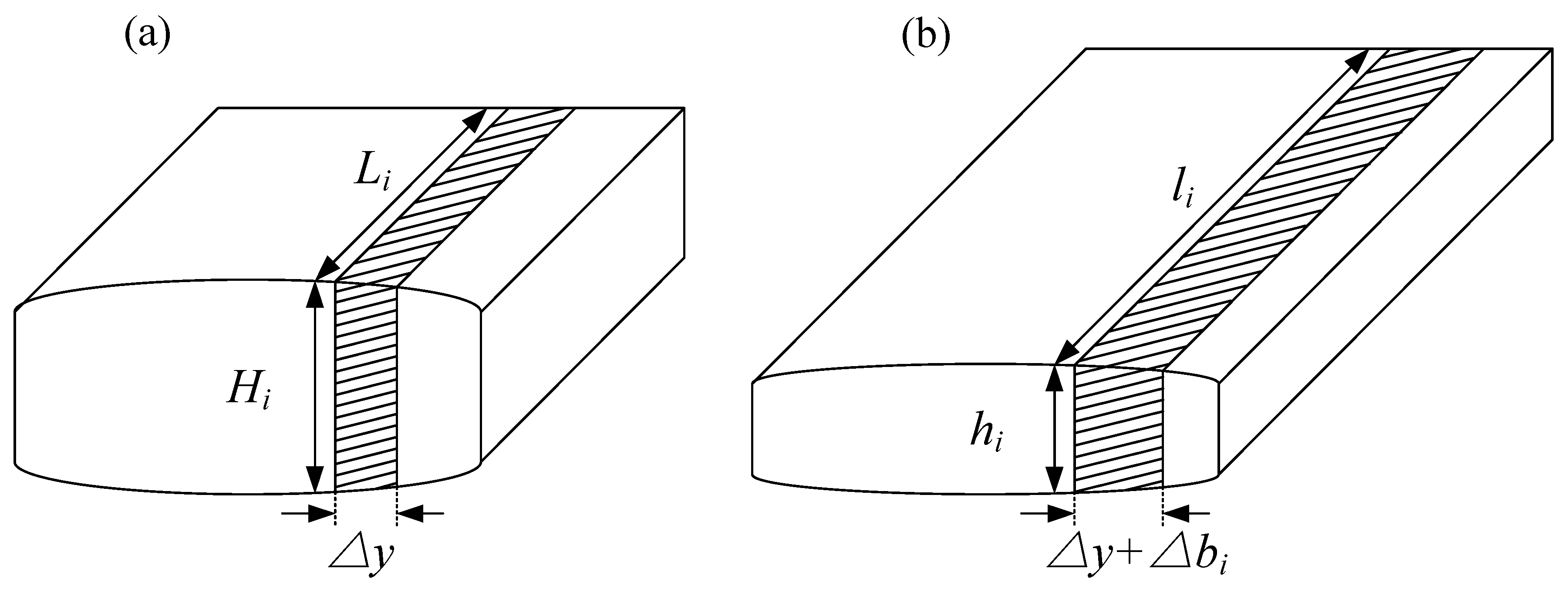
2.1. Calculation of Roll Gap Profile of SmartCrown Intermediate Roll

Equation (2) and Equation (3) define the roll profile of the SmartCrown intermediate roll. When the rolls shift a distance in the axial direction, the roll profile of upper and bottom roll can be calculated as Equation (4) and Equation (5), respectively.

$$y_{su1}\left(x\right)=A\sin \left(\frac{2Fai\left(\left(x\text{-}s\right)+C\right)}{L}\right)-B\left(\left(x\text{-}s\right)+C\right)$$

(4)

$$y_{sb1}\left(x\right)=-A\sin \left(\frac{2Fai\left(\left(x\text{-}s\right)-C\right)}{L}\right)+B\left(\left(x\text{-}s\right)-C\right)$$

(5)

The roll gap $g\left(x\right)$ along the roll barrel is obtained, as follows:

$$g\left(x\right)=-y_{su1}\left(x\right)-y_{sb1}\left(x\right)$$

(6)

The equivalent crown C_e of the roll gap is the difference of roll gap between the center and edge, which can be calculated as in Equation (7).

$$C_e=g\left(0\right)-g\left(\frac{L}{2}\right)$$

(7)

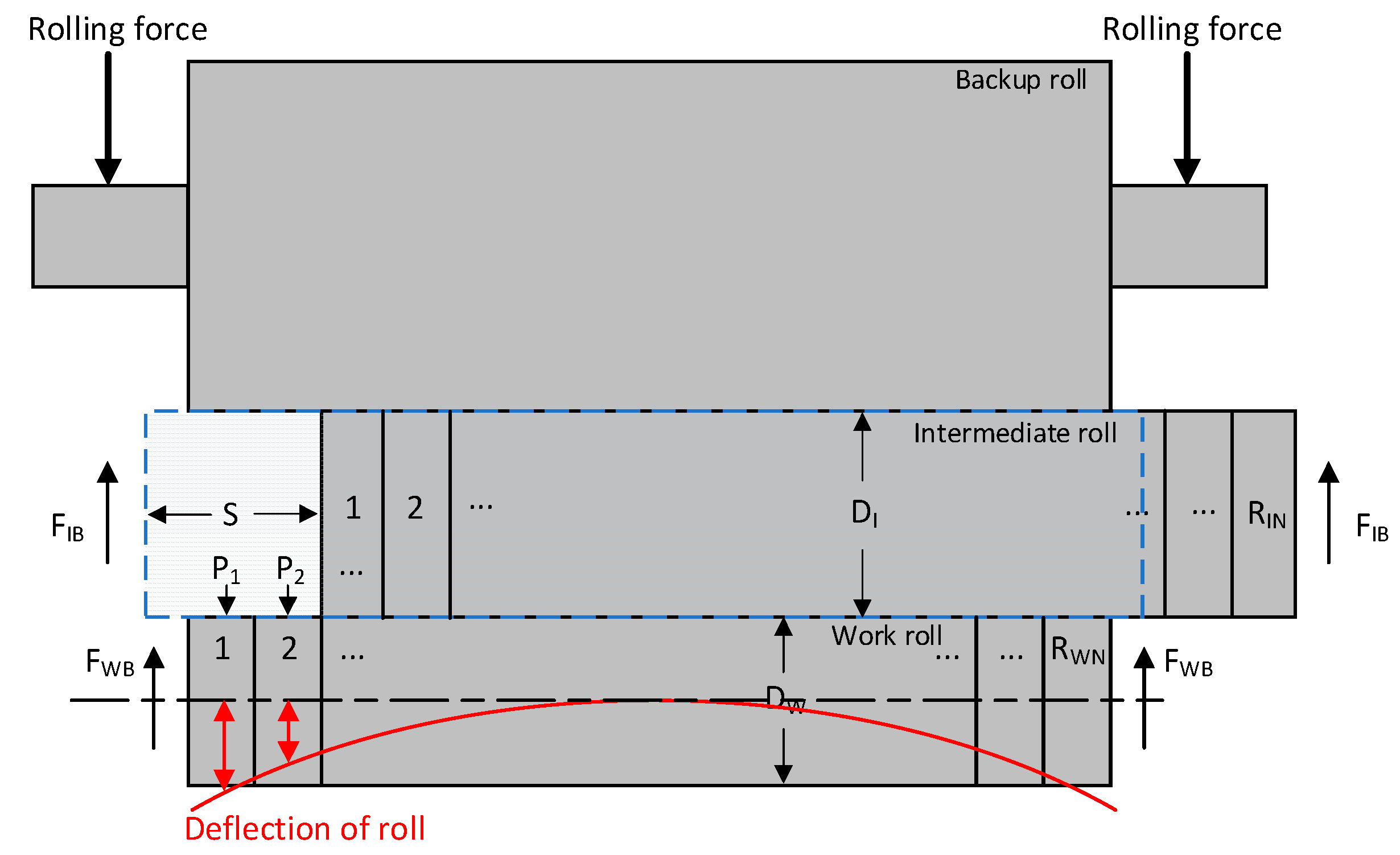
2.2. Calculation of Contact Pressure Distribution between Rolls

The contact pressure distribution between rolls is an important parameter for calculating the elastic deformation of rolls, and the rolling force distribution should be calculated before the calculation of contact pressure distribution. The diagram of the rolling process is shown in Figure 3, and the rolling force of unit i_i is calculated, as follows:

$$P_i=B_{\mathrm{s}}\cdot K\cdot T_P\cdot Q_P\cdot \sqrt{R^{\prime }\cdot \left(H_i-h_i\right)}$$

(8)

$T_P$ and $Q_P$ are calculated as Equation (9) and Equation (10), respectively.

$$T_P=\left(1-\frac{t_b}{K}\right)\cdot \left(1.05+0.1\cdot \frac{1-t_f/K}{1-t_b/K}-0.15\cdot \frac{1-t_b/K}{1-t_f/K}\right)$$

(9)

$$Q_P=1.08+1.79\cdot \frac{H_i-h_i}{H_i}\cdot \sqrt{1-\frac{H_i-h_i}{H_i}}\cdot \mu \cdot \sqrt{\frac{R^{\prime }}{h_i}}-1.02\cdot \frac{H_i-h_i}{H_i}$$

(10)

Assume that the contact pressure distribution between work roll and intermediate roll outside the contact region of work roll and the strip as in Equation (11).

$$q_i=F_{WB}/R_{WN}$$

(11)

Assume the contact pressure distribution between work roll and intermediate roll inside the contact region of work roll and the strip as Equation (12).

$$q_i=P_i+F_{WB}/R_{WN}$$

(12)

Similarly, the contact pressure between intermediate roll and backup roll is assumed as Equation (13) and Equation (14).

$$Q_i=F_{IB}/R_{IN}$$

(13)

$$Q_i=q_i+F_{IB}/R_{IN}$$

(14)

The rolls will deflect and flat during the cold rolling process, and Figure 4 shows the deflection and flatten of rolls. The elastic deflection of the work roll is calculated as in Equation (15).

$$Y{W}_i=GW\times q_j$$

(15)

GW can be defined as in Equation (16).

$$GW=\left[\begin{array}{ccc}gw\left(1,1\right)& \cdots & gw\left(1,n\right)\\ ⋮& & ⋮\\ gw\left(n,1\right)& \cdots & gw\left(n,n\right)\end{array}\right]$$

(16)

Similarly, we can obtain the elastic deflection of the intermediate roll (YI_i). The equation of deformation coordinate relationship between work roll and intermediate roll is shown as in Equation (17).

$$YW{I}_i=YW{I}_{L/2}+Y{I}_i-Y{W}_i-M{I}_i-M{W}_i$$

(17)

YWI_L/2 can be calculated as in Equation (18).

$$YW{I}_{L/2}=q_{L/2}\left(\frac{1-{\nu }_W{}^2}{\pi E_W}+\frac{1-{\nu }_I{}^2}{\pi E_I}\right)\ln \frac{\sqrt[3]{e^2}\left(D_W+D_I\right)}{2q_{L/2}\left[\left(1-{\nu }_W{}^2/\pi E_W\right)+\left(1-{\nu }_I{}^2/\pi E_I\right)\right]}$$

(18)

The influence function matrix of roll flatten can be defined as in Equation (19).

$$GWI=\left[\begin{array}{ccc}gwi\left(1,1\right)& \cdots & gwi\left(1,n\right)\\ ⋮& & ⋮\\ gwi\left(n,1\right)& \cdots & gwi\left(n,n\right)\end{array}\right]$$

(19)

The flatten between work roll and intermediate roll YWI_i, which is described in Equation (20).

$$YW{I}_i=GWI\times q_{ci}$$

(20)

Substitute Equation (17) and Equation (19) to Equation (20), we can obtain q_ci. When the difference between q_ci and q_i is higher than the required accuracy, q_i needs to be corrected by Equation (21), and then recalculate q_ci, until the accuracy is satisfied.

$$q_i^m=q_i^{m-1}+\lambda \left[q_{ci}^m-q_i^{m-1}\right]$$

(21)

In addition, the condition of static equilibrium should be satisfied as in Equation (22).

$${\displaystyle \sum P}+F_{WB}-{\displaystyle \sum q}<\epsilon$$

(22)

The calculation of contact pressure between intermediate roll and backup roll is similar to the calculation of contact pressure between work roll and intermediate roll. Figure 5 shows the deflection and flatten of rolls.

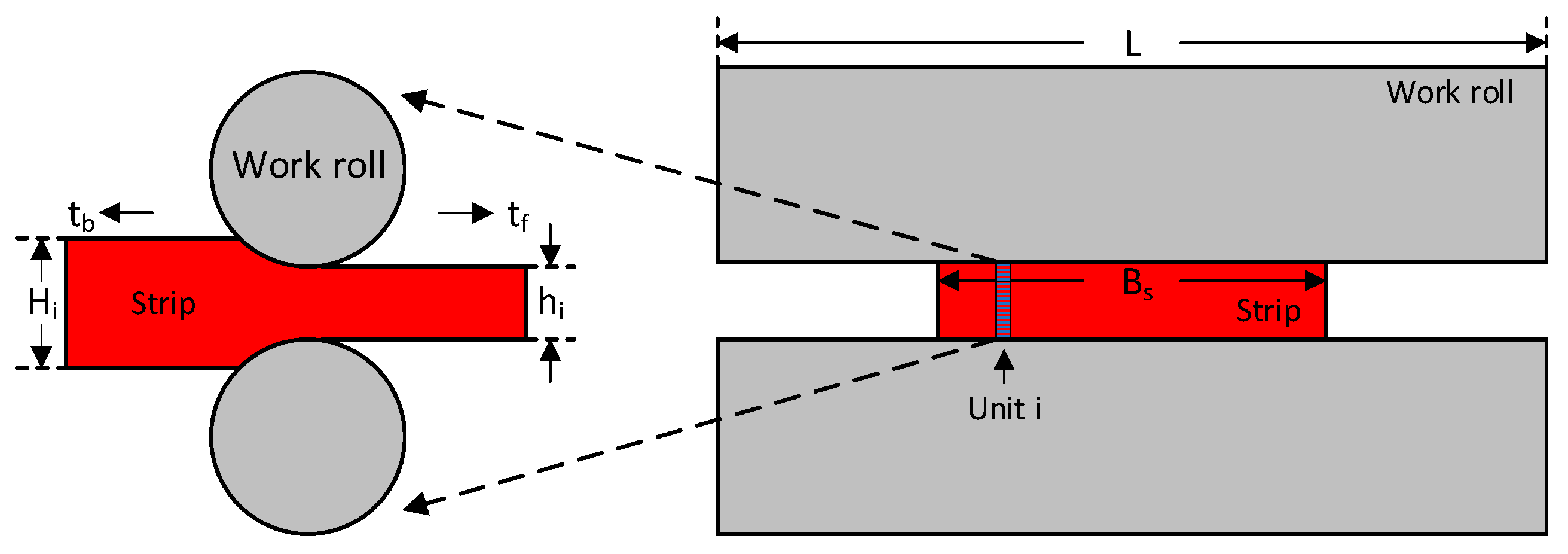
2.3. Calculation of Cold Rolled Strip Flatness

The thickness distribution (h_i) of cold rolled strip is calculated as in Equation (23).

$$h_i=h_{L/2}+\left(YW{S}_i-YW{S}_{L/2}\right)+2\left(M{W}_i-Y{W}_i\right)$$

(23)

Figure 6 shows the strip section profile before and after rolling.

According to the law of volume constancy, Equation (24) can be obtained.

$$H_i{L}_i\Delta y=h_i{l}_i\left(\Delta y+\Delta b_i\right)$$

(24)

$\Delta b_i$ can be calculated, as follows.

$$\Delta b_i=0.61{\left(\frac{H_i}{\Delta y}\right)}^{1.27}\exp \left[-0.38\left(\frac{H_i}{\sqrt{R^{\prime }\left(H_i-h_i\right)}}\right)\right]$$

(25)

Add incremental at both sides of the Equation (24) instead, then Equation (26) is obtained.

$$\left(H_i+\Delta H_i\right)\left(L_i+\Delta L_i\right)=\left(h_i+\Delta h_i\right)\left(l_i+\Delta l_i\right)+\Delta b_i$$

(26)

Expand Equation (26), then Equation (27) is obtained.

$$H_i{L}_i+H_i\Delta L_i+L_i\Delta H_i+\Delta H_i\Delta L_i=h_i{l}_i+h_i\Delta l_i+l_i\Delta h_i+\Delta h_i\Delta l_i+\Delta b_i$$

(27)

Equation (27) divide by Equation (24), and then Equation (28) is obtained.

$$\frac{\Delta l_i}{l_i}=\frac{\Delta L_i}{L_i}+\frac{\Delta H_i}{H_i}-\frac{\Delta h_i}{h_i}-\Delta b_i$$

(28)

Thus, the influence of strip flatness before rolling, strip thickness profile before and after rolling on strip flatness after rolling, as follows.

$$\frac{\Delta l_i}{\overline{l}}=\frac{\Delta L_i}{\overline{L}}+\frac{\Delta H_i}{\overline{H}}-\frac{\Delta h_i}{\overline{h}}-\Delta b_i$$

(29)

Note that, $\frac{\Delta L_i}{\overline{L}}$ is the strip flatness before rolling.

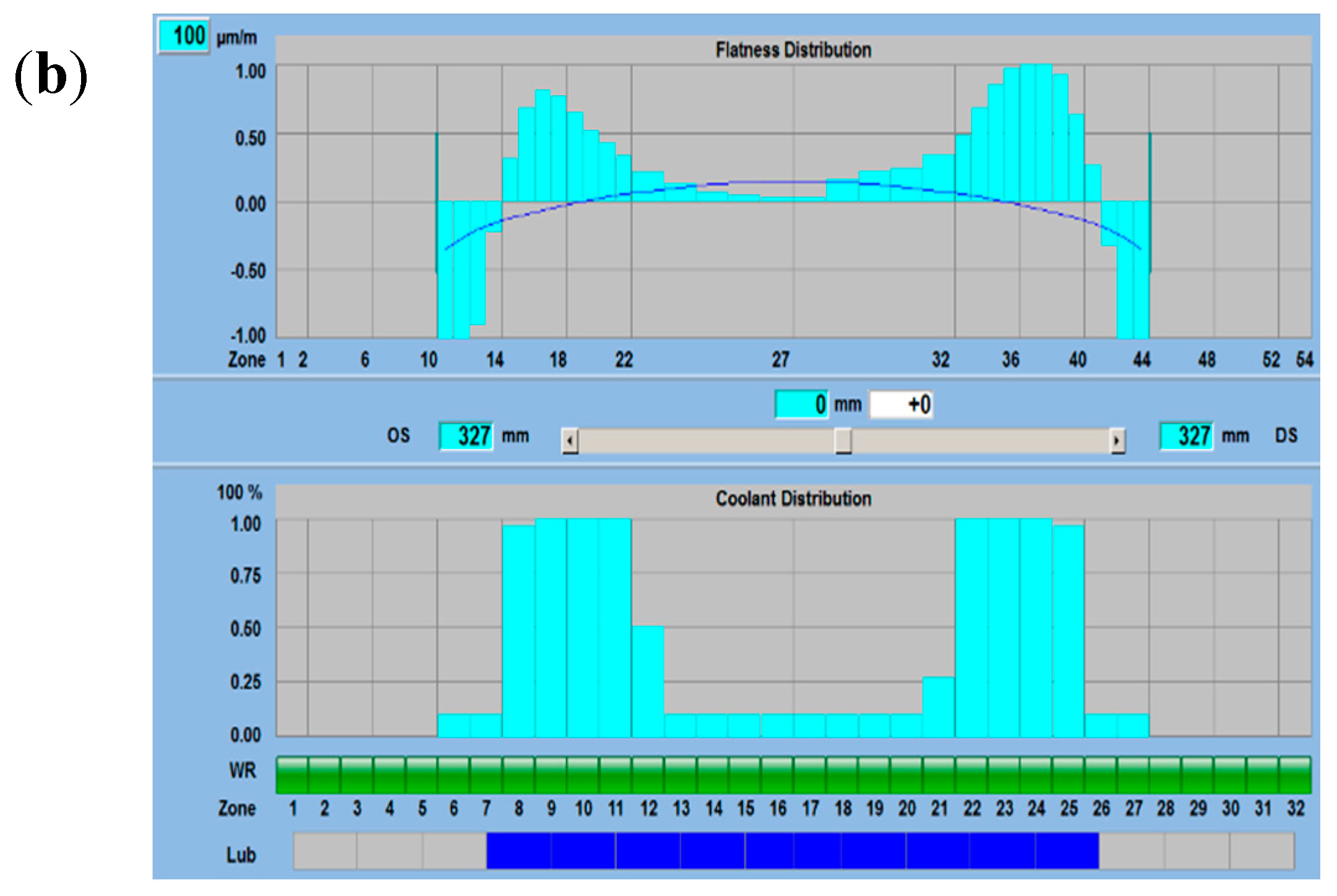
2.4. Verification of the Coupling Model

The flatness model is verified in a tandem cold rolling mills, by comparing the rolling force and strip flatness after rolling between the actual measured values and calculation results. The steel sample is DP980 steel, and the experimental parameters are obtained from the Primary Data Input (PDI). Figure 7 provides the verification results. The relative error of the rolling force between simulation and measurement is less than 6.5%, as shown in Figure 7a. Meanwhile, the maximum absolute error of flatness of stand 5 is less than 10 IU, as shown in Figure 7b. The calculation time of the coupling model is two seconds.

3. Flatness Control Characteristics of SmartCrown Intermediate Roll

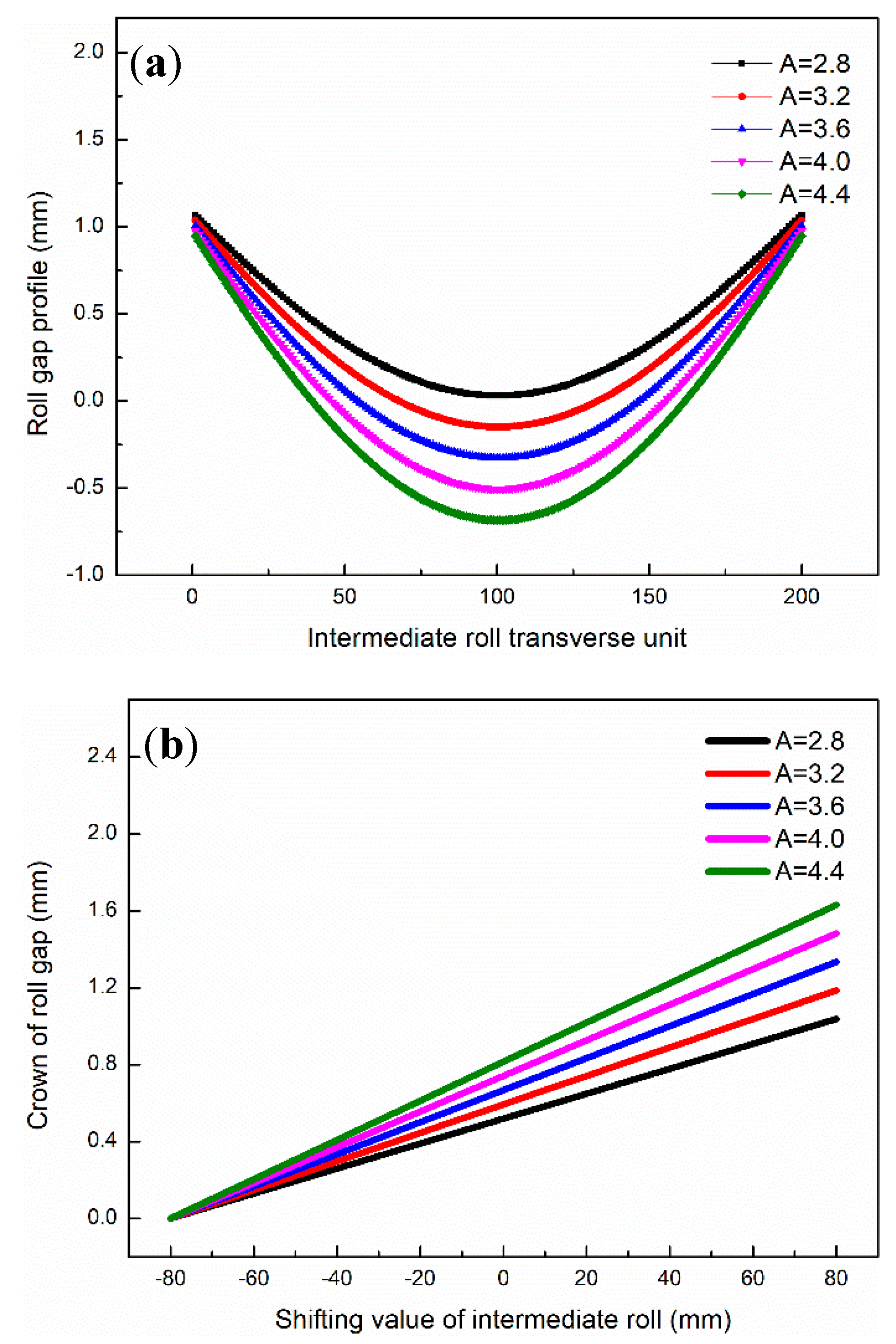
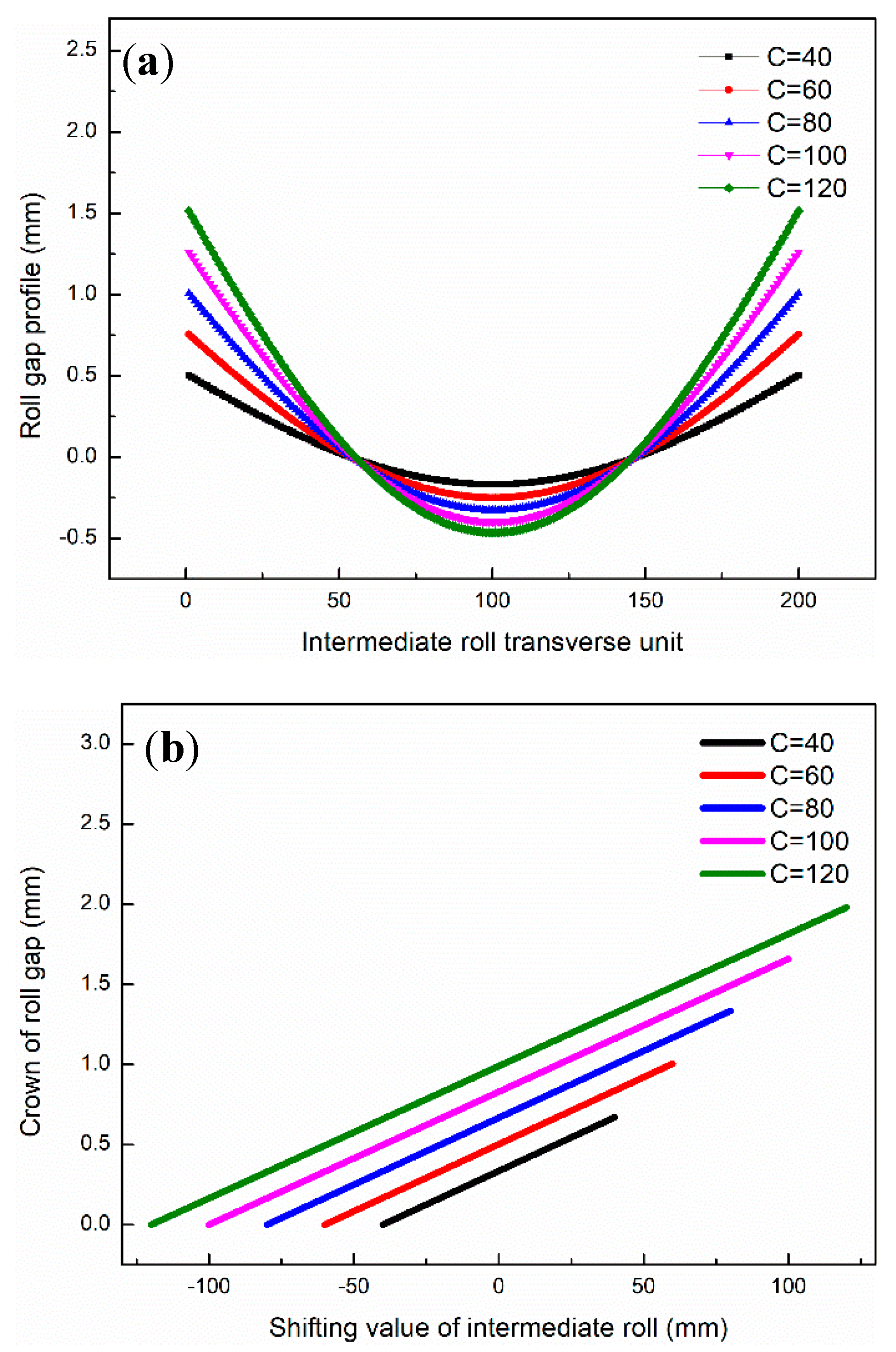
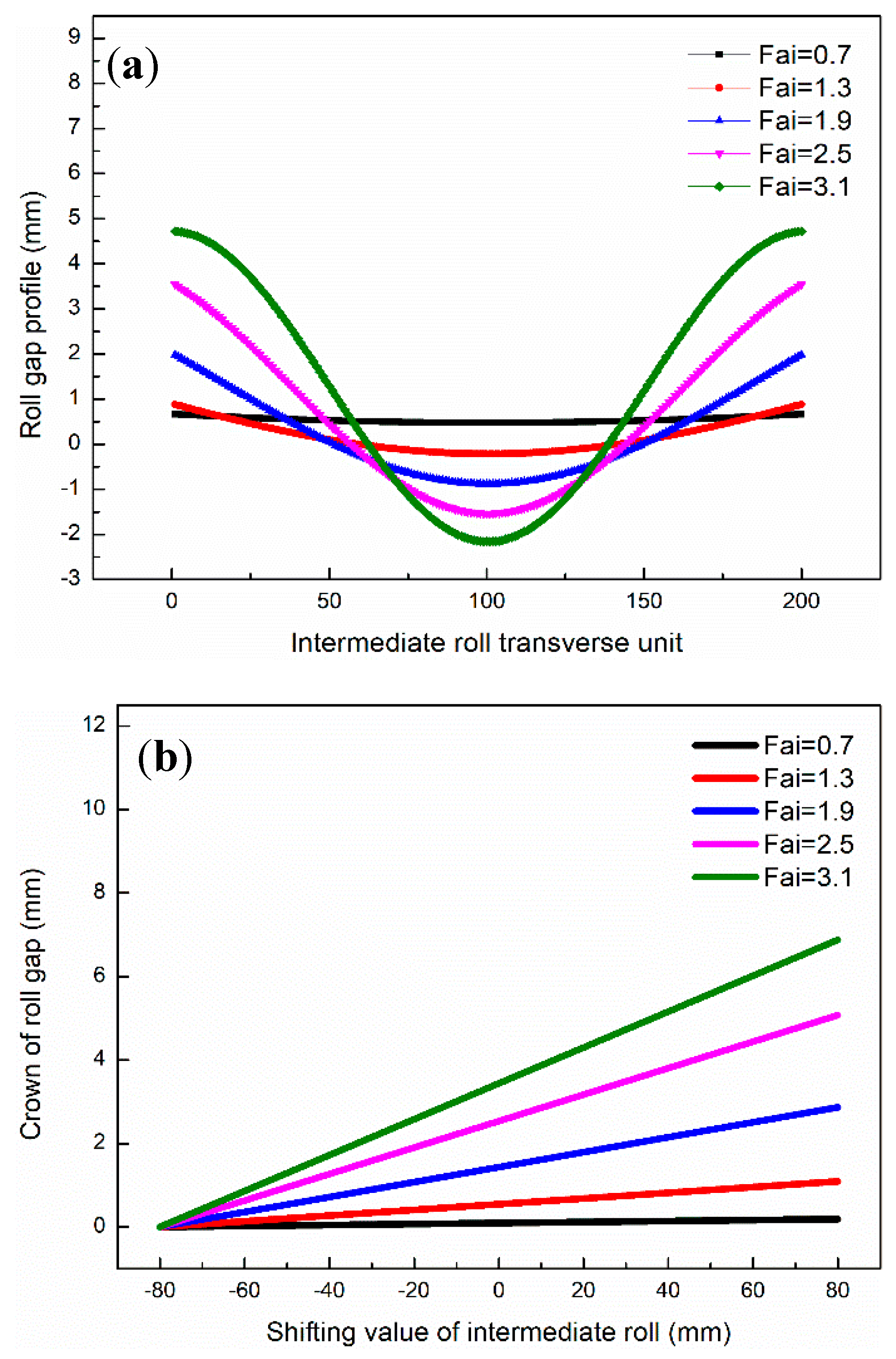
3.1. Effect of Profile Parameters on Roll Gap

The roll gap profile reflects the ability of strip profile control. The roll gap and the variation of roll gap crown with the shifting of intermediate roll under different A are calculated in order to analyze the effect of profile parameter A on the roll gap profile. A denotes the amplitude of the roll profile, in order to avoid the excessive difference of roll diameter, A cannot exceed 4.5. According to the manual experience, A is set to 2.8, 3.2, 3.6, 4.0, and 4.4. B, C, and Fai are set to a constant value (B = 0.004, C = 80, and Fai = 1.3) when A is analyzed. Figure 8 shows the calculation results.

As indicated in Figure 8a, the roll gap crown increased with the increase of A. Figure 8b gives the adjustment range of the roll gap crown. With A increasing from 2.8 to 4.4, the adjustment range of roll gap crown by intermediate roll shifting increased from 1.038 mm to 1.63 mm.

The roll profile parameter B denotes the position of the roll profile relative to the average radius. B cannot exceed 0.005 in order to avoid the excessive difference of roll diameter. According to the manual experience, B is set to 0.003, 0.0035, 0.004, 0.0045, and 0.005. A, C, and Fai are set to a constant value (A = 3.6, C = 80, and Fai = 1.3) when A is analyzed, and the calculation results, as shown in Figure 9. As indicated in Figure 9a and Figure 9b, the roll gap crown and the adjustment range of roll gap crown by intermediate roll shifting were not changed with the increasing B.

The roll profile parameter C denotes the maximum distance of the intermediate roll shifting. The maximum intermediate roll shifting distance of SmartCrown 6-high cold rolling mill for the simulation is 120 mm, so C cannot exceed 120 and C is set to 40, 60, 80, 100, and 120. A, B, and Fai are set to constant values (A = 3.6, B = 0.004, and Fai = 1.3) when C is analyzed, and the calculation results are shown in Figure 10. The roll gap crown increased with the increase of C, as indicated in Figure 10. With C increased from 40 to 120, the adjustment range of roll gap crown by intermediate roll shifting increased from 0.671 mm to 1.979 mm.

Fai is called the profile angle (in radians), which is the most critical parameter of the SmartCrown intermediate roll profile. Fai determines the span of the roll profile in the standard sine function (as shown in Figure 11). The sine has more than one period when Fai exceeds 3.14, which goes against the grinding of the roll profile and flatness control. Hence, Fai is set to 0.7, 1.3, 1.9, 2.5, and 3.1, according to the manual experience. A, B, and C are set to a constant value (A = 3.6, B = 0.004 and C = 80) when Fai is analyzed, and the calculation results are shown in Figure 12.

As indicated in Figure 12, with the increase of Fai, the roll gap profile transformed from quadratic shape to quartic shape, which indicated that Fai had a significant effect on controlling the quadric strip flatness. The adjustment range of roll gap crown by intermediate roll shifting increased from 0.671 mm to 1.979 mm with Fai risen from 0.7 to 3.1.

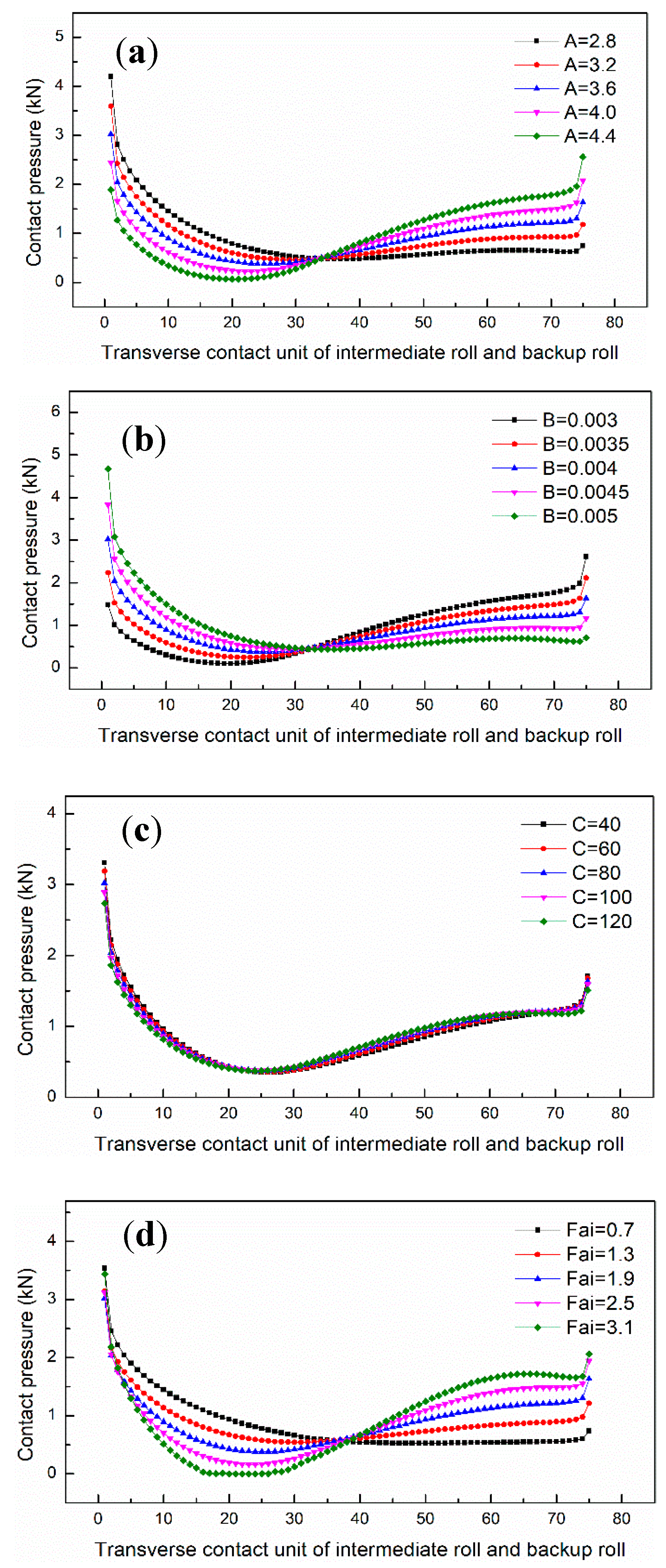
3.2. Effect of Profile Parameters on Contact Pressure Between Rolls

The uniform contact pressure between the rolls is helpful in reducing the nonuniform wear of rolls and improve the strip flatness control ability. Hence, the uniform contact pressure between rolls is an essential object of roll profile design. The contact pressure between rolls is calculated based on the roll profile parameters that are set in Section 3.1; the rolling parameters are shown in

Table 1. The rolling parameters for the calculation.

Name	Value
Work roll diameter/length (mm)	430/1740
Intermediate roll diameter/length (mm)	500/1990
Backup roll diameter/length (mm)	1310/1750
Strip width (mm)	1250
Strip thickness before/after rolled (mm)	2.3/1.7
Material	DP780
Front/back tension (MPa)	140/110
Work roll/intermediate roll bending force (kN)	300/300
Intermediate roll shifting (mm)	0

and the results are shown in Figure 13 and Figure 14.

The contact pressure between work roll and intermediate roll (denoted by QWI. Similarly, Figure 13 shows the contact pressure between intermediate roll and backup roll is denoted by QIB) under different profile parameters. As indicated in Figure 13a, with the increase of A, the QWI in the drive side (DS) decreased and the operating side (OS) increased. Meanwhile, the difference of QWI between DS and OS increased. On the contrary, the QWI in the drive side (DS) increased and in the operating side (OS) decreased with the B increased, and the difference of QWI between DS and OS decreased, as shown in Figure 13b. Figure 13c indicated that the QWI changed little with the change of C. From Figure 13d, the influence trend of Fai on QWI was similar to A. The maximum difference of QWI was located in the 1/4 region of both sides.

Figure 14 shows the QIB under different roll profile parameters. Similar to the QWI, the peak of QIB was located in the DS. Increasing B and C could effectively reduce the peak QIB at DS, but increased the peak QIB in OS.

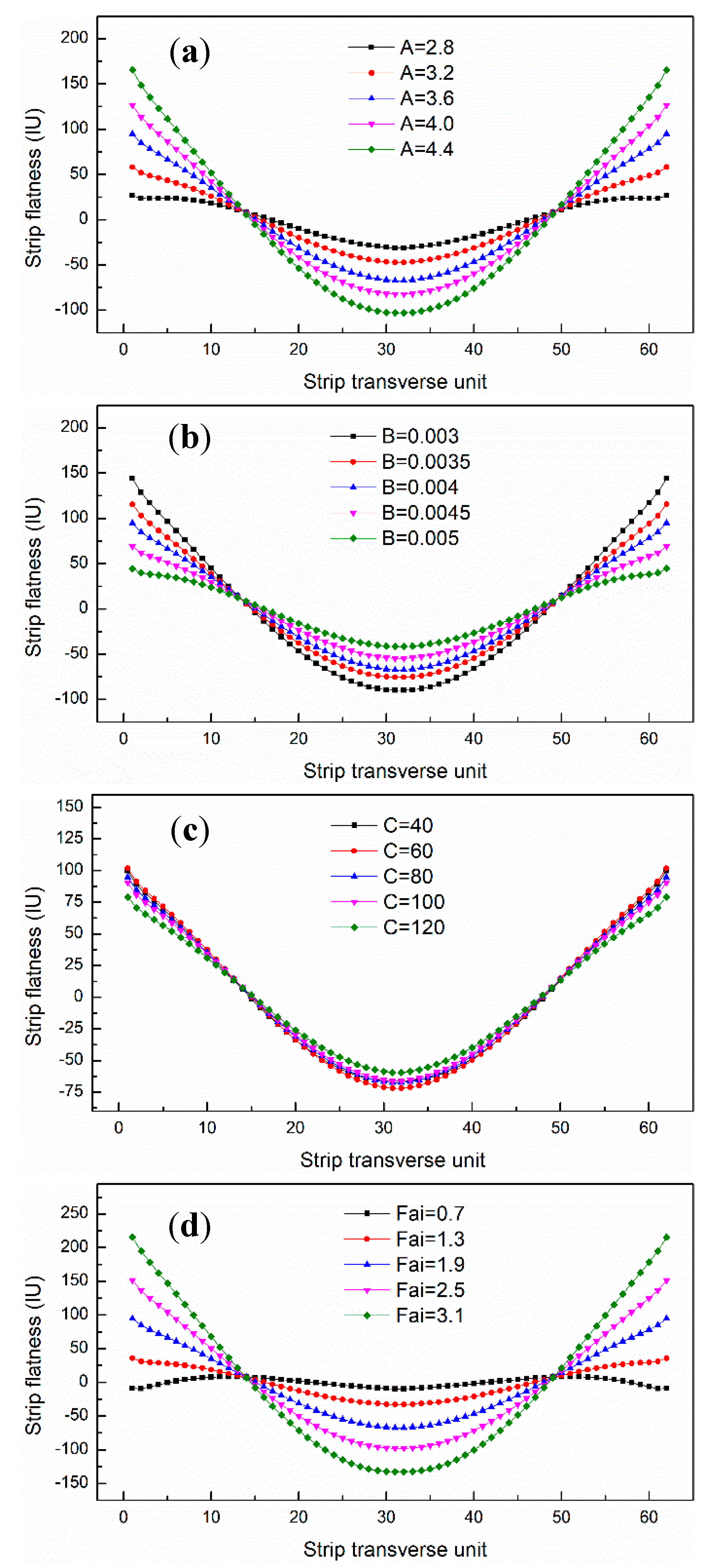
3.3. Effect of Profile Parameters on Strip Flatness

To analyse the profile parameters on strip flatness, the cold rolled strip flatness under different parameters were calculated, and the results are shown in Figure 15. As shown in Figure 15a,d, with the increased of A and Fai, the strip flatness transformed from flat to edge wave. Instead, the strip flatness transformed from edge wave to flat with the increase of B. C had little effect on the strip flatness.

4. Multi-Objective Optimization of SmartCrown Intermediate Roll

Section 3 systematically analyzed the effect of roll profile parameters on roll gap profile, QWI, QIB, and strip flatness. The roll profile parameters should be further optimized by the optimization algorithm. The NSGA-II has been successfully applied in searching the multi-objective optimal solution of parameters of the engineering problem [19,20], which is used to determine the optimal roll profile parameters in this section.

4.1. Multi-Objective Functions

The roll gap crown adjustment range should be as wide as possible to enhance the flatness control ability of cold rolling mill. Hence, combined with Equation (7), the objective function of roll gap crown adjustment range J₁ can be defined, as follows:

$$J_1=\max \left[g\left(0\right)-g\left(\frac{L}{2}\right)\right]$$

(30)

Uniform contact pressure between rolls leads to the uniform roll wear, which could improve the flatness control. The objective function of the contact pressure difference between rolls J₂ can be defined, as follows.

$$J_2=\min \left(QW{I}_{\max }-QW{I}_{\min }\right)$$

(31)

4.2. Constraint Conditions

The bearings of rolls are prone to damage under excessive axial force. Hence, the axial force should be controlled within the limit of the equipment. The axial force F is calculated, as follows:

$$F=P_0\left[y_{su1}\left(\frac{L+B_s}{2}\right)-y_{su1}\left(\frac{L-B_s}{2}\right)\right]$$

(32)

The constraint is defined, as follows:

$$F\le \frac{3}{1000}{\displaystyle \sum P}$$

(33)

The roll profile parameters have to be kept within its upper and lower limits, as follows:

$$\{\begin{array}{l}2.8\le A\le 4.4\\ 0.003\le B\le 0.005\\ 40\le C\le 120\\ 0.7\le Fai\le 3.1\end{array}$$

(34)

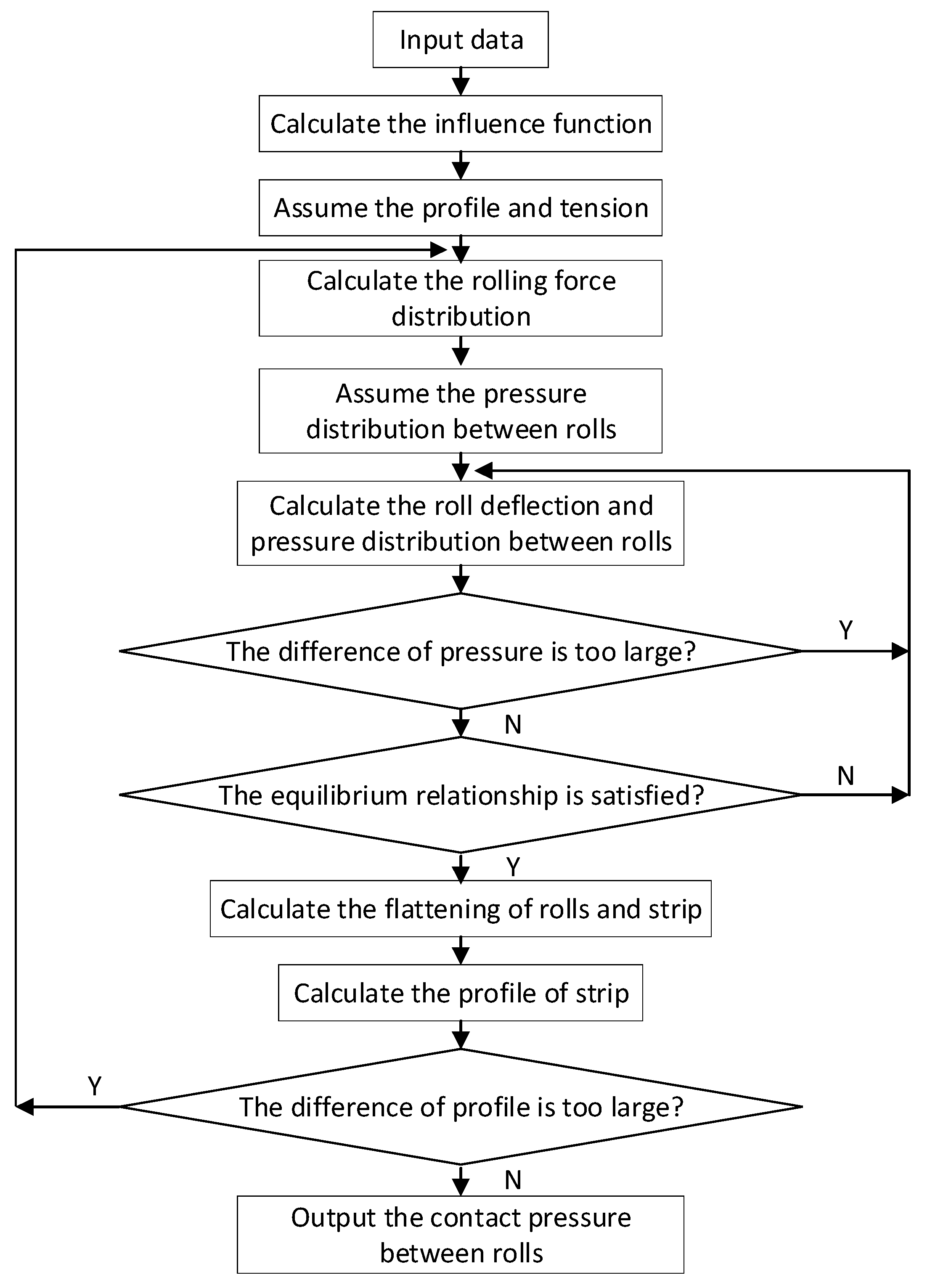
4.3. Roll Profile Parameters Optimization Procedure

The steps of roll profile parameters optimization are as follows.

Step 1: Randomly generate a set of roll profile parameters.

Step 2: Use the NSGA-II to search the pareto-optimal solutions within decision space.

Step 3: The optimal roll profile parameters are output if the number of iterations satisfies the evolutionary generation, otherwise return to Step 2.

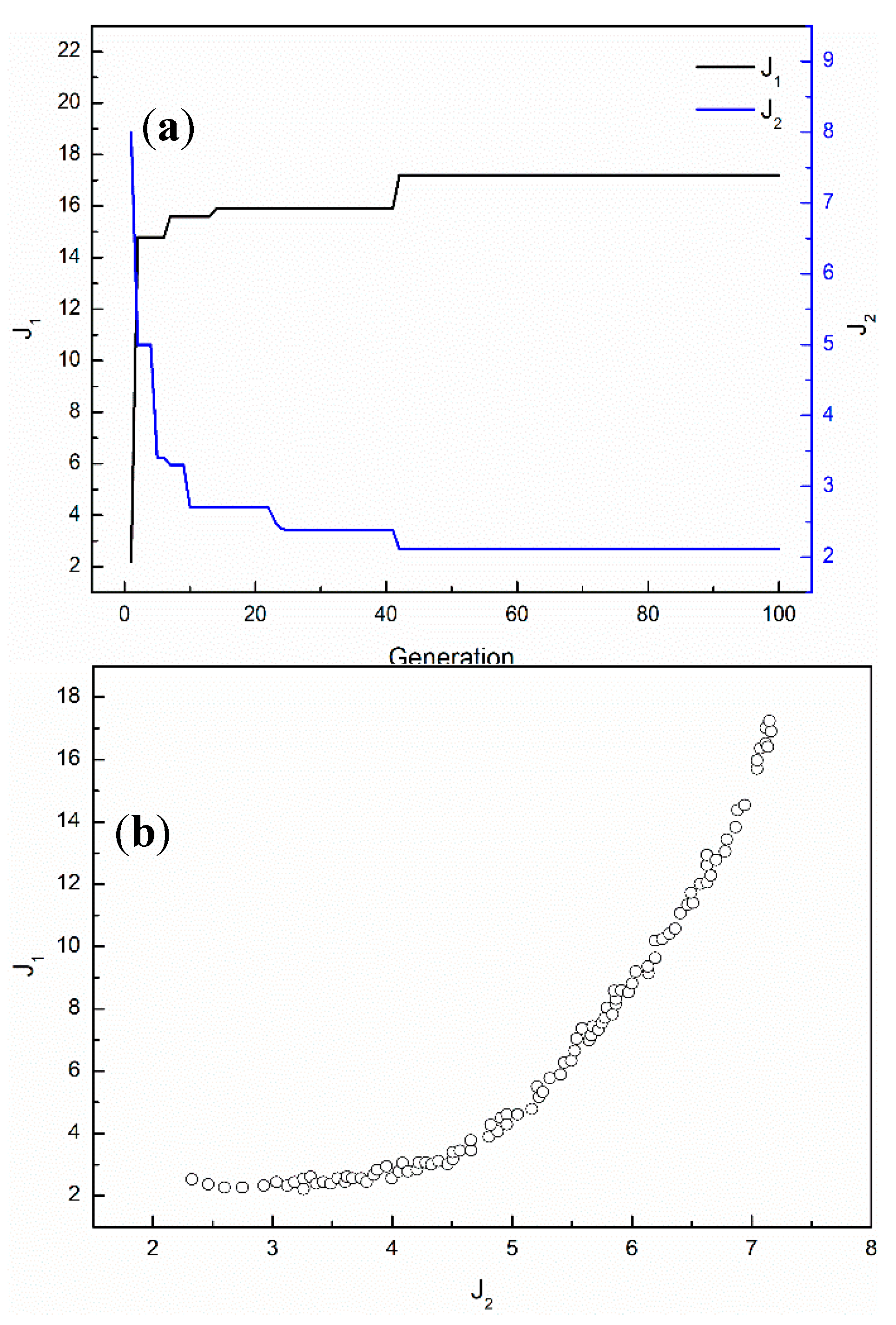
4.4. Multi-Objective Optimization Results

The optimization method was applied to a tandem cold rolling mill. Table 1 shows the rolling parameters. Figure 16a gives the evolution of objective function 1 and 2 with the generation, and Figure 16b gives the Pareto-optimal solution at the end of the evolution. The two objective functions reach steady state after 40 generations, as indicated in Figure 16a.

The objective of J₁ is to find the maximum value and the objective of J₂ is to find the minimum value, as shown in Figure 16b. Hence, there is a conflicted relationship between J₁ and J₂. Therefore, a decision-making method that is based on the weighted-sum approach is used to select the trade-off solution form the Pareto front. The weighted-sum objective function J is defined, as follows:

$$J={\alpha }_1\cdot \frac{J_1-J_{1\min }}{J_{1\max }-J_{1\min }}+{\alpha }_2\cdot \frac{J_2-J_{2\min }}{J_2{}_{\max }-J_{2\min }}$$

(35)

Figure 17 shows the roll gap crown adjustment range and QWI under different ${\alpha }_1$ and ${\alpha }_2$. In this study, set ${\alpha }_1$ = 0.3, ${\alpha }_2$ = 0.7, and the optimal roll profile parameters of 3.919, 0.004804, 78, and 1.396 are proposed for A, B, C, and Fai, respectively.

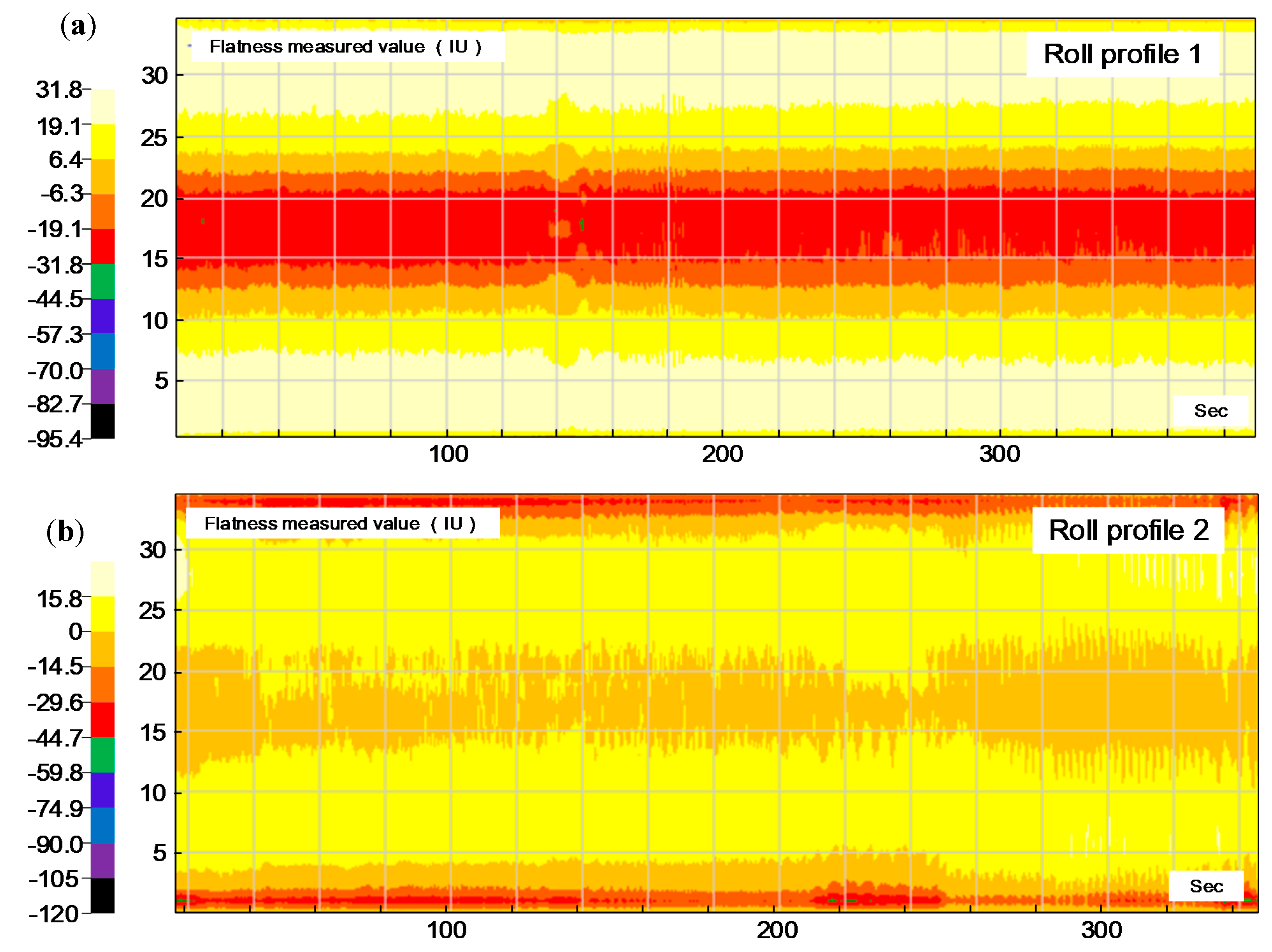
5. Industrial Test and Application

Rolling experiments were carried out in a 1740 mm six-high five stand tandem cold rolling mills in order to verify the optimization results of roll profile parameters. The diameter of work roll, intermediate roll, and backup roll are 420–470 mm, 500–580 mm, and 1300–1465 mm, respectively. The minimum and maximum product thickness of the mills are 0.2 mm and 2.5 mm, respectively. The max total rolling force on strip is 32000 kN. The test material is DP780. Two types of SmartCrown intermediate roll profile were carried out in the stand 5 of the tandem cold rolling mills. Roll profile 1 is the profile before optimized and the roll profile parameters are 3.662, 0.004342, 120, and 1.221 for A, B, C, and Fai, respectively. Roll profile 2 is the profile that is optimized in Section 4.

Figure 18 shows the measured flatness of a certain moment. The quartic flatness defects were obvious when used the Roll profile 1, and the local flatness at the 1/4 region of the strip was more than 20 IU, as shown in Figure 18a. When compared with Roll profile 1, the flatness was significantly improved when using Roll profile 2, as shown in Figure 18b.

Figure 19 indicated the flatness measured value of a whole coil, the flatness all over the strip when used Roll profile 2 within 10 IU, as shown in Figure 19b. The results of optimization results are verified by the rolling experiments.

6. Conclusions

• A Coupling model of roll profile and strip flatness was established and verified. The relative error of the rolling force that was calculated by the model was less than 6.5%, and the absolute error of flatness was within 10 IU. The provided coupling model has an acceptable accuracy to meet the requirements of the present study.
• The influence trend of roll profile parameters A and B on contact pressure between rolls and strip flatness is quite the opposite. Fai had a significant effect on controlling the quadric strip flatness.
• The roll profile parameters were optimized based on the NSGA-II, and the optimal roll profile parameters of 4.419, 0.004804, 78, and 1.396 are proposed for A, B, C, and Fai, respectively. The optimal roll profile parameters were applied to a 1740 mm six-high five stand tandem cold rolling mills, and the flatness quality was significantly improved.