Abstract
A fixture hardening process for aerospace gear box components of alloy S156 (16NiCrMo16-5, 1.6722) is investigated by thermomechanical metallurgical 2D axisymmetric Finite Element simulations. Material parameters are experimentally determined. Contact and transformation plasticity effects among others are implemented in Abaqus® with user subroutines. The study aims to optimize the mandrel diameter of a fixture hardening tool for processing of planet gears. Plasticity, transformation plasticity, arising contact forces, and pressure depending on different mandrel sizes are investigated in depth. Distortion is evaluated and an optimal setting is derived from the calculations. Results show that cylindricity, defined here as the difference between maximum and minimum radius of the part, and maximum contact pressure, both can be reduced by increasing the mandrel radius. Physical effects and distortion evolve strongly nonlinear. Analysis methods highlighting cylindricity depending on the different mandrel diameters are developed to illustrate this nonlinear behavior and to enhance knowledge about the process.
1. Introduction
Gears in aerospace applications require highly accurate production processes with minimal resulting distortion to satisfy safety requirements and to maximize service time in high speed and load environments. Press quenching or fixture hardening is a heat treatment technique utilized to control dimension and form changes of parts by constraining their shrinkage during quenching [1,2,3]. Important mechanisms and variables encountered are heat transfer by the cooling medium, thermal and transformation strains, transformation plasticity, and transformation kinetics [4,5]. Phase transformation during the quenching process leads to significant dimensional changes and plasticity effects. The specific tool design, e.g., oil flow guidance and mandrel dimension are key parameters of the tool.
Mandrel size together with heat transfer coefficient dictate the exact time of contact and thus the temperature of the part as well as the developing contact pressure. Setting the correct mandrel size is therefore critical in order to achieve high quality results. Due to highly nonlinear physical phenomena, exact forecast of shrinkage for an individual steel grade is extremely challenging [6].
This work represents an expansion with substantial additional investigations of a previously published conference paper by the author [7]. In this study the influence of the mandrel radius of a fixture hardening process on the global distortion is analyzed by Finite Element Method (FEM) simulations. A model of a gear without teeth is used enabling axial symmetry and reduction of the modeling domain from 3D to 2D since gear teeth are not included in the geometry. The diameter of the model is set to the pitch diameter of the gear in order to maintain a similar volume to that of the original gear. The investigated fixture hardening process consists of two main steps leading to the part’s final geometry:
(1) First, the carburized gear is austenitized, which leads to an expansion of approximately one percent [5], and then it is placed onto a mandrel followed by rapid oil quenching inside the tool. The oil has a temperature of 60 °C and circulates in the fixture with high velocities. Shrinkage of the part onto the mandrel restricts dimensional and shape changes.
(2) The quenched part is pressed out at room temperature to remove the mandrel. During press out, significant form changes take place due to the release of elastic energy.
Common practice in industry is to carry out initial parameter setting trials starting with a mandrel diameter slightly larger than expected and to iteratively reduce the diameter by grinding the mandrel. To the authors’ best knowledge, general procedures or guidelines based on scientific principles for setting the mandrel size are not published currently. Two different aspects are investigated in this study, a practical and a methodological one:
(i) The influence of the mandrel size on distortion of a fixture hardened part.
(ii) The influence of modeling the mandrel as a rigid body vs. modeling the mandrel as an elastic-plastic body.
The paper is structured as follows. In Section 2, the implemented mathematical framework is discussed briefly with a focus on the description of strain in the model. Experimental determination of material parameters is described and parameters for the austenite to martensite transformation are presented. Fundamental aspects of the implemented FE model, geometry, boundary conditions, meshing, heat transfer, and simulated process steps are explained next. In the results section, temperature curves are evaluated, and distortion of the inner and outer radii of the part is discussed in detail. A discussion of important aspects and a short summary form the conclusion of the paper.
2. Materials and Methods
The gear material and the methodology of the fixture hardening process model is introduced in the following section. Briefly, the mathematical framework, selected material data, geometry, and mesh, as well as boundary conditions and specifics of the simulated heat treatment are presented. Extensive information on modeling of steel heat treatment can be found in [4,8]. Gear steel is S156 (16NiCrMo16-5, 1.6722), a high-strength aerospace steel grade with a carbon content of 0.16 wt.%. The mandrel is made of a hardened alloy.
2.1. Mathematical Framework
A coupled thermomechanical–metallurgical model of a fixture hardening process of a power transmission gear blank was implemented within a FEM framework [9,10,11]. Temperature is calculated by Fourier’s heat equation and carbon diffusion is modelled via Fick’s second law. Diffusion based phase transformations are described by a combined approach according to Johnson–Mehl-Avrami (JMA) and Leblond [12,13,14]. The diffusionless martensitic transformation is modeled by the Koistinen-Marburger equation [15]. The strain rate equilibrium of the mechanical field divided into individual contributions is given by
where is total strain rate composed of —elastic, —plastic, —thermal, —isotropic phase transformation, and transformation plasticity strain rates. Linear mixture rules are applied for all described effects. Elasticity strain rates are given in terms of the Young’s modulus and Poisson’s coefficient [16]. Thermal and phase transformation strain is calculated in a combined approach according to [17]
Density of the phases is calculated from the sum of thermal and transformation strain. The transformation plasticity effect is implemented using a linearized approach [18] as follows,
In integral form:
where is the transformation plasticity constant and is the deviatoric stress tensor. Kinetics are affected by the saturation function . The Ramberg-Osgood model for isotropic hardening of the austenitic and martensitic phases is used [19]:
where is stress, is the hardening parameter, is plastic strain, and is the hardening exponent.
2.2. Material Data
The gear steel for this study is S156 (16NiCrMo16-5, 1.6722) having a chemical composition (wt.%): 0.2 C, 0.4 Mn, 0.2 Si, 1.0 Cr, 2.0 Ni, 4.0 Mo and 0.1 Cu. Dilatometer experiments with through carburized specimens with different carbon contents have been carried out to determine phase transformation parameters. The experiments yielded martensitic transformations only, for a wide range of cooling rates. Retained austenite was measured by X-ray diffraction for the dilatometer specimens at room temperature. Based on these experiments phase transformation material data has been obtained by fitting recorded dilatometry data to the JMA and Koistinen-Marburger equations using the retained austenite data as validation for the transformed phase volumes. Martensitic transformation is modeled by the Koistinen-Marburger equation [15].
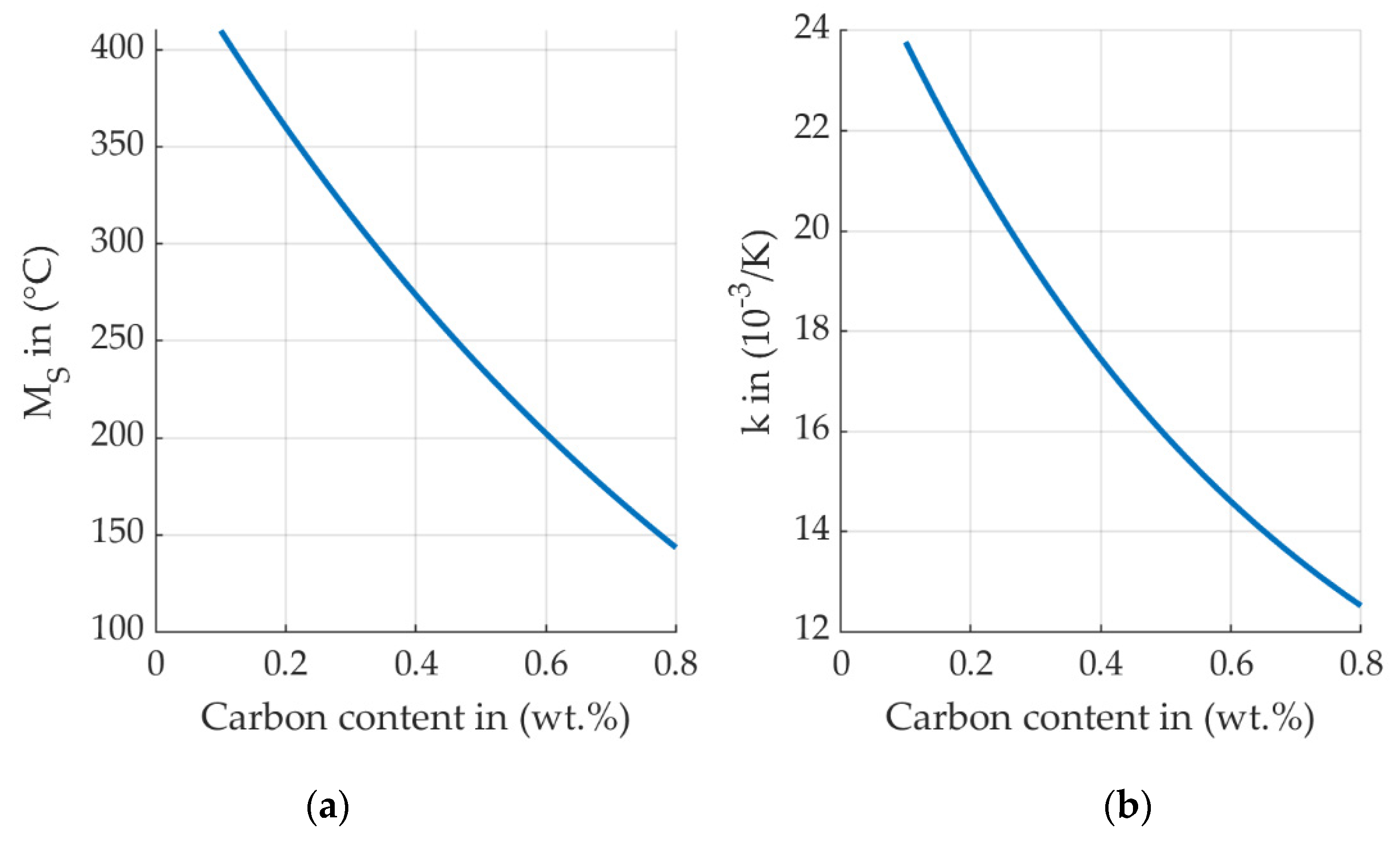
where is the martensite fraction, is the martensite start temperature, and is the Koistinen-Marburger coefficient. Material and phase transformation parameters were implemented as carbon and phase dependent, see Equations (7) and (8). Exponential dependency of first order on carbon content is assumed for martensite start, MS, and for the Koistinen-Marburger parameter k, see Figure 1.
where and are coefficents describing carbon dependency of and , respectively.
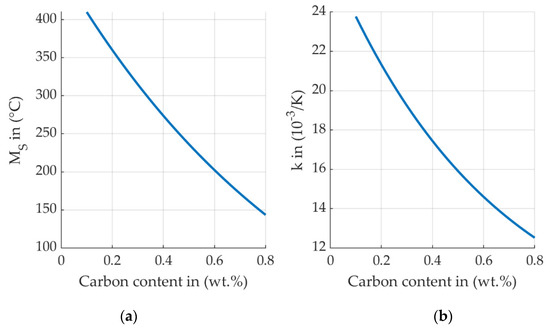
Figure 1.
(a) Calculated martensite start temperature and (b) parameter k of the Koistinen-Marburger equation for steel S156.
Due to confidentiality some of the measured data, e.g., values for Martensite Start temperatures and the fitted k parameter cannot be made available for this publication. These parameters can be calculated with good agreement with measurement data based on empirical models, which take the composition range into account, described in [20]. According to formulas given in [20], the author of this study calculated the values given in Figure 1 and Table 1 for the composition of steel S156.

Table 1.
Calculated carbon dependent values for MS for steel S156.
In general, temperature and, if applicable, carbon dependency of material parameters are given in polynomial form:
Transformation plasticity, for the austenite to martensite transformation, for Equation (3) according to [21] is (-). Parameters to calculate plastic deformations as described in Equation (6) are given in Table 2:

Table 2.
Hardening parameters for steel SAE 5120 according to work in [21,22].
Thermophysical data was partially taken from a dataset for alloy SAE 5120 (20MnCr5, 1.7147) published in [21]. This data set is also used as material data for the mandrel. Further unpublished data from the SFB 570, Distortion Engineering program, and from a material data base provided by a project partner was implemented. Linear carbon dependency is assumed for all other parameters. Data used for simulations is summarized here. The initial density is . The following values are used for thermal conductivity, specific heat, elastic modulus, and poisson’s ratio (Table 3).

Table 3.
Thermophysical parameters used for simulations [21,22].
2.3. Model Geometry
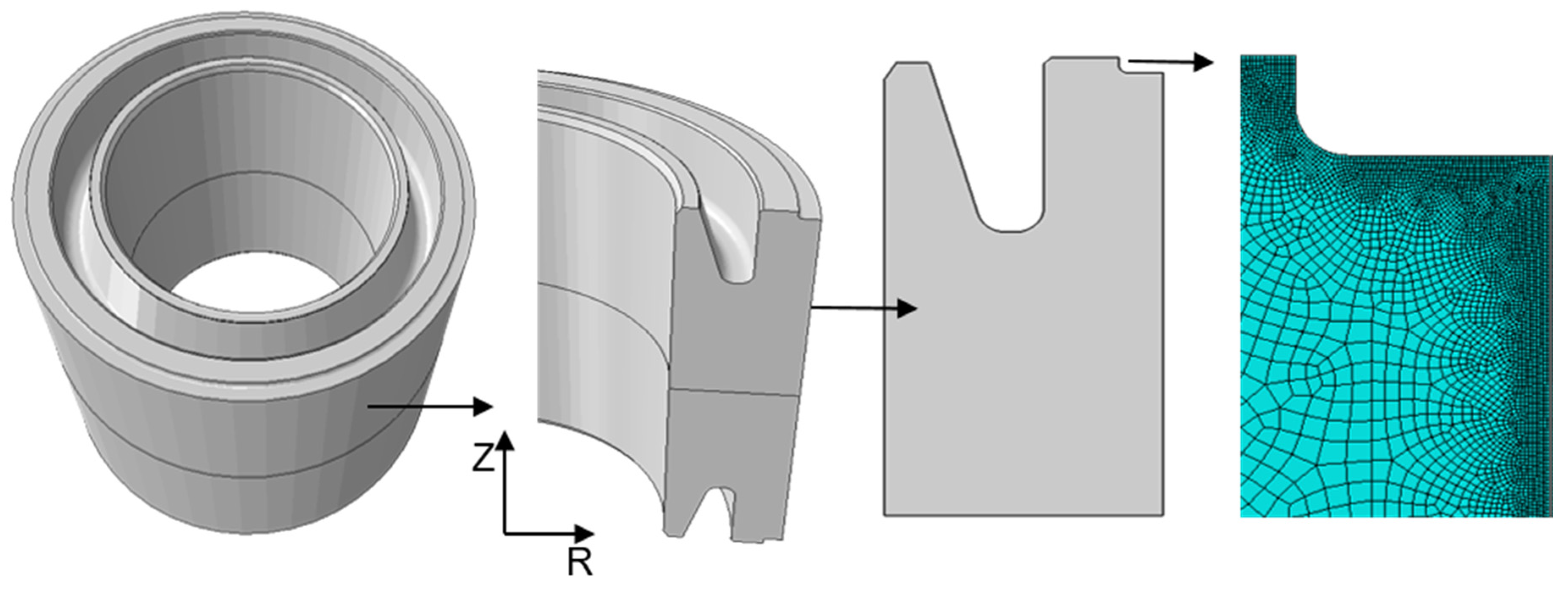
The model geometry was implemented based on a 3D CAD model of a gear blank according to Figure 2.
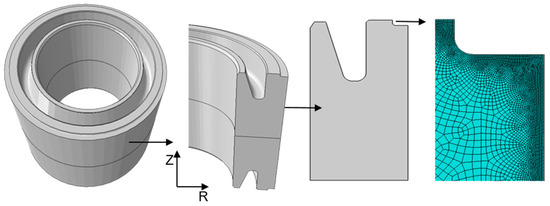
Figure 2.
Implemented gear blank geometry and near surface mesh of the 2D axisymmetric model derived from 3D geometry.
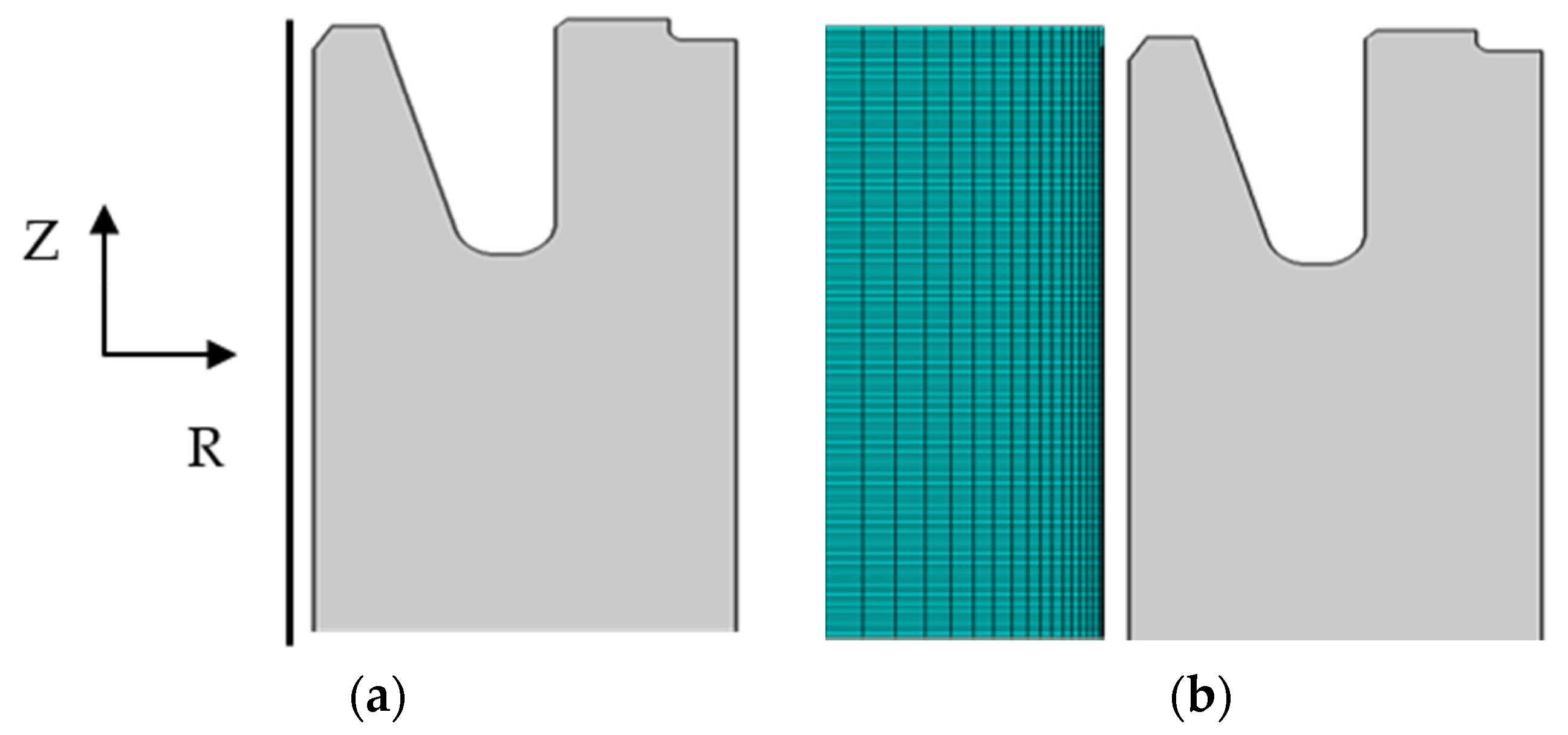
Rotational symmetry enables a 2D representation of the gear blank. Only one half of the gear blank along the z-axis is simulated because of mirror symmetry along the height. A 4-node axisymmetric quadrilateral bilinear displacement temperature element type was used. The mesh consists of 65088 elements, with refinements underneath the surface in order to account for steep gradients in those areas. Mesh optimization for convergence was carried out. The mandrel is represented by an analytical rigid body in case I, and by a solid body in case II. Figure 3 depicts the two cases with the meshed solid body for case II.
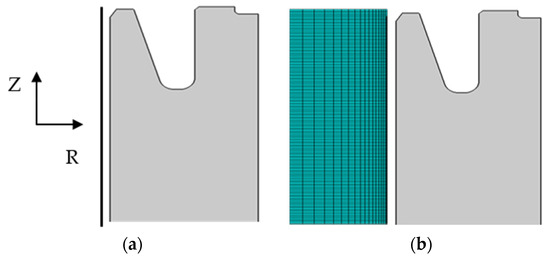
Figure 3.
2D axial symmetric geometry of gear blank and mandrel for two evaluated set-ups: (a) Mandrel as analytical rigid body. (b) Mandrel as solid body with elastic plastic properties.
2.4. Boundary and Initial Conditions
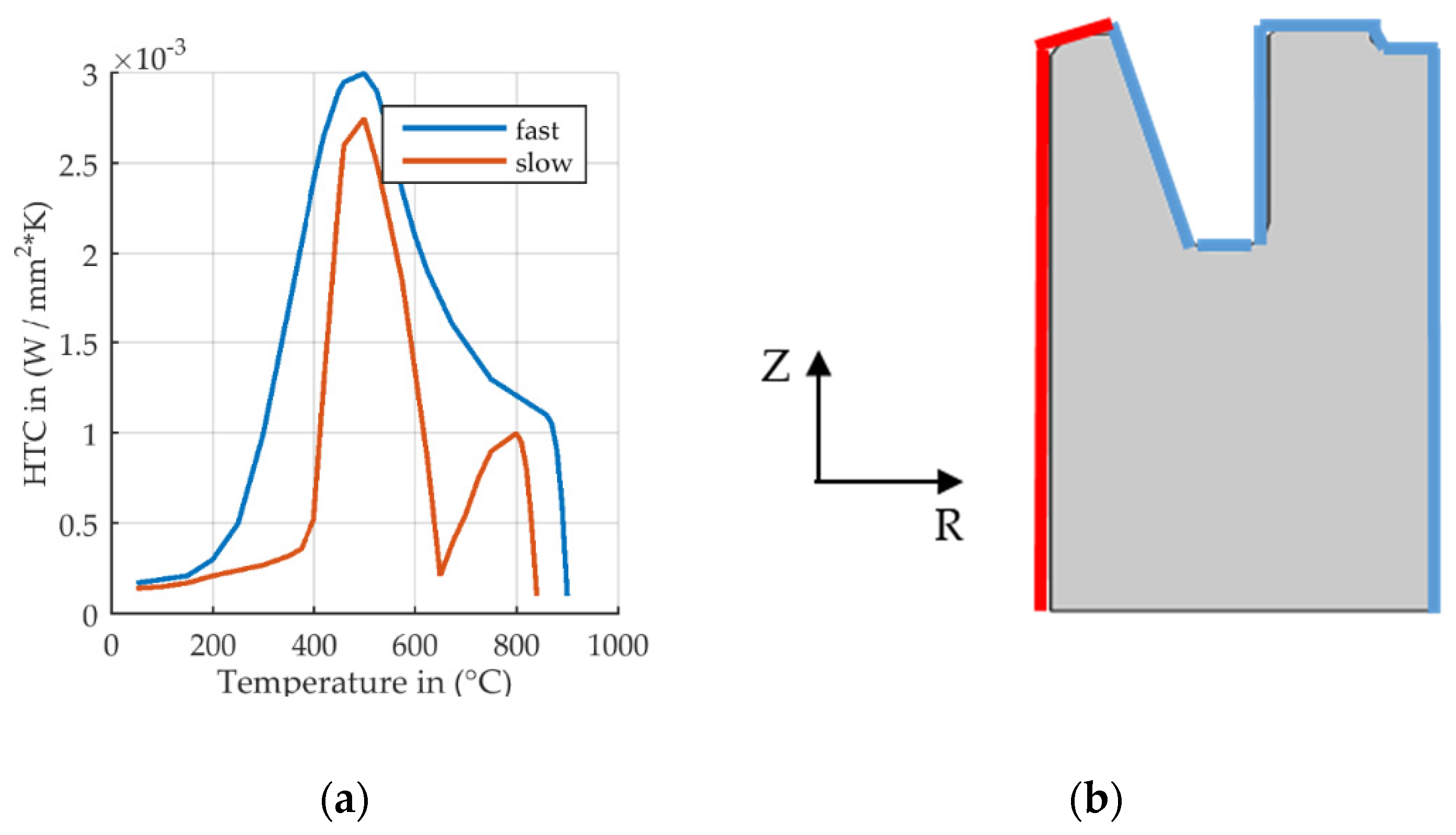
Mechanical boundary conditions consider rotational symmetry about the cylinder axis and mirror symmetry about the height of the gear blank. Thermal boundary conditions depend on the process step: During heating and furnace cooling, a constant Heat Transfer Coefficient (HTC) is applied. During quenching, two different temperature-dependent HTCs are considered, see Figure 4.
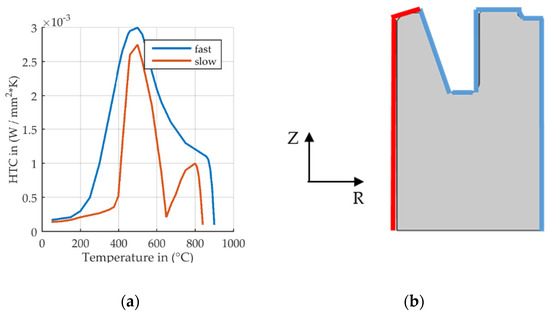
Figure 4.
Heat transfer coefficient for two different flow velocities, slow and fast. (a) Temperature dependent heat transfer coefficient. (b) Model geometry with two windows on the surface for application of two different HTCs.
Approximations for these HTCs have been obtained based on computational fluid dynamics simulations for the oil flow velocity in the fixture. These fluid dynamics simulations and HTC approximations have been carried out by project partners and have been provided to the author. Heat transfer between the part and the tool is not considered in the simulations. The mandrel is not thermally conductive and cooling with the applied HTC takes place, as well as when contact is established. This simplification can be justified by analyzing the global cooling of the part rather than looking at individual contributions that lead to the global cooling. Zero oil flow velocity is assumed to occur on the inner radius, colored red, whereas a higher oil flow is assumed to be present on the outer radius, colored blue. An augmented Lagrangian based surface to surface contact was implemented with separation after contact enabled and hard contact property definitions.
The following initial conditions apply before the first simulated process step. The initial microstructure assumed in the model consists of a mixture of ferrite and pearlite and initial temperature is uniform at 20 °C. Residual stresses are zero everywhere in the model. Conditions at the end of a process step are transferred to the next one.
2.5. Simulated Process Steps
The heat treatment process is simulated in five steps, as shown in Figure 5, with different physical effects contributing to the resulting displacements and distortion after each step.

Figure 5.
Simulated process steps.
Gears are carburized and hardened at typical case hardening temperatures, details for the heat treatment is decribed in [23]. Prior to carburizing the material is austenitized. The main effects during austenitizing are strain due to thermal expansion and phase transformation-related effects such as changes in volume and density as well as transformation plasticity. The next steps are carburizing, followed by furnace cooling with a constant and homogeneous HTC. Furnace cooling is a controlled slow cooling step in order to reach the desired hardening temperature. In the fixture hardening step, quenching with the described HTCs as shown in Figure 4 is simulated. Thermal shrinkage, phase transformations and contact lead to considerable displacements and to distortion. Press out, the final step, takes place at room temperature and leads to the release of elastic energy which can introduce further distortion [5]. The press out step is modeled as a Boolean operation, without applied loads or friction effects. The mandrel elements are instantly deleted which leads to deformations of the part due to a redistribution of stresses and due to the stored elastic energy. This simplified approach is chosen because of a lack of measurement data of the actual press out process.
2.6. Study Parameter
(1) Nine different mandrel radii are evaluated in 2D axisymmetric simulations. The minimum applied radius is 0.1 mm smaller than the nominal one and is modified in 0.05 mm intervals to a maximum of +0.3 mm.
(2) A second focus is the investigation of the simplification of modeling the mandrel as rigid body. Resulting distortion is compared for the fixture hardening process with mandrel as rigid body and the mandrel as a solid part made with elastic plastic properties.
2.7. Numerical Aspects
Numerical convergence studies have been carried out. Mesh element size and solver tolerances for time steps, maximum temperature and strain changes per increment have been tested and optimized. The maximum allowed transformed phase volume per increment was set to two percent. This tolerance controls time and temperature changes per increment. Maximum penetration depth in contact simulations has not exceeded 10−7 mm.
2.8. Model Validation
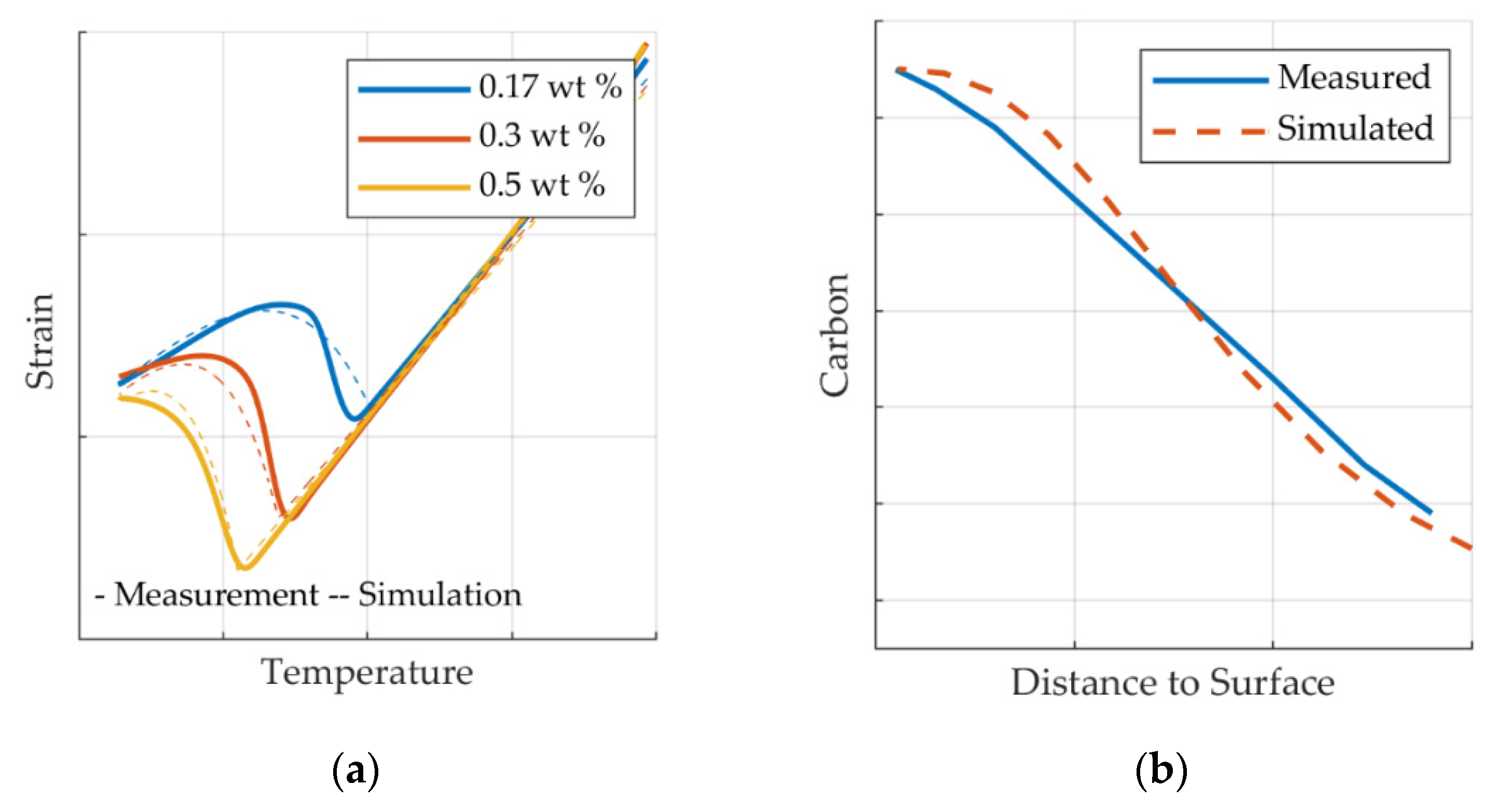
Extensive dilatometer studies as well as heat treatment trials in industry heat treating furnaces have been carried out in preparation of the material data set. Micrographs after each process step have been made to verify the simulated phase volumes. For fitting the phase transformation material parameters dilatometer measurements, retained austenite measurements and carbon profiles have been recorded experimentally. Dilatometer specimens with three different carbon contents, corresponding to the values of the experimental carbon profiles were studied. Transformation kinetics and the transformed phase volumes—martensite and austenite—have been used as a measure of the quality of the simulations. A comparison of numerical results with experimental results shows good agreement as shown in Figure 6.
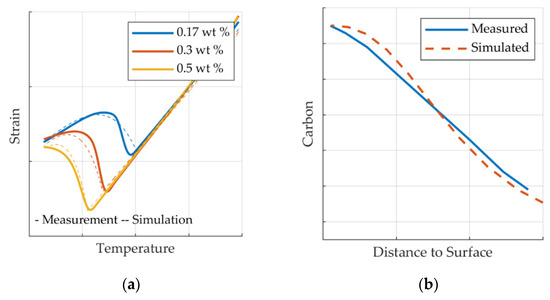
Figure 6.
Validation of material parameters. Comparison of simulated and measured values of dilatometer and carburizing trials. (a) Dilatometry. (b) Carburizing.
Explicit values for strain and for the carbon profile cannot be published due to confidentiality. The displayed expansion of the austenitic phase in the plot on the left shows almost no differences between simulation and experiment. The final strain and thus also the final phase volumes also match well. Differences can be observed for the kinetics of the austenite to martensite transformations. The optimization routine yields these differences because of weighting factors attributed to the transformed volume fraction of phases. With respect to the final distortion, the fitting was focused on thermal expansion of austenite and martensite as well as the transformed volume rather than the kinetics. The simulated carbon profile yields the exact surface carbon content and also yields the correct case depth according to the material specification. Even though the exact profile is not replicated the crucial parameters are correct and the values are within standard industry tolerances.
3. Results
Simulation results are discussed by analyzing cooling curves, contact pressure, and the resulting displacements. The most important output parameter of the present study is cylindricity, which is defined here as the difference between the maximum and minimum displacement in radial direction. Cylindricity is calculated separately for the inner and outer radii.
3.1. Temperature Curves
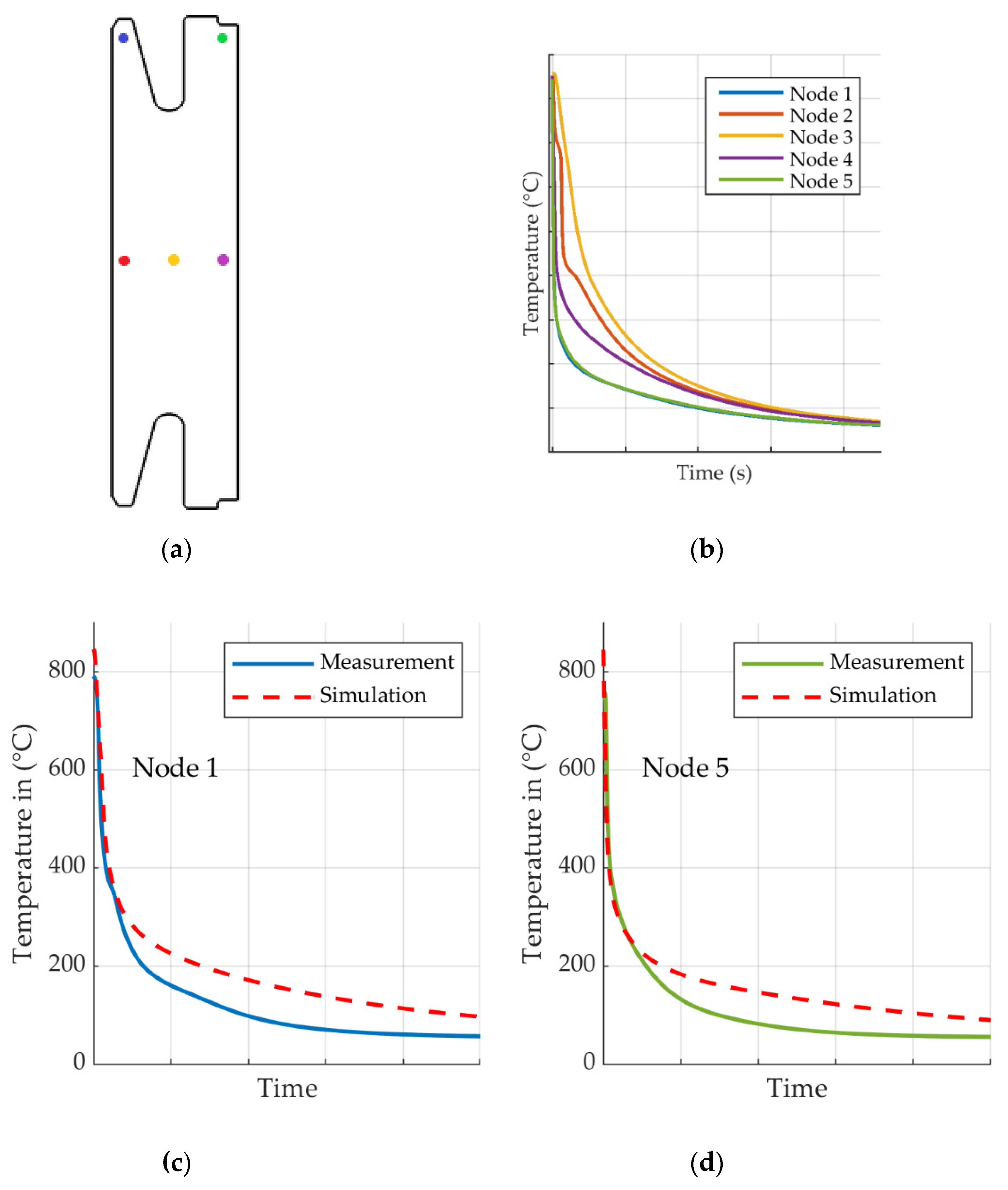
Simulated cooling curves as shown in Figure 7 are evaluated at five different locations with different expected quench rates and cooling characteristics.
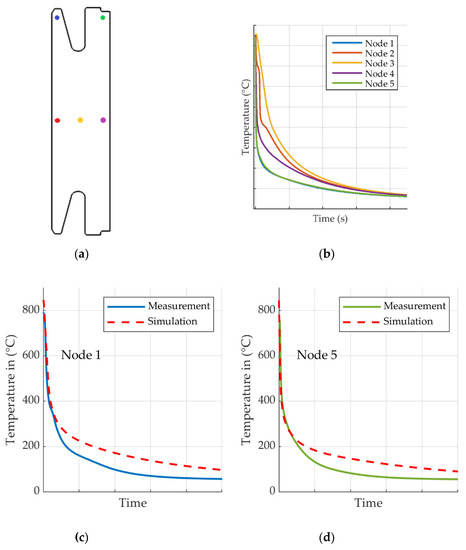
Figure 7.
Simulated cooling curves at five different locations. (a) Thermocouple measurement and simulation evaluation location. (b) Simulated temperature curves. (c) Comparison of simulated and measured temperature curves. (d) Comparison of simulated and measured temperature curves.
The effective temperature curves are dictated by the applied HTCs and by the thickness of the part in each region. Predicted cooling curves can be divided into separate qualitative groups by cooling rate: The fastest cooling occurs in the thinner section of the part with the highest HTC. The thin gear arms—nodes one and five—cool fast and will also most likely start to deform before the gear body starts to deform. On the outside of the massive mid-section, at node four, cooling is slower due to heat flow from the gear body. Cooling on the inner radius, node two, exhibits distinct boiling and convection phases which is related to the HTC for 0 m/s velocity, Figure 4. The massive mid-section of the gear cools faster on the outside and slower on the inside which leads to thermal stresses and subsequently to displacements and possibly to distortion. Figure 7c,d shows a comparison between measured and simulated temperatures. Two nodes in regions with different HTCs, one close to the inner diameter and one close to the outer diameter, are chosen. The initial quenching process with the steepest temperature gradients is replicated with high agreement for both nodes. Starting below 250 °C measurements and simulations start to deviate from each other and a larger error develops.
3.2. Comparison of Measured and Simulated Radial Profile
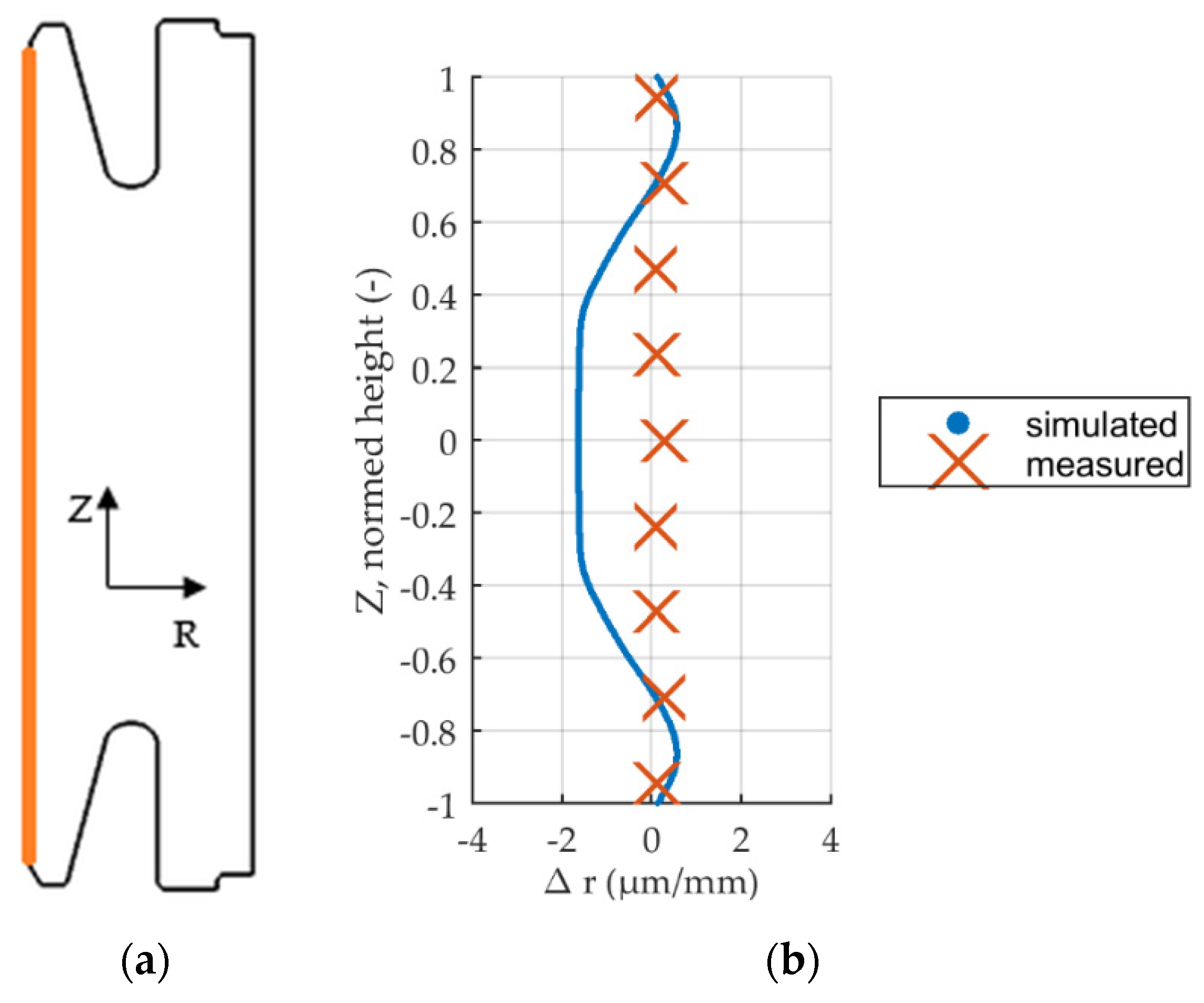
To validate the model and to assess the quality of the tested simulated variations, the simulated radial profile of the inner diameter is compared to measurement data. The radius has been measured by a coordinate measurement machine at nine evenly spaced positions along the height of the gear blank. Measurements have been carried out before and after quenching by the industry partner. Figure 8 shows the relative displacement over height in µm/mm.
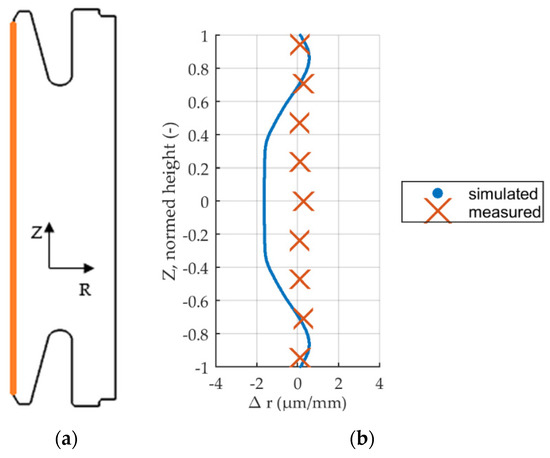
Figure 8.
Relative displacement after press out, nominal mandrel diameter. Comparison of measured and simulated profiles. (a) Measurement location. (b) Comparison of profiles.
The profile comparison yields good agreement between measured and simulated relative radial displacement for top and bottom of the gear blank. The model overpredicts shrinkage in the middle section between normed height [−0.6…0.6]. The characteristic bending towards the inner bore of top and bottom due to the recesses is captured well and agrees with measurement data. For a further comparison, the percentage deviation between measured and simulated profiles is shown in Figure 9.
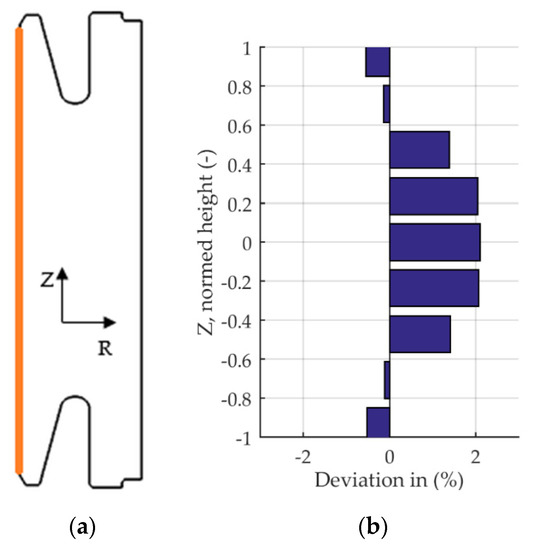
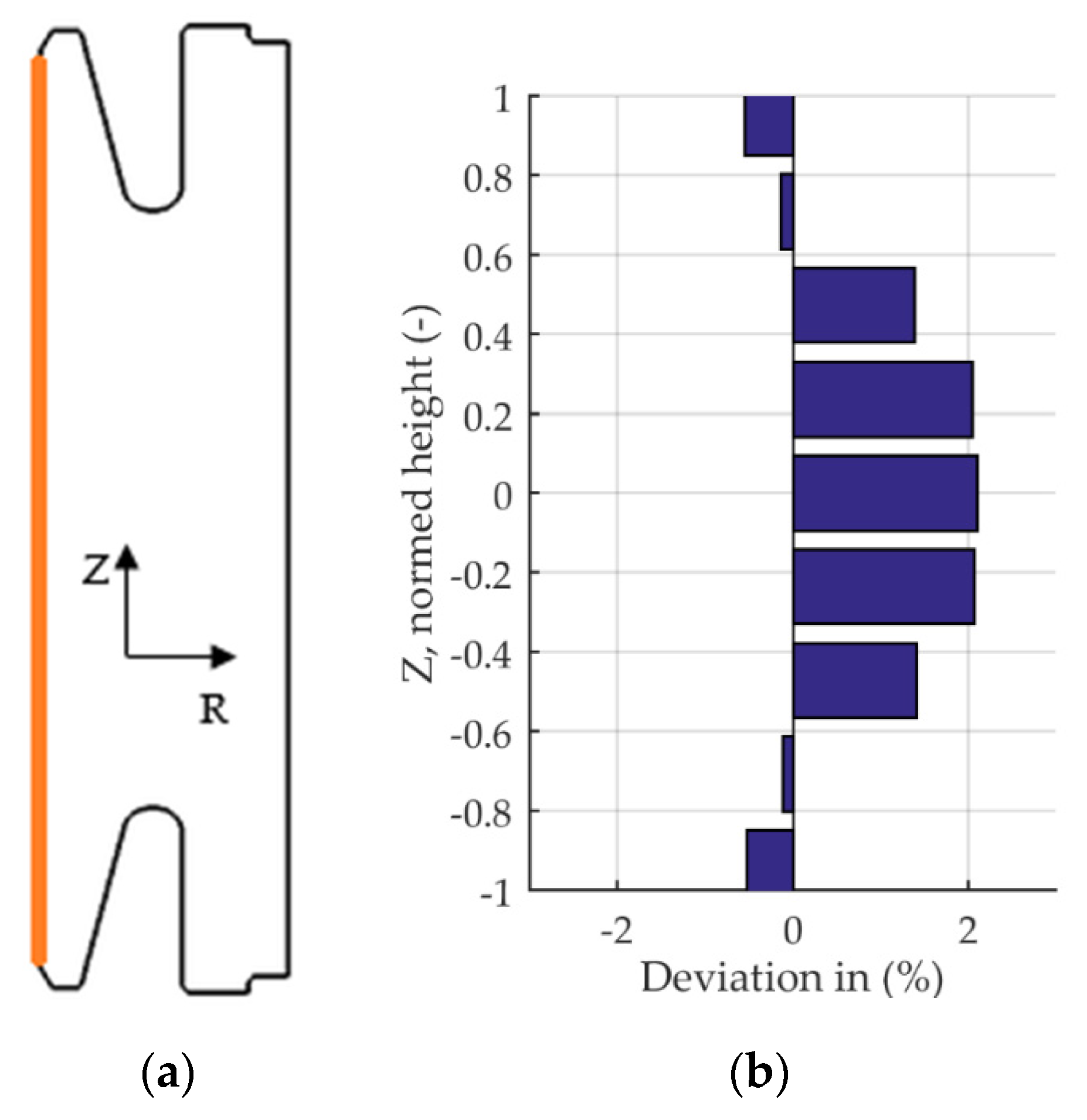
Figure 9.
Percentage deviation of measured and simulated radial displacement at the bore at nine measurement positions. (a) Measurement location. (b) Percentage deviation of displacement.
The largest deviation of 2.1% is present in the middle section along the height. The smallest deviation, 0.1%, can be found just below the top and bottom at the second measurement position respectively. The overprediction of shrinkage in the middle section allows the conclusion that the elastic strain is too large in the model or that the implemented hardening parameters still have errors which lead to a modeled material that does yield sufficient plastic deformation.
3.3. Influence of Mandrel Diameter
Cooling curves in Figure 7 show that the slowest cooling is present in the middle of the gear at node three. Different cooling rates lead to high thermal gradients within the part. Therefore, thermal shrinkage takes place in a nonuniform complex way. Distortion of the part is influenced by three main events: thermal shrinkage, contact with the mandrel, and phase transformations, which lead to volume and density changes. The resulting distortion is discussed in the following section; Figure 10 depicts the gear in austenitized state before quenching starts and in the quenched state, shrank, and in contact with the mandrel.
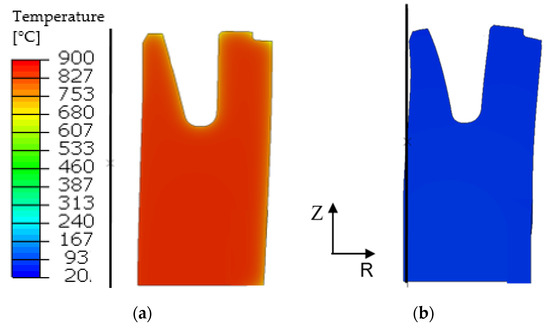
Figure 10.
Deformation scale factor: 15. Surface plots in (a) austenitized and (b) quenched state. The mandrel is a rigid body that does not deform. Figure 8b reveals a gap between the gear blank and the mandrel in the quenched state when in contact.
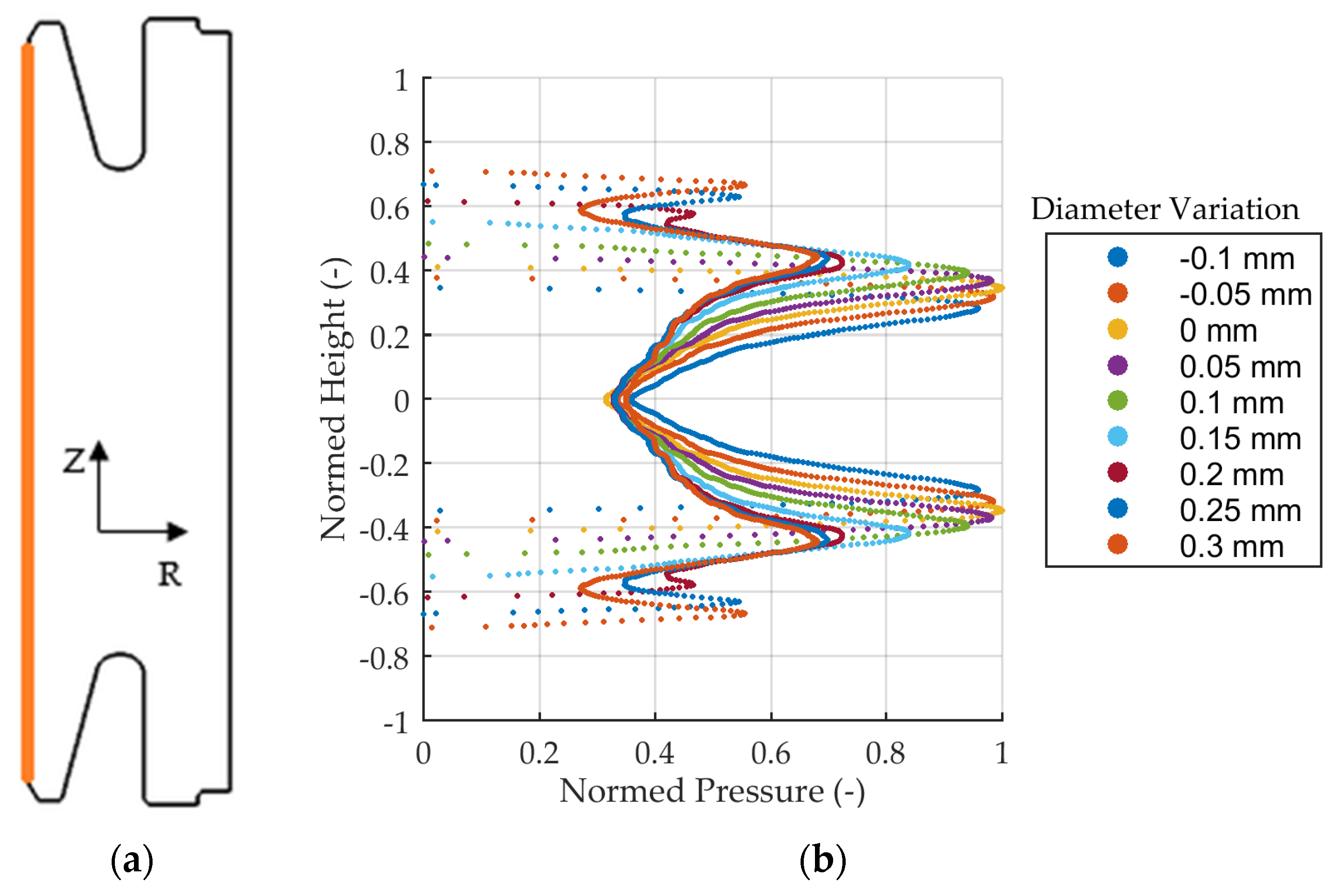
In the austenitized state, see Figure 10a, the model predicts a slight buckling of the gear due to stronger expansion in radial direction of the upper half of the gear where the recess is located. This means that distortion is present when the quenching process starts. In the quenched state, see Figure 10b right image, the model shows the inner of the two arms bending towards the axis of rotation while the outer gear arm bends in the opposite direction, outwards. Shrinkage of the part onto the mandrel is not complete. A gap between gear blank and mandrel is present located in the upper region of the gear length. Contact area between part and mandrel after quenching is a key property influencing cylindricity and the direction of the observed bending of outer and inner radii. Peak pressure and average pressure are important parameters showing the influence and complex resulting shrinkage of the mandrel diameter variation. Contact pressure is linked to strain via residual stresses and thus directly impacts distortion. Figure 11 and Figure 12 show the predicted pressure at the inner radius at the end of the fast quenching process.
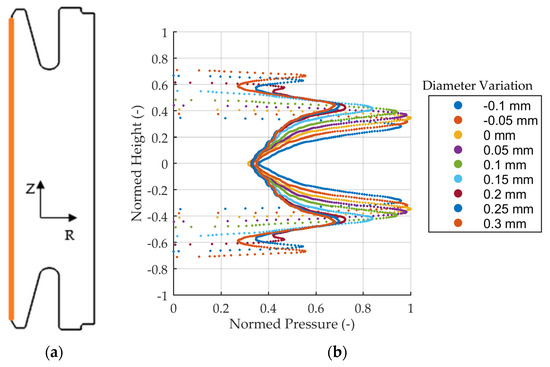
Figure 11.
Pressure over height after quenching, in contact with the mandrel. (a) Measurement location. (b) Pressure over height.
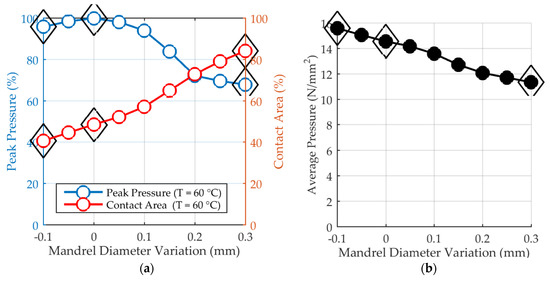
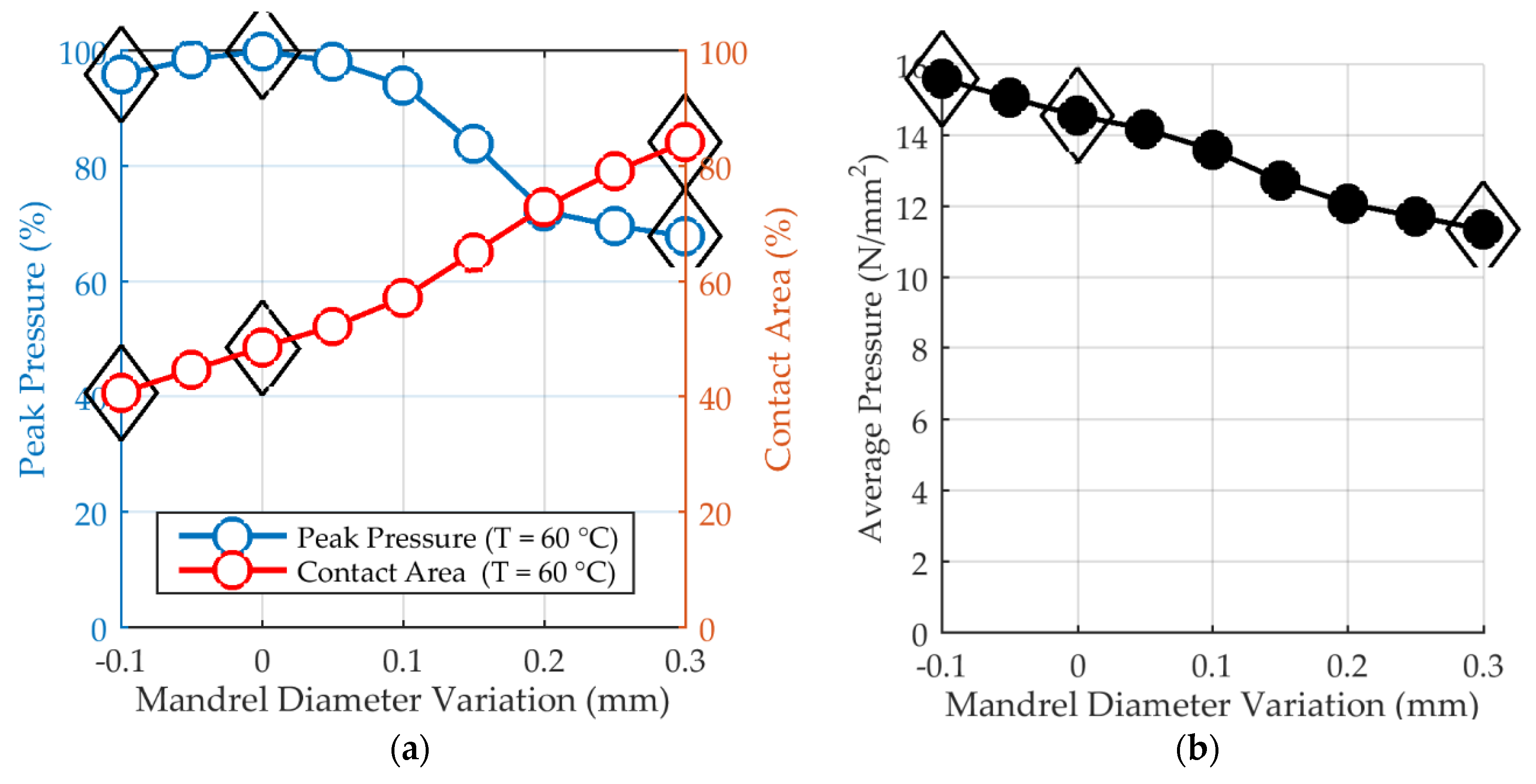
Figure 12.
(a) Peak contact pressure and contact area between part and mandrel indicating incomplete shrinkage of the part onto the mandrel. (b) Average pressure over mandrel diameter variation.
The model reveals two different types of pressure over normalized height curves depending on the mandrel diameter variation: The three largest diameters—Φ +0.2 mm, Φ +0.25 mm, and Φ +0.3 mm—show four peaks: two small ones between height ±0.5 and height ±1 and two larger peaks around the middle. All other diameters only have two pressure peaks. It can also clearly be seen that shrinkage onto the mandrel is not complete and that contact area more than doubles for a 0.3 mm larger diameter mandrel. At the middle of the gear at height zero, the nominal diameter yields the smallest pressure and the smallest diameter yields the largest pressure. In Figure 12a, peak pressure values and contact area show opposite trends. The smallest, nominal, and largest diameters are marked by a diamond. Smaller diameters result in a higher pressure and a smaller contact area. The development of peak pressure though is nonlinear. Highest peak pressure values are calculated for the nominal diameter, whereas the largest diameter yields the smallest peak pressure. Despite smaller contact area, peak pressure for the two smallest diameters, Φ −0.05 mm and Φ −0.1 mm, decreases by 5% and 2%, respectively, compared to the nominal diameter’s peak pressure. For a further analysis, pressure is integrated over height and radius and then averaged by division by the corresponding contact area, see Figure 12b. In spite of the nonlinear development of peak pressure, the average pressure decreases roughly linear with increasing mandrel diameter. Peak pressure and the average force are important for process control since the tool can only exhibit a limited press out force without damaging the gear blank.
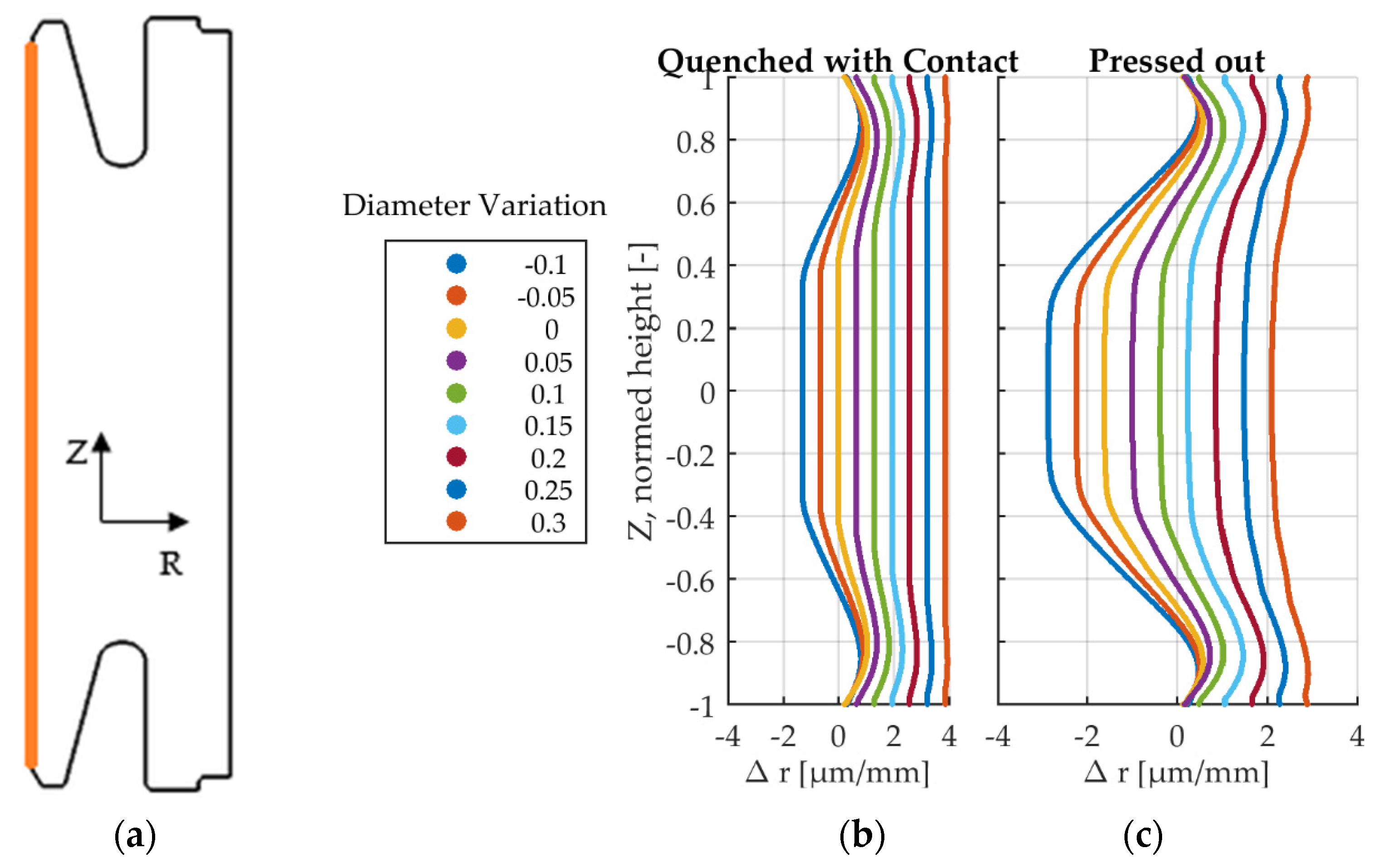
Following the analysis of temperature curves and pressure distribution the resulting deformations of the inner diameter are analyzed. Deformations after fixture hardening and after mandrel removal are presented in Figure 13.
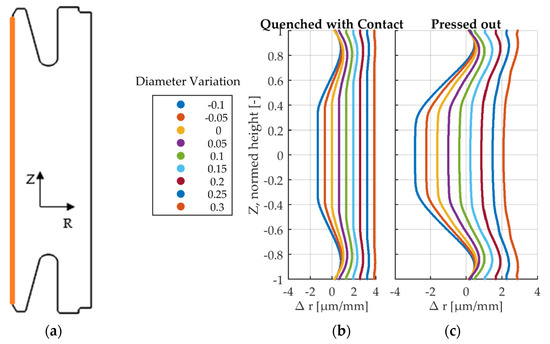
Figure 13.
Relative displacement in µm/mm. (a) Measurement location. (b) Quenched, in contact with mandrel; (c) Pressed out, no contact, release of elastic energy.
The area of the part that has been in contact shows a larger displacement after mandrel removal. With increasing contact area, the resulting shape changes become smaller, see largest diameter Φ +0.3 mm. For the smaller diameters, the contact area does not extend beyond half the nominal height. This results in high peak pressure and consequently in larger deformations due to release of elastic energy after mandrel removal, see Figure 13b, blue and red curves for diameters Φ −0.1 mm and Φ −0.05 mm. Much larger displacements are calculated for diameters Φ −0.1 mm and Φ +0.1 mm than for Φ +0.3 mm. A dimensional change is present for the largest mandrel diameter but the shape change is the smallest. Smaller contact area on the inner radius and high pressures lead to larger influence of elasticity on deformations of the gear blank. Next, the outer diameter is qualitatively examined in Figure 14.
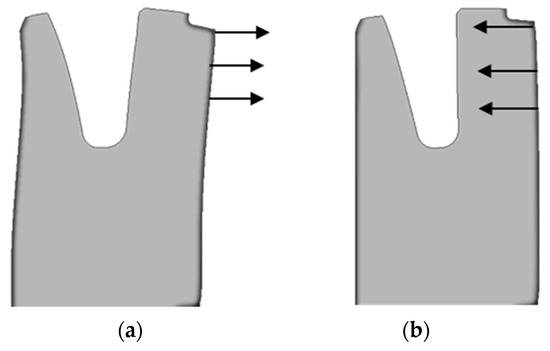
Figure 14.
Displacement scaled by factor 15. (a) Smallest mandrel diameter (−0.1 mm). Quenched state with contact, smallest mandrel diameter yields outward bending of outer radius. (b) Largest mandrel diameter (+0.3 mm). Quenched state with contact, largest mandrel diameter yields inward bending of outer radius.
Two fundamentally different shapes of the outer radius are depicted in Figure 14. The small mandrel shows outward bending while the large mandrel shows inward bending of the outer radius. To avoid small bending effects from the edges of the geometry, the bending is analyzed from a height of 0.4 to 0.9, which is the height where the influence of the recess is strongly in effect. The middle section is not included. The relative displacement is fitted to the following function,
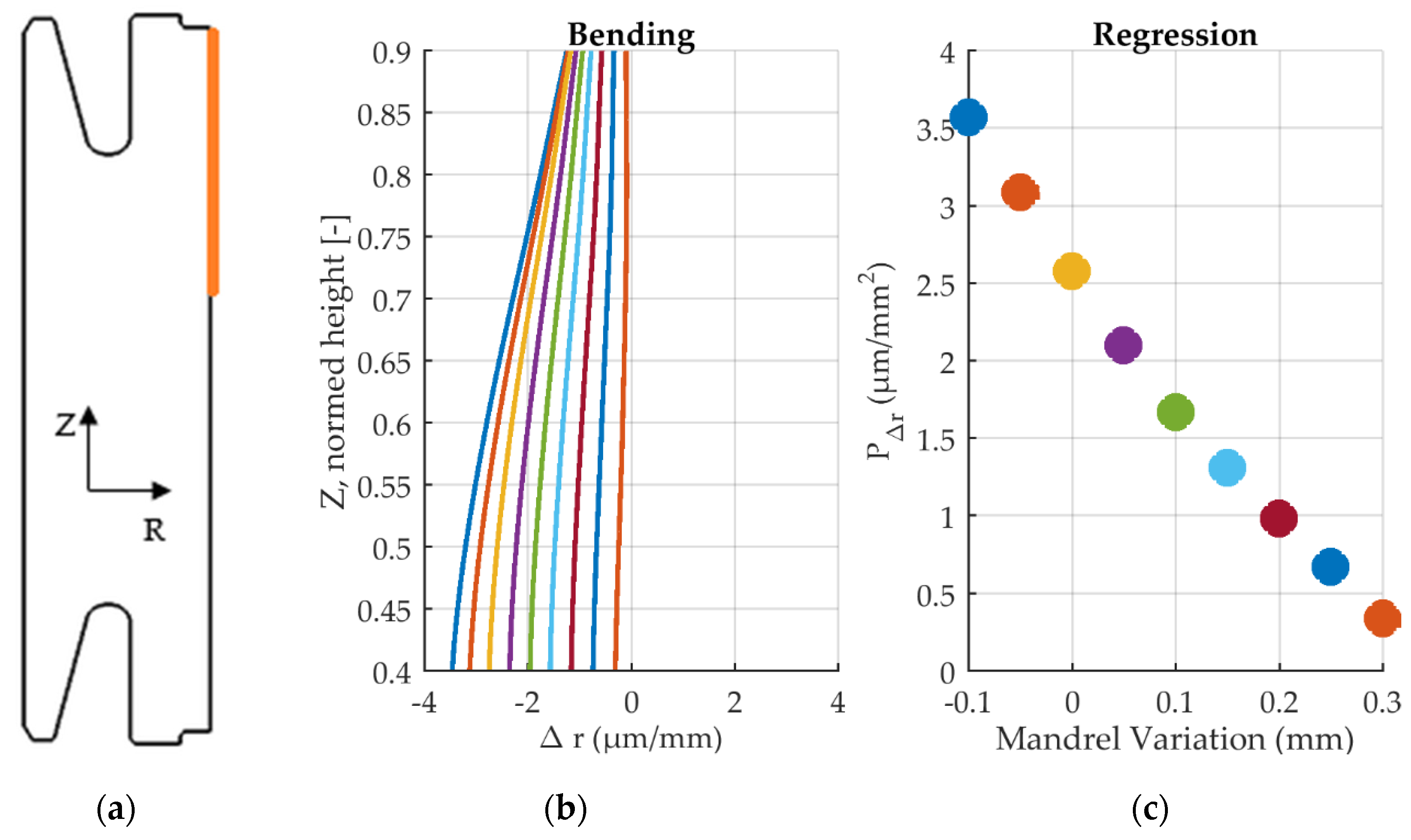
where r0 is the radius at height z equal to zero and coefficient P∆r is the gradient describing the bending depending on height z. The bending direction that is illustrated in Figure 14 is quantified by the coefficient P∆r. The results are plotted over the mandrel diameter variation in Figure 15.
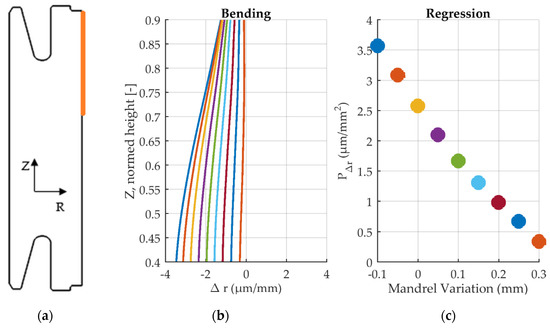
Figure 15.
Bending of outer radius for all mandrel diameter variations in quenched state with contact between part and mandrel. (a) Evaluated area. (b) Bending between height 0.4 and 0.9. (c) Regression coefficients over mandrel diameter variation.
The straightest geometry’s coefficient has a value of zero. Positive coefficients indicate bending away from the axis of rotation and negative coefficients indicate bending towards the axis of rotation. It follows that Φ +0.2 mm, which has the smallest coefficient P∆r, also yields the smallest distortion. This result is valid in the quenched state.
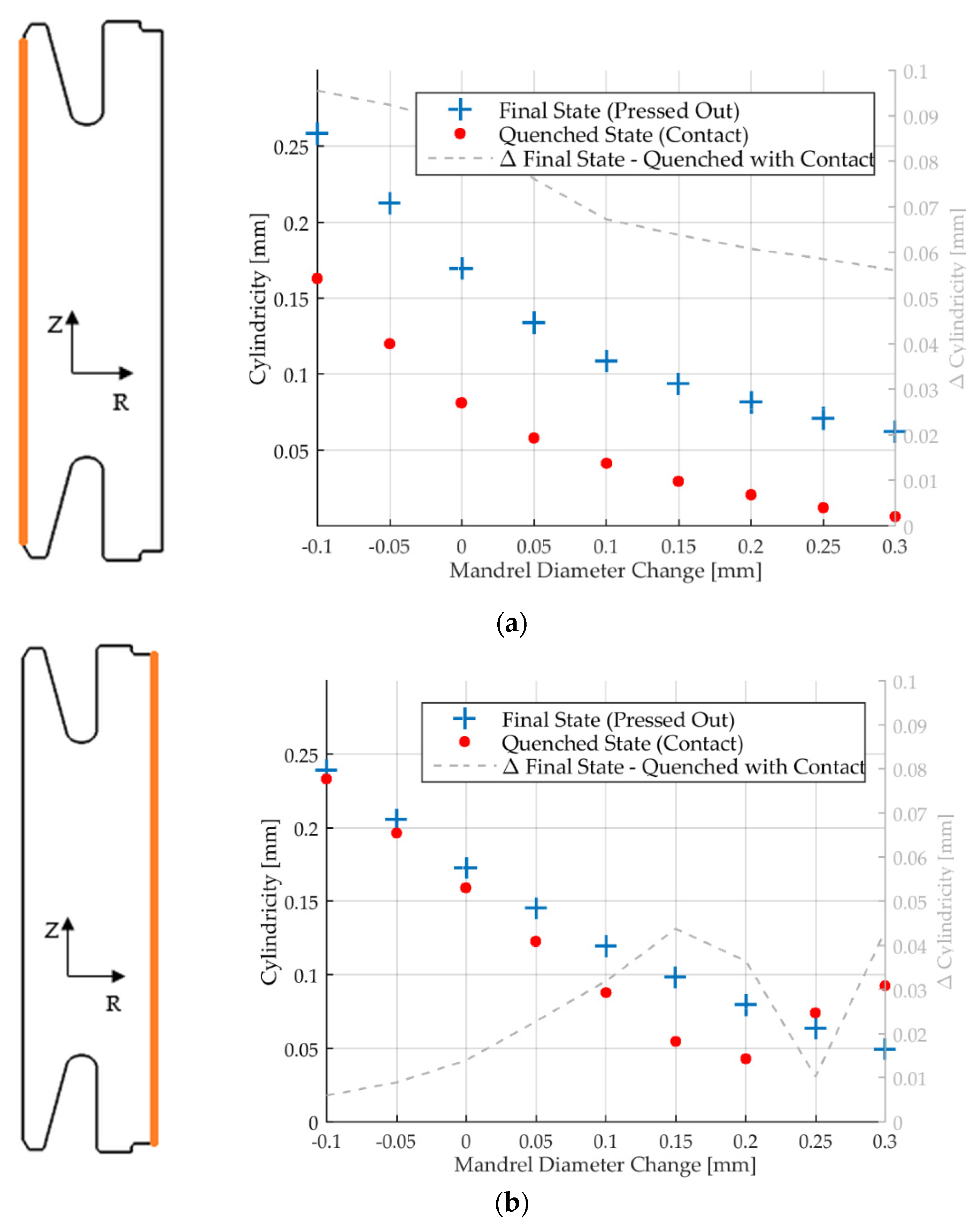
For a further analysis cylindricity in the quenched and pressed out states for inner and outer radius is calculated. Cylindricity in this analysis is defined as the difference between the maximum and minimum displacement, measured on either the inner or outer radius. Figure 16 shows cylindricity for inner and outer radius in the quenched and final states.
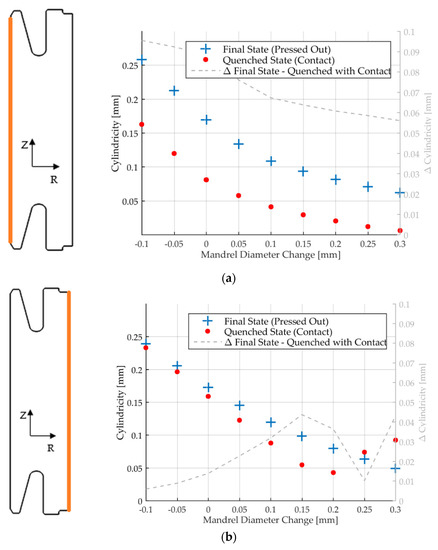
Figure 16.
Model prediction of cylindricity in quenched and final states and difference between the two states. (a) Inner radius. (b) Outer radius.
The smallest mandrel diameter results in the highest cylindricity and the largest mandrel diameter yields the lowest cylindricity, this observation is valid for inner and outer radius in the final state. The dashed curve shows the difference in cylindricity between quenching and mandrel removal. This delta value gives an indication of the amount and relevance of the release of stored elastic energy. A large difference designates a large spring back due to elasticity. A strong nonlinear development of the cylindricity difference for the outer radius can be observed. The maximum difference is present for Φ +0.15 mm. To explain the underlying mechanisms, it is important to understand the role of the mandrel radius and the height of contact on the inner radius. The contact area increases from 40% to nearly 80% with increasing mandrel radius. This seems to induce different bending moments on the outer radius. The zero-crossing of the calculated bending gradient P∆r, see Figure 12 Φ +0.2 mm, indicates the change of the bending direction. A reversal of the inward bending to an outward bending takes place for mandrel diameters larger than Φ +0.2 mm.
However, cylindricity values in the final state, see Figure 16, show that the observed bending directions of the outer radius are not preserved after removal of the part from the fixture. Release of stored elastic energy evens out these effects and the largest mandrel diameter yields the lowest cylindricity.
3.4. Influence of Mandrel Properties
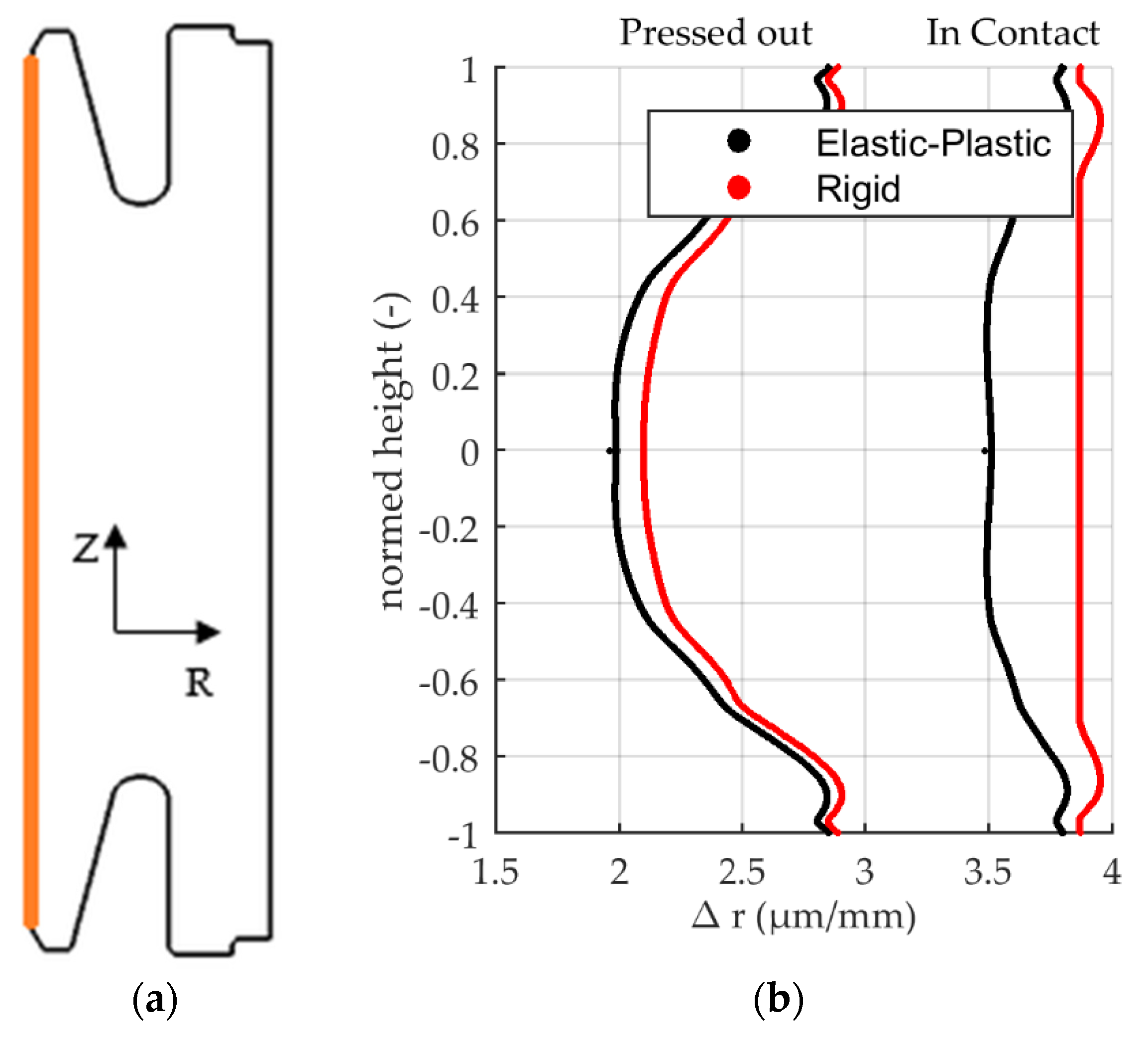
The influence of modeling the mandrel as a rigid body versus modeling the mandrel as an elastic-plastic body is discussed in the following. In industry, the mandrel is commonly hardened but in the present study the non-hardened state was chosen to maximize the effect of elastic deformations of the mandrel. To scrutinize the modeling assumptions regarding plasticity and elasticity of the mandrel, the resulting displacements on the inner radius for the largest mandrel diameter are compared in Figure 17.
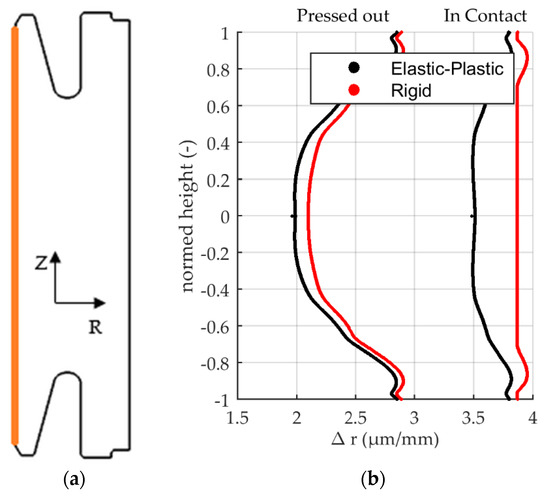
Figure 17.
(a) Analysis location. (b) Relative displacement of the inner radius in µm/mm. Elastic-plastic vs rigid mandrel. Two process steps are shown: (1) Quenched, still in contact with the mandrel. (2) Pressed out after release of elastic energy.
Model results show that the mandrel’s displacement is elastic only. After mandrel removal the mandrel returns to its original shape. Elasticity of the mandrel leads to larger shrinkage in both states, quenched and in the final state. The difference in shrinkage in the final stage is as small as 0.1 µm/mm. The shape of the inner radius in quenched state differs from the rigid model to the elastic-plastic model: For the elastic-plastic model, a very slight “w” shape is present around zero mm nominal height (black curve). In this region shrinkage is smaller. The rigid model yields a perfectly flat inner radius where the part is in contact with the mandrel. When removing the mandrel these differences in the quenched state are leveled and only a dimensional change remains.
4. Summary and Conclusions
A parametric study of a fixture hardening process was successfully implemented in a 2D axisymmetric FEM framework. Material parameters have been experimentally determined and verified. The mandrel diameter of a fixture hardening tool was varied and the influence on distortion was analyzed. Cylindricity and bending was quantified in the analysis.
The applied HTCs in connection with the geometry, especially the recess, lead to thermal gradients and nonuniform shrinkage of the part. Nonuniform shrinkage leads to incomplete contact with the mandrel. The upper and lower parts of the gear blank are not in contact with the mandrel. The size of the area which is in contact with the mandrel has a significant influence on the developing peak contact pressure and average force. Contact area or shrinkage onto the mandrel is identified as a key influence on cylindricity as well. On the outer radius different bending directions occur depending on the mandrel size. Methodological tests concerning elasticity of the mandrel show that the mandrel can be modeled as rigid. By doing so, only small dimensional changes are neglected that do not diminish the quality of the calculated displacements.
Simplifications, e.g., concerning the modeled process steps, the heat transfer and the chosen geometry still require validation by measurement results. Important parameters and effects during press out, which are currently not modeled, are the applied load and the resulting friction, which leads to a transformation of mechanical energy into heat [24]. This step is time dependent and influences surface temperature and stresses and results in elastic and possibly plastic deformations. The influence and the sensitivity of these effects on the resulting displacements, however, cannot be measured in the real process which makes determination of modeling parameters and validation data difficult. It is planned to model the press out step more realistically with a variation of friction coefficients for lubricated steel from literature.
Differences between the measured and the simulated temperature profiles are relatively large for temperature regions below 250 °C. Above 250 °C, the simulated temperature matches the measured one well. To evaluate the influence of these observed deviations on the predicted displacements, the development of the process at this time has to be analyzed. For the bulk material with a base carbon content of 0.17 wt. %, the austenite to martensite transformation is finished when the temperature error becomes larger. Contact of the part and the mandrel is well established by this time as well. After the transformation for most of the material is finished and contact is established mostly uniform shrinkage due to thermal expansion will occur. Thus, it can be concluded that the introduced error by an underestimated HTC possibly leads to quantitative differences but not a qualitative one.
Regarding the implemented material data some differences between simulated and measurement data, as shown in Figure 6, exist. The simulated carbon profile lies within the tolerances given in the specification for the modeled part therefore this deviation does not introduce an error but rather represents a typical variation that would also be encountered in a production environment. The calculated dilatometer curves show a difference in the transformation kinetics. This difference possibly introduces an error in the calculated displacements. The sensitivity of the final distortion to the transformation kinetics have not been the subject of this study.
This parametric study serves the purpose of demonstrating modeling capabilities, identifying areas where improvements of the modeling strategy are necessary, and gaining fundamental qualitative knowledge about the real fixture hardening process. To the best of the authors’ knowledge, no systematic approaches dealing with the setup of the optimal mandrel diameter in a fixture hardening process can be found in the scientific literature. It was the aim of this study to analyze the complex nonlinear quenching process and to better explain effects and dependencies that lead to the resulting distortion. The present paper delivers an in depth explanation of the influence of the mandrel diameter on displacement. Ongoing work involves the experimental validation of the calculated final displacements and refinement of applied boundary conditions and process steps. A conclusion of the present study is that an increased mandrel radius yields lower cylindricity. In theory a mandrel that is too large requires very high press out forces that might damage the part.
5. Concluding Remarks
(1) The present study shows that within the tested range, the largest mandrel diameter also yields the lowest contact pressure and lowest force per area. These results allow the conclusion that an optimal mandrel diameter exists which yields low distortion and low peak pressure at the same time.
(2) The final press out step is modeled in a simplified manner without considering loads or friction. This simplification introduces a systematic error that remains to be quantified.
(3) Future research should expand the modeling domain from 2D to 3D to capture effects of fixture hardening on the outer diameter and especially on the teeth of the gear.
Author Contributions
Conceptualization, H.B. and T.L.; Funding acquisition, H.B.; Investigation, H.B. and B.T.; Methodology, H.B. and T.L.; Supervision, T.L.; Validation, H.B.; Writing—original draft, H.B.; Writing—review & editing, T.L. and B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry for Economic Affairs and Energy (BMWi) and Aerospace Transmission Technologies (ATT) within the research program “Luftfahrtforschungsprogramm” (LuFo), grant reference number 20T1505.
Acknowledgments
The authors would like to thank Hector Pous Romero and Christopher Watson (Rolls Royce) for insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Reardon, A. Press Quenching. In ASM Handbook, Steel Heat Treating Fundamentals and Processes; Dossett, J., Totten, G., Eds.; ASM International: Material park, OH, USA, 2013; Volume 4a. [Google Scholar]
- Boyer, H.E.; Archambault, P.; Moreaux, F. Techniques of Quenching. In Quenching Theory and Technology; Lišcic, B.E.A., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 486–507. [Google Scholar]
- Zhang, Y.; Wang, G.; Shi, W.; Yang, L.; Li, Z. Optimization of Process Parameters for the Axial Distortion and Distortion Range During Die Quenching of a Spiral Bevel Gear. J. Mater. Eng. Perform. 2018, 27, 3803–3811. [Google Scholar] [CrossRef]
- Gur, H.; Pan, J. Handbook of Thermal Process Modeling Steels; CRC Press: Boston, MA, USA, 2001. [Google Scholar]
- Lübben, T. Basics of Distortion and Stress Generation during Heat Treatment. In ASM Handbook Steel Heat Treating Technologies; Dosset, J., Totten, G.E., Eds.; ASM International: Material park, OH, USA, 2014; Volume 48, pp. 339–354. [Google Scholar]
- Streng, T.; Heeß, K.; Lübben, T. Dimensionally and geometrically accurate quenching of ringshaped components in fully-automated hardening presses. In Proceedings of the 19th ASM Heat Treating Society Conference, Cincinatti, OH, USA, 1–4 November 1999. [Google Scholar]
- Birkhofer, H.; Flach, H.; Lübben, T. Optimizing Mandrel Dimensions for a Fixture Hardening Process by Finite-Element-Simulation. In Proceedings of the International Conference on Quenching and Distortion Engineering, Nagoya, Japan, 24–27 November 2018. [Google Scholar]
- Simsir, C. Modeling and Simulation of Steel Heat Treatment—Prediction of Microstructure, Distortion, Residual Stresses, and Cracking. In ASM Handbook, Steal Heat Treating Technologies; Dossett, J., Totten, G.E., Eds.; ASM International: Material park, OH, USA, 2014; Volume 4b, pp. 409–466. [Google Scholar]
- Simsir, C.; Hunkel, M.; Luetjens, J.; Rentsch, R. Process-chain simulation for prediction of the distortion of case-hardened gear blanks. Mater. Werkst. 2012, 43, 163–170. [Google Scholar] [CrossRef]
- Schicchi, D.; Caggiano, A.; Lübben, T.; Hunkel, M.; Hoffmann, F. On the mesoscale fracture initiation criterion of heterogeneous steels during quenching. Mater. Perform. Charact. 2017, 1, 80–104. [Google Scholar] [CrossRef]
- Simsir, C.; Gür, H.C. A FEM based framework for simulation of thermal treatments: Application to steel quenching. Comput. Mater. Sci. 2008, 44, 588–600. [Google Scholar] [CrossRef]
- Avrami, M.A. Kinetics of phase change II, transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Johnson, W.A.; Mehl, R.F. Reaction kinetics in process of nucleation and growth. Trans. AIME 1939, 135, 416–458. [Google Scholar]
- Leblond, J.B.; Devaux, J.; Devaux, J.C. Mathematical modelling of transformation plasticity in steels I: Case of ideal-plastic phases. Int. J. Plast. 1989, 5, 551–572. [Google Scholar] [CrossRef]
- Koistinen, R.; Marburger, D. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels. Acta Metall. 1959, 7, 59. [Google Scholar] [CrossRef]
- Chen, W.F.; Han, D.J. Plasticity for Structural Engineers; Springer: New York, NY, USA, 1988. [Google Scholar]
- Jablonka, A.; Harste, K.; Schwerdtfeger, K. Thermomechanical properties of iron and iron-carbon alloys: Density and thermal contraction. Steel Res. Int. 1991, 62, 24–33. [Google Scholar] [CrossRef]
- Wolff, M.; Böhm, M.; Dalgic, M.; Hüßler, I. Evaluation of models for TRIP and stress-dependent transformation behaviour for the martensitic transformation of the steel 100Cr6. Comput. Mater. Sci. 2008, 43, 108–114. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee For Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Van Bohemen, S.M. Bainite and martensite start temperature calculated with exponential carbon dependence. Mater. Sci. Technol. 2012, 28, 487–495. [Google Scholar] [CrossRef]
- Franc, R. Numerische Untersuchung des Einflusses von Faserverlauf und Abschreckbedingungen auf das Verzugsverhalten von Scheiben. Diploma Thesis, Universität Bremen, Bremen, Germany, 2012. [Google Scholar]
- Hunkel, M.; Kagathara, J.; Prahl, U. The Influence of Segregations after Forming on the Heat Treatment Result of Bevel Gears. Steel Res. Int. 2019, 90, 1800427. [Google Scholar] [CrossRef]
- Easton, D.; Aylott, C.; Shaw, B.; Rahimi, S. Residual Stresses in Case Hardened Steel Gears. In American Gear Manufacturers Association; Trans Tech Publications Ltd.: Alexandria, VA, USA, 2018. [Google Scholar]
- Kennedy, F.E. Frictional Heating and Contact Temperatures. In Modern Tribology Handbook; Bhushan, B., Ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).