Development of a Mass and Energy Balance Model and Its Application for HBI Charged EAFs
Abstract
1. Introduction
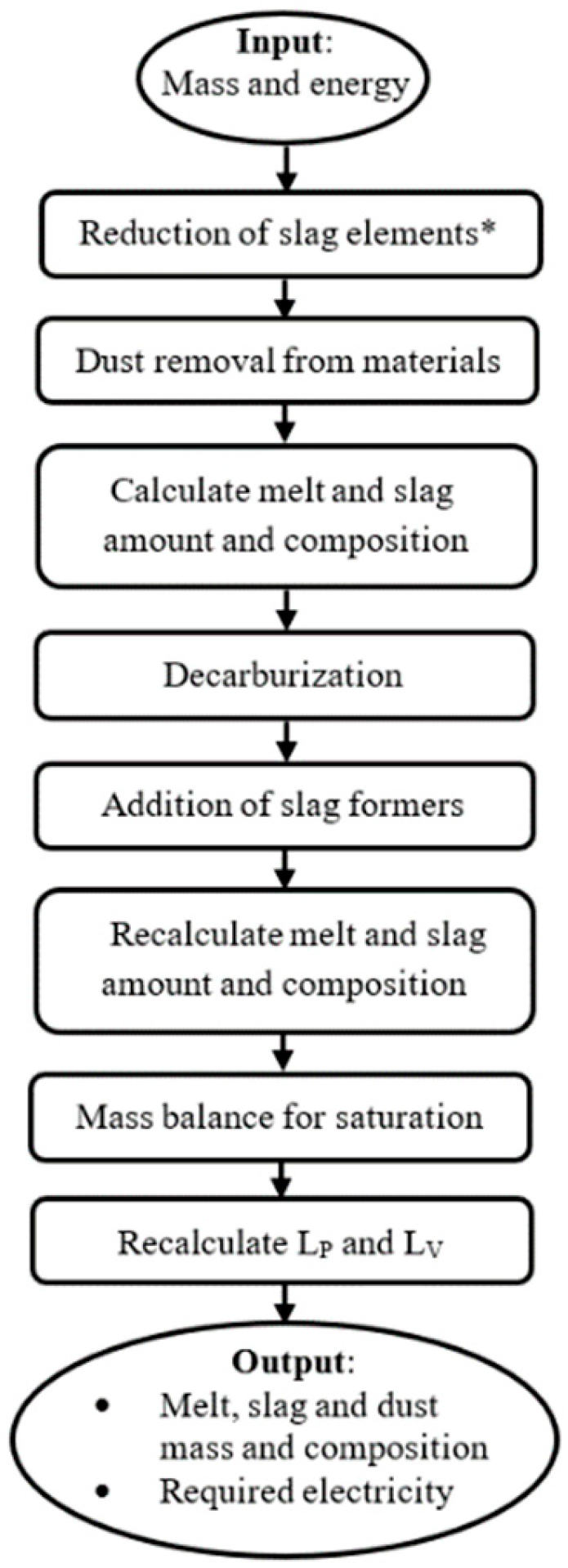
2. Model Development
3. Model Description
3.1. Mass Balance
- Raw materials, which include different types of scraps, DRI/HBIs, and carbon powders
- Hot heel
- Slag formers, consisting of lime and dolomite
- Refractory components, which can be dissolved into slag
- Oxygen injected through lances and consumed during the metal oxidation, decarburization, powder carbon oxidation, fuel combustion in burners and post-combustion
- Fuel additions through the burners
- Molten steel
- Molten slag, which can also, possibly, contain solid MgO components
- Hot heel
- Dust components in metal oxide forms
- Gas, which can consist of CO, CO2, and N2.
3.1.1. Reactions
- Oxidation of metallic elements present in steel that goes into the slag, which has the following general form for element X:
- Reduction of iron, manganese, chromium, phosphorus and vanadium oxides (XO):
3.1.2. Metal and Slag Composition
3.1.3. Dust
3.2. Energy Balance
- Enthalpy of charged material, , which is described as follows:where is the enthalpy of formation of component i at temperature 298 K and is the enthalpy of mixing. Furthermore, is the mole number of component i in the charged material, which is a mixture of scraps, DRI/HBI, slag formers, refractory and also hot heel which can be left from a previous heat.
- Electricity,
- Energy of fuel combustion in burners,
- Energy of oxidation powder carbon,
- Energy of cementite formation in DRI, , which is calculated as follows:
- Enthalpy of molten steel at the tapping temperature,
- Enthalpy of molten slag at the tapping temperature,
3.3. Slag Model
4. Model Calibration and Validation
4.1. Furnace Data
4.2. Calibration
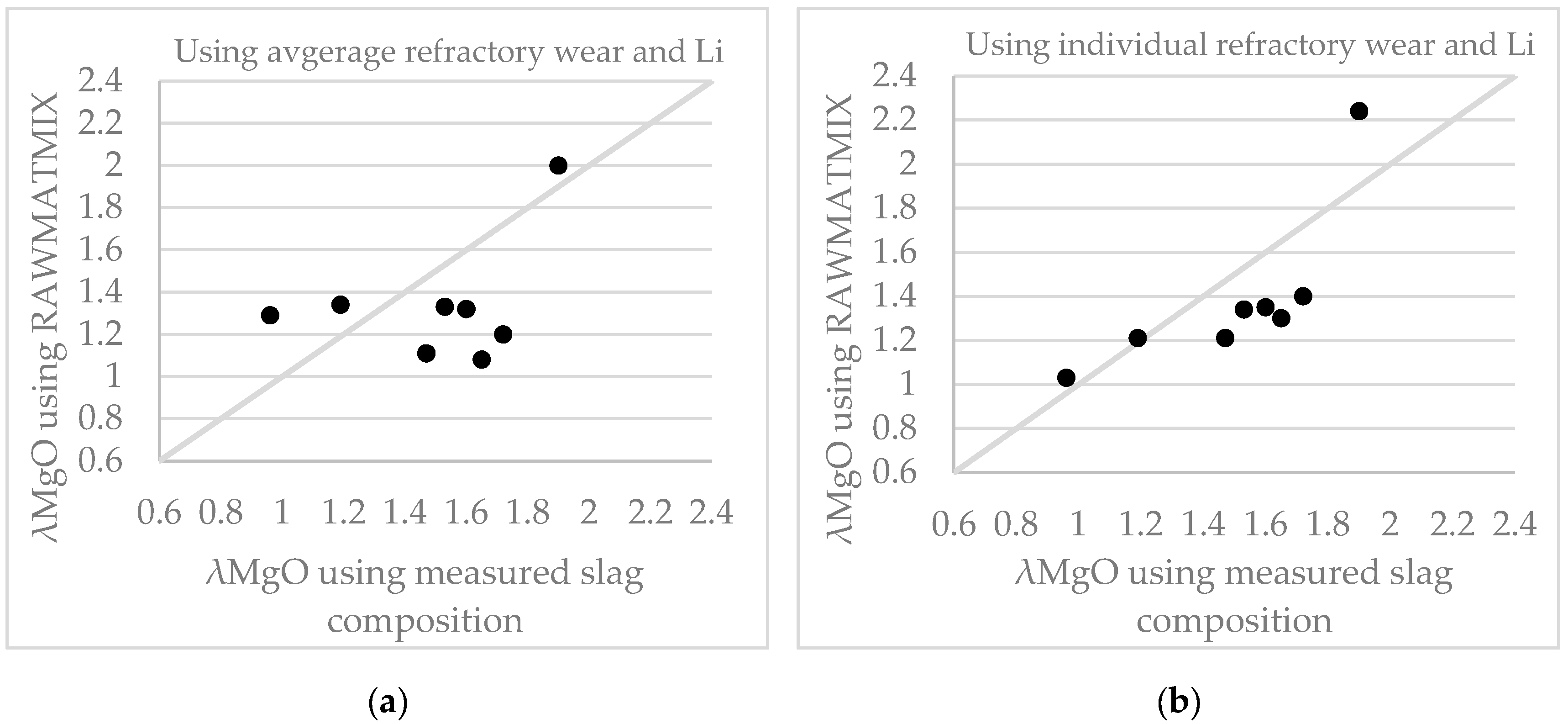
4.2.1. Slag Composition
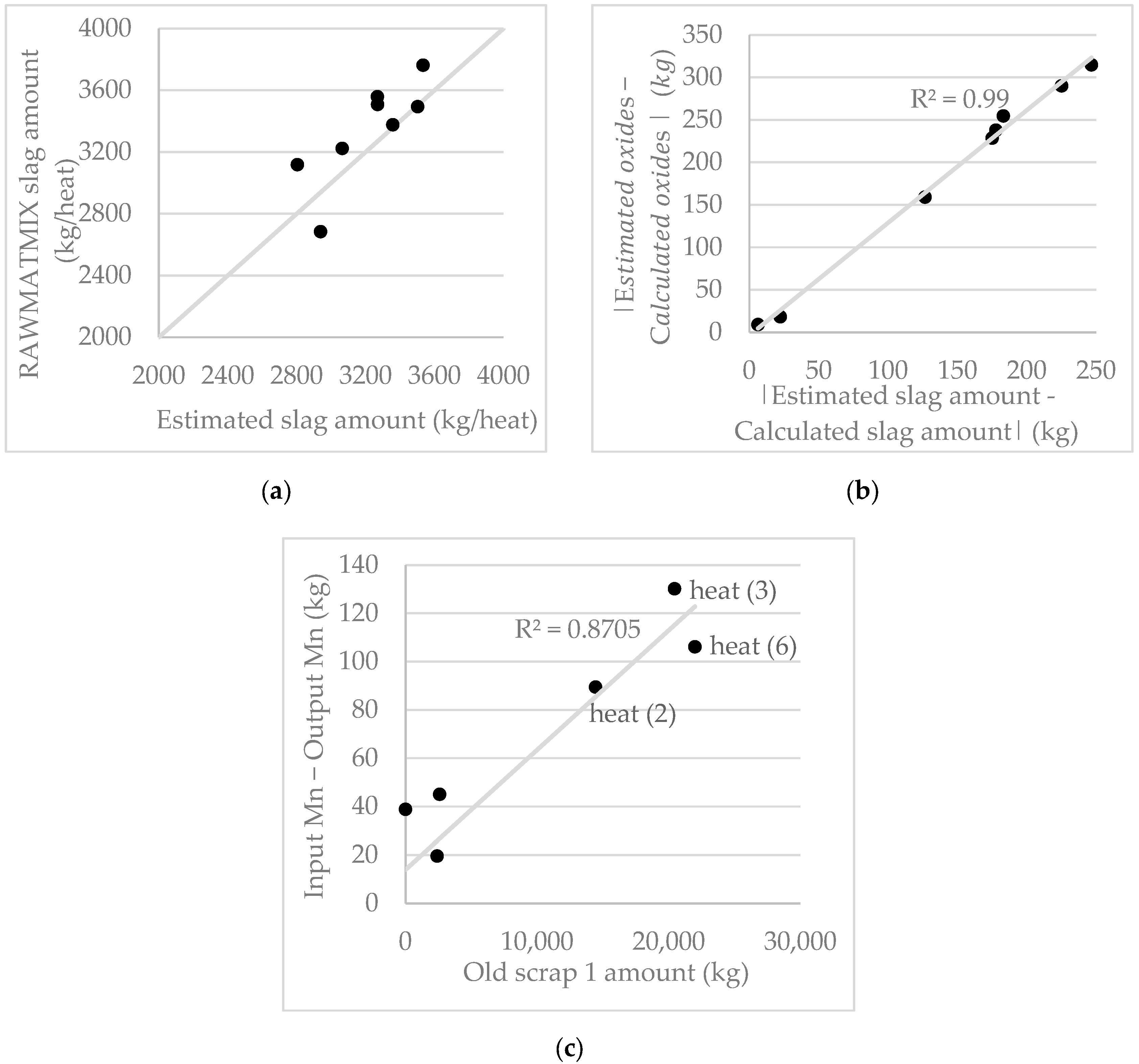
4.2.2. Slag Mass
4.2.3. Metal Composition
4.2.4. Distribution Ratios
4.2.5. Dust Calculation
4.2.6. Other Estimations
5. Model Application
6. Results and Discussion
6.1. Calibration Results
6.1.1. Slag
6.1.2. Dust
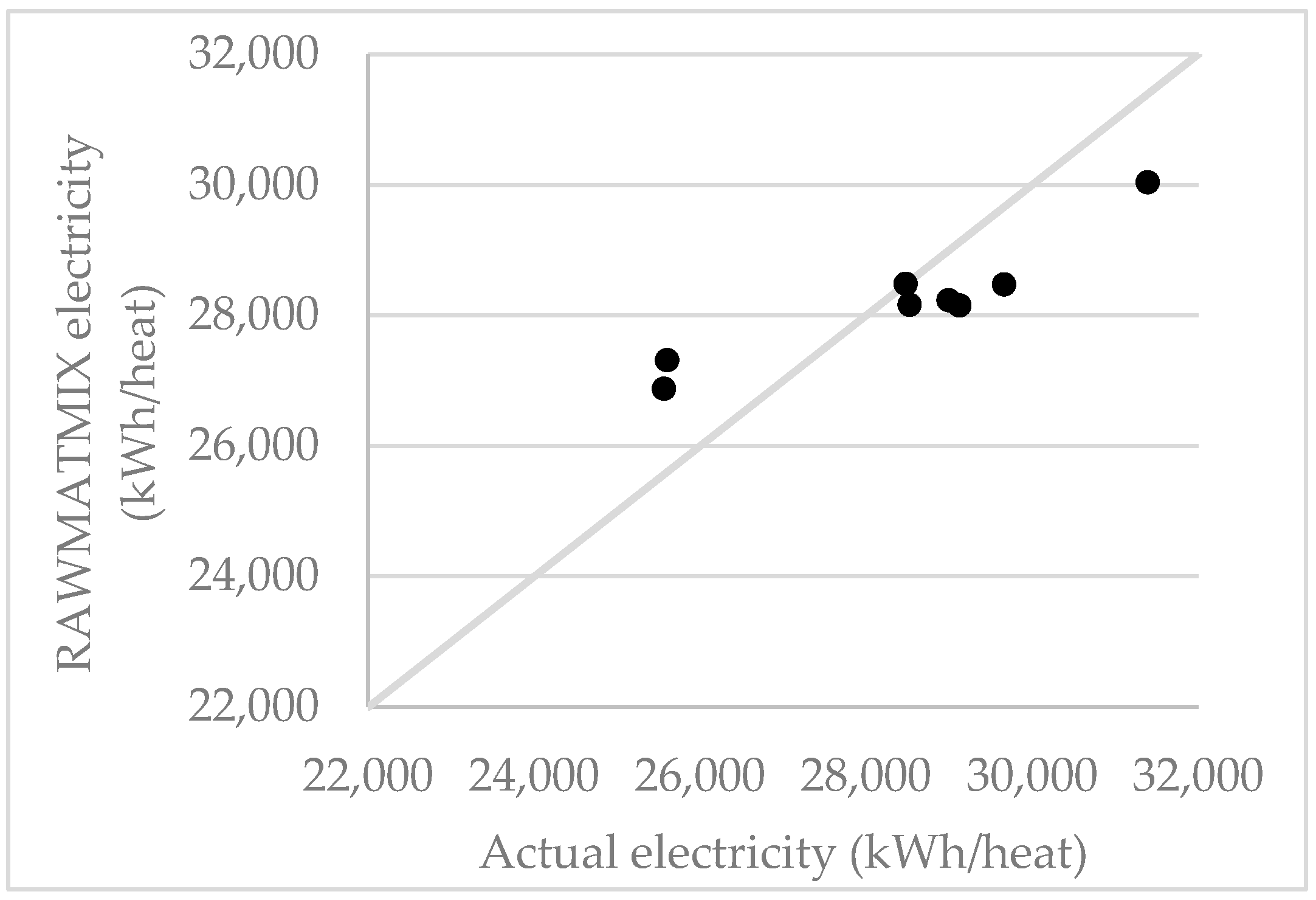
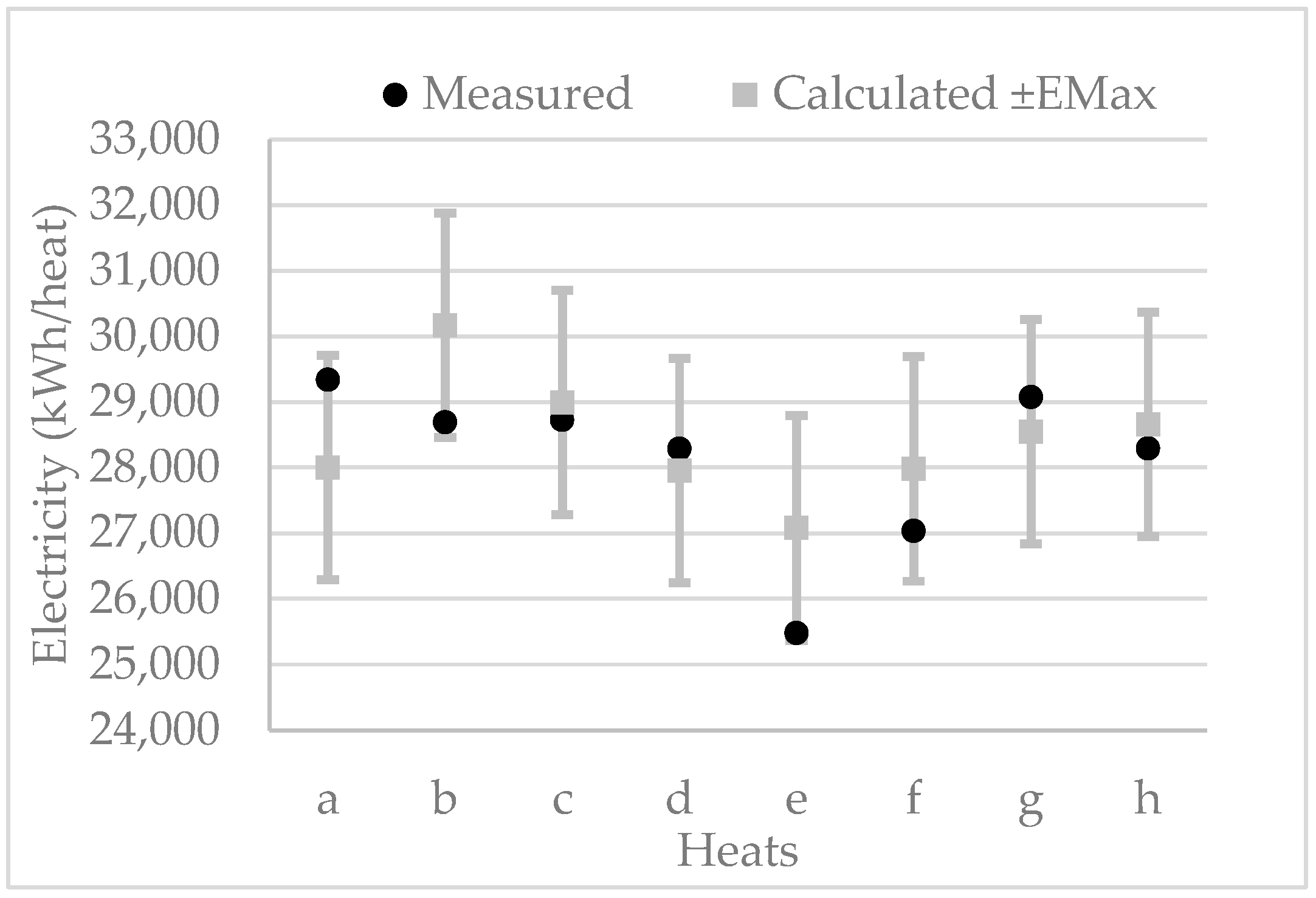
6.1.3. Electricity
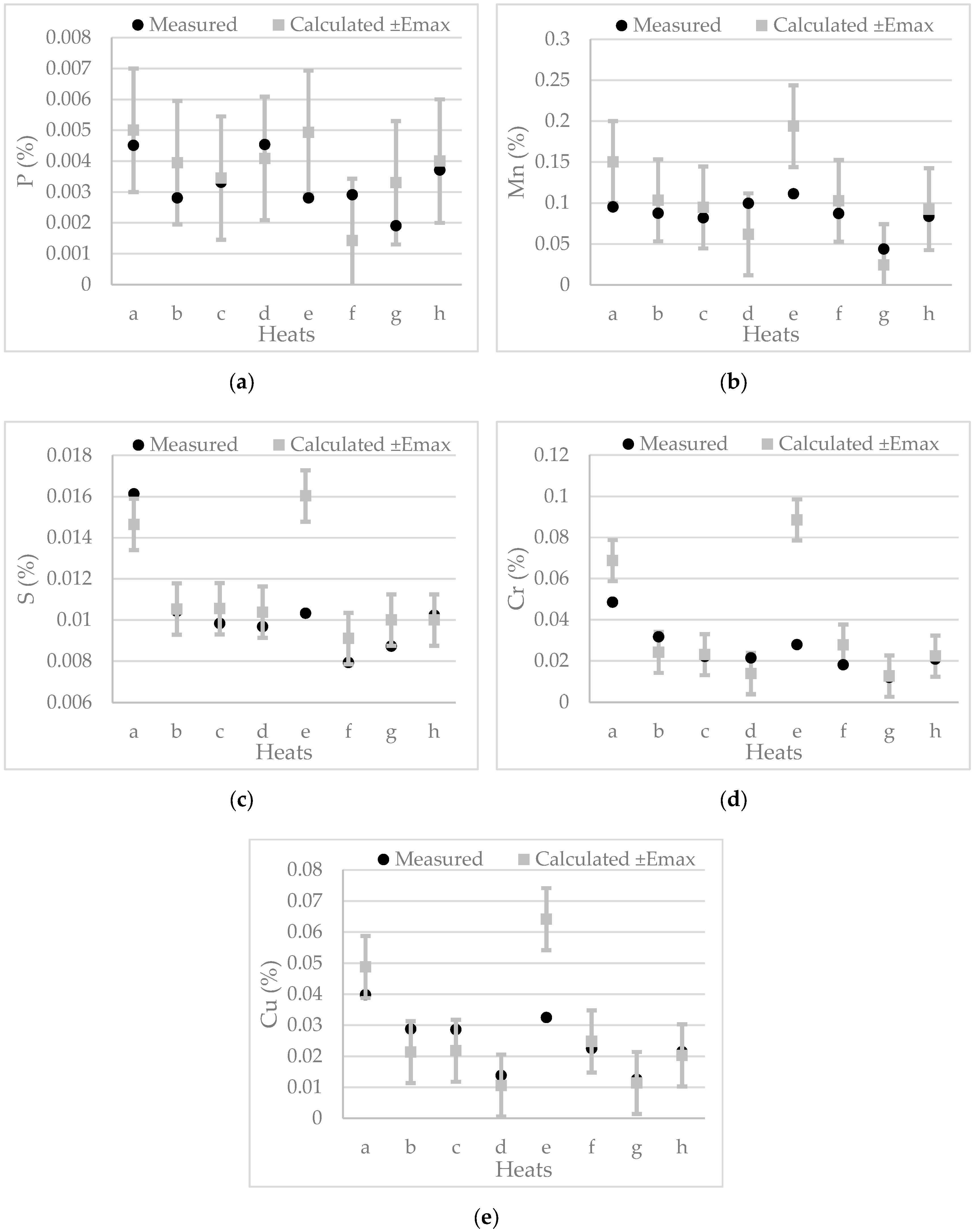
6.1.4. Melt Composition
6.2. Validation Results
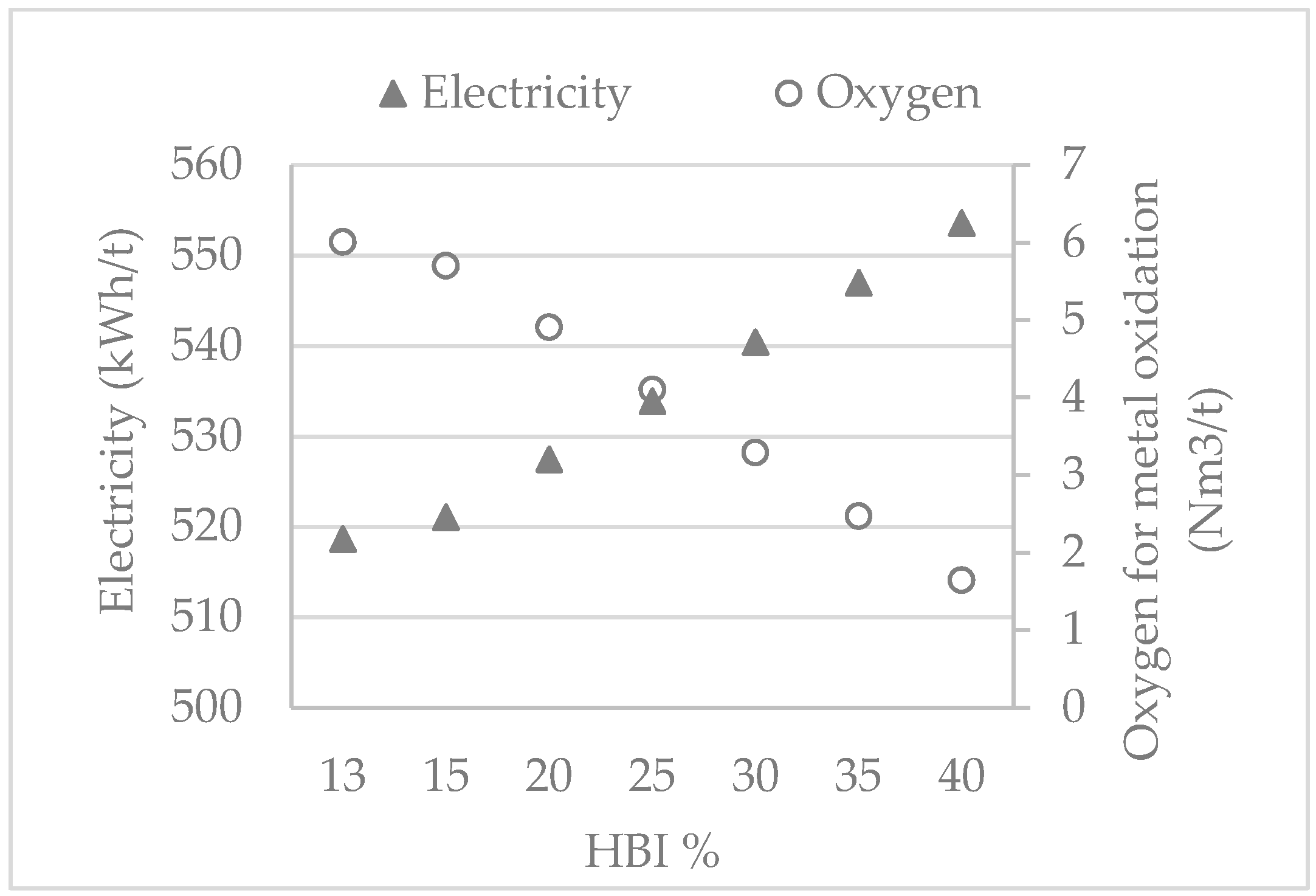
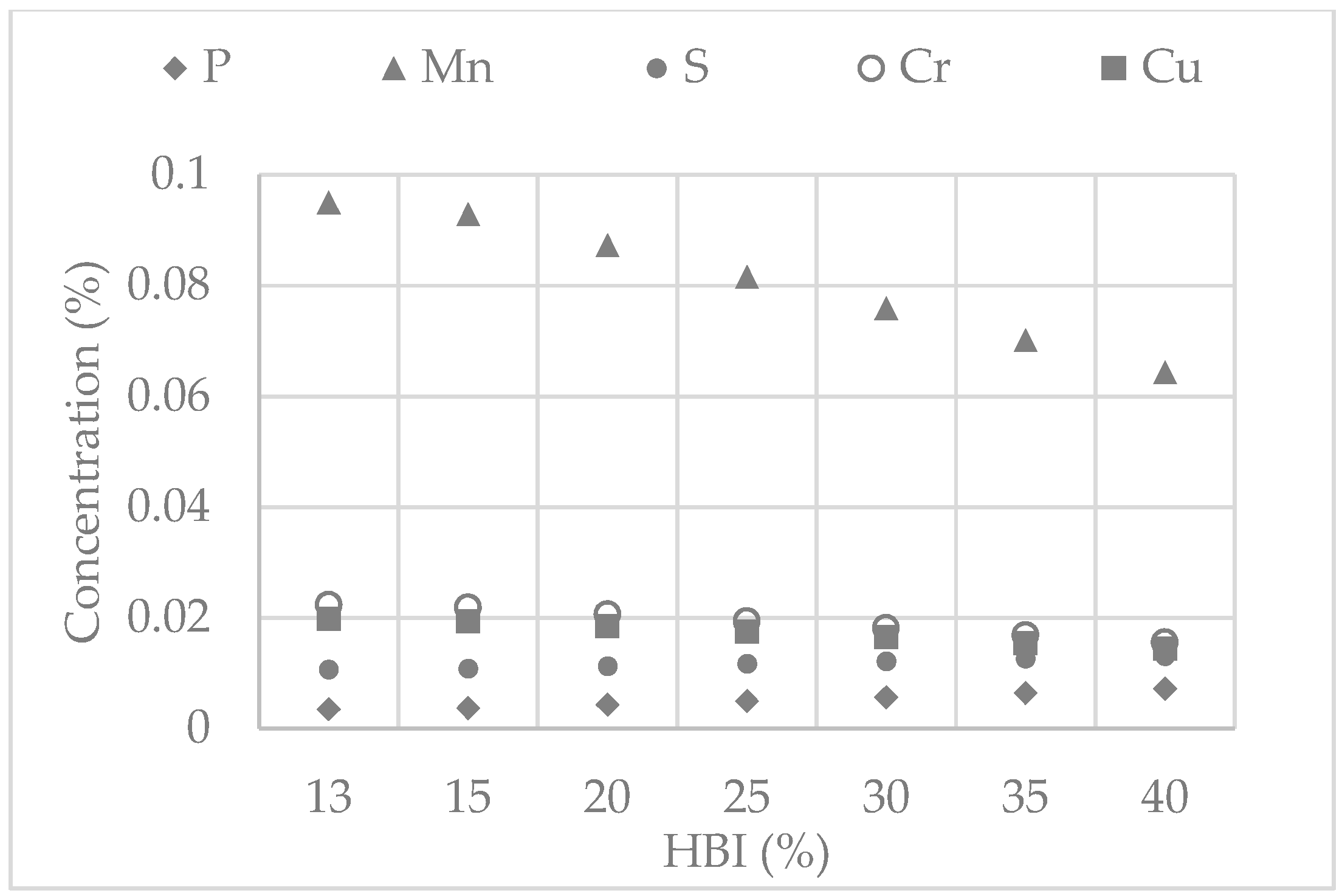
6.3. Model Application Results
Adjustment of Slag Formers
7. Conclusions
- an increased electricity demand of 1.29 kWh/t
- a decreased amount of 0.16 Nm3/t of oxygen for metal oxidation
- an increased amount of slag by 34 kg
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Element | Molar Mass (g/mol) | H298 (kJ/mol) | H1700 (kJ/mol) | Hmix (kJ/mol) | Cp1700 (J/mol) | Cp298 (J/mol) |
|---|---|---|---|---|---|---|
| C | 12.01 | 0.00 | 28.03 | 22.59 | 24.40 | 8.53 |
| Si | 28.09 | 0.00 | 86.67 | −131.50 | 27.22 | 20 |
| Mn | 54.94 | 0.00 | 73.24 | 4.08 | 46.06 | 26.3 |
| P | 30.97 | 71.90 | 97.35 | −122.17 | 18.85 | 23.84 |
| S | 32.06 | 64.38 | 89.93 | −135.06 | 18.83 | 22.6 |
| Cr | 52.00 | 0.00 | 46.55 | 19.25 | 47.15 | 23.3 |
| Ni | 58.69 | 0.00 | 63.83 | −20.92 | 43.13 | 26.1 |
| Mo | 95.94 | 0.00 | 39.87 | 27.61 | 35.12 | 24.1 |
| Ti | 47.87 | 0.00 | 46.54 | −31.13 | 25.69 | 25 |
| Cu | 63.55 | 0.00 | 53.34 | 33.47 | 31.41 | 24.43 |
| V | 50.94 | 0.00 | 65.38 | −42.26 | 41.88 | 24.9 |
| Fe | 55.85 | 0.00 | 67.98 | 0.00 | 46.06 | 25.1 |
| Element | Mol Mass (g/mol) | H298 (kJ/mol) | H1700 (kJ/mol) | Cp1700 (J/mol) | Cp298 (J/mol) |
|---|---|---|---|---|---|
| SiO2 | 60.09 | −909.13 | −814.07 | 73.96 | 73.96 |
| Al2O3 | 101.96 | −1676.72 | −1507.73 | 136.74 | 136.73 |
| FeO | 71.85 | −261.01 | −160.23 | 68.20 | 68.2 |
| MnO | 70.94 | −385.26 | −309.68 | 61.65 | 61.65 |
| CaO | 56.08 | −634.84 | −560.81 | 58.07 | 58.07 |
| MgO | 40.30 | −601.76 | −531.80 | 54.68 | 54.68 |
| P2O5 | 141.94 | −1506.24 | −1247.71 | 162.50 | 162.5 |
| VO2 | 181.88 | −1559.05 | −1242.72 | 190.95 | 74.68 |
| TiO2 | 79.90 | −945.56 | −844.20 | 84.23 | 84.23 |
| Cr2O3 | 151.97 | −1130.65 | −954.60 | 67.53 | 67.52 |
| NiO | 74.70 | −240.79 | −162.14 | 62.90 | 62.9 |
| Heat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| HBI | 6900 | 6700 | 7300 | 8500 | 0 | 6950 | 6600 | 6700 |
| Pig Iron 1 | 1100 | 1050 | 1600 | 1250 | 0 | 1200 | 1000 | 1550 |
| Pig Iron 2 | 3050 | 3450 | 3700 | 3150 | 0 | 3350 | 3400 | 3300 |
| Old scrap 1 | 2400 | 14,450 | 20,450 | 1150 | 0 | 22,000 | 0 | 2600 |
| Old scrap 2 | 0 | 6900 | 10,100 | 0 | 0 | 11,000 | 0 | 0 |
| Old scrap 3 | 3250 | 0 | 0 | 4450 | 0 | 0 | 3950 | 3350 |
| New scrap 1 | 12,400 | 9300 | 0 | 10,100 | 18,600 | 0 | 12,400 | 8150 |
| New scrap 2 | 12,400 | 11,250 | 1350 | 10,150 | 12,100 | 0 | 10,500 | 9850 |
| New scrap 3 | 11,200 | 0 | 0 | 9450 | 18,800 | 0 | 12,850 | 13,950 |
| Return 1 | 0 | 4250 | 6750 | 3650 | 0 | 2500 | 1500 | 2550 |
| Return 2 | 0 | 0 | 0 | 0 | 3000 | 0 | 0 | 0 |
| Sculls | 0 | 0 | 0 | 0 | 0 | 1850 | 0 | 0 |
| Return 3 | 0 | 0 | 2050 | 1500 | 0 | 3300 | 0 | 0 |
| Hot heel type | 1 | - | 2 | 1 | 3 | 2 | 1 | 1 |
| Coke | 870 | 794 | 799 | 725 | 806 | 799 | 718 | 722 |
| Lime | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| Dolomite | 650 | 650 | 600 | 700 | 600 | 800 | 500 | 600 |
| Heat | a | b | c | d | e | f | g | h |
| HBI | 7200 | 8300 | 8800 | 9300 | 6400 | 0 | 10,250 | 6750 |
| Pig Iron 1 | 900 | 1000 | 1000 | 1800 | 800 | 0 | 3000 | 1200 |
| Pig Iron 2 | 2950 | 2900 | 2700 | 3950 | 3300 | 0 | 4250 | 3100 |
| Old scrap 1 | 17,500 | 2050 | 2450 | 0 | 23,450 | 2100 | 0 | 2150 |
| Old scrap 2 | 6450 | 0 | 0 | 0 | 11,500 | 0 | 0 | 0 |
| Old scrap 3 | 0 | 4900 | 4500 | 0 | 0 | 3500 | 0 | 3350 |
| New scrap 1 | 5350 | 9600 | 9300 | 12,450 | 0 | 8400 | 0 | 9100 |
| New scrap 2 | 3100 | 11,400 | 12,450 | 10,650 | 0 | 23,100 | 32,550 | 10,500 |
| New scrap 3 | 0 | 12,450 | 9950 | 10,850 | 0 | 13,300 | 0 | 13,100 |
| Return 1 | 8750 | 3550 | 2050 | 0 | 3300 | 1550 | 2350 | 2700 |
| Return 2 | 0 | 0 | 0 | 1700 | 0 | 0 | 0 | 0 |
| Sculls | 950 | 0 | 0 | 1950 | 2200 | 0 | 0 | 0 |
| Return 3 | 0 | 1900 | 1150 | 0 | 1500 | 0 | 0 | 0 |
| hot heel | 5000 | 0 | 5000 | 5000 | 5000 | 5000 | 5000 | 5000 |
| Hot heel type | 2 | 2 | 1 | 3 | 3 | 1 | 1 | 1 |
| Coke | 799 | 794 | 724 | 800 | 797 | 723 | 719 | 723 |
| Lime | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| Dolomite | 750 | 600 | 600 | 550 | 550 | 700 | 600 | 600 |
| Input Material | Fe | FeO | Si | Pb | As | C | Sn | Ca | Ti | Cu | Mo |
| HBI | 83.964 | 9 | 0.005 | 0 | 0 | 1 | 0 | 0 | 0 | 0.0014 | 0 |
| Pig Iron 1 | 95.007 | 0 | 0.15 | 0 | 0 | 4.25 | 0 | 0 | 0.005 | 0 | 0 |
| Pig Iron 2 | 94.157 | 0 | 1 | 0 | 0 | 4.25 | 0 | 0 | 0.005 | 0 | 0 |
| Old scrap 1 | 98.022 | 0 | 0.3 | 0 | 0.001 | 0.4 | 0.01 | 0 | 0.001 | 0.1 | 0.02 |
| Old scrap 2 | 98.717 | 0 | 0.02 | 0 | 0 | 0.05 | 0.005 | 0 | 0.001 | 0.1 | 0.04 |
| Old scrap 3 | 97.07 | 0 | 0.35 | 0 | 0 | 0.05 | 0 | 0 | 0 | 0.1 | 0 |
| New scrap 1 | 98.586 | 0 | 0.01 | 0.009 | 0 | 0.02 | 0.001 | 0.0015 | 0.002 | 0.015 | 0.004 |
| New scrap 2 | 98.786 | 0 | 0.01 | 0.009 | 0 | 0.02 | 0.001 | 0.0015 | 0.002 | 0.015 | 0.004 |
| News crap 3 | 98.586 | 0 | 0.01 | 0.009 | 0 | 0.02 | 0.001 | 0.0015 | 0.002 | 0.015 | 0.004 |
| Return 1 | 97.619 | 2 | 0.002 | 0 | 0 | 0.3 | 0 | 0 | 0.001 | 0.03 | 0 |
| Return 2 | 98.675 | 0 | 0 | 0 | 0 | 0.4 | 0 | 0 | 0 | 0 | 0.84 |
| Sculls | 98.877 | 0 | 0.002 | 0.011 | 0 | 0.399 | 0.003 | 0.001 | 0.001 | 0.061 | 0.016 |
| Return 3 | 97.619 | 2 | 0.002 | 0 | 0 | 0.3 | 0 | 0 | 0.001 | 0.03 | 0 |
| Hot heel type 1 | 99.494 | 0 | 0.0015 | 0 | 0.006 | 0.3 | 0 | 0 | 0.0015 | 0.022 | 0.0085 |
| Hot heel type 2 | 99.373 | 0 | 0.001 | 0.001 | 0 | 0.3 | 0.0017 | 0 | 0.001 | 0.048 | 0.016 |
| Hot heel type 3 | 99.561 | 0 | 0.001 | 0.006 | 0 | 0.2 | 0.001 | 0 | 0.002 | 0.019 | 0.028 |
| Input Material | Mn | W | V | Co | P | Ni | S | Cr | Zn | Nb | Al |
| HBI | 0 | 0 | 0 | 0 | 0.02 | 0 | 0.02 | 0 | 0 | 0 | 0 |
| Pig Iron 1 | 0.013 | 0 | 0.015 | 0 | 0.029 | 0 | 0.006 | 0.025 | 0 | 0 | 0 |
| Pig Iron 2 | 0.013 | 0 | 0.015 | 0 | 0.029 | 0 | 0.006 | 0.025 | 0 | 0 | 0 |
| Old Scrap 1 | 0.8 | 0 | 0.001 | 0 | 0.02 | 0.1 | 0.025 | 0.2 | 0 | 0 | 0 |
| Old Scrap 2 | 0.8 | 0 | 0.001 | 0.001 | 0.005 | 0.15 | 0.01 | 0.1 | 0 | 0 | 0 |
| Old Scrap 3 | 1.2 | 0 | 0 | 0 | 0.02 | 0.1 | 0.01 | 0.1 | 1 | 0 | 0 |
| New Scrap 1 | 0.3 | 0.001 | 0.001 | 0 | 0.005 | 0.015 | 0.007 | 0.02 | 1 | 0.003 | 0 |
| New Scrap 2 | 0.1 | 0.001 | 0.001 | 0 | 0.005 | 0.015 | 0.007 | 0.02 | 1 | 0.003 | 0 |
| New Scrap 3 | 0.3 | 0.001 | 0.001 | 0 | 0.005 | 0.015 | 0.007 | 0.02 | 1 | 0.003 | 0 |
| Return 1 | 0.01 | 0 | 0.005 | 0 | 0.01 | 0.005 | 0.013 | 0.002 | 0 | 0 | 0.003 |
| Return 2 | 0.08 | 0 | 0 | 0 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sculls | 0.13 | 0.004 | 0.001 | 0 | 0.006 | 0.046 | 0.014 | 0.066 | 0 | 0.004 | 0.03 |
| Return 3 | 0.01 | 0 | 0.005 | 0 | 0.01 | 0.005 | 0.013 | 0.002 | 0 | 0 | 0.003 |
| Hot heel 1 | 0.01 | 0 | 0.005 | 0 | 0.01 | 0.005 | 0.013 | 0.002 | 0 | 0 | 0.03 |
| Hot heel 2 | 0.115 | 0.002 | 0.001 | 0 | 0.006 | 0.036 | 0.014 | 0.051 | 0 | 0.0035 | 0.03 |
| Hot heel 3 | 0.098 | 0.001 | 0.001 | 0 | 0.0025 | 0.022 | 0.008 | 0.016 | 0.0035 | 0.03 |
Appendix B
References
- Toulouevski, Y.N.; Zinurov, I.Y. Innovation in Electric Arc Furnaces; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–22. [Google Scholar]
- Rathaba, P.L.; Craig, I.K.; Pistorius, P.C. Influence of Oxyfuel Burner Subsystem on the EAF Process. IFAC Autom. Min. Miner. Met. Process. 2004, 37, 215–220. [Google Scholar] [CrossRef]
- Madias, J. Electric Furnace Steelmaking. In Treatise in Process Metallurgy; Elsevier: Oxford, UK, 2014; Volume 3, pp. 271–272. [Google Scholar]
- Morris, A.E.; Fine, H.A.; Geiger, G. Handbook on Material and Energy Balance Calculations in Material Processing; John Willey & Sons: Hoboken, NJ, USA, 2011; p. 582. [Google Scholar]
- Hasanbeigi, A.; Price, L.K.; McKane, A.T. The State-of-the-Art Clean Technologies (SOACT) for Steelmaking Handbook. Available online: https://www.jisf.or.jp/business/ondanka/eco/docs/SOACT-Handbook-2nd-Edition.pdf (accessed on 4 February 2020).
- Von Starck, A.; Mühlbauer, A.; Kramer, C. Handbook of Thermoprocessing Technologies; Vulkan-Verlag GmbH: Essen, Germany, 2005; p. 298. [Google Scholar]
- Alaneddine, S.; Bowman, B. Particularities of Melting DRI in AC and Dc arc furnaces. Arch. Metall. Mater. 2008, 53, 411–417. [Google Scholar]
- Du, C.; Zhu, M.; Sun, L.; Dong, S. Metallurgical Characteristics and Effectiveness of Metallic Heats in Electric Arc Furnace. Asia Pac. J. Chem. Eng. 2006, 14, 353–362. [Google Scholar]
- Morales, R.D.; Ruben Lule, G.; Lopez, F.; Camacho, J.; Romero, J.A. The Slag Foaming Practice in EAF and its influence on the steelmaking Shop Productivity. ISIJ Int. 1995, 35, 1054–1062. [Google Scholar] [CrossRef]
- Kirschen, M.; Badr, K.; Cappel, J. Chemical Energy and Bottom Stirring Systems-Cost Effective Solutions for a Better Performing EAF. Int. J. ISSI 2009, 6, 1–8. [Google Scholar]
- Bekker, J.G.; Craig, I.K.; Pistorius, P.C. Modeling and Simulation of an Electric Arc Furnace, Furnace. ISIJ Int. 1999, 39, 23–32. [Google Scholar] [CrossRef]
- MacRosty, R.D.M.; Swartz, C.L.E. Dynamic Modeling of an Industrial Electric Arc Furnace. Ind. Eng. Chem. Res. 2005, 44, 8067–8083. [Google Scholar] [CrossRef]
- Logar, V.; Dovžan, D.; Škrjanc, I. Modeling and Validation of an Electric Arc Furnace: Part 1, Heat and Mass Transfer. ISIJ Int. 2012, 52, 402–412. [Google Scholar] [CrossRef]
- Hay, T.; Reimann, A.; Echterhof, T. Improving the Modelling of slag and Steel Bath Chemistry in an Electric Arc Furnace Process Model. Metall. Mater. Trans. B 2019, 50, 2377–2388. [Google Scholar] [CrossRef]
- Kirschen, M.; Badr, K.; Pfeifer, H. Influence of Direct Reduced Iron on the Energy Balance of the Electric Arc Furnace in Steel Industry. Energy 2011, 36, 6146–6155. [Google Scholar] [CrossRef]
- Andersson, A. A Study on Selected Hot-Metal and Slag Components for Improved Blast Furnace Control. Licentiate Thesis, Royal Institute of Technology, Stockholm, Sweden, 2003. [Google Scholar]
- Barin, I.; Knacke, O.; Kubaschewski, O. Thermochemical Properties of Inorganic Substances; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Selin, R. The Role of Phosphorus, Vanadium and Slag Forming Oxides in Direct Reduction Based Steelmaking. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 1987. [Google Scholar]


| Heat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Oxygen lance (Nm3) | 110 | 116 | 260 | 137 | 225 | 275 | 81 | 104 |
| Burner (kWh) | 500 | 620 | 480 | 480 | 460 | 730 | 745 | 735 |
| Tap temperature (°C) | 1644 | 1693 | 1652 | 1613 | 1639 | 1619 | 1662 | 1649 |
| Heat | a | b | c | d | e | f | g | h |
| Oxygen lance (Nm3) | 111 | 310 | 147 | 116 | 123 | 206 | 99 | 83 |
| Burner (kWh) | 480 | 480 | 470 | 480 | 480 | 710 | 730 | 735 |
| Tap temperature (°C) | 1681 | 1670 | 1651 | 1620 | 1660 | 1625 | 1658 | 1621 |
| Heat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| MnO | 2.79 | 2.45 | 2.07 | 3.43 | 3.80 | 4.13 | 2.59 | 2.28 |
| P2O5 | 0.45 | 0.35 | 0.25 | 0.43 | 0.43 | 0.44 | 0.41 | 0.41 |
| S | 0.05 | 0.07 | 0.12 | 0.04 | 0.05 | 0.05 | 0.06 | 0.06 |
| Cr2O3 | 0.24 | 0.39 | 0.26 | 0.35 | 0.30 | 0.39 | 0.29 | 0.23 |
| NiO | 0.01 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| NbO | 0.07 | 0.05 | 0.08 | 0.06 | 0.07 | 0.07 | 0.07 | 0.05 |
| SiO2 | 16.70 | 12.33 | 14.33 | 15.06 | 10.23 | 12.86 | 11.63 | 13.89 |
| V2O5 | 0.08 | 0.09 | 0.11 | 0.09 | 0.08 | 0.08 | 0.10 | 0.15 |
| TiO2 | 1.15 | 0.75 | 0.65 | 1.28 | 0.95 | 0.74 | 1.38 | 1.43 |
| Al2O3 | 8.30 | 5.59 | 6.55 | 7.69 | 5.50 | 5.91 | 4.26 | 4.74 |
| CaO | 40.36 | 41.39 | 40.75 | 40.08 | 42.79 | 41.13 | 44.83 | 43.13 |
| MgO | 7.81 | 14.53 | 12.80 | 9.47 | 13.79 | 12.19 | 12.36 | 11.62 |
| FeO | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
| Heat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| C | 0.615 | 0.740 | 0.592 | 0.449 | 0.175 | 0.332 | 0.342 | 0.333 |
| Mn | 0.105 | 0.109 | 0.122 | 0.084 | 0.098 | 0.114 | 0.074 | 0.067 |
| P | 0.005 | 0.008 | 0.006 | 0.003 | 0.003 | 0.004 | 0.003 | 0.003 |
| S | 0.010 | 0.014 | 0.017 | 0.010 | 0.008 | 0.011 | 0.009 | 0.011 |
| Cr | 0.0249 | 0.058 | 0.068 | 0.026 | 0.016 | 0.026 | 0.023 | 0.019 |
| Ni | 0.020 | 0.033 | 0.049 | 0.022 | 0.022 | 0.028 | 0.022 | 0.020 |
| Cu | 0.018 | 0.051 | 0.064 | 0.026 | 0.019 | 0.028 | 0.023 | 0.021 |
| Nb | 0.004 | 0.004 | 0.003 | 0.004 | 0.004 | 0.004 | 0.004 | 0.004 |
| Si | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.003 | 0.001 |
| Mo | 0.010 | 0.017 | 0.014 | 0.017 | 0.028 | 0.019 | 0.004 | 0.004 |
| Sn | 0.001 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.000 | 0.000 |
| Ca | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| V | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| W | 0.002 | 0.005 | 0.001 | 0.003 | 0.001 | 0.001 | 0.003 | 0.004 |
| Pb | 0.006 | 0.007 | 0.006 | 0.006 | 0.006 | 0.006 | 0.006 | 0.006 |
| Ti | 0.002 | 0.001 | 0.001 | 0.001 | 0.002 | 0.001 | 0.002 | 0.001 |
| Al | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Zr | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| Fe | 99.1 | 98.9 | 99 | 99.3 | 99.6 | 99.4 | 99.4 | 99.4 |
| Element (i) | Li | σL |
|---|---|---|
| Mn | 24 | 7 |
| S | 5.4 | 1.4 |
| Cr | 4.5 | 2 |
| Ni | 0.48 | 0.2 |
| Cu | 0 | 0 |
| Nb | 15.4 | 3.3 |
| Si | 1467 | 1405 |
| Mo | 0 | 0 |
| P | 49.2 | 22 |
| Ti | 453 | 191 |
| V | 0.22 | 6.7 |
| Al | 111 | 28 |
| C | CaO | MnO | Cr2O3 | S | Fe2O3 | ZnO | CuO | PbO | Cd |
|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 4.77 | 1.732 | 0.1 | 0.02 | 41.14 | 44.96 | 0.06 | 7.2 | 0.001 |
| Mn (%) | Cr (%) | Fe (%) | Cu (%) | Pb (%) | S (%) | Zn (%) |
|---|---|---|---|---|---|---|
| 11 | 5 | 0.8 | 13 | 71 | 6 | 100 |
| Raw material | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 |
|---|---|---|---|---|---|---|---|
| HBI (%) | 13 | 15 | 20 | 25 | 30 | 35 | 40 |
| Old scrap 1 (kg) | 2400 | 2342 | 2190 | 2038 | 1887 | 1735 | 1583 |
| Old scrap 3 (kg) | 3250 | 3172 | 2966 | 2760 | 2555 | 2349 | 2144 |
| New scrap 1 (kg) | 12,400 | 12,101 | 11,316 | 10,532 | 9747 | 8963 | 8178 |
| New scrap 2 (kg) | 12,400 | 12,101 | 11,316 | 10,532 | 9747 | 8963 | 8178 |
| New scrap 3 (kg) | 11,200 | 10,930 | 10,221 | 9513 | 8804 | 8095 | 7387 |
| Element | P | Mn | S | Cr | Cu |
|---|---|---|---|---|---|
| R | 0.82 | 0.75 | 0.99 | 0.98 | 0.98 |
| EMax | 0.0021 | 0.07 | 0.0006 | 0.061 | 0.032 |
| Case | 4 | 5 | 6 | 7 |
|---|---|---|---|---|
| HBI (%) | 25 | 30 | 35 | 40 |
| lime (kg) | 1168 | 1228 | 1288 | 1347 |
| Dolomite (kg) | 594 | 716 | 838 | 961 |
| slag mass (kg) | 3921 | 4317 | 4713 | 5109 |
| λMgO | 1 | 1 | 1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arzpeyma, N.; Gyllenram, R.; Jönsson, P.G. Development of a Mass and Energy Balance Model and Its Application for HBI Charged EAFs. Metals 2020, 10, 311. https://doi.org/10.3390/met10030311
Arzpeyma N, Gyllenram R, Jönsson PG. Development of a Mass and Energy Balance Model and Its Application for HBI Charged EAFs. Metals. 2020; 10(3):311. https://doi.org/10.3390/met10030311
Chicago/Turabian StyleArzpeyma, Niloofar, Rutger Gyllenram, and Pär G. Jönsson. 2020. "Development of a Mass and Energy Balance Model and Its Application for HBI Charged EAFs" Metals 10, no. 3: 311. https://doi.org/10.3390/met10030311
APA StyleArzpeyma, N., Gyllenram, R., & Jönsson, P. G. (2020). Development of a Mass and Energy Balance Model and Its Application for HBI Charged EAFs. Metals, 10(3), 311. https://doi.org/10.3390/met10030311





