Simulation on the Effect of Porosity in the Elastic Modulus of SiC Particle Reinforced Al Matrix Composites
Abstract
1. Introduction
2. Numerical Modeling
2.1. Linear Elasticity Equations
2.2. Finite Element Implementation
3. Results and Discussions
3.1. Comparison of FEA Predictions with Experimental Data
3.2. SiC Particle Reinforced Aluminum Composites
3.2.1. Pore-Free Al-Matrix and Pore-Free SiC-Particle
3.2.2. Porous Al-Matrix and Pore-Free SiC Particle
3.2.3. Pore Free Al-matrix and Porous SiC Particle
3.2.4. Porous Al-Matrix and Porous SiC Particle
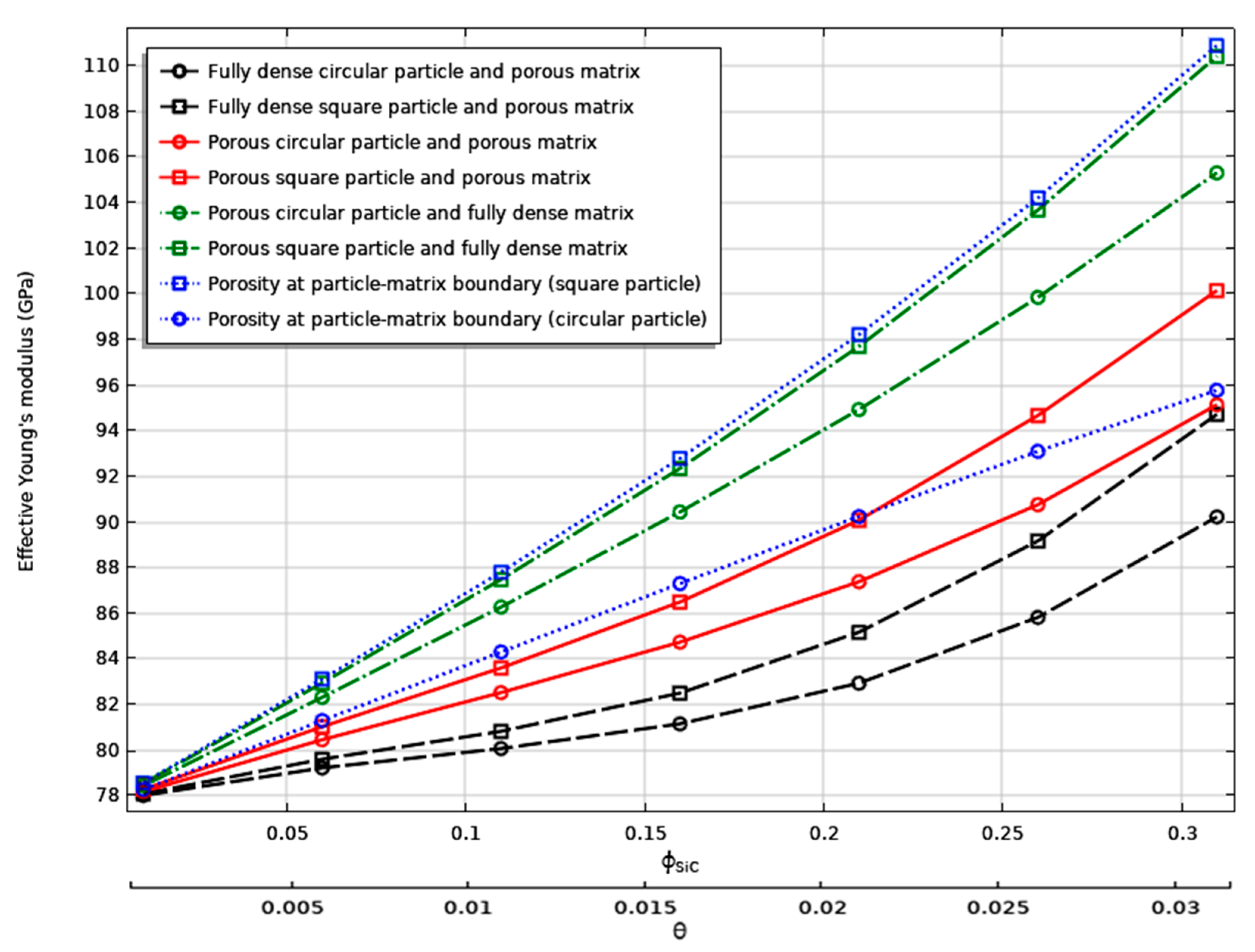
3.2.5. Porosity at Matrix–Particle Interface
3.2.6. REV Models with SiC Particles Representing 2D Real Microstructures
4. Conclusions
- (1)
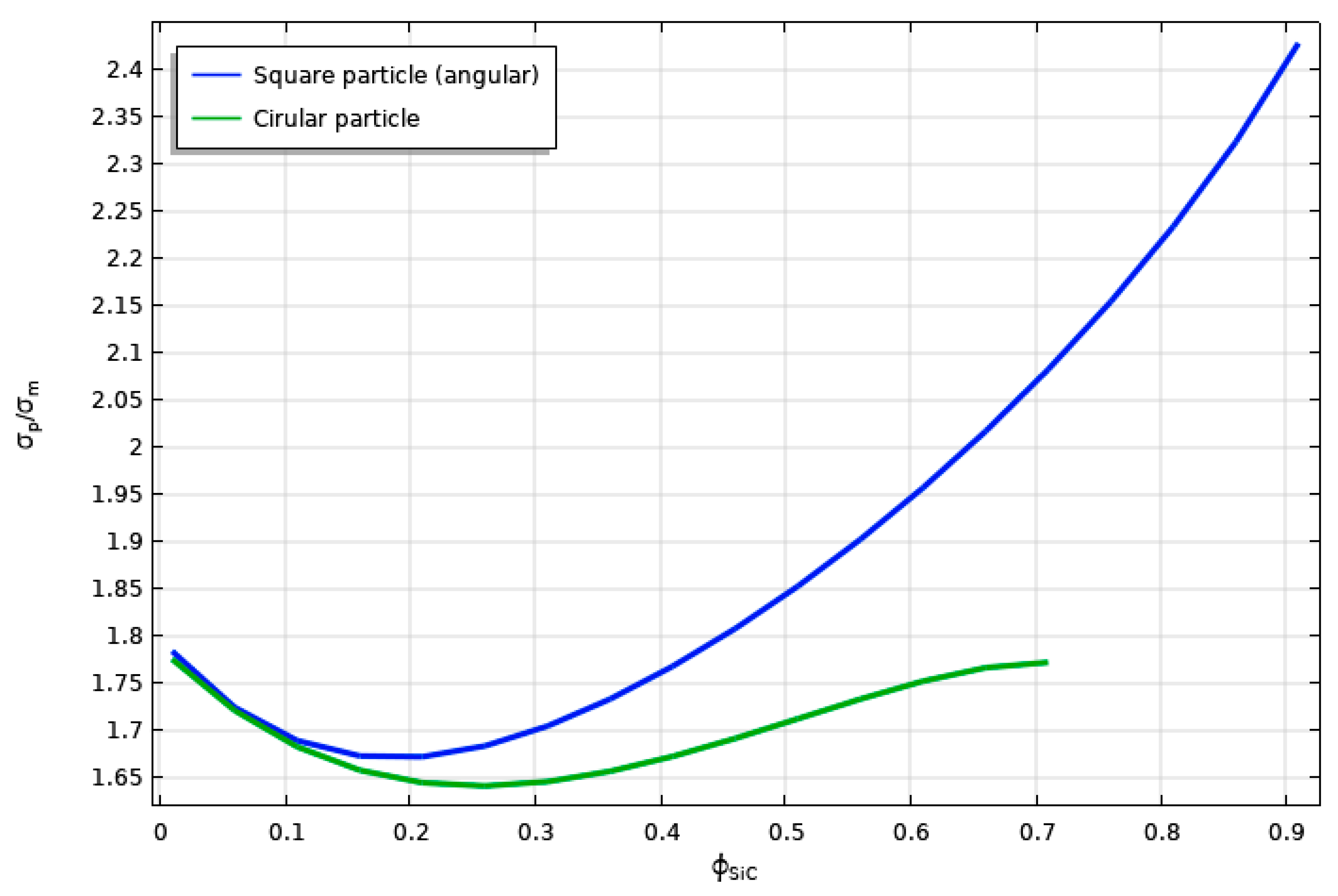
- In the case of fully dense SiC particles and fully dense Al-matrix, the square and circular particles endure the same load to the volume fraction up to 11%. However, above this reinforcement content, the angular particle endures more load. Therefore, the effective elastic modulus of the MMC is independent of the morphology when the reinforcement content is lower to 11%.
- (2)
- Despite the presence of pore in the composite, stress transfer from the soft matrix to the hard particle is effective in all cases, except in the case of fully dense circular particle and porous matrix.
- (3)
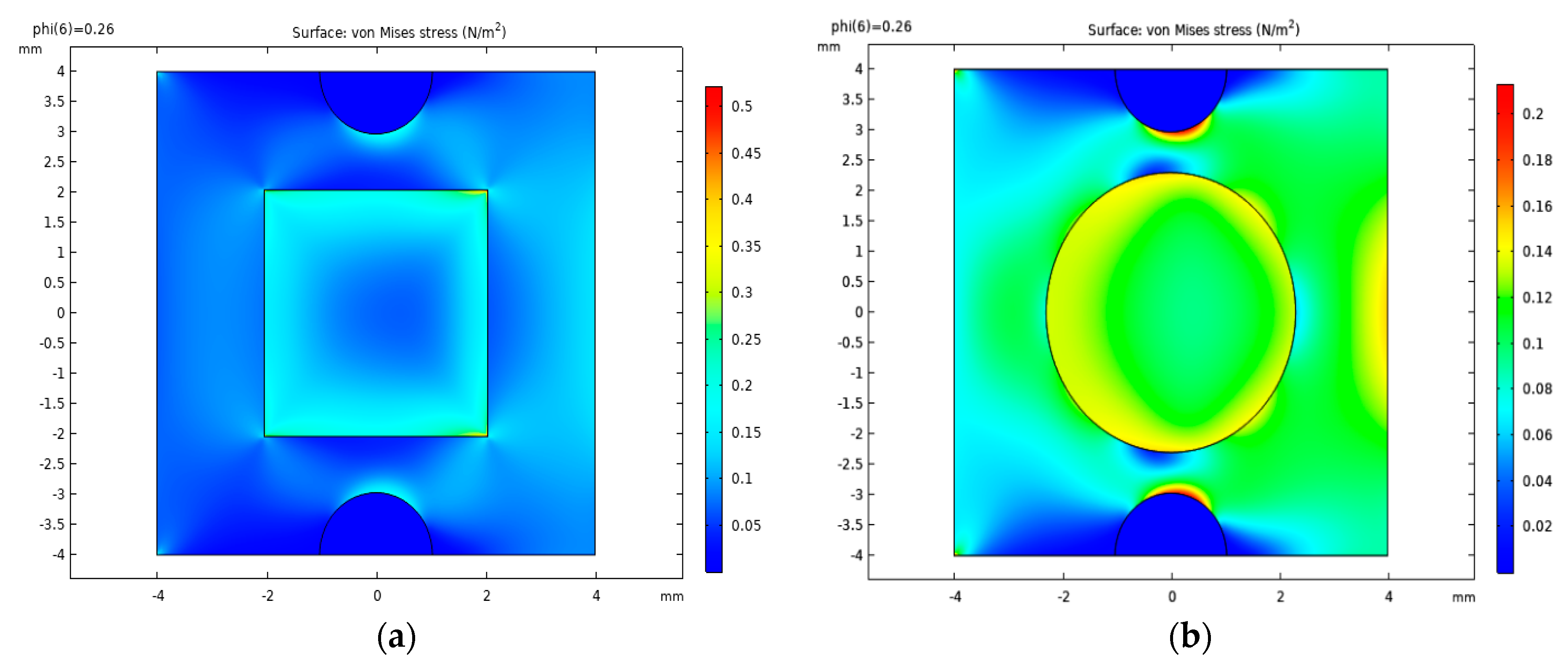
- For pores within the particles, the stress concentration around the pore is higher for the circular particles than the square ones.
- (4)
- The elastic modulus is more sensitive to porosity in the matrix, which is a common defect in MMC.
- (5)
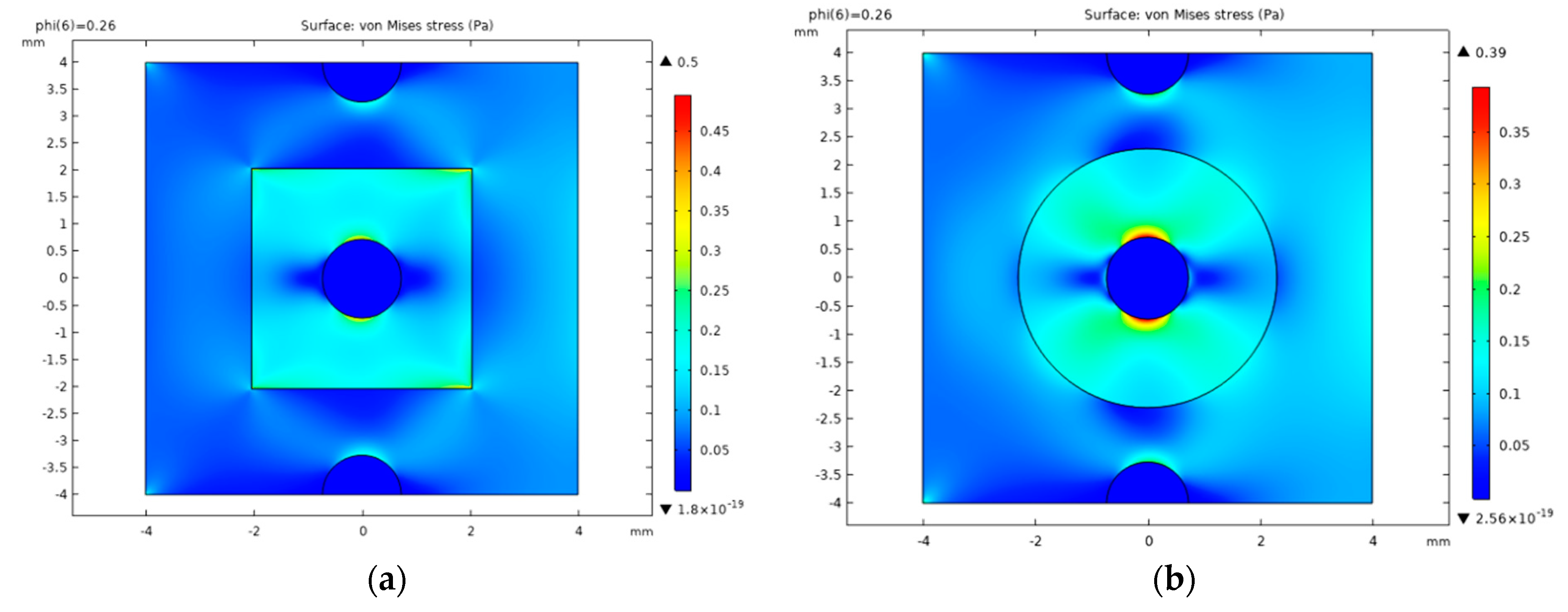
- For the square or angular particles, the pore within the particle affects the load transfer mechanism in the same way to the pore located at the particle matrix interface.
- (6)
- For the porosity at the particle–matrix interface, the contact points among the particle, matrix, and the pore acts as a stress concentrator.
- (7)
- The porosity plays a significant role in the strength of the composites, and for a given porosity in the matrix, it impairs the Young’s modulus in the same way independently of the shape of the SiC-reinforcement.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arreola-Herrera, R.; Cruz-Ramírez, A.; Rivera-Salinas, J.E.; Romero-Serrano, J.A.; Sánchez-Alvarado, R.G. The effect of non-metallic inclusions on the mechanical properties of 32 CDV 13 steel and their mechanical stress analysis by numerical simulation. Theor. Appl. Fract. Mech. 2018, 94, 134–146. [Google Scholar] [CrossRef]
- Kulkarni, S.G.; Achchhe, L.; Menghani, J.V. Effect of reinforcement type and porosity on strength of metal matrix composite. Int. J. Comput. Mater. Sci. Eng. 2016, 5, 1650006. [Google Scholar] [CrossRef]
- Shen, L.; Finot, M.; Needleman, A.; Suresh, S. Effective plastic response of two-phase composites. Acta Metall. Mater. 1995, 43, 1701–1722. [Google Scholar] [CrossRef]
- Chawla, N.; Chawla, K.K. Microstructure-based modeling of the deformation behavior of particle reinforced metal matrix composites. J. Mater. Sci. 2006, 41, 913–925. [Google Scholar] [CrossRef]
- Nasher, N.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials, 2nd ed.; Elsevier: North-Holland, The Netherlands, 1999. [Google Scholar]
- Gentieu, T.; Catapano, A.; Jume, J.; Broughton, J. Computational modeling of particulate-reinforced materials up to high volume fractions: Linear elastic homogenization. J. Mater. Des. Appl. 2019, 233, 1101–1116. [Google Scholar]
- Hassani, A.; Bagherpour, E.; Qods, F. Influence of pores on workability of porous Al/SiC composites fabricated through powder metallurgy + mechanical alloying. J. Alloys Compd. 2014, 591, 132–142. [Google Scholar] [CrossRef]
- Schöbel, M.; Requena, G.; Fiedler, G.; Tolnai, D.; Vaucher, S.; Degischer, H.P. Void formation in metal matrix composites by solidification and shrinkage of an AlSi7 matrix between densely packed particles. Compos. Part A Appl. Sci. Manuf. 2014, 66, 103–108. [Google Scholar] [CrossRef]
- Arif, M.N.; Bukhari, M.Z.; Brabazon, D.; Hashmi, M.S.J. Coefficient of thermal expansion (CTE) study in metal matrix composite of CuSiC vs. AlSiC. IOP Conf. Ser. Mater. Sci. Eng. 2019, 701, 012057. [Google Scholar] [CrossRef]
- Podymova, N.B.; Kalashnikov, I.E.; Bolotova, L.K.; Kobeleva, L.I. Laser-ultrasonic nondestructive evaluation of porosity in particulate reinforced metal-matrix composites. Ultrasonics 2019, 99, 105959. [Google Scholar] [CrossRef]
- Schöbel, M.; Altendorfer, W.; Degischer, H.P.; Vaucher, S.; Buslaps, T.; Di Michiel, M.; Hofmann, M. Internal stresses and voids in SiC particle reinforced aluminum composites for heat sink applications. Compos. Sci. Technol. 2011, 71, 724–733. [Google Scholar] [CrossRef]
- Voigt, W. Uber die Beziehung zwischen den beiden Elastizitatskonstanten Isotroper Korper. Wied. Ann.Phys. 1889, 38, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fliessgrense von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behavior of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Arunachalam, V. Effective elastic moduli of porous solids. J. Mater. Sci. 1990, 25, 3930–3937. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Arunachalam, V. Effective elastic moduli of porous ceramic materials. J. Am. Ceram. Soc. 1993, 76, 2745–2752. [Google Scholar] [CrossRef]
- Chawla, N.; Shen, Y. Mechanical behavior of particle reinforced metal matrix composites. Adv. Eng. Mater. 2001, 6, 357–370. [Google Scholar] [CrossRef]
- Chawla, N.; Ganesh, V.; Wunsch, B. Three-dimensional (3D) microstructure visualization and finite element modeling of the mechanical behavior of SiC particle reinforced aluminum composites. Scr. Mater. 2004, 51, 161–165. [Google Scholar] [CrossRef]
- Dong, C. Effects of process-induced voids on the properties of fibre reinforced composites. J. Mater. Sci. Technol. 2016, 32, 597–604. [Google Scholar] [CrossRef]
- Deng, X.; Koopman, M.; Chawla, K.K.; Scarritt, S. Measurement and prediction of Young’s modulus of a Pb-free solder. J. Mater. Sci. Mater. Electron. 2004, 15, 385–388. [Google Scholar]
- Kukshal, V.; Gangwar, S.; Patnaik, A. Experimental and finite element analysis of mechanical and fracture behavior of SiC particulate filled A356 alloy composites: Part I. J. Mater. Des. Appl. 2015, 229, 91–105. [Google Scholar] [CrossRef]
- Hashim, J.; Looney, M.; Hashmi, M.S.J. The enhancement of wettability of SiC particles in cast aluminum matrix composites. J. Mater. Process. Technol. 1999, 1, 329–335. [Google Scholar]
- Ray, S. Review Synthesis of cast metal matrix particulate composite. J. Mater. Sci. 1993, 28, 539–5413. [Google Scholar] [CrossRef]
- Sun, C.; Song, M.; Wang, Z.; He, Y. Effect of particle size on the microstructures and mechanical properties of SiC-reinforced pure aluminum composites. J. Mater. Eng. Perform. 2011, 20, 1606–1612. [Google Scholar] [CrossRef]
- Koopman, M.; Chawla, K.K.; Coffin, C.; Patterson, B.R.; Deng, X.; Patel, B.V.; Fang, Z.; Lockwood, G. Determination of elastic constants inWC/Co metal matrix composites by resonant ultrasound spectroscopy and impulse excitation. Adv. Eng. Mater. 2002, 4, 37–42. [Google Scholar] [CrossRef]
- Eroshkin, O.; Tsukrov, I. On micromechanical modeling of particulate composites with inclusions of various shapes. Int. J. Solids Struct. 2005, 42, 409–427. [Google Scholar] [CrossRef]
- Fish, J.; Belytschko, T. A Fist Course in Finite Elements; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Tillmann, W.; Klusemann, B.; Nebel, J.; Svendsen, B. Analysis of the mechanical properties of an Arc-sprayed WC-FeCSiMn coating: Nanoindentation and simulation. J. Therm. Spray Technol. 2011, 20, 328–335. [Google Scholar] [CrossRef]
- Ganesh, V.V.; Chawla, N. Effect of particle orientation anisotropy on the tensile behavior of metal matrix composites: Experiments and microstructure-based simulation. Mater. Sci. Eng. A 2005, 391, 342–353. [Google Scholar] [CrossRef]
- Clayne, T.W.; Withers, P.J. An Introduction to Metal Matrix Composites; Cambridge University Press: Cambdrige, UK, 1995. [Google Scholar]
- McDaniels, D.L. Analysis of stress-strain, fracture, and ductility behavior of aluminum matrix composites containing discontinuous silicon carbide reinforcement. Metall. Trans. A 1985, 16, 1105–1115. [Google Scholar] [CrossRef]
- Upadhy, A.; Ramvir, S. Prediction of effective elastic modulus of biphasic composite materials. Mod. Mech. Eng. 2012, 2, 6–13. [Google Scholar] [CrossRef]
- Qu, S.G.; Lou, H.S.; Li, X.Q. Influence of particle size distribution on properties of SiC particles reinforced aluminum matrix composites with high SiC particle content. J. Compos. Mater. 2016, 50, 1049–1058. [Google Scholar] [CrossRef]
- Sherif El-Eskandarany, M. Mechanical solid state mixing for synthesizing of SiCp/Al nanocomposites. J. Alloys Compd. 1998, 279, 263–271. [Google Scholar] [CrossRef]
- Santhosh Kumar, S.; Seshu Bai, V.; Rajkumar, K.V.; Sharma, G.K.; Jayakumar, T.; Rajasekharan, T. Elastic modulus of Al–Si/SiC metal matrix composites as a function of volume fraction. J. Phys. D Appl. Phys. 2009, 42, 175504. [Google Scholar] [CrossRef]
- Liaw, P.K.; Shannon, R.E.; Clark, W.G.; Harrigan, W.C.; Jeong, H.; Hsu, D.K. Nondestructive characterization of material properties of metal-matrix composites. Mater. Chem. Phys. 1995, 39, 220–228. [Google Scholar] [CrossRef]

 ), experimental data (
), experimental data ( ) [25], numerical data (square
) [25], numerical data (square  , circle
, circle  ) and V–R bounds (
) and V–R bounds ( ) for the Young’s modulus for Co-WC system.
) for the Young’s modulus for Co-WC system.
 ), experimental data (
), experimental data ( ) [25], numerical data (square
) [25], numerical data (square  , circle
, circle  ) and V–R bounds (
) and V–R bounds ( ) for the Young’s modulus for Co-WC system.
) for the Young’s modulus for Co-WC system.
 ), experimental data (
), experimental data ( ) [16] and numerical data (square
) [16] and numerical data (square  , circle
, circle  ).
).
 ), experimental data (
), experimental data ( ) [16] and numerical data (square
) [16] and numerical data (square  , circle
, circle  ).
).


 ), experimental data [32,33,34,35,36,37], numerical data (square
), experimental data [32,33,34,35,36,37], numerical data (square  , circle
, circle  ) and V–R bounds (
) and V–R bounds ( ).
).





| Material | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|
| Al | 74 | 0.33 |
| SiC | 410 | 0.19 |
| SiC Volume Fraction | 10% | - | 20% | - | 30% | - |
| Shape of the Particle | 1% in porosity | % reduction | 2% in porosity | % reduction | 3% in porosity | % reduction |
| Square | 88.2 GPa * 80.8 GPa † | 8.3 | 99.3 GPa * 85.1 GPa † | 14.3 | 113.15 GPa * 94.7 GPa † | 16.3 |
| Circular | 87.3 GPa * 80.0 GPa † | 8.3 | 97.1 GPa * 82.9 GPa † | 14.6 | 109.0 GPa * 90.2 GPa † | 17.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera-Salinas, J.E.; Gregorio-Jáuregui, K.M.; Romero-Serrano, J.A.; Cruz-Ramírez, A.; Hernández-Hernández, E.; Miranda-Pérez, A.; Gutierréz-Pérez, V.H. Simulation on the Effect of Porosity in the Elastic Modulus of SiC Particle Reinforced Al Matrix Composites. Metals 2020, 10, 391. https://doi.org/10.3390/met10030391
Rivera-Salinas JE, Gregorio-Jáuregui KM, Romero-Serrano JA, Cruz-Ramírez A, Hernández-Hernández E, Miranda-Pérez A, Gutierréz-Pérez VH. Simulation on the Effect of Porosity in the Elastic Modulus of SiC Particle Reinforced Al Matrix Composites. Metals. 2020; 10(3):391. https://doi.org/10.3390/met10030391
Chicago/Turabian StyleRivera-Salinas, Jorge E., Karla M. Gregorio-Jáuregui, José A. Romero-Serrano, Alejandro Cruz-Ramírez, Ernesto Hernández-Hernández, Argelia Miranda-Pérez, and Víctor H. Gutierréz-Pérez. 2020. "Simulation on the Effect of Porosity in the Elastic Modulus of SiC Particle Reinforced Al Matrix Composites" Metals 10, no. 3: 391. https://doi.org/10.3390/met10030391
APA StyleRivera-Salinas, J. E., Gregorio-Jáuregui, K. M., Romero-Serrano, J. A., Cruz-Ramírez, A., Hernández-Hernández, E., Miranda-Pérez, A., & Gutierréz-Pérez, V. H. (2020). Simulation on the Effect of Porosity in the Elastic Modulus of SiC Particle Reinforced Al Matrix Composites. Metals, 10(3), 391. https://doi.org/10.3390/met10030391





