Multiscale Simulation of Non-Metallic Inclusion Aggregation in a Fully Resolved Bubble Swarm in Liquid Steel
Abstract
:1. Introduction
2. Numerical Methods
2.1. Modeling of Collision Dynamics at Mesoscopic Scale
2.1.1. LBM-IBM Simulation Framework
2.1.2. Simulation Setup
2.1.3. Determination of Collision Efficiency
2.2. Modeling of the Bubbly Flow at Macroscopic Scale
2.2.1. Physical Modeling
2.2.2. Numerical Modeling
3. Results and Discussion
3.1. Collision Efficiencies in Shear Driven Aggregation
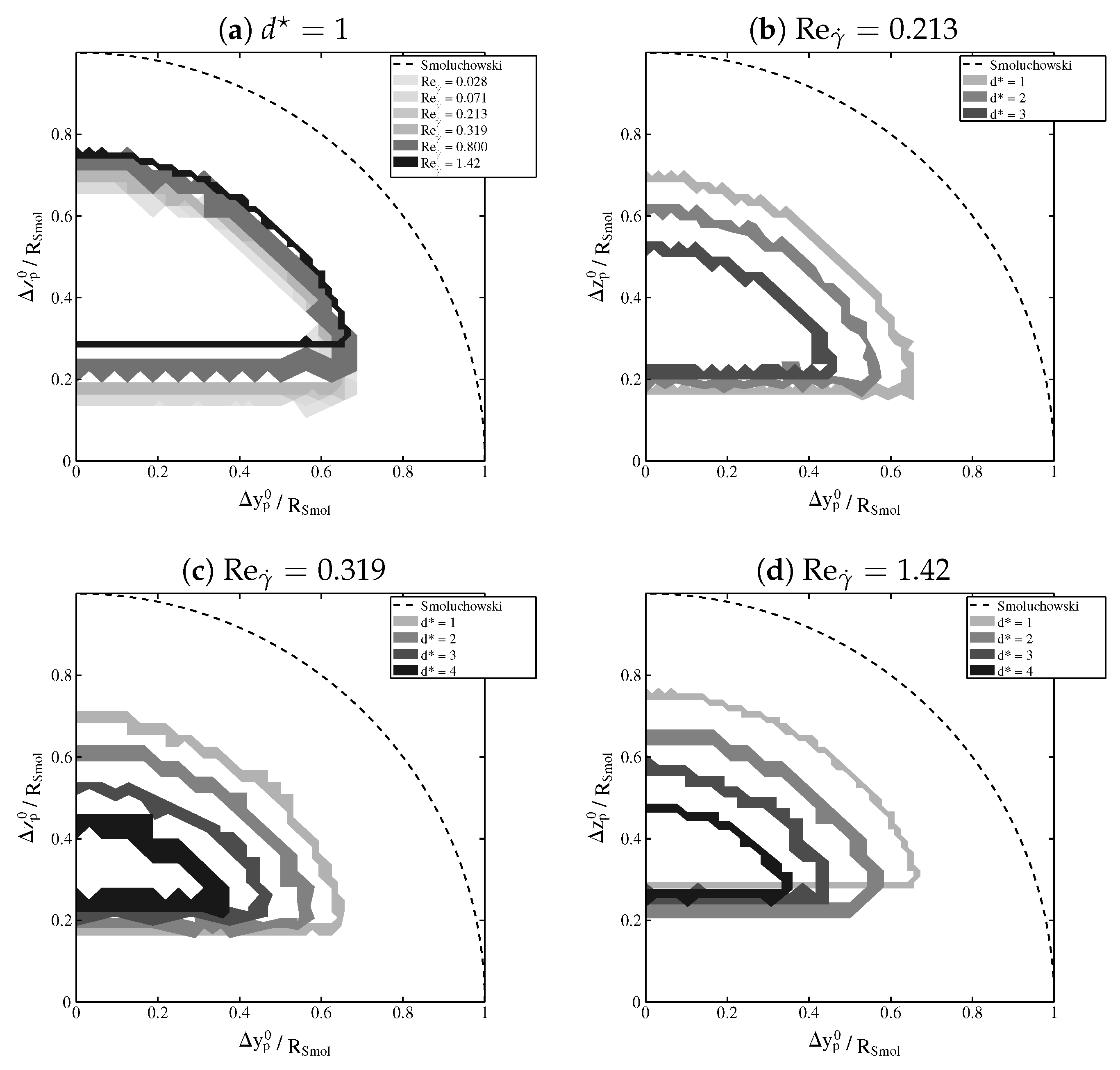
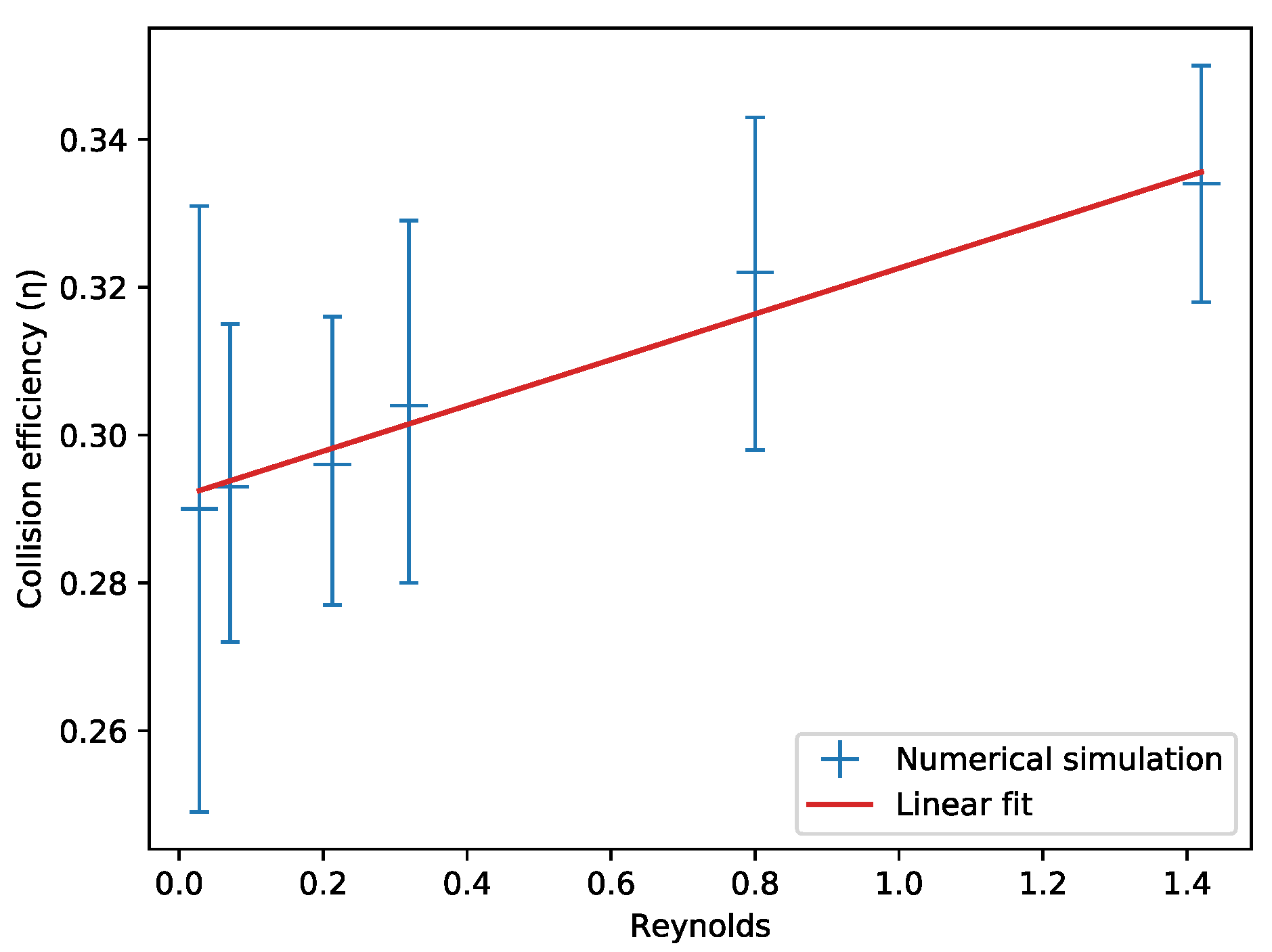
3.1.1. Impact of Reynolds Number on Collision Dynamics
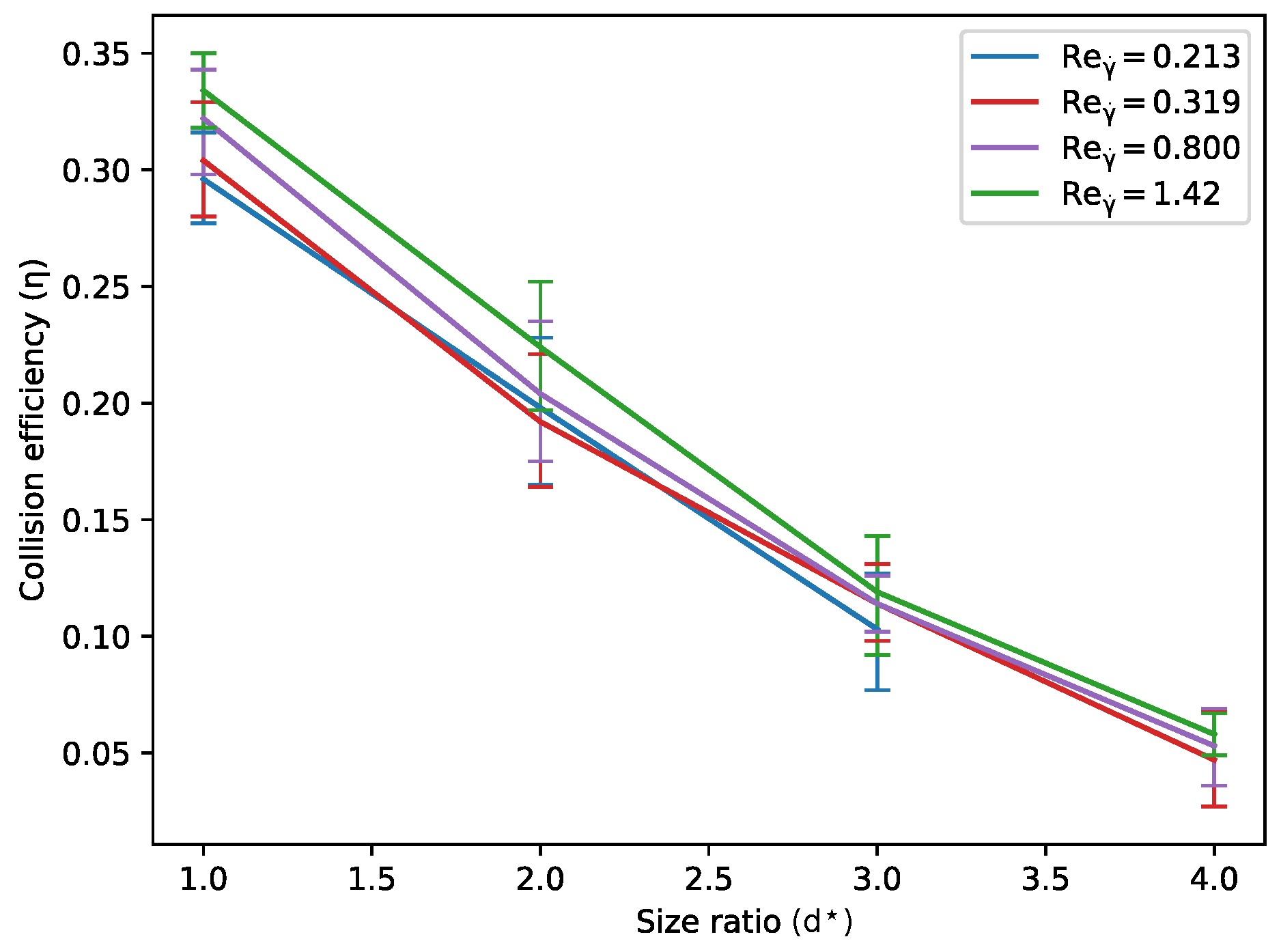
3.1.2. Impact of Particle Size Ratio
3.1.3. Binary Collision Efficiency
3.2. Aggregation Kinetics in a Bubbly Flow
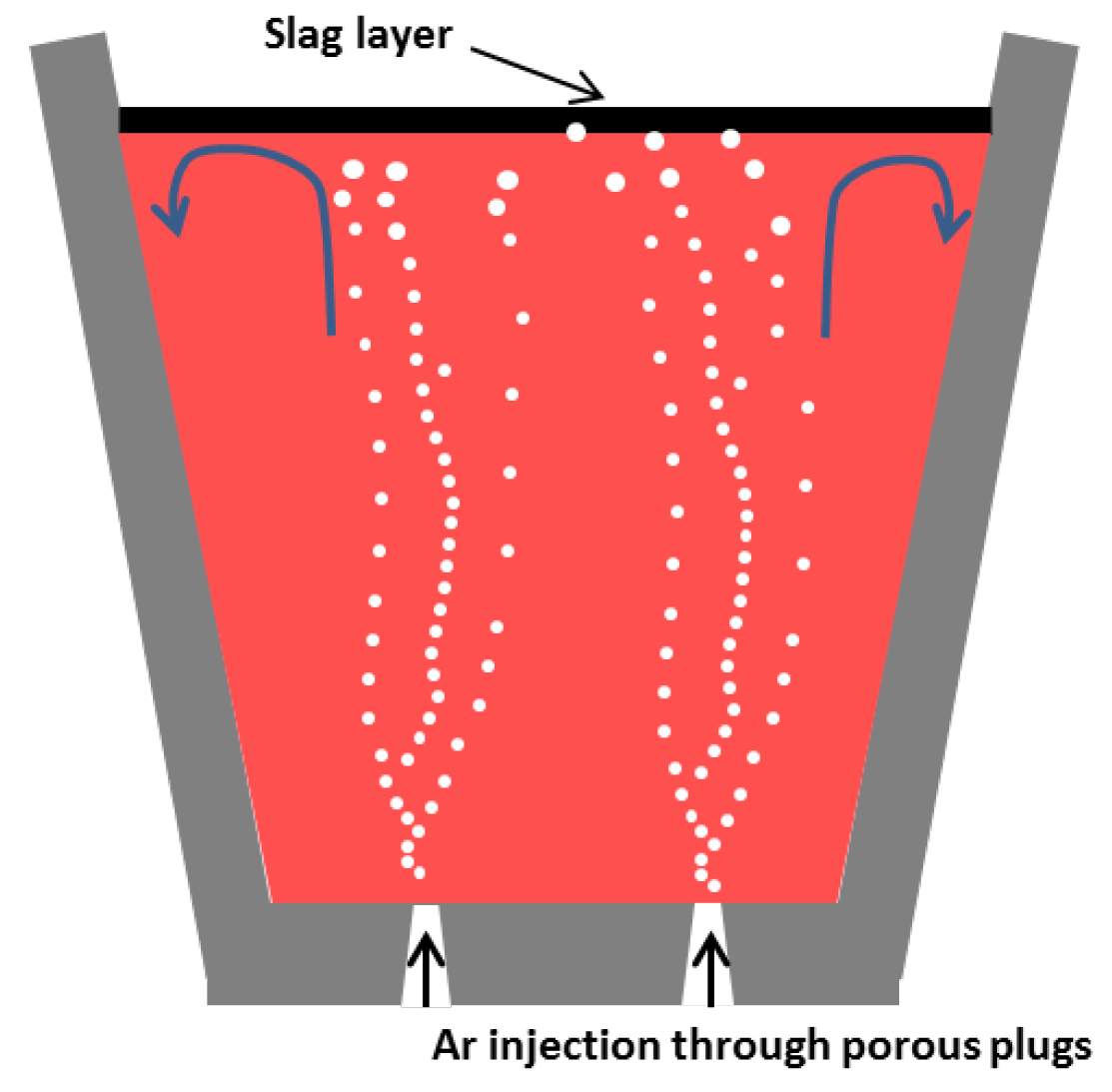
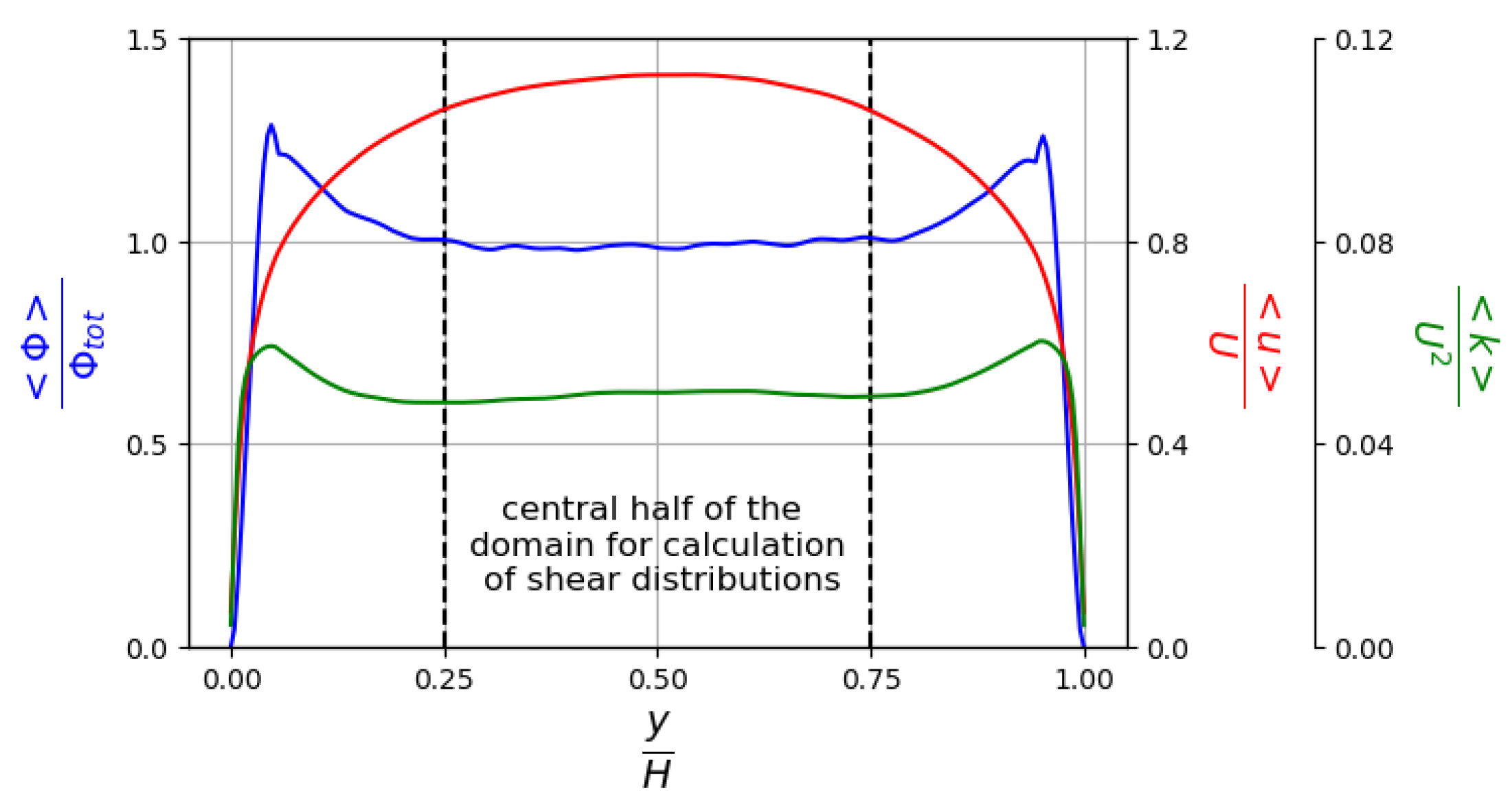
3.2.1. Channel Configuration
3.2.2. Turbulent Liquid Steel and Argon Flow
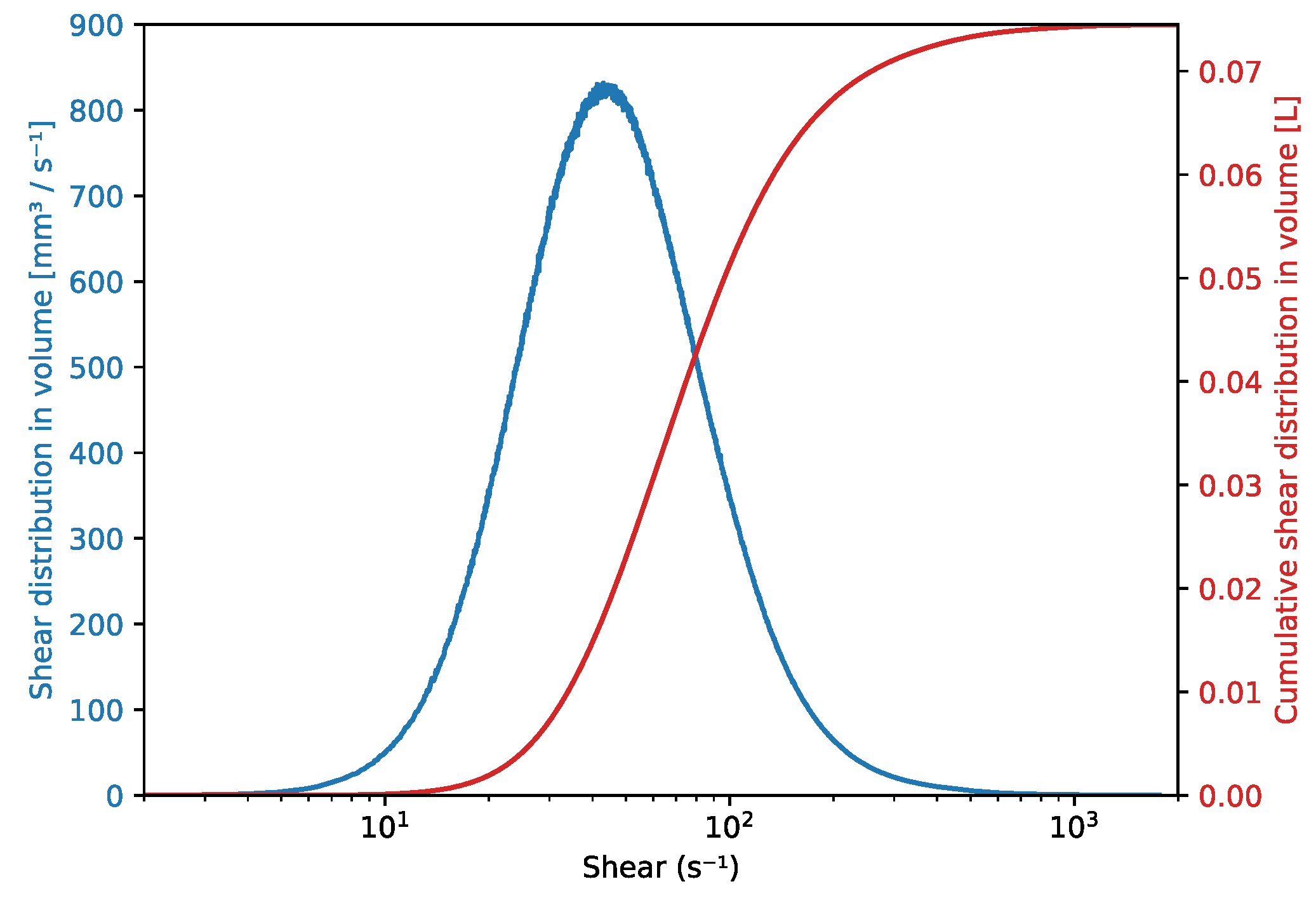
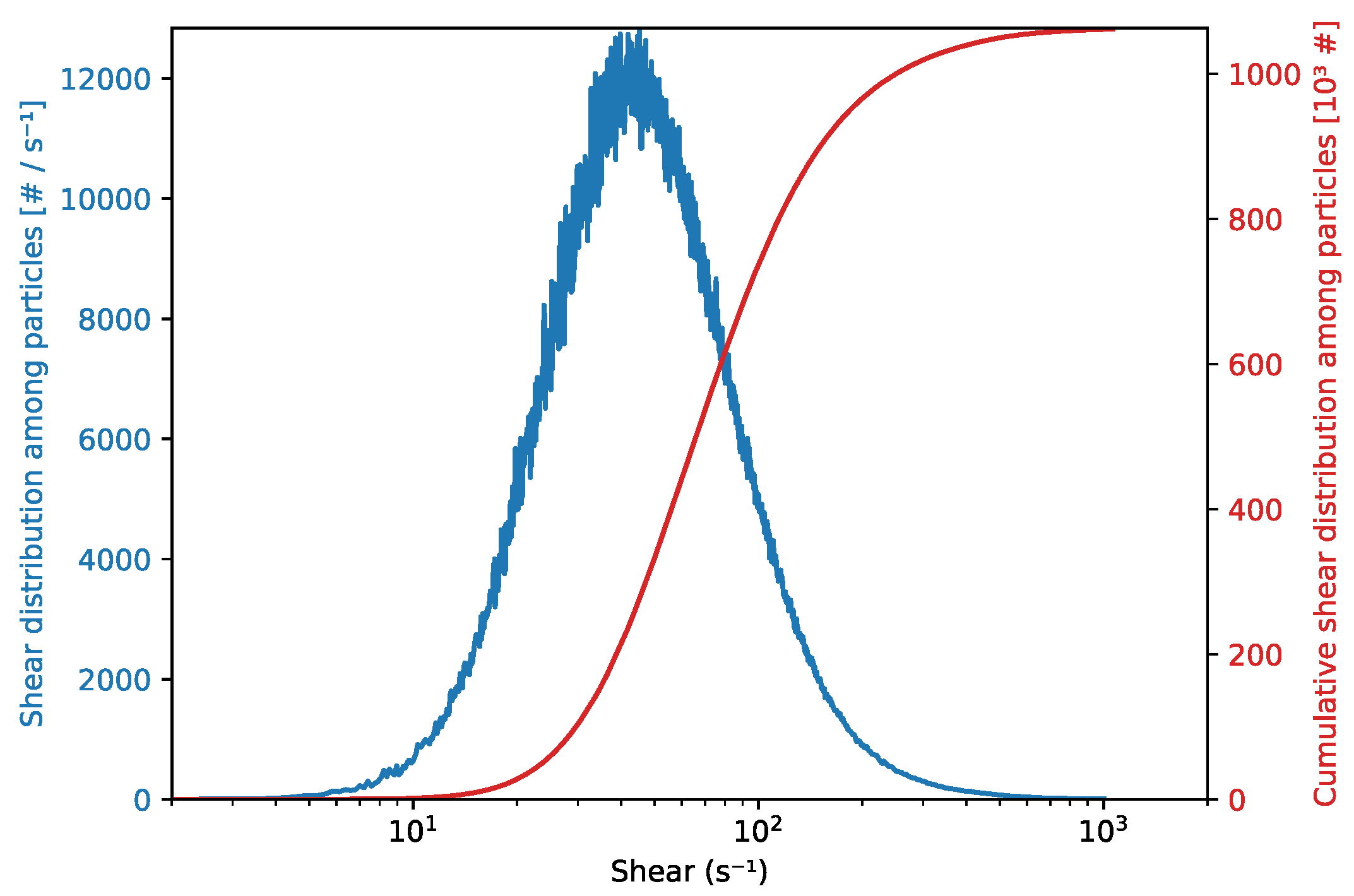
3.2.3. Determination of Collision Frequency
3.2.4. Results for Collision Rates
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Thomas, B.G. State of the art in evaluation and control of steel cleanliness. ISIJ Int. 2003, 43, 271–291. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Li, Y.; Ren, Y. Fundamentals of Non-Metallic Inclusions in Steel: Part II. Evaluation Method of Inclusions and Thermodynamics of Steel Deoxidation. Iron Steel 2013, 12, 1–8. [Google Scholar]
- Cournil, M.; Gruy, F.; Gardin, P.; Saint-Raymond, H. Modelling of solid particle aggregation dynamics in non-wetting liquid medium. Chem. Eng. Process. Process. Intensif. 2006, 45, 586–597. [Google Scholar] [CrossRef]
- Bellot, J.P.; De Felice, V.; Dussoubs, B.; Jardy, A.; Hans, S. Coupling of a CFD and a PBE calculations to simulate the behavior of an inclusion population in a gas-stirred ladle. Metall. Mater. Trans. B 2014, 45, 13–21. [Google Scholar] [CrossRef]
- De Felice, V.; Daoud, I.L.A.; Dussoubs, B.; Jardy, A.; Bellot, J.-P. Numerical modelling of inclusion behaviour in a gas-stirred ladle. ISIJ Int. 2012, 52, 1274–1281. [Google Scholar] [CrossRef] [Green Version]
- Lou, W.; Zhu, M. Numerical Simulations of Inclusion Behavior in Gas-Stirred Ladles. Metall. Mater. Trans. B 2013, 45, 762–782. [Google Scholar] [CrossRef]
- Bellot, J.-P.; Kroll-Rabotin, J.-S.; Gisselbrecht, M.; Joishi, M.; Saxena, A.; Sanders, R.S.; Jardy, A. Toward better control of inclusion cleanliness in a gas stirred ladle using multiscale numerical modeling. Materials 2018, 11, 1179. [Google Scholar] [CrossRef] [Green Version]
- Saffman, P.G.F.; Turner, J.S. On the collision of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef] [Green Version]
- Higashitani, K.; Ogawa, R.; Hosokawa, G.; Matsuno, Y. Kinetic theory of shear coagulation for particles in a viscous fluid. J. Chem. Eng. Jpn. 1982, 15, 299–304. [Google Scholar] [CrossRef] [Green Version]
- Van de Ven, T.G.M.; Mason, S.G. The microrheology of colloidal dispersions VII. Orthokinetic doublet formation of spheres. Colloid Polym. Sci. 1977, 255, 46–479. [Google Scholar] [CrossRef]
- Bülow, F.; Nirschl, H.; Dörfler, W. Simulating orthokinetic heterocoagulation and cluster growth in destabilizing suspensions. Particuology 2017, 31, 117–128. [Google Scholar] [CrossRef]
- Vanni, M.; Baldi, G. Coagulation efficiency of colloidal particles in shear flow. Adv. Colloid Interface Sci. 2002, 97, 151–177. [Google Scholar] [CrossRef]
- Frungieri, G.; Vanni, M. Dynamics of a shear-induced aggregation process by a combined Monte Carlo-Stokesian Dynamics approach. In Proceedings of the 9th International Conference on Multiphase Flow, Florence, Italy, 22–27 May 2016. [Google Scholar]
- Frungieri, G.; Vanni, M. Shear-induced aggregation of colloidal particles: A comparison between two different approaches to the modelling of colloidal interactions. Can. J. Chem. Eng. 2017, 95, 1768–1780. [Google Scholar] [CrossRef] [Green Version]
- Haddadi, H.; Morris, J.F. Topology of pair-sphere trajectories in finite inertia suspension shear flow and its effects on microstructure and rheology. Phys. Fluids 2015, 14, 043302. [Google Scholar] [CrossRef]
- Santarelli, C.; Fröhlich, J. Direct Numerical Simulations of spherical bubbles in vertical turbulent channel flow. Influence of bubble size and bidispersity. Int. J. Multiph. Flow 2016, 81, 27–45. [Google Scholar] [CrossRef]
- Gisselbrecht, M.; Kroll-Rabotin, J.-S.; Bellot, J.-P. Aggregation kernel of globular inclusions in local shear flow: application to aggregation in a gas-stirred ladle. Metall. Res. Technol. 2019, 116, 512. [Google Scholar] [CrossRef]
- Eggels, J.G.M.; Somers, J.A. Numerical simulation of free convective flow using the lattice-Boltzmann scheme. Int. J. Heat Fluid Flow 1995, 16, 357–364. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T.; Peng, Y. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows. Phys. Lett. A 2006, 354, 173–182. [Google Scholar] [CrossRef]
- Gisselbrecht, M. Simulation des Interactions Hydrodynamiques Entre Inclusions Dans un méTal Liquide: éTablissement de Noyaux d’agrégation dans les Conditions Représentatives du Procédé de Flottation. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2019. (In French). [Google Scholar]
- Smoluchowski, M.V. Drei Vorträge über Diffusion, Brownsche Bewegung und Koagulation von Kolloidteilchen. Z. Fur Phys. 1916, 17, 557–585. (In German) [Google Scholar]
- Aland, S.; Schwarz, S.; Fröhlich, J.; Voigt, A. Modeling and numerical approximations for bubbles in liquid metal. Eur. Phys. J. Spec. Top. 2013, 220, 185–194. [Google Scholar] [CrossRef]
- Heitkam, S.; Drenckhan, W.; Fröhlich, J. Packing Spheres Tightly: Influence of Mechanical Stability on Close-Packed Sphere Structures. Phys. Rev. Lett. 2012, 108, 148302. [Google Scholar] [CrossRef] [PubMed]
- Schiller, L.; Naumann, A. A Drag Coefficient Correlation. Z. Des Vereins Dtsch. Ingenieure 1935, 77, 318–320. (In German) [Google Scholar]
- Kempe, T.; Fröhlich, J. An improved immersed boundary method with direct forcing for the simulation of particle laden flows. J. Comput. Phys. 2012, 9, 3663–3684. [Google Scholar] [CrossRef]
- Tschisgale, S.; Kempe, T.; Fröhlich, J. A general implicit direct forcing immersed boundary method for rigid particles. Comput. Fluids 2018, 170, 285–298. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef] [Green Version]
- May, R.; Gruy, F.; Fröhlich, J. Impact of particle boundary conditions on the collision rates of inclusions around a single bubble rising in liquid metal. Proc. Appl. Math. Mech. 2018, 18, e201800029. [Google Scholar] [CrossRef]
- Ma, T.; Santarelli, C.; Ziegenhein, T.; Lucas, D.; Fröhlich, J. Direct numerical simulation–based Reynolds-averaged closure for bubble-induced turbulence. Phys. Rev. Fluids 2017, 2, 034301. [Google Scholar] [CrossRef]

 1,
1,  2,
2,  3,
3,  4.
4.
 1,
1,  2,
2,  3,
3,  4.
4.


| 0.028 | 0.071 | 0.213 | 0.319 | 0.800 | 1.42 | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| Quantity | Symbol | Value | |
|---|---|---|---|
| Liquid steel properties | |||
| Fluid density | [] | ||
| Kinematic viscosity | [] | ||
| Surface tension | [] | ||
| Channel width | H | [m] | |
| Upward bulk velocity | U | [m/s] | |
| Argon properties | |||
| Bubble density | [] | ||
| Bubble diameter | [m] | ||
| Bubble gas fraction | |||
| Inclusion properties | |||
| Particle density | [] | ||
| Particle diameter | [m] | ||
| Numerical parameters | |||
| Domain size | [] | = [] | |
| Number of cells | [] | = [] | |
| Time step | |||
| Number of bubbles | |||
| Number of particles | (initial) | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kroll-Rabotin, J.-S.; Gisselbrecht, M.; Ott, B.; May, R.; Fröhlich, J.; Bellot, J.-P. Multiscale Simulation of Non-Metallic Inclusion Aggregation in a Fully Resolved Bubble Swarm in Liquid Steel. Metals 2020, 10, 517. https://doi.org/10.3390/met10040517
Kroll-Rabotin J-S, Gisselbrecht M, Ott B, May R, Fröhlich J, Bellot J-P. Multiscale Simulation of Non-Metallic Inclusion Aggregation in a Fully Resolved Bubble Swarm in Liquid Steel. Metals. 2020; 10(4):517. https://doi.org/10.3390/met10040517
Chicago/Turabian StyleKroll-Rabotin, Jean-Sébastien, Matthieu Gisselbrecht, Bernhard Ott, Ronja May, Jochen Fröhlich, and Jean-Pierre Bellot. 2020. "Multiscale Simulation of Non-Metallic Inclusion Aggregation in a Fully Resolved Bubble Swarm in Liquid Steel" Metals 10, no. 4: 517. https://doi.org/10.3390/met10040517
APA StyleKroll-Rabotin, J.-S., Gisselbrecht, M., Ott, B., May, R., Fröhlich, J., & Bellot, J.-P. (2020). Multiscale Simulation of Non-Metallic Inclusion Aggregation in a Fully Resolved Bubble Swarm in Liquid Steel. Metals, 10(4), 517. https://doi.org/10.3390/met10040517





