Extension of Barlat’s Yield Criterion to Tension–Compression Asymmetry: Modeling and Verification
Abstract
:1. Introduction
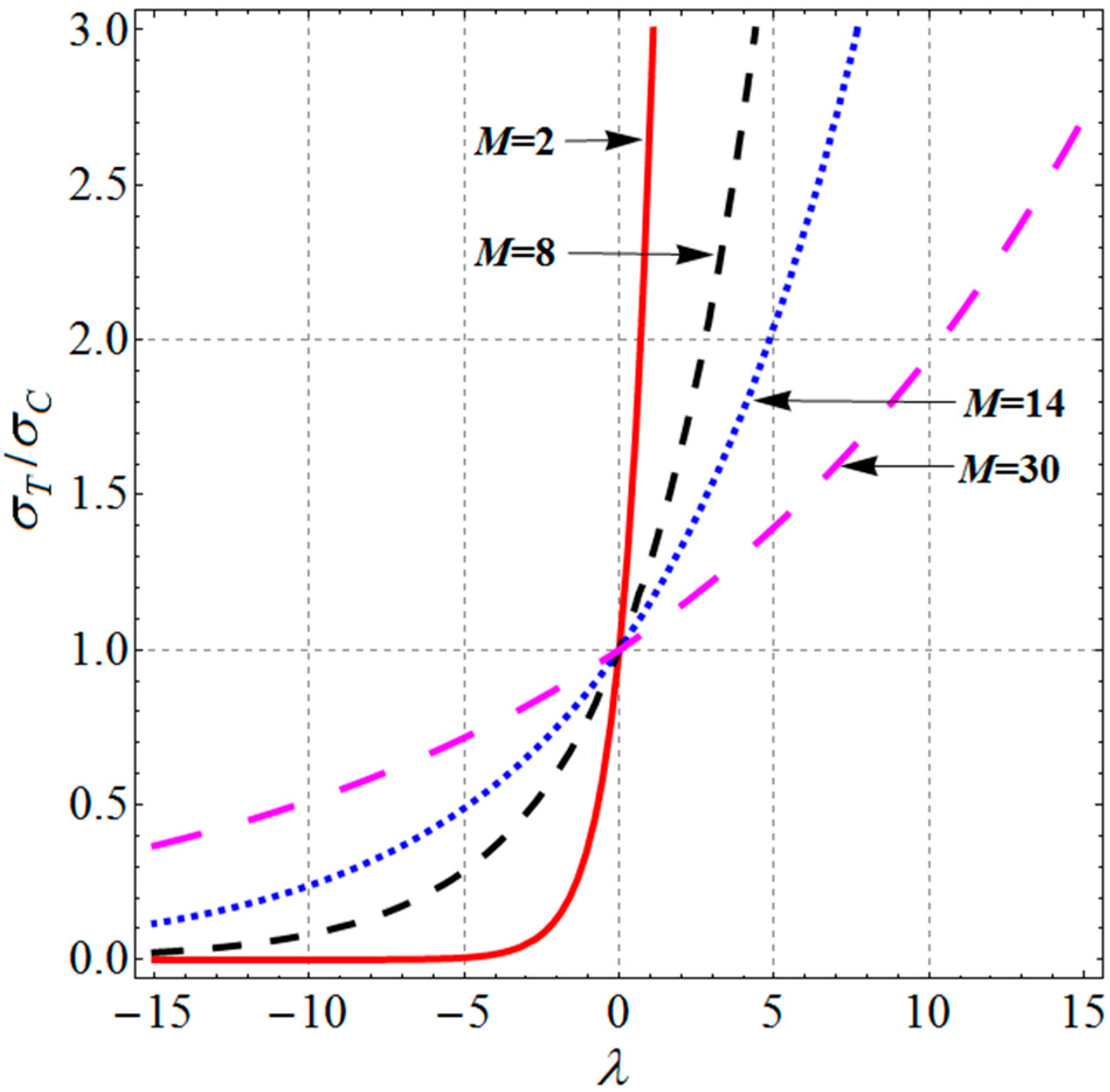
2. Extension of Barlat (1987) Isotropic Yield Criterion to Tension–Compression Asymmetry
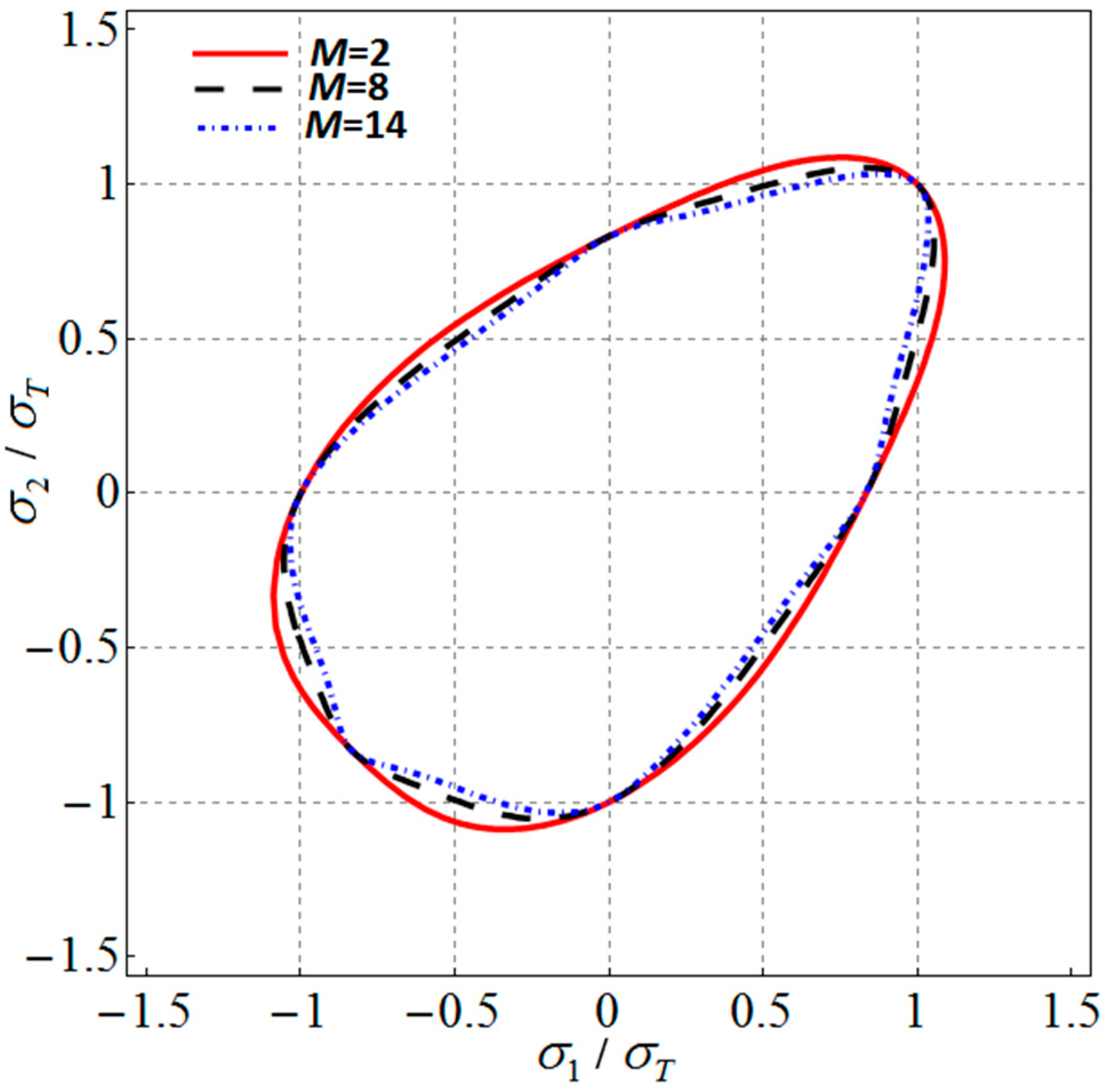
3. Extension of Barlat (1989) Anisotropic Yield Criterion to Tension–Compression Asymmetry
4. Validation and Discussion
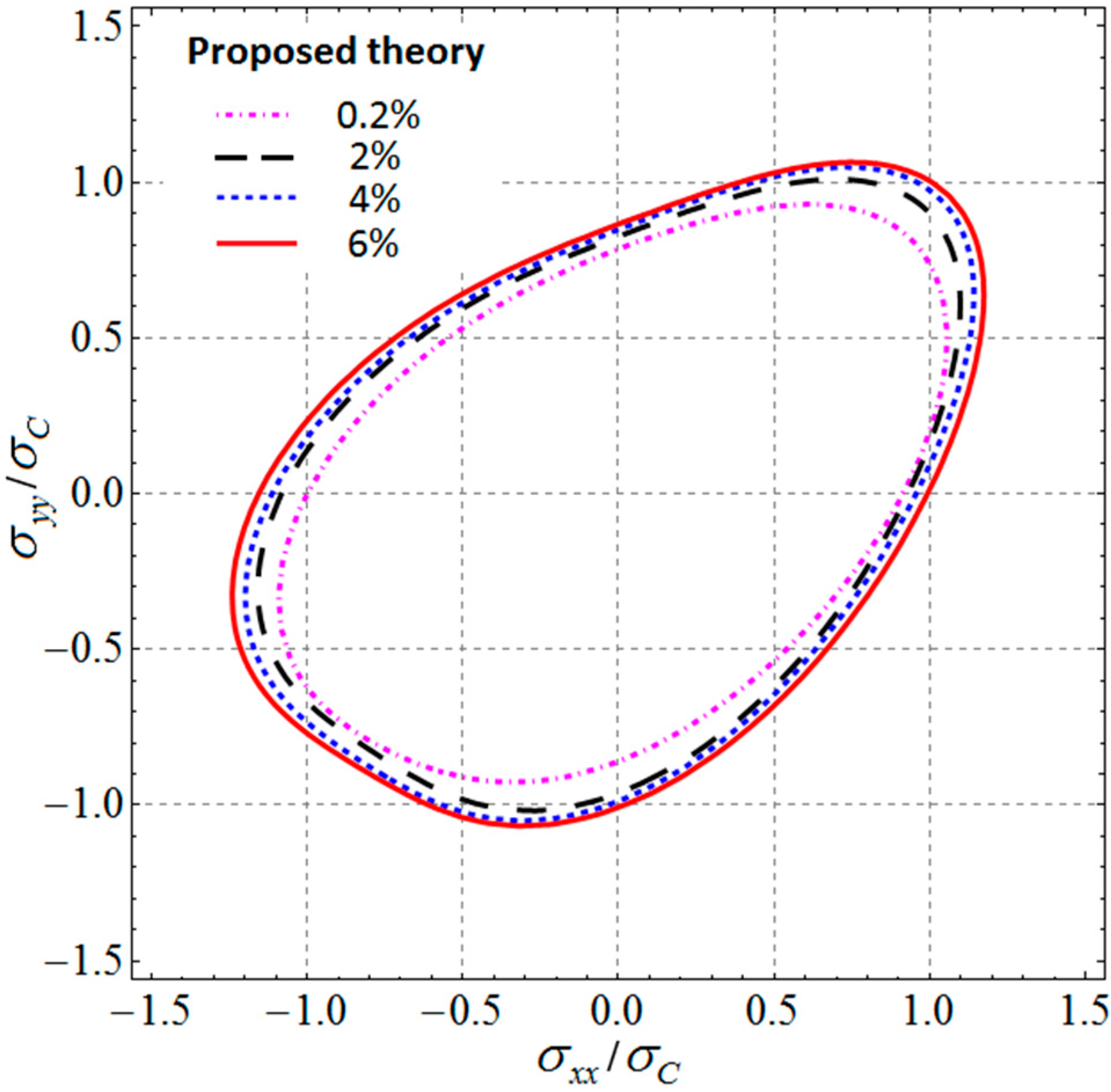
4.1. Applications to Titanium Ti-6Al-4V
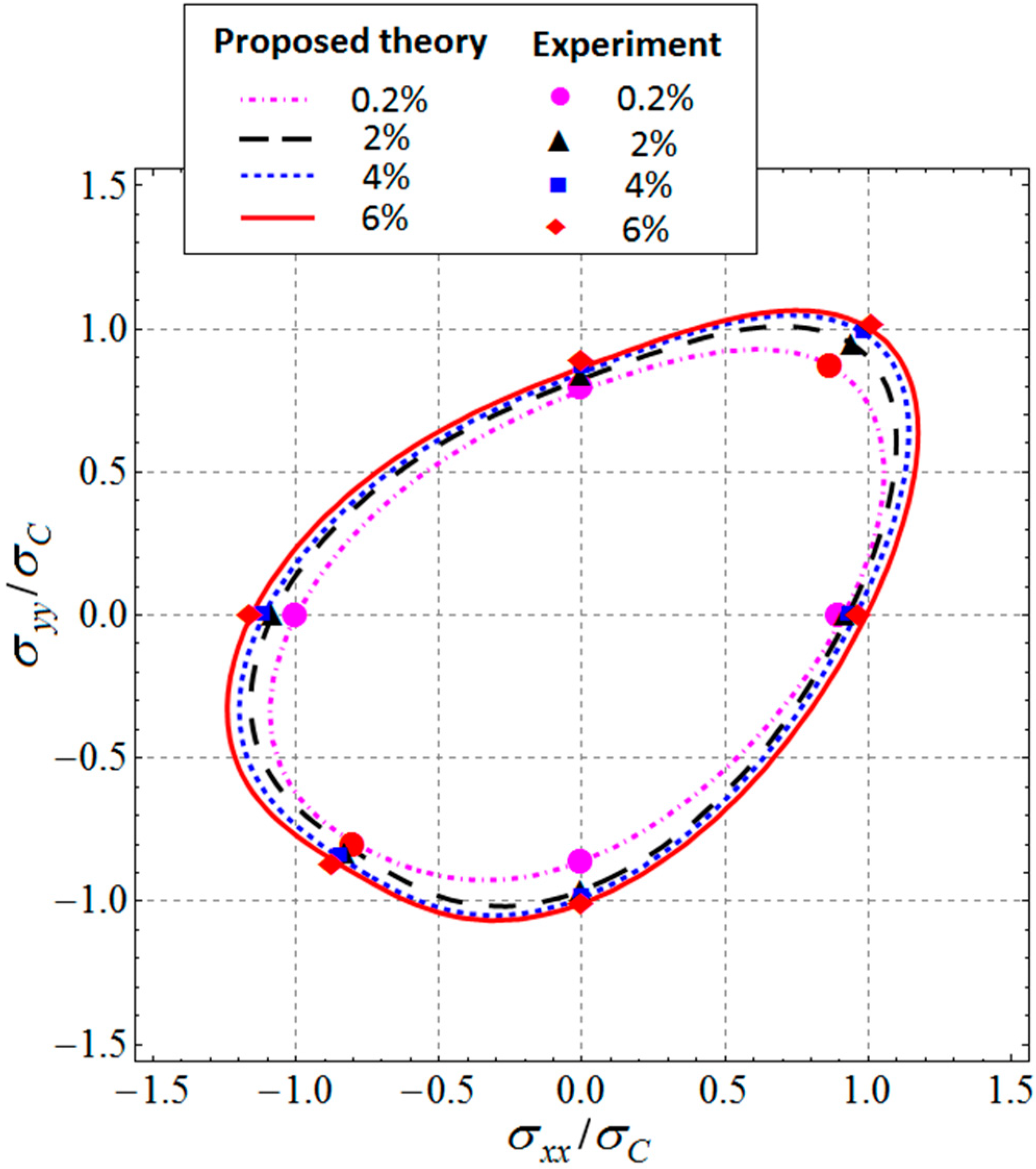
4.2. Applications to Shape Memory Alloy Cu-Al-Be
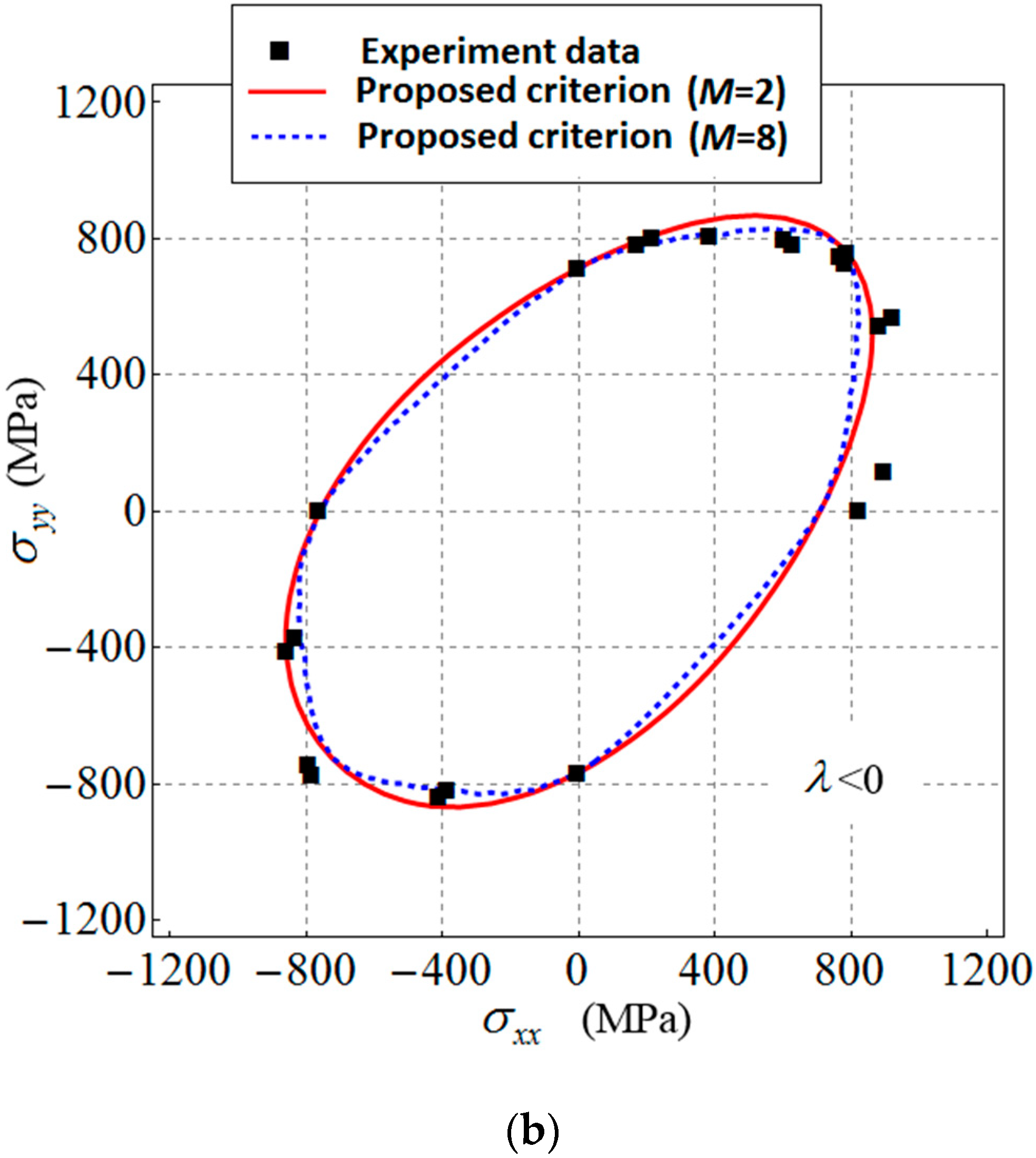
4.3. Applications to Ni3Al Based Intermetallic Alloy IC10
- I.
- the difference between experimental value and theoretical prediction in the case of uniaxial stress states;
- II.
- the normal distance between experimental point and the predicted yield locus in the case of biaxial stress states.
4.4. Applications to DP980 Steel and 6022-T4 Aluminum
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
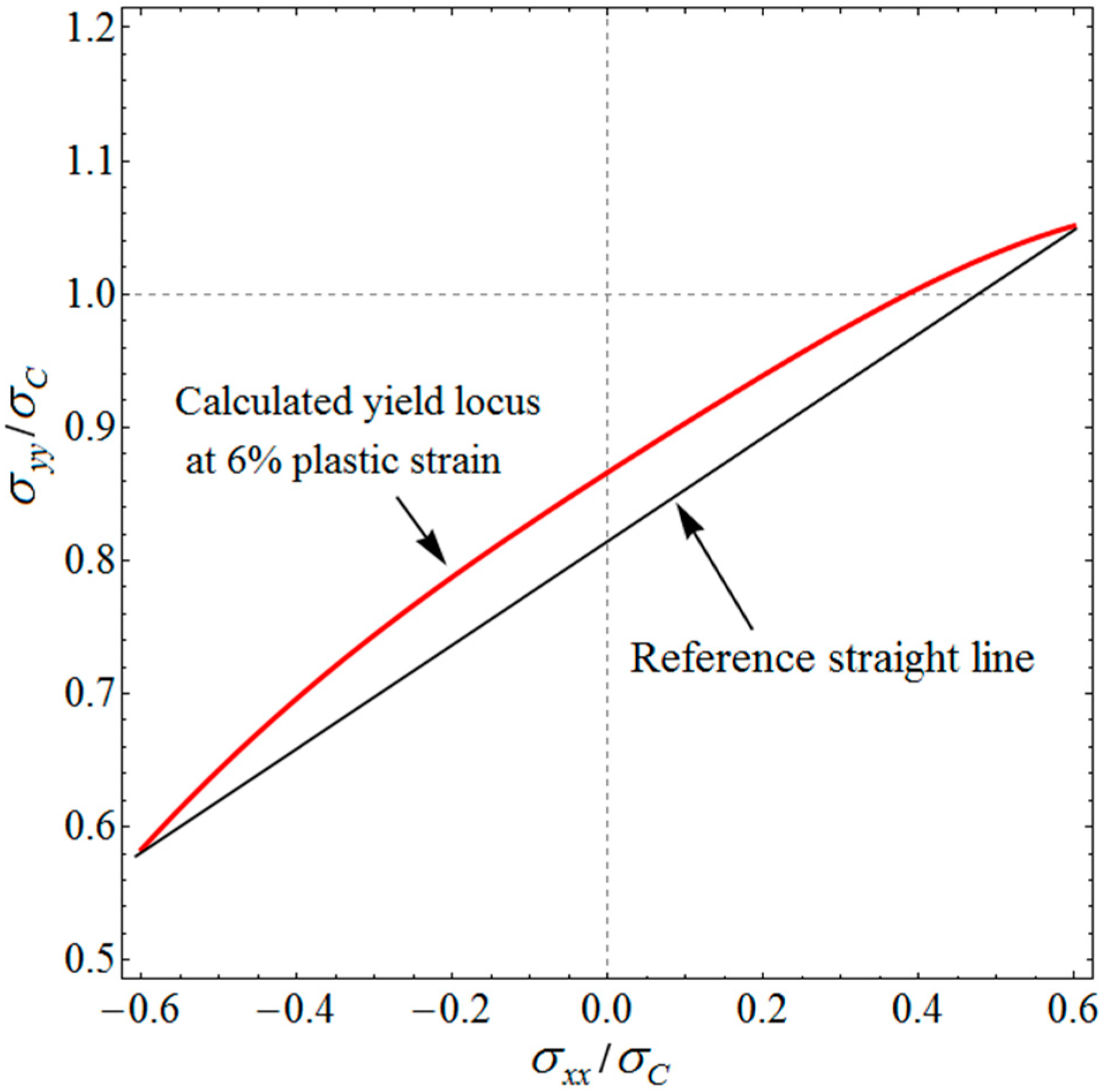
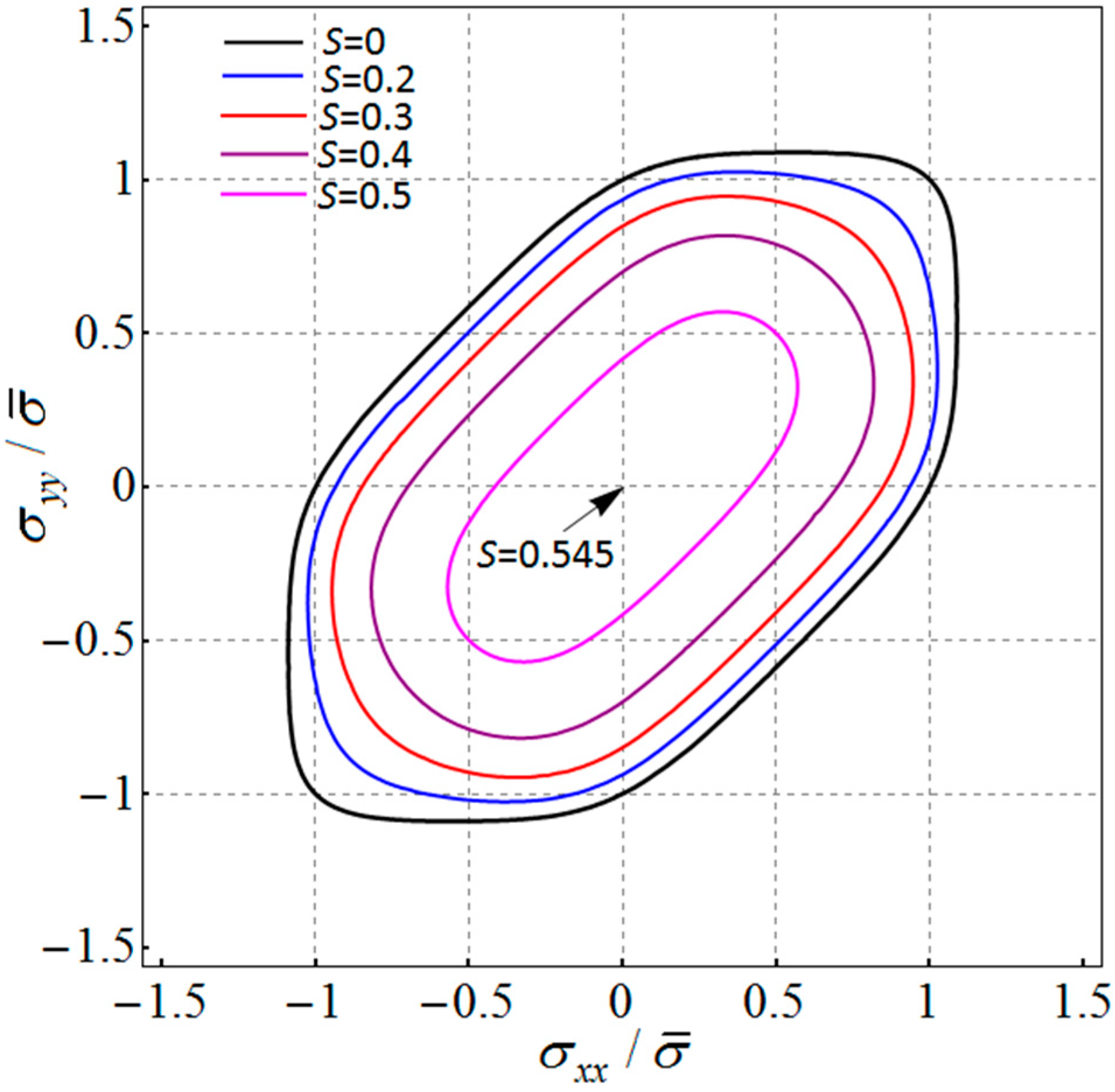
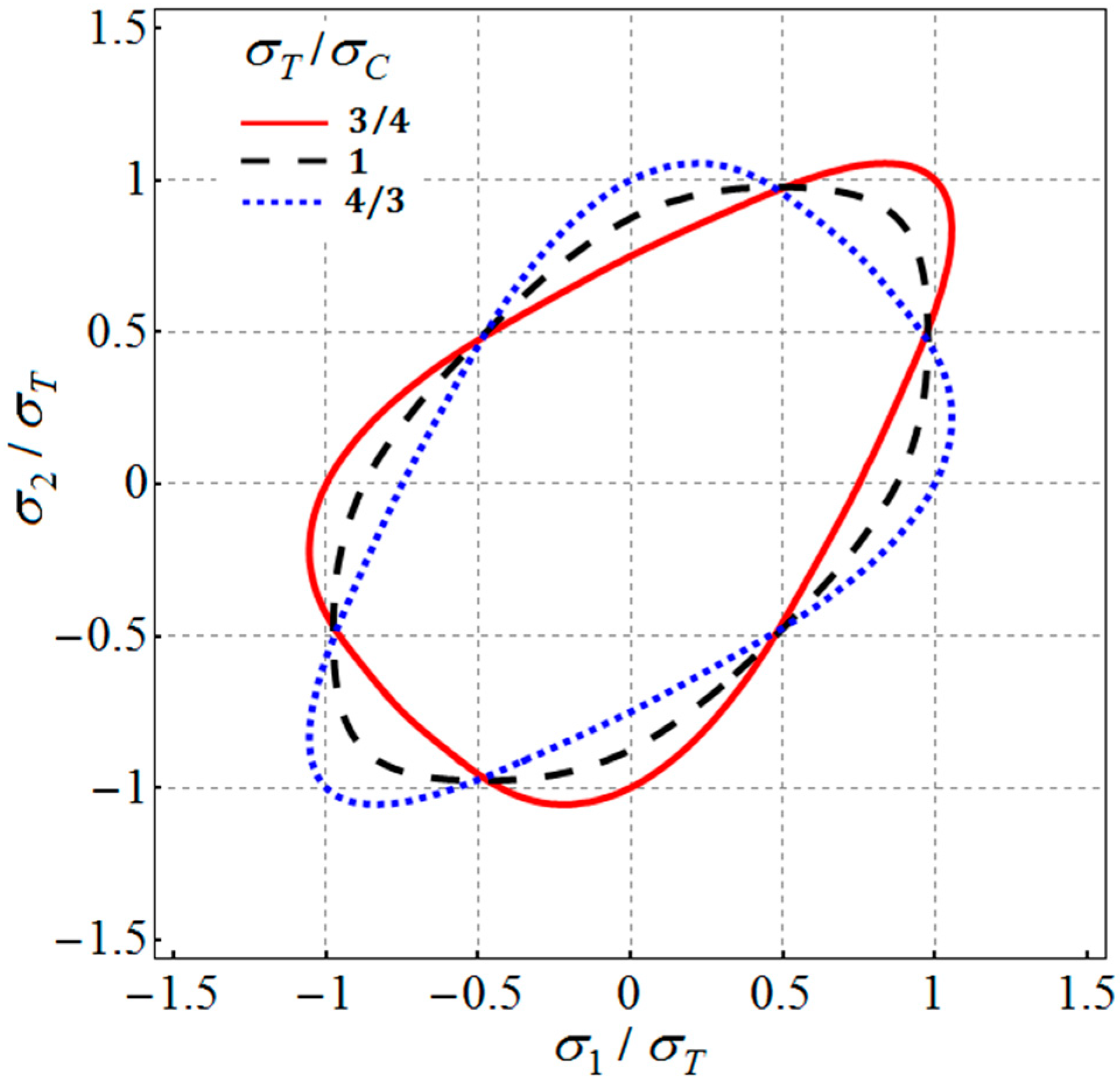
Appendix A. Discussion on the Convexity of the Proposed Yield Function
References
- Gantar, G.; Pepelnjak, T.; Kuzman, K. Optimization of sheet metal forming processes by the use of numerical simulations. J. Mater. Process. Technol. 2002, 130, 54–59. [Google Scholar] [CrossRef]
- Yang, H.; Fan, X.G.; Sun, Z.C.; Guo, L.G.; Zhan, M. Recent developments in plastic forming technology of titanium alloys. Sci. China Technol. Sci. 2011, 54, 490–501. [Google Scholar]
- Zhang, F.F.; Chen, J.S.; Chen, J.; Huang, X.Z.; Lu, J. Review on development and experimental validation for anisotropic yield criterions. Adv. Mech. 2012, 42, 68–80. (In Chinese) [Google Scholar]
- Drucker, D.C. Relation of experiments to mathematical theories of plasticity. J. Appl. Mech. 1949, 16, 349–357. [Google Scholar]
- Hershey, A.V. The plasticity of an isotropic aggregate of anisotropic face centered cubic crystals. J. Appl. Mech. Trans. ASME 1954, 21, 241–249. [Google Scholar]
- Yu, M.H.; He, L.N.; Song, L.Y. Twin shear stress strength theory and its generalization. Sci. China Ser. A 1985, 12, 1113–1120. (In Chinese) [Google Scholar]
- Zhang, S.H.; Guan, M.; Wu, G.J.; Gao, S.W.; Chen, X.D. An ellipsoidal yield criterion for porous metals with accurate descriptions of theoretical strength and Poisson’s ratio. Acta Mech. 2017, 228, 4199–4210. [Google Scholar] [CrossRef]
- Cazacu, O. New yield criteria for isotropic and textured metallic materials. Int. J. Solids Struct. 2018, 139–140, 200–210. [Google Scholar] [CrossRef]
- Zhang, S.H.; Jiang, X.R.; Xiang, C.C.; Deng, L.; Li, Y.X. Proposal and application of a new yield criterion for metal plastic deformation. Arch. Appl. Mech. 2020. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. Soc. London A 1948, 193, 281–297. [Google Scholar]
- Banabic, D. Anisotropy of Sheet Metal. In Formability of Metallic Materials; Banabic, D., Ed.; Springer: Berlin, Germany, 2000; pp. 119–172. [Google Scholar]
- Yu, M.H. Advances in strength theories for materials under complex stress state in the 20th Century. Appl. Mech. Rev. 2002, 55, 198–218. [Google Scholar] [CrossRef]
- Hill, R. Theoretical plasticity of textured aggregates. Math. Proc. Camb. Phil. Soc. 1979, 85, 179–191. [Google Scholar] [CrossRef]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hill, R. A user-friendly theory of orthotropic plasticity in sheet metals. Int. J. Mech. Sci. 1993, 35, 19–25. [Google Scholar] [CrossRef]
- Hill, R.; Hecker, S.S.; Stout, M.G. An investigation of plastic flow and differential work hardening in orthotropic brass tubes under fluid pressure and axial load. Int. J. Solids Struct. 1994, 31, 2999–3021. [Google Scholar] [CrossRef]
- Hosford, W.F. Texture strengthening. Met. Eng. Quart. 1966, 6, 13–19. [Google Scholar]
- Hosford, W.F. A generalized isotropic yield criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Hosford, W.F.; Allen, T.J. Twining and directional slip as a cause for strength differential effect. Met. Trans. 1973, 4, 1424–1425. [Google Scholar] [CrossRef]
- Barlat, F.; Richmond, O. Prediction of tricomponent plane stress yield surfaces and associated flow and failure behavior of strongly textured F.C.C. polycrystalline sheets. Mater. Sci. Eng. 1987, 95, 15–29. [Google Scholar] [CrossRef]
- Barlat, F.; Lian, J. Plastic behavior and stretchability of sheet Metals. Part I: Yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dicke, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.H.; Chuh, E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Barlat, F.; Yoon, J.W.; Cazacu, O. On linear transformations of stress tensors for the description of plastic anisotropy. Int. J. Plast. 2007, 23, 876–896. [Google Scholar] [CrossRef]
- Cazacu, O. New mathematical results and explicit expressions in terms of the stress components of Barlat et al. (1991) orthotropic yield criterion. Int. J. Solids Struct. 2019, 176, 86–95. [Google Scholar] [CrossRef]
- Gröger, R.; Vitek, V. Impact of non-Schmid stress components present in the yield criterion for bcc metals on the activity of {110}<111> slip systems. Comput. Mater. Sci. 2019, 159, 297–305. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, B.K.; Pang, Y. Numerical investigation of evolution of earing, anisotropic yield and plastic potentials in cold rolled FCC aluminum alloy based on the crystallographic texture measurements. Eur. J. Mech. A Solids 2019, 75, 41–55. [Google Scholar] [CrossRef]
- Lou, Y.S.; Yoon, J.W. Alternative approach to model ductile fracture by incorporating anisotropic yield function. Int. J. Solids Struct. 2019, 164, 12–24. [Google Scholar] [CrossRef]
- Wang, X.S.; Hu, W.L.; Huang, S.J.; Ding, R. Experimental investigations on extruded 6063 aluminum alloy tubes under complex tension–compression stress states. Int. J. Solids Struct. 2019, 168, 123–137. [Google Scholar] [CrossRef]
- Cazacu, O. New expressions and calibration strategies for Karafillis and Boyce (1993) yield criterion. Int. J. Solids Struct. 2020, 186, 410–422. [Google Scholar] [CrossRef]
- Ezz, S.S.; Pope, D.P.; Paidar, V. The tension/compression flow stress asymmetry in Ni3 (Al, Nb) single crystals. Acta Metall. 1982, 30, 921–926. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals. Int. J. Plast. 2004, 20, 2027–2045. [Google Scholar] [CrossRef]
- Plunkett, B.; Cazacu, O.; Barlat, F. Orthotropic yield criteria for description of the anisotropy in tension and com-pression of sheet metals. Int. J. Plast. 2008, 24, 847–866. [Google Scholar] [CrossRef]
- Cazacu, O.; Ioan, R.I.; Yoon, J.W. Orthotropic strain rate potential for the description of anisotropy in tension and compression of metals. Int. J. Plast. 2010, 26, 887–904. [Google Scholar] [CrossRef]
- Lou, Y.S.; Huh, H.; Yoon, J.W. Consideration of strength differential effect in sheet metals with symmetric yield functions. Int. J. Mech. Sci. 2013, 66, 214–223. [Google Scholar] [CrossRef]
- Chen, L.; Wen, W.D.; Cui, H.T. Generalization of Hill’s yield criterion to tension–compression asymmetry materials. Sci. China Technol. Sci. 2013, 56, 89–97. [Google Scholar] [CrossRef]
- Cazacu, O.; Stewart, J.B. Analytical criterion for porous solids containing cylindrical voids in an incompressible matrix exhibiting tension–compression asymmetry. Philos. Mag. 2013, 93, 1520–1548. [Google Scholar] [CrossRef]
- Yoon, J.W.; Lou, Y.S.; Yoon, J.H.; Glazoff, M.V. Asymmetric yield function based on the stress invariants for pressure sensitive metals. Int. J. Plast. 2014, 56, 184–202. [Google Scholar] [CrossRef]
- Tang, B.T.; Wang, Z.M.; Guo, N.; Wang, Q.L.; Liu, P.X. An Extended Drucker Yield Criterion to Consider Tension–Compression Asymmetry and Anisotropy on Metallic Materials: Modeling and Verification. Metals 2020, 10, 20. [Google Scholar] [CrossRef] [Green Version]
- Verma, R.K.; Kuwabara, T.; Chung, K.; Haldar, A. Experimental evaluation and constitutive modeling of non-proportional deformation for asymmetric steels. Int. J. Plast. 2011, 27, 82–101. [Google Scholar] [CrossRef]
- Steglich, D.; Brocks, W.; Bohlen, J.; Barlat, F. Modeling direction-dependent hardening in magnesium sheet forming simulations. Int. J. Mater Form. 2011, 4, 243–253. [Google Scholar] [CrossRef] [Green Version]
- Andar, M.O.; Kuwabara, T.; Steglich, D. Material modeling of AZ31 Mg sheet considering variation of r-values and asymmetry of the yield locus. Mater. Sci. Eng. A 2012, 549, 82–92. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Worswick, M.J. Application of an Evolving Non-Associative Anisotropic-Asymmetric Plasticity Model for a Rare-Earth Magnesium Alloy. Metals 2018, 8, 1013. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.S.; Yu, S.J.; Liu, H.W. Deformation induced anisotropic responses of Ti–6Al–4V alloy Part II: A strain rate and temperature dependent anisotropic yield criterion. Int. J. Plast. 2012, 7, 14–26. [Google Scholar] [CrossRef]
- Khan, A.S.; Yu, S.J. Deformation induced anisotropic responses of Ti–6Al–4V alloy, Part I: Experiments. Int. J. Plast. 2012, 38, 1–13. [Google Scholar] [CrossRef]
- Bouvet, C.; Calloch, S.; Lexcellent, C. Mechanical behavior of a Cu–Al–Be shape memory alloy under multiaxial proportional and non-proportional loadings. J. Eng. Mater. Technol. 2002, 124, 112–124. [Google Scholar] [CrossRef]
- Zhao, X.H.; Huang, Z.H.; Tan, Y.N.; Zhang, Q.; Jia, X.Y.; Xu, H.B. New Ni3Al-based directionally-solidified superalloy IC10. J. Aeronaut. Mater. 2006, 26, 20–24. (In Chinese) [Google Scholar]
- Chen, L.; Wen, W.D.; Cui, H.T. Yielding description for a Ni3Al based intermetallic alloy. Mater Des. 2012, 41, 192–197. [Google Scholar] [CrossRef]
- Hama, T.; Kuroda, M.; Kuwabara, T.; Takahashi, S.; Yamanaka, A. DP980 material characterization for benchmark 1 of Numisheet 2018. In Proceedings of the 11th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes, Tokyo, Japan, 30 July–3 August 2018. [Google Scholar]
- Barlat, F.; Maeda, Y.; Chung, K.; Yanagawa, M.; Brem, J.C.; Hayashida, Y.; Lege, D.J.; Matsui, K.; Murtha, S.J.; Hattori, S.; et al. Yield function development for aluminum alloy sheets. J. Mech. Phys. Solids 1997, 45, 1727–1763. [Google Scholar] [CrossRef]




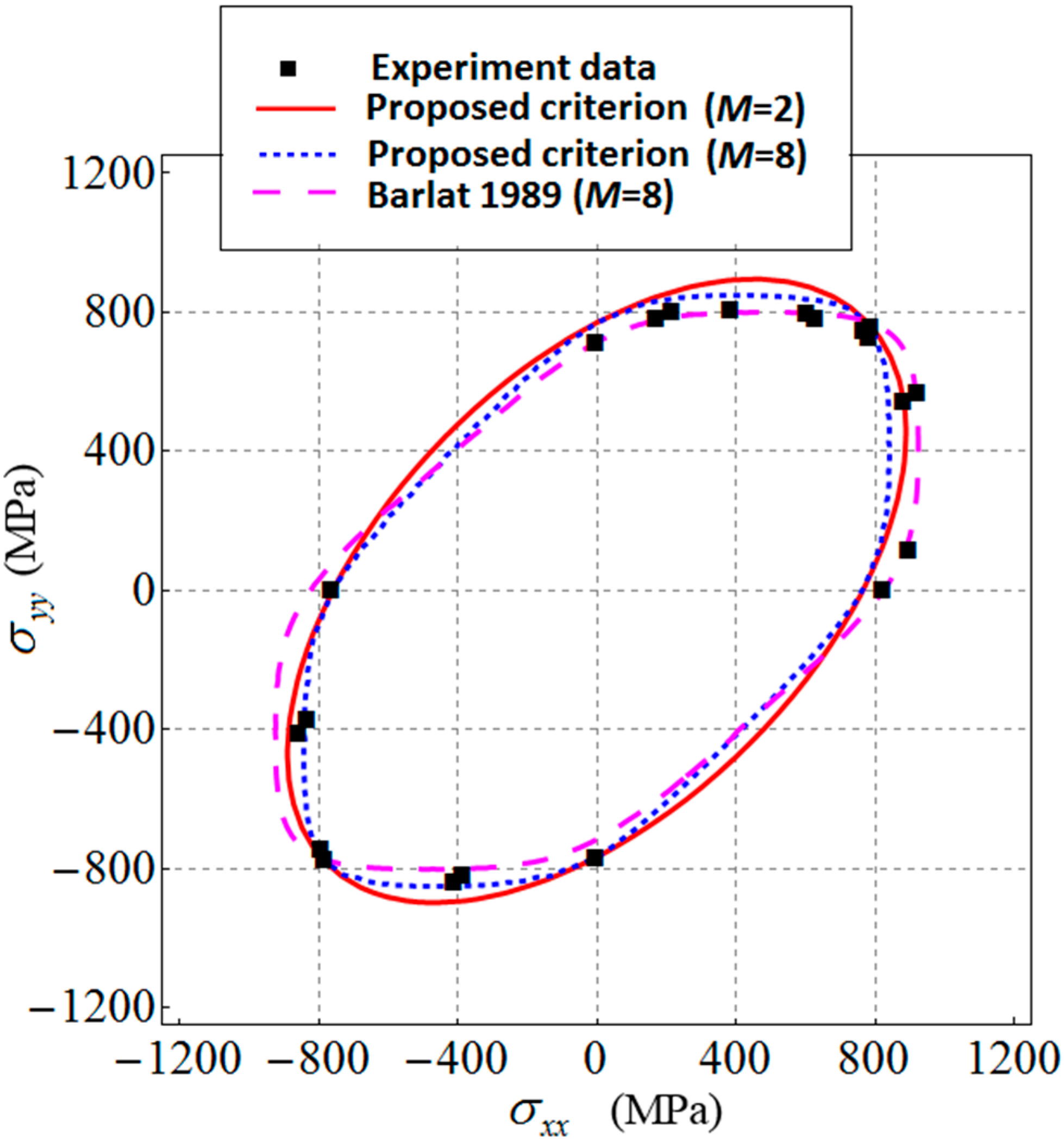
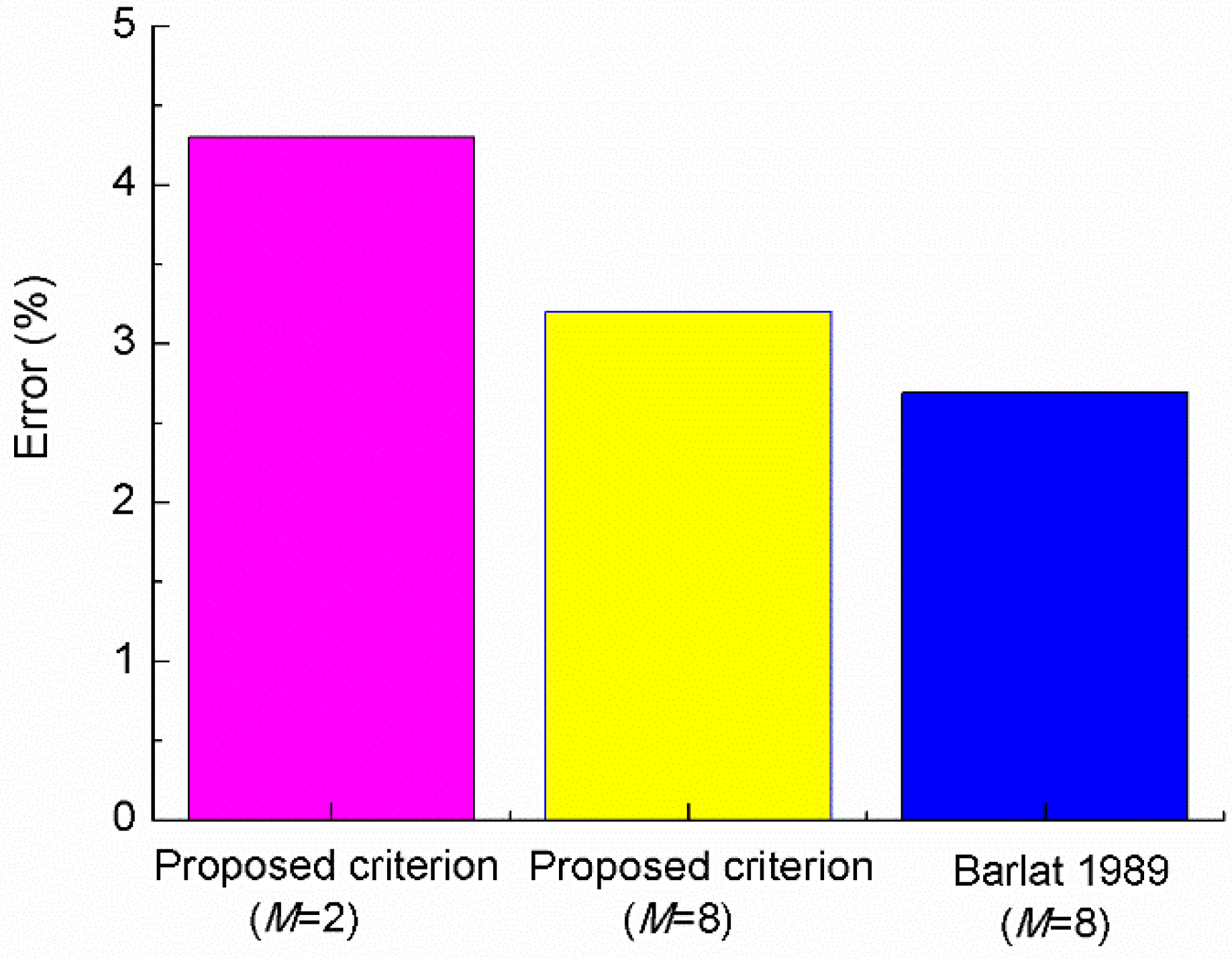
| Cazacu 2004 [32] | Chen 2013 [36] | Yoon 2014 [38] | Present Paper |
|---|---|---|---|
| 11 | 7 | 9 | 5 |
| Plastic Strain | ||||||
|---|---|---|---|---|---|---|
| 0.2% 2% 4% 6% | 0.900 0.920 0.936 0.967 | 1.000 1.082 1.113 1.156 | 0.800 0.863 0.868 0.890 | 0.860 0.962 0.988 1.008 | 0.870 0.946 0.985 1.013 | 0.800 0.830 0.845 0.870 |
| Plastic Strain | h | a | c | |
|---|---|---|---|---|
| 0.2% 2% 4% 6% | 1.163 1.125 1.127 1.147 | 0.557 0.491 0.452 0.426 | 0.443 0.363 0.356 0.322 | −0.089 −0.151 −0.151 −0.152 |
| Yield Criterion | h | a | c | |
|---|---|---|---|---|
| Extended Barlat 1989 (M = 2) Extended Barlat 1989 (M = 8) Barlat 1989 (M = 8) | 1.03 1.03 1.03 | 4.572 × 10−5 3.483 × 10−17 0.882 | 4.854 × 10−5 4.412 × 10−17 1.118 | −0.196 −0.784 - |
| Plastic Strain | |||||
|---|---|---|---|---|---|
| 0.2% | 825 | 760 | 715 | 766 | 775 |
| Yield Criterion | h | a | c | ||
|---|---|---|---|---|---|
| Extended Barlat 1989 (M = 2) Extended Barlat 1989 (M = 8) | 0.992 0.992 | 8.39 × 10−7 3.963 × 10−24 | 8.923 × 10−7 5.022 × 10−24 | 0.082 0.328 | −0.069 −0.276 |
| Yield Criterion | h | a | c | |
|---|---|---|---|---|
| Extended Barlat 1989 (M = 2) Extended Barlat 1989 (M = 8) Barlat 1989 (M = 8) | 0.992 0.992 1.154 | 8.39 × 10−7 3.963 × 10−24 0.796 | 8.923 × 10−7 5.022 × 10−24 1.204 | 0.007 0.026 - |
| Yield Criterion | h | a | c | p | |
|---|---|---|---|---|---|
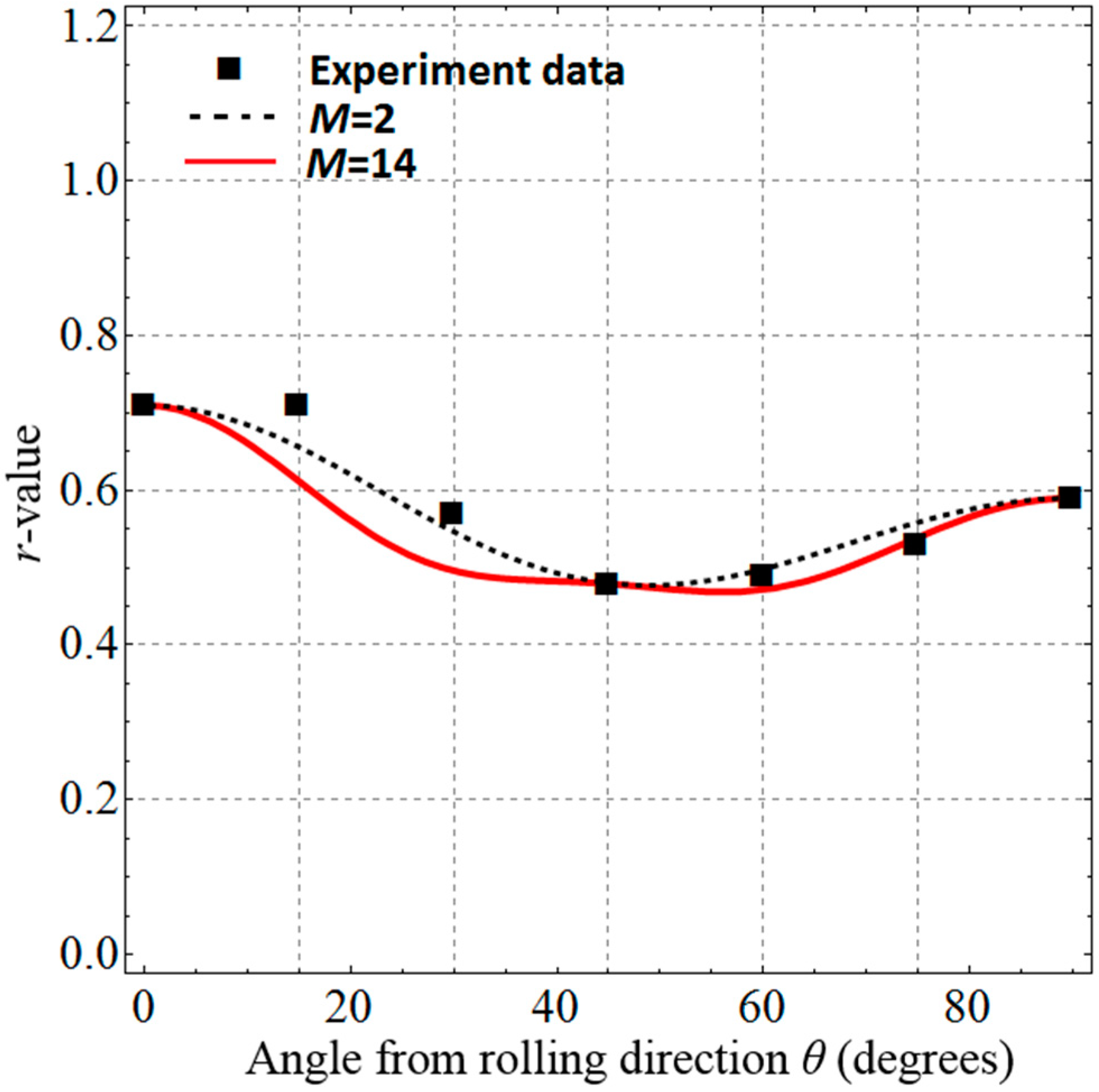
| Extended Barlat 1989 (M = 2) Extended Barlat 1989 (M = 8) | 0.915 0.915 | 1.108 1.108 | 0.892 0.892 | 0.739 0.852 | 0 0 |
| Yield Criterion | h | a | c | p | |
|---|---|---|---|---|---|
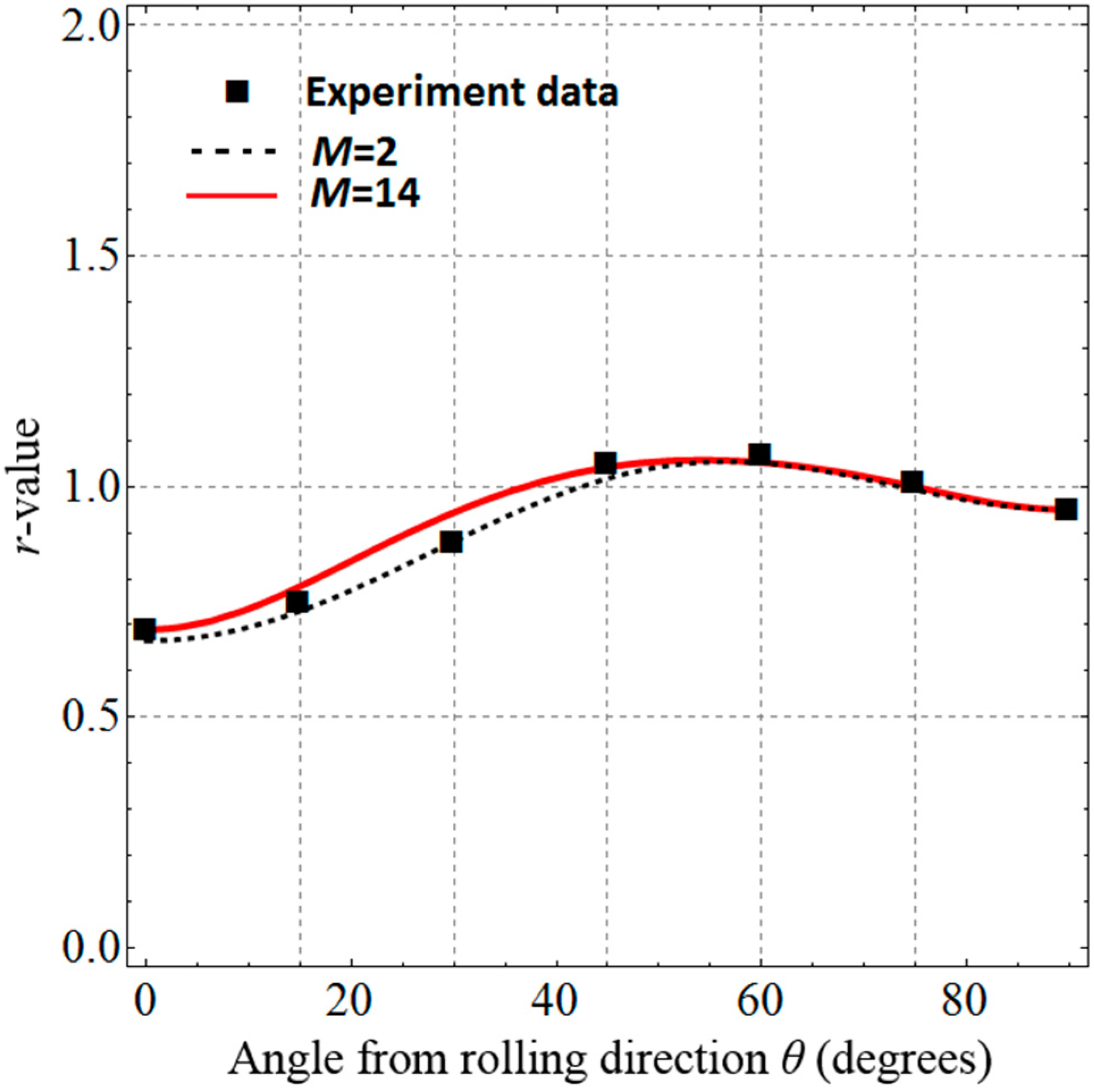
| Extended Barlat 1989 (M = 2) Extended Barlat 1989 (M = 14) | 1.058 1.058 | 1.215 1.215 | 0.785 0.758 | 0.672 0.809 | 0 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhang, H.; Song, M. Extension of Barlat’s Yield Criterion to Tension–Compression Asymmetry: Modeling and Verification. Metals 2020, 10, 713. https://doi.org/10.3390/met10060713
Chen L, Zhang H, Song M. Extension of Barlat’s Yield Criterion to Tension–Compression Asymmetry: Modeling and Verification. Metals. 2020; 10(6):713. https://doi.org/10.3390/met10060713
Chicago/Turabian StyleChen, Lei, Hongying Zhang, and Mitao Song. 2020. "Extension of Barlat’s Yield Criterion to Tension–Compression Asymmetry: Modeling and Verification" Metals 10, no. 6: 713. https://doi.org/10.3390/met10060713
APA StyleChen, L., Zhang, H., & Song, M. (2020). Extension of Barlat’s Yield Criterion to Tension–Compression Asymmetry: Modeling and Verification. Metals, 10(6), 713. https://doi.org/10.3390/met10060713




