CFD Investigation of Bath Flow and Its Related Alumina Transmission in Aluminum Reduction Cells: Slotted Anodes and Busbar Designs
Abstract
1. Introduction
2. Model Description and Cases Design
2.1. Model Description
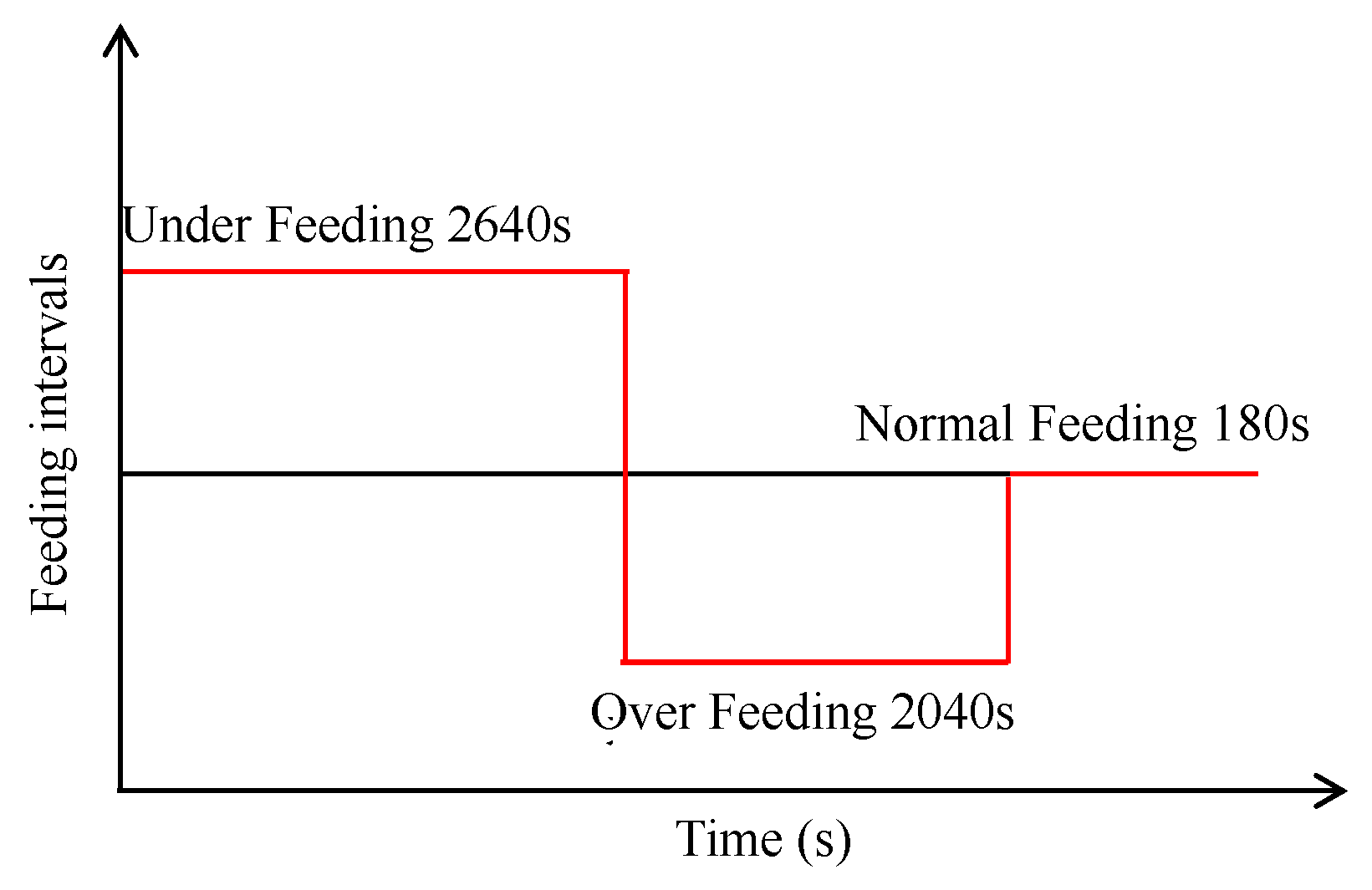
Step 1: Bath Flow
Step 2: Alumina Transmission
2.2. Case Design
3. Results and Discussion
3.1. Base Case
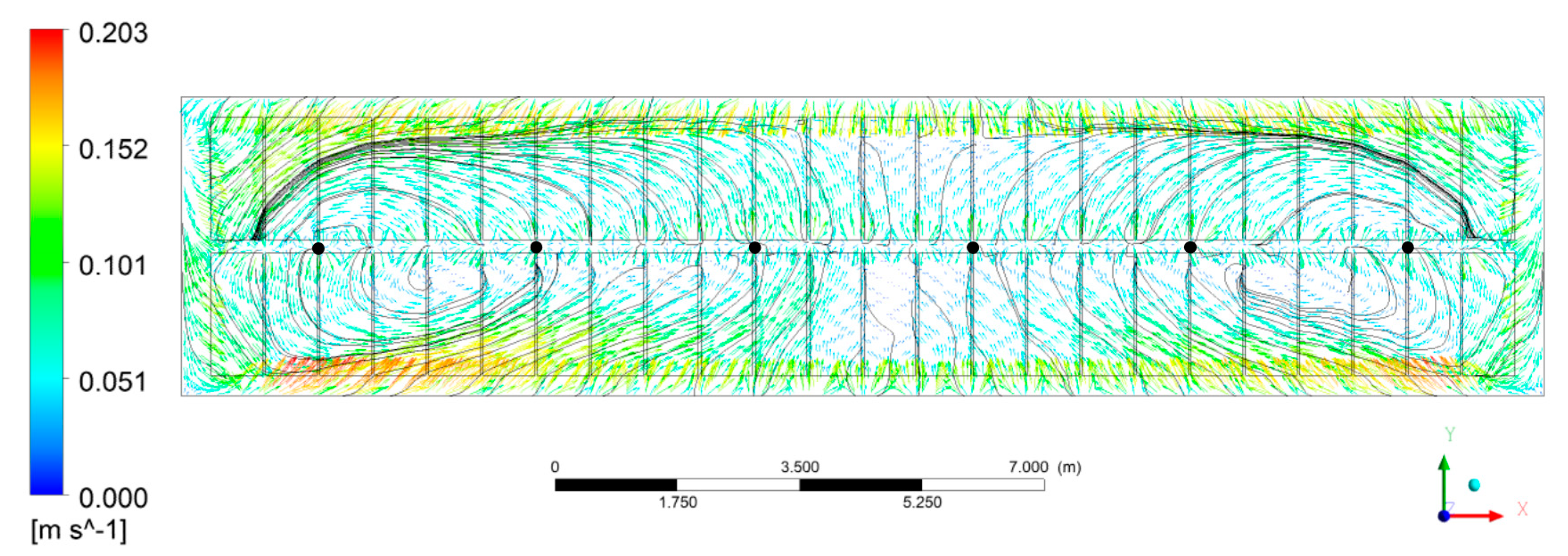
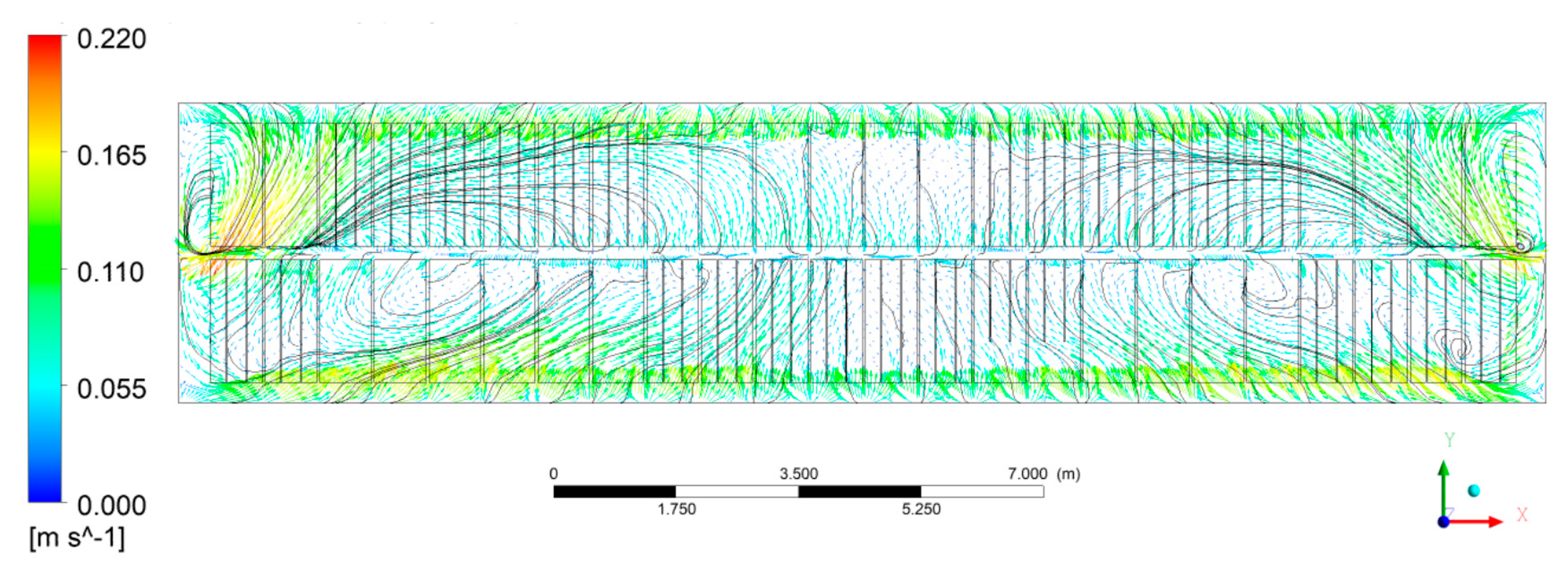
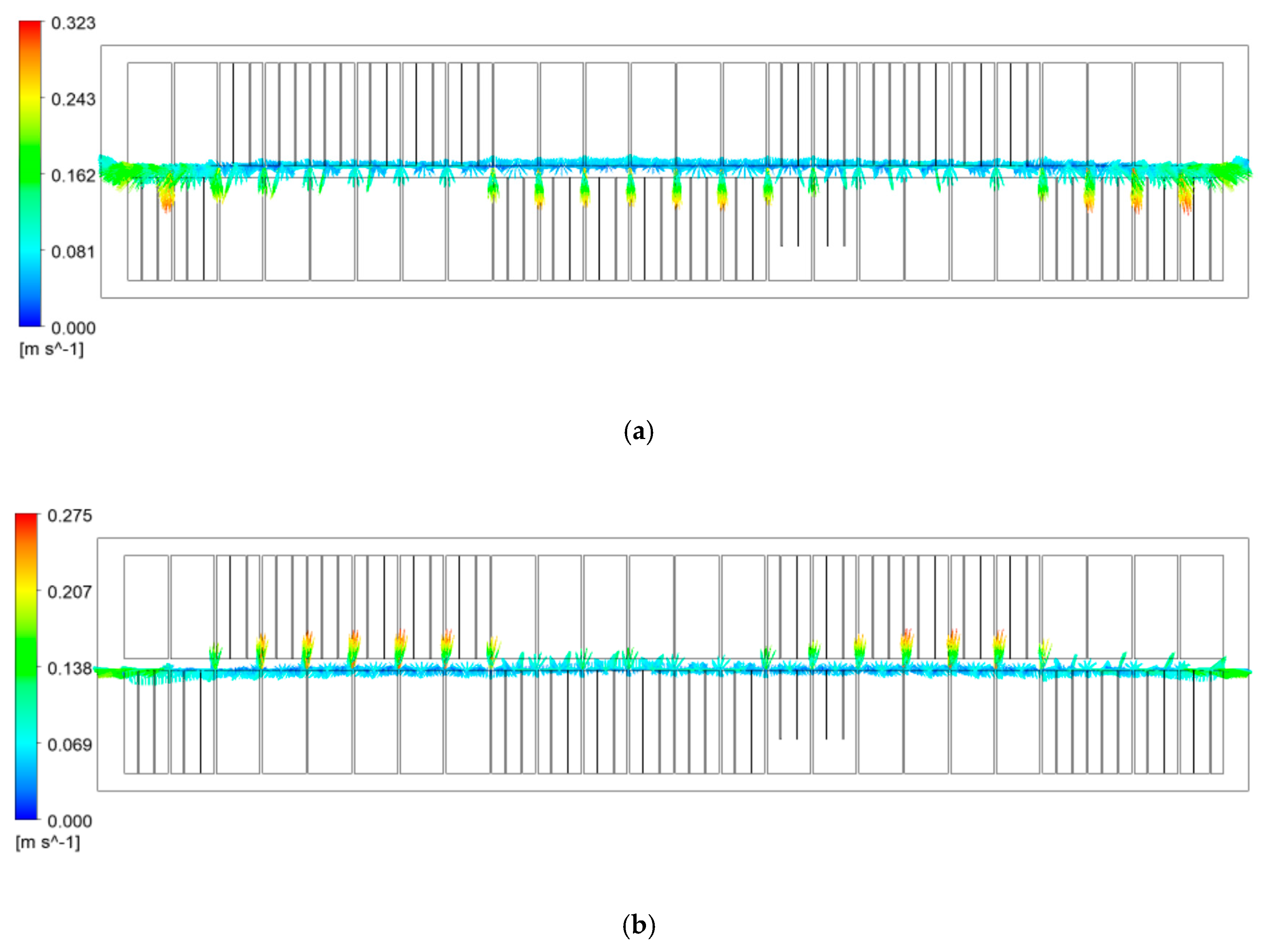
3.1.1. Bath Flow
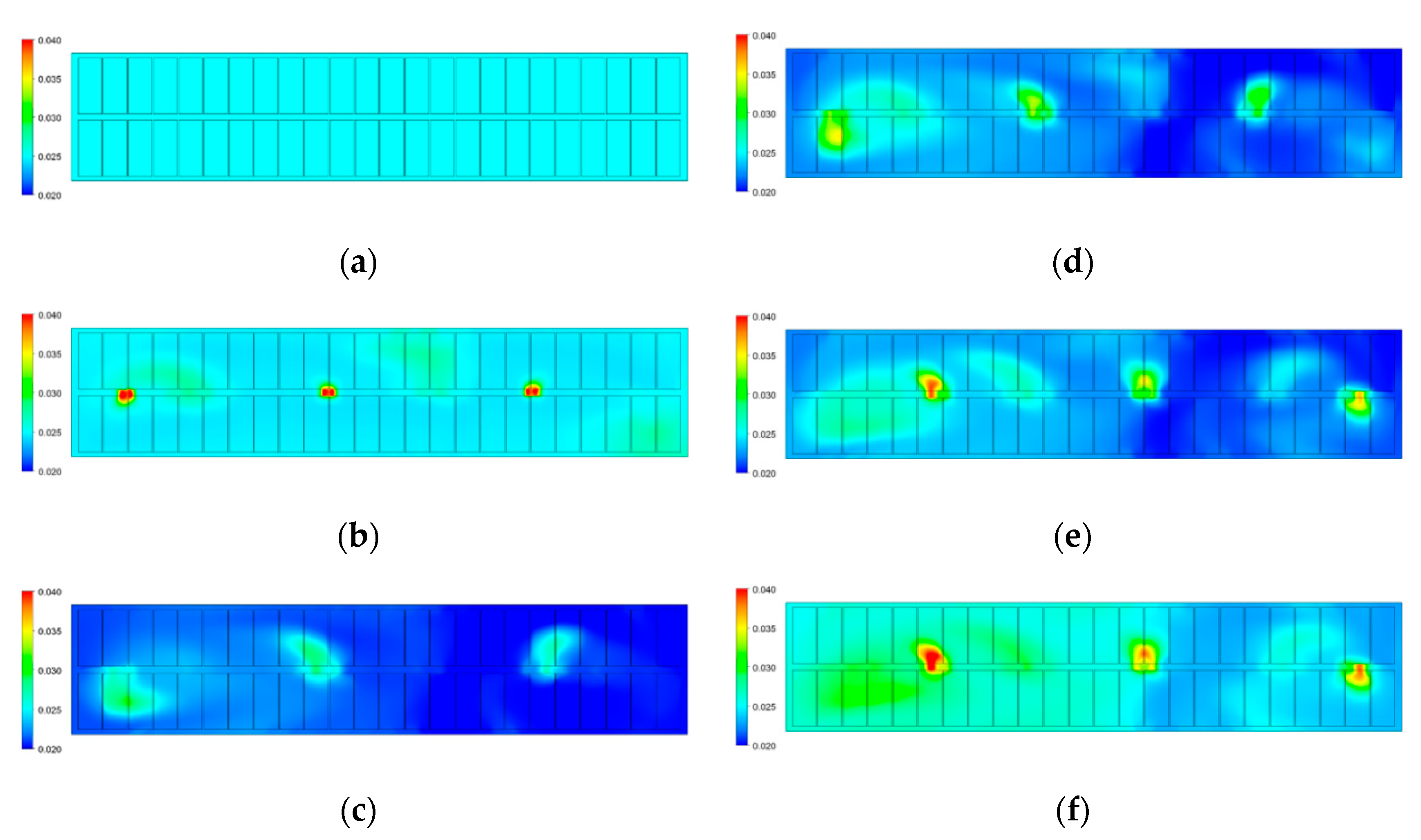
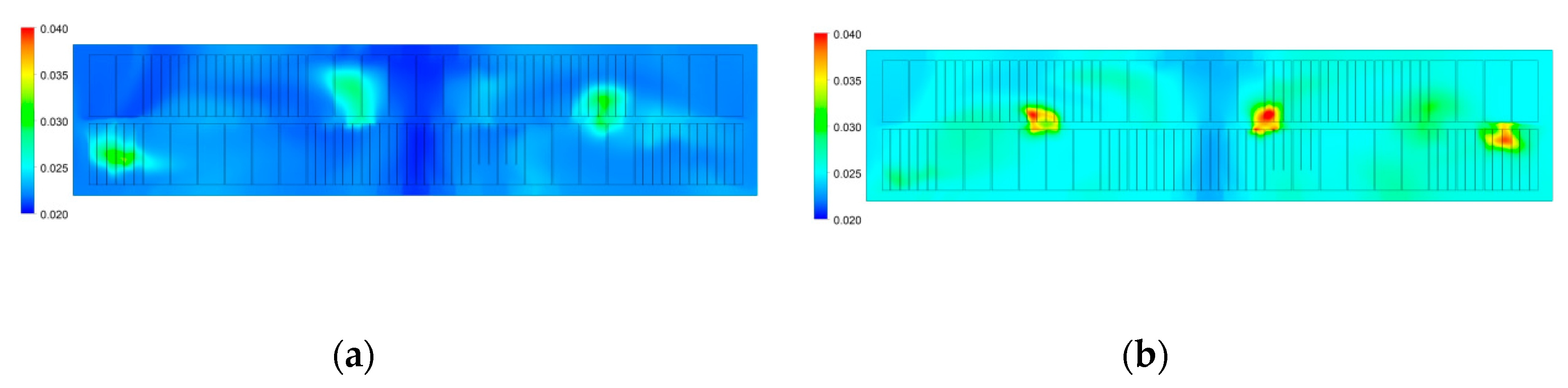
3.1.2. Characteristics of Alumina Distribution
3.2. Effect of Slots
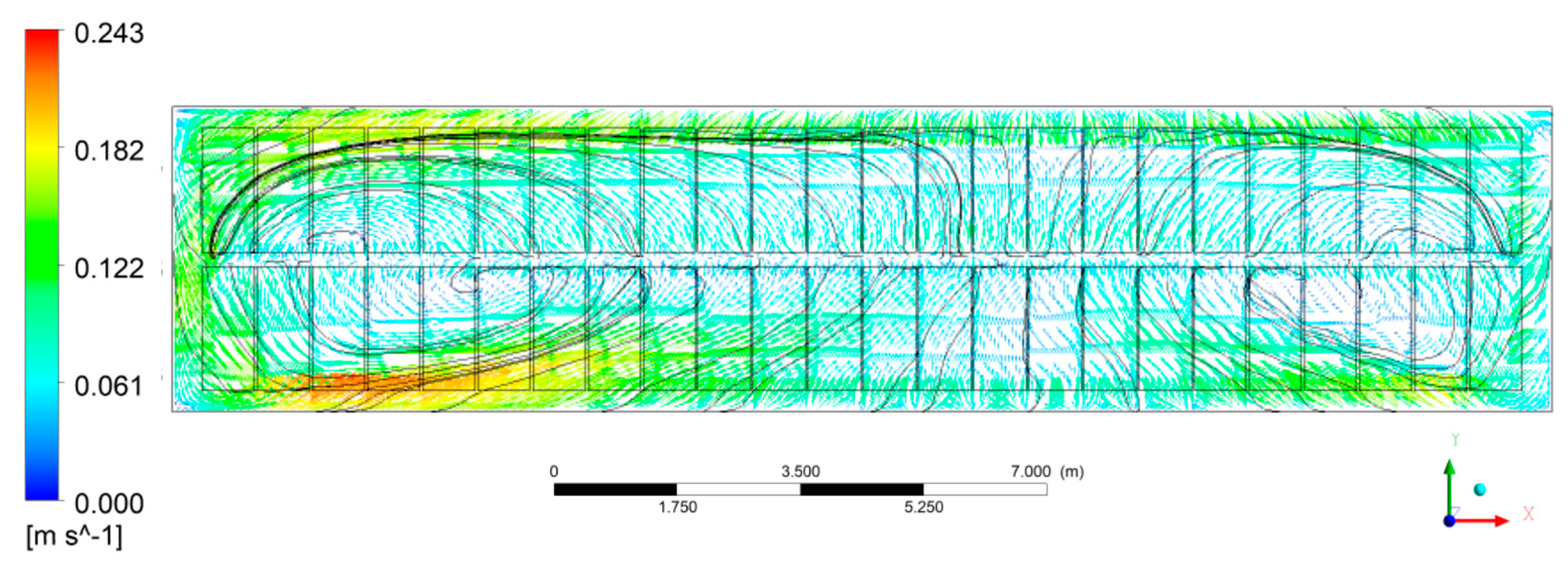
3.2.1. Bath Flow
3.2.2. Alumina Transmission
3.3. Effect of Busbar Design
3.3.1. Bath Flow
3.3.2. Alumina Transmission
4. Conclusions
- The bath flow driven by bubbles, electromagnetic force, and aluminum drag force presents two different size vortices in the horizontal plane in the middle of the ACD region, of which the larger one at the duct end occupied the region of feeding points 4, 5, and 6, while the smaller one near to the tap end covered the area of feeding points 1 and 2. Feeding point 3 was located on the boundary of the two vortices.
- The larger velocity or stronger turbulence presented at the cross section of the inter-anode gaps and the center channel would be beneficial to heat the cold alumina added from the feeding points here.
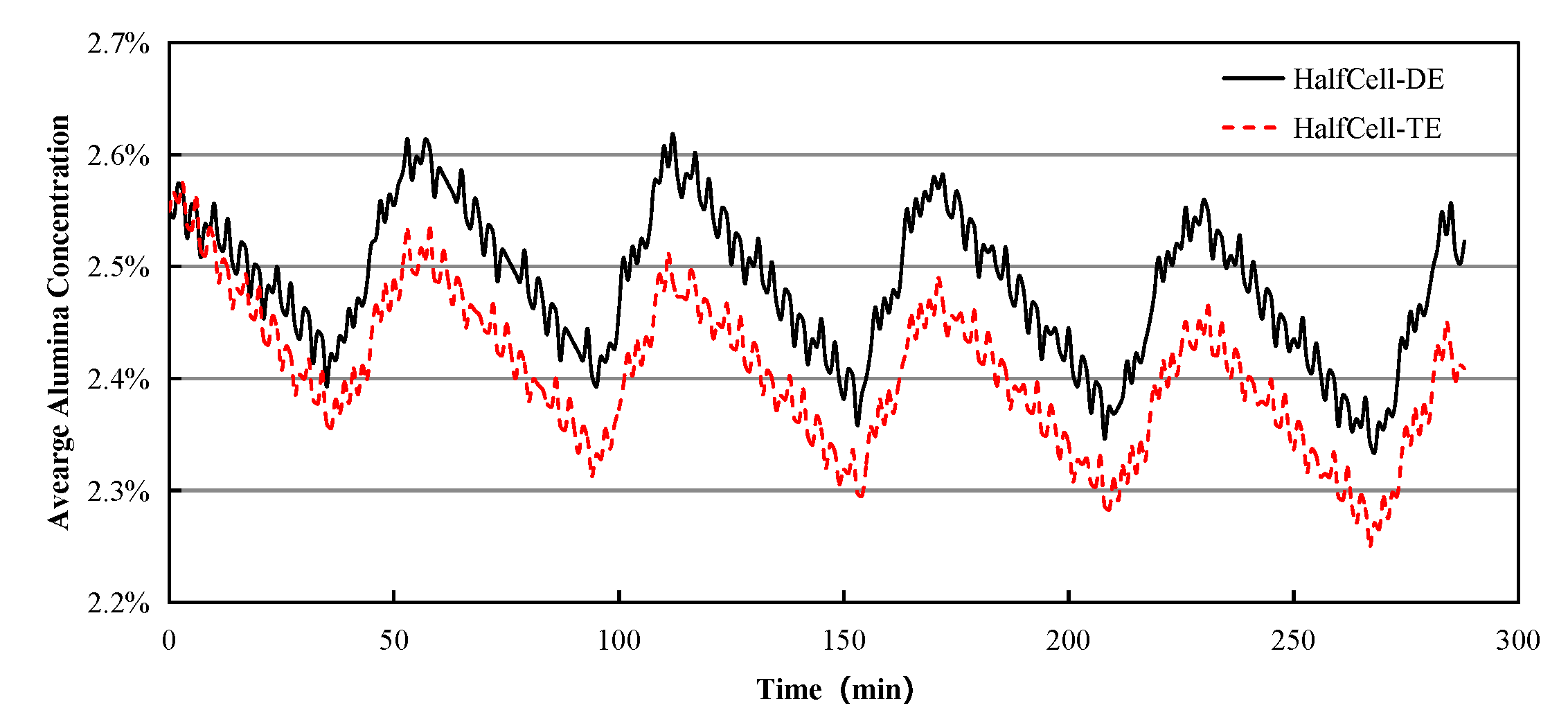
- Both numerical results and industrial data show the average concentration of alumina within the half-cell at the duct end is larger than that at the tap end. This is possibly related to the bath flow characteristics and the locations of feeding points.
- In general, the global flow patterns and alumina distribution of the slotted case are very similar to the unslotted case. However, with the application of slotted anodes, the maximum velocity in the horizontal plane was increased, while the average velocity was decreased slightly. Therefore, the alumina distribution of the slotted case is more uniform than that of the unslotted case.
- Since the busbar structure was upgraded from A to B, the symmetry of the two vortices became more obvious and the maximum flow velocity was significantly reduced, especially at the ends of the aluminum reduction cell. Consequently, the alumina concentration is more uniform within the bath for busbar net B.
Author Contributions
Funding
Conflicts of Interest
References
- Qiu, Z. Principle and Application of Aluminium Electrolysis, 2nd ed.; China University of Mining and Technology Press: Xuzhou, China, 1998; pp. 8–16. [Google Scholar]
- Zhu, J.; Li, J. Transient simulation of bath temperature inside aluminum reduction cells. Metals 2020, 10, 379. [Google Scholar] [CrossRef]
- Zhu, J.; Li, J. Influence of Alumina Feeding Dose Distribution on Superheat Based on Computational Simulation. Available online: https://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijspm (accessed on 30 April 2020).
- Chrenková, M.; Danek, V.; Silný, A.; Utigard, T. Density, electrical conductivity and viscosity of low melting baths for aluminum electrolysis. In Proceedings of the TMS Light Metals, Warrendale, PA, USA, 4–8 February 1996; pp. 227–232. [Google Scholar]
- Choudhary, G. Electrical conductivity for aluminum cell electrolyte between 950–1025 °C by regression equation. Electrochem. Soc. 1973, 120, 381–383. [Google Scholar] [CrossRef]
- Grjotheim, K.; Krohn, C.; Malinovsky, M.; Matiasovsky, K.; Thonstad, J. Aluminium Electrolysis, 2nd ed.; Aluminium-Verlag: Dusseldorf, Germany, 1982; p. 131. [Google Scholar]
- Rye, K.; Konigsson, M.; Solberg, I. Current redistribution among individual anode carbons in a Hall-Héroult prebake cell at low alumina concentrations. In Proceedings of the TMS Light Metals, San Antonio, TX, USA, 15–19 February 1998; pp. 241–246. [Google Scholar]
- Dion, L.; Kiss, L.; Lagace, C.; Victor, R.; Evans, J. On-line monitoring of individual anode currents to understand and improve the process control at alouette. In Proceedings of the TMS Light Metals, Orlando, FL, USA, 15–19 March 2015; pp. 723–728. [Google Scholar]
- Moxnes, B.; Solheim, A.; Liane, M.; Svinsas, E.; Halkjelsvik, A. Improved cell operation by redistribution of the alumina feeding. In Proceedings of the TMS Light Metals, San Antonio, TX, USA, 15–19 February 2009; pp. 461–466. [Google Scholar]
- Bilek, M.; Zhang, W.; Stevens, J. Modelling of electrolyte flow and its related transport processes in aluminium reduction cells. In Proceedings of the TMS Light Metals, San Francisco, CA, USA, 27 February–3 March 1994; pp. 323–331. [Google Scholar]
- Zhou, N.; Xia, X.; Bao, C. Effect of electromagnetic force and anode gas on electrolyte flow in aluminum electrolysis cell. J. Cent. South. Univ Technol. 2006, 13, 496–500. [Google Scholar] [CrossRef]
- Doheim, M.A.; El-Kersh, A.M.; Ali, M.M. Computational modeling of flow in aluminum reduction cells due to gas bubbles and electromagnetic forces. Metall. Mater. Trans. B 2007, 38, 113–119. [Google Scholar] [CrossRef]
- Liu, W.; Hu, H.; Zhou, D.; Yang, X.; Feng, Y.; Witt, P. Numerical modeling of bath-bubble two phase flow and alumina mixing in aluminum reduction cell. Light Metals 2016, 1, 25–29. (In Chinese) [Google Scholar]
- Zhao, Z.; Tao, S.; Liu, W.; Yang, X. Industrial measurement and numerical simulation on alumina distribution in large-scale prebaked aluminum reduction cell. Light Metals 2019, 6, 20–24. (In Chinese) [Google Scholar]
- Zhang, H.; Yang, S.; Zhang, H.; Li, J.; Xu, Y. Numerical simulation of alumina-mixing process with a multicomponent flow model coupled with electromagnetic forces in aluminum reduction cells. JOM 2014, 66, 1210–1217. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, W.; Cooksey, M.; Schwarz, P. Development of bubble driven flow CFD model applied for aluminium smelting cells. J. Comput. Multiph. Flows 2010, 2, 179–188. [Google Scholar] [CrossRef]
- Feng, Y.; Cooksey, M.; Schwarz, M. CFD modelling of alumina mixing in aluminium reduction cell. In Proceedings of the TMS Light Metals, Washington, DC, USA, 14–18 February 2010; pp. 455–460. [Google Scholar]
- Li, J.; Zhang, H.; Zhang, H.; Xu, Y.; Yang, S.; Lai, Y. Numerical simulation on vertical structures of electrolyte flow field in large aluminium reduction cells. Trans. Nonferr. Metal. Soc. 2012, 22, 2082–2089. (In Chinese) [Google Scholar]
- Jiang, N.; Qiu, Z.; Zhang, H.; Zhang, H.; Yang, S.; Li, J.; Liu, Q. Numerical simulation of alumina concentration field in 500 kA aluminum reduction cell. Trans. Nonferr. Metal. Soc. 2015, 25, 799–805. (In Chinese) [Google Scholar]
- Zhan, S.; Li, M.; Zhou, J.; Yang, J.; Zhou, Y. CFD simulation of dissolution process of alumina in an aluminum reduction cell with two-particle phase population balance model. Appl. Therm. Eng. 2014, 73, 805–818. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Wang, Z.; Tao, T.; Li, T.; Zhao, Z. CFD modeling of alumina diffusion and distribution in aluminum smelting cells. JOM 2019, 71, 764–771. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, Y.; Schwarz, M.; Witt, P.; Wang, Z.; Cooksey, M. Numerical modeling of flow dynamics in the aluminum smlting process: Comparsion between air-water and CO2-cryolite systems. Metall. Mater. Trans. B 2017, 48, 1200–1216. [Google Scholar] [CrossRef]
- Feng, N. Aluminum Electrolysis, 1st ed.; Chemical Industry Press: Beijing, China, 2006; p. 271. [Google Scholar]
- Zhao, Z.; Zhou, D.; Liu, W.; Hu, H.; Feng, Y.; Wang, Z. Numerical assessment on effects of longitudinal slots and its application in aluminium reduction cells. JOM 2020, 66, 1210–1217. [Google Scholar] [CrossRef]
- Skybakmoen, E.; Solheim, A.; Sterten, A. Alumina solubility in molten salt systems of interest for aluminum electrolysis and related phase diagram data. Metall. Mater. Trans. B 1997, 28, 81–86. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Z.; Gao, B.; Feng, Y.; Shi, Z.; Hu, X. Anodic bubble behavior and voltage drop in a laboratory transparent aluminium electrolysis cell. Metall. Mater. Trans. B 2016, 47, 1962–1975. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, B.; Feng, Y.; Huang, Y.; Wang, Z.; Shi, Z.; Hu, X. Effects of anode wettability and slots on anodic bubble behavior using transparent aluminium electrolytic cells. JOM 2017, 69, 281–291. [Google Scholar] [CrossRef]
- Wang, X.; Tarcy, G.; Whelan, S.; Porto, S.; Ritter, C.; Kiss Ouellet, B.; Homley, G.; Morphett, A.; Proulx, G.; Lindsay, S.; et al. Development and deployment of slotted anode technology at Alcoa. In Proceedings of the TMS Light Metals, Warrendale, PA, USA, 25 February–1 March 2007; pp. 539–544. [Google Scholar]
- Zhao, Z.; Li, R.; Liu, W.; Tao, S.; Wang, Z. Fundamental study and plant trail on slotted anodes technology in aluminum reduction cell. Light Metals 2020, 1, 24–28. (In Chinese) [Google Scholar]
- Liu, W.; Zhou, D.; Zhao, Z. Progress in application of energy-saving measures in aluminum reduction cells. JOM 2019, 71, 2420–2429. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, J.; Li, J.; Sun, K.; Xiao, J. Evolution of the busbar structure in large-scale aluminum reduction cells. JOM 2017, 69, 307–314. [Google Scholar] [CrossRef]




| Down-stream (Side B) | ||||||||||||||||||||||||
| Anode No. | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| H2 (mm) | 0 | 0 | 185 | 185 | 110 | 110 | 20 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 215 | 215 | 140 | 140 | 50 | 50 | 0 | 0 | 0 | 0 |
| H1 (mm) | 0 | 0 | 215 | 215 | 140 | 140 | 50 | 50 | 0 | 0 | 0 | 0 | 0 | 0 | 245 | 245 | 170 | 170 | 80 | 80 | 5 | 5 | 0 | 0 |
| Center Chanel | ||||||||||||||||||||||||
| H1 (mm) | 65 | 65 | 0 | 0 | 0 | 0 | 0 | 0 | 230 | 230 | 155 | 155 | 95 | 95 | 20 | 20 | 0 | 0 | 0 | 0 | 260 | 260 | 185 | 155 |
| H2 (mm) | 35 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 200 | 125 | 125 | 65 | 65 | 0 | 0 | 0 | 0 | 0 | 0 | 230 | 230 | 155 | 185 |
| Anode No. | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Up-stream (Side A) | ||||||||||||||||||||||||
| Cases | No Slots | Slots | Busbar Net A | Busbar Net B | 6 Feeders |
|---|---|---|---|---|---|
| Case 0 | √ | × | × | √ | √ |
| Case 1 | × | √ | × | √ | √ |
| Case 2 | √ | × | √ | × | √ |
| Meshes | Mesh 1.00 | Mesh 1.11 | Mesh 1.25 |
|---|---|---|---|
| Divisions Number of X_Side_Channel | 10 | 11 | 12 |
| Divisions Number of X_Anode_Width | 15 | 16 | 18 |
| Divisions Number of X_Inter_Anode_Gap | 5 | 5 | 6 |
| Divisions Number of Y_Side_Channel | 10 | 11 | 12 |
| Divisions Number of Y_Center_Channel | 30 | 33 | 37 |
| Divisions Number of Y_Anode_Length | 10 | 11 | 12 |
| Divisions Number of Z_Anode_Height | 8 | 9 | 10 |
| Divisions Number of Z_ACD | 5 | 5 | 5 |
| Maximum Velocity at Middle Plane of ACD | 20.3 cm/s | 20.7 cm/s | 21.2 cm/s |
| Time (min) | No. | SP1 | SP2 | SP3 | SP4 | SP5 | SP6 | Ave. | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Overfeeding | S1 | 1.36 | 1.30 | 1.74 | 2.42 | 2.00 | 1.32 | 1.69 |
| 3 | S2 | 1.42 | 1.44 | 1.60 | 1.96 | 2.10 | 1.42 | 1.66 | |
| 6 | S3 | 1.24 | 1.30 | 1.84 | 2.42 | 1.64 | 1.28 | 1.62 | |
| 9 | S4 | 1.38 | 1.34 | 2.02 | 2.32 | 1.80 | 1.34 | 1.70 | |
| 12 | S5 | 1.48 | 1.48 | 2.48 | 2.24 | 1.70 | 1.70 | 1.85 | |
| 15 | S6 | 1.76 | 2.16 | 2.06 | 2.36 | 2.18 | 1.92 | 2.14 | |
| 20 | Underfeeding | S7 | 2.04 | 2.10 | 2.62 | 2.30 | 2.00 | 1.86 | 2.15 |
| 25 | S8 | 1.96 | 2.06 | 2.32 | 2.36 | 2.54 | 1.88 | 2.23 | |
| 30 | S9 | 1.88 | 2.02 | 2.26 | 2.10 | 2.18 | 1.96 | 2.07 | |
| 35 | S10 | 2.08 | 1.80 | 2.00 | 2.02 | 2.00 | 1.74 | 1.94 | |
| 40 | S11 | 2.28 | 1.82 | 1.92 | 2.18 | 1.76 | 1.62 | 1.93 | |
| 45 | S12 | 1.82 | 1.60 | 1.72 | 2.36 | 1.72 | 1.70 | 1.82 | |
| Ave. | 1.70 | 1.70 | 2.05 | 2.25 | 1.97 | 1.65 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Li, J.; Zhang, H. CFD Investigation of Bath Flow and Its Related Alumina Transmission in Aluminum Reduction Cells: Slotted Anodes and Busbar Designs. Metals 2020, 10, 805. https://doi.org/10.3390/met10060805
Zhu J, Li J, Zhang H. CFD Investigation of Bath Flow and Its Related Alumina Transmission in Aluminum Reduction Cells: Slotted Anodes and Busbar Designs. Metals. 2020; 10(6):805. https://doi.org/10.3390/met10060805
Chicago/Turabian StyleZhu, Jiaming, Jie Li, and Hongliang Zhang. 2020. "CFD Investigation of Bath Flow and Its Related Alumina Transmission in Aluminum Reduction Cells: Slotted Anodes and Busbar Designs" Metals 10, no. 6: 805. https://doi.org/10.3390/met10060805
APA StyleZhu, J., Li, J., & Zhang, H. (2020). CFD Investigation of Bath Flow and Its Related Alumina Transmission in Aluminum Reduction Cells: Slotted Anodes and Busbar Designs. Metals, 10(6), 805. https://doi.org/10.3390/met10060805





