A Newly Discovered Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit for Metallic Materials
Abstract
1. Introduction
2. Methods and Materials
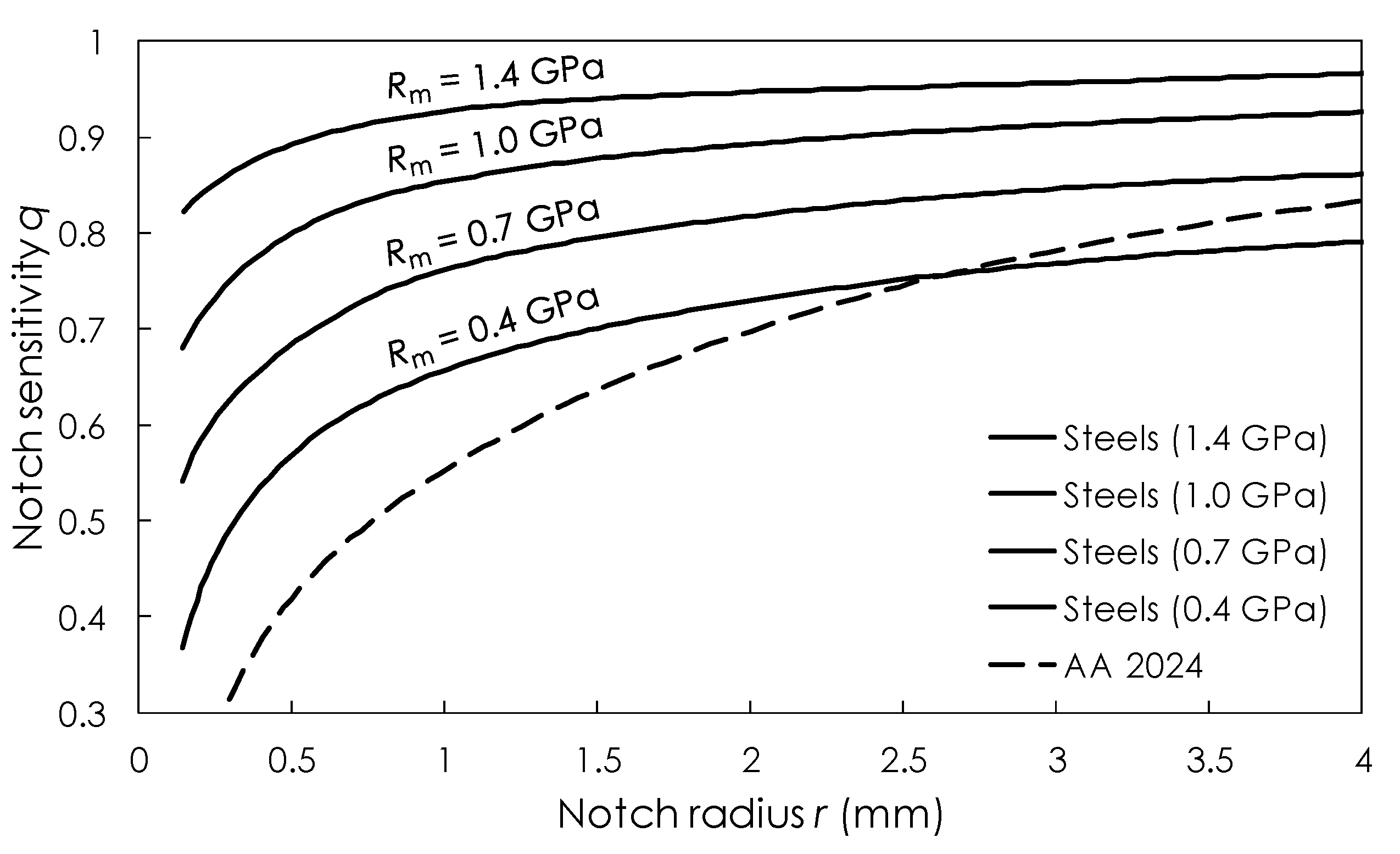
2.1. Methods and Reference to Previous Work
2.2. Materials
2.3. New Insights into Previous Work
3. Results
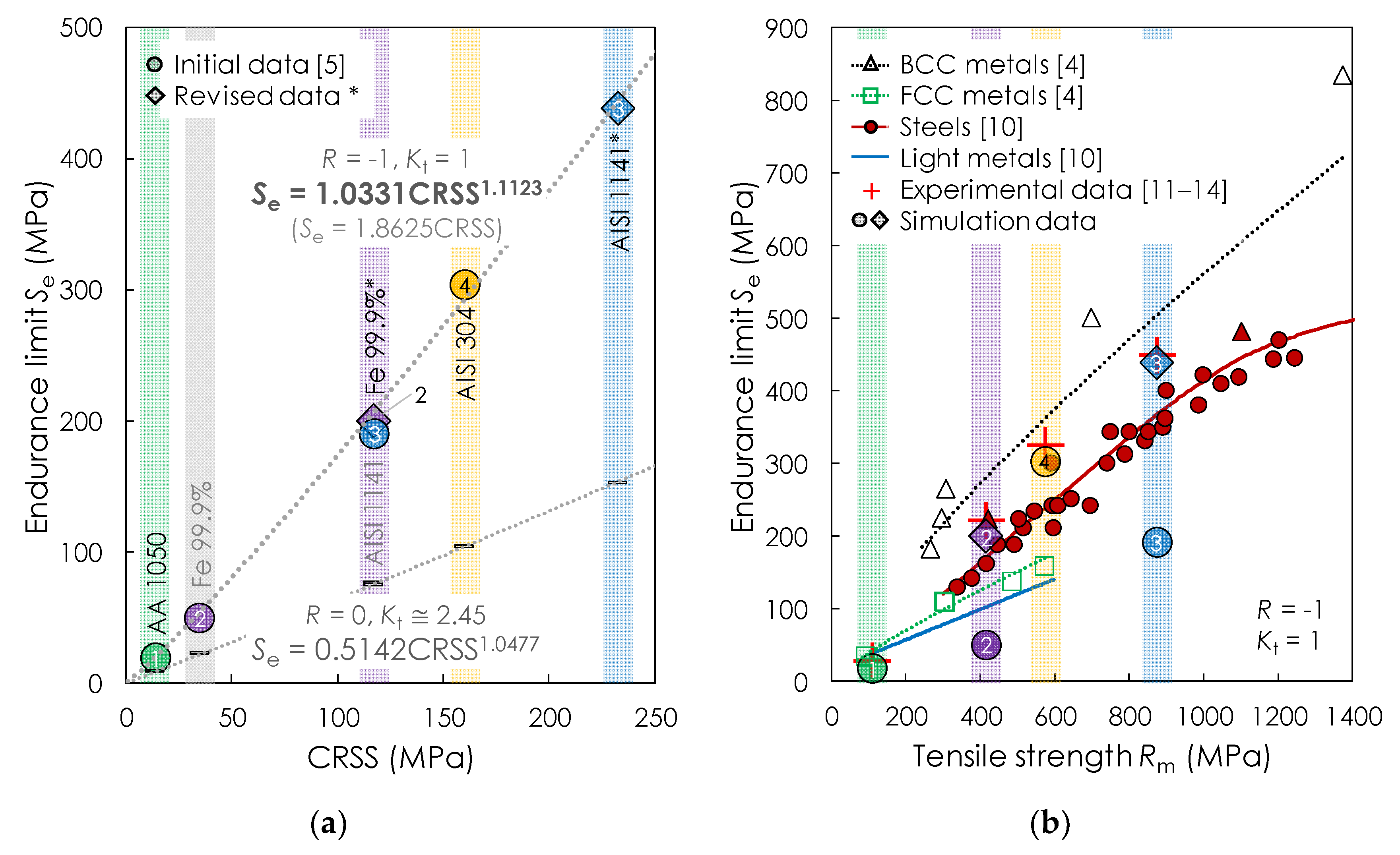
3.1. Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit
3.2. Application of the Newly Discovered Relation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Material | Se (MPa) R = 0 Kt ≅ 2.45 | Kt | q | Kfat | Se (MPa) R = 0 Kt = 1 | Sm (MPa) | Rm (MPa) | Se (MPa) R = −1 Kt = 1 (Axial) |
|---|---|---|---|---|---|---|---|---|
| AISI 304 | 103 [5] | 2.53 | 0.83 | 2.27 | 233.8 | 233.8 | 574 [31] | 303.7 |
| AISI 1141 * | 152 | 2.39 | 0.90 | 2.25 | 342.2 | 342.2 | 875 [13] | 438.5 |
| AISI 1141 | 76 [5] | 2.39 | 0.90 | 2.25 | 171.1 | 171.1 | 875 [13] | 190.7 |
| Fe 99.9% * | 74 | 2.41 | 0.80 | 2.13 | 157.5 | 157.5 | 414 [33] | 200.0 |
| Fe 99.9% | 22 [5] | 2.41 | 0.80 | 2.13 | 46.8 | 46.8 | 414 [33] | 49.7 |
| AA 1050 | 8 [5] | 2.46 | 0.84 | 2.23 | 17.8 | 17.8 | 110 [34] | 19.5 |
| Material | Se (MPa) | R | L | Kt | q | Kfat | Se (MPa) R = 0 Kt = 1 | Sm (MPa) | Rm (MPa) | Se (MPa) R = −1 Kt = 1 (Axial) |
|---|---|---|---|---|---|---|---|---|---|---|
| AISI 304 | 217 [14] | −1 | a | 1.6 | 0.83 | 1.50 | -> | - | 574 [31] | 325 |
| AISI 1141 | 155 [13] | 0 | a | 2.39 | 0.90 | 2.25 | 348.9 | 348.9 | 875 [13] | 450 |
| Fe 99.9% | 150 [12] | −1 | a | 1.6 | 0.80 | 1.48 | -> | - | 414 [33] | 222 |
| AA 1050 | 34.5 [11] | −1 | b | 1 | - | - | -> | - | 110 [34] | 29 |
References
- Ferro, A.; Montalenti, G. On the effect of the crystalline structure on the form of fatigue curves. Philos. Mag. 1964, 10, 1043. [Google Scholar] [CrossRef]
- Ferro, A.; Mazzetti, P.; Montalenti, G. On the effect of the crystalline structure on fatigue: Comparison between body-centred metals (Ta, Nb, Mo and W) and face-centred and hexagonal metals. Phil. Mag. J. Theor. Exp. Appl. Phys. 1965, 12, 867–875. [Google Scholar] [CrossRef]
- Buck, A. Fatigue properties of pure metals. Int. J. Fract. Mech. 1967, 3, 145–152. [Google Scholar] [CrossRef]
- Grosskreutz, J.C. Fatigue mechanisms in the sub-creep range. ASTM 1971, 495, 5–60. [Google Scholar]
- Mlikota, M.; Schmauder, S. On the critical resolved shear stress and its importance in the fatigue performance of steels and other metals with different crystallographic structures. Metals 2018, 8, 883. [Google Scholar] [CrossRef]
- Jennings, A.T.; Burek, M.J.; Greer, J.R. Microstructure versus Size: Mechanical properties of electroplated single crystalline Cu nanopillars. Phys. Rev. Lett. 2010, 104, 135503. [Google Scholar] [CrossRef] [PubMed]
- Rogne, B.R.S.; Thaulow, C. Strengthening mechanisms of iron micropillars. Philos. Mag. 2015, 95, 1814–1828. [Google Scholar] [CrossRef]
- Božić, Ž.; Schmauder, S.; Mlikota, M.; Hummel, M. Multiscale fatigue crack growth modelling for welded stiffened panels. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 1043–1054. [Google Scholar] [CrossRef]
- Monnet, G.; Pouchon, M.A. Determination of the critical resolved shear stress and the friction stress in austenitic stainless steels by compression of pillars extracted from single grains. Mater. Lett. 2013, 98, 128–130. [Google Scholar] [CrossRef]
- Dietmann, H. Einführung in die Elastizitäts- und Festigkeitslehre; Alfred Kröner Verlag: Stuttgart, Germany, 1991. [Google Scholar]
- MatWeb—The Online Materials Information Resource. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=db0307742df14c8f817bd8d62207368e (accessed on 7 May 2020).
- Islam, M.A.; Sato, N.; Tomota, Y. Tensile and plane bending fatigue properties of pure iron and iron-phosphorus alloys at room temperature in the air. Trans. Indian Inst. Met. 2011, 64, 315–320. [Google Scholar] [CrossRef]
- Fatemi, A.; Zeng, Z.; Plaseied, A. Fatigue behavior and life predictions of notched specimens made of QT and forged microalloyed steels. Int. J. Fatigue 2004, 26, 663–672. [Google Scholar] [CrossRef]
- Atzori, B.; Meneghetti, G.; Ricotta, M. Analysis of the fatigue strength under two load levels of a stainless steel based on energy dissipation. Frattura Integr. Strutt. 2011, 17, 15–22. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Mlikota, M.; Schmauder, S.; Božić, Ž. Calculation of the Wöhler (S-N) curve using a two-scale model. Int. J. Fatigue 2018, 114, 289–297. [Google Scholar] [CrossRef]
- Mlikota, M.; Schmauder, S. Virtual testing of plasticity effects on fatigue crack initiation. In Advances in Engineering Materials, Structures and Systems: Innovations, Mechanics and Applications; Zingoni, A., Ed.; CRC Press: London, GB, 2019; pp. 587–592. [Google Scholar]
- Tanaka, K.; Mura, T. A dislocation model for fatigue crack initiation. J. Appl. Mech. 1981, 48, 97–103. [Google Scholar] [CrossRef]
- Tanaka, K.; Mura, T. A theory of fatigue crack initiation at inclusions. Metall. Trans. A 1982, 13, 117–123. [Google Scholar] [CrossRef]
- Mlikota, M.; Staib, S.; Schmauder, S.; Božić, Ž. Numerical determination of Paris law constants for carbon steel using a two-scale model. J. Phys. Conf. Ser. 2017, 843, 012042. [Google Scholar] [CrossRef]
- Glodež, S.; Jezernik, N.; Kramberger, J.; Lassen, T. Numerical modelling of fatigue crack initiation of martensitic steel. Adv. Eng. Softw. 2010, 41, 823–829. [Google Scholar] [CrossRef]
- Jezernik, N.; Kramberger, J.; Lassen, T.; Glodež, S. Numerical modelling of fatigue crack initiation and growth of martensitic steels. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 714–723. [Google Scholar] [CrossRef]
- Mlikota, M.; Schmauder, S.; Božić, Ž.; Hummel, M. Modelling of overload effects on fatigue crack initiation in case of carbon steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1182–1190. [Google Scholar] [CrossRef]
- Mlikota, M.; Schmauder, S. Numerical determination of component Wöhler curve. DVM Bericht 2017, 1684, 111–124. [Google Scholar]
- Božić, Ž.; Schmauder, S.; Mlikota, M.; Hummel, M. Multiscale fatigue crack growth modeling for welded stiffened panels. In Handbook of Mechanics of Materials; Schmauder, S., Chen, C.-S., Chawla, K.K., Chawla, N., Chen, W., Kagawa, Y., Eds.; Springer: Singapore, 2018; pp. 1–21. [Google Scholar]
- Huang, X.; Brueckner-Foit, A.; Besel, M.; Motoyashiki, Y. Simplified three-dimensional model for fatigue crack initiation. Eng. Fract. Mech. 2007, 74, 2981–2991. [Google Scholar] [CrossRef]
- Briffod, F.; Shiraiwa, T.; Enoki, M. Fatigue crack initiation simulation in pure iron polycrystalline aggregate. Mater. Trans. 2016, 57, 1741–1746. [Google Scholar] [CrossRef]
- Božić, Ž.; Mlikota, M.; Schmauder, S. Application of the ΔK, ΔJ and ΔCTOD parameters in fatigue crack growth modelling. Tech. Gaz. 2011, 18, 459–466. [Google Scholar]
- Božić, Ž.; Schmauder, S.; Mlikota, M. Fatigue growth models for multiple long cracks in plates under cyclic tension based on ΔKI, ΔJ-integral and ΔCTOD parameter. Key Eng. Mater. 2011, 488–489, 525–528. [Google Scholar]
- Jin, H.-H.; Ko, E.; Kwon, J.; Hwang, S.S.; Shin, C. Evaluation of critical resolved shear strength and deformation mode in proton-irradiated austenitic stainless steel using micro-compression tests. J. Nucl. Mater. 2016, 470, 155–163. [Google Scholar] [CrossRef]
- Krompholz, K.; Ullrich, G. Investigations into the fatigue crack initiation and propagation behaviour in austenitic stainless steel X5 CrNi 18 9 (1. 4301). Materialwiss. Werkstofftech. 1985, 16, 270–276. [Google Scholar] [CrossRef]
- Bao, W.P.; Xiong, Z.P.; Ren, X.P.; Wang, F.M. Effect of strain rate on mechanical properties of pure iron. Adv. Mater. Res. 2013, 705, 21–25. [Google Scholar] [CrossRef]
- Keil, B.; Devletian, J. Comparison of the mechanical properties of steel and ductile iron pipe materials. In Pipelines 2011: A Sound Conduit for Sharing Solutions, Proceedings of the Pipelines Conference 2011, Seattle, WA, USA, 23–27 July 2011; Jeong, D.H.S., Pecha, D., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1301–1312. [Google Scholar]
- Lorenzino, P.; Navarro, A.; Krupp, U. Naked eye observations of microstructurally short fatigue cracks. Int. J. Fatigue 2013, 56, 8–16. [Google Scholar] [CrossRef]
- Yang, L.; Fatemi, A. Impact resistance and fracture toughness of vanadium-based microalloyed forging steel in the as-forged and Q&T conditions. J. Eng. Mater. Technol. 1996, 118, 71–79. [Google Scholar]
- Schijve, J. Fatigue of Structures and Materials; Springer Netherlands: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Bhaduri, A. Mechanical Properties and Working of Metals and Alloys; Springer Nature: Singapore, 2018. [Google Scholar]
- Marin, J. Mechanical Behavior of Engineering Materials; Prentice Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]


| Material | E (GPa) | G (GPa) | υ | Rp0.2 (MPa) | Rm (MPa) | d (µm) | CRSS (MPa) |
|---|---|---|---|---|---|---|---|
| AISI 304 | 188 | 79.0 | 0.26 | 322 [31] | 574 [31] | 30 | 160 [9] |
| AISI 1141 | 200 | 78.125 | 0.28 | 564 [13] | 875 [13] | 60 | 117 [8] |
| Fe 99.9% | 205 | 81.0 | 0.28 | 260 [32] | 414 [33] | 65 | 35 [7] |
| AA 1050 | 72 | 26.0 | 0.33 | 95 [34] | 110 [34] | 65 | 14 [6] |
| Material | Lattice | CRSS (MPa) | Se (MPa)/Sim. R = 0, Kt ≅ 2.45 | Se (MPa)/Sim. R = −1, Kt = 1 | Se (MPa)/Exp. R = −1, Kt = 1 |
|---|---|---|---|---|---|
| AISI 304 | FCC | 160 [9] | 103 [5] | 303.7 | 325 [14] |
| AISI 1141 | BCC | 117 [8] | 76 [5] | 190.7 | 450 [13] |
| Fe 99.9% | BCC | 35 [7] | 22 [5] | 49.7 | 222 [12] |
| AA 1050 | FCC | 14 [6] | 8 [5] | 19.5 | 29 [11] |
| Material | Rm (MPa) | CRSS (MPa) | Se (MPa)/Sim. R = 0, Kt ≅ 2.45 | Se (MPa)/Sim. R = −1, Kt = 1 | Se (MPa)/Exp. R = −1, Kt = 1 |
|---|---|---|---|---|---|
| AISI 304 | 574 [31] | 160 [9] | 103 [5] | 303.7 | 325 [14] |
| AISI 1141 * | 875 [13] | 232.5 (Equation (2)) | 152 | 438.5 | 450 [13] |
| AISI 1141 | 875 [13] | 117 [8] | 76 [5] | 190.7 | 450 [13] |
| Fe 99.9% * | 414 [33] | 117 [8] | 74 | 200 | 222 [12] |
| Fe 99.9% | 414 [33] | 35 [7] | 22 [5] | 49.7 | 222 [12] |
| AA 1050 | 110 [34] | 14 [6] | 8 [5] | 19.5 | 29 [11] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlikota, M.; Schmauder, S. A Newly Discovered Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit for Metallic Materials. Metals 2020, 10, 803. https://doi.org/10.3390/met10060803
Mlikota M, Schmauder S. A Newly Discovered Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit for Metallic Materials. Metals. 2020; 10(6):803. https://doi.org/10.3390/met10060803
Chicago/Turabian StyleMlikota, Marijo, and Siegfried Schmauder. 2020. "A Newly Discovered Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit for Metallic Materials" Metals 10, no. 6: 803. https://doi.org/10.3390/met10060803
APA StyleMlikota, M., & Schmauder, S. (2020). A Newly Discovered Relation between the Critical Resolved Shear Stress and the Fatigue Endurance Limit for Metallic Materials. Metals, 10(6), 803. https://doi.org/10.3390/met10060803







