Next Article in Journal
Gauge-Strain-Controlled Air and PWR Fatigue Life Data for 304 Stainless Steel—Some Effects of Surface Finish and Hold Time
Next Article in Special Issue
Interstitial Atom Engineering in Magnetic Materials
Previous Article in Journal
Effect of Grain Size on the Friction-Induced Martensitic Transformation and Tribological Properties of 304 Austenite Stainless Steel
Previous Article in Special Issue
Effect of the Sputtering Power on the Structure, Morphology and Magnetic Properties of Fe Films
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 10
Issue 9
10.3390/met10091247
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Magnetic and Magnetocaloric Effect of Laves Phase Compounds Er(Fe0.8−xMn0.2−yCox+y)2 with x, y = 0.0 or 0.1

by
Safa Othmani
1,
Ichrak Chaaba
2,
Sonia Haj-Khlifa
3,
Patricia de Rango
3 and
Daniel Fruchart
3,*
1
Unité de Recherche sur les Hétéro-Epitaxies et Applications, Faculté des Sciences de Monastir 5019, Université de Monastir, Monastir 5000, Tunisia
2
Laboratoire des Technologies des Systèmes Smart, C.R.I. Multimédia et Traitement Numérique des Données, Technopôle de Sfax, B.P 275, Sfax 3029, Tunisia
3
Institut Néel & Université Grenoble Alpes, B.P. 166, 38042 Grenoble CEDEX 9, France
*
Author to whom correspondence should be addressed.
Metals 2020, 10(9), 1247; https://doi.org/10.3390/met10091247
Submission received: 5 August 2020 / Revised: 5 September 2020 / Accepted: 7 September 2020 / Published: 16 September 2020
(This article belongs to the Special Issue Advanced Magnetic Materials)
Browse Figures
Versions Notes

Abstract

:
Magnetic and magnetocaloric effect (MCE) of the Er(Fe0.8−xMn0.2−yCox+y)2 Laves phase-type compounds have been investigated. X-ray diffraction (XRD) analysis has revealed that these compounds crystallize with the C15 type Laves phase structure (Space Group Fd-3m). The magnetization curves indicate a ferri-magnetic-ordering resulting of the antiparallel coupling between the moments of the heavy rare earth Er and the transition metal (TM). The partial substitution of Fe/Mn by Co increases the Curie temperature from 355 K for Er(Fe0.8Mn0.2)2 to 475, 550, and 555 K for Er(Fe0.7Mn0.2Co0.1)2, Er(Fe0.8Mn0.1Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2, respectively. According to the nature of the TM elements, arguments were presented forwards either Molecular Field or Spin Fluctuation Theory, even Stoner type pictures should be considered for. MCE was calculated according to the Maxwell relation based on isotherm magnetization measurements. The magnetic entropy change (−∆SM) observed on a 300–400 K temperature range can be understood in terms of a Spin Fluctuation Theory picture supported by both the different magnetic polarization levels that were shared by the TM elements and the related interatomic exchange forces.

1. Introduction

Magnetocaloric effect (MCE), which is considered as a foundation for the development of magnetic refrigeration, has attracted considerable attention during recent years [1,2,3]. Additionally, fundamental investigations of MCE phenomena reveal of high interest for a better knowledge of the local magnetic polarization, the exchange forces, and elastic couplings with the lattice [4,5]. Generally speaking, the MCE is characterized by determining both the isothermal magnetic entropy change (ΔS) and the adiabatic temperature change (ΔTad) of a material when exposed to a variation magnetic field. Most of the investigations on the MCE materials have focused on temperature ranges where occurs either a first order or a second order phase transition [1,2,3,4,5,6]. Usually, for the first order magnetic phase transition materials, large ΔS may be obtained in the vicinity of the magnetic transition temperature, owing to a sharp change of magnetization [1,2,3,4,6,7,8,9,10,11,12]. Accordingly, considerable attention has been paid to that type of materials for the development of efficient magnetic refrigeration systems, as was corroborated by early results. However, magnetic phenomena that may hinder the MCE yield narrow the magnetic refrigeration application of first order transition materials [12,13,14]. Besides, no magnetic/thermal hysteresis occurs along a wider temperature range, thus making the second order transition materials attracting to investigate as well [14]. In fact, quite different series of high performance MCE materials were extensively considered for their fundamental properties as well for potential applications, e.g., in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Among such series, magnetic Laves phases R(Fe1−xTMx)2-type compounds, where R is a heavy rare earth metal sharing a high magnetic moment and transition metal (TM) is a magnetic transition metal, have retained our attention. The synthesis procedures and structural aspects remain rather simple comparison made with other types of compounds. In addition, the magnetic and electronic properties reveal particularly flexible in terms of saturation magnetization, ordering temperature, and type of transition order. The RFe2 series exhibit ferri-magnetic arrangements with rather high ordering temperatures (second order type) and compensation points when MR(T) = −MTM(T) [20,21,22,23]. Interestingly, in the RCo2 binaries, the magnetic polarization on Co is typically driven by its itinerant electron character leading to rather low ordering temperature that was reported being of first order type [15]. The substitution of Fe to Co was expected, extending enough the ordering temperature towards room temperature, with the potential benefit of rather large variations of magnetic entropy (S) at the transition [24,25,26,27]. In order to lower and adjust the Curie temperature, even to suppress the compensation point, we have investigated the Er(Fe1−xCox)2 and R(Fe1−xCox)2Hy hydrides with R = Ho, Er for their magnetic and magnetocaloric properties, as shown in ref. [28,29]. For all cases, a rather flat magnetic entropy variation was revealed, extending on a large range of temperature (e.g., 100 to 400 K), which remains of limited intensity. However, a sharp and marked S signal was evidenced in the lowest temperature range for the hydrogenated compounds, similar to that found for the pure ErCo2 binary [15].
Besides, investigations of Er(Fe1−xMnx)2 compounds revealed that substitutions of Fe by Mn lead to remarkable impacts on both crystal structure and magnetic properties, since manganese tends superimpose antiferromagnetic (AFM) TM-TM exchange couplings [30,31,32].
In the present work, we report on the structural, magnetic, and magnetocaloric properties of Co- substituted Er(Fe0.8Mn0.2)2 compounds. Small Mn contents only where chosen in order to maintain the cubic MgCu2 (C15 type) structure. The counterbalance effects of Co to Mn were considered for, since Co favors ferromagnetic interactions in spite of sharing a low magnetic moment and Mn drives AFM exchange couplings with a possibly high magnetic moment. For this doing, the Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.2Co0.2)2 compounds were synthesized, and their structure, magnetic, and magnetocaloric properties were analyzed.

2. Materials and Methods

All of the samples were prepared from high-purity elements Er(3N), Mn(4N), Fe(3N8), and Co(4N) using high frequency melting under purified Ar atmosphere (5 N). A small excess of Mn was added to the starting compositions to prevent any loss due to its high vapor pressure. The homogeneity of the ingots was insured with five successive melting procedures.
Systematic X-ray diffraction analyses were carried out at room temperature using a Siemens reflection diffractometer D5000R (Bruker AXS GmbH, Östliche Rheinbrückenstr. 49, 76187 Karlsruhe Germany) operating at λCo,Kα1 wavelength.
Magnetization traces were recorded using the two extraction-type magnetometers developed at Institut Néel, respectively, for high temperature (300–900 K) and for low temperature (5–330 K) ranges. For the different compounds, the magnetic transition temperatures were determined by determining the position of the first derivative (dM/dT) peaks of traces recorded under a low magnetic field of 0.05 T. The magnetic entropy change S, which allows determine the MCE, was established using the Maxwell’s relation from isothermal magnetization plots recorded versus magnetic field.

3. Results

3.1. Structure Analysis

Figure 1 shows the room temperature X-ray diffraction (XRD) patterns of Er(Fe0.8−xMn0.2−yCox+y)2 (x, y = 0.0 or 0.1) compounds. Profile-type structure refinements were carried out using the Fullprof tool [33]. A single phase-material is observed for the substituted compounds without any impurity apart a tiny amount of Er2O3 for Er(Fe1−xMnx)2. All of the compounds were found crystallizing in the MgCu2-type cubic Laves phase structure (C15-type, Space Group Fd-3m).
However, for Er(Fe0.8Mn0.2)2, very small additional peaks are notified, which may correspond to the erbium oxide (Er2O3), in amount not exceeding 3 mol.%. It may arise from the grinding of the ingot to fine powder needed for the XRD measurements. Figure 2 shows the indexation of patterns.
For example, Figure 2 discloses the experimental XRD pattern of Er(Fe0.8Mn0.1Co0.1)2 as compared with the calculated profile. Table 1 lists the refined cell parameters for all the studied compounds. Please note that, for Er(Fe0.8Mn0.2)2, the present results fairly well agree with previously established data received on the Er(Fe1−xMnx)2 (0 < x < 0.6) system [31].
For the Co-substituted compounds, the unit-cell volume decreases comparison made to that of Er(Fe0.8Mn0.2), since the Co atomic radius is smaller than that of Fe and Mn with rMn = 1.61 Å, rFe = 1.56 Å, and rCo = 1.52 Å, the calculated values accounting for the d-block contraction [34]. Accordingly, the Mn-richest compounds exhibit the largest unit cell volumes.

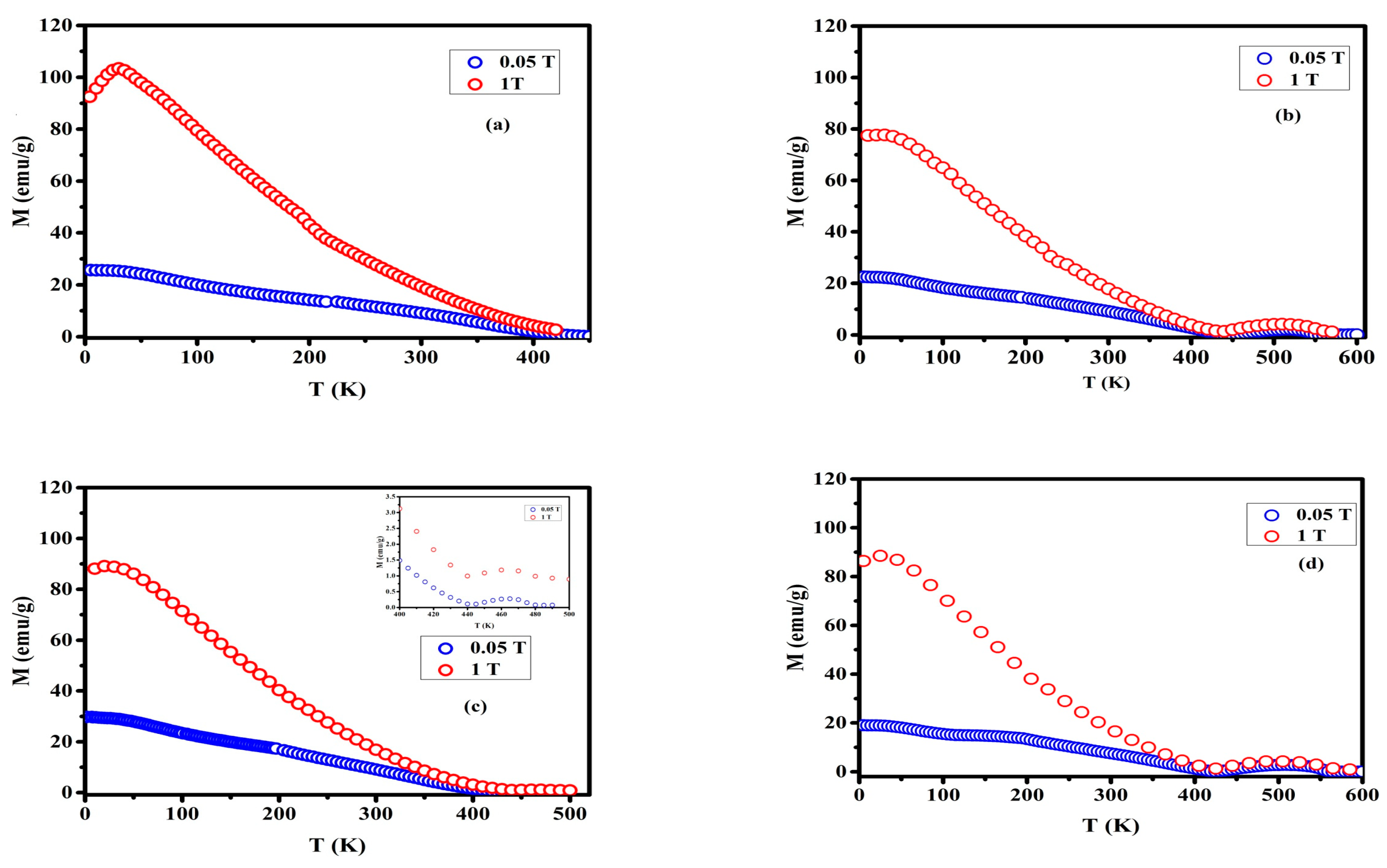
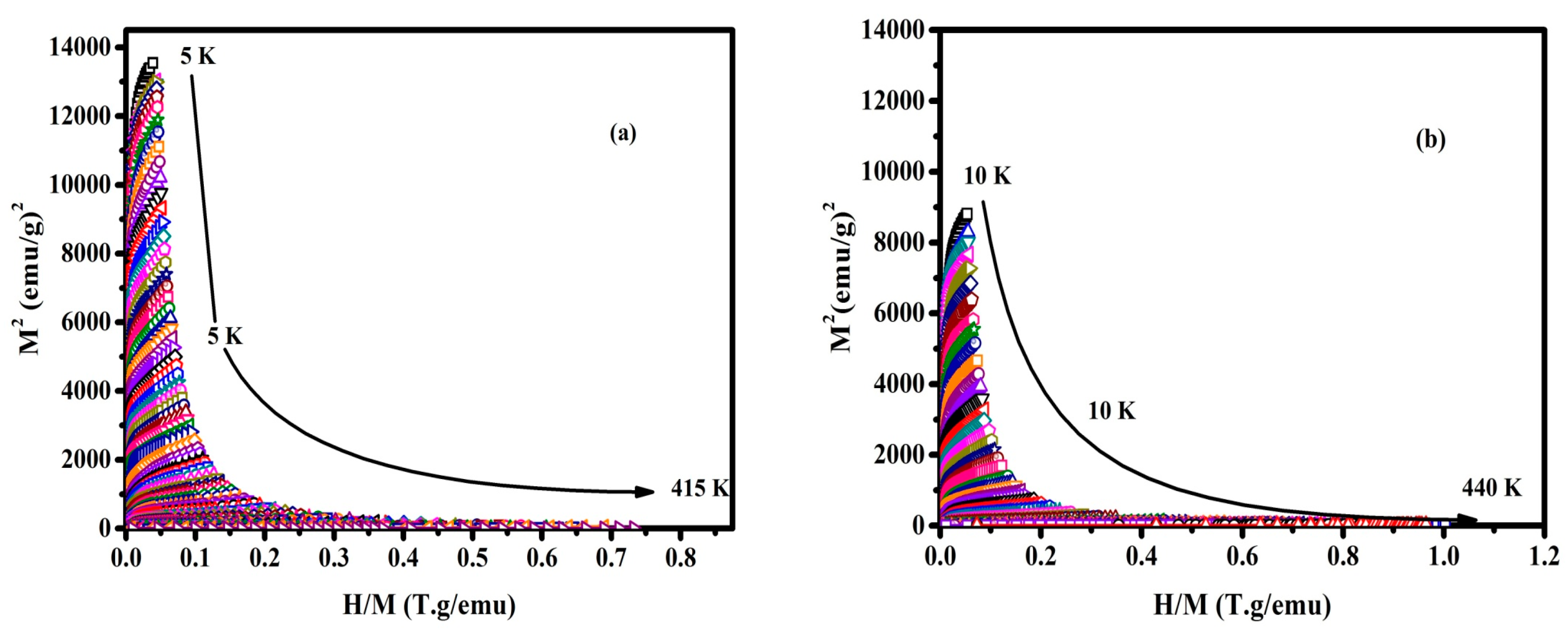
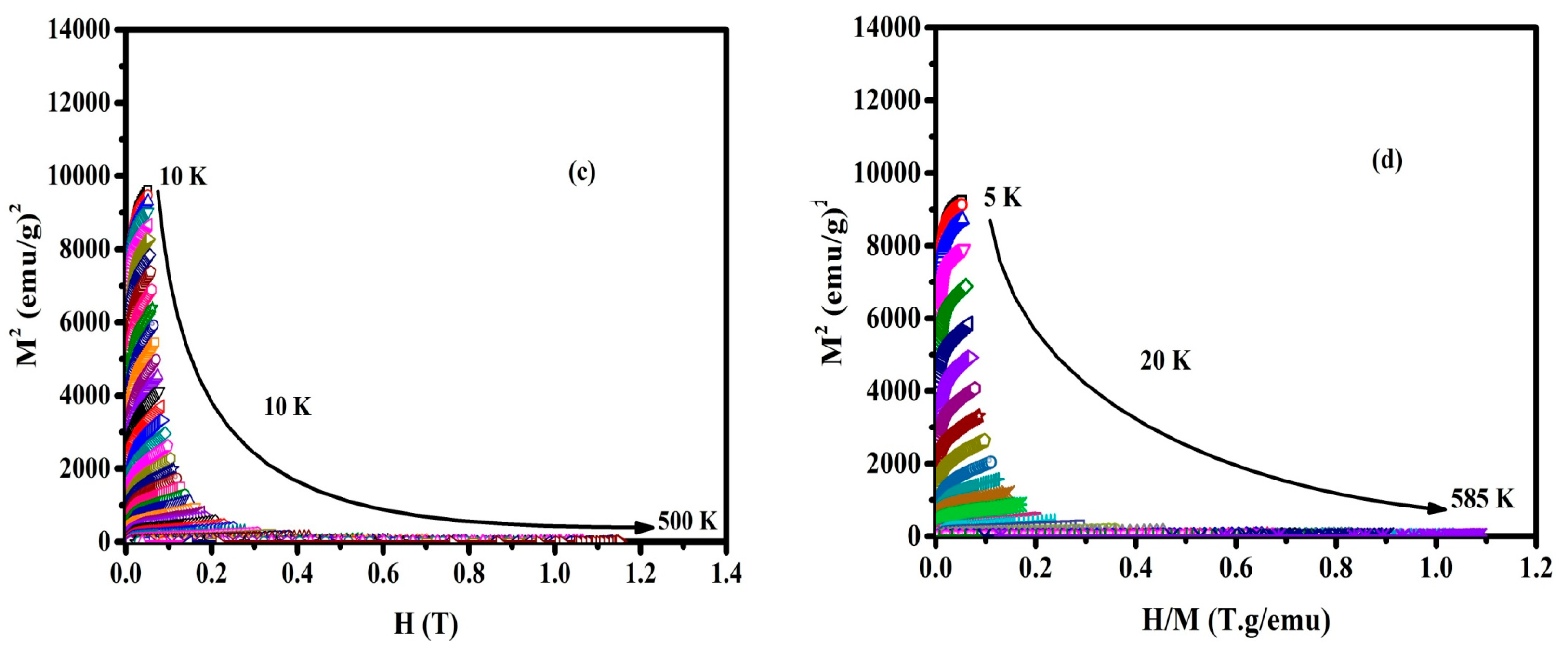
3.2. Magnetic Properties

Figure 3 shows the magnetization variation versus temperature of the Er(Fe0.8−xMn0.2−yCox+y)2 compounds established in external magnetic field of 0.05 and 1 T.
The M-T curves of all samples show smooth variations suggesting that the magnetic ordering transitions are of second order. However, the derivative trace reveals for all compounds a marked change of the susceptibility versus temperature nearby 50 K. This phenomenon should result of a differential thermal behavior of the anisotropy contribution of the erbium Crystal Electric Field (CEF) which was reported to increase at low temperature [35,36,37], whereas the molecular field addressed by the (Fe-TM) sublattice should be considered as almost unchanged [21,35,36,37].
All of the compounds are ferrimagnet (FI), according to the Russell–Saunders rules leading to antiparallel configurations between a TM(3d) moment and a heavy rare earth R(4f) moment via the R(5d)-TM(3d) overlapping orbitals. According to literature, the Er moment can be considered as fully saturated (~9 µB) [38,39,40], so being larger than twice the TM-3d one. At 355 K, Er(Fe0.8Mn0.2)2 exhibits a transition from ferri- (FI) to paramagnet (PM) states, as shown Figure 3a. In principle, the Er and TM magnetizations align antiparallel, but, when temperature increases high enough, the Er magnetization is known to decrease faster than that of TM sublattices [35,36,37]. Accordingly, when |µEr| = |Σ(µFe) + Σ(µMn) + Σ(µCo), a compensation point appears (Tcomp) on the magnetization trace. This occurs for the three Co-substituted compounds for which Co shares a smaller magnetic moment, but the Co–Co and Co–Fe exchange interactions are known to increase markedly. The substitution of Co to Mn or Fe induces noticeable changes in the magnetic characteristics, as shown Figure 3. TC increases from 355 K for Er(Fe0.8Mn0.2)2 to 550, 475, and 555 K for Er(Fe0.8Mn0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2, respectively, and in all cases a compensation point Tcomp. is observed close to 450 K.
For all compounds, 5 K-isothermal magnetization traces measured in magnetic fields ranging from 0 to 7 T are shown in Figure 4. Please recall the equivalence of units emu/g (CGS) ≡ Am2/kg (SI).
The net magnetization increases rapidly for applied fields lower than 1 T and then evolves almost linearly for H > 1.5 T. An approach to saturation magnetization was expressed fitting the 5 K magnetization traces [38]:
M ( H ) = M s a t − a H
with a being a phenomenology parameter.
Table 2 reports the saturation magnetization values of the samples. One can see that Msat decreases from 6.01 µB for Er(Fe0.8Mn0.2)2 to 4.93, 5.26, and 5.00 µB for Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2. Estimates of the mean <TM> magnetic moments reported in Table 2 were simply derived as MTM = (MEr − Msat)/2, with respect to free ion value of ~9 µB attributed to the Er moment [38,39].
In a first attempt to derive each of the TM contributions to the overall <TM> magnetization, we have considered the <TM> values both expressed from the 1–2 and 3–4 formula differences (as numbered in Table 2), assuming µEr and µFe almost constant. For these differences, the |µMn − µCo| values are found of 5.5 and 1.65 µB, respectively.
Accordingly, markedly different (or unrealistic) results suggest that, in these series of Er(Fe-Mn-Co)2 compounds, some of the TM moments are far to exhibit determined values. Howbeit, the values estimated from magnetic saturation approach should be as well questioned. Otherwise, it was considered that the anisotropic magnetic hyperfine interaction at the Fe(TM) nuclei should play a role on the magnetic polarization level and orientation of the Fe(TM) moment in the RFe2 binaries [39]. However, in most RFe2 and particularly in the ErFe2, the Fe moment was shown to behave almost smoothly as early reported e.g., in [20,21,30,31,35,36,37,38,39,40,41]. Back to the values that were received from saturation magnetization measurements undertaken on the simple Er(Co1−xFex)2 system [28], the Fe and Co moments were found to be equal to 1.97 and 1.47 µB, respectively. For the border compositions, one can remark that the Fe and Co moments undergo an exact reduction of 0.22 µB reference to their 3d metal values. Moreover, for the intermediate composition Er(Co0.875Fe0.125)2 the mean <µTM> value of 1.54 µB fairly corresponds to the Co/Fe ratio contributions. Accordingly, it should be anticipated that, here, the Mn moment support most of the TM magnetization dispersion in the four studied compounds. More fundamental analyses devoted to the magnetic characteristics of the R(TM)2 compounds of C15 type with TM = Mn, Fe, and Co, lead to, concluding that, in R-Mn binaries as well as many Mn based intermetallics, low-temperature magnetic instabilities are related to trends for antiferromagnetic ordering [42,43]. Often, both the 4f–3d and 3d–3d interactions are negative leading either to complex non-collinear magnetic structures, or weakening the (even no) local magnetic moment as for Tb1−xYxMn2 [42], Y(Fe1−xMnx)2 [43], Th6Mn23 [44,45,46], (Fe1−xMnx)B [40] This is especially the case for structures sharing a CN12 tetrahedral-close-compact TM network (based on Friauf-polyhedra or cuboctahedra).
Conversely, the mean moment of the TM site increases when Co is substituted to Mn. If at low temperature in the binary RCo2, cobalt exhibits band paramagnetism, it is promptly polarized by internal or external fields, as mentioned in ref. [41]. Subsequently, according to the generalized Slater-Pauling chart, the magnetic moment shared by the TM lattice increases with the Co content [38]. Assuming for µFe and µCo almost constant values of 2.0 and 1.5 µB, as mentioned above, a simple evaluation based on the µ3d values reported in Table 2 leads estimating roughly the µMn values to −0.75, 2.9, 1.6, and 3.0 µB for Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2, respectively. This means that, in the Mn-richest compound, Er(Fe0.8Mn0.2)2, Mn should be lower-even-negative magnetically polarized.
The molecular field picture of Curie temperature TC of a ferrimagnetic R-TM system leads write:
TC = ½[TTM + TR + ((TTM − TR)2 + 4T2R-TM)1/2]
where TTM, TR, and TR-TM represent the contributions to TC due to TM-TM, R-R, and R-TM exchange interactions respectively. Reference to classical notations, the respective Curie temperature are defined from the respective CTM and CR Curie constants and molecular field coefficients nTM-TM, nR-TM and nR-R, respectively [47]. Note that T2R-TM is proportional to the de Gennes’ factor of the rare earth element with G(J) = (gJ − 1)2J(J + 1). Hence, if one considers that the TR-R contribution is negligible (a few % of TTM) and TR-TM << TTM [47,48] (here nR-TM said constant with temperature [49]), so TC − TTM should be proportional to G(J). Experimentally, the Curie temperature of ErFe2 is found to be approximately 10 K higher than that of LuFe2 (Lu non-magnetic) of 570 K [50,51], allowing quantifies the value of de Gennes’ type contribution. Subsequently, one may consider the expression (2) as a simplified following writing introducing a phenomenological coefficient:
TC/TTM ~ [1 + (1 − 4α)1/2]
Accordingly, from the µTM magnetization values derived from Table 2 and the Curie temperature values reported in Table 3, ones can establish that the ratio TC/(<µTM>)2 remains almost constant and equal to 1.35 ± 0.3 for the three Co-containing compounds, but its value is much higher (1.69) for Er(Fe0.8Mn0.2)2 the Mn-only substituted to Fe compound. Here, the coefficient must be negative, leading to conclude that, in the latter binary, the Mn-TM(Fe,Co) couplings are negative in agreement to the value of −0.75 µB found above. Additionally, the cell volume differences that correspond to the 2–1 and 4–3 formulas are, respectively, of 7.64 and 5.6 Å3 for similar TM atom substitutions (Co0.1 − Mn0.1)/u.f. This would suggest the existence of a volume anomaly ω = k·µMn2 [42], where k relates with the various magneto-elastic contributions.
Figure 5a displays the isothermal magnetization traces of Er(Fe0.8Mn0.2)2 measured under magnetic fields ranging from 0 to 5 T. When increasing the magnetic field, magnetization increases very few in the paramagnetic state (T > TC), conversely in the ordered state (T < TC) the magnetization traces M (H) evidence a rapid saturation above 1 T. For all Co-substituted compounds, Figure 5b–d display the isothermal magnetization traces on both sides of Tcomp. One can see that all of the compounds saturate easily for T < Tcomp insomuch as the high symmetry of the Er site makes the magneto-crystalline anisotropy of [111] axis-type, very weak [52]. As aforementioned, the compounds are ferri-magnetic with the larger Er moment oriented antiparallel to the smaller <TM> moments [15,50,51,52]. When increasing temperature, both the TM and Er moments decrease, but the depolarization of the Er moment is faster than the TM ones [49]. Therefore, the saturation field gradually decreases with the increasing temperature. The M(H) traces recorded above Tcomp are shown in Figure 5b’–d’ and for a given field, magnetization increases first and then decreases when temperature increases from Tcomp up to TC. For the Er(Fe0.7Mn0.2Co0.1)2 compound, the linear shape of the traces recorded at 460 K clearly indicates that Tcomp is close to TC, additionally with a resulting weak magnetization level of 2µTM − µEr, as shown Figure 5c’.
Subsequently, an Arrott plot-type analysis [53] is used in order to define the character of the magnetic phase transitions, as shown in Figure 6. Reference to the Banerjee’s criterion, the type of magnetic transition is determined from the slope of the isotherms curves, where a negative slope corresponds to a First Order Magnetic Transition (FOMT), while a positive slope corresponds to a Second Order Magnetic Transition (SOMT). For all of our compounds, the Arrott plots exhibit a positive slope confirming the SOMT character.

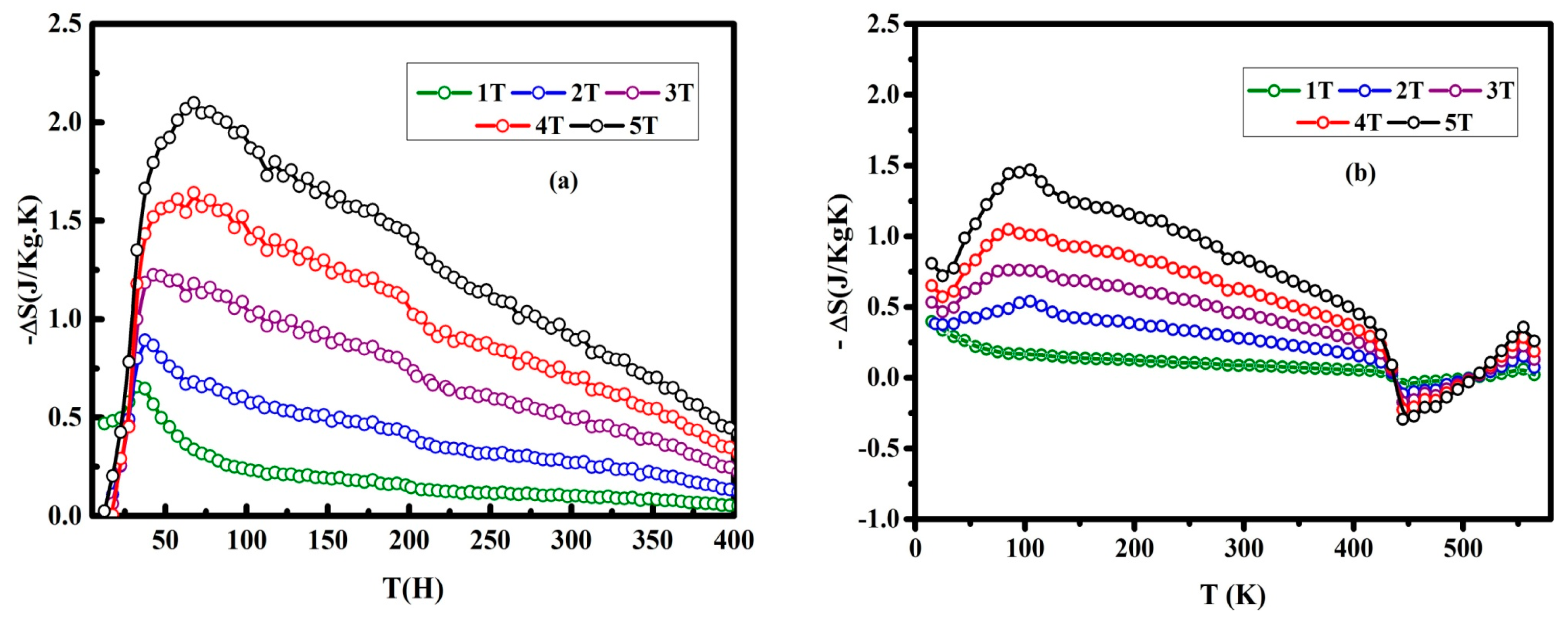
3.3. Magnetocaloric Properties

In a magnetization–demagnetization process, the magnetocaloric effect (MCE) is related to the change of the isothermal magnetic entropy change SM observed when applying or removing an external magnetic field to a specific sample [54]. The magnitude of the MCE of a magnetic material is also characterized by the adiabatic temperature change ∆Tad upon the magnetic field variation.
In the present work, magnetization isotherms were recorded in order to determine the total magnetic entropy change | Δ S M | of all of the samples as a function of temperature and magnetic field change. According to the Maxwell relation, | Δ S M | can be evaluated through the classical formula:
Δ S M ( T , H ) = S M ( T , H ) − S M ( T , 0 ) = ∫ 0 H max ( ∂ M ∂ T ) H d H
For magnetization measured at discrete field and temperature intervals, the magnetic entropy change that is defined in Equation (4) can be approximated by Equation (5) [5,55]:
− Δ S M = ∑ i M i − M i + 1 T i + 1 − T i Δ H i
where Mi and Mi+1 are the experimental values of magnetization measured at temperatures Ti and Ti+1, respectively, under an applied magnetic field Hi.
Figure 7 shows the temperature dependence of |ΔSM| upon a magnetic field change H = 1 to 5 T for all the studied compounds.
For all of the cases, the maximum of |ΔSM| exhibits a linear increase when the applied maximum field is increased. As shown for Er(Fe0.8Mn0.2)2 in Figure 7a, the |ΔSM| trace found when applying a rather weak field change of [0–1 T] mimics the susceptibility trace itself as shown on Figure 3a. But for larger magnetic field changes of [0–2 T] to [0–5 T] a wide bump of ΔSM extends over ~400 K, making the ΔSM (T) trace rather untypical, in comparison with classical MCE materials.
For the three Co-containing compounds, apart the first ΔSM (T) peak setting at TC, a second anomaly is pointed out, as shown Figure 7b–d. The latter phenomenon is related to the compensation temperature TComp. At TC, the ΔSM (T) value is negative as for a classical direct MCE effect, but it is positive at TComp as for a reverse MCE effect. The present phenomena fairly confirm what was found for the binary R-Fe compounds [56]. Once more, here the temperature-wide bumps of ΔSM appear and extend over ~400 K, but are systematically ~1/3 less marked (~1.5 J·kg−1·K−1) than that found for Er(Fe0.8Mn0.2)2 (~2.2 J·kg−1·K−1) for a magnetic field change of [0–5 T]. The | Δ S M max | determinated on both side of the compensation temperature under a change of applied magnetic field of 5 T are reported in Table 3.

4. Discussion

The structural, magnetic, and magnetocaloric properties of the Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2 compounds were investigated. The XRD results confirm that partial substitution of Co to Mn on the TM site preserves the MgCu2-type structure. Around 450 K, a compensation temperature is found for the Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2 and Er(Fe0.7Mn0.1Co0.2)2 compounds, involving a ferri-magnetic arrangement between the Er and TM magnetic sublattices.
However, the magnetic properties of the Er(Fe1−xTMx)2 Laves phase compounds with TM = (Mn, Co) and x = 0.2 or 0.3 are not so obvious to describe and understand. Hereafter, the main characteristics of members of cubic RTM2 C15-type compounds will be briefly recalled, mainly focusing on the R = Er systems, with TM = Fe, Co, and Mn successively.
The bulk magnetic properties of the ErFe2 binary has been well described while using a molecular field type model with negative magnetic exchange couplings in between the heavy rare earth element (e.g., Er) centering the Friauf type polyhedron formed by TM (Fe) atoms. The magnetic moments of both elements correspond almost well to the free metal values [38,39,40] the main coupling exchange interactions to consider are the positive Fe-Fe and the negative Er-Fe one which is addressed via the 3d–5d–4f path. As a matter of proof, hydrogen insertion to form ErFe2Hx hydrides leads to 1–a progressive decrease of the Hhf field transferred from the Fe sites that generates 2–a reduction of the J(Er) kinetic momentum, 3–a subsequent decrease of the 4f(Er) magnetic polarization, and 4–a weakening of the 3d(Fe)–5d(Er) overlap efficiency upon changes of conduction electron density at the Fermi level EF via the 1s(H)–3d(Fe) hybridization. Consequently, the 3d(Fe) local moment appears slightly diminished, but a decrease of the Fe-Fe and Fe-Er exchange forces lead to a net decrease of both TC and TComp [35,57,58,59,60,61,62]. All of these changes can be well described using a molecular field type picture.
The case of the RCo2 binary with the C15 cubic structure was recently recalled in a recent paper that was dedicated to MCE interests [28]. In fact ErCo2 is a typical example of RCo2 compounds which magnetism is beyond the limits of Co itinerant electron meta-magnetism [58,59,60] leading to a 1st order magnetic ordering at TC ~43 K only. This occurs thanks to the Er hyperfine transferred field, so, after substituting with a few amount of Fe to Co, the paramagnetic level is increased related to a Density of State (DOS) band transfer, leading to extend the magnetic ordering up to highest temperature, as we observed in ref [28].
In the R-Mn binary compounds, Mn was shown to induce very spectacular magnetic features, as e.g., for the isotypes Y6Mn23–ferromagnetic (FM with TC ~500 K)/Th6Mn23 Pauli paramagnet and Y6Mn23H~23 Pauli paramagnet/Th6Mn23H23–FM (TC ~350 K) [44,45,46,62]. It is worth to note that the R6TM23 series (SG Fm3m) and the RTM2 C15 series (SG Fd-3m) exhibit very close structure coordination features that consist in CN12 TM-coordination number of the R atom, forming a cuboctahedron for the former and a Friauf-type polyhedron for the latter. For such high coordination numbers, the formation (or loss) of a local 3d magnetic moment apart a critical Mn-Mn distance was proposed and questioned by several authors [63,64]. Effectively, the magnetic moment configurations are very different in the RMn2 series with very low magnetic ordering transitions (e.g., ~10–30 K), evidence of several type AFM ordering, weak (<1 µB) or no 3d-magnetic moment [42,43,63,64]. When using interstitial hydrogen as a distance spacer the situation was observed to evolve, then the change of electron s-type density must also be accounted for [44,45,61]. In ref. [42], the nature of magnetic polarization and interactions was analyzed more systematically, aiming distinguish the model of Mn-Mn critical distance effect to d-band meta-magnetism considerations, reference to that a deep minimum of DOS should occur at EF. Accordingly, it depends whether or not the JTM-TM exchange forces are positive (Co-Co), negative (Mn-Mn), or intermediate (e.g., Fe-Mn), also accounting for the JR-TM coupling forces.
Subsequently, several groups have questioned the magnetic characteristics of R(TM1−xTM’x)2 pseudo-ternary compounds, TM,TM’ є {Mn, Fe, Co, Ni}. Ref [65] provides one of the more extended and recent overviews on the magnetoelastic and magnetocaloric properties of such C15 based Laves phase compounds.
Back to the more complex situation organized here with the Er(Fe1−x(Mn-Co)x)2 compounds, the elementary analysis developed here tends to demonstrate that Mn could achieve very different levels and signs in its magnetic polarization up to temperatures rather high. This apparent type of meta-magnetism appears to be enhanced by both the rather robust 3d-Fe and 4f-Er magnetism, and the relative force of the exchange interactions shared by Co substitutions.
A more detailed knowledge of each particular TM element contributions seems difficult to establish more ahead either from bulk magnetization analysis or by using neutron diffraction. In fact, a non-collinear magnetic ordering, depending on the hydrogen content, has yet been proposed by using the latter technique to characterize the magnetic structure in the ErFe2-H system [66]. Besides, and very recently, meta-magnetic transitions were pointed out in the derivate parent system Y1−xErxFe2(H,D)4.2 involving inversion from AFM to FM couplings in between Er and Fe lattices [67]. However, for these large hydrogen content, the cubic symmetry of the C15 crystal structure is lowered to a monoclinic space group (C2/m, even better Pc), due to a specific ordering on the tetrahedral site occupancy by H(D). So, a simple parallel teaching is not made possible to establish.
Here, the high symmetry of the 8a (Er) and 16d (TM) sites forming the Friauf coordination and the random distribution of the three TM elements lead to global information, only. Subsequently, magnetoresistance measurements and e.g., local probes, such as XMCD, 57Fe (reference to the systematic work [39]), 57Co and 166Er Mössbauer spectroscopy, also NMR spectroscopies… should be considered to detail the magnetic properties of the Er(Fe1−x(Co-Mn)x)2 series. However, the concluding statements found in [67], as well as several refs herein mentioned, are of interest, since focusing on a meta-magnetic process is related to an itinerant electron meta-magnetic behavior of the Fe(TM) sublattice and corresponding to peculiarities (or changes) of DOS at the Fe Fermi level.
Furthermore, the very detailed work, but mainly dedicated to R-Co binaries or pseudo-binaries, could serve as reference guide [68]. Accordingly, the Spin Fluctuation Theory (SFT) [69] expressed under the Gaussian approximation [70] looks to be considered here (temperature and field dependencies, 2nd order transition). Complementary, electronic structure calculations leading to derive theoretical trends of the magnetic and elastic properties e.g., as recently reported for TbFe2 and TbCo2 systems in ref. [71] should be of interest to compare after using a KKR-CPA code, the present Er(Fe1−xTMx)2 compounds, as well to their hydrides.

5. Conclusions

The entropy variation ΔSM recorded on the present compounds versus a small field variation mimics rather well the magnetic susceptibility behavior versus temperature. Upon application of larger and larger magnetic field variations, the ΔSM contribution increases almost linearly up to significant levels (−1.5 to 2.2 J/kg·K); moreover, within a large temperature range of 300 to 400 K. Even if these contributions remain modest in comparison with what is received from performant magnetocaloric compounds [1,2,3,4,5,6,7], but in a restricted temperature range, here the ΔSM contributions at TC (even at Tcomp.) remain especially weak. Reference made between the Stoner and the Spin Fluctuation theories [70], only the binary ErCo2 [15,72] undergoing a first order transition can be related directly to a Stoner type model [58,59]. Conversely the Er(Fe1−xTMx)2 with TM = Co, Mn, are relevant for a SFT model with no marked entropy effect at the second type transition.
Even if they display rather modest performances, the present Er(Fe1−xTMx)2 compounds may serve as magneto-caloric elements for cryogenic applications, as effective in a wide range of temperature. This can appear as an interesting alternative to prefer the use composites of binary RCo2 mixtures with R = Tb, Dy, Ho, Er… [61,72,73,74]. Anyway, quasi binary R(Co0.88Fe0.12)2 compounds based on the latter series were recently investigated for their peculiar characteristics down to Curie temperature [75]. High field susceptibility temperature dependence was evidenced to take place in intermediate to low temperature ranges and interpreted in terms of the “weak magnetic sublattice” model. One more, such behavior supports the interest of more systematic magnetic characterizations of the RTM2 series of Laves type compounds, with R being a heavy rare earth metal and TM being a solution of magnetic 3d metals. Otherwise, a structure spacer, such as inserted hydrogen atoms, might be of interest to modify i.e., the DOS in the vicinity of EF and then the magnetic couplings and configurations, as already mentioned here above [29,35,44,45,46,67].

Author Contributions

Conceptualization, S.O., P.d.R. and D.F.; methodology, D.F. and P.d.R.; validation, D.F.; formal analysis, I.C., S.O. and D.F.; resources, S.O. and P.d.R.; experiment & data curation, I.C., S.H.-K.; writing—original draft preparation S.O.; writing—review and editing, D.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This study was supported by Faculté des Sciences de Sfax and Institut Néel, Grenoble.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pecharsky, V.K.; Gschneidner, J.K.A. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
  2. Fujieda, S.; Hasegawa, Y.; Fujita, A.; Fukamichi, K. Direct measurement of magnetocaloric effects in itinerant-electron metamagnets La(FexSi1−x)13 compounds and their hydrides. J. Magn. Magn. Mater. 2004, 272, 2365–2366. [Google Scholar] [CrossRef]
  3. Tegus, O.; Brück, E.; Buschow, K.H.J.; De Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef]
  4. von Ranke, P.J.; De Campos, A.; Caron, L.; Coelho, A.A.; Gama, S.; De Oliveira, N.A. Calculation of the giant magnetocaloric effect in the MnFeP0.45As0.55 compound. Phys. Rev. B 2004, 70, 094410. [Google Scholar] [CrossRef]
  5. Tishin, A.M. Magnetocaloric effect: Current situation and future trends. J. Magn. Magn. Mater. 2007, 316, 351–357. [Google Scholar] [CrossRef]
  6. Brück, E.; Tegus, O.; Thanh, D.; Buschow, K. Magnetocaloric refrigeration near room temperature (invited). J. Magn. Magn. Mater. 2007, 310, 2793–2799. [Google Scholar] [CrossRef]
  7. Wada, H.; Tanabe, Y. Giant magnetocaloric effect of MnAs1−xSbx. Appl. Phys. Lett. 2001, 79, 3302–3304. [Google Scholar] [CrossRef]
  8. Han, Z.D.; Wang, D.H.; Zhang, C.; Xuan, H.C.; Gu, B.X.; Du, Y.W. Low-field inverse magnetocaloric effect in Ni50−xMn39+xSn11 Heusler alloys. Appl. Phys. Lett. 2007, 90, 042507. [Google Scholar] [CrossRef]
  9. Trung, N.T.; Zhang, L.; Caron, L.; Buschow, K.H.J.; Brück, E. Giant magnetocaloric effects by tailoring the phase transitions. Appl. Phys. Lett. 2010, 96, 172504. [Google Scholar] [CrossRef]
  10. Trung, N.T.; Biharie, V.; Zhang, L.; Caron, L.; Buschow, K.H.J.; Brück, E. From single- to double-first-order magnetic phase transition in magnetocaloric Mn1−xCrxCoGe compounds. Appl. Phys. Lett. 2010, 96, 162507. [Google Scholar] [CrossRef] [Green Version]
  11. Liu, E.; Wang, W.; Feng, L.; Zhu, W.; Li, G.; Chen, J.; Zhang, H.; Wu, G.; Jiang, C.; Xu, H.; et al. Stable magnetostructural coupling with tunable magnetoresponsive effects in hexagonal ferromagnets. Nat. Commun. 2012, 3, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  12. Liu, J.; Gottschall, T.; Skokov, K.P.; Moore, J.D.; Gutfleisch, O. Giant magnetocaloric effect driven by structural transitions. Nat. Mater. 2012, 11, 620–626. [Google Scholar] [CrossRef] [PubMed]
  13. Pecharsky, A.O.; Gschneidner, J.K.; Pecharsky, V.K. The giant magnetocaloric effect of optimally prepared Gd5Si2Ge2. J. Appl. Phys. 2003, 78, 4722–4728. [Google Scholar]
  14. Hu, F.-X.; Qian, X.L.; Sun, J.R.; Wang, G.J.; Zhang, X.X.; Cheng, Z.H.; Shen, B.G. Magnetic entropy change and its temperature variation in compounds La(Fe1−xCox)11.2Si1.8. J. Appl. Phys. 2002, 92, 3620–3623. [Google Scholar] [CrossRef]
  15. Wada, H.; Tomekawa, S.; Shiga, M. Magnetocaloric effect of ErCo2. J. Magn. Magn. Mater. 1999, 196, 689–690. [Google Scholar] [CrossRef]
  16. Nikitin, S.; Myalikgulyev, G.; Tishin, A.; Annaorazov, M.; Asatryan, K.; Tyurin, A. The magnetocaloric effect in Fe49Rh51 compound. Phys. Lett. A 1990, 148, 363–366. [Google Scholar] [CrossRef]
  17. Tohei, T.; Wada, H.; Kanomata, T. Large magnetocaloric effect of Mn3−xCoxGaC. J. Magn. Magn. Mater. 2004, 272, E585–E586. [Google Scholar] [CrossRef]
  18. Provenzano, V.; Shapiro, A.J.; Shull, R.D. Reduction of hysteresis losses in the magnetic refrigerant Gd5Ge2Si2 by the addition of iron. Nature 2004, 429, 853–857. [Google Scholar] [CrossRef]
  19. Xie, Z.G.; Geng, D.; Zhang, Z.D. Reversible room-temperature magnetocaloric effect in Mn5PB2. Appl. Phys. Lett. 2010, 97, 202504. [Google Scholar] [CrossRef]
  20. Buschow, K.H.J.; Van Stapele, R.P. Magnetic Properties of the intermetallic compounds RFe2. Le J. de Phys. Colloq. 1971, 32, C1-672. [Google Scholar] [CrossRef]
  21. Buschow, K.H.J. Magnetic Properties of some Cubic Rare-Earth-Iron Compounds of the Type RFe2 and RxY1−xFe2. J. Appl. Phys. 1970, 41, 4066. [Google Scholar] [CrossRef]
  22. Mican, S.; Benea, D.; Mankovsky, S.; Polesya, S.; Gînscă, O.; Tetean, R. Magnetic behaviour of Er1−xZrxFe2 intermetallic compounds. J. Physics Condens. Matter 2013, 25, 466003. [Google Scholar] [CrossRef]
  23. Haldar, A.; Singh, N.K.; Mudryk, Y.; Nayak, A.K.; Suresh, K.G.; Nigam, A.K.; Pecharsky, V.K. Magnetostructural transition in Ce(Fe0.975Ga0.025)2 compound. J. Appl. Phys. 2010, 107, 09E133. [Google Scholar] [CrossRef] [Green Version]
  24. Anikin, M.S.; Tarasov, E.N.; Kudrevatykh, N.V.; Zinin, A.V. Untypical Temperature Dependence of the Magnetocaloric Effect in the Dy(Co1−xFex)2 (x = 0.10; 0.15) Compounds. Solid State Phenom. 2015, 233, 247–250. [Google Scholar] [CrossRef]
  25. Anikin, M.S.; Tarasov, E.; Kudrevatykh, N.; Osadchenko, V.; Zinin, A. About the Role of Fe-Ions in the Formation of Magnetocaloric Effect in Ho(Co1−xFex)2 Compounds. Acta Phys. Pol. A 2015, 127, 635–637. [Google Scholar] [CrossRef]
  26. Halder, M.; Yusuf, S.; Mukadam, M.D.; Shashikala, K. Magnetocaloric effect and critical behavior near the paramagnetic to ferrimagnetic phase transition temperature in TbCo2−xFex. Phys. Rev. B 2010, 81, 174402. [Google Scholar] [CrossRef] [Green Version]
  27. Zou, J.-D.; Shen, B.-G.; Sun, J.-R. Magnetic properties and magnetocaloric effect in TbCo2−xFex compounds. Chin. Phys. 2007, 16, 3843. [Google Scholar]
  28. Chaaba, I.; Othmani, S.; Haj-Khlifa, S.; Fruchart, D.; Cheikhrouhou-Koubaa, W.; Cheikhrouhou, A.; De Rango, P. Magnetic and magnetocaloric properties of Er(Co1−xFex)2 intermetallic compounds. J. Magn. Magn. Mater. 2017, 439, 269–276. [Google Scholar] [CrossRef]
  29. Chaaba, I.; Othmani, S.; Haj-Khlifa, S.; De Rango, P.; Fruchart, D. Effect of Hydrogen on the Structure, Magnetic and Magnetocaloric Properties of Laves Phase Type-Compounds RE(Fe0.25Co0.75)2Hy with RE = Ho and Er, y = 0.0, 3.0, 3.5. Solid State Phenom. 2019, 289, 102–107. [Google Scholar] [CrossRef]
  30. Ilyushin, A.; Wallace, W. Magnetic and structural studies of rare earth-iron-manganese laves phase ternaries I. J. Solid State Chem. 1976, 17, 131–133. [Google Scholar] [CrossRef]
  31. Ilyushin, A.; Wallace, W. Magnetic and structural studies of rare earth-iron-manganese laves phase ternaries II. J. Solid State Chem. 1976, 17, 373–376. [Google Scholar] [CrossRef]
  32. Merches, M.; Narasimhan, K.S.V.L.; Wallace, W.E.; Ilyushin, A. Magnetic Properties of R(Fe1−xMnx)2 Compounds (R = Gd, Tb, By, Ho or Er). AIP Conf. Proc. 1976, 34, 233. [Google Scholar] [CrossRef]
  33. Rodriguez-Carvajal, J. Fullprof. 2k, Version 4.6 c. Physica B 2002, 55, 192. Available online: https://scholar.google.com/citations?user=mJgatLIAAAAJ&hl=en (accessed on 4 September 2017).
  34. Clementi, E.; Raimond, D.I.; Reinhardt, W.P. Atomic Screening Constants from SCF Functions II. J. Chem. Phys. 1967, 47, 1300. [Google Scholar] [CrossRef]
  35. De Saxce, T.; Berthier, Y.; Fruchart, D. Magnetic and structural properties of the ternary hydride phases of ErFe2. J. Less Common Met. 1985, 107, 35–43. [Google Scholar] [CrossRef]
  36. Dariel, M.P.; Atzmony, U. Bulk magnetic anisotropy constants of the rare-earth iron Laves compounds. Int. J. Magn. 1973, 4, 213. Available online: www.iaea.org›inis›collection›NCLCollectionStore›_PublicPDF (accessed on 16 June 2020).
  37. Bargouth, M.O.; Will, G. Neutron diffraction study of ErFe2. Le J. Phys. Colloq. 1971, 32, C1-675. [Google Scholar] [CrossRef]
  38. du Tremolet de Lacheisserie, E.; Gignoux, D.; Schenker, M. Magnetism; Grenoble Sciences: Grenoble, France, 2005; ISBN 0 387 22967 1. E-book ISBN 0 387 23062 9. [Google Scholar]
  39. Bowden, G.J.; Bunbury, D.S.P.; Guimaraes, A.P. Mössbauer Studies of Iron-Rare Earth Intermetallics. J. Appl. Phys. 1968, 39, 1323. [Google Scholar] [CrossRef]
  40. Wallace, W.E. Mössbauer Effect Measurements of Hyperfine Interactions in Laves Phases Containing Fe Combined with Ti, Zr, Y, and the Lanthanide Metals. J. Chem. Phys. 1964, 41, 3857. [Google Scholar] [CrossRef]
  41. Burzo, E. On the magnetic properties of Y(FexCo1−x)2 compounds. Solid State Commun. 1978, 25, 825–828. [Google Scholar] [CrossRef]
  42. Gaidukova, I.Y.; Dubenko, I.S.; Levitin, R.Z.; Markosyan, A.S.; Pirogov, A.N. Nature of the magnetism of the subsystem in RMn2 compounds. Zh. Eksp. Teor. Fiz. 1988, 94, 236242. [Google Scholar]
  43. Schaafsma, A.; Besnus, M.; Vincze, I.; Van Der Woude, F. Effect of Mn on the magnetic moments of Fe in intermetallic compounds. J. Magn. Magn. Mater. 1980, 1149–1150. [Google Scholar] [CrossRef]
  44. Malik, S.; Takeshita, T.; Wallace, W. Hydrogen induced magnetic ordering in Th6Mn23. Solid State Commun. 1977, 23, 599–602. [Google Scholar] [CrossRef]
  45. Commandré, M.; Fruchart, D.; Rouault, A.; Sauvage, D.; Shoemaker, C.; Shoemaker, D. Etude par diffraction neutronique des composés Mn23Y6Dx. J. Phys. Lett. 1979, 40, 639–642. [Google Scholar] [CrossRef]
  46. Buschow, K.H.J.; Sherwood, R.C. Magnetic properties and hydrogen absorption in rare-earth intermetallics of the type RMn2 and R6Mn23. J. Appl. Phys. 1977, 48, 4643–4648. [Google Scholar] [CrossRef]
  47. Mitchell, I.V.; Coey, J.M.D.; Givord, D.; Harris, I.R.; Hanitsch, R. Concerted European Action on Magnets (CEAM); Springer Science & Business Media: New York, NY, USA, 2012; pp. 72–73. [Google Scholar]
  48. Belorizky, E.; Fremy, M.A.; Gavigan, J.P.; Givord, D.; Li, H.S. Evidence in rare-earth (R)–transition metal (M) intermetallics for a systematic dependence of R-M exchange interactions on the nature of the R atom. J. Appl. Phys. 1987, 61, 3971–3973. [Google Scholar] [CrossRef]
  49. Buschow, K.H.J.; de Boer, F.R. Physics of Magnetism and Magnetic Materials; Springer Science & Business Media: New York, NY, USA, 2007; ISBN 978-0-306-48408-7. [Google Scholar]
  50. Fruchart, D.; Berthier, Y.; De Saxce, T.; Vulliet, P. Etudes structurales et magnetiques des formes cubiques et rhomboedriques LnFe2Hx, Ln = Er, Tb. J. Solid State Chem. 1987, 67, 197–209. [Google Scholar] [CrossRef]
  51. Pontonnier, L.; Fruchart, D.; Soubeyroux, J.; Triantafillidis, G.; Berthier, Y. Structural and magnetic behaviour of LuFe2Hx. J. Less Common Met. 1991, 172, 191–197. [Google Scholar] [CrossRef]
  52. Talik, E.; Kulpa, M.; Mydlarz, T.; Kusz, J.; Böhm, H. Magnetic properties of ErMn2 single crystals. J. Alloys Compd. 2003, 348, 12–17. [Google Scholar] [CrossRef]
  53. Banerjee, B. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
  54. Yu, B.; Gao, Q.; Zhang, B.; Meng, X.; Chen, Z. Review on research of room temperature magnetic refrigeration. Int. J. Refrig. 2003, 26, 622–636. [Google Scholar] [CrossRef]
  55. Gschneidner, K.A.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Res. 2000, 30, 387–429. [Google Scholar] [CrossRef] [Green Version]
  56. Nikitin, S.A.; Talalaeva, E.V.; Chernikova, L.A.; Andreenko, A.S. Magnetocaloric effects in rare-earth magnetic materials. Zh. Eksp. Teor. Fiz. 1973, 65, 2058. [Google Scholar]
  57. Rhyne, J.J.; Sankar, S.G.; Wallace, W.E. Sublattice magnetization of ErFe2—H. In Rare Earths in Modern Science and Technology; McCarthy, G.J., Rhyne, J.J., Eds.; Plenum Press: New York, NY, USA, 1978; ISBN 978-1-4613-3054-7. [Google Scholar]
  58. Cyrot, M.; Gignoux, D.; Givord, F.; Lavagna, M. Magnetism of the rare earth, 3d–Theoretical review. J. Phys. Colloq. 1979, 40, C5-171. [Google Scholar] [CrossRef]
  59. Cyrot, M.; Lavagna, M. Density of states and magnetic properties of the rare-earth compounds RFe2, RCo2 and RNi2. J. Phys. 1979, 40, 763–771. [Google Scholar] [CrossRef]
  60. Khmelevskyi, S.; Mohn, P. The order of the magnetic phase transitions in RCo2 (R = rare earth) intermetallic compounds. J. Phys. Condens. Matter 2000, 12, 9453–9464. [Google Scholar] [CrossRef]
  61. Balli, M.; Fruchart, D.; Gignoux, D. Magnetic behaviour and experimental study of the magnetocaloric effect in the pseudobinary Laves phase Er1−xDyxCo2. J. Alloy. Compd. 2011, 509, 3907–3912. [Google Scholar] [CrossRef]
  62. Wallace, W.E.; Malik, S.K.; Takeshita, T.; Sankar, S.G.; Gualtieri, D.M. Magnetic properties of hydrides of the rare earths and rare earth intermetallics. J. Appl. Phys. 1978, 49, 1486–1491. [Google Scholar] [CrossRef]
  63. Hardman, K. Site magnetization of cubic and hexagonal HoMn2. J. Appl. Phys. 1982, 53, 1944. [Google Scholar] [CrossRef]
  64. Shiga, M. Magnetic ordering and frustration in itinerant systems: RMn2. J. Magn. Mag. Mat. 1994, 4, 17. [Google Scholar]
  65. Tepëшина, И.; Cwik, J.; Tereshina, E.; Politova, G.A.; Burkhanov, G.; Chzhan, V.; Ilyushin, A.; Miller, M.; Zaleski, A.; Nenkov, K.; et al. Multifunctional Phenomena in Rare-Earth Intermetallic Compounds With a Laves Phase Structure: Giant Magnetostriction and Magnetocaloric Effect. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
  66. Shashikala, K.; Raj, P.; Sathyamoorthy, A.; Rao, T.V.C.; Siruguri, V.; Paranjpe, S.K. ErFe2–H2 system. II. Non-collinear magnetic ordering. Philos. Mag. B 1999, 79, 1195–1203. [Google Scholar] [CrossRef]
  67. Paul-Boncour, V.; Isnard, O.; Shtender, V.; Skourski, Y.; Guillot, M. Origin of the metamagnetic transitions in Y1−xErxFe2(H,D)4.2 compounds. J. Magn. Magn. Mater. 2020, 512, 167018. [Google Scholar] [CrossRef]
  68. Duc, N.H.; Brommers, P.E. Aspects of Rare Earth-Transition metal Intermetallics. In Advanced Magnetism and Magnetic Materials—Volume 1; Duc, N.H., Ed.; Vietnam National University Press: Ho Chi Minh City, Vietnam, 2014; ISBN 978-604-62-4371-7. [Google Scholar]
  69. Moriya, T. Developments of the theory of spin fluctuations and spin fluctuation-induced superconductivity. Proc. Jpn. Acad. Ser. B 2006, 82, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  70. Melnikov, N.B.; Reser, B.I.; Grebennikov, V. Spin-fluctuation theory beyond Gaussian approximation. J. Phys. A Math. Theor. 2010, 43, 195004. [Google Scholar] [CrossRef] [Green Version]
  71. Bentouaf, A.; Mebsout, R.; Rached, H.; Amari, S.; Reshak, A.H.; Aissa, B. Theoretical investigation of the structural, electronic, magnetic and elastic properties of binary cubic C15-Laves phases TbX2 (X = Co and Fe). J. Alloy. Compd. 2016, 689, 885–893. [Google Scholar] [CrossRef]
  72. Duc, N.; Anh, D.K.; Brommer, P. Metamagnetism, giant magnetoresistance and magnetocaloric effects in RCo2-based compounds in the vicinity of the Curie temperature. Phys. B Condens. Matter 2002, 319, 1–8. [Google Scholar] [CrossRef]
  73. Valiev, E. Entropy and magnetocaloric effect in ferrimagnets RCo2. J. Exp. Theor. Phys. 2017, 124, 968–974. [Google Scholar] [CrossRef]
  74. Balli, M.; Fruchart, D.; Gignoux, D. A study of magnetism and magnetocaloric effect in Ho1−xTbxCo2 compounds. J. Magn. Mag. Mat. 2007, 314, 16–20. [Google Scholar] [CrossRef]
  75. Anikin, M.S.; Tarasov, E.N.; Kudrevatykh, N.V.; Volegov, A.S.; Zinin, A.V. Magnetic properties of R(Co0.88Fe0.12)2 quasi-biany compounds. J. Phys. Conf. Ser. 2019, 1389, 012061. [Google Scholar] [CrossRef]
Metals 10 01247 g001 550
Figure 1. X-ray diffraction (XRD) patterns of Er(Fe0.2Mn0.8)2, (black), Er(Fe0.8Mn0.1Co0.1)2 (green), Er(Fe0.7Mn0.2Co0.1)2 (blue), and Er(Fe0.7Mn0.1Co0.2)2 (red). A tiny amount of Er2O3 impurity was detected for Er(Fe0.2Mn0.8)2.
Figure 1. X-ray diffraction (XRD) patterns of Er(Fe0.2Mn0.8)2, (black), Er(Fe0.8Mn0.1Co0.1)2 (green), Er(Fe0.7Mn0.2Co0.1)2 (blue), and Er(Fe0.7Mn0.1Co0.2)2 (red). A tiny amount of Er2O3 impurity was detected for Er(Fe0.2Mn0.8)2.
Metals 10 01247 g001
Metals 10 01247 g002 550
Figure 2. Observed (red) and calculated (black) XRD patterns of Er(Fe0.8Mn0.2 Co0.1)2. The difference pattern is plotted at the bottom. Bragg reflections are indicated by ticks.
Figure 2. Observed (red) and calculated (black) XRD patterns of Er(Fe0.8Mn0.2 Co0.1)2. The difference pattern is plotted at the bottom. Bragg reflections are indicated by ticks.
Metals 10 01247 g002
Metals 10 01247 g003 550
Figure 3. Temperature dependence of the magnetization under 0.05 T (blue) and 1 T (red) for (a) Er(Fe0.8Mn0.2)2 (b) Er(Fe0.8Mn0.1Co0.1)2 (c) Er(Fe0.7Mn0.2Co0.1)2 and (d) Er(Fe0.7Mn0.1Co0.2)2. The inset of Figure 3 (c) allows distinguish in more details the magnetization behavior in between Tcomp. and TC.
Figure 3. Temperature dependence of the magnetization under 0.05 T (blue) and 1 T (red) for (a) Er(Fe0.8Mn0.2)2 (b) Er(Fe0.8Mn0.1Co0.1)2 (c) Er(Fe0.7Mn0.2Co0.1)2 and (d) Er(Fe0.7Mn0.1Co0.2)2. The inset of Figure 3 (c) allows distinguish in more details the magnetization behavior in between Tcomp. and TC.
Metals 10 01247 g003
Metals 10 01247 g004 550
Figure 4. Magnetization traces at 5K of Er(Fe0.2Mn0.8)2 (black), Er(Fe0.8Mn0.1Co0.1)2 (green), Er(Fe0.7Mn0.2Co0.1)2 (blue), and Er(Fe0.7Mn0.1Co0.2)2 (red) upon increasing the applied field up to 7 T.
Figure 4. Magnetization traces at 5K of Er(Fe0.2Mn0.8)2 (black), Er(Fe0.8Mn0.1Co0.1)2 (green), Er(Fe0.7Mn0.2Co0.1)2 (blue), and Er(Fe0.7Mn0.1Co0.2)2 (red) upon increasing the applied field up to 7 T.
Metals 10 01247 g004
Metals 10 01247 g005a 550Metals 10 01247 g005b 550
Figure 5. Variation of magnetization versus the applied magnetic field up to 5T at different temperatures for (a) Er(Fe0.8Mn0.2)2, (b,c,d) at the temperature range T < Tcomp and (b’,c’,d’) at T > Tcomp for (Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn01Co0.2)2, respectively.
Figure 5. Variation of magnetization versus the applied magnetic field up to 5T at different temperatures for (a) Er(Fe0.8Mn0.2)2, (b,c,d) at the temperature range T < Tcomp and (b’,c’,d’) at T > Tcomp for (Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn01Co0.2)2, respectively.
Metals 10 01247 g005aMetals 10 01247 g005b
Metals 10 01247 g006a 550Metals 10 01247 g006b 550
Figure 6. M2 vs. µ0H/M isotherm traces plotted apart from Curie temperature for (a) Er(Fe0.2Mn0.8)2, (b) Er(Fe0.8Mn0.1Co0.1)2, (c) Er(Fe0.7Mn0.2Co0.1)2, and (d) Er(Fe0.7Mn0.1Co0.2)2.
Figure 6. M2 vs. µ0H/M isotherm traces plotted apart from Curie temperature for (a) Er(Fe0.2Mn0.8)2, (b) Er(Fe0.8Mn0.1Co0.1)2, (c) Er(Fe0.7Mn0.2Co0.1)2, and (d) Er(Fe0.7Mn0.1Co0.2)2.
Metals 10 01247 g006aMetals 10 01247 g006b
Metals 10 01247 g007a 550Metals 10 01247 g007b 550
Figure 7. Magnetic entropy difference −ΔSM versus temperature for various magnetic field shifts for (a) Er(Fe0.2Mn0.8)2, (b) Er(Fe0.8Mn0.1Co0.1)2, (c) Er(Fe0.7Mn0.2Co0.1)2, and (d) Er(Fe0.7Mn0.1Co0.2)2. The inser of Figure 7c allows to better illustrate the thermal and field behavior of the MCE in between Tcomp. and TC.
Figure 7. Magnetic entropy difference −ΔSM versus temperature for various magnetic field shifts for (a) Er(Fe0.2Mn0.8)2, (b) Er(Fe0.8Mn0.1Co0.1)2, (c) Er(Fe0.7Mn0.2Co0.1)2, and (d) Er(Fe0.7Mn0.1Co0.2)2. The inser of Figure 7c allows to better illustrate the thermal and field behavior of the MCE in between Tcomp. and TC.
Metals 10 01247 g007aMetals 10 01247 g007b
Table
Table 1. Cell parameters at 300 K for Er(Fe0.8Mn0.2)2, Er(Fe0.8Co0.1Mn0.1 Co0.1)2, Er(Fe0.7Mn0.2 Co0.1)2, and Er(Fe0.7Mn0.1 Co0.2)2 refined from XRD.
Table 1. Cell parameters at 300 K for Er(Fe0.8Mn0.2)2, Er(Fe0.8Co0.1Mn0.1 Co0.1)2, Er(Fe0.7Mn0.2 Co0.1)2, and Er(Fe0.7Mn0.1 Co0.2)2 refined from XRD.
CompoundsCell Parameter (Å)Cell Volume (Å3)
Er(Fe0.8Mn0.2)217.313(3)391.18(3)
Er(Fe0.8Mn0.1Co0.1)227.265(5)383.54(2)
Er(Fe0.7Mn0.2Co0.1)237.281(1)386.02(1)
Er(Fe0.7Mn0.1Co0.2)247.246(1)380.42(2)
Table
Table 2. Total magnetic moments and TM moments for Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2 compounds at 5 K.
Table 2. Total magnetic moments and TM moments for Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2 compounds at 5 K.
CompoundsMolar Mass (g/mol.)Msat
(emu/g)		Msat
(µB/f.u.)		<µ3d>
(µB/f.u.)
Er(Fe0.8Mn0.2)21278.586122.386.101.45
Er(Fe0.8Mn0.1Co0.1)22279.385100.045.002.00
Er(Fe0.7Mn0.2Co0.1)23279.204105.235.261.87
Er(Fe0.7Mn0.1Co0.2)24280.00398.414.932.04
Table
Table 3. Transition temperature and maximum magnetic entropy change for Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2 for a (0–5 T) field change.
Table 3. Transition temperature and maximum magnetic entropy change for Er(Fe0.8Mn0.2)2, Er(Fe0.8Mn0.1Co0.1)2, Er(Fe0.7Mn0.2Co0.1)2, and Er(Fe0.7Mn0.1Co0.2)2 for a (0–5 T) field change.
CompoundsCompensation
Temperature (K)		Curie Temperature TC (K)−ΔSM (J·kg−1·K−1)
T<Tcomp/T> Tcomp
Er(Fe0.8Mn0.2)21no3552.11
Er(Fe0.8Mn0.1Co0.1)224355501.47/0.37
Er(Fe0.7Mn0.2Co0.1)234454751.5/0.07
Er(Fe0.7Mn0.1Co0.2)244255551.53/0.29

Share and Cite

MDPI and ACS Style

Othmani, S.; Chaaba, I.; Haj-Khlifa, S.; de Rango, P.; Fruchart, D. Magnetic and Magnetocaloric Effect of Laves Phase Compounds Er(Fe0.8−xMn0.2−yCox+y)2 with x, y = 0.0 or 0.1. Metals 2020, 10, 1247. https://doi.org/10.3390/met10091247

AMA Style

Othmani S, Chaaba I, Haj-Khlifa S, de Rango P, Fruchart D. Magnetic and Magnetocaloric Effect of Laves Phase Compounds Er(Fe0.8−xMn0.2−yCox+y)2 with x, y = 0.0 or 0.1. Metals. 2020; 10(9):1247. https://doi.org/10.3390/met10091247

Chicago/Turabian Style

Othmani, Safa, Ichrak Chaaba, Sonia Haj-Khlifa, Patricia de Rango, and Daniel Fruchart. 2020. "Magnetic and Magnetocaloric Effect of Laves Phase Compounds Er(Fe0.8−xMn0.2−yCox+y)2 with x, y = 0.0 or 0.1" Metals 10, no. 9: 1247. https://doi.org/10.3390/met10091247

APA Style

Othmani, S., Chaaba, I., Haj-Khlifa, S., de Rango, P., & Fruchart, D. (2020). Magnetic and Magnetocaloric Effect of Laves Phase Compounds Er(Fe0.8−xMn0.2−yCox+y)2 with x, y = 0.0 or 0.1. Metals, 10(9), 1247. https://doi.org/10.3390/met10091247

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop