Design and Simulation of Meshing Performance of Modified Straight Bevel Gears
Abstract
:1. Introduction
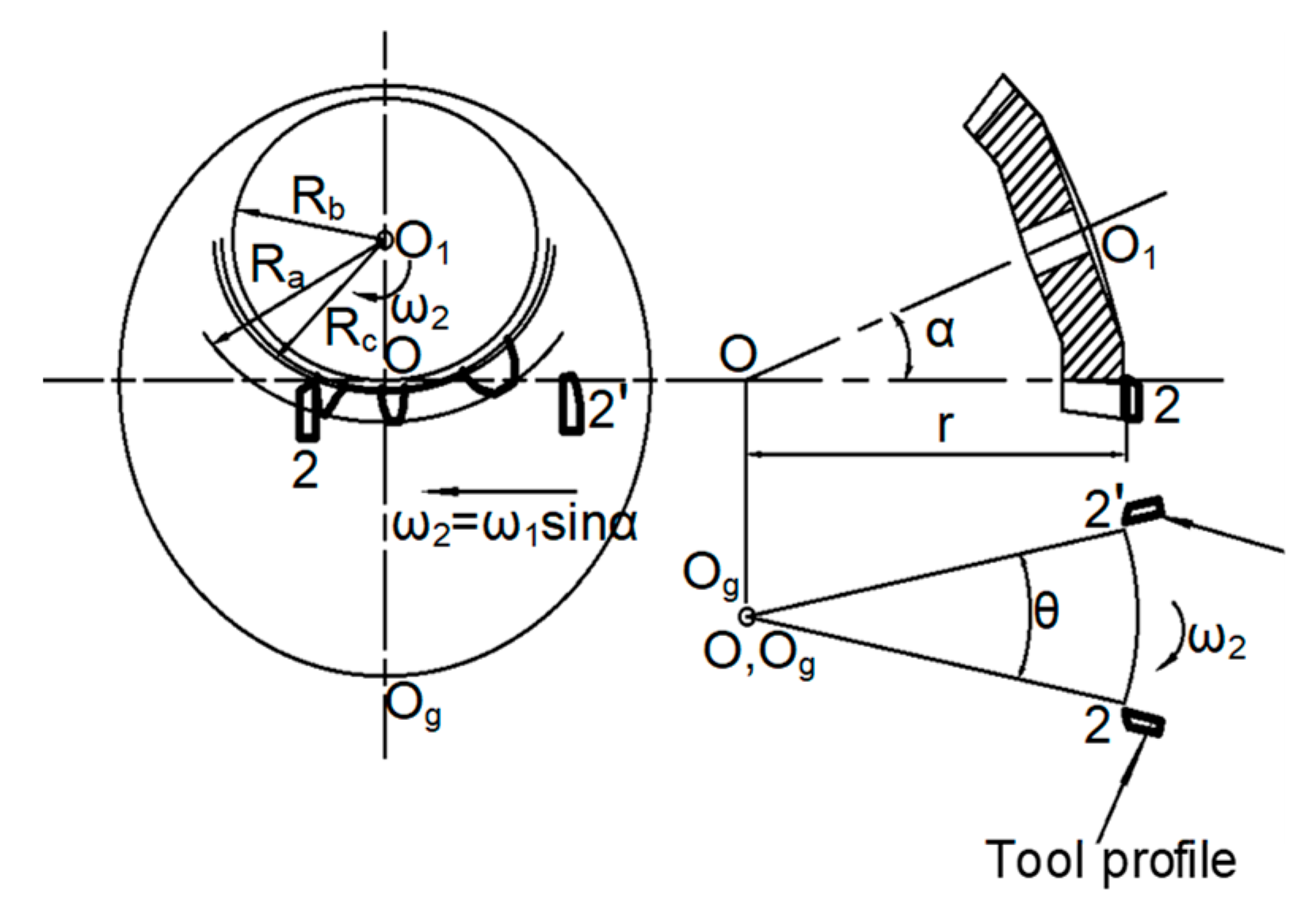
2. Theoretical Background
3. Establishment of Finite Element Models
4. Analysis of the Circumferential Displacements of Tooth
5. Determination of the Axial Modification of the Tooth
5.1. Derivation of Symmetric Crowned Modification Gear Tooth Surface
5.2. Derivation of Tooth End Relief Gear Tooth Surface
6. Results and Discussions
6.1. Influence of Modification on the Tooth Contact Area
6.2. Influence of Modification on the Tooth Contact Stress
6.3. Influence of Modification on the Distribution of Tooth Contact Stress
6.4. Influence of Modification on the Distribution of Tooth Bending Stress
6.5. Influence of Modification on the Transmission Error
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| θ | Angle between two bevel gear planing tools (deg) |
| θa | Angle of tip cone (deg) |
| θb | Angle of base cone (deg) |
| θc | Angle of cutting beginning cone (deg) |
| ΔΦ1 | Rotation angle of driving pinion (deg) |
| z | Number of teeth |
| Radius vector of gear tooth surface point | |
| Radius vector of point at base circle of gear planing tool | |
| rd | Radius of the bottom rim of the pinion (mm) |
| Mi | Matrix (N·m) |
| α | Pressure angle (deg) |
| Δδi | Circumferential displacement difference at critical position (mm) |
| δim | Circumferential displacement of meshing tooth along contact line at critical position (mm) |
| δiu | Circumferential displacement without mesh along contact line (mm) |
| δ | Circumferential displacement of nodes on bottom rim of pinion under loaded (mm) |
| b | Tooth width (mm) |
| ΔTi | Modification dimension |
| ΔLi | Relief length (mm) |
| ΔP | Axial displacement of pinion (mm) |
| ΔG | Axial displacement of gear (mm) |
| ΔE | Change of center distance (mm) |
| Δγ | Change of crossing angle (deg) |
References
- Xie, C. Improved analytical models for mesh stiffness and load sharing ratio of spur gears considering structure coupling effect. Mech. Syst. Signal Process. 2018, 111, 331–347. [Google Scholar] [CrossRef]
- Ouyang, T.; Huang, H.; Zhang, N.; Mo, C.; Chen, N. A model to predict tribo-dynamic performance of a spur gear pair. Tribol. Inter. 2017, 116, 449–459. [Google Scholar] [CrossRef]
- Wang, B.; Hua, L. Computerized design and FE simulation of meshing of involute spiral bevel gears with alignment errors. Adv. Mater. Res. 2011, 199–200, 386–391. [Google Scholar] [CrossRef]
- Lin, T.; He, Z. Analytical method for coupled transmission error of helical gear system with machining errors, assembly errors and tooth modifications. Mech. Syst. Signal Process. 2017, 91, 167–182. [Google Scholar] [CrossRef]
- Litvin, F.L.; Vecchiato, D.; Yukishima, K.; Azar, A.F. Reduction of noise of loaded and unloaded misaligned gear drives. Comput. Method. Appl. Mech. Eng. 2006, 195, 5523–5536. [Google Scholar] [CrossRef]
- Zhu, C.; Song, C.; Lim, T.C.; Peng, T. Pitch cone design and influence of misalignments on tooth contact behaviors of crossed beveloid gears. Mech. Mach. Theory 2013, 59, 48–64. [Google Scholar] [CrossRef]
- Chen, X.; Tang, J. Tooth contact analysis of spur face gear drives with alignment errors. In Proceedings of the 2011 Second International Conference on Digital Manufacturing and Automation, Hunan, China, 5–7 August 2011; pp. 1368–1371. [Google Scholar]
- Zhang, F.; Tian, X.; Cui, H. The modification design of involute straight bevel gear. IERI Procedia 2012, 3, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Song, C.; Zhu, C.; Ni, G. Effects of tooth modifications on mesh characteristics of crossed beveloid gear pair with small shaft angle. Mech. Mach. Theory 2018, 119, 142–160. [Google Scholar] [CrossRef]
- Motahar, H.; Samani, F.S.; Molaie, M. Nonlinear vibration of the bevel gear with teeth profile modification. Nonlinear Dyn. 2015, 83, 1875–1884. [Google Scholar] [CrossRef]
- Cao, X.; Lou, J.; Ma, Z. Sensitivity analysis of installation errors of the straight bevel gear modification tooth surface. J. Mech. Trans. 2014, 38, 40–43. (In Chinese) [Google Scholar]
- Simon, V.V. Influence of tooth modifications on tooth contact in face-hobbed spiral bevel gears. Mech. Mach. Theory 2011, 46, 1980–1998. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, H.; Han, X. Computerized design and simulation of meshing of modified double circular-arc helical gears by tooth end relief with helix. Mech. Mach. Theory 2010, 45, 46–64. [Google Scholar] [CrossRef]
- Samani, F.S.; Molaie, M.; Pellicano, F. Nonlinear vibration of the spiral bevel gear with a novel tooth surface modification method. Meccanica 2019, 54, 1071–1081. [Google Scholar] [CrossRef]
- Chen, X. The Modification Methods of Straight Bevel Gear. Ph.D. Thesis, Hua Zhong University of Science and Technology, Wuhan, China, 2006; pp. 73–90. (In Chinese). [Google Scholar]
- Shunmugam, M.S.; Narayana, S.V.R.S.; Jayarakash, V. Establishing gear tooth surface geometry and normal deviation. Mech. Mach. Theory 1998, 33, 525–534. [Google Scholar] [CrossRef]
- Han, X.; Hua, L.; Deng, S.; Luo, Q. Influence of alignment errors on contact pressure during straight bevel gear meshing process. Chin. J. Mech. Eng. 2015, 28, 1089–1099. [Google Scholar] [CrossRef]
- Deng, S.; Hua, L.; Han, X.; Hunag, S. Finite element analysis of contact fatigue and bending fatigue of a theoretical assembling straight bevel gear pair. J. Cent. South. Univ. 2013, 20, 279–292. [Google Scholar] [CrossRef]
- Shuting, L. Effect of addendum on contact strength bending strength and basic performance parameters of a pair of spur gears. Mech. Mach. Theory 2008, 13, 1543–1556. [Google Scholar]






















| Parameter | Jiangsu Pacific Gear Transmission Co. LTD, Taizhou, China | Driving Pinion | Driven Gear |
|---|---|---|---|
| Module (mm) | mn | 3.7792 | 3.7792 |
| Shaft angle (deg) | Σ | 90 | 90 |
| Number of teeth | z | 10 | 14 |
| Pressure angle (deg) | α | 22.5 | 22.5 |
| Modification coefficient of height | x | −0.1812 | 0.1812 |
| Shearing modification coefficient | xt | 0.05 | −0.05 |
| Addendum coefficient | ha* | 0.8 | 0.8 |
| Headspace coefficient | c | 0.188 | 0.188 |
| Face width (mm) | b | 9.75 | 9.75 |
| Gear aperture (mm) | Rc | 7.0275 | 10 |
| Jiangsu Pacific Gear Transmission Co. LTD, Taizhou, China | Modification Method | Modification Parameter |
|---|---|---|
| Case1 | Symmetric crowned modification | ΔT = 11 μm |
| Case2 | Symmetric crowned modification | ΔT = 15 μm |
| Case3 | Tooth end relief | ΔT1 = ΔT2 = Δ11 μm |
| Case4 | Tooth end relief | ΔT1 = 11 μm, ΔT2 = Δ15 μm |
| Names of Parameters | Value |
|---|---|
| Axial displacement of pinion, ΔP (mm) | 0.1 |
| Axial displacement of gear, ΔG (mm) | 0.1 |
| Change of center distance, ΔE (mm) | −0.02, 0.02 |
| Change of crossing angle, Δγ (deg) | 1 |
| Jiangsu Pacific Gear Transmission Co. LTD, Taizhou, China | Without Misalignment/MPa | ΔP = 0.1 /MPa | ΔG = 0.1 /MPa | ΔE = −0.02 /MPa | ΔE = 0.02 /MPa | Δγ = 1 /MPa |
|---|---|---|---|---|---|---|
| Unmodified gear | 594.4 | 698.3 | 849.5 | 705.4 | 661.4 | 602.4 |
| Case1 | 465.9 | 483.9 | 476.2 | 471.1 | 471.0 | 475.3 |
| Case2 | 491.5 | 508.0 | 496.0 | 491.1 | 496.4 | 493.8 |
| Case3 | 443.7 | 504.4 | 522.7 | 489.1 | 431.1 | 449.3 |
| Case4 | 441.3 | 494.9 | 503.8 | 482.6 | 419.0 | 442.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Xiong, X.; Zhuang, W. Design and Simulation of Meshing Performance of Modified Straight Bevel Gears. Metals 2021, 11, 33. https://doi.org/10.3390/met11010033
Chen M, Xiong X, Zhuang W. Design and Simulation of Meshing Performance of Modified Straight Bevel Gears. Metals. 2021; 11(1):33. https://doi.org/10.3390/met11010033
Chicago/Turabian StyleChen, Mingzhang, Xiaoshuang Xiong, and Wuhao Zhuang. 2021. "Design and Simulation of Meshing Performance of Modified Straight Bevel Gears" Metals 11, no. 1: 33. https://doi.org/10.3390/met11010033
APA StyleChen, M., Xiong, X., & Zhuang, W. (2021). Design and Simulation of Meshing Performance of Modified Straight Bevel Gears. Metals, 11(1), 33. https://doi.org/10.3390/met11010033






