Molten Steel Flow, Heat Transfer and Inclusion Distribution in a Single-Strand Continuous Casting Tundish with Induction Heating

Abstract

The electrical magnetic field plays an important role in controlling the molten steel flow, heat transfer and migration of inclusions. However, industrial tests for inclusion distribution in a single-strand tundish under the electromagnetic field have never been reported before. The distribution of non-metallic inclusions in steel is still uncertain in an induction-heating (IH) tundish. In the present study, therefore, using numerical simulation methods, we simulate the flow and heat transfer characteristics of molten steel in the channel-type IH tundish, especially in the channel. At the same time, industrial trials were carried out on the channel-type IH tundish, and the temperature distribution of the tundish with or without IH under different pouring ladle furnace was analyzed. The method of scanning electron microscopy was employed to obtain the distribution of inclusions on different channel sections. The flow characteristics of molten steel in the channel change with flow time, and the single vortex and double vortex alternately occur under the electromagnetic field. The heat loss of molten steel can be compensated in a tundish with IH. As heating for 145 s, the temperature of the molten steel in the channel increases by 31.8 K. It demonstrates that the temperature of the molten steel in the tundish can be kept at the target value of around 1813 K, fluctuating up and down 3 K after using electromagnetic IH. In the IH channel, the large inclusions with diameters greater than 9 μm are more concentrated at the edge of the channel, and the effect of IH on the inclusion with diameters less than 9 μm has little effect.

1. Introduction

In the continuous casting process, the tundish is not only a distributor of molten steel pouring from ladle to mold, but also a reaction vessel to ensure the homogenization of temperature and composition for molten steel [1,2]. Additionally, the stability of the pouring temperature of the molten steel in the tundish is an essential factor affecting the productivity of the casting machine and the quality of the slab [3]. The temperature fluctuation of molten steel due to the temperature of molten steel in the tundish decreasing during ladle changing at the initial or end of the pouring stage seriously affects the quality of the slab, and also reduces the productivity and yield of continuous casting [4]. Moreover, the heat lost through the ladle and tundish pool surfaces and the refractory wall during the entire casting process is inevitable during the casting process. The temperature of the molten steel in the tundish inevitably has large fluctuations. Hence, the control of the molten steel temperature is of great significance for continuous casting production.

So far, many innovative experiments [5,6] and new technologies [7,8,9] have been conducted and various process optimization has been established to homogenize the composition and temperature of molten steel. Particularly, electromagnetic metallurgical technology [10,11,12] utilizes the force or heat effect of the electromagnetic field or simultaneously uses the force and heat effect [13,14,15] to control molten metal flow, heat transfer and inclusion migration in the metallurgical process [16,17]. Plasma heating [18] and induction heating (IH) [19] are the leading heating methods in the process of heating molten steel in the continuous-casting tundish [20,21]. A channel-type IH tundish is developed by utilizing the thermal and force effects of electromagnetic fields [22,23,24]. The thermal effect of the electromagnetic field can fully compensate the molten steel temperature, reduce the fluctuation of the molten steel temperature in the tundish and effectively control the temperature in the tundish [25]. Moreover, the electromagnetic force can produce the “pinch effect”, so that the non-metallic inclusion particles with poor conductivity move toward the channel wall and finally adhere to the channel wall to remove [16]. The channel-type electromagnetic IH technology can not only heat the molten steel but also purify the molten steel and other metals and alloys, which has good application value and prospects [26].

A channel-type IH tundish as a new technology for achieving low superheated constant temperature casting and removal of non-metallic inclusions in molten steel was studied by water modeling [27] and numerical simulation [28,29,30]. In water modeling, the electromagnetic force and Joule heating cannot be considered. It is not comprehensive to ignore the electromagnetic force or Joule heating in the research of the molten steel flow field, temperature field, and non-metallic inclusion removal under the electromagnetic field. In general, experimental research is costly and cannot fully provide the entire state of heat and mass transfer of molten steel in the tundish.

Recently, numerical simulation has become more and more accepted as an alternative method for studying external electromagnetic fields and chemical reactions. The flow field, temperature field and the residence time distribution (RTD) for a single-strand tundish with IH were investigated [31,32]. Tang et al. [8] and Wang et al. [33,34] comprehensively analyzed the flow and heat transfer in multi-strand tundishes with IH by using the method of water simulation and numerical simulation. This work provides a novel design idea and application case for the upgraded trough IH tundish for the production of high-quality steel. To optimize the design of the horizontal channel to remove inclusions, understanding the impact of magnetic field parameters, the removal of inclusions in horizontal channels under AC (alternating current) magnetic field was numerically calculated [35]. Wang [36] established a generalized three-dimensional mathematical model of the movement of inclusions in the channel-type IH tundish, and the movement law of inclusions was investigated using the Euler–Lagrange method. However, in the numerical simulation, due to the uncertainty of the boundary conditions, the composition and quantity of inclusions and the limitations of calculation, it is difficult to accurately and comprehensively simulate the migration, collision and aggregation of inclusions. Therefore, in the numerical simulation, the distribution of inclusions is difficult to fully reflect the situation of real inclusions [30,36]. Moreover, the understanding of the flow field and temperature field of locally heated molten steel under electromagnetic force, as well as the unsteady flow and heat transfer characteristics, is still uncertain. Thus, it is necessary to obtain the distribution of inclusions in the molten steel channel under the IH, which is of great significance for understanding the migration mechanism of non-metallic inclusions in molten steel channel.

Based on the industrial trials data, the temperature of molten steel in the continuous-casting tundish during multi-ladle furnace (six furnaces) was recorded under conditions with and without IH. The distribution of inclusions at different positions of the channel in the tundish after IH under industrial conditions is analyzed in detail. In this work, the numerical simulation method is used to study the molten steel flow and heat transfer in the tundish with IH. The temperature data of molten steel in industrial trials was analyzed with and without IH. The numbers of inclusions in the channel steel rod cross sections were compared statistically by the surface scan method.

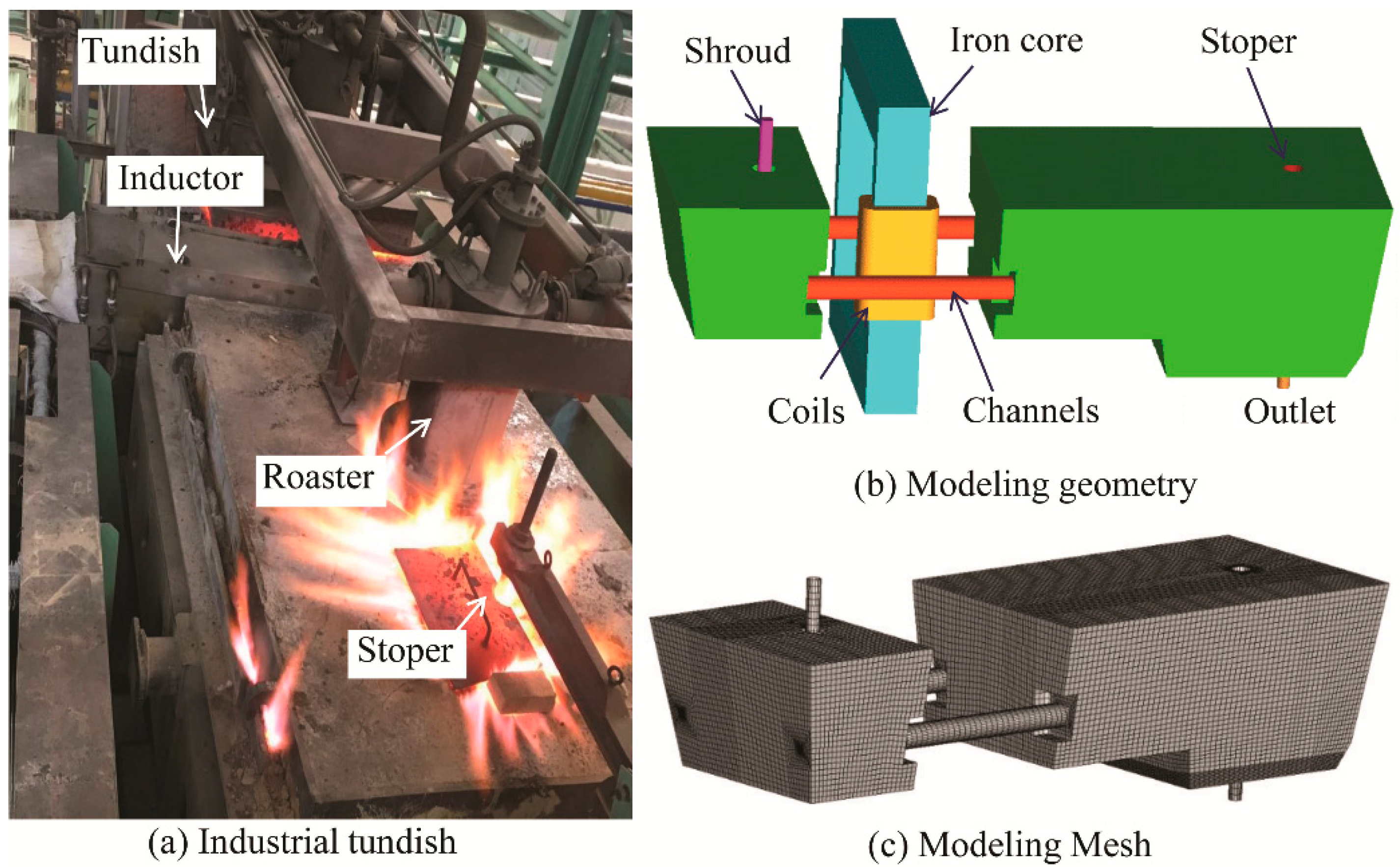
2. Model Description

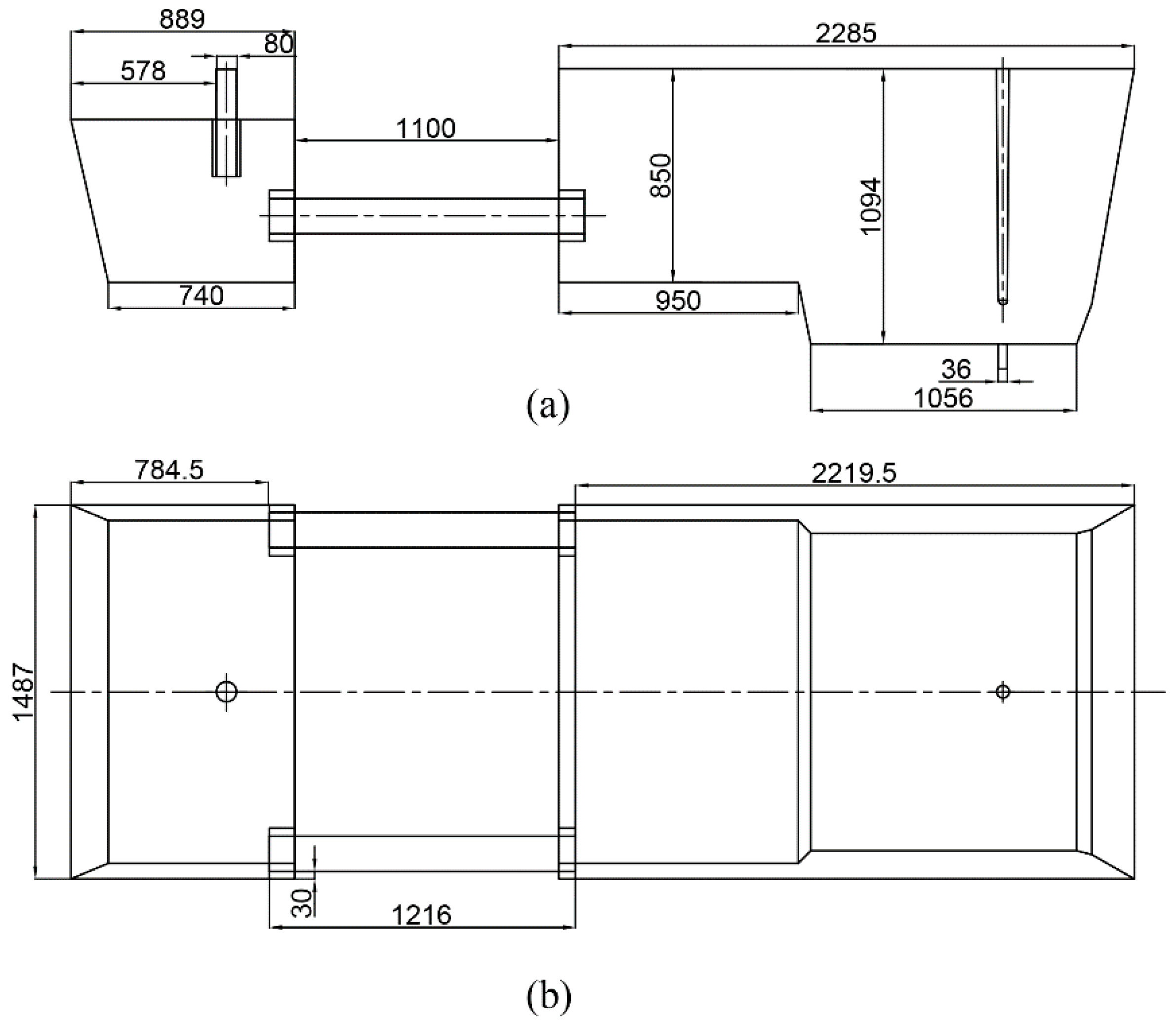
2.1. Main Dimensions of Model

The main characteristic of an industrial experiment on the single-strand slab tundish and numerical modeling are depicted in Figure 1. Two channels of an electromagnetic IH slab continuous-casting tundish are symmetrically located at the bottom of the tundish. The pouring zone and distribution zone of the tundish are connected by two channels. The IH device is composed of an iron core and an induction coil. The numerical modeling includes controlling the device stopper. The channel-type IH tundish mesh is mapped in whole hexahedron cells. The relevant dimensions of the IH tundish are described in Figure 2, where the front view (a) and top view (b) are shown. The direction of the channel axis is along the z-coordinate position to display the details of the induction channels.

2.2. Mathematical Modeling and Methodology

2.2.1. Fluid Flow and Heat Transfer Model

Given that the fluid is incompressible, the modified conservation equations take the following forms.

Continuity equation:

$$\frac{\partial \left(\rho \right)}{\partial \tau }+\frac{\partial \left(\rho u_i\right)}{\partial x_i}=0$$

(1)

Momentum equation:

$$\frac{\partial \left(\rho u_i\right)}{\partial \tau }+\frac{\partial \left(\rho u_i{u}_j\right)}{\partial x_j}=-\frac{\partial P}{\partial x_i}+\frac{\partial }{\partial x_j}\left[{\mu }_{\mathrm{eff}}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]+\rho \mathrm{g}+F$$

(2)

where τ, ρ and u represent flow time, fluid density and fluid velocity, respectively. g is gravity acceleration, and F is an electromagnetic force, i and j represent subscript index.

Turbulence kinetic energy (k) equation:

$$\frac{\partial \left(\rho u_{j}k\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left(\frac{{\mu }_{\mathrm{eff}}}{{\sigma }_k}\times \frac{\partial k}{\partial x_j}\right)+G-\rho \epsilon$$

(3)

Turbulence kinetic energy dissipation rate (ε) equation:

$$\frac{\partial \left(\rho u_j\epsilon \right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left(\frac{{\mu }_{\mathrm{eff}}}{{\sigma }_{\epsilon }}\times \frac{\partial \epsilon }{\partial x_j}\right)+\frac{\left(C_{1}G\epsilon -C_2\rho {\epsilon }^2\right)}{k}$$

(4)

where

$$G={\mu }_t\frac{\partial u_j}{\partial x_i}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$

(5)

Effective viscosity is:

$${\mu }_{\mathrm{eff}}=\mu +{\mu }_t=\mu +\rho C_{\mu }\frac{k^2}{\epsilon }$$

(6)

In order to take thermal natural convection into consideration, the buoyancy can be simplified by using a Boussinesq’s model. Thus, the relationship between the density and temperature of molten steel in this study is represented by [25].

$$\rho =8523-0.8358T\left(\mathrm{kg}·{\mathrm{m}}^{-3}\right)$$

(7)

2.2.2. Heat Transfer Model

Energy equation:

$$\frac{\partial \left(\rho C_{p}T\right)}{\partial t}+\nabla \left(\rho C_{p}uT\right)=\nabla \left(\lambda \nabla T\right)+Q+S_T$$

(8)

where τ, T and λ represent heat capacity, temperature and thermal conductivity, respectively. Q is electromagnetic Joule heating and S_T is viscous dissipation effect. The velocity field and temperature field are coupled with the molten steel density, which relates to its temperature. The calculation method and results of the source term can be referred to our previous work [13].

2.2.3. Boundary Condition and Parameters

The boundary conditions for the molten steel flow and heat transfer in IH tundish can be summarized as:

(1)

The tundish inlet is at speed entry and the inlet turbulence intensity is 8%. The inlet boundary condition is set as velocity magnitude, the outlet is set as the outflow boundary condition, zero shear stress is applied to the free surface of the tundish and no-slip boundary conditions are set to the other walls.

(2)

The constant value of the inlet temperature of molten steel is 1800 K.

(3)

The molten steel dynamic viscosity is constant 0.0061 kg/(m·s), specific heat is 750 J/(kg·K), thermal conductivity is 41 W/(m·K) [19].

(4)

The surface radiation and surface heat flux of each wall are considered as reference parameters [32], values of other boundary conditions and parameters for molten steel flow and heat transfer are listed in

Table 1. Parameters of the molten steel and boundary condition of flow and heat transfer.

Parameters	Value
Coefficient of thermal expansion of liquid steel, K−1	1.2 × 10−4
Inlet velocity, m s−1	0.72
Top wall heat flux, W m−2	15,000
Bottom wall heat flux, W m−2	1800
Longitudinal walls flux, W m−2	4600
Transversal walls flux, W m−2	4000
Channel walls flux, W m−2	1200
Tundish IH power, kW	900

.

2.2.4. Solution Method

The molten steel flow and heat transfer behavior in the channel-type IH tundish involves the coupling calculation of the velocity field and the temperature field. A commercial CFD software program, Fluent, was used to investigate single-phase fluid flow and heat transfer. The flow and heat transfer calculation are about 765,860 hexahedron cells. The time step of 10⁻⁴ s is used. For the velocity and temperature field, the convergence criteria are that the values are less than 10⁻⁴ and 10⁻⁶, respectively. The Joule heat and electromagnetic force in the tundish channel are obtained by solving Maxwell’s equation [13].

2.2.5. Model Validation

IH has a significant effect on molten steel flow, temperature rise, and inclusion movement. Therefore, before the mathematical model is used in numerical experiments, it is necessary to verify the applicability of the mathematical model in predicting the IH effect. In the numerical simulation, the tundish with the IH channel was simulated using the same current density and frequency. The model validation of the electromagnetic field can be found in our previous paper [13,32].

3. Results and Discussion

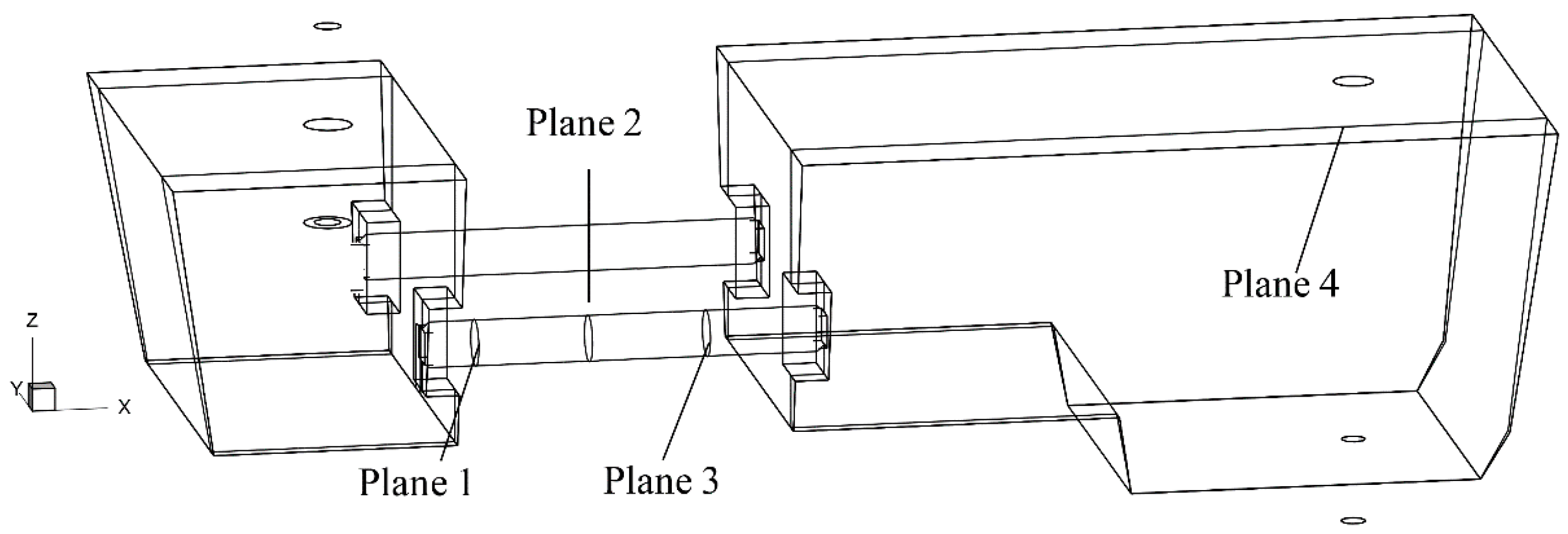
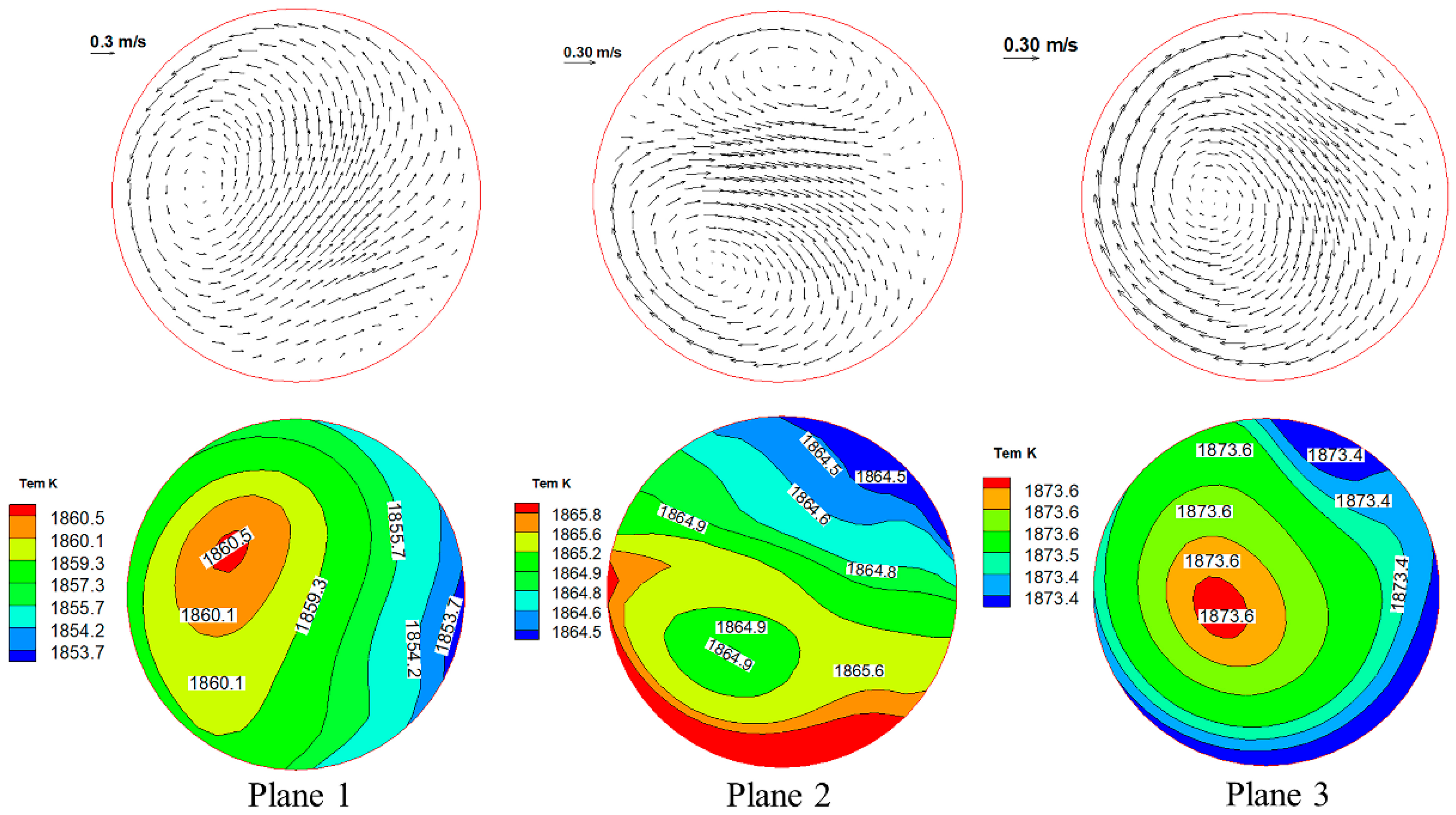
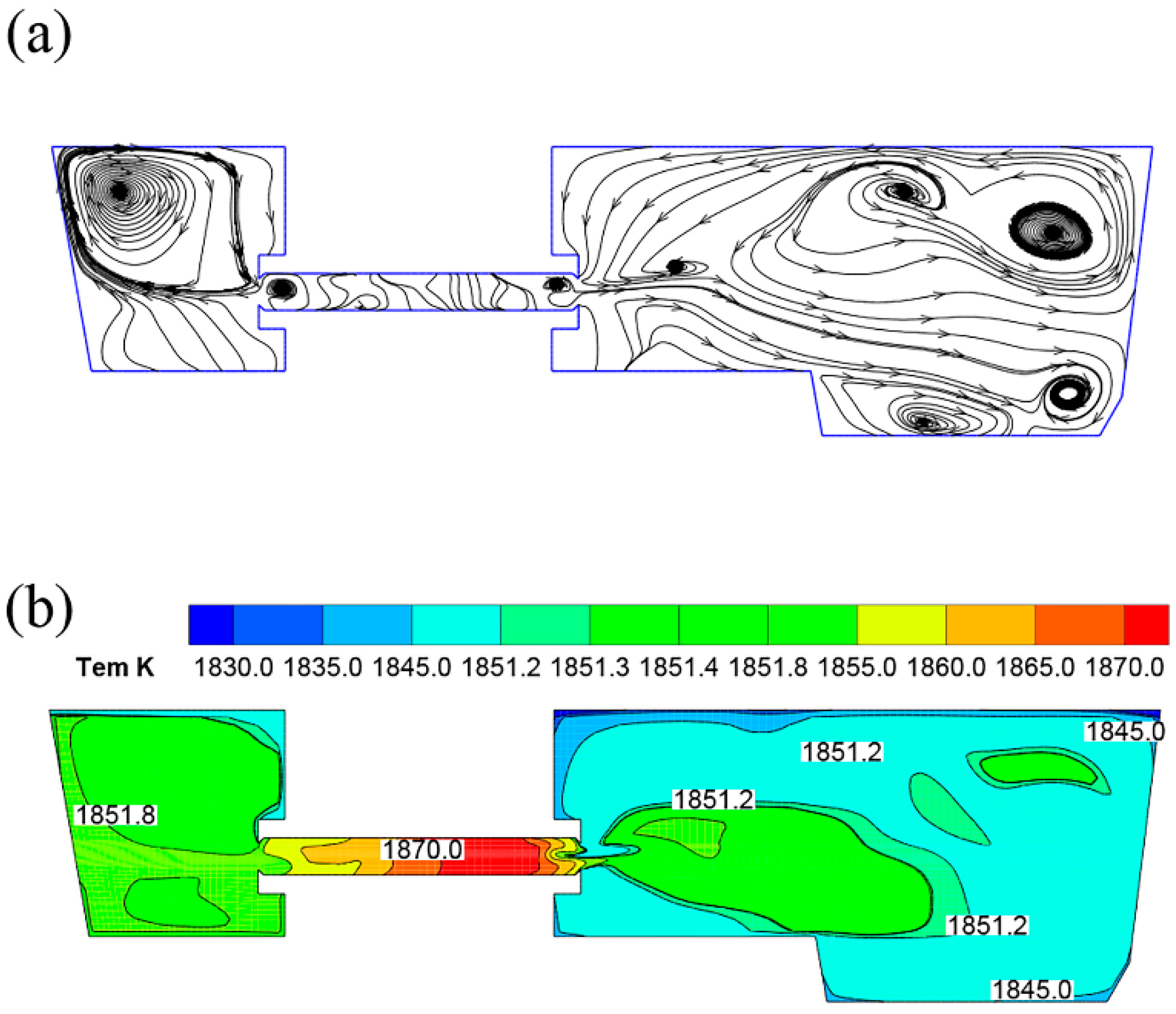
3.1. Velocity and Temperature Field

In order to clearly describe the specific locations of the sections and lines, we marked the following locations. The cross sections x = 0.35 m, x = 0.70 m and x = 1.05 m at channel 1 are named Plane 1, Plane 2 and Plane 3, respectively, for illustrating the distribution of velocity and temperature at different sections in the same channel. Plane1, Plane 2 and Plane 3 are the cross sections along Channel 1. Figure 3 displays the section position of the IH tundish. There are no IH devices, such as IH coils and iron cores, in the fluid calculation domain. The IH tundish uses single-core and single-coil heating devices. The iron cores and coils were arranged on the exterior of Channel 1. The molten steel flowing through the two channels was heated by Joule heating under an electromagnetic field.

Figure 4 shows that the velocity vector and temperature contour of molten steel at Planes 1, 2 and 3 at IH lasts for 30 s. As seen in Figure 4, the flow direction of the molten steel changes under the Joule heating and electromagnetic force of the electromagnetic field. Because the direction of the electromagnetic force comes from the circumferential direction to the center of the channel cross section [19], Plane 1 is close to the entrance section of molten steel flowing through Channel 1. Plane 2 lies in the centre of Channel 1, and Plane 3 is located near the exit of Channel 1, as shown in Figure 3. From the velocity vectors of Plane 1, Plane 2 and Plane 3, it can be seen that the vortex direction of molten steel changes from single vortex to double vortex under the electromagnetic force. The molten steel begins to generate swirling flow with centripetal force. The rotation direction of molten steel in Plane 1 is counterclockwise, and the rotation direction of molten steel in Plane 2 is counterclockwise in the upper part and clockwise in the lower part. The rotation direction of Plane 3 is counterclockwise, but there is a small counterclockwise vortex in the upper right corner. The double vortex swirl in Plane 3 is not obvious, but the double vortex swirl in Plane 2 is markedly noticeable. The position and quantity of the rotating vortex constantly keep changing under the electromagnetic force. With the increase in the flow distance of the molten steel in the channel, the time that molten steel subjected to electromagnetic forces in the channel also increases.

The thermal effect of the electromagnetic field heats the molten steel flowing through the channel. As can be seen from the temperature contours, the molten steel in the channel is gradually increased with the increase in the heating time under the electromagnetic field. The high-temperature region of the front region of the heating channel is close to the distribution of Joule heating [8]. With the increase in flow distance, the molten steel temperature increases gradually. The maximum temperature of molten steel at Plane 1, Plane 2 and Plane 3 in the channel is 1860.5 K, 1865.8 K and 1873.6 K, respectively.

Figure 5 draws the path line and temperature contour of the molten steel through the channel longitudinal section (Plane 4) when heated for 30 s under IH. The path line of molten steel in Figure 5 shows that there are multiple vortices in the molten steel in this section, which are distributed in the injection region and pouring region. From the contour of the molten steel temperature distribution, it can be found that the molten steel flowing through the channel is heated under the electromagnetic field. Although the molten steel is heated in the channel, the temperature of the molten steel rises, and the density of the molten steel decreases, but the molten steel flowing out of the channel outlet does not rush to the free surface. Due to the electromagnetic force directed to the center of the channel [13], the molten steel at the exit of the channel does not flow to the liquid surface, but disperses forward, because of the existence of strong swirl.

With the increase in electromagnetic IH time, the rotation direction and temperature of molten steel in the channel gradually changes. As shown in Figure 6, when IH lasts for 145 s, the rotation direction and temperature distribution of molten steel in Planes 1, 2 and 3 change under the Joule heat and electromagnetic force of the electromagnetic field. The flow of molten steel in different planes of the channel changes due to the continuous eccentric electromagnetic force [32]. The vortex of molten steel at Plane 1 changes from a single counterclockwise vortex to a double vortex, while the vortex in the lower layer is not obvious and the flow is weak. The double vortex in Plane 2 is obvious. Compared with the flow at 30 s, there is basically no change in the direction of rotation of molten steel. The double vortex in Plane 3 at 145 s is more evident than that vortex at 30 s, and the trend of the vortex in the upper part is even stronger. As the IH time and flow distance of molten steel in the channel increase, the temperature of the molten steel also gradually increases. The heating time was increased from 30 s to 145 s, the temperature of the molten steel in the channel increased, and the temperature of the section was still uneven. The highest temperature of the molten steel at channel Planes 1, 2 and 3 increased from 1860.5 K, 1864.9 K and 1873.6 K to 1860.7 K, 1866.6 K and 1879.1 K, respectively, as the heating time increased from 30 s to 145 s.

As the IH time increases, the molten steel flowing through the channel is heated to different degrees, and the temperature at different locations is different. When the IH time reaches 145 s, compared with the IH time of 30 s, it causes drastic changes in the temperature distribution on the longitudinal section. Figure 7 depicts a graph showing the velocity vector and temperature contour of molten steel in the longitudinal section (Plane 4) of the channel for 145 s of IH. With the increase in heating time, the temperature of the molten steel flowing out of the channel changes little. The number and shape of vortices on Plane 4 change, the number of vortices in the pouring zone decreases, and the vortices become inconspicuous, as can be seen from the velocity vector diagram on Plane 4. The high-temperature area at Plane 4 is mainly distributed in the middle and lower part of the tundish. Therefore, the channel arrangement is changed from horizontal to an upwardly inclined channel arrangement scheme, which could make the high-temperature area of the molten steel move upward.

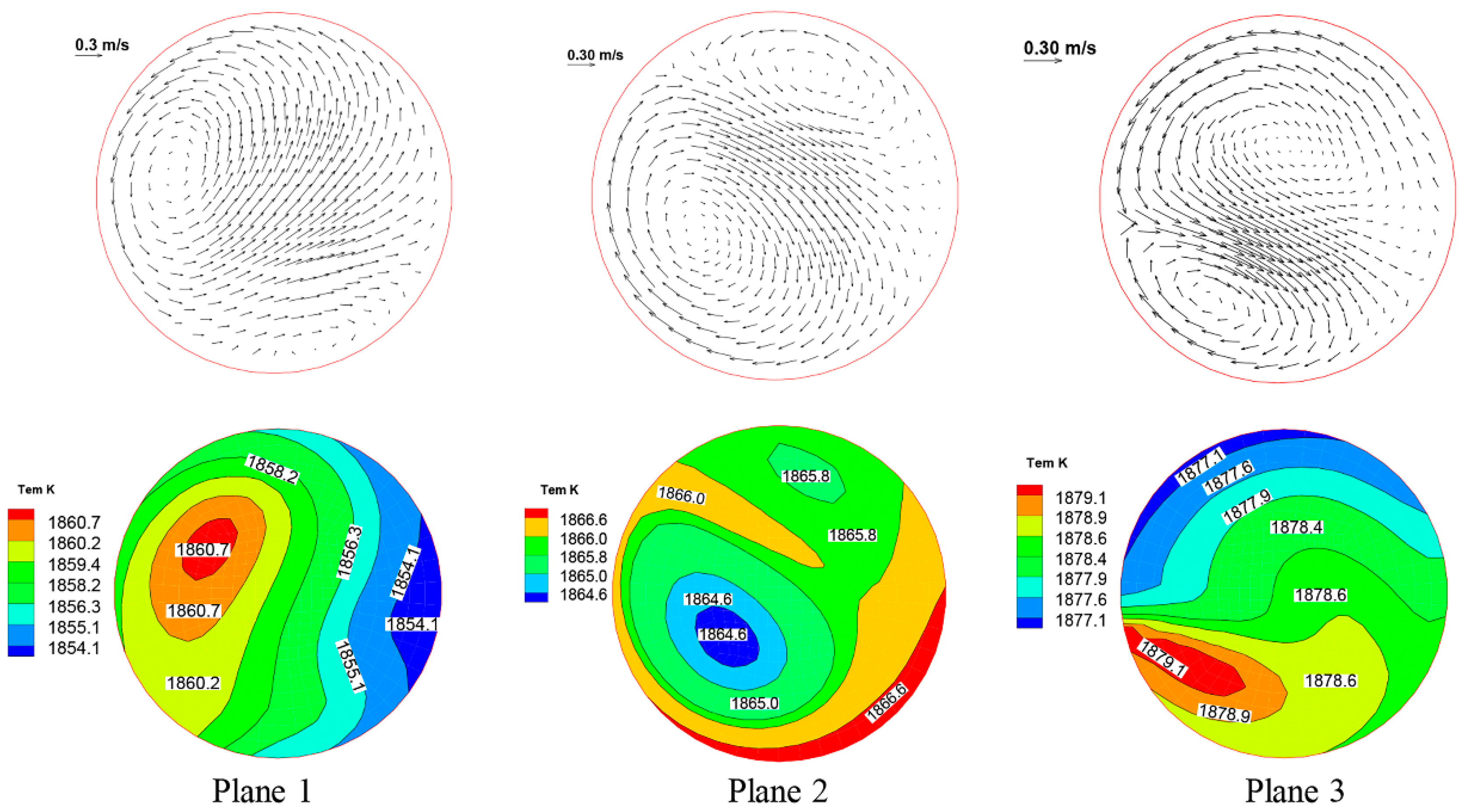
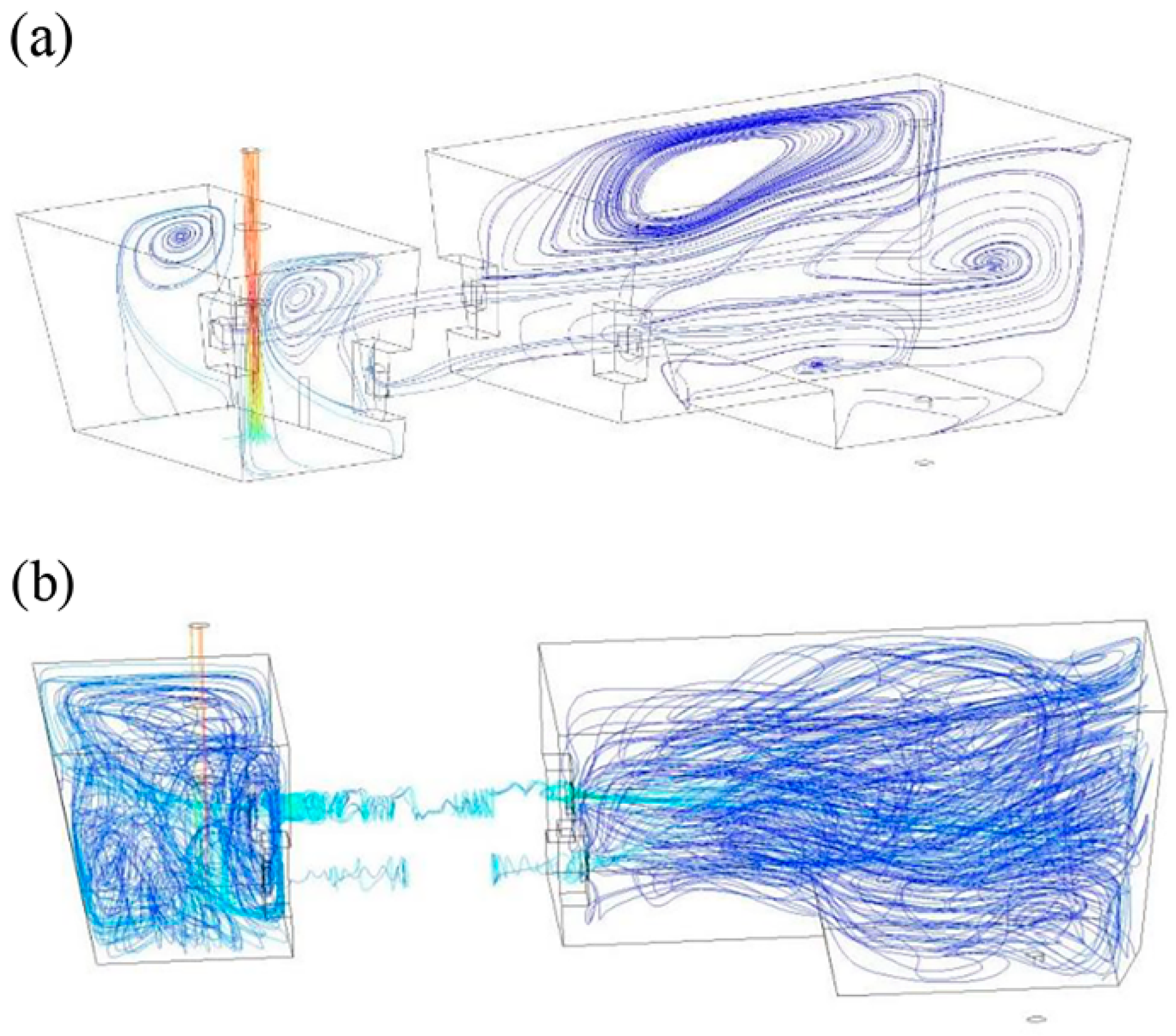
3.2. Path Lines of Flow Field

Figure 8 shows the path line of the three-dimensional flow of molten steel with or without IH. As seen from the figure, the path for molten steel to flow through the shroud to the bottom of the tundish is relatively short without IH. The vortex flow is formed at the bottom of the tundish, and the flow path of the molten steel in the channel is a straight line. This flow method may cause short-circuit flow of molten steel in the tundish or reduce the average residence time of molten steel in the tundish. The flow direction of the molten steel in the tundish channel without IH is mainly along the axial direction, and the tangential rotational speed of the cross section of the channel is small. The molten steel is subjected to a combination of centripetal electromagnetic forces and Joule heating in the IH condition. The molten steel flows spirally in the channel, and the molten steel flowing out of the channel still has a large rotational speed and flows to the tundish outlet. The path line and the flow field vector of the molten steel are consistent. The tangential rotation linear velocity of molten steel in the tundish channel is large under IH conditions. Another function of tundish metallurgy is to increase the average residence time of molten steel to facilitate the removal of non-metallic inclusions in molten steel. It is noticeable from the path line of the molten steel in the tundish that the rotation of the molten steel in the channel is strengthened under the electromagnetic field. The increase in the tangential velocity of the molten steel in the channel is beneficial to increasing the average residence time of the molten steel. From this perspective, the continuous casting tundish with IH helps to remove non-metallic inclusions in molten steel. The average horizontal velocity of molten steel in the channel changes little under the condition of certain molten steel flow rate in the channel with or without the electromagnetic field. However, in the circumferential direction of the channel, the velocity changes greatly, the motion path of molten steel increases, and the average residence time will increase, which is beneficial to the floating removal of inclusions, but the rotating flow in the channel may change the motion trajectory of inclusions; thus, it has a certain impact on the floating removal rate.

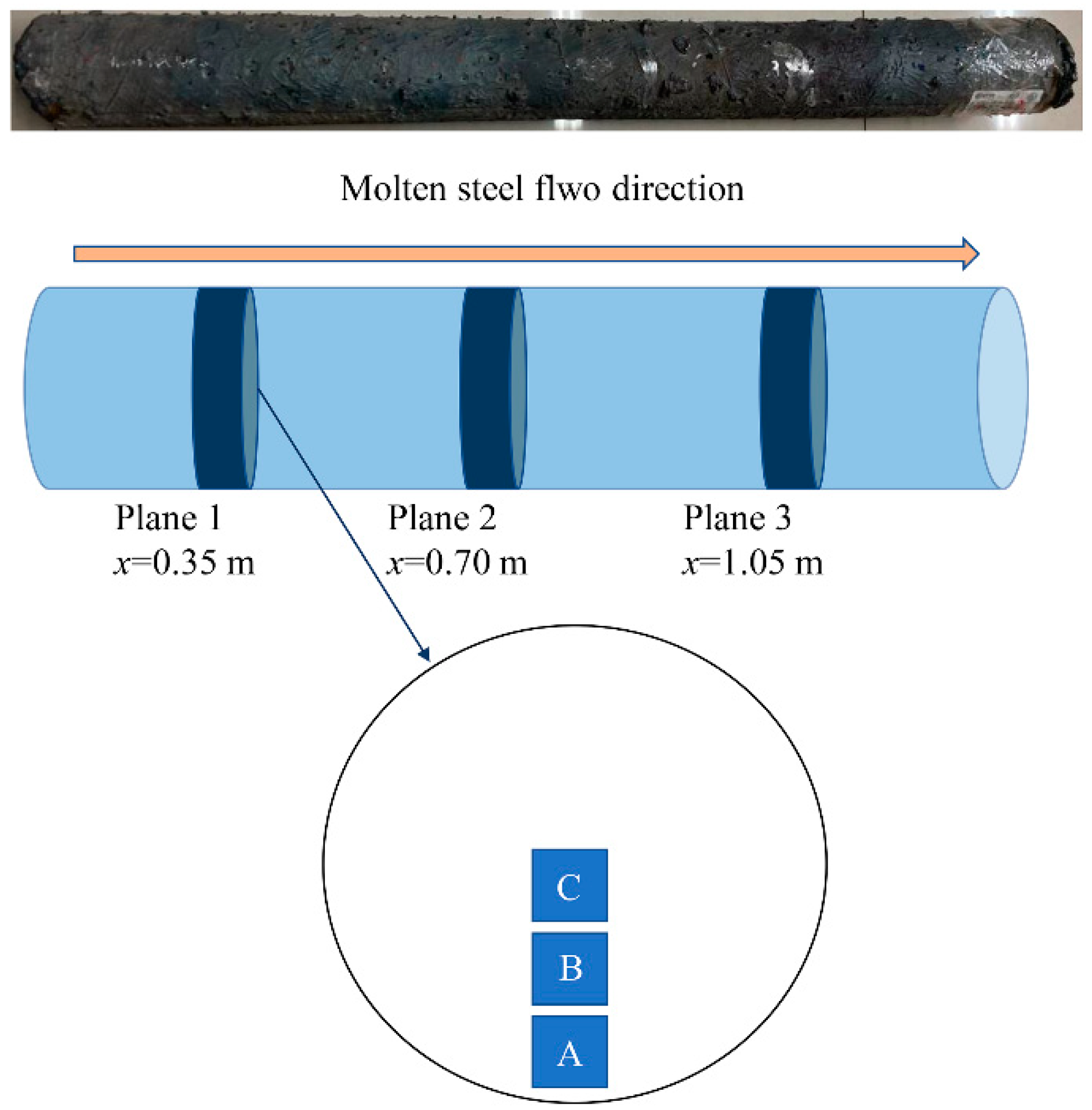
3.3. Industrial Trials

Molten steel with low superheat has excellent effects on constant temperature casting for improving the quality and stable operation of a slab, and it is one of the most effective methods to optimize the solidification structure and enhance the quality of a product. The use of tundish electromagnetic IH can control the temperature of molten steel in the casting process within an ideal range and can compensate the molten steel for heat in a timely manner, thereby decreasing the current temperature fluctuation of the molten steel in the tundish, and achieving constant temperature casting with a low superheat. The temperature of molten steel in the tundish is monitored to investigate the influence of electromagnetic IH on the temperature compensation. The frequency of data collection is ten times per minute, the ladle casting period is approximately fifty minutes, and five hundred temperature points are obtained during each ladle casting. Here, we continuously recorded the six ladle casting periods. The temperature change curve is plotted in Figure 9 without and with IH in different casting periods.

It is evident from the figures that when the electromagnetic IH equipment is introduced, the molten steel temperature fluctuation decreases. The initial temperature of molten steel entering the tundish is 1830 K and 1819 K, respectively, without (Figure 9a) or with (Figure 9b) induction heating. The initial temperature of molten steel with the IH tundish is 11 K lower than that without IH. The net weight of the molten steel in the ladle is 50 tons. In a single ladle pouring period, as the casting time increases, the heat loss of the molten steel increases and the temperature of the molten steel decreases in the late pouring period. The temperature drops to about 1803 K without electromagnetic IH. In the first ladle pouring period, the temperature of the molten steel dropped by 27 K, and during subsequent pouring, the temperature of the molten steel dropped by 18 K. After using the electromagnetic IH equipment, the molten steel temperature can be required to target the temperature around 1813 K. The target value was kept at 1813 ± 3 K. The entire casting process can almost maintain constant temperature casting, which reduces production costs and improves production efficiency. It has important practical significance for improving the quality of the slab. The slab continuous casting tundish adopts channel electromagnetic IH technology, which plays a role in the temperature compensation and flow control of molten steel, especially for molten steel in the superheat range. The overheating of the molten steel is controlled near the target value to lower the tapping temperature of the converter and to compensate for the temperature drop of the molten steel in the tundish. The tundish with IH provides the necessary support for low superheat and constant temperature pouring in the continuous casting process.

In order to analyze the distribution of inclusions at different positions of the channel along the flow direction, the Aspex surface scan method (scanning starts at 1 μm) was used to statistically count the number of inclusions in the channel steel rod cross sections. Figure 10 shows the different sections located at Plane 1, Plane 2 and Plane 3, respectively. The diameter of the channel steel rod is 0.14 m and the length is 1.10 m. The thickness of the cylinder is 0.10 m. Areas A, B and C lie at the circle of the channel steel rod edge to center, which is shown in Figure 10. Area A is at the bottom of the channel.

Figure 11 depicts the number of inclusions distribution histogram of the channel steel rod at different cross sections. At the position of Plane 1 from the center to the edge, the number of small inclusions does not change much, while the number of large inclusions decreases, which is shown in Figure 11a. The number of inclusions greater than 9 μm does not change significantly. Figure 11b shows the number of inclusions from the center to the edge at Plane 2 of the channel steel rod. The total number of inclusions at the position of Plane 2 of the channel steel rod are at the highest level of the three areas. In particular, the proportion of the increase in the number of inclusions greater than 9 μm is the most obvious. Compared with the distribution of inclusions at Plane 2 of the channel, the large inclusions at Plane 2 of the channel are more obviously distributed in the center. From the center to the edge, the small inclusions are slightly reduced, and the large inclusions are significantly reduced. The change in the number of inclusions at Plane 3 at the center to the edge of the channel histogram is shown in Figure 11c. From Area C to Areas B and A, the number of large-size inclusions whose diameters are greater than 9 μm shows an increasing trend, the number of small-size inclusions whose diameters are less than 9 μm increase first and then decrease.

There is no obvious change in the distribution of small-size inclusions with diameters less than 9 μm in Plane 1 and Plane 2 of the channel steel sample. The number of inclusions in Areas A, B, and C is similar. Compared with the channel steel rod section at Plane 1 and Plane 2, in the channel steel rod section at Plane 3, the large inclusions with diameters greater than 9 μm are more concentrated on the edge, which may be related to the migration of large inclusions to the channel wall under the electromagnetic gradient force. At the same time, it also shows that the electromagnetic field has a small effect on the inclusions with a particle size of less than 9 μm in the molten steel in the channel.

It should be pointed out that the mathematical model we established only considers the flow and heat transfer of single-phase fluid, which is insufficient for the very important two-phase transport phenomenon of inclusion migration. At present, we record the temperature of molten steel in the continuous casting tundish of multiple ladle furnaces with or without IH according to the industrial test data. The distribution of inclusions at different positions of the tundish channel after IH in the tundish under industrial conditions is analyzed in detail. In the follow-up study, we will analyze and evaluate the electromagnetic field effect for the inclusion movement and migration behavior through further calculation and experiments.

4. Conclusions

The mathematical model of the slab continuous casting tundish with IH is established. The changes in the flow field and temperature field in the tundish under IH at different times were discussed. The temperature change of molten steel in the tundish was investigated with or without IH and the distribution of inclusions in the channel were performed. The main conclusions could be drawn as the following:

(1)

The molten steel in the channel changes from straight flow to spiral flow under the electromagnetic field. The flow characteristics of molten steel in the channel change with time, showing an alternating flow of single vortex and double vortex.

(2)

The heat loss of the molten steel in the tundish with IH can be compensated, and the temperature of the molten steel in the channel increases by 31.8 K after heating for 145 s. The temperature of molten steel in the tundish can keep the target value at 1813 ± 3 K after using the electromagnetic IH equipment in industrial trials.

(3)

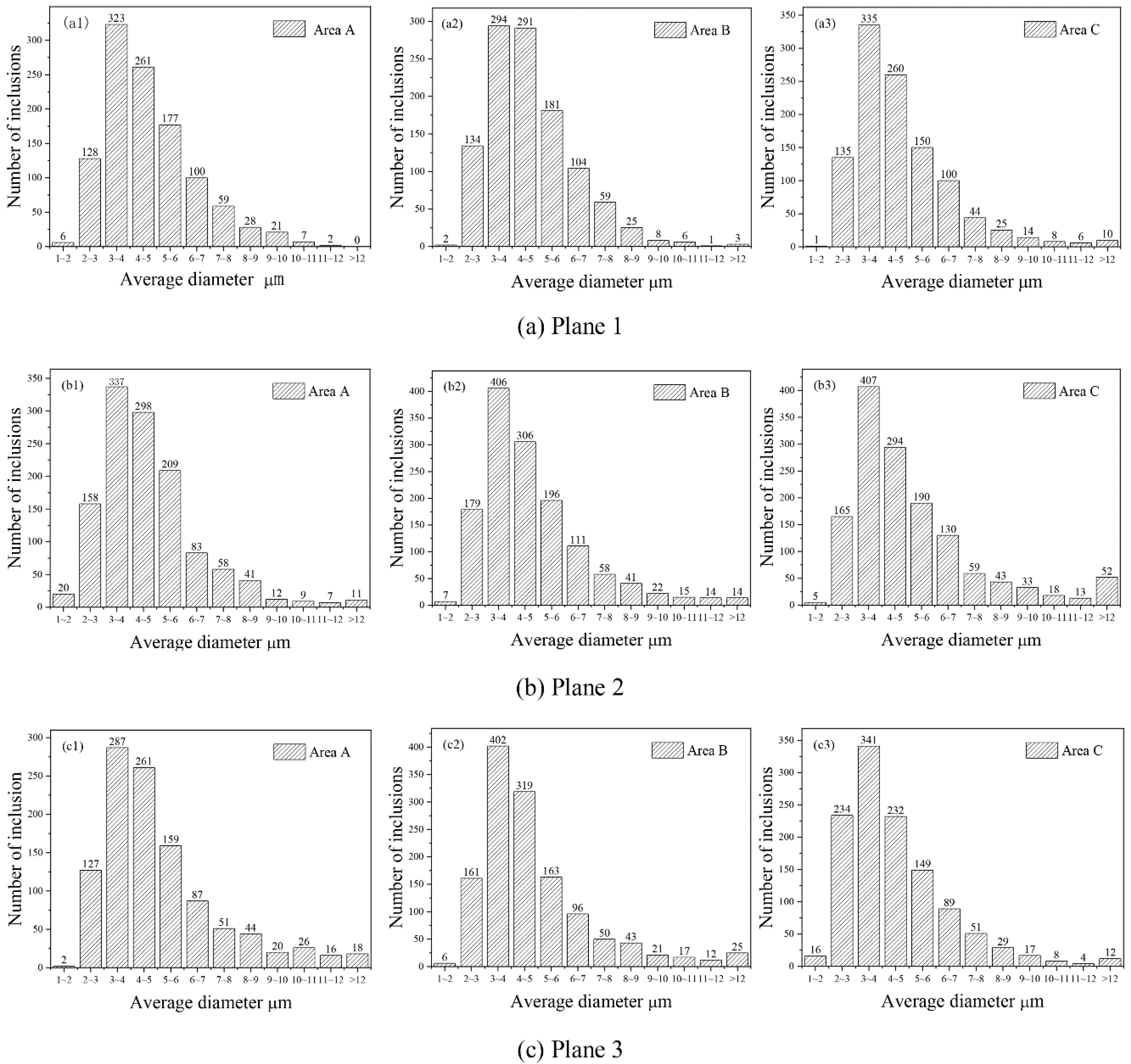
The electromagnetic field has little effect on the inclusions with diameters less than 9 μm in the molten steel in the channel of the IH tundish. The number of inclusions with diameters greater than 9 μm at the edge of the channel is greater than that at the center and other positions of the IH tundish channel.