Assessment of Dislocation Density by Various Techniques in Cold Rolled 1050 Aluminum Alloy
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
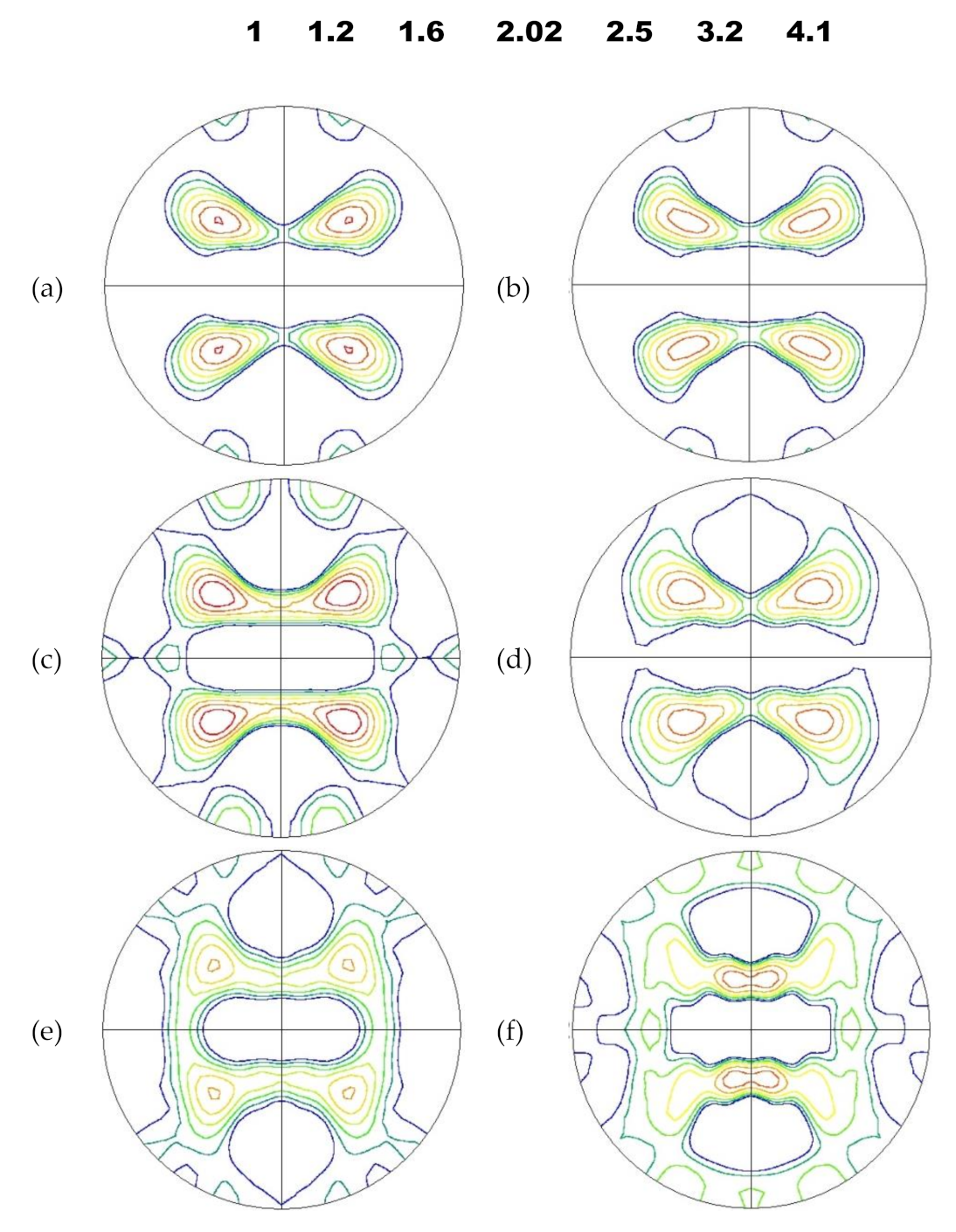
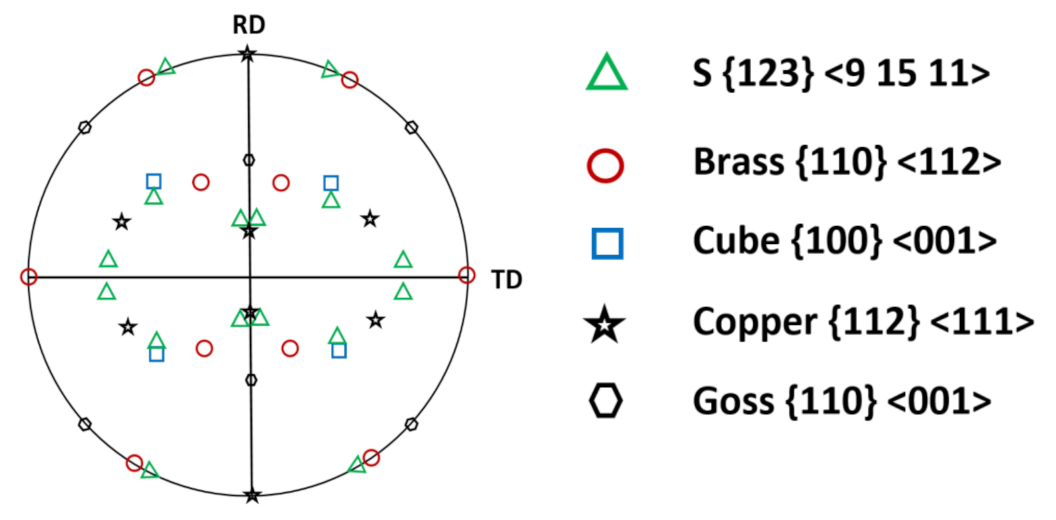
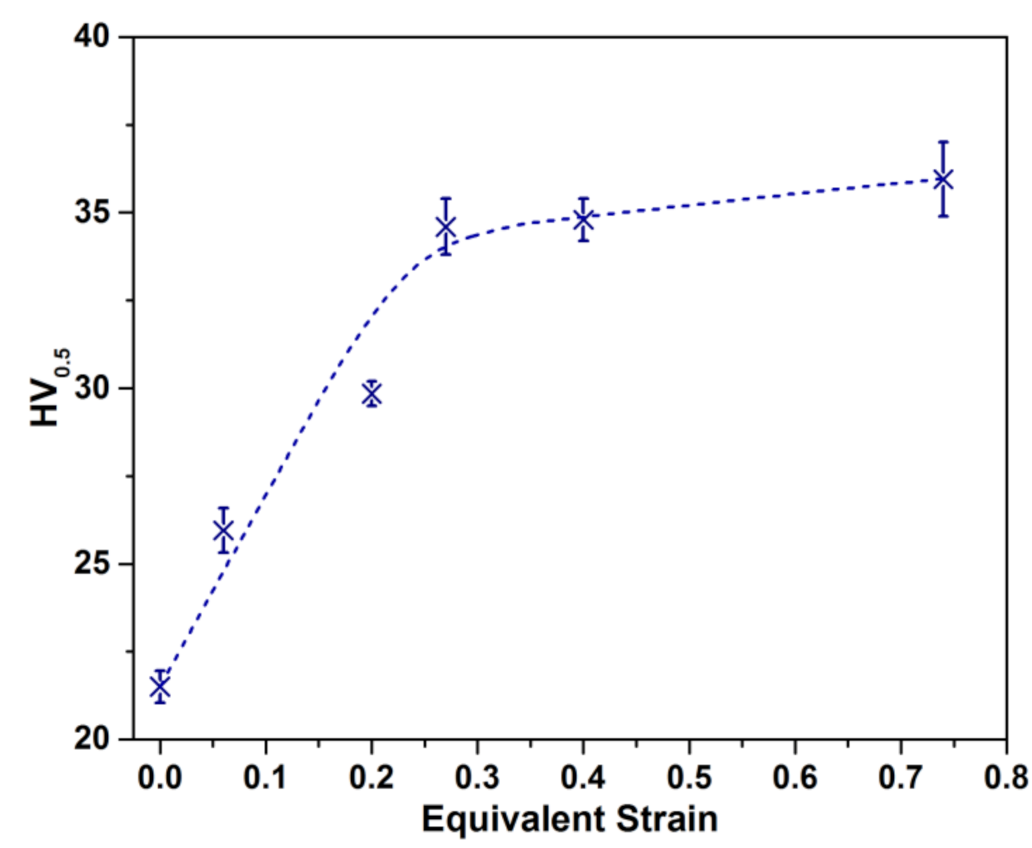
3.1. Evolution of Microstructure, Texture, and Hardness
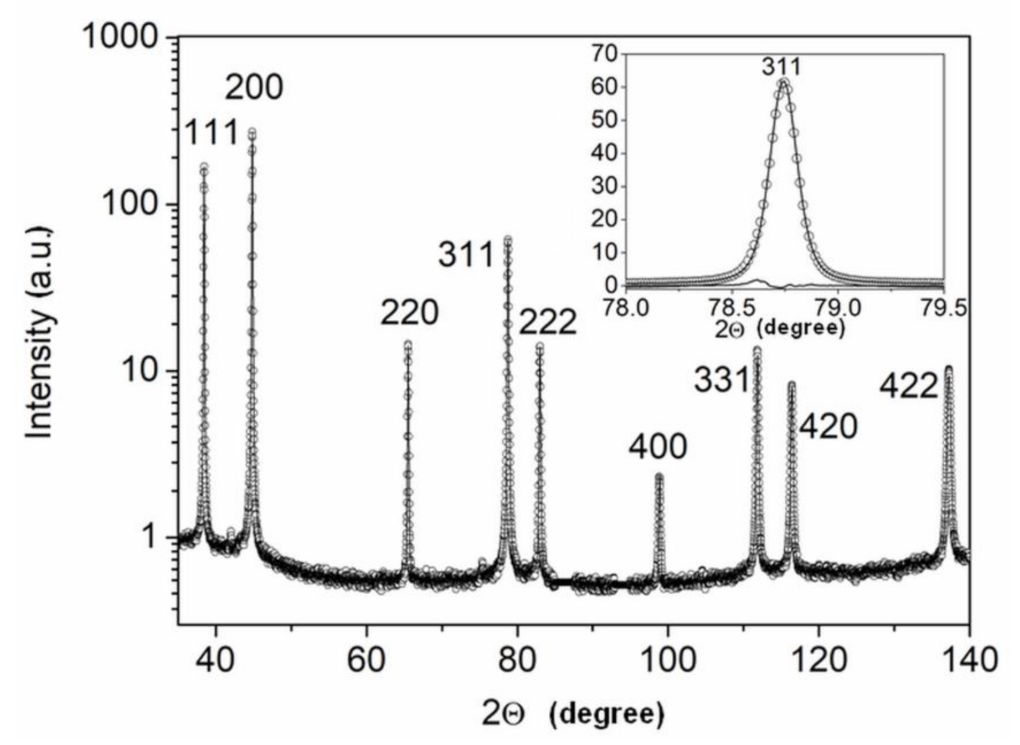
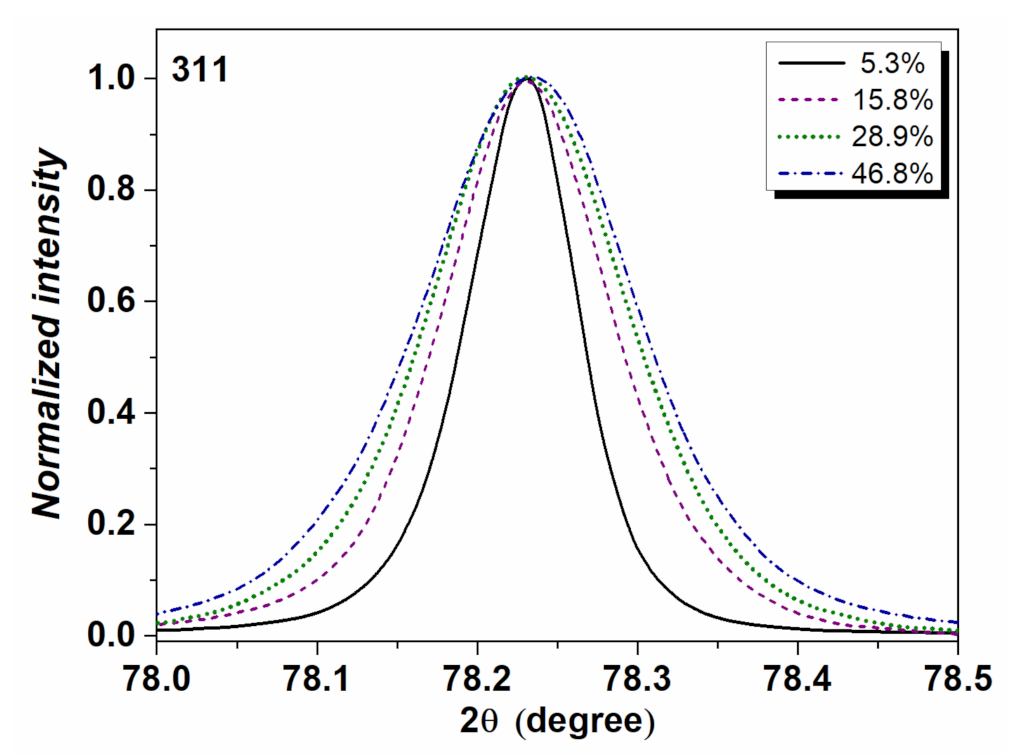
3.2. Estimation of Dislocation Density by XLPA
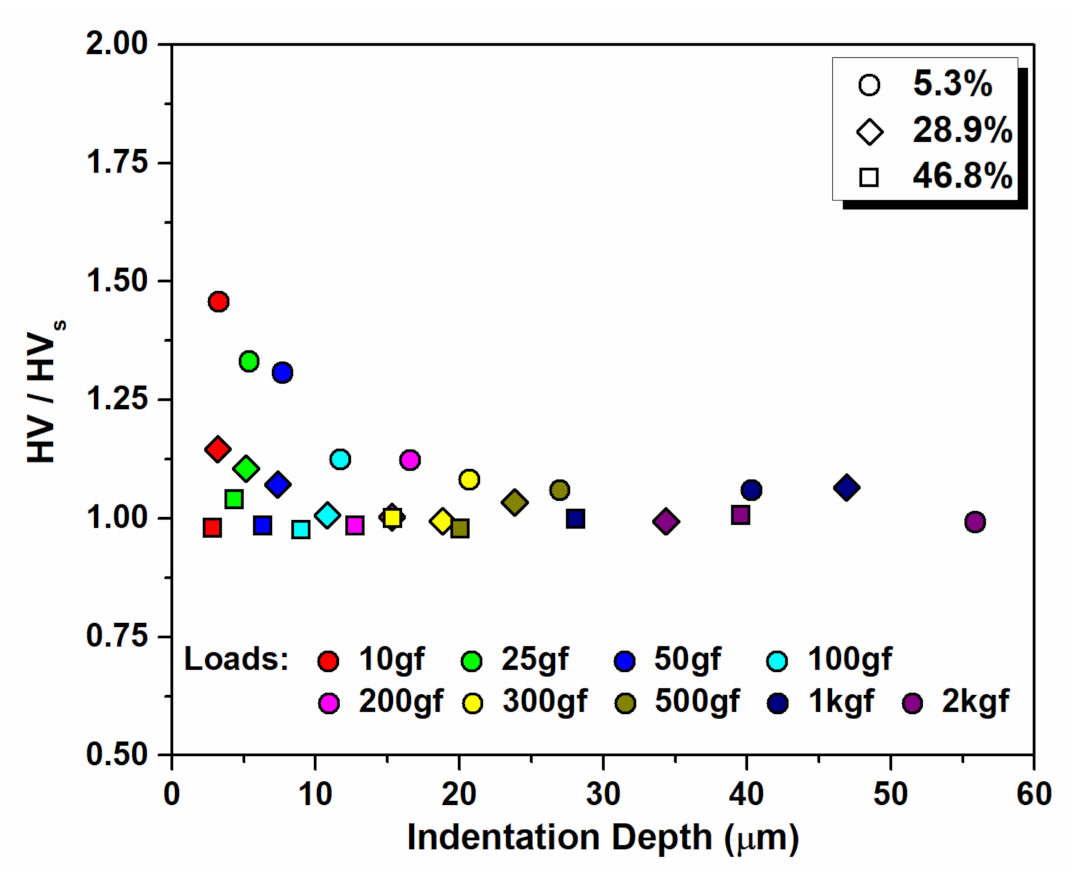
3.3. Indentation
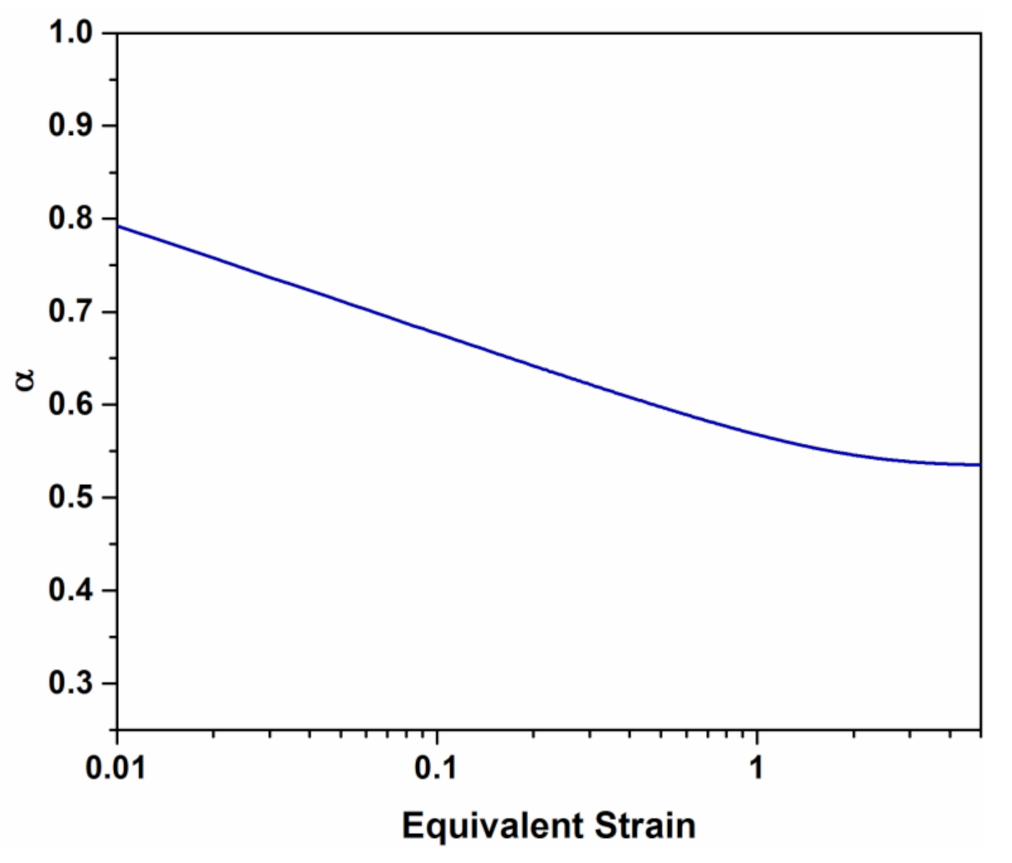
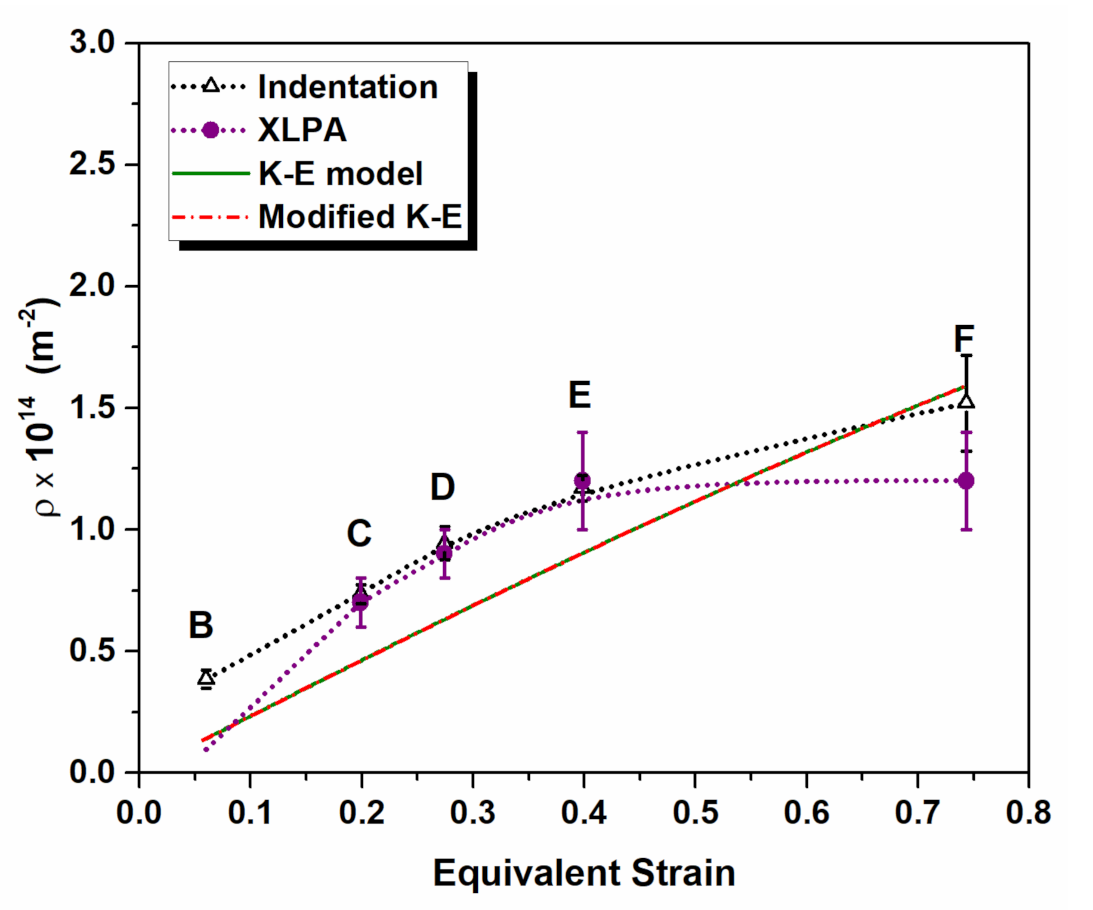
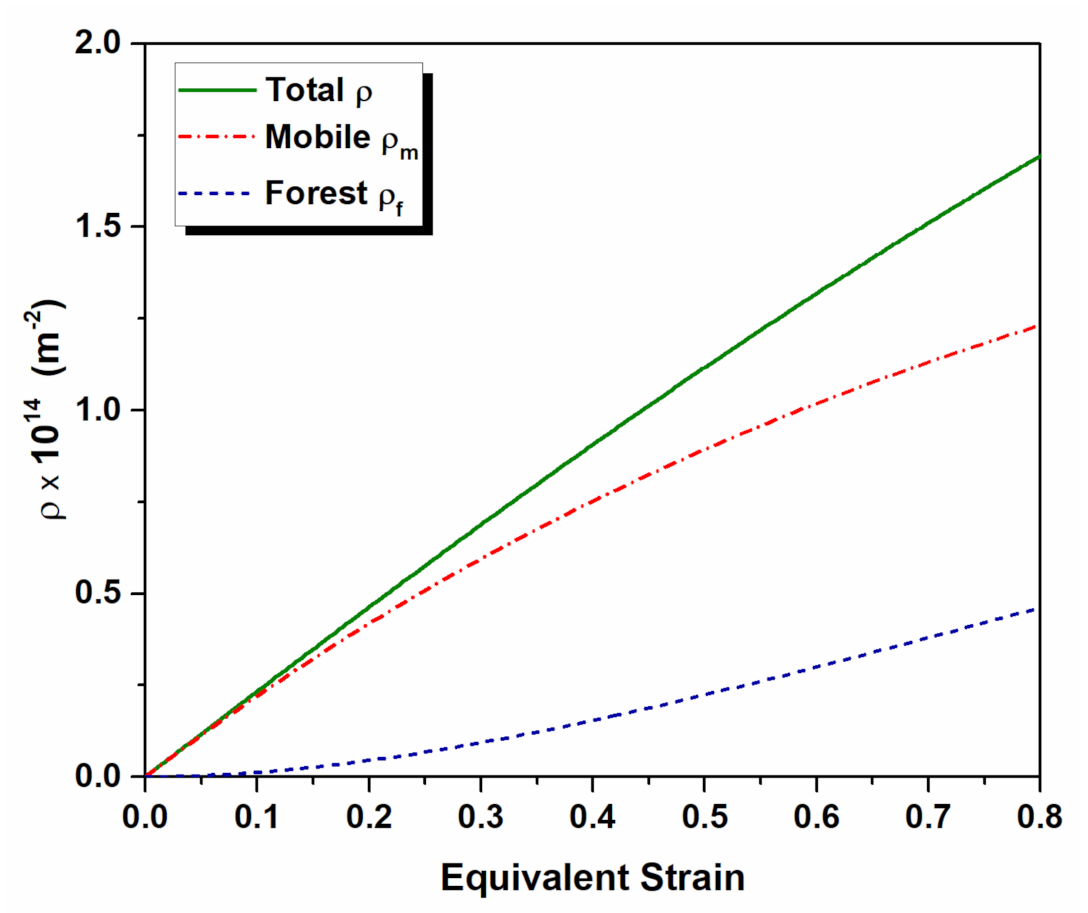
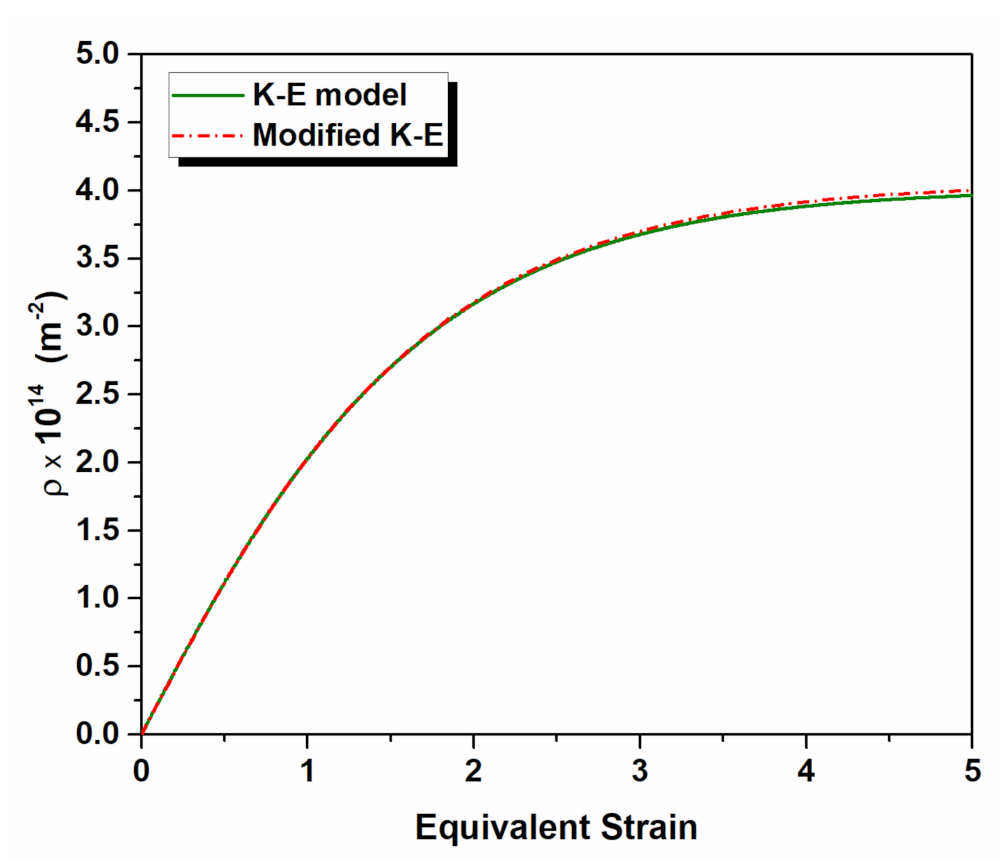
3.4. Numerical Assesment of Dislocation Density
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voyiadjis, G.Z.; Yaghoobi, M. Size Effects in Plasticity: From Macro to Nano; Elsevier: Amsterdam, The Netherland, 2020; p. 394. [Google Scholar]
- Nye, J.F. Some geometrical relations in dislocated crystals. Acta Metall. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Phil. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Humphreys, J.; Rohrer, G.S.; Rollett, A. Recrystallization and Related Annealing Phenomena, 3rd ed.; Elsevier: Amsterdam, The Netherland, 2017; p. 704. [Google Scholar]
- Sidor, J.J.; Kestens, L.A.I. Analytical description of rolling textures in face-centred-cubic metals. Scripta Mater. 2013, 68, 273–276. [Google Scholar] [CrossRef]
- Gubicza, J.; Ungár, T. Characterization of defect structures in nanocrystalline materials by x-ray line profile analysis. Z. Kristallographie 2007, 222, 567–579. [Google Scholar] [CrossRef] [Green Version]
- Gubicza, J. Defect structure in nanomaterials; Woodhead Publishing: Sawston, UK, 2012; p. 358. [Google Scholar]
- Gubicza, J. X-ray line profile analysis in Materials Science; IGI-Global: Hershey, PA, USA, 2014; p. 369. [Google Scholar]
- Taheri, M.; Weiland, H.; Rollett, A. A method of measuring stored energy macroscopically using statistically stored dislocations in commercial purity aluminum. Metall. Mater. Trans. A 2006, 37, 19–25. [Google Scholar] [CrossRef]
- Field, D.P.; Merriman, C.C.; Allain-Bonasso, N.; Wagner, F. Quantification of dislocation structure heterogeneity in deformed polycrystals by EBSD. Modelling Simul. Mater. Sci. Eng. 2012, 20, 024007. [Google Scholar] [CrossRef]
- Ribárik, G.; Ungár, T.; Gubicza, J. MWP-fit: A program for multiple whole-profile fitting of diffraction peak profiles by ab initio theoretical functions. J. Appl. Cryst. 2001, 34, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Warren, B.E.; Averbach, B.L. The Effect of Cold-Work Distortion on X-Ray Patterns. J. Appl. Physics. 1950, 21, 595–599. [Google Scholar] [CrossRef]
- Bertaut, E.F. Raies de Debye-Scherrer et repartition des dimensions des domains de Bragg dans les poudres polycrystallines. Acta Crystallographica 1950, 3, 14–18. [Google Scholar] [CrossRef]
- Wilkens, M. The determination of density and distribution of dislocations in deformed single crystals from broadened X-ray diffraction profiles. Phys. Stat. Sol. 1970, 2, 359–370. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mannan, P.; Tome, C.N.; Pereloma, E.V. On the evolution and modelling of Cube texture during dynamic recrystallisation of Ni-30Fe-Nb-C model alloy. J. Alloys Compd. 2018, 748, 620–636. [Google Scholar] [CrossRef]
- Durst, K.; Backes, B.; Göken, M. Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 2005, 52, 1093–1097. [Google Scholar] [CrossRef]
- Graça, S.; Colaço, R.; Carvalho, P.A.; Vilar, R. Determination of dislocation density from hardness measurements in metals. Mater. Lett. 2008, 62, 3812–3814. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effect in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Busby, J.T.; Hash, M.C.; Was, G.S. The relationship between hardness and yield stress in irradiated austenitic and ferritic steels. J. Nucl. Mater. 2005, 336, 267–278. [Google Scholar] [CrossRef]
- Arsenlis, A.; Parks, D.M. Crystallographic aspects of geometrically necessary and statistically- stored dislocation density. Acta Mater. 1999, 47, 1597–1611. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y. Geometrically necessary dislocation and size-dependent plasticity. Scr. Mater. 2003, 48, 113–118. [Google Scholar] [CrossRef]
- Field, D.P.; Trivedi, P.B.; Wright, S.I.; Kumar, M. Analysis of local orientation gradients in deformed single crystals. Ultramicroscopy 2005, 103, 33–39. [Google Scholar] [CrossRef]
- Moussa, C.; Bernacki, M.; Besnard, R.; Bozzolo, N. About quantitative EBSD analysis of deformation and recovery substructures in pure Tantalum. 2015 IOP Conf. Ser. Mater. Sci. Eng. 2015, 89, 012038. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E. Dislocation Densities in Some Annealed and Cold-Worked Metals from Measurements on the X-ray Debye-Scherrer Spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Smallman, R.E.; Westmacott, K.H. Stacking faults in face-centred cubic metals and alloys. Philos. Mag. 1957, 2, 669–683. [Google Scholar] [CrossRef]
- Ma, K.; Wen, H.; Hu, T.; Topping, T.D.; Isheim, D.; Seidman, D.N.; Lavernia, E.J.; Schoenung, J.M. Mechanical behavior and strengthening mechanisms in ultrafine grain precipitation-strengthened aluminum alloy. Acta Mater. 2014, 62, 141–155. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liao, X.Z.; Jin, Z.; Valiev, R.Z.; Zhu, Y.T. Microstructures and mechanical properties of ultrafine grained 7075 Al alloy processed by ECAP and their evolutions during annealing. Acta Mater. 2004, 52, 4589–4599. [Google Scholar] [CrossRef]
- Wang, X.; Guo, M.; Zhang, Y.; Xing, H.; Li, Y.; Luo, J.; Zhang, J.; Zhuang, L. The dependence of microstructure, texture evolution and mechanical properties of Al-Mg-Si-Cu alloy sheet on final cold rolling deformation. J. Alloys Compd. 2016, 657, 906–916. [Google Scholar] [CrossRef]
- Csanádi, T.; Chinh, N.Q.; Gubicza, J.; Langdon, T.G. Plastic behavior of fcc metals over a wide range of strain: Macroscopic and microscopic descriptions and their relationship. Acta Mater. 2011, 59, 2385–2391. [Google Scholar] [CrossRef]
- Csanádi, T.; Chinh, N.Q.; Gubicza, J.; Vörös, G.; Langdon, T.G. Characterization of stress–strain relationships in Al over a wide range of testing temperatures. Int. J. Plast. 2014, 54, 178–192. [Google Scholar] [CrossRef]
- Pešička, J.; Kužel, R.; Dronhofer, A.; Eggeler, G. The evolution of dislocation density during heat treatment and creep of tempered martensite ferritic steels. Acta Mater. 2003, 51, 4847–4862. [Google Scholar] [CrossRef]
- Sidor, J.J.; Petrov, R.H.; Kestens, L.A.I. Modeling the crystallographic texture changes in aluminum alloys during recrystallization. Acta Mater. 2011, 59, 5735–5748. [Google Scholar] [CrossRef]
- Decroos, K.; Sidor, J.; Seefeldt, M. A new analytical approach for the velocity field in rolling processes and its application in through-thickness texture prediction. Metall. Mater. Trans. A 2014, 45, 948–961. [Google Scholar] [CrossRef] [Green Version]
- Sidor, J.J. Assessment of Flow-Line Model in Rolling Texture Simulations. Metals 2019, 9, 1098. [Google Scholar] [CrossRef] [Green Version]
- Groma, I.; Ungar, T.; Wilkens, M. Asymmetric X-ray Line Broadening of Plastically Deformed Crystals. I. Theory. J. Appl. Crystallogr. 1988, 21, 47–53. [Google Scholar] [CrossRef]
- Gil Sevillano, J.; Van Houtte, P.; Aernoudt, E. Large Strain Work Hardening and Textures. Prog. Mater. Sci. 1980, 25, 69–412. [Google Scholar] [CrossRef]
- Müllner, P.; Solenthaler, C. On the effect of deformation twinning on defect densities. Mater. Sci. Eng. A 1997, 230, 107–115. [Google Scholar] [CrossRef]
- Nes, E. Modelling of work hardening and stress saturation in fcc metals. Prog. Mater. Sci. 1998, 41, 129–193. [Google Scholar] [CrossRef]
- Kubin, L.P.; Estrin, Y. Evolution of dislocation densities and the critical conditions for the Portevin-Le Chatelier effect. Acta Metall. Mater. 1990, 38, 697–708. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Met. 1981, 29, 1865–1875. [Google Scholar]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Met. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Beyerlein, I.J.; Lesar, R. Plastic anisotropy in fcc single crystals in high rate deformation. Int. J. Plast. 2009, 25, 26–48. [Google Scholar] [CrossRef]

| Sample | Reduction (%) | Grain Size (μm) | M | e |
|---|---|---|---|---|
| A | 0 | 74.8 | 3.09 | 0 |
| B | 5.3 | 70.0 | 3.1 | 0.06 |
| C | 15.8 | 66.4 | 3.1 | 0.20 |
| D | 21.1 | 64.2 | 3.1 | 0.27 |
| E | 28.9 | 61.0 | 3.1 | 0.40 |
| F | 46.8 | 54.7 | 3.16 | 0.74 |
| Sample | ρ × 1014 (m−2) | d (μm) |
|---|---|---|
| A | <0.1 | - |
| B | <0.1 | 1.9 |
| C | 0.7 ± 0.1 | 1.1 |
| D | 0.9 ± 0.1 | 1 |
| E | 1.2 ± 0.2 | 0.9 |
| F | 1.2 ± 0.2 | 0.7 |
| Sample | ρ × 1014 (m−2), (α = 0.5) | ρ × 1014 (m−2), (α by Equation (7)) |
|---|---|---|
| B | 1.02 ± 0.13 | 0.38 ± 0.04 |
| C | 1.47 ± 0.07 | 0.73 ± 0.04 |
| D | 1.76 ± 0.11 | 0.94 ± 0.07 |
| E | 1.99 ± 0.07 | 1.17 ± 0.05 |
| F | 2.25 ± 0.51 | 1.52 ± 0.20 |
| Sample | K–E | Modified K–E |
|---|---|---|
| B | 0.14 | 0.14 |
| C | 0.46 | 0.46 |
| D | 0.62 | 0.63 |
| E | 0.90 | 0.90 |
| F | 1.59 | 1.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidor, J.J.; Chakravarty, P.; Bátorfi, J.G.; Nagy, P.; Xie, Q.; Gubicza, J. Assessment of Dislocation Density by Various Techniques in Cold Rolled 1050 Aluminum Alloy. Metals 2021, 11, 1571. https://doi.org/10.3390/met11101571
Sidor JJ, Chakravarty P, Bátorfi JG, Nagy P, Xie Q, Gubicza J. Assessment of Dislocation Density by Various Techniques in Cold Rolled 1050 Aluminum Alloy. Metals. 2021; 11(10):1571. https://doi.org/10.3390/met11101571
Chicago/Turabian StyleSidor, Jurij J., Purnima Chakravarty, János Gy. Bátorfi, Péter Nagy, Qingge Xie, and Jenő Gubicza. 2021. "Assessment of Dislocation Density by Various Techniques in Cold Rolled 1050 Aluminum Alloy" Metals 11, no. 10: 1571. https://doi.org/10.3390/met11101571
APA StyleSidor, J. J., Chakravarty, P., Bátorfi, J. G., Nagy, P., Xie, Q., & Gubicza, J. (2021). Assessment of Dislocation Density by Various Techniques in Cold Rolled 1050 Aluminum Alloy. Metals, 11(10), 1571. https://doi.org/10.3390/met11101571








