Fracture Areas Quantitative Investigating of Bending-Torsion Fatigued Low-Alloy High-Strength Steel
Abstract
:1. Introduction
2. Materials and Methods
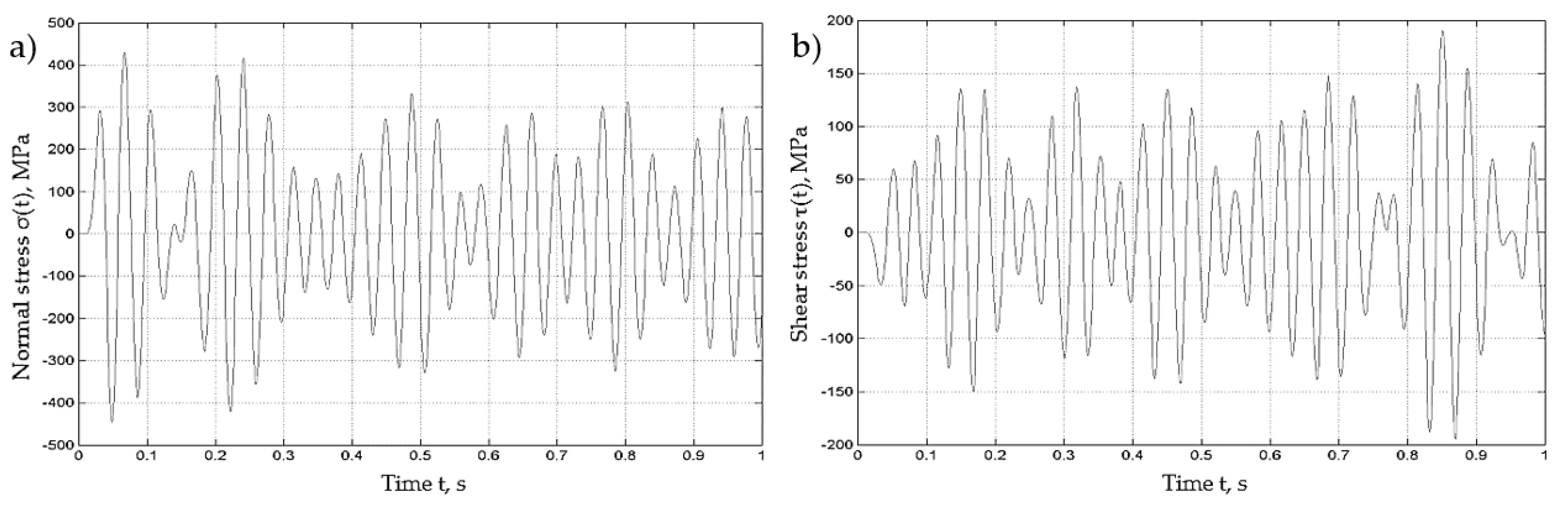
2.1. Bending-Torsion Fatigue Test
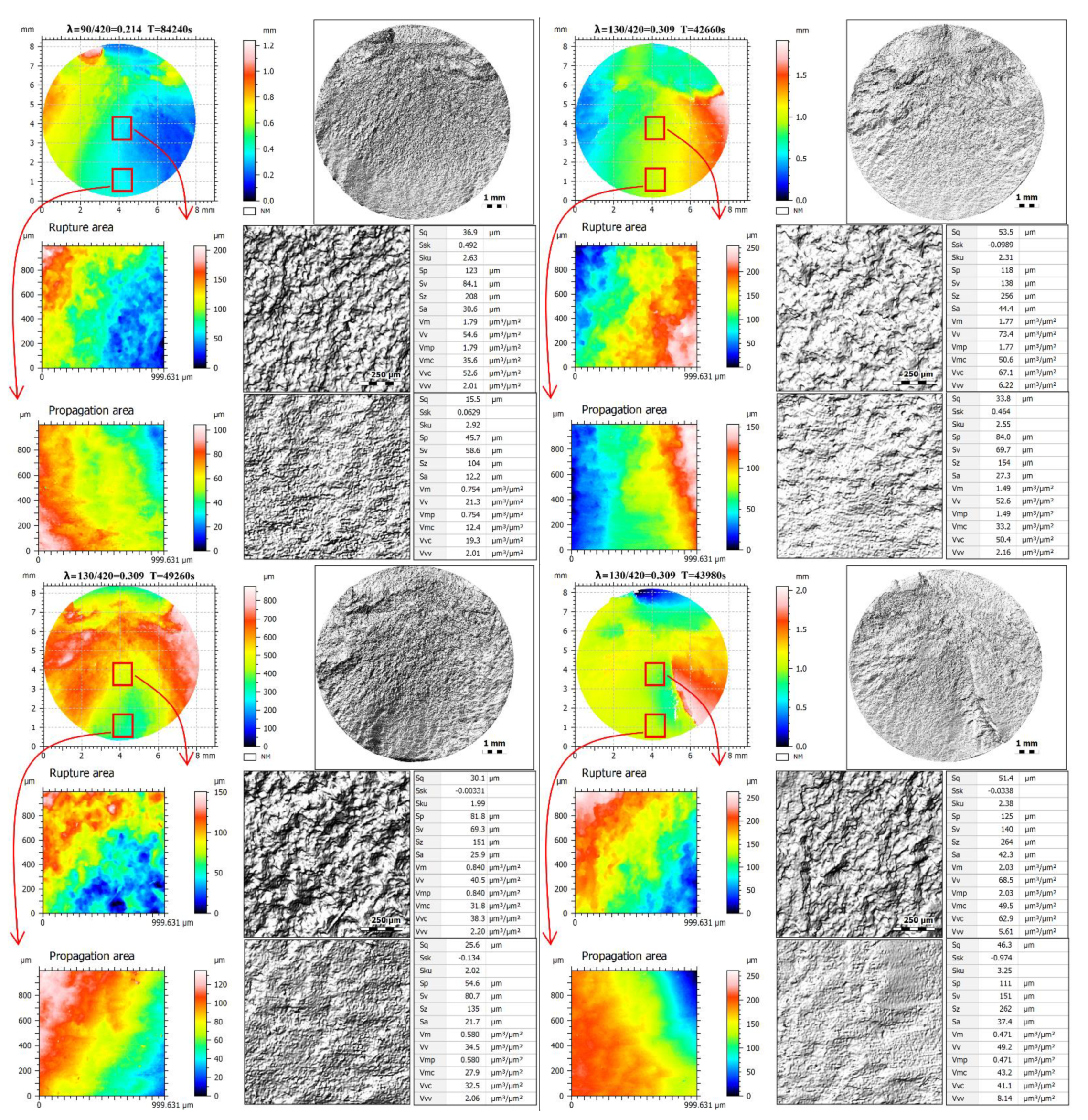
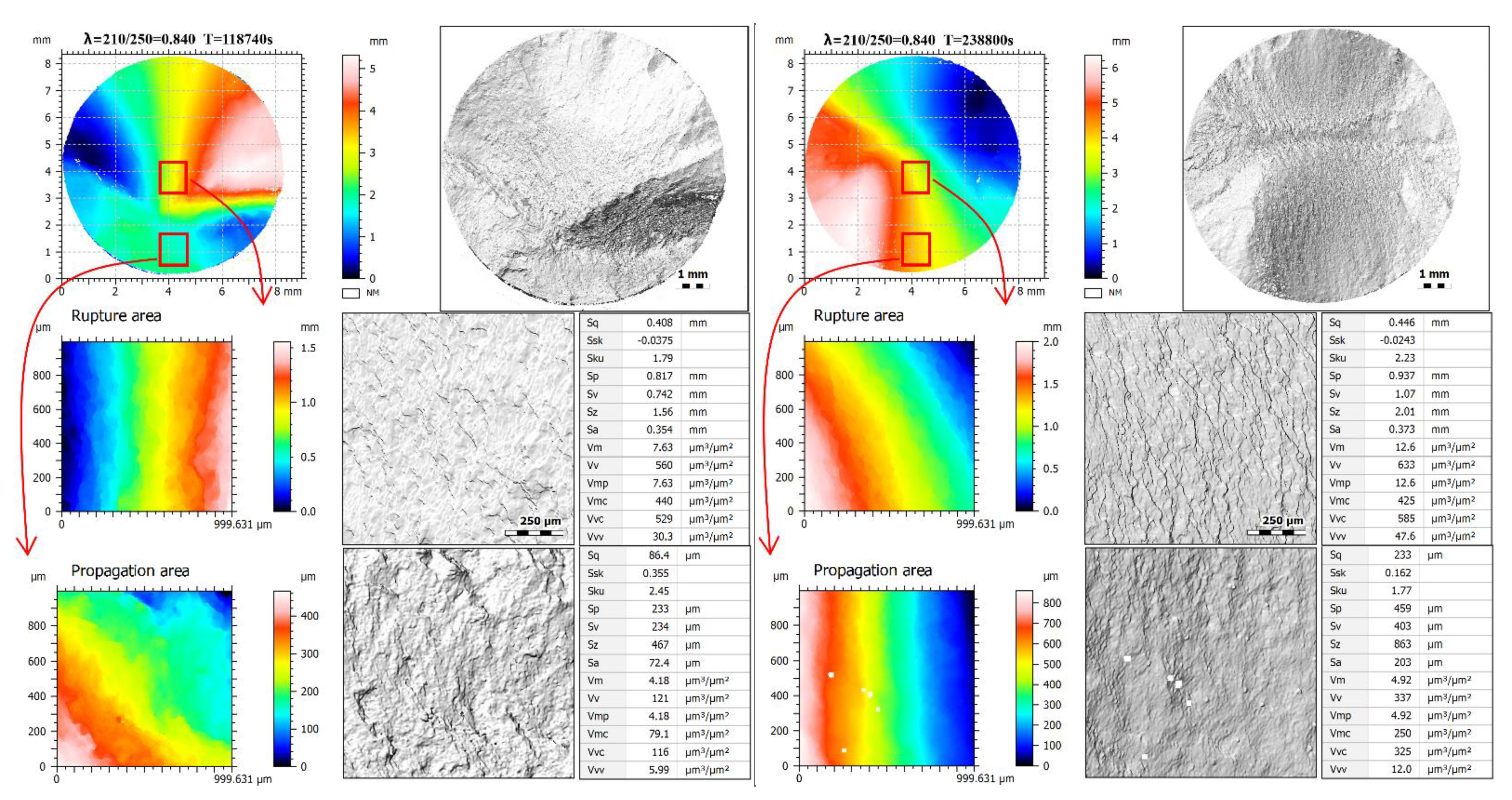
2.2. Fracture Surface Topography Measurement
3. Results
4. Discussion
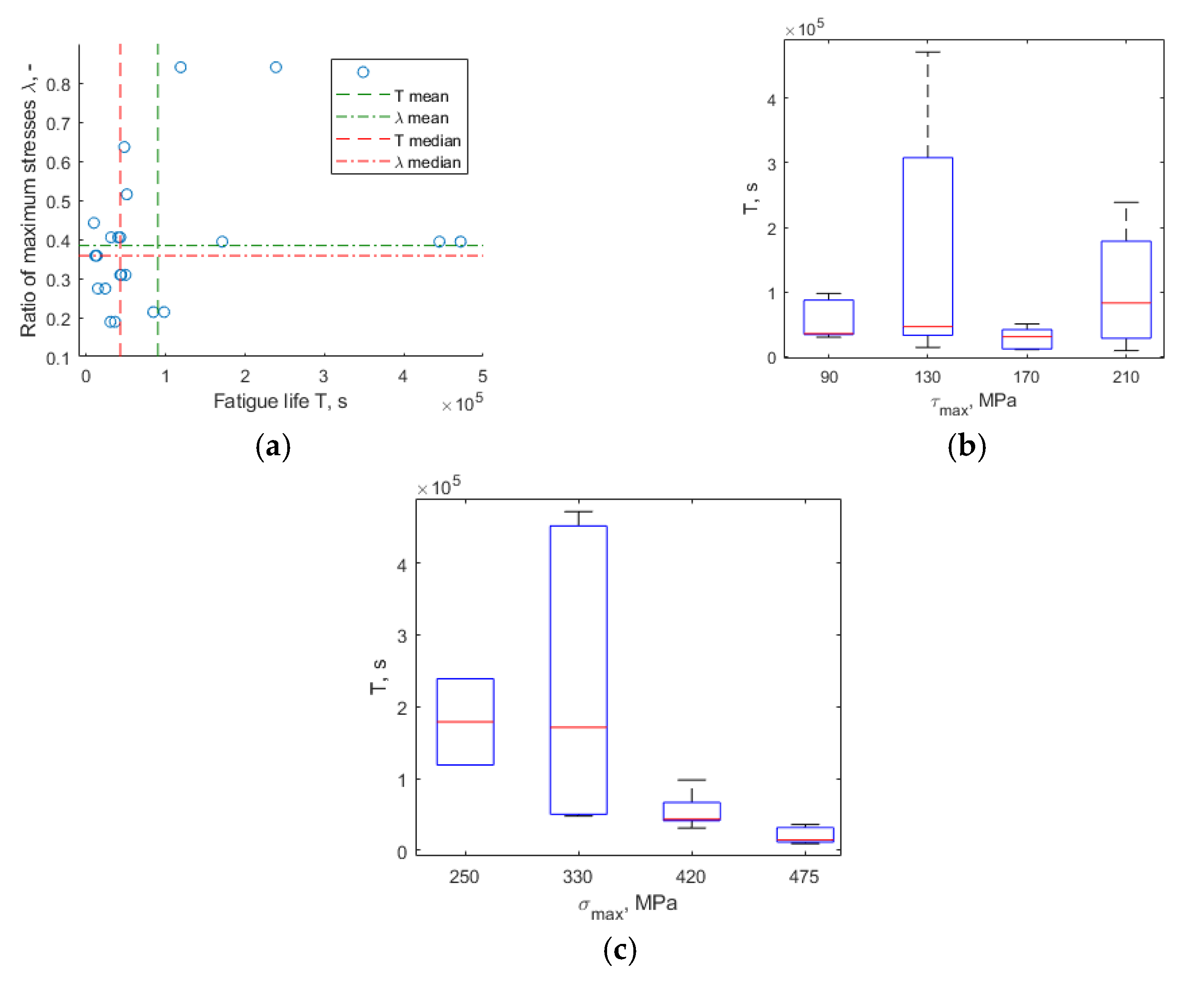
4.1. The Influence of the Maximum Normal and Shear Stresses Share on Fatigue Life
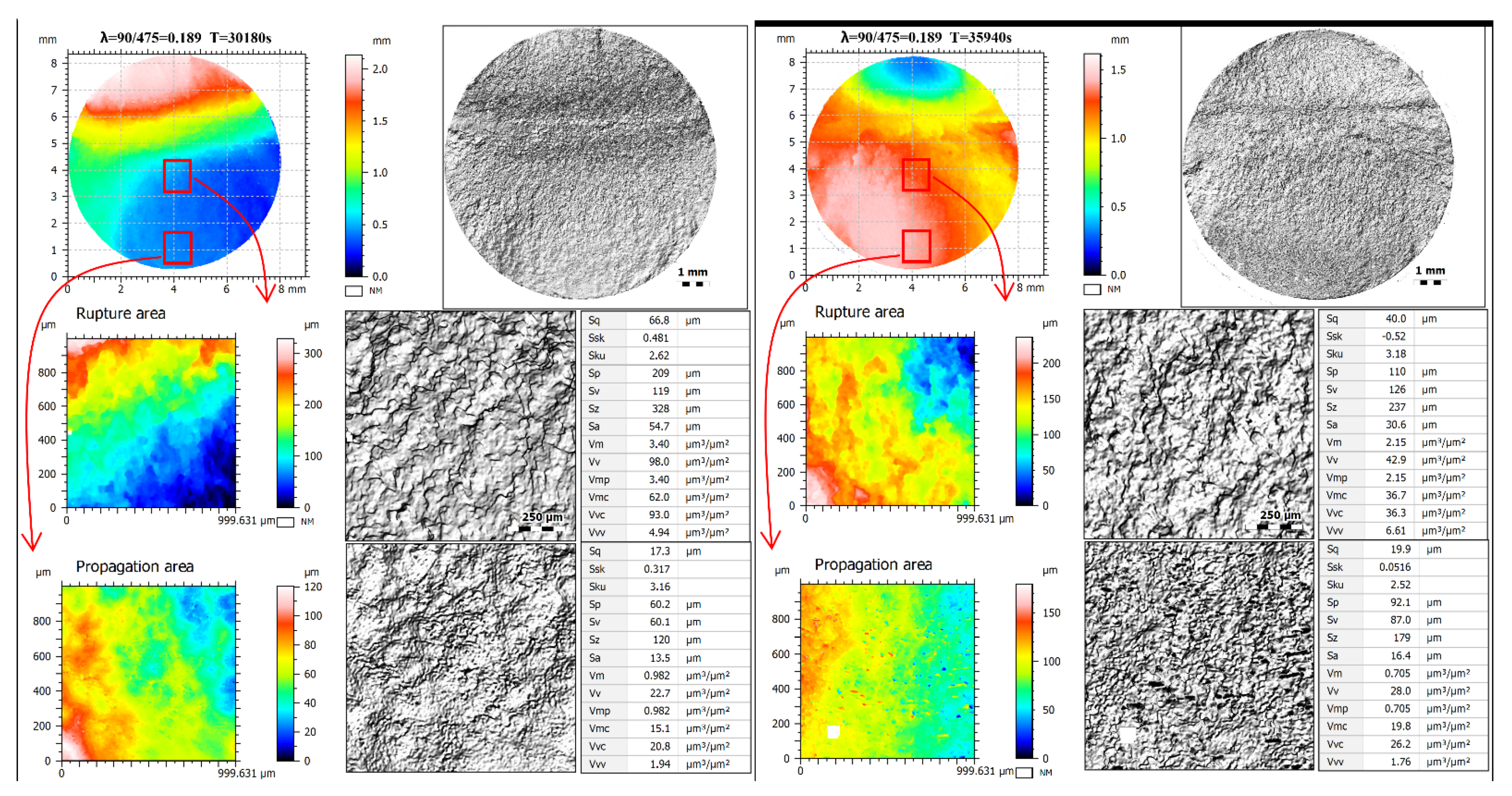
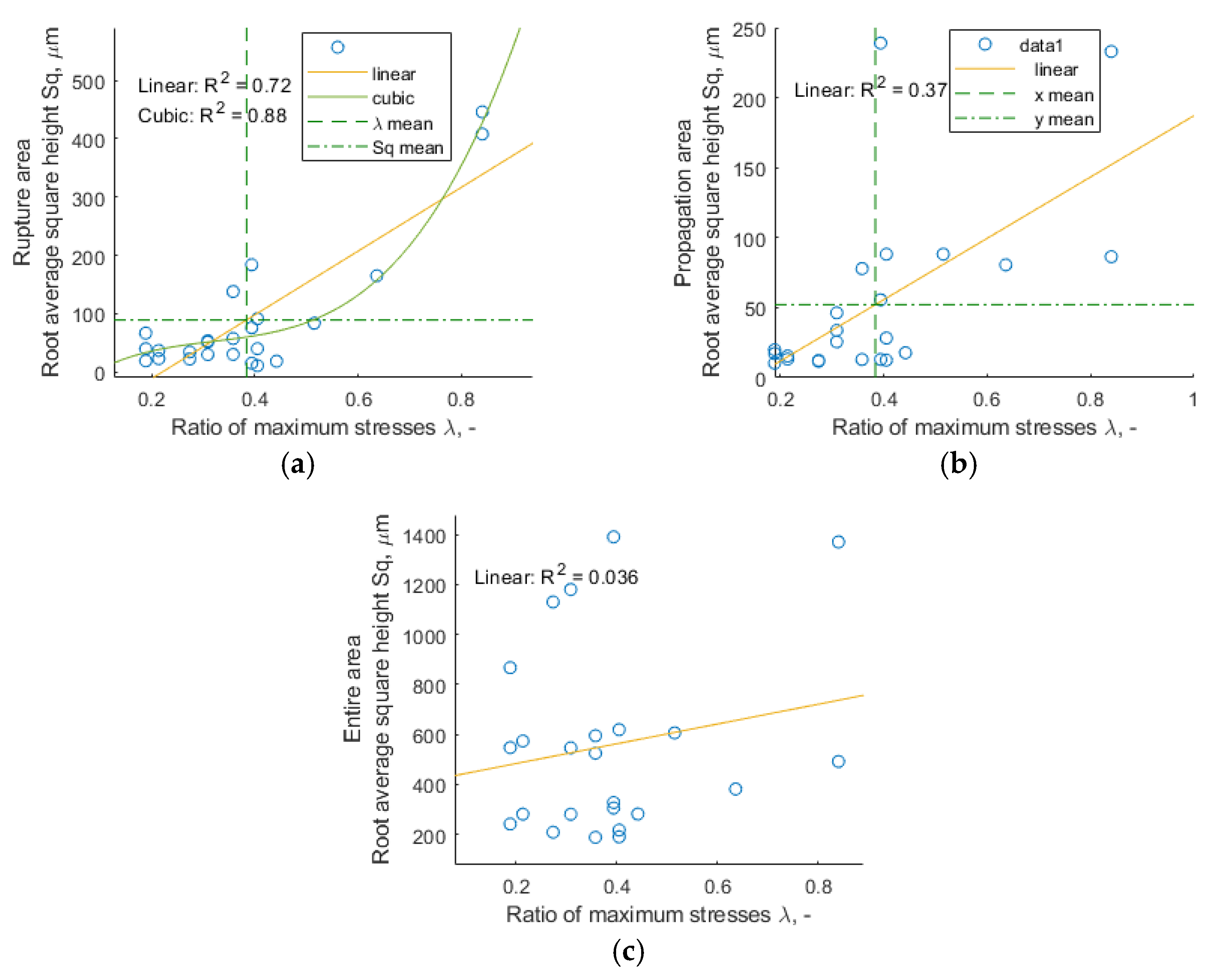
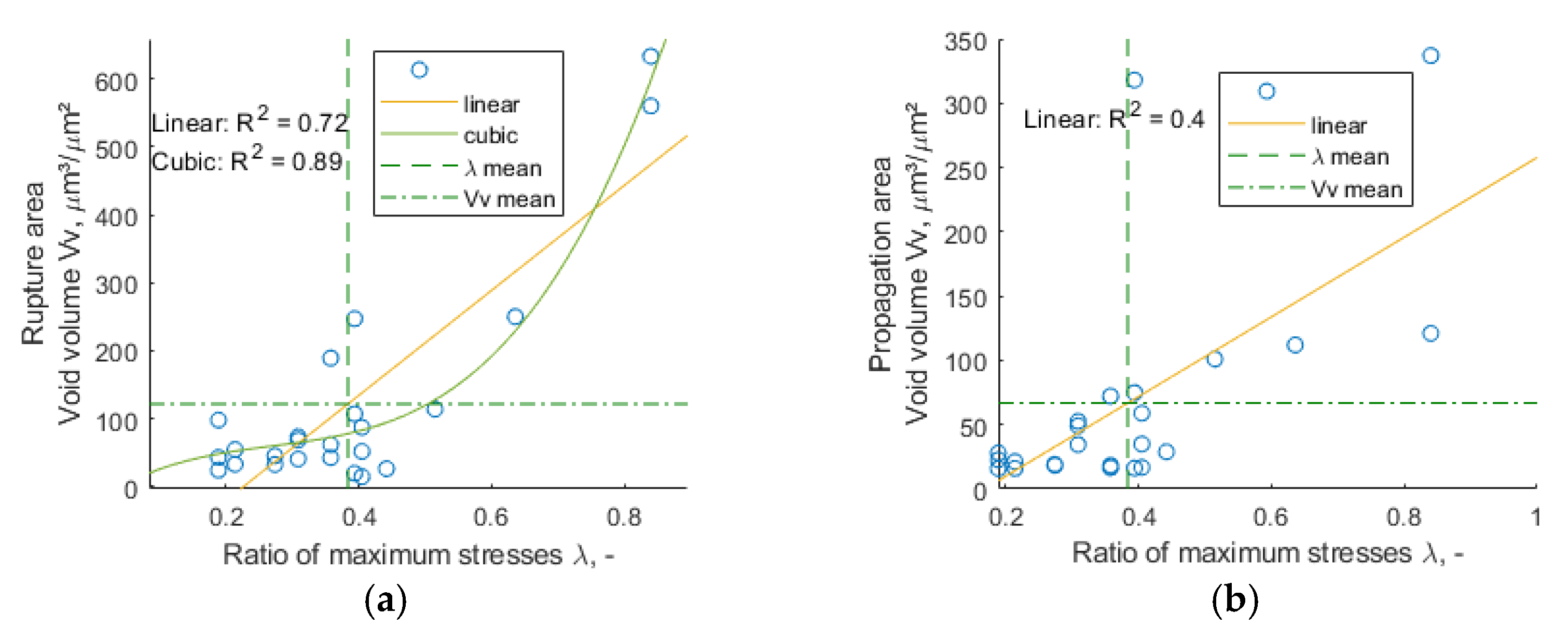
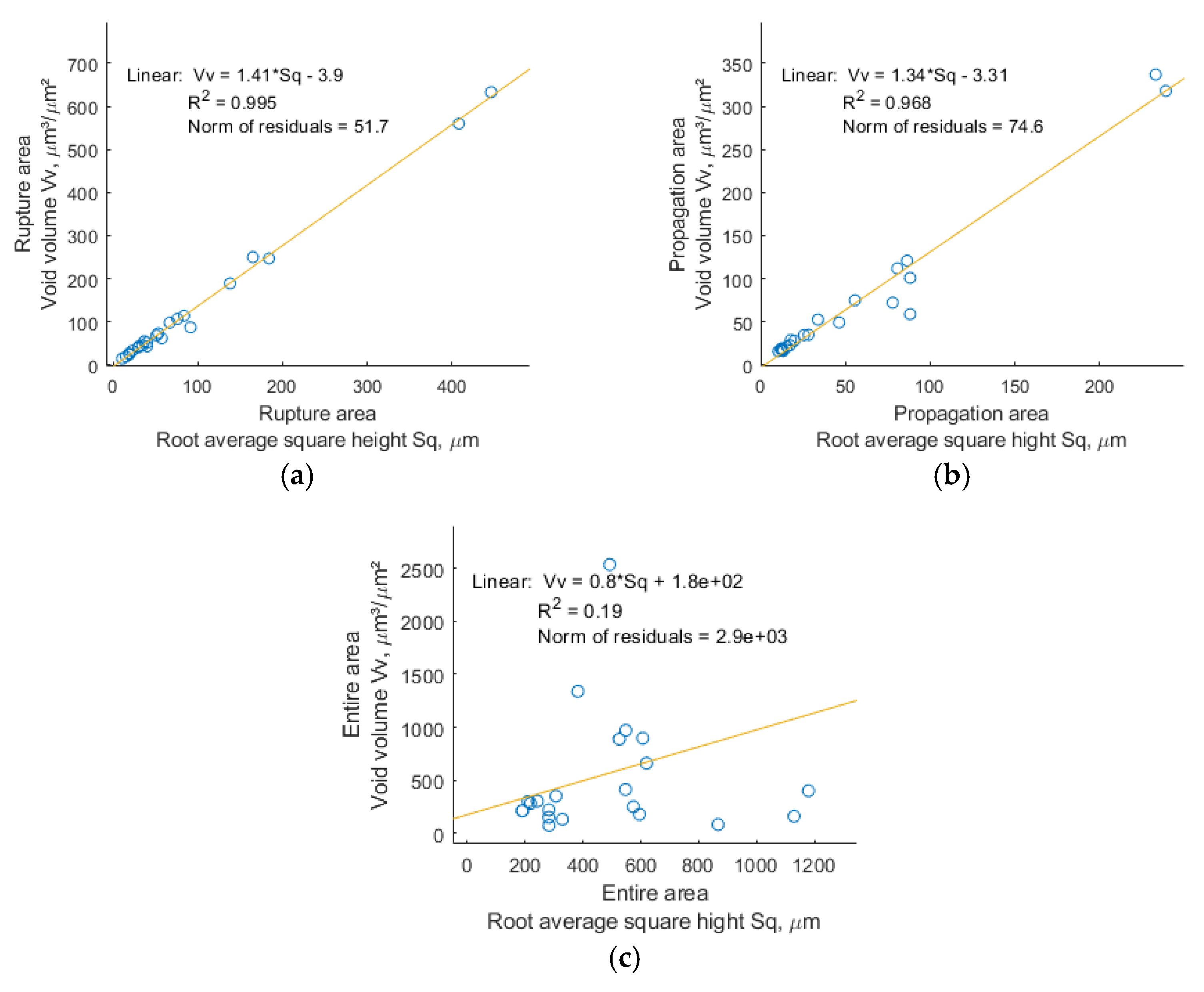
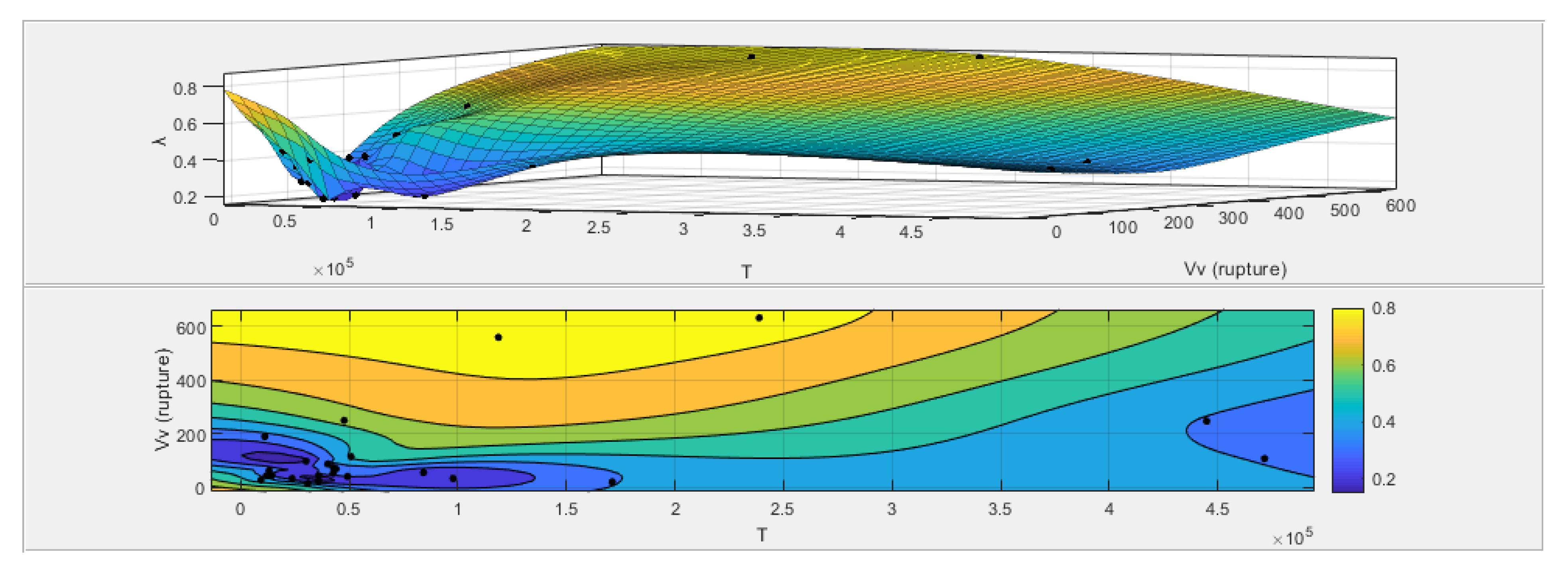
4.2. The Influence of the Ratio of Maximum Stresses λ on Fracture Surface Parameters
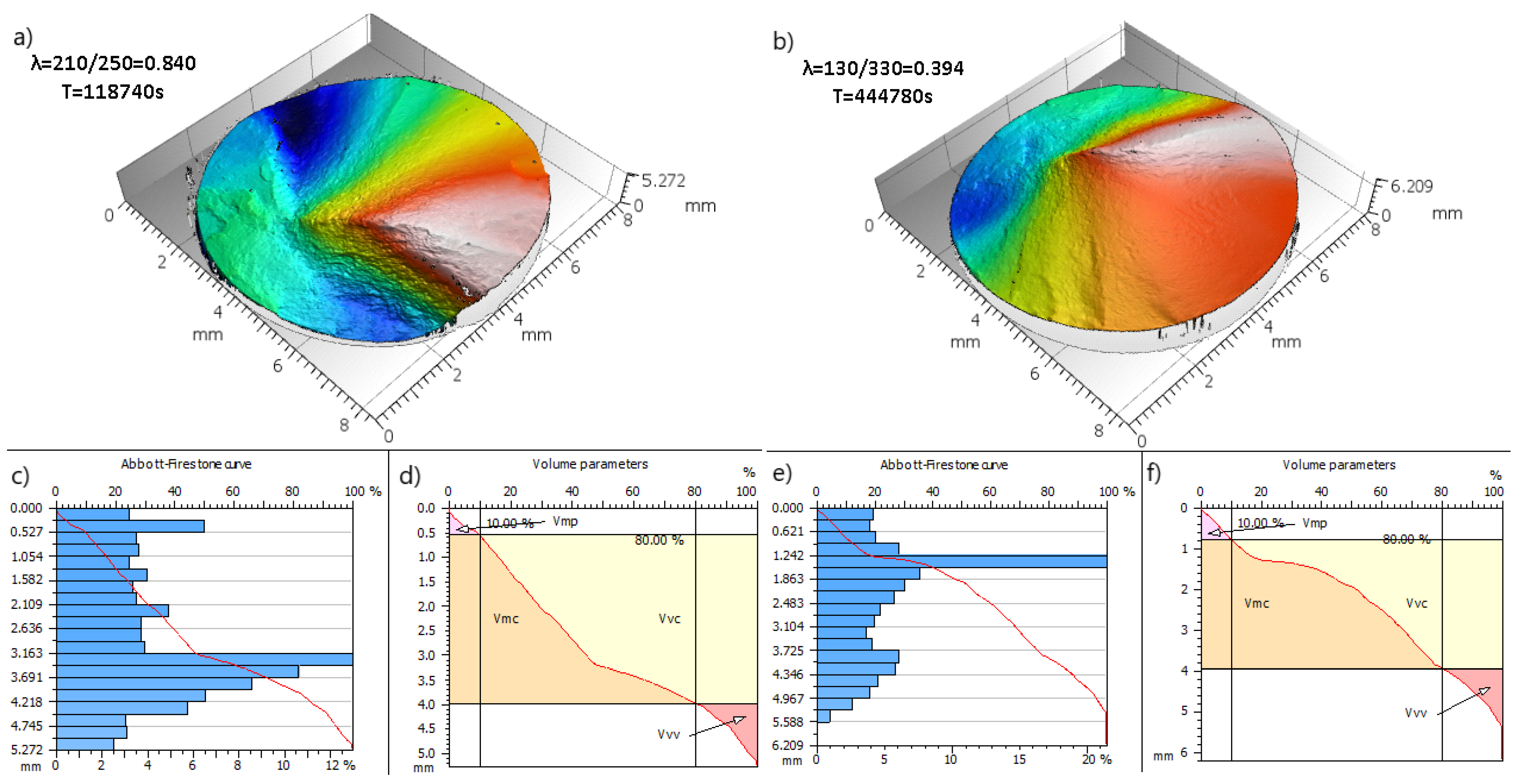
4.3. Fracture Surface Parameters for Maximum Vv Cases
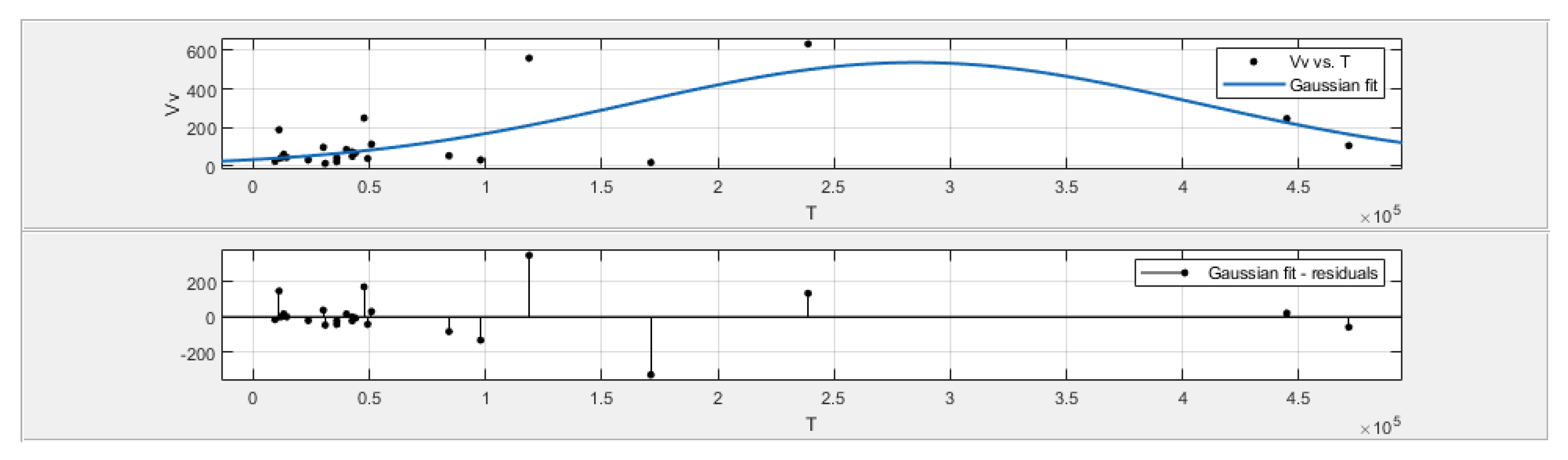
4.4. Summary of the Optimal Fractographic Parameter Vv with Fatigue Life T and Ratio of Maximum Stresses λ
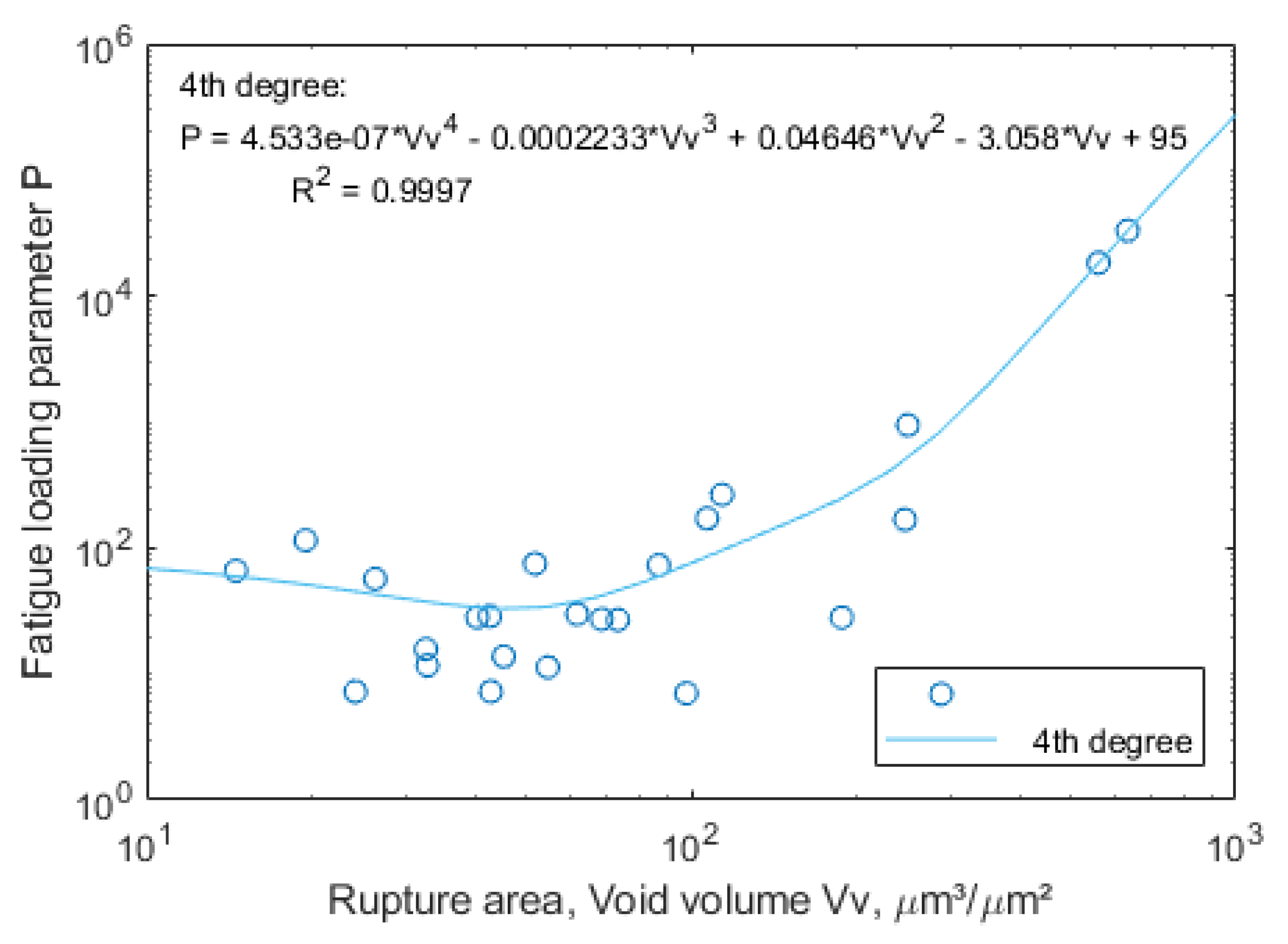
4.5. Loading and Fatigue Life Prediction Model Based on Void Volume Vv Parameter for the Rupture Area
5. Conclusions
- Fatigue life T depends more on the share of maximum normal stress σmax than on the maximum shear stress τmax;
- The best correlation with respect to ratio of maximum stresses λ was demonstrated by the void volume Vv parameter for the rupture area, and the best was Cubic fit with R2 around 0.89;
- The loading factors also affect the shape of the Abbott–Firestone curve as well as the extent Vx volume parameters (Vmp, Vmc, Vvc and Vvv);
- Fatigue life T, in the case of the analyzed data, is not well correlated with the surface topography parameters and the best was Gaussian fit with R2 around 0.434;
- New fatigue loading parameter P shows a rather good fit to void volume Vv parameter for the rupture area, with R2=0.9997, but within the specified range of loading combinations.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| h | µm | height |
| P | - | fatigue loading parameter |
| R2 | - | coefficient of determination |
| Sa | µm | arithmetical mean height |
| Sk | µm | core height |
| Smr1, Smr2 | ||
| Smr, Smrx | % | areal material ratio |
| Spk | µm | reduced peak height |
| Svk | µm | reduced dale height |
| Sq | µm | root mean square height |
| T | s | fatigue life |
| t | s | time |
| Vmc | µm³/µm² | core material volume |
| Vmp | µm³/µm² | peak material volume |
| Vv | µm³/µm² | void volume |
| Vvc | µm³/µm² | core void volume |
| Vvv | µm³/µm² | pit void volume |
| σ(t) | MPa | normal stress in time |
| τ(t) | MPa | shear stress in time |
| σmax | MPa | maximum normal stress |
| τmax | MPa | maximum shear stress |
| λ | - | ratio of maximum stresses |
References
- Branco, R.; Berto, F. High-Strength Low-Alloy Steels. Metals 2021, 11, 1000. [Google Scholar] [CrossRef]
- Guo, F.; Wu, S.C.; Liu, J.X.; Zhang, W.; Qin, Q.B.; Yao, Y. Fatigue life assessment of bogie frames in high-speed railway vehicles considering gear meshing. Int. J. Fatigue 2020, 132, 105353. [Google Scholar] [CrossRef]
- Cruces, A.S.; Lopez-Crespo, P.; Moreno, B.; Antunes, F.V. Multiaxial Fatigue Life Prediction on S355 Structural and Offshore Steel Using the SKS Critical Plane Model. Metals 2018, 8, 1060. [Google Scholar] [CrossRef] [Green Version]
- Pawliczek, R.; Rozumek, D. The Effect of Mean Load for S355J0 Steel with Increased Strength. Metals 2020, 10, 209. [Google Scholar] [CrossRef] [Green Version]
- Riofrío, P.G.; Ferreira, J.A.M.; Capela, C.A. Imperfections and Modelling of the Weld Bead Profile of Laser Butt Joints in HSLA Steel Thin Plate. Metals 2021, 11, 151. [Google Scholar] [CrossRef]
- Jiménez-Peña, C.; Goulas, C.; Preußner, J.; Debruyne, D. Failure Mechanisms of Mechanically and Thermally Produced Holes in High-Strength Low-Alloy Steel Plates Subjected to Fatigue Loading. Metals 2020, 10, 318. [Google Scholar] [CrossRef] [Green Version]
- Fu, S.; Cheng, F.; Tjahjowidodo, T. Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination. Metals 2020, 10, 69. [Google Scholar] [CrossRef] [Green Version]
- Podulka, P. The Effect of Surface Topography Feature Size Density and Distribution on the Results of a Data Processing and Parameters Calculation with a Comparison of Regular Methods. Materials 2021, 14, 4077. [Google Scholar] [CrossRef]
- Dzierwa, A.; Reizer, R.; Pawlus, P.; Grabon, W. Variability of areal surface topography parameters due to the change in surface orientation to measurement direction. Scanning 2014, 36, 170–183. [Google Scholar] [CrossRef]
- ISO-ISO 25178-2:2012—Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. Available online: https://www.iso.org/standard/42785.html (accessed on 28 December 2020).
- Todhunter, L.D.; Leach, R.K.; Lawes, S.D.A.; Blateyron, F. Industrial survey of ISO surface texture parameters. CIRP J. Manuf. Sci. Technol. 2017, 19, 84–92. [Google Scholar] [CrossRef]
- Zak, K. Cutting mechanics and surface finish for turning with differently shaped CBN tools. Arch. Mech. Eng. 2017, 64, 347–357. [Google Scholar] [CrossRef] [Green Version]
- Wojciechowski, S.; Maruda, R.W.; Barrans, S.; Nieslony, P.; Krolczyk, G.M. Optimisation of machining parameters during ball end milling of hardened steel with various surface inclinations. Measurement 2017, 111, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Senin, N.; Thompson, A.; Leach, R.K. Characterisation of the topography of metal additive surface features with different measurement technologies. Meas. Sci. Technol. 2017. [Google Scholar] [CrossRef]
- Feng, X.; Senin, N.; Su, R.; Ramasamy, S.; Leach, R. Optical measurement of surface topographies with transparent coatings. Opt. Lasers Eng. 2019, 121, 261–270. [Google Scholar] [CrossRef]
- López-Sanz, S.; Guzmán Bernardo, F.J.; Rodríguez Martín-Doimeadios, R.C.; Ríos, Á. Analytical metrology for nanomaterials: Present achievements and future challenges. Anal. Chim. Acta 2019, 1059, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.A.; Bowen, W.P. Quantum metrology and its application in biology. Phys. Rep. 2016, 615, 1–59. [Google Scholar] [CrossRef] [Green Version]
- Pluta, K.; Florkiewicz, W.; Malina, D.; Rudnicka, K.; Michlewska, S.; Królczyk, J.B.; Sobczak-Kupiec, A. Measurement methods for the mechanical testing and biocompatibility assessment of polymer-ceramic connective tissue replacements. Measurement 2021, 171, 108733. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Liang, Z.; Wang, Y.; Wang, X. Fatigue life prediction model of metallic materials considering crack propagation and closure effect. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–11. [Google Scholar] [CrossRef]
- Derpeński, Ł.; Seweryn, A.; Bartoszewicz, J. Ductile fracture of notched aluminum alloy specimens under elevated temperature part 1—Experimental research. Theor. Appl. Fract. Mech. 2019, 102, 70–82. [Google Scholar] [CrossRef]
- Azevedo, C.R.F.; Marques, E.R. Three-dimensional analysis of fracture, corrosion and wear surfaces. Eng. Fail. Anal. 2010, 17, 286–300. [Google Scholar] [CrossRef]
- Lynch, S.P.; Moutsos, S. A brief history of fractography. J. Fail. Anal. Prev. 2006, 6, 54–69. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, S.; Withers, P.J.; Cao, H.; Chen, P.; Zhang, Y.; Shen, Z.; Vojtek, T.; Hutař, P. Corrosion fatigue lifetime assessment of high-speed railway axle EA4T steel with artificial scratch. Eng. Fract. Mech. 2021, 245, 107588. [Google Scholar] [CrossRef]
- Macek, W.; Owsiński, R.; Trembacz, J.; Branco, R. Three-dimensional fractographic analysis of total fracture areas in 6082 aluminium alloy specimens under fatigue bending with controlled damage degree. Mech. Mater. 2020, 147, 103410. [Google Scholar] [CrossRef]
- Macek, W. Fractal analysis of the bending-torsion fatigue fracture of aluminium alloy. Eng. Fail. Anal. 2019, 99, 97–107. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Korpyś, M.; Łagoda, T. Fractal dimension for bending-torsion fatigue fracture characterisation. Measurement 2021, 184, 109910. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Costa, J.D.; Pereira, C. Strain sequence effect on fatigue life and fracture surface topography of 7075-T651 aluminium alloy. Mech. Mater. 2021, 160, 103972. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Szala, M.; Marciniak, Z.; Ulewicz, R.; Sczygiol, N.; Kardasz, P. Profile and Areal Surface Parameters for Fatigue Fracture Characterisation. Materials 2020, 13, 3691. [Google Scholar] [CrossRef]
- Macek, W. Fracture surface formation of notched 2017A-T4 aluminium alloy under bending fatigue. Int. J. Fract. 2021, 9, 1–17. [Google Scholar] [CrossRef]
- Macek, W.; Marciniak, Z.; Branco, R.; Rozumek, D.; Królczyk, G.M. A fractographic study exploring the fracture surface topography of S355J2 steel after pseudo-random bending-torsion fatigue tests. Measurement 2021, 178, 109443. [Google Scholar] [CrossRef]
- Marciniak, Z.; Rozumek, D.; Macha, E. Verification of fatigue critical plane position according to variance and damage accumulation methods under multiaxial loading. Int. J. Fatigue 2014, 58, 84–93. [Google Scholar] [CrossRef]
- Marciniak, Z.; Rozumek, D.; Macha, E. Fatigue lives of 18G2A and 10HNAP steels under variable amplitude and random non-proportional bending with torsion loading. Int. J. Fatigue 2008, 30, 800–813. [Google Scholar] [CrossRef]
- Macek, W.; Mucha, N. Evaluation of Fatigue Life Calculation Algorithm of the Multiaxial Stress-Based Concept Applied to S355 Steel under Bending and Torsion. Mech. Mech. Eng. 2017, 21, 935–951. [Google Scholar]
- Abbott, E.J.; Firestone, F.A. Specifying surface quality. Mech. Eng. 1933, 65, 569–572. [Google Scholar]
- Pawlus, P.; Reizer, R.; Wieczorowski, M.; Krolczyk, G. Material ratio curve as information on the state of surface topography—A review. Precis. Eng. 2020, 65, 240–258. [Google Scholar] [CrossRef]
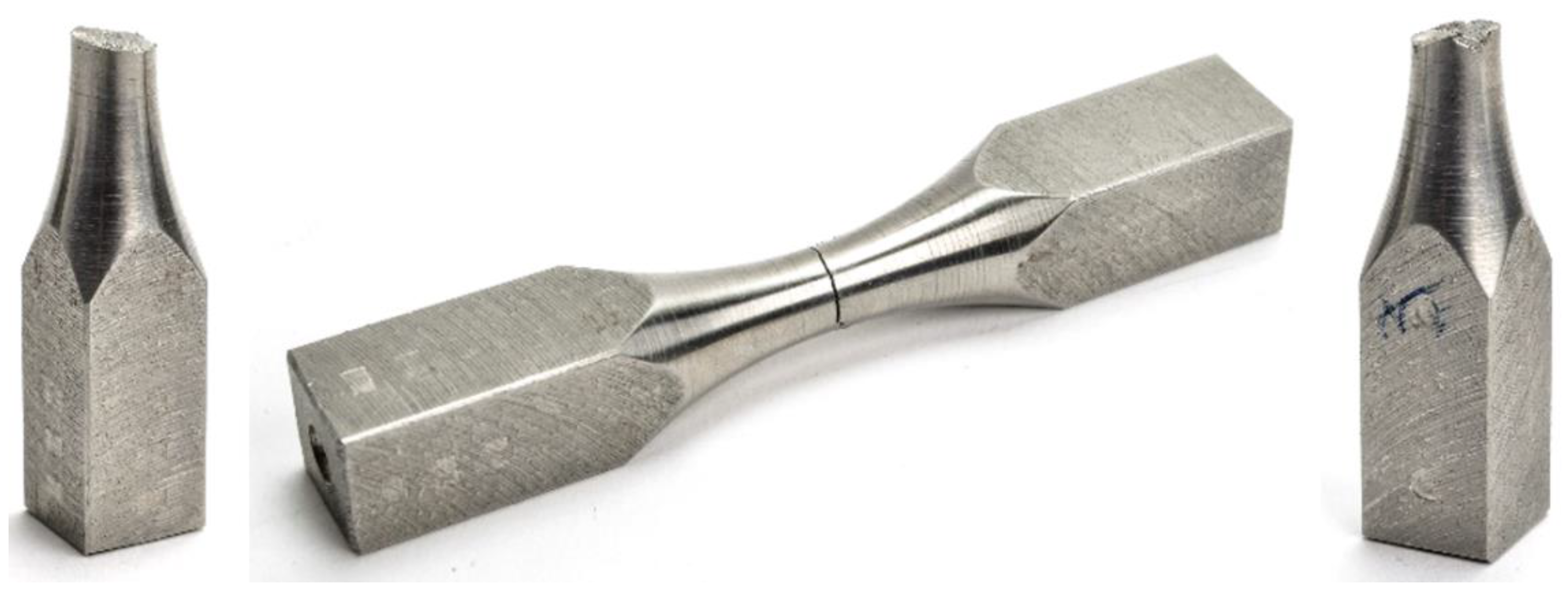







| Magnification | 10× |
|---|---|
| Vertical resolution | 79.6 nm |
| Lateral resolution | 3.91 µm |
| Number of images | 9 rows × 7 columns |
| Exposure time | 178 µs |
| Contrast | 0.53 |
| Curve Fitting, General Model Gauss1 | Goodness of Fit |
|---|---|
| f(x) = a1 × exp(−((x − b1)/c1)^2) | SSE: 3.351 × 105 |
| Coefficients (with 95% confidence bounds): | R2: 0.4336 |
| a1 = 537.1 (280, 794.2) | Adjusted R2: 0.3797 |
| b1 = 2.848 × 105 (2.379 × 105, 3.316 × 105) | RMSE: 126.3 |
| c1 = 1.721 × 105 (1.242 × 105, 2.2 × 105) |
| Thin-Plate Spline Interpolant | Goodness of Fit |
|---|---|
| f(x,y) = thin-plate spline computed from p | p = coefficient structure |
| x is normalized by mean 9.003 × 104 and std 1.256 × 105 | SSE: 7.196 × 10−26 |
| y is normalized by mean 121.5 and std 160.4 | R2: 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macek, W. Fracture Areas Quantitative Investigating of Bending-Torsion Fatigued Low-Alloy High-Strength Steel. Metals 2021, 11, 1620. https://doi.org/10.3390/met11101620
Macek W. Fracture Areas Quantitative Investigating of Bending-Torsion Fatigued Low-Alloy High-Strength Steel. Metals. 2021; 11(10):1620. https://doi.org/10.3390/met11101620
Chicago/Turabian StyleMacek, Wojciech. 2021. "Fracture Areas Quantitative Investigating of Bending-Torsion Fatigued Low-Alloy High-Strength Steel" Metals 11, no. 10: 1620. https://doi.org/10.3390/met11101620
APA StyleMacek, W. (2021). Fracture Areas Quantitative Investigating of Bending-Torsion Fatigued Low-Alloy High-Strength Steel. Metals, 11(10), 1620. https://doi.org/10.3390/met11101620






