The Microstructure in an Al–Ti Alloy Melt: The Wulff Cluster Model from a Partial Structure Factor
Abstract
:1. Introduction
2. Methods
2.1. Theoretical Methods
2.2. Experimental Methods
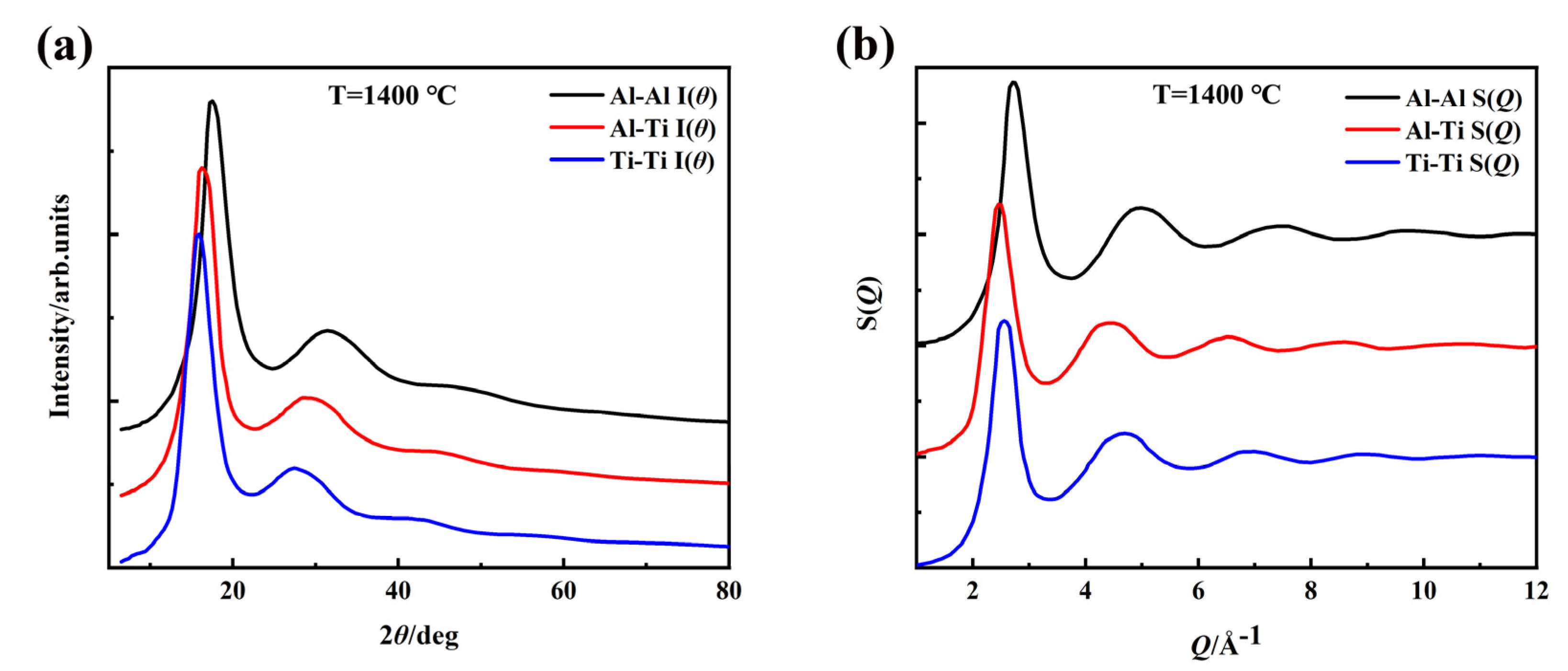
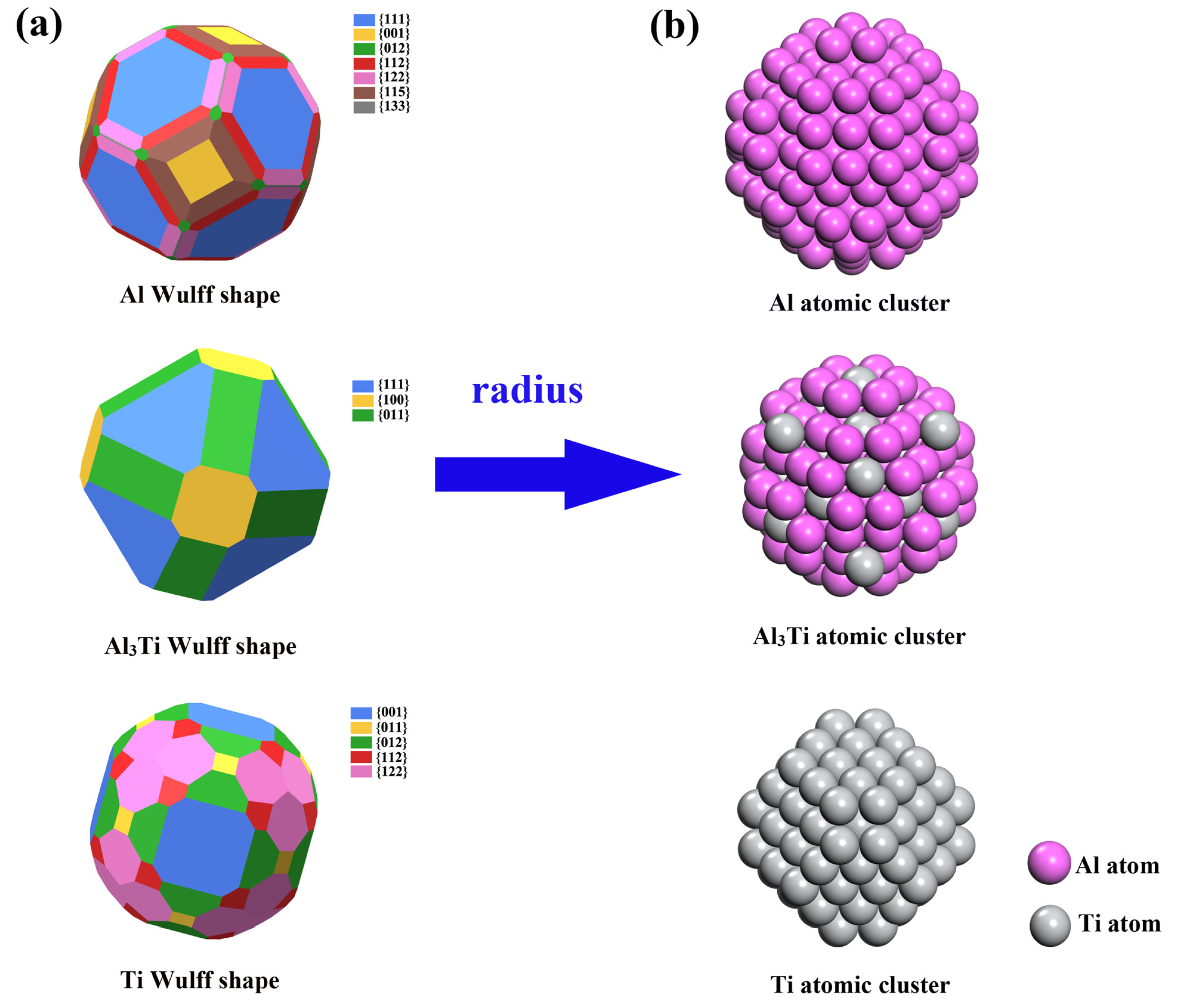
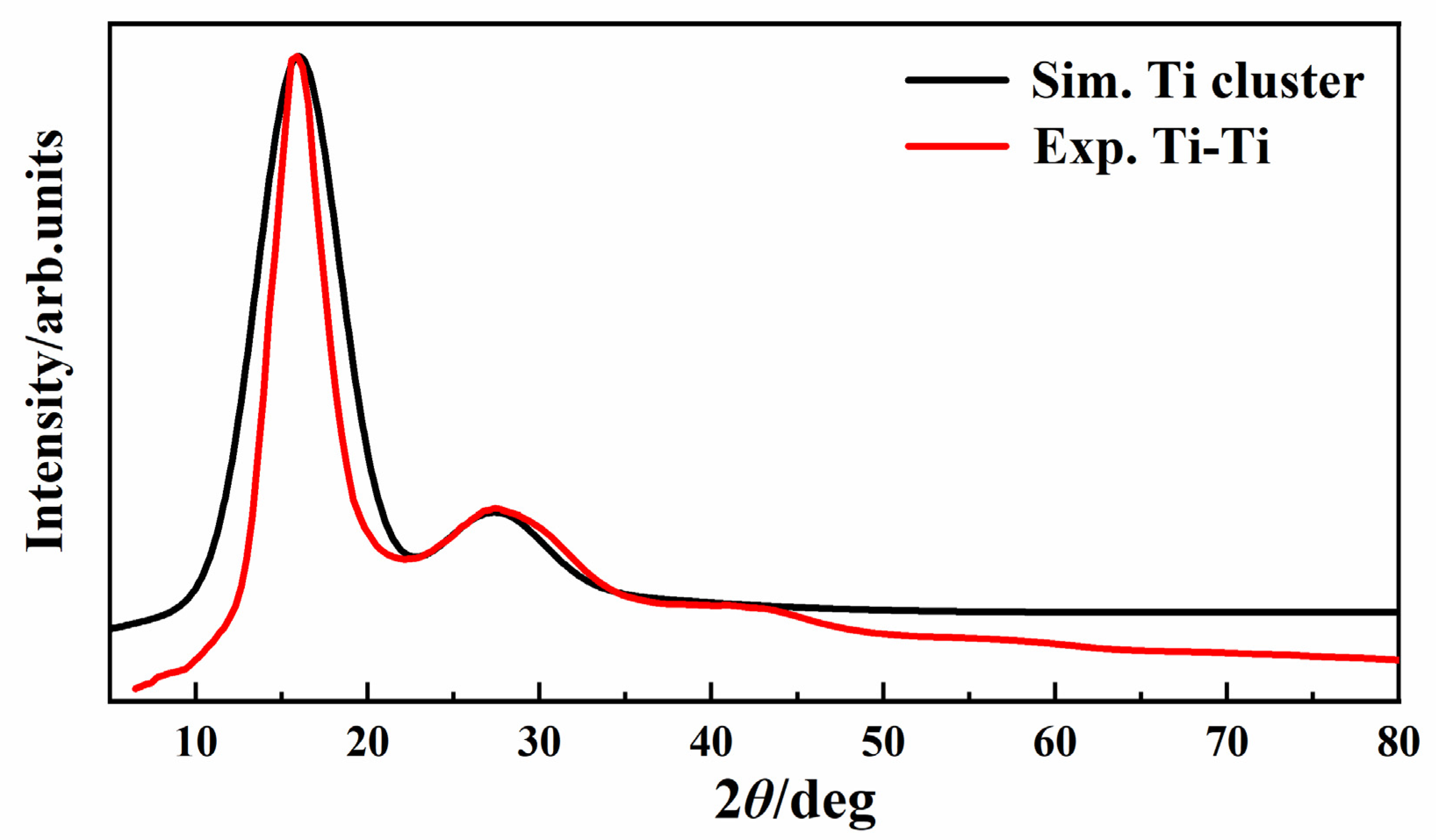
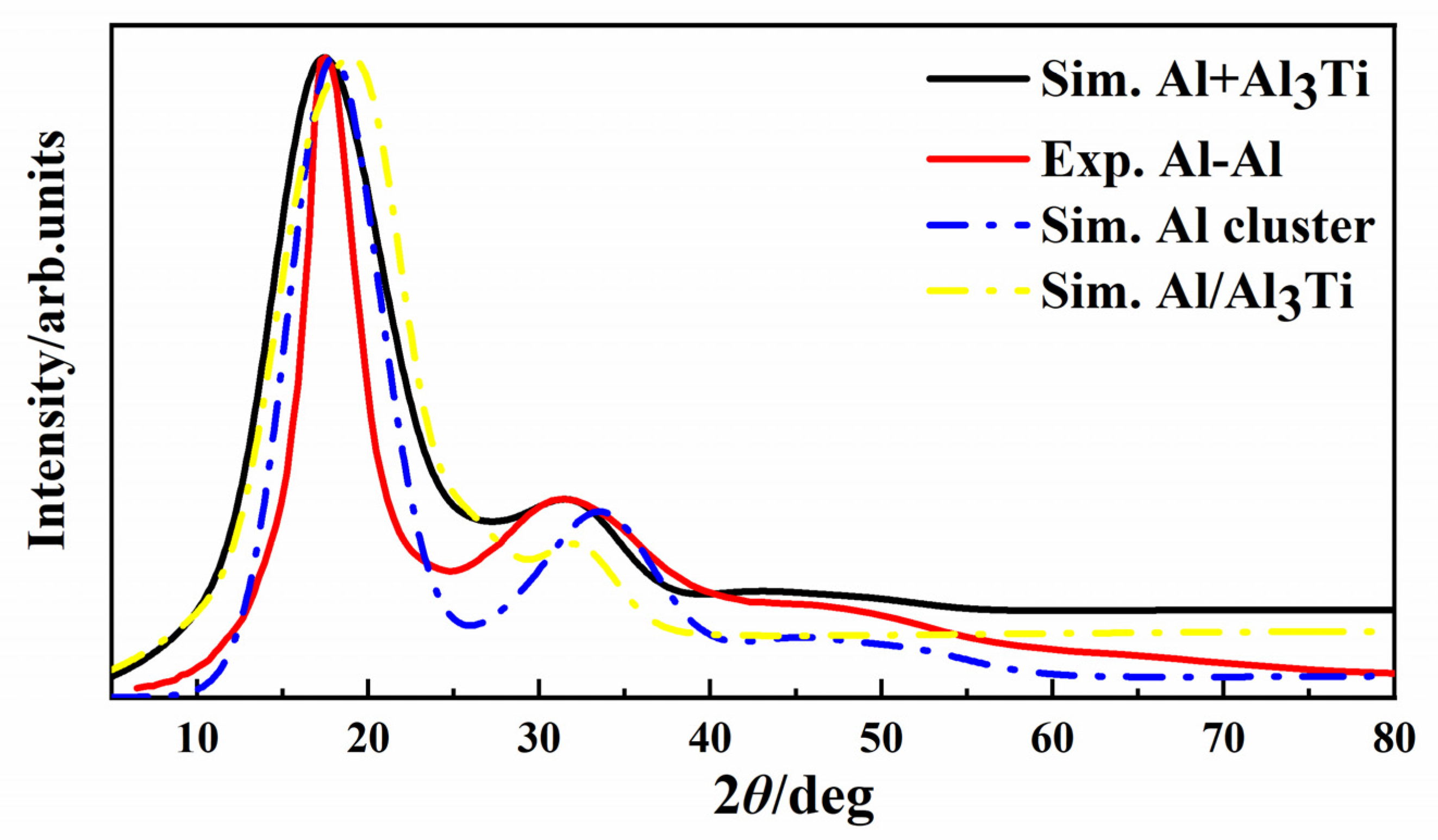
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilmametov, A.R.; Ivanisenko, Y.; Mazilkin, A.A.; Straumal, B.B.; Gornakova, A.S.; Fabrichnaya, O.B.; Kriegel, M.J.; Rafaja, D.; Hahn, H. The α→ω and β→ω phase transformations in Ti–Fe alloys under high-pressure torsion. Acta Mater. 2018, 144, 337–351. [Google Scholar] [CrossRef]
- Hennig, R.G.; Trinkle, D.R.; Bouchet, J.; Srinivasan, S.G.; Albers, R.C.; Wilkins, J.W. Impurities block the α to ω martensitic transformation in titanium. Nat. Mater. 2005, 4, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Pang, J.; Blackwood, D.J. Corrosion of titanium alloys in high temperature near anaerobic seawater. Corros. Sci. 2016, 105, 17–24. [Google Scholar] [CrossRef]
- Sedmák, P.; Pilch, J.; Heller, L.; Kopeček, J.; Wright, J.; Sedlák, P.; Frost, M.; Šittner, P. Grain-resolved analysis of localized deformation in nickel-titanium wire under tensile load. Science 2016, 353, 559–562. [Google Scholar] [CrossRef]
- Wang, S.Q.; Patel, V.K.; Bhole, S.D.; Wen, G.D.; Chen, D.L. Microstructure and mechanical properties of ultrasonic spot welded Al/Ti alloy joints. Mater. Des. 2015, 78, 33–41. [Google Scholar] [CrossRef]
- Lahiri, A.; Das, R. Spectroscopic studies of the ionic liquid during the electrodeposition of Al–Ti alloy in 1-ethyl-3-methylimidazolium chloride melt. Mater. Chem. Phys. 2012, 132, 34–38. [Google Scholar] [CrossRef]
- Chen, G.; Peng, Y.; Zheng, G.; Qi, Z.; Wang, M.; Yu, H.; Dong, C.; Liu, C.T. Polysynthetic twinned TiAl single crystals for high-temperature applications. Nat. Mater. 2016, 15, 876–881. [Google Scholar] [CrossRef]
- Srirangam, P.; Kramer, M.J.; Shankar, S. Effect of strontium on liquid structure of Al–Si hypoeutectic alloys using high-energy X-ray diffraction. Acta Mater. 2011, 59, 503–513. [Google Scholar] [CrossRef]
- Georgarakis, K.; Louzguine-Luzgin, D.V.; Antonowicz, J.; Vaughan, G.; Yavari, A.R.; Egami, T.; Inoue, A. Variations in atomic structural features of a supercooled Pd–Ni–Cu–P glass forming liquid during in situ vitrification. Acta Mater. 2011, 59, 708–716. [Google Scholar] [CrossRef]
- Bian, X.; Guo, J.; Lv, X.; Qin, X.; Wang, C. Prediction of glass-forming ability of metallic liquids. Appl. Phys. Lett. 2007, 91, 221910. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E. Atomic-level structure and structure–property relationship in metallic glasses. Prog. Mater. Sci. 2011, 56, 379–473. [Google Scholar] [CrossRef]
- Meyer, A. Self-diffusion in liquid copper as seen by quasielastic neutron scattering. Phys. Rev. B 2010, 81, 12102. [Google Scholar] [CrossRef]
- Susskind, H.; Becker, W. Random packing of spheres in non-rigid containers. Nature 1966, 212, 1564–1565. [Google Scholar] [CrossRef]
- Bernal, J.D. A geometrical approach to the structure of liquids. Nature 1959, 183, 141–147. [Google Scholar] [CrossRef]
- Huang, L.; Wang, C.Z.; Ho, K.M. Structure and dynamics of liquid Ni 36 Zr 64 by ab initio molecular dynamics. Phys. Rev. B 2011, 83, 184103. [Google Scholar] [CrossRef]
- Schenk, T.; Holland-Moritz, D.; Simonet, V.; Bellissent, R.; Herlach, D.M. Icosahedral short-range order in deeply undercooled metallic melts. Phys. Rev. Lett. 2002, 89, 75507. [Google Scholar] [CrossRef]
- Lou, H.; Wang, X.; Cao, Q.; Zhang, D.; Zhang, J.; Hu, T.; Mao, H.; Jiang, J. Negative expansions of interatomic distances in metallic melts. Proc. Natl. Acad. Sci. USA 2013, 110, 10068–10072. [Google Scholar] [CrossRef] [Green Version]
- Hui, L.; Xiufang, B.; Guanghou, W. Molecular dynamics study of the local order and defects in quenched states. Phys. Rev. B 2003, 67, 94202. [Google Scholar] [CrossRef]
- Hui, L.; Pederiva, F. Anomalies in liquid structure of Ni 3 Al alloys during a rapid cooling process. Phys. Rev. B 2003, 68, 54210. [Google Scholar] [CrossRef]
- Vasisht, V.V.; Saw, S.; Sastry, S. Liquid–liquid critical point in supercooled silicon. Nat. Phys. 2011, 7, 549–553. [Google Scholar] [CrossRef] [Green Version]
- Jakse, N.; Pasturel, A. Local order of liquid and supercooled zirconium by ab initio molecular dynamics. Phys. Rev. Lett. 2003, 91, 195501. [Google Scholar] [CrossRef]
- Ceschini, L.; Boromei, I.; Morri, A.; Seifeddine, S.; Svensson, I.L. Effect of Fe content and microstructural features on the tensile and fatigue properties of the Al–Si10–Cu2 alloy. Mater. Des. (1980–2015) 2012, 36, 522–528. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Doty, H.W.; Kaufman, M.J. The effects of Mn additions on the microstructure and mechanical properties of Al–Si–Cu casting alloys. Mater. Sci. Eng. A 2008, 488, 496–504. [Google Scholar] [CrossRef]
- Xue, X.; Bian, X.; Geng, H.; Qin, X. Structural evolution of medium range and short-range order with temperature in Cu-25 wt.% Sn. Mater. Sci. Eng. A 2003, 363, 134–139. [Google Scholar] [CrossRef]
- Song, L.; Tian, X.; Shao, A.; Li, L.; Zhang, Y.; Li, H.; Lin, X. The structure of metallic melts in binary homogenous alloys: A thermodynamical understanding from the Wulff cluster model. Phys. Chem. Chem. Phys. 2020, 22, 23237–23245. [Google Scholar] [CrossRef]
- Song, L.; Tian, X.; Yang, Y.; Qin, J.; Li, H.; Lin, X. Probing the microstructure in pure Al & Cu melts: Theory meets experiment. Front. Chem. 2020, 8, 607. [Google Scholar]
- Song, L.; Tian, X.; Shao, A.; Hua, M.; Li, L.; Li, H.; Lin, X. The structure of metallic melts in eutectic alloys based on the Wulff cluster model: Theory meets experiment. Phys. Chem. Chem. Phys. 2021, 23, 3606–3614. [Google Scholar] [CrossRef]
- Tyson, W.R.; Miller, W.A. Surface free energies of solid metals: Estimation from liquid surface tension measurements. Surf. Sci. 1977, 62, 267–276. [Google Scholar] [CrossRef]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef] [Green Version]
- Einstein, T.L. Equilibrium shape of crystals. In Handbook of Crystal Growth; Elsevier: Amsterdam, The Netherlands, 2015; pp. 215–264. [Google Scholar]
- Hui, L.; Pederiva, F.; Wang, B.L.; Wang, J.L.; Wang, G.H. How does the nickel nanowire melt? Appl. Phys. Lett. 2005, 86, 11913. [Google Scholar] [CrossRef]
- Hacene, M.; Anciaux Sedrakian, A.; Rozanska, X.; Klahr, D.; Guignon, T.; Fleurat Lessard, P. Accelerating VASP electronic structure calculations using graphic processing units. J. Comput. Chem. 2012, 33, 2581–2589. [Google Scholar] [CrossRef]
- Hutchinson, M.; Widom, M. VASP on a GPU: Application to exact-exchange calculations of the stability of elemental boron. Comput. Phys. Commun. 2012, 183, 1422–1426. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Harrison, M.J.; Woodruff, D.P.; Robinson, J.; Sander, D.; Pan, W.; Kirschner, J. Adsorbate-induced surface reconstruction and surface-stress changes in Cu (100)/O: Experiment and theory. Phys. Rev. B 2006, 74, 165402. [Google Scholar] [CrossRef] [Green Version]
- Bonzel, H.P.; Yu, D.K.; Scheffler, M. The three-dimensional equilibrium crystal shape of Pb: Recent results of theory and experiment. Appl. Phys. A 2007, 87, 391–397. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 84106. [Google Scholar] [CrossRef] [Green Version]
- Mathew, K.; Kolluru, V.C.; Mula, S.; Steinmann, S.N.; Hennig, R.G. Implicit self-consistent electrolyte model in plane-wave density-functional theory. J. Chem. Phys. 2019, 151, 234101. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Chen, D.; Fang, Q.; Chen, H.; Fan, T.; Liu, B.; Liu, F.; Tang, P. Effects of finite temperature on the surface energy in Al alloys from first-principles calculations. Appl. Surf. Sci. 2019, 479, 499–505. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Zydallis, J.B.; Lamont, G.B. Considerations in engineering parallel multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 144–173. [Google Scholar] [CrossRef]
- Engel, G.E.; Wilke, S.; König, O.; Harris, K.; Leusen, F. PowderSolve–a complete package for crystal structure solution from powder diffraction patterns. J. Appl. Crystallogr. 1999, 32, 1169–1179. [Google Scholar] [CrossRef] [Green Version]
- Pawley, G.S. Unit-cell refinement from powder diffraction scans. J. Appl. Crystallogr. 1981, 14, 357–361. [Google Scholar] [CrossRef]
- Tian, X.L.; Zhan, C.W.; Hou, J.X.; Chen, X.C.; Sun, J.J. Nanocrystal model for liquid metals and amorphous metals. J. Mater. Sci. Technol. 2010, 26, 69–74. [Google Scholar] [CrossRef]


| Types | γ (J/m2) | Types | γ (J/m2) | Types | γ (J/m2) |
|---|---|---|---|---|---|
| Ti(100) | 1.56 | Al(100) | 0.96 | Al3Ti (100)-1 | 1.85 |
| Ti(110) | 1.73 | Al(110) | 1.03 | Al3Ti (100)-2 | 1.23 |
| Ti(111) | 1.82 | Al(111) | 0.87 | Al3Ti (110)-1 | 1.93 |
| Ti(210) | 1.69 | Al(210) | 1.03 | Al3Ti (110)-2 | 1.15 |
| Ti(211) | 1.73 | Al(211) | 0.96 | Al3Ti (111) | 1.09 |
| Ti(221) | 1.69 | Al(221) | 0.96 | Al3Ti (210)-1 | 1.93 |
| Ti(310) | 1.72 | Al(310) | 1.03 | Al3Ti (210)-2 | 1.91 |
| Ti(311) | 1.81 | Al(311) | 0.99 | Al3Ti (211)-1 | 1.56 |
| Ti(511) | 1.78 | Al(511) | 0.98 | Al3Ti (211)-2 | 1.28 |
| Al3Ti (221) | 1.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Song, L.; Shao, A.; Hua, M.; Li, H.; Tian, X. The Microstructure in an Al–Ti Alloy Melt: The Wulff Cluster Model from a Partial Structure Factor. Metals 2021, 11, 1799. https://doi.org/10.3390/met11111799
Lin X, Song L, Shao A, Hua M, Li H, Tian X. The Microstructure in an Al–Ti Alloy Melt: The Wulff Cluster Model from a Partial Structure Factor. Metals. 2021; 11(11):1799. https://doi.org/10.3390/met11111799
Chicago/Turabian StyleLin, Xiaohang, Lin Song, Anchen Shao, Minghao Hua, Hui Li, and Xuelei Tian. 2021. "The Microstructure in an Al–Ti Alloy Melt: The Wulff Cluster Model from a Partial Structure Factor" Metals 11, no. 11: 1799. https://doi.org/10.3390/met11111799
APA StyleLin, X., Song, L., Shao, A., Hua, M., Li, H., & Tian, X. (2021). The Microstructure in an Al–Ti Alloy Melt: The Wulff Cluster Model from a Partial Structure Factor. Metals, 11(11), 1799. https://doi.org/10.3390/met11111799







