Experimental Investigation and Multi-Response Optimization of Machinability of AA5005H34 Using Composite Desirability Coupled with PCA
Abstract
1. Introduction
Applications of Research Work
2. Materials and Methods
2.1. Material
2.2. Cutting Process Parameters
2.3. Responses Variables
2.4. Experimentation
2.5. Optimization Methodology
3. Results and Discussion
3.1. Analysis of Variance (ANOVA)
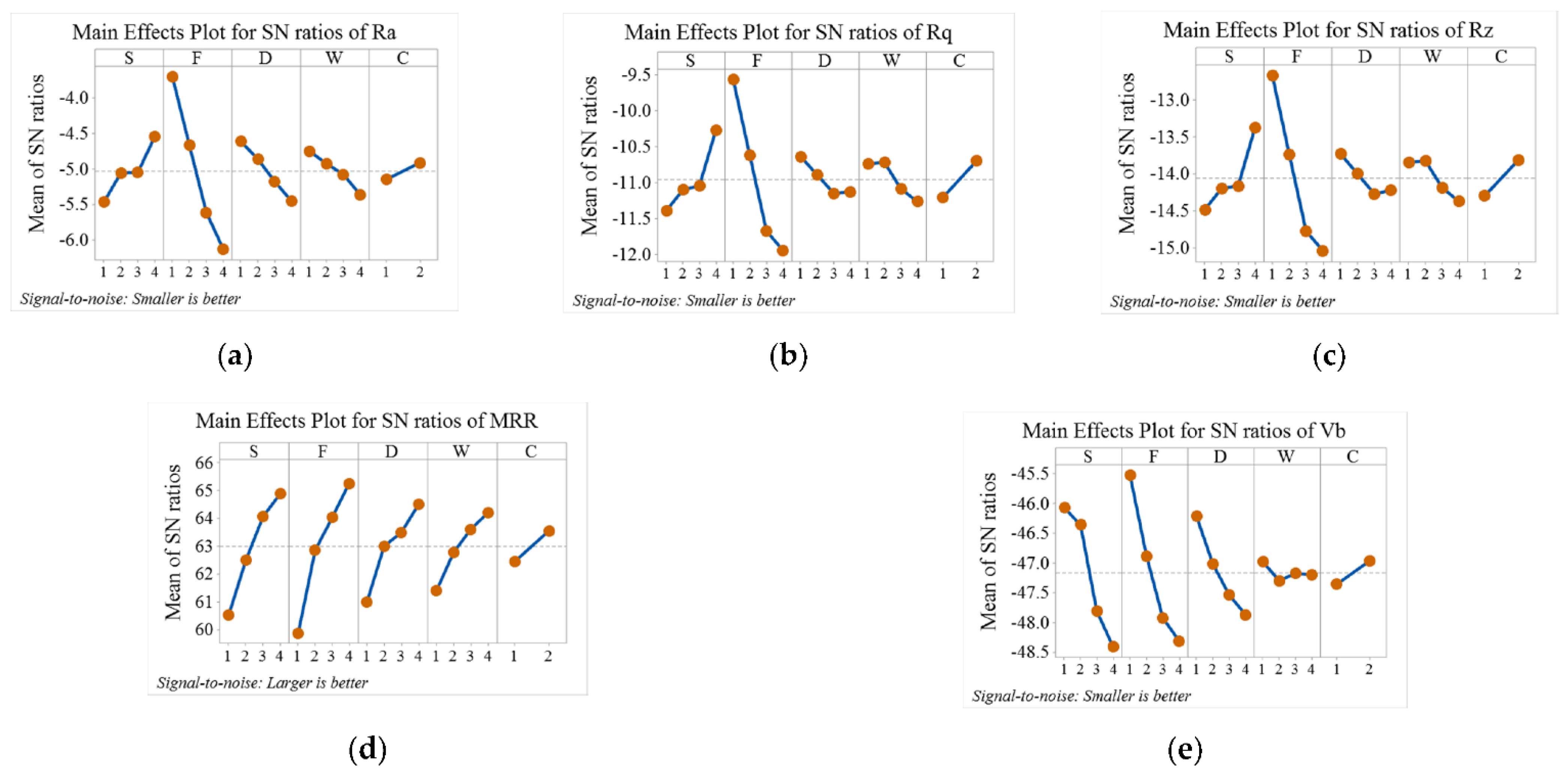
3.2. Main Effects Plots of Means for Individual Responses
3.3. Single Objective Optimization
3.4. Multi-Objective Optimization
4. Confirmatory Experiment
5. Conclusions
- The PCA-CDF method found S3F2D3W2C2 to be the optimal setting for the milling machining of aluminum 5005 H34.
- In terms of % contribution, the ANOVA revealed that the feed rate is the most influential machining parameter for the SR profile. For example, the % contributions of Ra, Rq, and Rz for feed rate are 68.74, 66.32, and 66.07, respectively.
- The Taguchi S/N ratio identified that the optimal cutting parameter for the minimization of SR (Ra, Rq, Rz) was S4F1D4W2C2T1—i.e., a spindle speed of 4000 rev/min, a feed rate of 250 mm/min, a depth of cut of 2.5 mm, a width of cut of 6 mm, and cutting conditions using MQL. The maximum MRR was achieved at S4F3D2W4 C1—i.e., spindle speed of 4000 rev/min, feed rate of 450 mm/min, depth of cut of 1.5 mm, width of cut of 14 mm, and dry cutting conditions. For the minimization of Vb, the optimal levels identified were S1F1D1W1C1—i.e., spindle speed of 1000 rev/min, feed rate of 250 mm/min, depth of cut of 1 mm, width of cut of 2 mm, and dry cutting conditions. The maximum MRR obtained under dry and MQL conditions was 2100 mm3/s and 2050 mm3/s, respectively.
- The contribution of the response variables in the principal component analysis in descending order was Ra at 23.43%, Rz at 22.66%, Rq at 22.56%, MRR at 16.32%, and Vb at 15.05%, respectively.
- The optimal machining parameters identified by the integrated approach of the PCA-CDF were spindle speed of 3000 rev/min, feed rate of 350 mm/min, depth of cut of 2 mm, width of cut of 6 mm, and MQL conditions.
- Finally, confirmatory experiments based on PCA-CDF list a significant diminishing of 21% in Ra, 23% in Rq, 18% in Rz, and 22% in Vb and an improvement of 30% in MRR. Therefore, the applied technique proved to be quite effective for multi-optimization.
- The application of MQL proved to be more efficient in comparison with dry machining due to its higher productivity, improved surface texture, and extended tool life.
- The experimental statistically optimized research findings can be offered as guidelines for the manufacturing sector. Additionally, these optimal machining conditions can be used as a baseline for improving the machinability of AA5005-H34.
- For future research work, the scope of the investigation could be enhanced by incorporating additional machining parameters to study their effect on quality responses. For example, the influence of the cutting reaction force, machining-induced stress, and nano-cutting fluids could be investigated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| MQL | minimum quantity lubricant |
| SEM | scanning electron microscope |
| PCA | principal component analysis |
| Ra | average roughness |
| Rq | root mean square |
| Rz | depth of peaks on the surface |
| MRR | material removal rate |
| SR | surface roughness |
| RSM | response surface methodology |
| PCA | principal component analysis |
| CDF | composite desirability function |
| Vb | flank wear |
| S | spindle speed |
| F | feed rate |
| D | depth of cut |
| W | width of cut |
| C | cutting condition |
| weight of the sample before machining | |
| weight of the sample after machining | |
| material density | |
| machining time | |
| Taguchi signal-to-noise ( | |
| LTB | larger-the-better (LTB) S/N ratio |
| STB | smaller-the-better (STB) S/N ratio |
| M | number of replications |
| experimental data. | |
| desirability value of quality response | |
| observed value of the response | |
| observed data at the kth response | |
| T | target value |
| assigned weight (varies 0.1–10) | |
| combined composite desirability | |
| desirability value of the rth response | |
| assigned weight to each response | |
| multi-criteria decision making | |
| multi-performance index (MPI) | |
| M | coefficient matrix |
| G | multi-response array |
| eigenvalues | |
| eigenvectors | |
| built-up edges (BUE) | |
| PC | principal component |
References
- Lian, Y.; Chen, H.; Mu, C.; Deng, J.; Lei, S. Experimental investigation and mechanism analysis of tungsten disulfide soft coated micro-nano textured self-lubricating dry cutting tools. Int. J. Precis. Eng. Manuf. Technol. 2018, 5, 219–230. [Google Scholar] [CrossRef]
- Mia, M.; Gupta, M.; Singh, G.; Krolczyk, G.; Pimenov, D.Y. An approach to cleaner production for machining hardened steel using different cooling-lubrication conditions. J. Clean. Prod. 2018, 187, 1069–1081. [Google Scholar] [CrossRef]
- Yusof, N.M.; Venkatesh, V.C.; Sharif, S. Dry turning of tempered martensitic stainless tool steel using coated cermet and coated carbide tools. J. Mater. Process. Technol. 2007, 185, 83–90. [Google Scholar] [CrossRef]
- Klocke, F.; Eisenblätter, G. Dry cutting. CIRP Ann. 1997, 46, 519–526. [Google Scholar] [CrossRef]
- Davoudinejad, A.; Tosello, G.; Annoni, M. Influence of the worn tool affected by built-up edge (BUE) on micro end-milling process performance: A 3D finite element modeling investigation. Int. J. Precis. Eng. Manuf. 2017, 18, 1321–1332. [Google Scholar] [CrossRef]
- Krolczyk, G.; Maruda, R.W.; Krolczyk, J.; Wojciechowski, S.; Mia, M.; Nieslony, P.; Budzik, G. Ecological trends in machining as a key factor in sustainable production—A review. J. Clean. Prod. 2019, 218, 601–615. [Google Scholar] [CrossRef]
- De Lacalle, L.L.; Angulo, C.; Lamikiz, A.; Sánchez, J. Experimental and numerical investigation of the effect of spray cutting fluids in high speed milling. J. Mater. Process. Technol. 2006, 172, 11–15. [Google Scholar] [CrossRef]
- Mia, M.; Gupta, M.K.; Lozano, J.A.; Carou, D.; Pimenov, D.Y.; Królczyk, G.; Dhar, N.R. Multi-objective optimi-zation and life cycle assessment of eco-friendly cryogenic N2 assisted turning of Ti-6Al-4V. J. Clean. Prod. 2019, 210, 121–133. [Google Scholar] [CrossRef]
- Katna, R.; Suhaib, M.; Agrawal, N. Nonedible vegetable oil-based cutting fluids for machining processes—A review. Mater. Manuf. Process. 2020, 35, 1–32. [Google Scholar] [CrossRef]
- Ahsan Ul Haq, M.; Khan, A.M.; Gong, L.; Xu, T.; Meng, L.; Hussain, S. A comparative study of face mill-ing of D2 steel using Al2O3 based nanofluid minimum quantity lubrication and minimum quantity lubri-cation. Adv. Sci. Technol. Res. J. 2018, 12, 99–105. [Google Scholar] [CrossRef]
- Gupta, M.K.; Mia, M.; Jamil, M.; Singh, R.; Singla, A.K.; Song, Q.; Liu, Z.; Khan, A.M.; Rahman, M.A.; Sarıkaya, M.; et al. Machinability investigations of hardened steel with biodegradable oil-based MQL spray system. Int. J. Adv. Manuf. Technol. 2020, 108, 735–748. [Google Scholar] [CrossRef]
- Khan, A.M.; Gupta, M.K.; Hegab, H.; Jamil, M.; Mia, M.; He, N.; Song, Q.; Liu, Z.; Pruncu, C.I. Energy-based cost integrated model-ling and sustainability assessment of Al-GnP hybrid nanofluid assisted turning of AISI52100 steel. J. Clean. Prod. 2020, 257, 120502. [Google Scholar] [CrossRef]
- Khan, A.M.; Jamil, M.; Salonitis, K.; Sarfraz, S.; Zhao, W.; He, N.; Zhao, G. Multi-objective optimization of en-ergy consumption and surface quality in nanofluid SQCL assisted face milling. Energies 2019, 12, 710. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Zhang, Y.; Wang, Y.; Jia, D.; Yang, M. Grinding temperature and energy ratio coefficient in MQL grinding of high-temperature nickel-base alloy by using different vegetable oils as base oil. Chin. J. Aeronaut. 2016, 29, 1084–1095. [Google Scholar] [CrossRef]
- Tao, F.; Cheng, J.; Qi, Q.; Zhang, M.; Zhang, H.; Sui, F. Digital twin-driven product design, manufac-turing and service with big data. Int. J. Adv. Manuf. Technol. 2018, 29, 3563–3576. [Google Scholar] [CrossRef]
- Nie, Z.; Lynn, R.; Tucker, T.M.; Kurfess, T. Voxel-based analysis and modeling of MRR computational accuracy in milling process. CIRP J. Manuf. Sci. Technol. 2019, 27, 78–92. [Google Scholar] [CrossRef]
- Gürbüz, H.; Emre Gönülaçar, Y. Optimization and evaluation of dry and minimum quantity lubri-cating methods on machinability of AISI 4140 using Taguchi design and ANOVA. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Abhang, L.B.; Hameedullah, M. Multi performance optimization in machining of En-31 steel alloy us-ing Taguchi-utility concept. J. Manuf. Technol. Res. 2011, 3, 265. [Google Scholar]
- Said, Z.; Gupta, M.; Hegab, H.; Arora, N.; Khan, A.M.; Jamil, M.; Bellos, E. A comprehensive review on mini-mum quantity lubrication (MQL) in machining processes using nano-cutting fluids. Int. J. Adv. Manuf. Technol. 2019, 105, 2057–2086. [Google Scholar] [CrossRef]
- Santos, M.C., Jr.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Debnath, S.; Reddy, M.M.; Yi, Q.S. Environmental friendly cutting fluids and cooling techniques in machining: A review. J. Clean. Prod. 2014, 83, 33–47. [Google Scholar] [CrossRef]
- Jebaraj, M.; Pradeep Kumar, M.; Yuvaraj, N.; Mujibar Rahman, G. Experimental study of the influ-ence of the process parameters in the milling of Al6082-T6 alloy. Mater. Manuf. Process. 2019, 34, 1411–1427. [Google Scholar] [CrossRef]
- Raju, K.V.M.K.; Janardhana, G.R.; Kumar, P.N.; Rao, V.D.P. Optimization of cutting conditions for surface roughness in CNC end milling. Int. J. Precis. Eng. Manuf. 2011, 12, 383–391. [Google Scholar] [CrossRef]
- Elsen, S.R.; Dhamodaran, K.; Aseer, J.R. Multi-Objective Optimization of End Milling Process Param-Eter for Stir Casted Alumina Reinforced Aluminium Metal Matrix Composite Using RSM. In Proceedings of the 2nd International Conference on Advances in Mechanical Engineering (ICAME 2018), Kattankulathur, India, 22–24 March 2018. [Google Scholar]
- Kumar, R.S.; Alexis, J.; Thangarasu, V. Optimization of high speed cnc end milling process of bsl 168 aluminium composite for aeronautical applications. Trans. Can. Soc. Mech. Eng. 2017, 41, 609–625. [Google Scholar] [CrossRef]
- Tsao, C.C. Grey–Taguchi method to optimize the milling parameters of aluminum alloy. Int. J. Adv. Manuf. Technol. 2009, 40, 41–48. [Google Scholar] [CrossRef]
- Lmalghan, R.; Rao, K.; ArunKumar, S.; Rao, S.S.; Herbert, M.A. Machining parameters optimization of aa6061 using response surface methodology and particle swarm optimization. Int. J. Precis. Eng. Manuf. 2018, 19, 695–704. [Google Scholar] [CrossRef]
- Rajeswari, B.; Amirthagadeswaran, K. Experimental investigation of machinability characteristics and multi-response optimization of end milling in aluminium composites using RSM based grey relational analysis. Measurement 2017, 105, 78–86. [Google Scholar] [CrossRef]
- Tosun, N.; Pihtili, H. Gray relational analysis of performance characteristics in MQL milling of 7075 Al alloy. Int. J. Adv. Manuf. Technol. 2010, 46, 509–515. [Google Scholar] [CrossRef]
- Abas, M.; Salah, B.; Khalid, Q.S.; Hussain, I.; Babar, A.R.; Nawaz, R.; Khan, R.; Saleem, W. Experimental investigation and statistical evaluation of optimized cutting process parameters and cutting conditions to minimize cutting forces and shape deviations in Al6026-T9. Materials 2020, 13, 4327. [Google Scholar] [CrossRef]
- Waseem, M.; Salah, B.; Habib, T.; Saleem, W.; Abas, M.; Khan, R.; Siddiqi, M.U.R. Multi-response optimization of tensile creep behavior of pla 3d printed parts using categorical response surface method-ology. Polymers 2020, 12, 2962. [Google Scholar] [CrossRef]
- Kamal, A.; Azfar, R.W.; Salah, B.; Saleem, W.; Abas, M.; Khan, R.; Pruncu, C.I. Quantitative analysis of sustainable use of construction materials for supply chain integration and construction industry perfor-mance through structural equation modeling (SEM). Sustainability 2021, 13, 522. [Google Scholar] [CrossRef]
- Markopoulos, A.; Karkalos, N.E.; Mia, M.; Pimenov, D.Y.; Gupta, M.K.; Hegab, H.; Khanna, N.; Balogun, V.A.; Sharma, S. Sustainability assessment, investigations, and modelling of slot milling characteristics in eco-benign machining of hardened steel. Metals 2020, 10, 1650. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Abbas, A.T.; Gupta, M.K.; Erdakov, I.; Soliman, M.S.; El Rayes, M.M. Investigations of surface quality and energy consumption associated with costs and material removal rate during face milling of AISI 1045 steel. Int. J. Adv. Manuf. Technol. 2020, 107, 3511–3525. [Google Scholar] [CrossRef]
- Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Mikolajczyk, T.; Soliman, M.S.; El Rayes, M.M. Optimization of cutting conditions using artificial neural networks and the Edgeworth-Pareto method for CNC face-milling operations on high-strength grade-H steel. Int. J. Adv. Manuf. Technol. 2019, 105, 2151–2165. [Google Scholar] [CrossRef]
- Muhammad, A.; Gupta, M.K.; Mikołajczyk, T.; Pimenov, D.Y.; Giasin, K. Effect of tool coating and cutting parameters on surface roughness and burr formation during micromilling of inconel 718. Metals 2021, 11, 167. [Google Scholar] [CrossRef]
- Sen, B.; Hussain, S.A.I.; Gupta, A.D.; Gupta, M.K.; Pimenov, D.Y.; Mikołajczyk, T. Application of Type-2 Fuzzy AHP-ARAS for Selecting Opti-mal WEDM Parameters. Metals 2021, 11, 42. [Google Scholar] [CrossRef]
- Saleem, W.; Salah, B.; Velay, X.; Ahmad, R.; Khan, R.; Pruncu, C.I. Numerical modeling and analysis of Ti6Al4V alloy chip for biomedical applications. Materials 2020, 13, 5236. [Google Scholar] [CrossRef]
- Abas, M.; Sayd, L.; Akhtar, R.; Khalid, Q.S.; Khan, A.M.; Pruncu, C.I. Optimization of machining pa-rameters of aluminum alloy 6026-T9 under MQL-assisted turning process. J. Mater. Res. Technol. 2020, 9, 10916–10940. [Google Scholar] [CrossRef]
- Bhushan, R.K.; Kumar, S.; Das, S. Effect of machining parameters on surface roughness and tool wear for 7075 Al alloy SiC composite. Int. J. Adv. Manuf. Technol. 2010, 50, 459–469. [Google Scholar] [CrossRef]
- Pereira, R.B.D.; Leite, R.R.; Alvim, A.C.; de Paiva, A.P.; Balestrassi, P.P.; Ferreira, J.R.; Davim, J.P. Multivariate robust modeling and optimization of cutting forces of the helical milling process of the aluminum alloy Al 7075. Int. J. Adv. Manuf. Technol. 2017, 95, 2691–2715. [Google Scholar] [CrossRef]
- Costa, D.M.D.; Belinato, G.; Brito, T.G.; Paiva, A.P.; Ferreira, J.R.; Balestrassi, P.P. Weighted principal component analysis combined with Taguchi’s signal-to-noise ratio to the multiobjective optimization of dry end milling process: A comparative study. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 1663–1681. [Google Scholar] [CrossRef]
- Tosun, N.; Huseyinoglu, M. Effect of MQL on surface roughness in milling of AA7075-T6. Mater. Manuf. Process. 2010, 25, 793–798. [Google Scholar] [CrossRef]
- Pillai, J.U.; Sanghrajka, I.; Shunmugavel, M.; Muthuramalingam, T.; Goldberg, M.; Littlefair, G. Opti-misation of multiple response characteristics on end milling of aluminium alloy using Taguchi-Grey relational approach. Measurement 2018, 124, 291–298. [Google Scholar] [CrossRef]
- Arokiadass, R.; Palaniradja, K.; Alagumoorthi, N. Predictive modeling of surface roughness in end milling of Al/SiCp metal matrix composite. Arch. Appl. Sci. Res. 2011, 3, 228–236. [Google Scholar]
- Tang, Z.; Liu, Z.; Pan, Y.; Wan, Y.; Ai, X. The influence of tool flank wear on residual stresses induced by milling aluminum alloy. J. Mater. Process. Technol. 2009, 209, 4502–4508. [Google Scholar] [CrossRef]
- Kelly, J.; Cotterell, M. Minimal lubrication machining of aluminium alloys. J. Mater. Process. Technol. 2002, 120, 327–334. [Google Scholar] [CrossRef]
- Aluminium Alloy 5005—Properties, Applications, Fabrication, Machinability and Weldability. Available online: https://www.azom.com/article.aspx?ArticleID=4244 (accessed on 27 August 2020).
- Babu, M.N.; Anandan, V.; Muthukrishnan, N.; Santhanakumar, M. End milling of AISI 304 steel us-ing minimum quantity lubrication. Measurement 2019, 138, 681–689. [Google Scholar] [CrossRef]
- Mia, M.; Gupta, M.K.; Pruncu, C.I.; Sen, B.; Khan, A.M.; Jamil, M. Six sigma optimization of multi-ple machining characteristics in hard turning under dry, flood, MQL and solid lubrication. J. Prod. Syst. Manuf. Sci. 2020, 1, 6. [Google Scholar]
- ISO. ISO 4287-1:1984 Surface Roughness—Terminology—Part 1: Surface and Its Parameters; ISO: Geneva, Switzerland, 1984. [Google Scholar]
- Kurt, H.I.; Oduncuoglu, M.; Yilmaz, N.F.; Ergul, E.; Asmatulu, R. A comparative study on the effect of welding parameters of austenitic stainless steels using artificial neural network and taguchi approaches with ANOVA analysis. Metals 2018, 8, 326. [Google Scholar] [CrossRef]
- Abas, M.; Naeem, K.; Habib, T.; Khan, I.; Farooq, U.; Khalid, Q.S.; Rahman, K. Development of prediction model for conductive pattern lines generated through positive displacement microdispensing system using artifi-cial neural network. Arab. J. Sci. Eng. 2020, 1–14. [Google Scholar] [CrossRef]
- Jan, Q.M.U.; Habib, T.; Noor, S.; Abas, M.; Azim, S.; Yaseen, Q.M. Multi response optimization of in-jection moulding process parameters of polystyrene and polypropylene to minimize surface roughness and shrinkage’s using integrated approach of S/N ratio and composite desirability function. Cogent Eng. 2020, 7. [Google Scholar] [CrossRef]
- Costa, N.R.; Lourenco, J.C.; Pereira, Z.L. Desirability function approach: A review and performance evaluation in adverse conditions. Chemom. Intell. Lab. Syst. 2011, 107, 234–244. [Google Scholar] [CrossRef]
- Pignatiello, J.J. An Overview of the strategy and tactics of taguchi. IIE Trans. 1988, 20, 247–254. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Chate, G.R.; Patel, G.C.M.; Kulkarni, R.M.; Vernekar, P.; Deshpande, A.S.; Parappagoudar, M. Study of the effect of nano-silica particles on resin-bonded moulding sand properties and quality of casting. Silicon 2018, 10, 1921–1936. [Google Scholar] [CrossRef]
- Javed, S.A.; Mahmoudi, A.; Khan, A.M.; Javed, S.; Liu, S. A critical review: Shape optimization of welded plate heat exchangers based on grey correlation theory. Appl. Therm. Eng. 2018, 144, 593–599. [Google Scholar] [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s entropy and multi attribute decision making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Qazi, M.I.; Akhtar, R.; Abas, M.; Khalid, Q.S.; Babar, A.R.; Pruncu, C. An integrated approach of GRA coupled with principal component analysis for multi-optimization of shielded metal arc welding (SMAW) process. Materials 2020, 13, 3457. [Google Scholar] [CrossRef]
- Sonawane, S.A.; Kulkarni, M. Optimization of machining parameters of WEDM for Nimonic-75 alloy using principal component analysis integrated with Taguchi method. J. King Saud Univ. Eng. Sci. 2018, 30, 250–258. [Google Scholar] [CrossRef]
- Lee, W.J.; Mendis, G.P.; Triebe, M.J.; Sutherland, J.W. Monitoring of a machining process using kernel principal component analysis and kernel density estimation. J. Intell. Manuf. 2019, 31, 1175–1189. [Google Scholar] [CrossRef]
- Das, R.; Ball, A.K.; Roy, S.S. Application of PCA-based hybrid methodologies for parameter optimi-zation of E-jet based micro-fabrication process: A comparative study. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 45. [Google Scholar] [CrossRef]
- Jones, B.; Montgomery, D.C. Design of Experiments: A Modern Approach; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730. [Google Scholar] [CrossRef]
- Sreejith, P. Machining of 6061 aluminium alloy with MQL, dry and flooded lubricant conditions. Mater. Lett. 2008, 62, 276–278. [Google Scholar] [CrossRef]
- Roy, P.; Sarangi, S.; Ghosh, A.; Chattopadhyay, A. Machinability study of pure aluminium and Al–12% Si alloys against uncoated and coated carbide inserts. Int. J. Refract. Met. Hard Mater. 2009, 27, 535–544. [Google Scholar] [CrossRef]
- Astakhov, V.P. Tribology of Metal Cutting; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
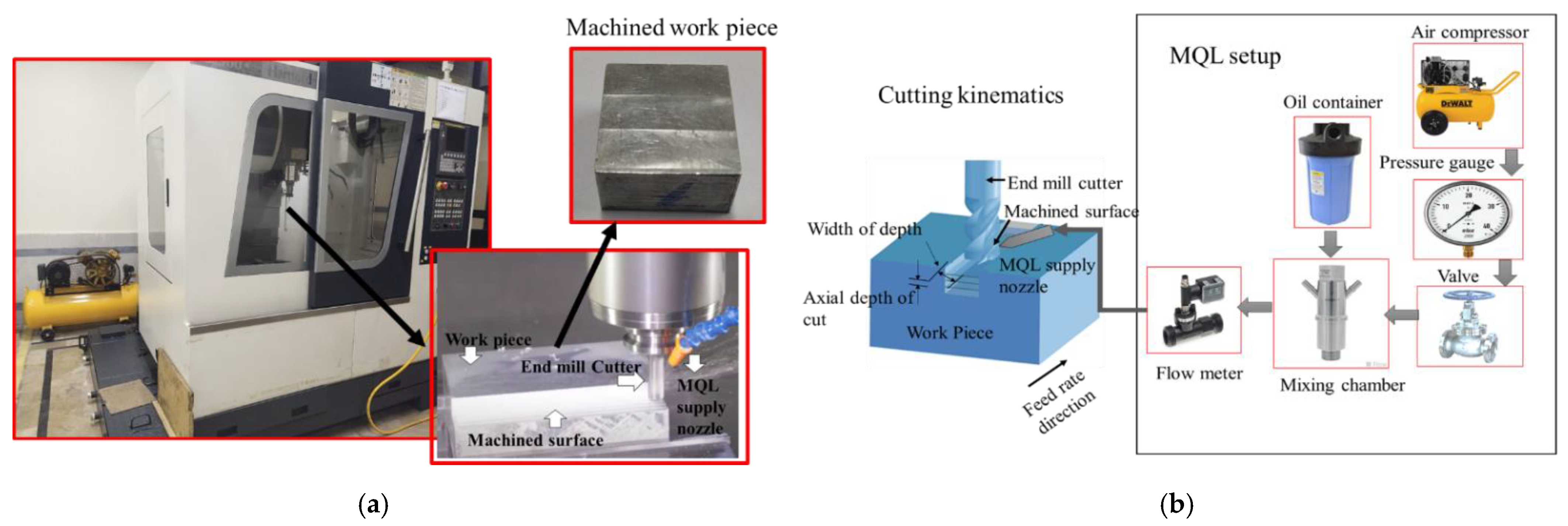



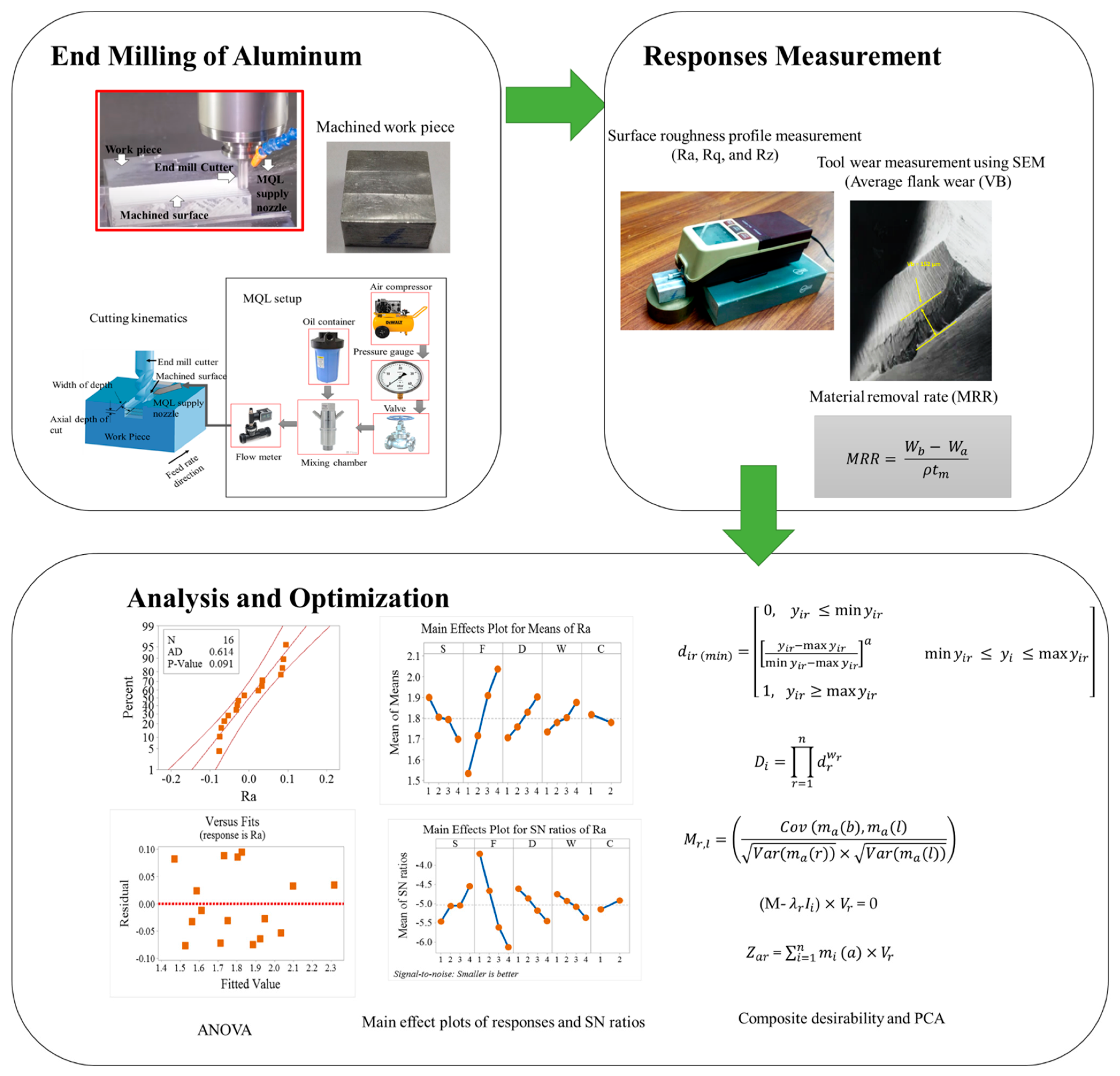



| Machining Method/Cutting Conditions | Material and Characteristics Studied | Investigation Approach | |
|---|---|---|---|
| [2] | Different cooling-lubrication | Hardened steel, machining parameters | Experimental invertigation |
| [5] | Micro end-milling | Tool wear | FEA, numerical investigation |
| [7] | Spray cutting fluids, high speed milling | Machining characteristics | Experimental and numerical investigation |
| [8] | Cryogenic N2 assisted turning | Ti-6Al-4V, tool life cycle assessment | Multi-objective optimization |
| [10] | Face milling, Al2O3 based MQL | D2 Steel | A comparative study |
| [11] | Biodegradable oil-based MQL | Hardened steel, machining characteristics | Experimental invertigation |
| [13] | Nanofluid SQCL assisted face milling | Aluminum, energy consumption, surface quality | Multi-objective optimization |
| [14] | MQL grinding, vegetable oils | Nickel-base alloy, grinding temperature, energy ratio coefficient | Experimental invertigation |
| [16] | Milling | MRR, computational accuracy | Voxel-based analysis |
| [17] | Dry, MQL milling | AISI 4140, machining characteristics | Taguchi design, ANOVA |
| [18] | Milling | En-31 steel alloy, machining characteristics | Multi performance optimization |
| [9,19,20,21] | Vegetable oil-based fluids, lubricants | Aluminum alloys and other materials | Review |
| [24] | End milling | Aluminum metal matrix composite | RSM |
| [26] | Milling parameters | Aluminum machining characteristics | Grey–Taguchi method |
| [27] | End milling | AA6061, machining parameters | RSM, particle swarm |
| [28] | Milling | Aluminum composites, machining parameters | RSM based grey relational analysis |
| [29] | MQL milling | 7075 Al alloy, machining parameters | Grey relational analysis |
| [30] | Turning under MQL | Al6026-T9, cutting forces | Statistical evaluation |
| [33] | Slot milling | AISI O1, machining parameters, surface quality | Regression analysis |
| [34] | Face milling | AISI 1045, surface quality, MRR | Multi-layer regression analysis |
| [35] | CNC Face milling | high-strength grade-H steel, cutting conditions | Artificial Neural Network (ANN) |
| [36] | Micro-milling | Inconel 718, cutting parameters, surface quality | Statistical evaluation |
| [38] | Milling under dry | Ti6Al4V alloy, cutting forces and temperature | Numerical analysis |
| [39] | MQL-assisted turning process | 6026-T9, machining parameters | Experimental invertigation |
| [40] | Dry CNC turning | 7075 Al composite, machining parameters | Experimental investigation |
| [41] | Helical milling | Al 7075 cutting forces | Multivariate optimization |
| [42] | Dry end milling | Weighted principal component analysis, Taguchi’s signal-to-noise ratio | Multi-objective optimization |
| [43] | Milling | Multiple response characteristics | Taguchi-Grey relational approach |
| [44] | End milling | Al/SiCp metal matrix composite, surface roughness | Predictive modeling |
| [45] | Milling | Aluminum, machining parameters | Taguchi-Grey approach |
| [46,47] | Milling, nano-fluids | Tool wear, residual stress | Experimental invertigation |
| Element | Al | Si | Mg | Fe | Cr | Cu | Mn | Zn | Others |
|---|---|---|---|---|---|---|---|---|---|
| % by weight | 97.63 | 0.30 | 1.10 | 0.07 | 0.10 | 0.20 | 0.20 | 0.25 | 0.15 |
| Factors | Symbols | Units | Levels | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| Spindle speed | S | rev/min | 1000 | 2000 | 3000 | 4000 |
| Feed rate | F | mm/min | 250 | 350 | 450 | 550 |
| Axial depth of cut | D | mm | 1 | 1.5 | 2 | 2.5 |
| Width of cut | W | mm | 2 | 6 | 10 | 14 |
| Cutting conditions | C | - | Dry | MQL | - | - |
| Exp. No. | Parameters | Responses | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | F | D | W | C | S | F | D | W | C | Ra (μm) | Rq (μm) | Rz (μm) | MRR (mm3/s) | Vb (mm) | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1000 | 250 | 1 | 2 | Dry | 1.55 | 3.16 | 4.51 | 450 | 152 |
| 2 | 1 | 2 | 2 | 2 | 1 | 1000 | 350 | 1.5 | 6 | Dry | 1.72 | 3.45 | 4.92 | 970 | 196 |
| 3 | 1 | 3 | 3 | 3 | 2 | 1000 | 450 | 2 | 10 | MQL | 1.98 | 3.98 | 5.69 | 1420 | 222 |
| 4 | 1 | 4 | 4 | 4 | 2 | 1000 | 550 | 2.5 | 14 | MQL | 2.35 | 4.38 | 6.25 | 2050 | 248 |
| 5 | 2 | 1 | 2 | 3 | 2 | 2000 | 250 | 1.5 | 10 | MQL | 1.53 | 3.07 | 4.39 | 1085 | 168 |
| 6 | 2 | 2 | 1 | 4 | 2 | 2000 | 350 | 1 | 14 | MQL | 1.64 | 3.28 | 4.69 | 1250 | 175 |
| 7 | 2 | 3 | 4 | 1 | 1 | 2000 | 450 | 2.5 | 2 | Dry | 1.92 | 3.88 | 5.52 | 1415 | 243 |
| 8 | 2 | 4 | 3 | 2 | 1 | 2000 | 550 | 2 | 6 | Dry | 2.13 | 4.26 | 6.09 | 1650 | 262 |
| 9 | 3 | 1 | 3 | 4 | 1 | 3000 | 250 | 2 | 14 | Dry | 1.6 | 3.22 | 4.61 | 1290 | 215 |
| 10 | 3 | 2 | 4 | 3 | 1 | 3000 | 350 | 2.5 | 10 | Dry | 1.89 | 3.78 | 5.41 | 1850 | 269 |
| 11 | 3 | 3 | 1 | 2 | 2 | 3000 | 450 | 1 | 6 | MQL | 1.82 | 3.62 | 5.18 | 1515 | 242 |
| 12 | 3 | 4 | 2 | 1 | 2 | 3000 | 550 | 1.5 | 2 | MQL | 1.86 | 3.68 | 5.27 | 1802 | 261 |
| 13 | 4 | 1 | 4 | 2 | 2 | 4000 | 250 | 2.5 | 6 | MQL | 1.45 | 2.62 | 3.75 | 1482 | 232 |
| 14 | 4 | 2 | 3 | 1 | 2 | 4000 | 350 | 2 | 2 | MQL | 1.61 | 3.12 | 4.48 | 1655 | 258 |
| 15 | 4 | 3 | 2 | 4 | 1 | 4000 | 450 | 1.5 | 14 | Dry | 1.92 | 3.88 | 5.55 | 2100 | 295 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | % Contribution | |
|---|---|---|---|---|---|---|---|
| Ra | S | 1 | 0.08 | 0.08 | 14.11 | 0.00 | 9.04 |
| F | 1 | 0.58 | 0.58 | 107.30 | 0.00 | 68.74 | |
| D | 1 | 0.09 | 0.09 | 16.23 | 0.00 | 10.40 | |
| W | 1 | 0.04 | 0.04 | 7.43 | 0.02 | 4.76 | |
| C | 1 | 0.01 | 0.01 | 1.03 | 0.33 | 0.66 | |
| Error | 10 | 0.05 | 0.01 | ||||
| Total | 15 | 0.85 | |||||
| Rq | S | 1 | 0.38 | 0.38 | 12.20 | 0.01 | 11.48 |
| F | 1 | 2.18 | 2.18 | 70.51 | 0.00 | 66.32 | |
| D | 1 | 0.16 | 0.16 | 5.11 | 0.05 | 4.81 | |
| W | 1 | 0.13 | 0.13 | 4.18 | 0.07 | 3.93 | |
| C | 1 | 0.13 | 0.13 | 4.30 | 0.07 | 4.04 | |
| Error | 10 | 0.31 | 0.03 | ||||
| Total | 15 | 3.29 | |||||
| Rz | S | 1 | 0.75 | 0.74 | 11.09 | 0.01 | 11.19 |
| F | 1 | 4.40 | 4.40 | 65.47 | 0.00 | 66.07 | |
| D | 1 | 0.33 | 0.33 | 4.88 | 0.05 | 4.92 | |
| W | 1 | 0.26 | 0.26 | 3.94 | 0.08 | 3.97 | |
| C | 1 | 0.25 | 0.25 | 3.72 | 0.08 | 3.75 | |
| Error | 10 | 0.67 | 0.07 | ||||
| Total | 15 | 6.66 | |||||
| MRR | S | 1 | 731,149 | 731,149 | 58.95 | 0.00 | 26.88 |
| F | 1 | 1,215,245 | 1,215,245 | 97.98 | 0.00 | 44.68 | |
| D | 1 | 345,056 | 345,056 | 27.82 | 0.00 | 12.69 | |
| W | 1 | 275,186 | 275,186 | 22.19 | 0.00 | 10.12 | |
| C | 1 | 29,241 | 29,241 | 2.36 | 0.16 | 1.08 | |
| Error | 10 | 124,029 | 12,403 | ||||
| Total | 15 | 2,719,906 | |||||
| Vb | S | 1 | 9159.20 | 9159.20 | 57.10 | 0.00 | 36.26 |
| F | 1 | 10,857.80 | 10,857.80 | 67.69 | 0.00 | 42.98 | |
| D | 1 | 3001.30 | 3001.30 | 18.71 | 0.00 | 11.88 | |
| W | 1 | 39.20 | 39.20 | 0.24 | 0.63 | 0.16 | |
| C | 1 | 600.30 | 600.30 | 3.74 | 0.08 | 2.38 | |
| Error | 10 | 1604.00 | 160.40 | ||||
| Total | 15 | 25,261.80 |
| Exp. No. | S/N Ratio of Responses | ||||
|---|---|---|---|---|---|
| Ra | Rq | Rz | MRR | Vb | |
| 1 | −3.81 | −9.99 | −13.08 | 53.06 | −43.64 * |
| 2 | −4.71 | −10.76 | −13.84 | 59.74 | −45.85 |
| 3 | −5.93 | −12.00 | −15.10 | 63.05 | −46.93 |
| 4 | −7.42 | −12.83 | −15.92 | 66.24 | −47.89 |
| 5 | −3.69 | −9.74 | −12.85 | 60.71 | −44.51 |
| 6 | −4.30 | −10.32 | −13.42 | 61.94 | −44.86 |
| 7 | −5.67 | −11.78 | −14.84 | 63.02 | −47.71 |
| 8 | −6.57 | −12.59 | −15.69 | 64.35 | −48.37 |
| 9 | −4.08 | −10.16 | −13.27 | 62.21 | −46.65 |
| 10 | −5.53 | −11.55 | −14.66 | 65.34 | −48.60 |
| 11 | −5.20 | −11.17 | −14.29 | 63.61 | −47.68 |
| 12 | −5.39 | −11.32 | −14.44 | 65.12 | −48.33 |
| 13 | −3.23 * | −8.37 * | −11.48 * | 63.42 | −47.31 |
| 14 | −4.14 | −9.88 | −13.03 | 64.38 | −48.23 |
| 15 | −5.67 | −11.78 | −14.89 | 66.44 * | −49.40 |
| 16 | −5.15 | −11.08 | −14.13 | 65.34 | −48.69 |
| Optimum | S4F1D4W2C2 | S4F1D4W2 C2 | S4F1D4W2 C2 | S4F3D2W4C1 | S1F1D1W1 C1 |
| Exp. No. | Composite Desirability Values | ||||
|---|---|---|---|---|---|
| Ra | Rq | Rz | MRR | Vb | |
| 1 | 0.889 | 0.693 | 0.696 | 0.000 | 1.000 |
| 2 | 0.700 | 0.528 | 0.532 | 0.315 | 0.692 |
| 3 | 0.411 | 0.227 | 0.224 | 0.588 | 0.510 |
| 4 | 0.000 | 0.000 | 0.000 | 0.970 | 0.329 |
| 5 | 0.911 | 0.744 | 0.744 | 0.385 | 0.888 |
| 6 | 0.789 | 0.625 | 0.624 | 0.485 | 0.839 |
| 7 | 0.478 | 0.284 | 0.292 | 0.585 | 0.364 |
| 8 | 0.244 | 0.068 | 0.064 | 0.727 | 0.231 |
| 9 | 0.833 | 0.659 | 0.656 | 0.509 | 0.559 |
| 10 | 0.511 | 0.341 | 0.336 | 0.848 | 0.182 |
| 11 | 0.589 | 0.432 | 0.428 | 0.645 | 0.371 |
| 12 | 0.544 | 0.398 | 0.392 | 0.819 | 0.238 |
| 13 | 1.000 | 1.000 | 1.000 | 0.625 | 0.441 |
| 14 | 0.822 | 0.716 | 0.708 | 0.730 | 0.259 |
| 15 | 0.478 | 0.284 | 0.280 | 1.000 | 0.000 |
| 16 | 0.600 | 0.455 | 0.464 | 0.848 | 0.161 |
| Component | PC 1 | PC 2 | PC 3 | PC 4 | PC 5 |
|---|---|---|---|---|---|
| Eigenvalue | 3.852 | 1.027 | 0.0993 | 0.0216 | 0.0001 |
| Variation (%) | 0.77 | 0.205 | 0.02 | 0.004 | 0 |
| Cumulative (%) | 0.77 | 0.976 | 0.996 | 1 | 1 |
| Eigenvector | 0.484 | −0.271 | −0.281 | 0.783 | −0.013 |
| 0.475 | −0.351 | 0.155 | −0.347 | 0.712 | |
| 0.476 | −0.346 | 0.149 | −0.372 | −0.702 | |
| −0.404 | −0.564 | 0.659 | 0.291 | −0.01 | |
| 0.388 | 0.605 | 0.664 | 0.207 | −0.004 |
| Response Variable | Contribution |
|---|---|
| Ra | 0.2343 |
| Rq | 0.2256 |
| Rz | 0.2266 |
| MRR | 0.1632 |
| Vb | 0.1505 |
| Exp. No. | Weighted Composite Desirability Values | Overall Desirability () | Rank | ||||
|---|---|---|---|---|---|---|---|
| Ra | Rq | Rz | MRR | Vb | |||
| 1 | 0.97 | 0.92 | 0.92 | 0.00 | 1.00 | 0.0000 | 14 |
| 2 | 0.92 | 0.87 | 0.87 | 0.83 | 0.95 | 0.5402 | 6 |
| 3 | 0.81 | 0.72 | 0.71 | 0.92 | 0.90 | 0.3443 | 12 |
| 4 | 0.00 | 0.00 | 0.00 | 0.99 | 0.85 | 0.0000 | 14 |
| 5 | 0.98 | 0.94 | 0.94 | 0.86 | 0.98 | 0.7196 | 2 |
| 6 | 0.95 | 0.90 | 0.90 | 0.89 | 0.97 | 0.6619 | 3 |
| 7 | 0.84 | 0.75 | 0.76 | 0.92 | 0.86 | 0.3746 | 11 |
| 8 | 0.72 | 0.55 | 0.54 | 0.95 | 0.80 | 0.1625 | 13 |
| 9 | 0.96 | 0.91 | 0.91 | 0.90 | 0.92 | 0.6513 | 4 |
| 10 | 0.85 | 0.78 | 0.78 | 0.97 | 0.77 | 0.3956 | 10 |
| 11 | 0.88 | 0.83 | 0.83 | 0.93 | 0.86 | 0.4845 | 7 |
| 12 | 0.87 | 0.81 | 0.81 | 0.97 | 0.81 | 0.4457 | 9 |
| 13 | 1.00 | 1.00 | 1.00 | 0.93 | 0.88 | 0.8187 | 1 |
| 14 | 0.96 | 0.93 | 0.92 | 0.95 | 0.82 | 0.6365 | 5 |
| 15 | 0.84 | 0.75 | 0.75 | 1.00 | 0.00 | 0.0000 | 14 |
| 16 | 0.89 | 0.84 | 0.84 | 0.97 | 0.76 | 0.4593 | 8 |
| Cutting Parameters | Mean of | Delta | Rank | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| Cutting speed | 0.221 | 0.480 | 0.494 * | 0.478 | 0.2731 | 2 |
| Feed rate | 0.547 | 0.558 * | 0.301 | 0.269 | 0.2917 | 1 |
| Depth of cut | 0.401 | 0.426 | 0.448 * | 0.397 | 0.0514 | 5 |
| Width of Cut | 0.364 | 0.501 * | 0.479 | 0.328 | 0.1732 | 4 |
| Cutting conditions | 0.329 | 0.513 * | - | - | 0.1910 | 3 |
| Responses | Initial Condition S2F3D4W1C1 | PCA-CDF | % Improvement from Initial Condition |
|---|---|---|---|
| Ra | 1.92 | 1.51 | 21 |
| Rq | 3.88 | 3.02 | 23 |
| Rz | 5.52 | 4.52 | 18 |
| MRR | 1415 | 1851 | 30 |
| Vb | 243 | 198 | 22 |
| Optimal Condition | - | S3F2D3W2C2 | - |
| 0.375 | 0.460 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qazi, M.I.; Abas, M.; Khan, R.; Saleem, W.; Pruncu, C.I.; Omair, M. Experimental Investigation and Multi-Response Optimization of Machinability of AA5005H34 Using Composite Desirability Coupled with PCA. Metals 2021, 11, 235. https://doi.org/10.3390/met11020235
Qazi MI, Abas M, Khan R, Saleem W, Pruncu CI, Omair M. Experimental Investigation and Multi-Response Optimization of Machinability of AA5005H34 Using Composite Desirability Coupled with PCA. Metals. 2021; 11(2):235. https://doi.org/10.3390/met11020235
Chicago/Turabian StyleQazi, Mohsin Iqbal, Muhammad Abas, Razaullah Khan, Waqas Saleem, Catalin Iulian Pruncu, and Muhammad Omair. 2021. "Experimental Investigation and Multi-Response Optimization of Machinability of AA5005H34 Using Composite Desirability Coupled with PCA" Metals 11, no. 2: 235. https://doi.org/10.3390/met11020235
APA StyleQazi, M. I., Abas, M., Khan, R., Saleem, W., Pruncu, C. I., & Omair, M. (2021). Experimental Investigation and Multi-Response Optimization of Machinability of AA5005H34 Using Composite Desirability Coupled with PCA. Metals, 11(2), 235. https://doi.org/10.3390/met11020235










