Earing Reduction by Varying Blank Holding Force in Deep Drawing with Deep Neural Network
Abstract
:1. Introduction
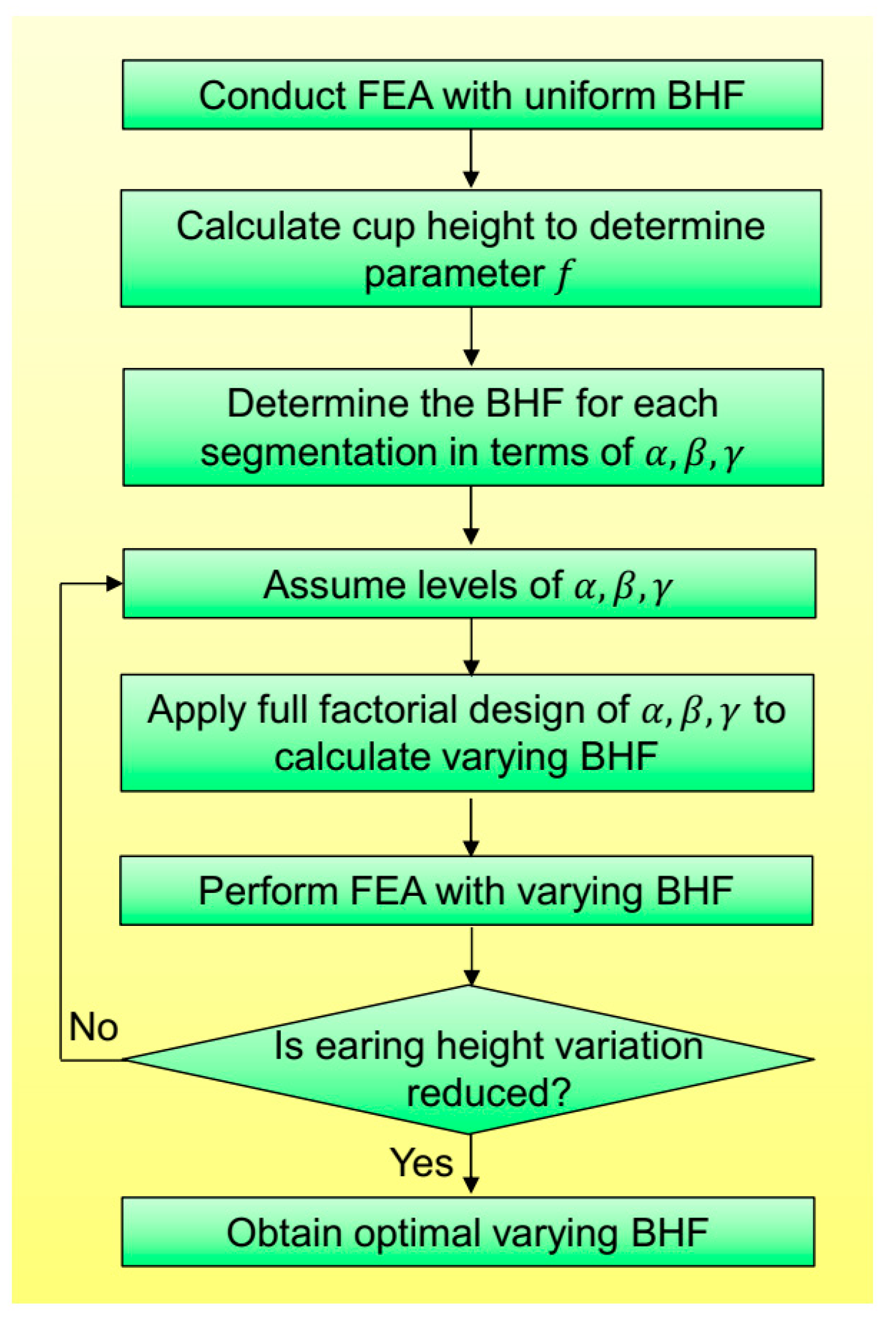
2. Analytical Theory for Determination of Varying Blank Holding Force (BHF)
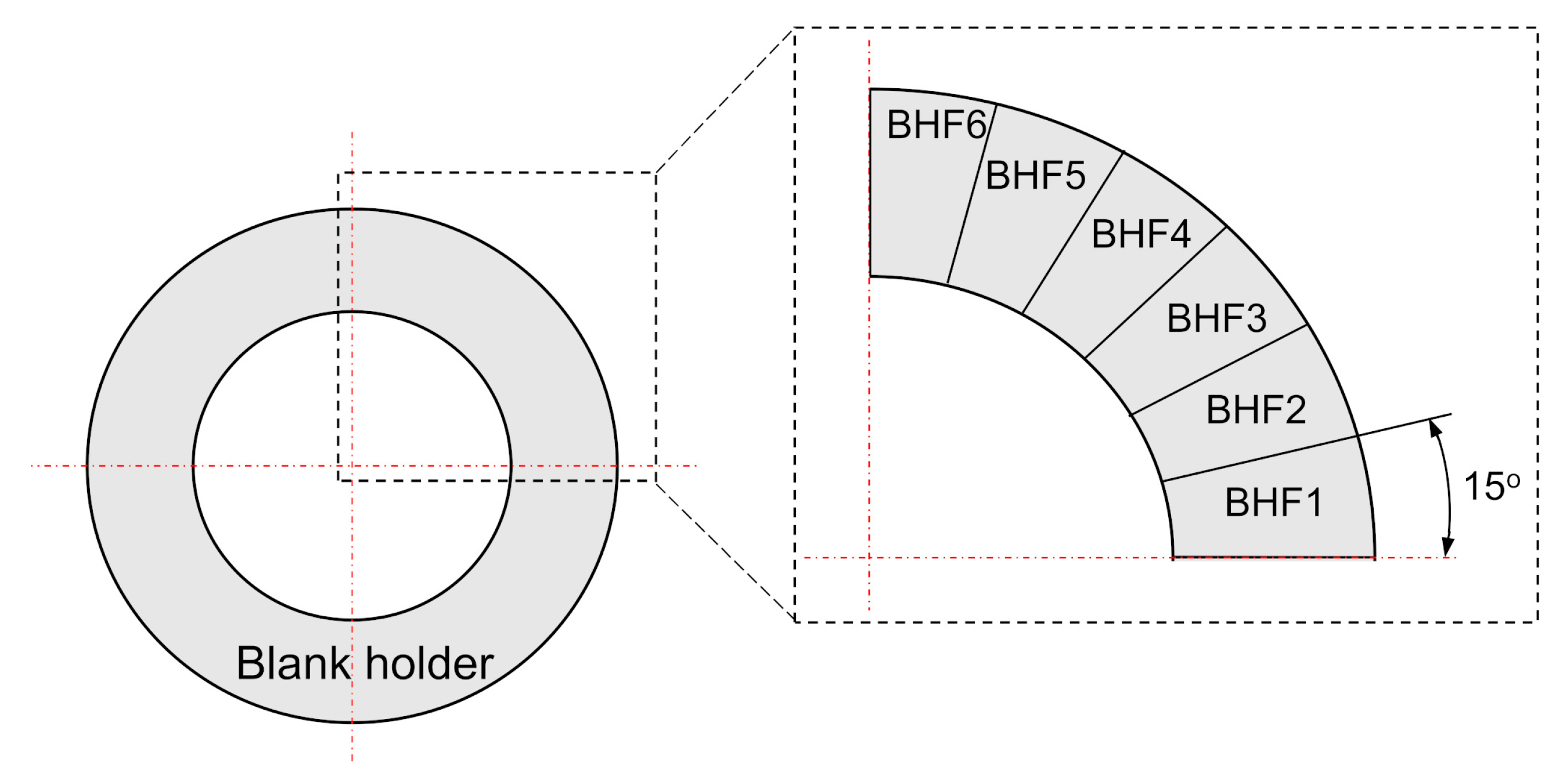
2.1. Design of Segmental Blank Holder
2.2. Analytical Model for Varying Blank Holding Force (BHF) with Segmental Blank Holder
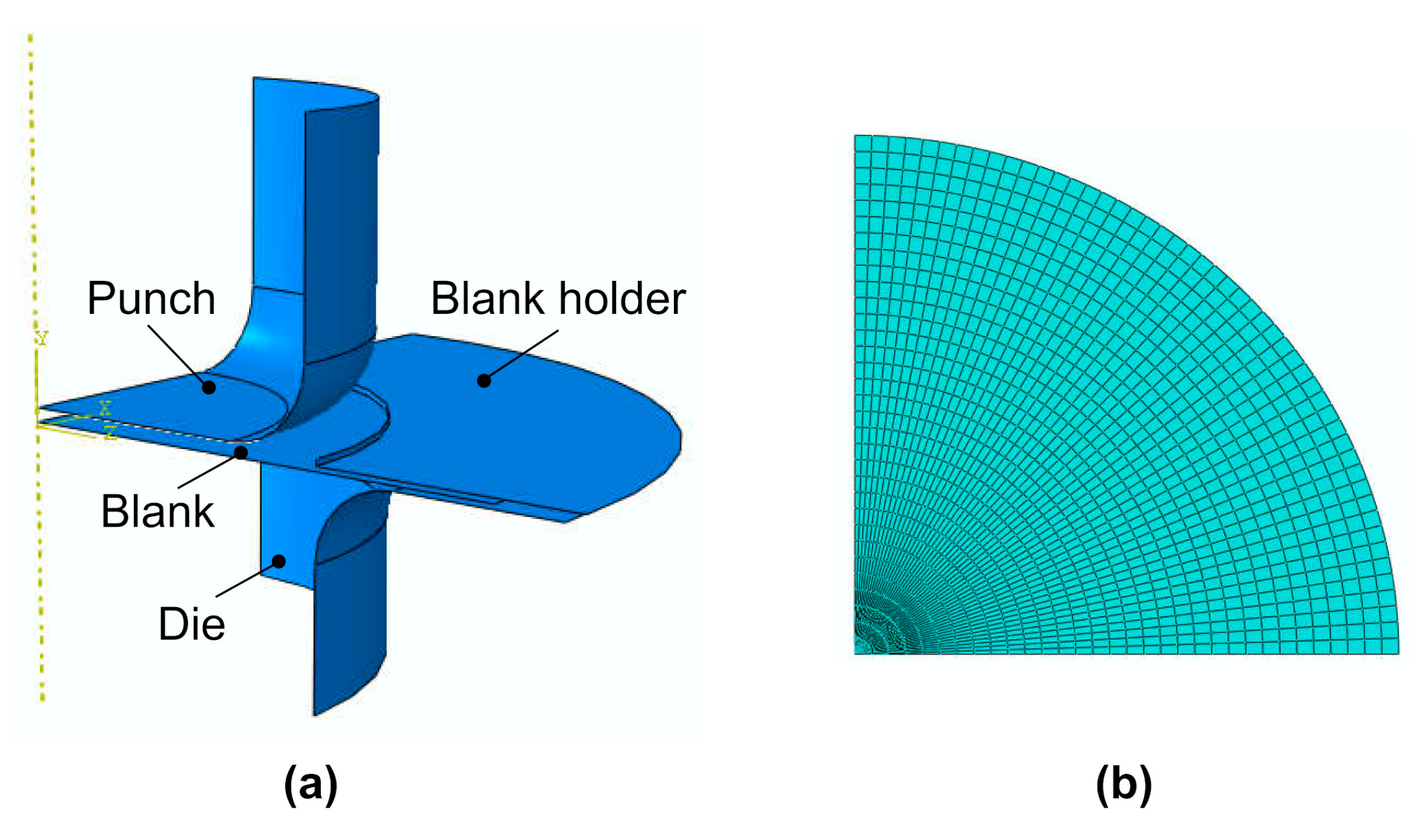
2.3. Finite Element Simulation of Deep Drawing
3. Integration of Deep Neural Network (DNN) with Genetic Algorithm (GA) for Optimization of Varying BHF
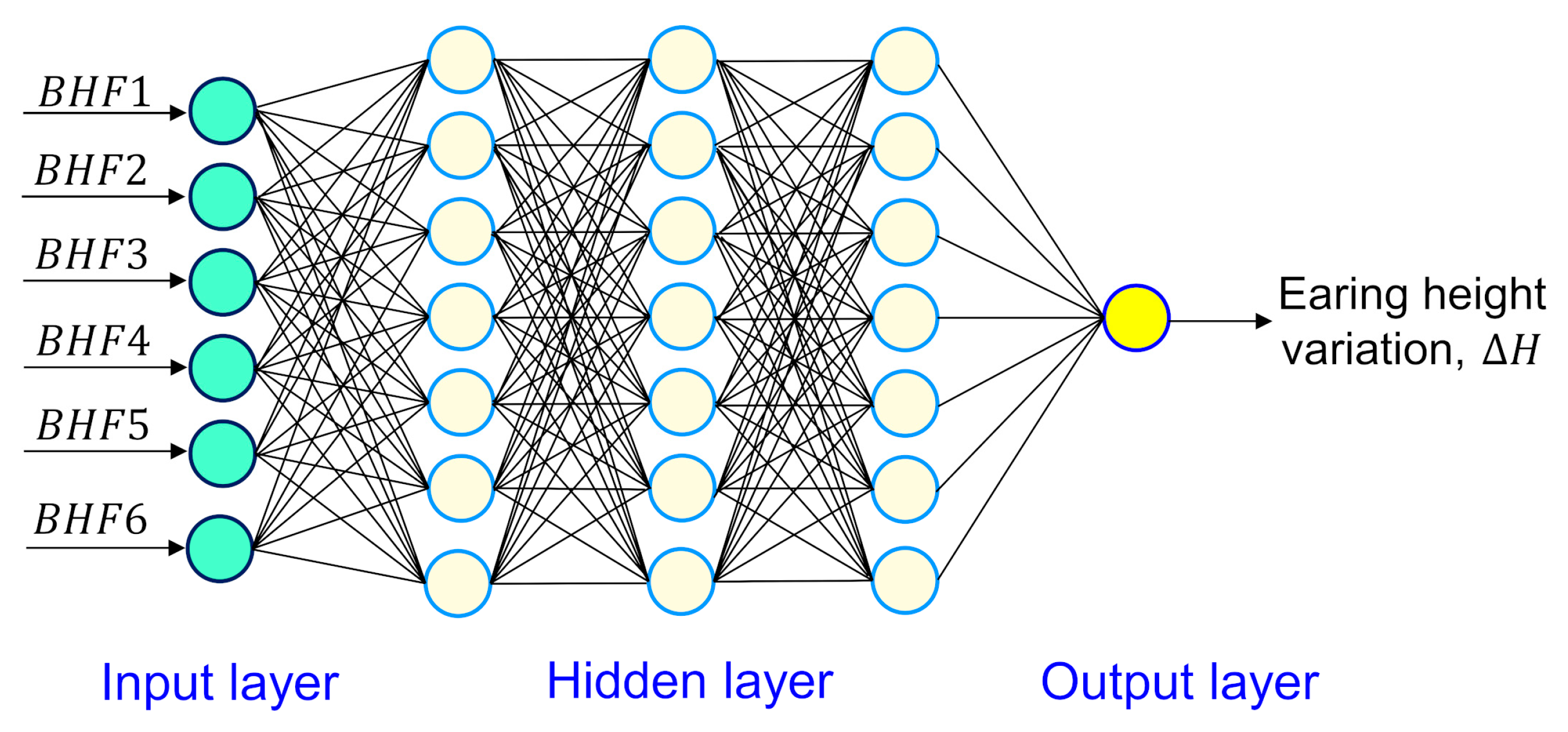
3.1. Deep Neural Network (DNN) Model
3.2. DNN-Genetic Algorithm (GA) Optimization Model
4. Results
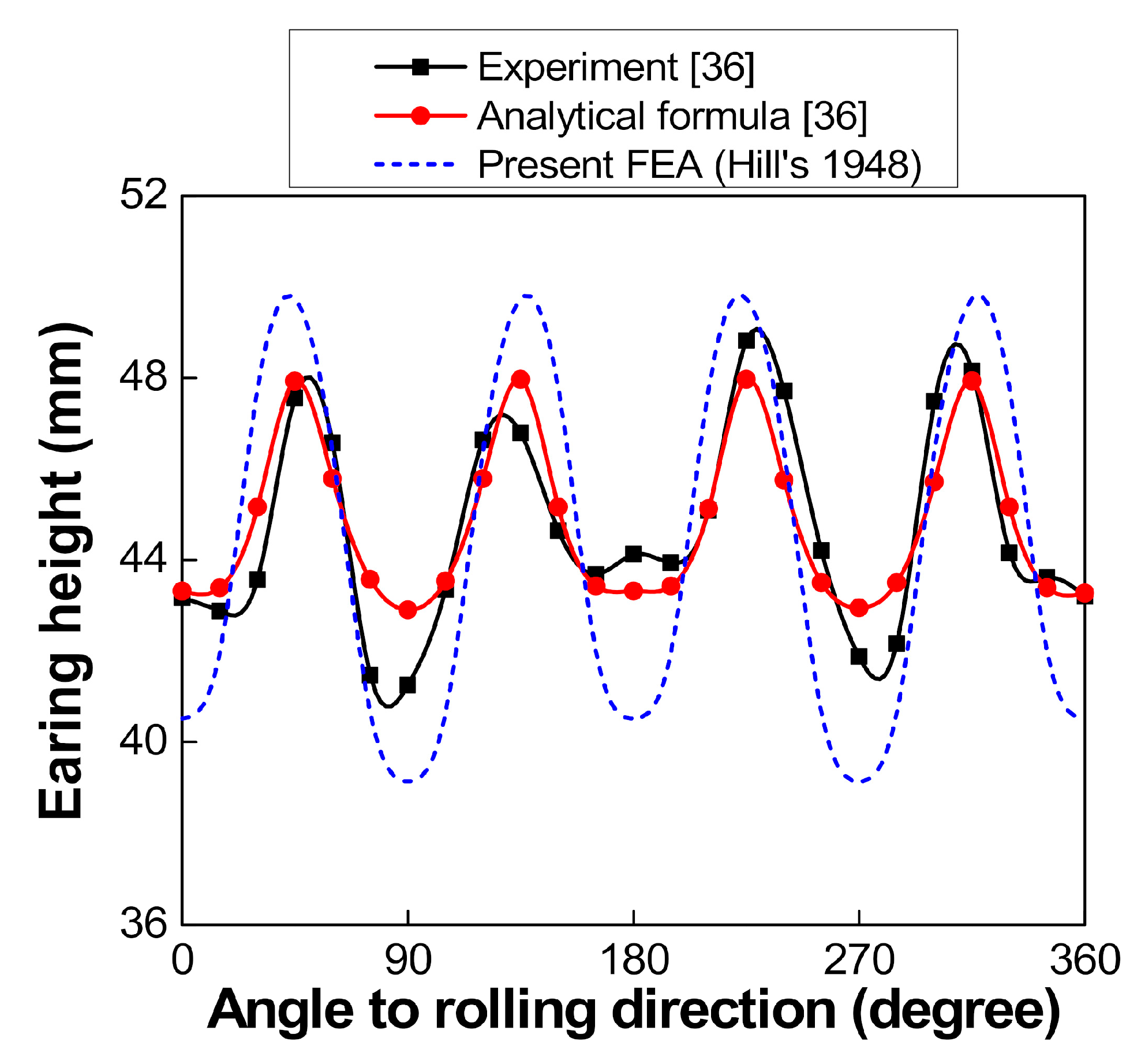
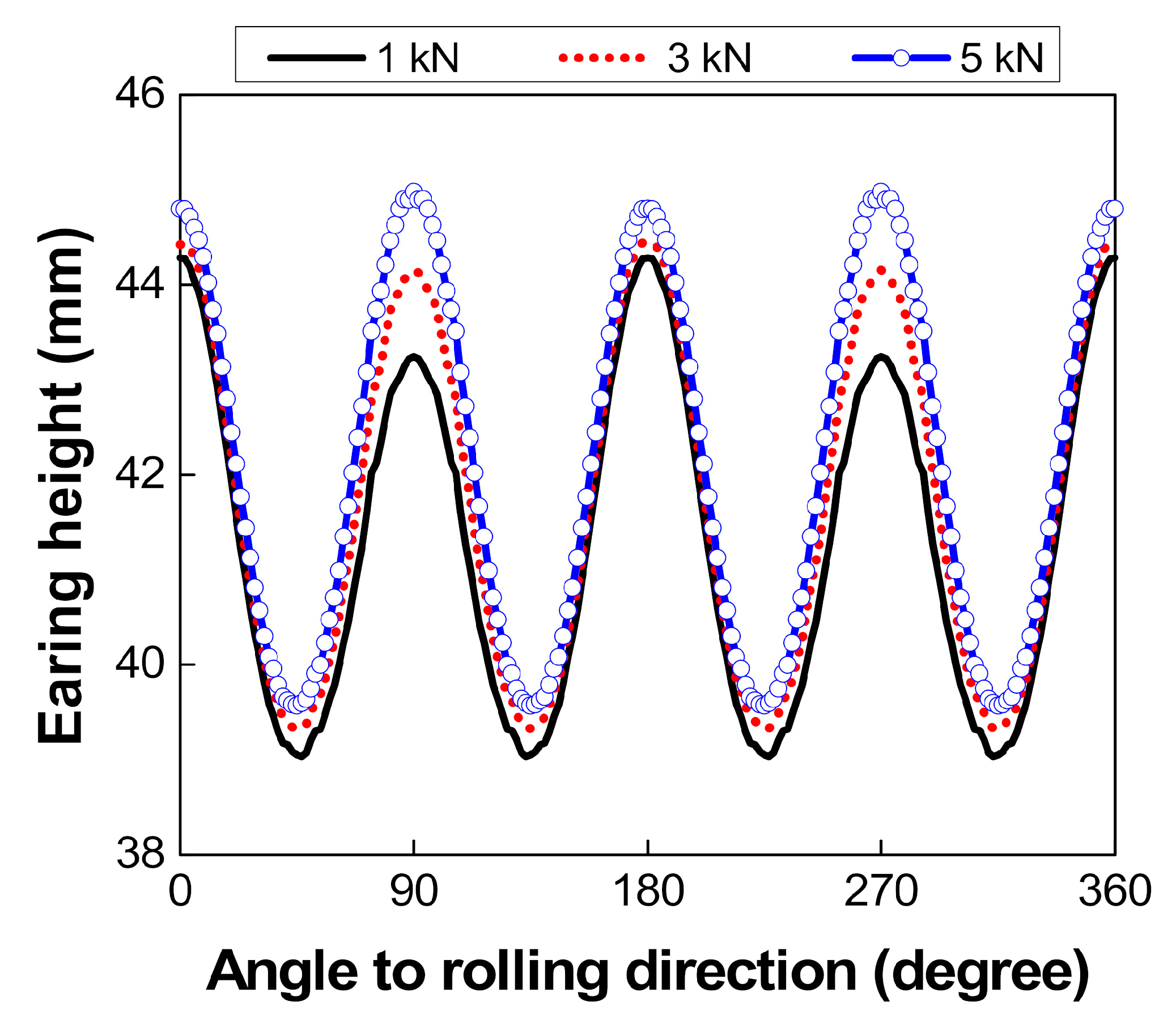
4.1. Verification of the Present Finite Element Analysis (FEA)
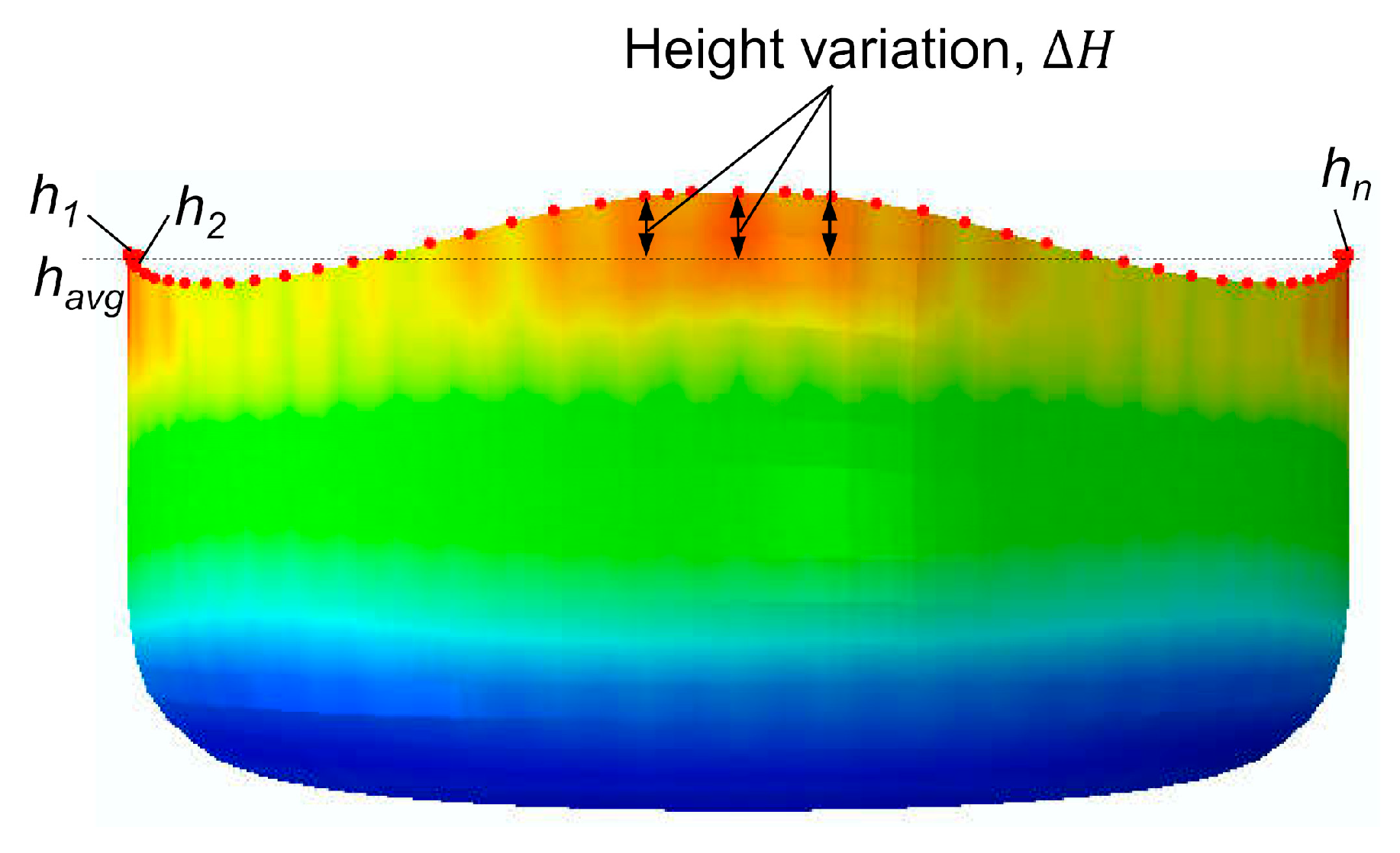
4.2. Prediction of Earing by Using the Uniform BHF
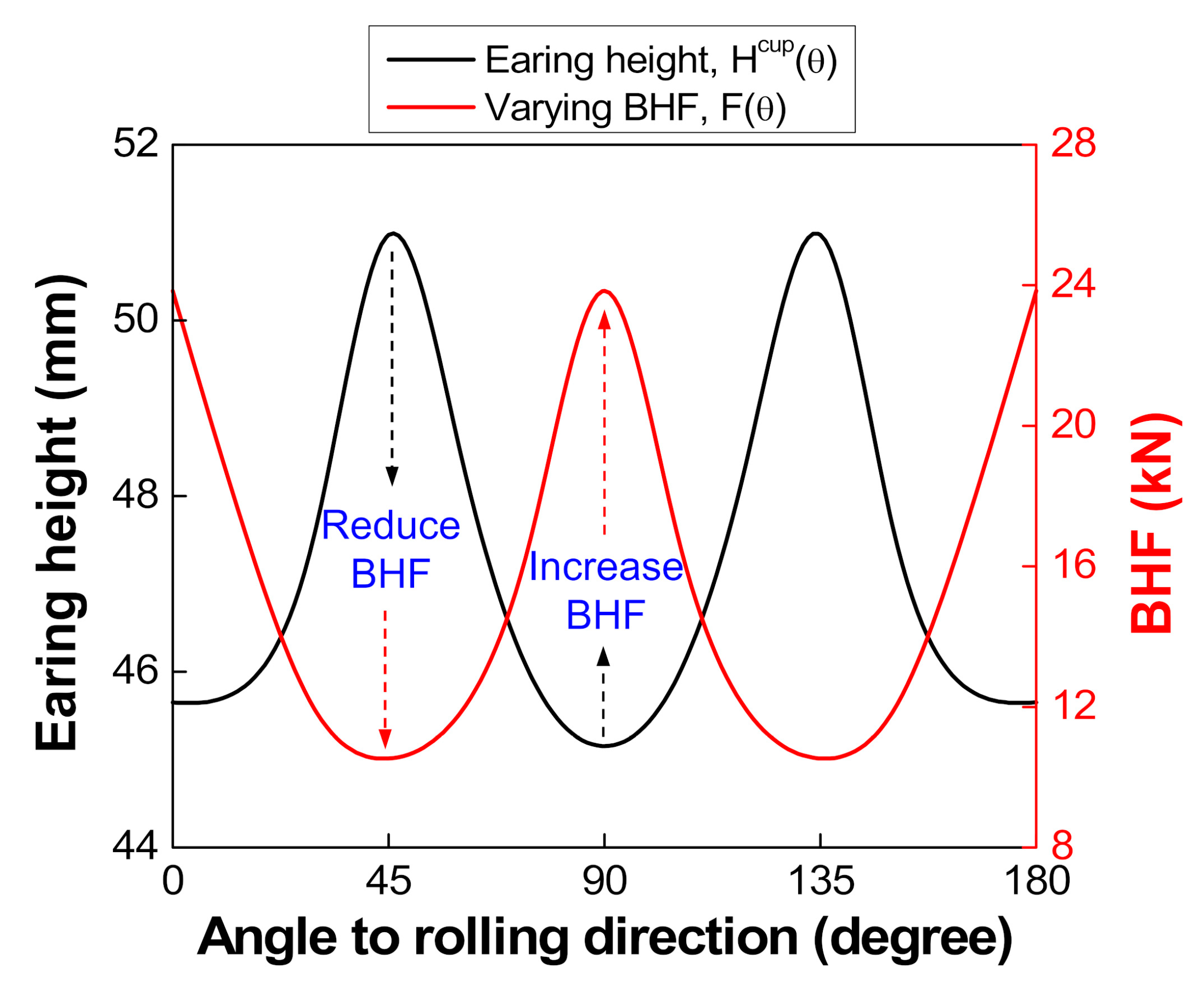
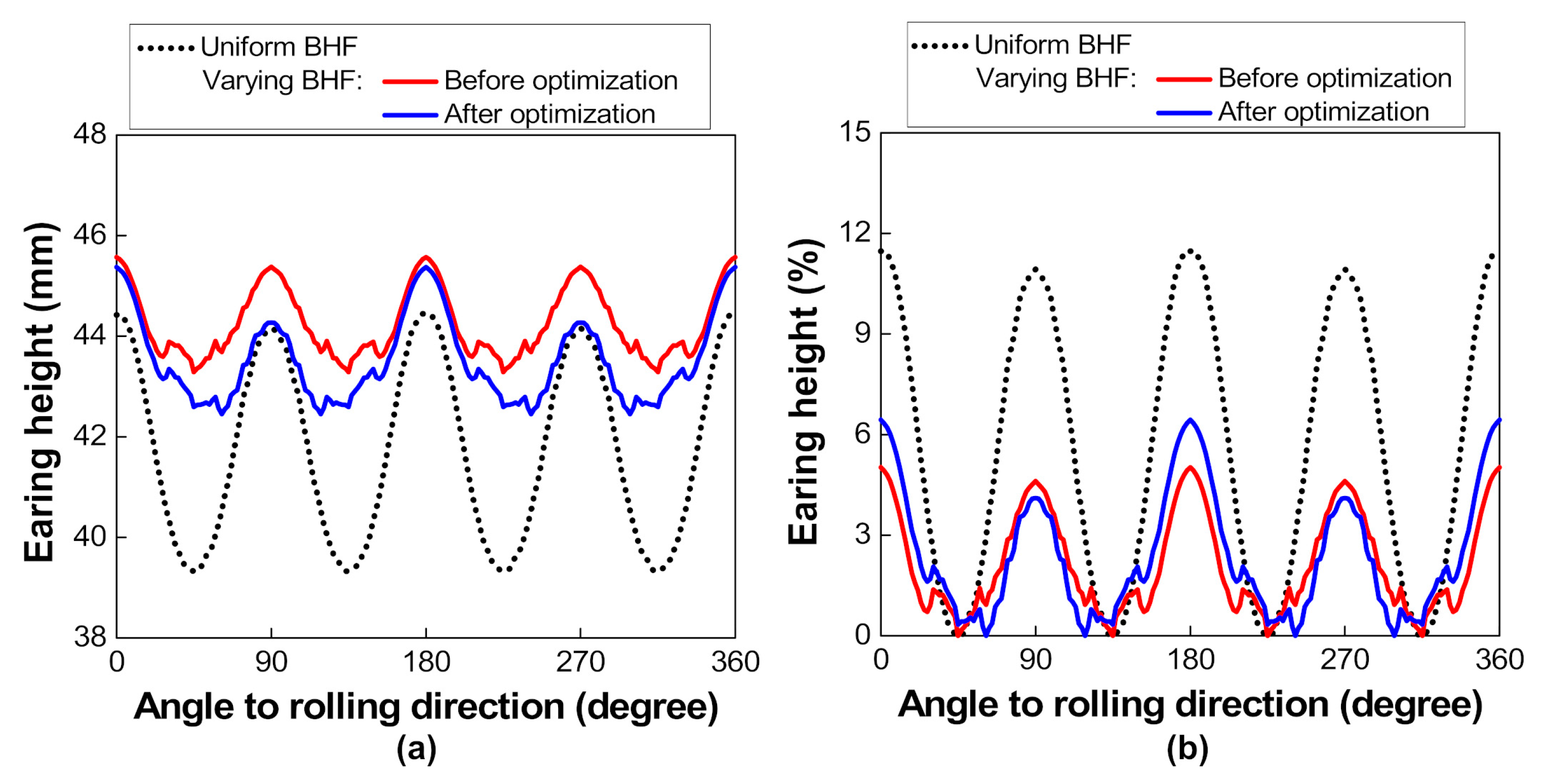
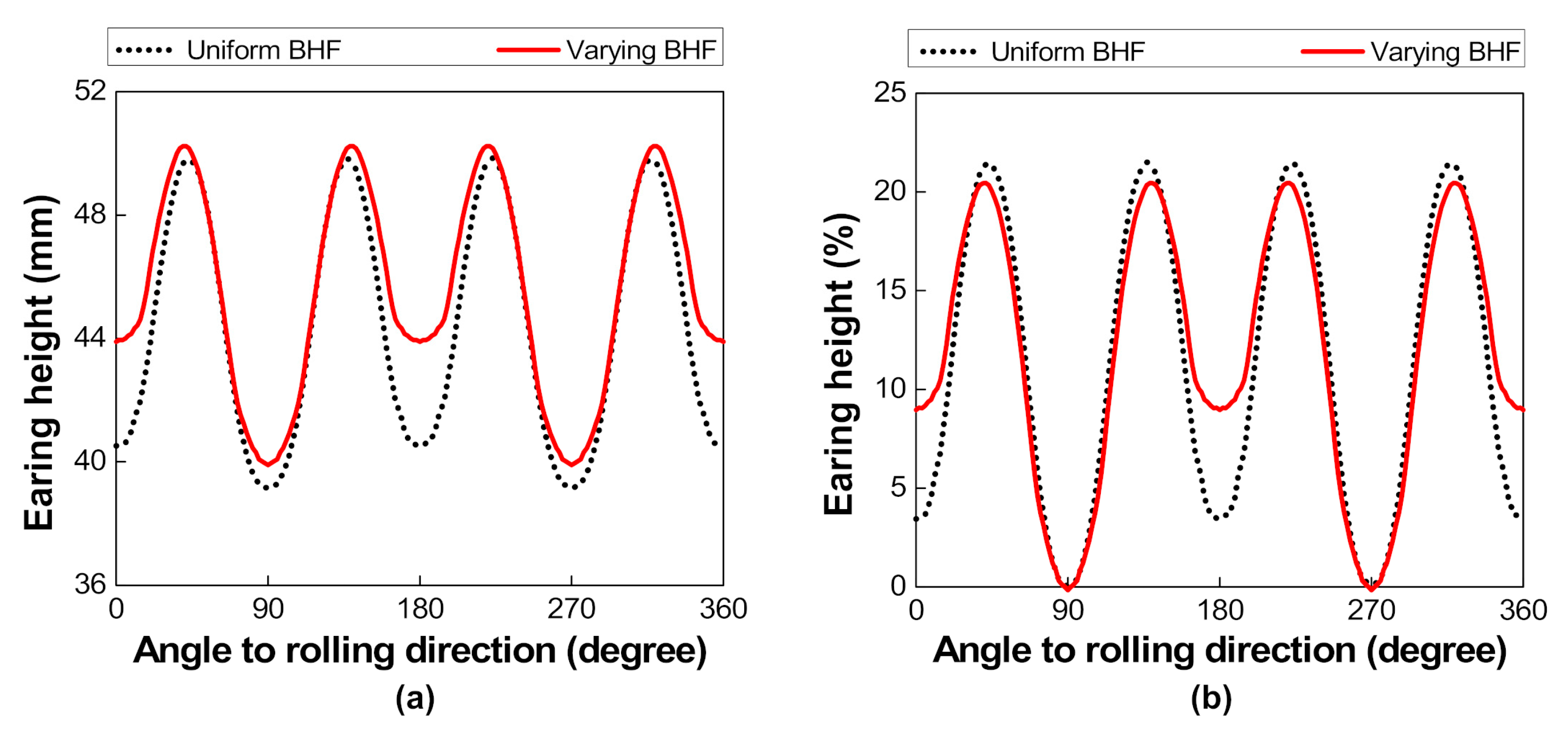
4.3. Effect of Varying BHF on Earing Reduction
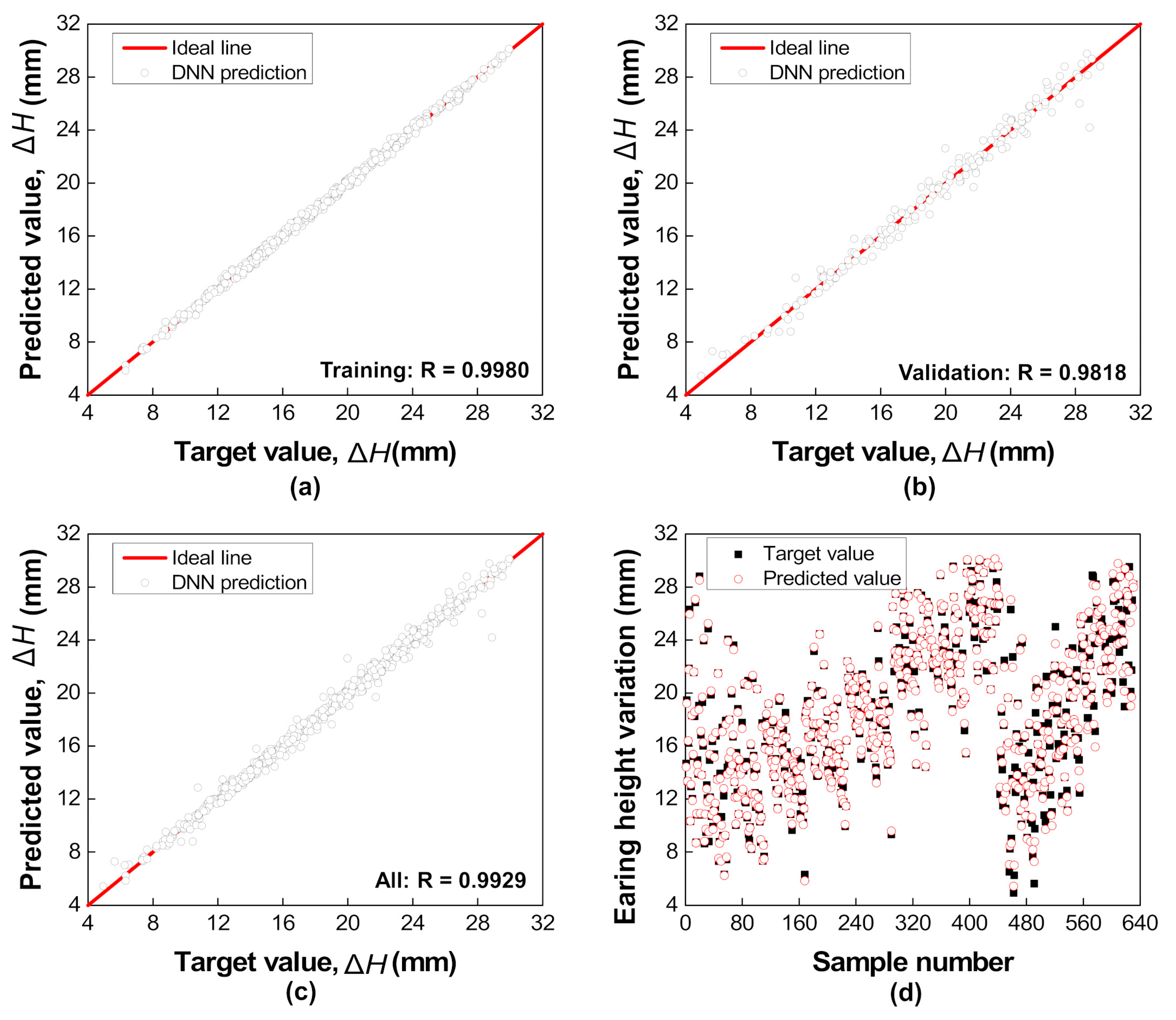
4.4. Prediction of Earing Height Variation by the DNN Model
4.5. Optimization of Varying BHF with Integrated DNN-GA Model
5. Discussion
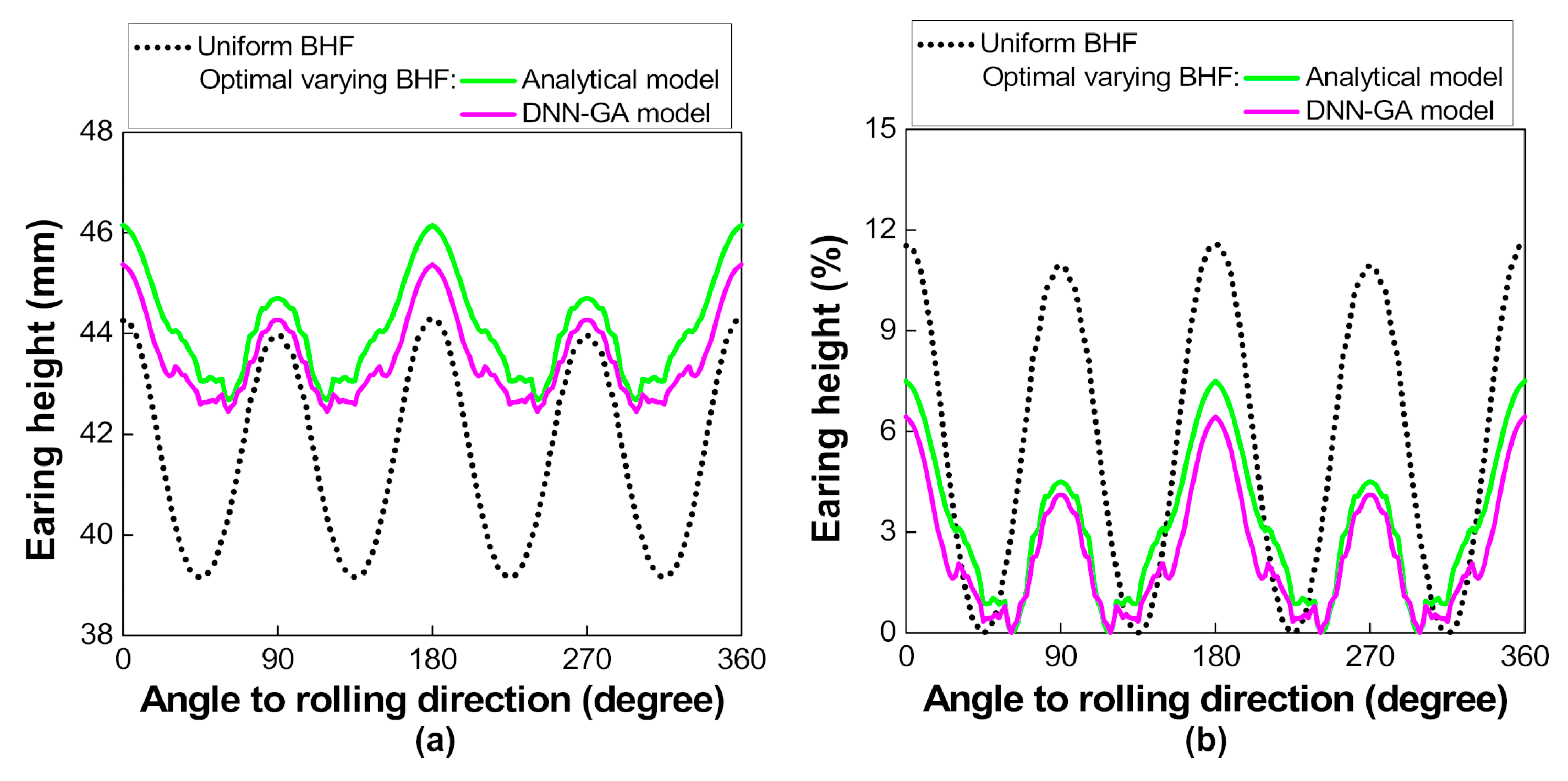
5.1. Comparison of Analytical and DNN-GA Models
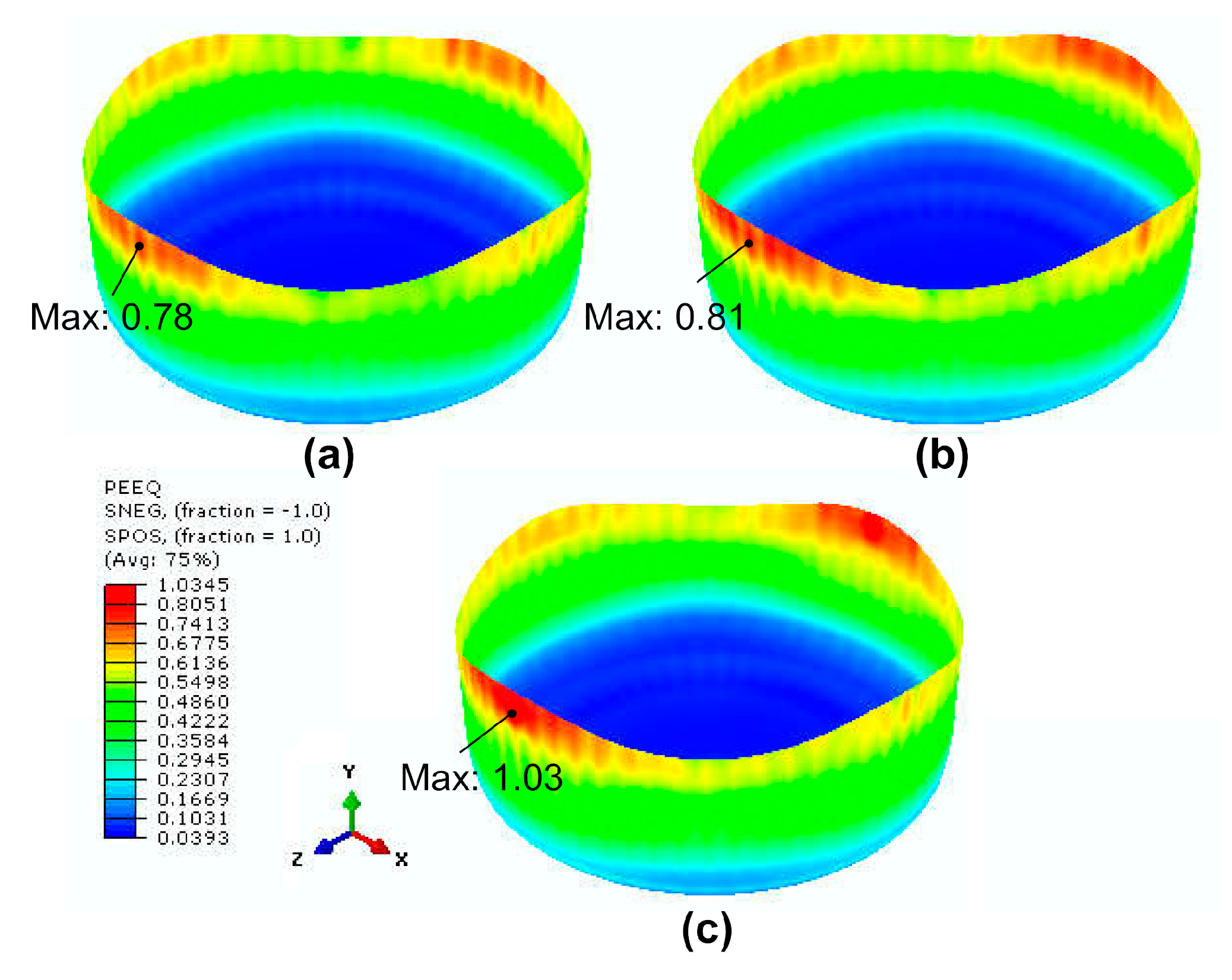
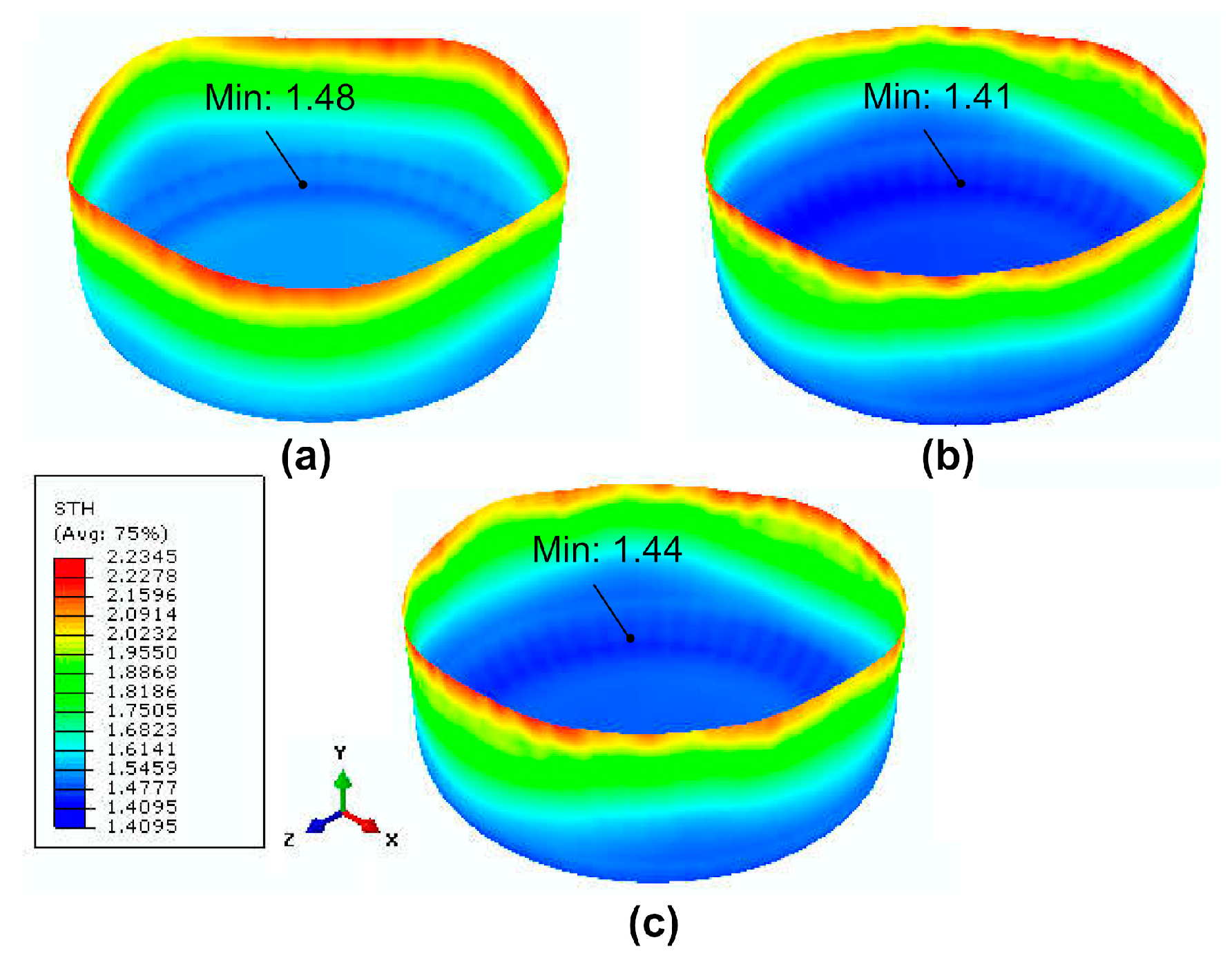
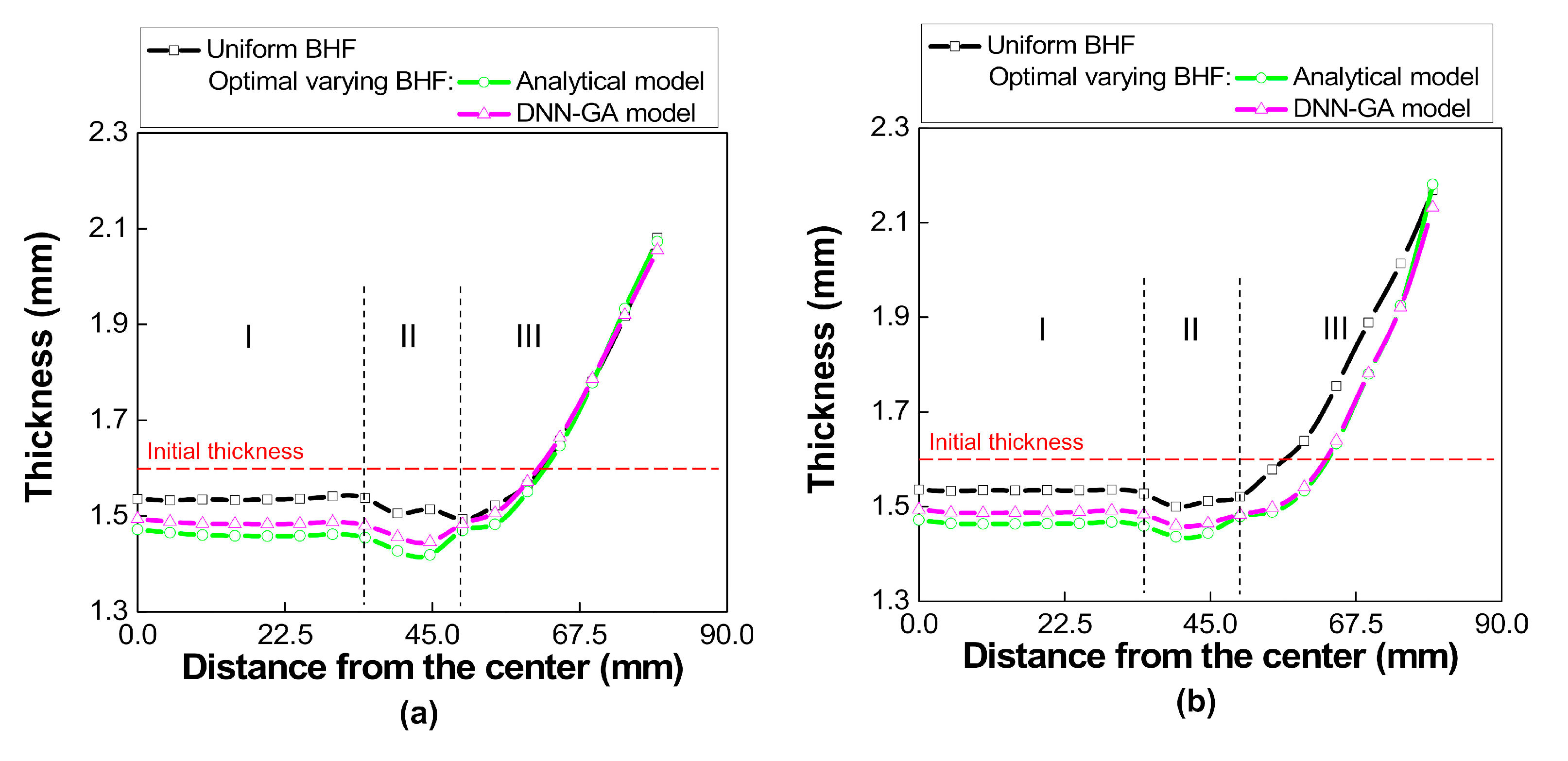
5.2. Thickness Variation in Different Directions
5.3. Effect of the Material Properties on Earing Reduction
6. Conclusions
- (i)
- With an interval holder-segment angle of 15°, the different varying BHFs obtained by the analytical model resulted in the different influences on earing reduction. The noticeable decrease of earing height variation by ~45% was revealed by the optimal varying BHF, indicating a more reasonable technique with varying BHF than the uniform BHF for earing reduction in deep drawing.
- (ii)
- The developed deep neural network (DNN) model with the integration of genetic algorithm (GA) revealed the optimization of varying BHF with a considerable reduction in earing height by ~52%, which showed a superior result to the analytical model. This confirmed that the proposed DNN-GA model effectively predicted and optimized the process parameters in this study.
- (iii)
- For a volume consistency, the non-uniform thickness distribution was observed with an increase of thickness in the transverse direction at the cup wall region by varying BHF, which indicated an improvement in deep-drawability. Although BHF of a segmental holder was held constant in the present study, the time dependence of the BHF seems to be important for further study.
- (iv)
- Furthermore, the present study revealed that, due to the effect of material properties on earing formation, the lower the material strength, the greater the effect on the earing reduction in deep drawing with the varying BHF will be.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Benke, M.; Schweitzer, B.; Hlavacs, A.; Mertinger, V. Prediction of Earing of Cross-Rolled Al Sheets from {h00} Pole Figures. Metals 2020, 10, 192. [Google Scholar] [CrossRef] [Green Version]
- Engler, O.; Knarbakk, K. Temper rolling to control texture and earing in aluminium alloy AA 5050A. J. Mater. Process. Technol. 2021, 288, 116910. [Google Scholar] [CrossRef]
- Guo, N.; Wang, J.; Sun, C.; Zhang, Y.; Fu, M. Analysis of size dependent earing evolution in micro deep drawing of TWIP steel by using crystal plasticity modeling. Int. J. Mech. Sci. 2020, 165, 105200. [Google Scholar] [CrossRef]
- Hlavacs, A.; Szucs, M.; Mertinger, V.; Benke, M. Prediction of Earing of Hot-Rolled Al Sheets from Pole Figures. Metals 2021, 11, 99. [Google Scholar] [CrossRef]
- Kishor, N.; Kumar, D.R. Optimization of initial blank shape to minimize earing in deep drawing using finite element method. J. Mater. Process. Technol. 2002, 130, 20–30. [Google Scholar] [CrossRef]
- Singh, A.; Basak, S.; PS, L.P.; Roy, G.G.; Jha, M.N.; Mascarenhas, M.; Panda, S.K. Prediction of earing defect and deep drawing behavior of commercially pure titanium sheets using CPB06 anisotropy yield theory. J. Manuf. Process. 2018, 33, 256–267. [Google Scholar] [CrossRef]
- Aretz, H.; Engler, O. Accuracy analysis of earing compensation procedures. Int. J. Solids Struct. 2020, 191–192, 418–433. [Google Scholar] [CrossRef]
- Jankree, R.; Thipprakmas, S. Achievements of Nearly Zero Earing Defects on SPCC Cylindrical Drawn Cup Using Multi Draw Radius Die. Metals 2020, 10, 1204. [Google Scholar] [CrossRef]
- Zhao, Z.; Mao, W.; Roters, F.; Raabe, D. A texture optimization study for minimum earing in aluminium by use of a texture component crystal plasticity finite element method. Acta Mater. 2004, 52, 1003–1012. [Google Scholar] [CrossRef]
- Engler, O.; Aegerter, J.; Calmer, D. Control of texture and earing in aluminium alloy AA 8011A-H14 closure stock. Mater. Sci. Eng. A 2020, 775, 775. [Google Scholar] [CrossRef]
- Vahdat, V.; Santhanam, S.; Chun, Y.W. A numerical investigation on the use of drawbeads to minimize ear formation in deep drawing. J. Mater. Process. Technol. 2006, 176, 70–76. [Google Scholar] [CrossRef]
- Feng, Y.; Hong, Z.; Gao, Y.; Lu, R.; Wang, Y.; Tan, J. Optimization of variable blank holder force in deep drawing based on support vector regression model and trust region. Int. J. Adv. Manuf. Technol. 2019, 105, 4265–4278. [Google Scholar] [CrossRef]
- Kitayama, S.; Koyama, H.; Kawamoto, K.; Miyasaka, T.; Yamamichi, K.; Noda, T. Optimization of blank shape and segmented variable blank holder force trajectories in deep drawing using sequential approximate optimization. Int. J. Adv. Manuf. Technol. 2016, 91, 1809–1821. [Google Scholar] [CrossRef]
- Zhong-Qin, L.; Wu-Rong, W.; Guan-Long, C. A new strategy to optimize variable blank holder force towards improving the forming limits of aluminum sheet metal forming. J. Mater. Process. Technol. 2007, 183, 339–346. [Google Scholar] [CrossRef]
- Demirci, H.I.; Esner, C.; Yasar, M. Effect of the blank holder force on drawing of aluminum alloy square cup: Theoretical and experimental investigation. J. Mater. Process. Technol. 2008, 206, 152–160. [Google Scholar] [CrossRef]
- Van, T.P.; Jöchen, K.; Böhlke, T. Simulation of sheet metal forming incorporating EBSD data. J. Mater. Process. Technol. 2012, 212, 2659–2668. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, S.; Cao, L.; Meng, L.; Zhang, Q.; Li, C. Research on Deep Drawing Process Using Radial Segmental Blank Holder based on Electro-permanent Magnet Technology. J. Manuf. Process. 2020, 59, 636–648. [Google Scholar] [CrossRef]
- Hassan, M.; Takakura, N.; Yamaguchi, K. Friction aided deep drawing using newly developed blank-holder divided into eight segments. Int. J. Mach. Tools Manuf. 2003, 43, 637–646. [Google Scholar] [CrossRef]
- Han, J.; Yamazaki, K.; Makino, S.; Shirasawa, T. Optimization of Deep Drawing Process for Circular Cup Forming. In Proceedings of the 10th World Congress on Structural and Multidisciplinary Optimization, Orlando, FL, USA, 19–24 May 2013. [Google Scholar]
- Kim, D.-K.; Kim, J.-M.; Park, W.-W.; Lee, H.W.; Im, Y.-T.; Lee, Y.-S. Three-dimensional crystal plasticity finite element analysis of microstructure and texture evolution during channel die compression of IF steel. Comput. Mater. Sci. 2015, 100, 52–60. [Google Scholar] [CrossRef]
- Neto, D.; Oliveira, M.; Santos, A.; Alves, J.; Menezes, L. Influence of boundary conditions on the prediction of springback and wrinkling in sheet metal forming. Int. J. Mech. Sci. 2017, 122, 244–254. [Google Scholar] [CrossRef] [Green Version]
- Irthiea, I. Experimental and numerical evaluation of micro flexible deep drawing technique using floating ring. J. Manuf. Process. 2019, 38, 556–563. [Google Scholar] [CrossRef]
- Türköz, M.; Cora Ömer, N.; Gedikli, H.; Dilmeç, M.; Halkacı, H.S.; Koç, M. Numerical optimization of warm hydromechanical deep drawing process parameters and its experimental verification. J. Manuf. Process. 2020, 57, 344–353. [Google Scholar] [CrossRef]
- Correia, J.D.M.; Ferron, G.; Moreira, L. Analytical and numerical investigation of wrinkling for deep-drawn anisotropic metal sheets. Int. J. Mech. Sci. 2003, 45, 1167–1180. [Google Scholar] [CrossRef]
- Saxena, R.K.; Dixit, P. Prediction of flange wrinkling in deep drawing process using bifurcation criterion. J. Manuf. Process. 2010, 12, 19–29. [Google Scholar] [CrossRef]
- Shi, Y.; Jin, H.; Wu, P. Analysis of cup earing for AA3104-H19 aluminum alloy sheet. Eur. J. Mech. A Solids 2018, 69, 1–11. [Google Scholar] [CrossRef]
- Tikhovskiy, I.; Raabe, D.; Roters, F. Simulation of earing during deep drawing of an Al–3% Mg alloy (AA 5754) using a texture component crystal plasticity FEM. J. Mater. Process. Technol. 2007, 183, 169–175. [Google Scholar] [CrossRef]
- Walde, T.; Riedel, H. Simulation of earing during deep drawing of magnesium alloy AZ31. Acta Mater. 2007, 55, 867–874. [Google Scholar] [CrossRef]
- Petkar, P.M.; Gaitonde, V.N.; Karnik, S.R.; Kulkarni, V.N.; Raju, T.K.G.; Davim, J.P. Analysis of Forming Behavior in Cold Forging of AISI 1010 Steel Using Artificial Neural Network. Metals 2020, 10, 1431. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Li, X.; Xie, Z.; Liu, R.; Liu, W.; Zhang, Y.; Xu, Y.; Liu, C. Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals 2020, 10, 234. [Google Scholar] [CrossRef] [Green Version]
- Murugesan, M.; Sajjad, M.; Jung, D.W. Hybrid Machine Learning Optimization Approach to Predict Hot Deformation Behavior of Medium Carbon Steel Material. Metals 2019, 9, 1315. [Google Scholar] [CrossRef] [Green Version]
- Rong-Ji, W.; Xin-Hua, L.; Qing-Ding, W.; Lingling, W. Optimizing process parameters for selective laser sintering based on neural network and genetic algorithm. Int. J. Adv. Manuf. Technol. 2008, 42, 1035–1042. [Google Scholar] [CrossRef]
- Shen, C.; Wang, L.; Li, Q. Optimization of injection molding process parameters using combination of artificial neural network and genetic algorithm method. J. Mater. Process. Technol. 2007, 183, 412–418. [Google Scholar] [CrossRef]
- Tsai, M.-J.; Li, C.-H.; Chen, C.-C. Optimal laser-cutting parameters for QFN packages by utilizing artificial neural networks and genetic algorithm. J. Mater. Process. Technol. 2008, 208, 270–283. [Google Scholar] [CrossRef]
- Yin, F.; Mao, H.; Hua, L. A hybrid of back propagation neural network and genetic algorithm for optimization of injection molding process parameters. Mater. Des. 2011, 32, 3457–3464. [Google Scholar] [CrossRef]
- Yoon, J.W.; Dick, R.E.; Barlat, F. A new analytical theory for earing generated from anisotropic plasticity. Int. J. Plast. 2011, 27, 1165–1184. [Google Scholar] [CrossRef]
- Tang, B.; Wu, F.; Wang, Z.; Zhang, S. Study on non-associated plasticity with various forward Euler stress integration algorithms and its prediction of earing in cylindrical cup drawing. Int. J. Mech. Sci. 2019, 157-158, 384–402. [Google Scholar] [CrossRef]
- Yoon, J.; Barlat, F.; Dick, R.; Karabin, M. Prediction of six or eight ears in a drawn cup based on a new anisotropic yield function. Int. J. Plast. 2006, 22, 174–193. [Google Scholar] [CrossRef]
- Yoon, J.W.; Barlat, F.; Gracio, J.; Rauch, E. Anisotropic strain hardening behavior in simple shear for cube textured aluminum alloy sheets. Int. J. Plast. 2005, 21, 2426–2447. [Google Scholar] [CrossRef]
- Hu, P.; Liu, Y.; Wang, J. Numerical study of the flange earring of deep-drawing sheets with stronger anisotropy. Int. J. Mech. Sci. 2001, 43, 279–296. [Google Scholar] [CrossRef]
- Seo, H.Y.; Jin, C.K.; Gil Kang, C. Effect on Blank Holding Force on Blank Deformation at Direct and Indirect Hot Deep Drawings of Boron Steel Sheets. Metals 2018, 8, 574. [Google Scholar] [CrossRef] [Green Version]
- Basak, S.; Panda, S.K.; Lee, M.-G. Formability and fracture in deep drawing sheet metals: Extended studies for pre-strained anisotropic thin sheets. Int. J. Mech. Sci. 2020, 170, 105346. [Google Scholar] [CrossRef]
- Cho, J.-H.; Han, S.-H.; Lee, G.Y. Microstructure and Texture Evolutions During Deep Drawing of Mg–Al–Mn Sheets at Elevated Temperatures. Materials 2020, 13, 3608. [Google Scholar] [CrossRef] [PubMed]
- Izadpanah, S.; Ghaderi, S.H.; Gerdooei, M. Material parameters identification procedure for BBC2003 yield criterion and earing prediction in deep drawing. Int. J. Mech. Sci. 2016, 552–563. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Cazacu, O.; Yoon, J.W.; Dick, R.E. Earing predictions for strongly textured aluminum sheets. Int. J. Mech. Sci. 2010, 52, 1563–1578. [Google Scholar] [CrossRef]
- Saxena, R.K.; Dixit, P.M. Finite element simulation of earing defect in deep drawing. Int. J. Adv. Manuf. Technol. 2009, 45, 219–233. [Google Scholar] [CrossRef]
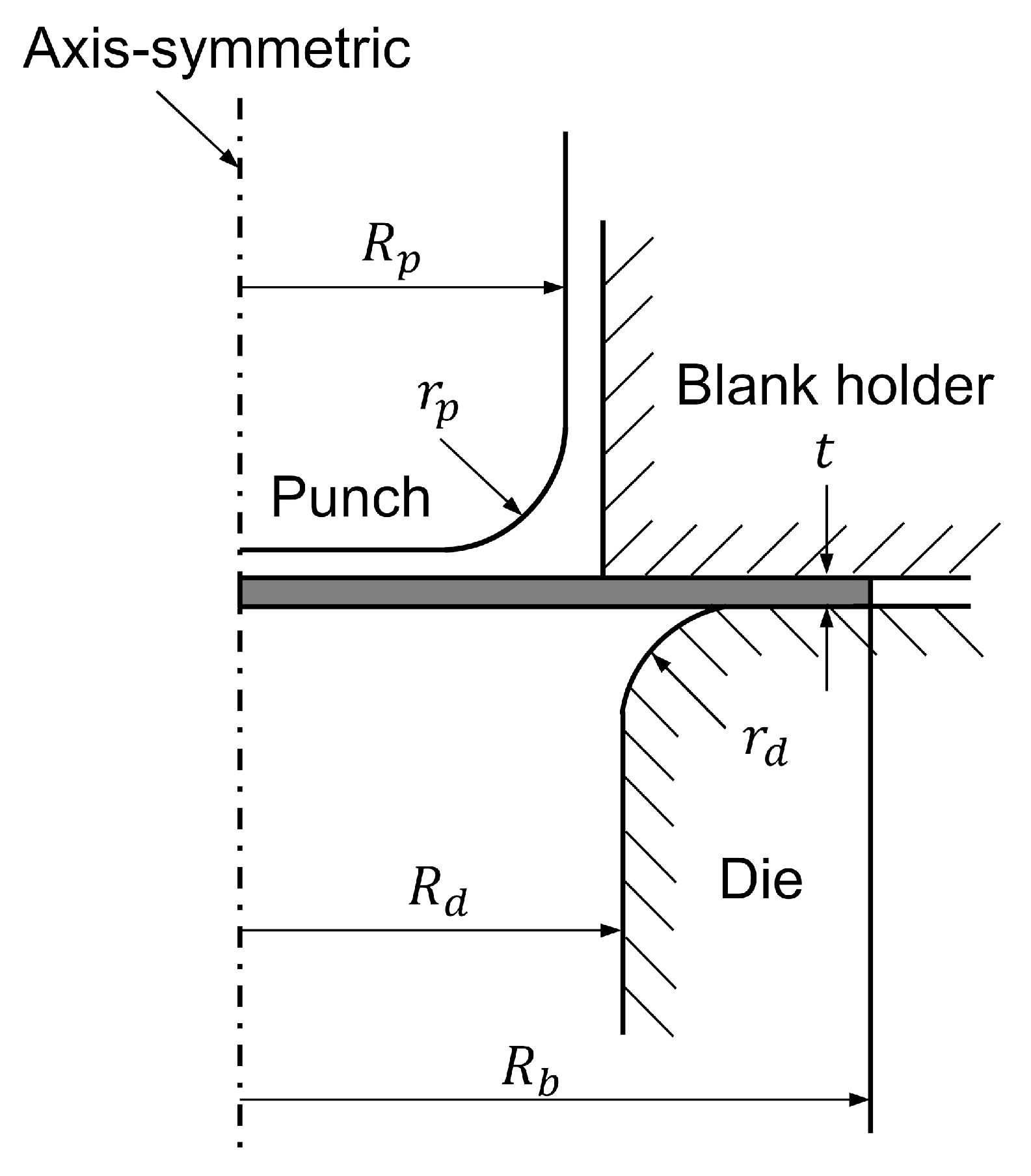





| Parameters | Dimensions (mm) |
|---|---|
| Punch diameter | 97.46 |
| Punch profile radius | 12.70 |
| Die opening diameter | 101.48 |
| Die profile radius | 12.70 |
| Blank sheet diameter | 158.76 |
| Blank sheet thickness | 1.60 |
| Properties | AA1050-O [39] | AA2090-T3 [38] |
|---|---|---|
| Young’s modulus (E), GPa | 70 | 68 |
| Poisson’s ratio | 0.33 | 0.33 |
| Stress-strain equation, MPa | ||
| r0 | 0.610 | 0.212 |
| r45 | 0.210 | 1.577 |
| r90 | 0.870 | 0.692 |
| Δr | 0.530 | −1.125 |
| Blank Holding Force (N) | Before Optimization (Best Choice in Full Factorial Design) | After Optimization (DNN-GA) | Analytical Model |
|---|---|---|---|
| BHF1 | 100 | 163 | 128 |
| BHF2 | 100 | 131 | 778 |
| BHF3 | 4900 | 4600 | 4685 |
| BHF4 | 4900 | 4426 | 4410 |
| BHF5 | 100 | 106 | 642 |
| BHF6 | 100 | 177 | 107 |
| ΔH (mm) | 4.94 | 6.24 | 7.09 |
| Compare to uniform BHF | −62% | −52% | −45% |
| K (MPa) | ∆r | 0.53 | 0.77 | 1.04 |
|---|---|---|---|---|
| 132 | - | 45% | 30% | 26% |
| 250 | 24% | 21% | 17% | |
| 500 | 12% | 9% | 8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.T.; Shan, Z.; Lee, H.W.; Kim, D.-K. Earing Reduction by Varying Blank Holding Force in Deep Drawing with Deep Neural Network. Metals 2021, 11, 395. https://doi.org/10.3390/met11030395
Tran MT, Shan Z, Lee HW, Kim D-K. Earing Reduction by Varying Blank Holding Force in Deep Drawing with Deep Neural Network. Metals. 2021; 11(3):395. https://doi.org/10.3390/met11030395
Chicago/Turabian StyleTran, Minh Tien, Zhengtong Shan, Ho Won Lee, and Dong-Kyu Kim. 2021. "Earing Reduction by Varying Blank Holding Force in Deep Drawing with Deep Neural Network" Metals 11, no. 3: 395. https://doi.org/10.3390/met11030395
APA StyleTran, M. T., Shan, Z., Lee, H. W., & Kim, D.-K. (2021). Earing Reduction by Varying Blank Holding Force in Deep Drawing with Deep Neural Network. Metals, 11(3), 395. https://doi.org/10.3390/met11030395







