Numerical Analysis of the Welding Behaviors in Micro-Copper Bumps
Abstract
:1. Introduction
2. Methodology
2.1. Simulation Assumptions
- The silicon wafer was assumed to be linear, elastic, and isotropic.
- Except for the silicon wafers, the other properties of the materials had bilinear isotropic characteristics.
- Negligible heat loss during simulated bonding.
- With the exception of copper blocks, the material parameters at high temperatures were assumed to be the same as those at room temperature.
- The boundary conditions at the bottom of the Si wafer layer had zero degrees of freedom in the x, y, and z directions.
2.2. Modeling and Setting of Finite Element Analysis
2.3. Geometry and Dimensions
2.4. Boundary Conditions, Load, and Contact Settings
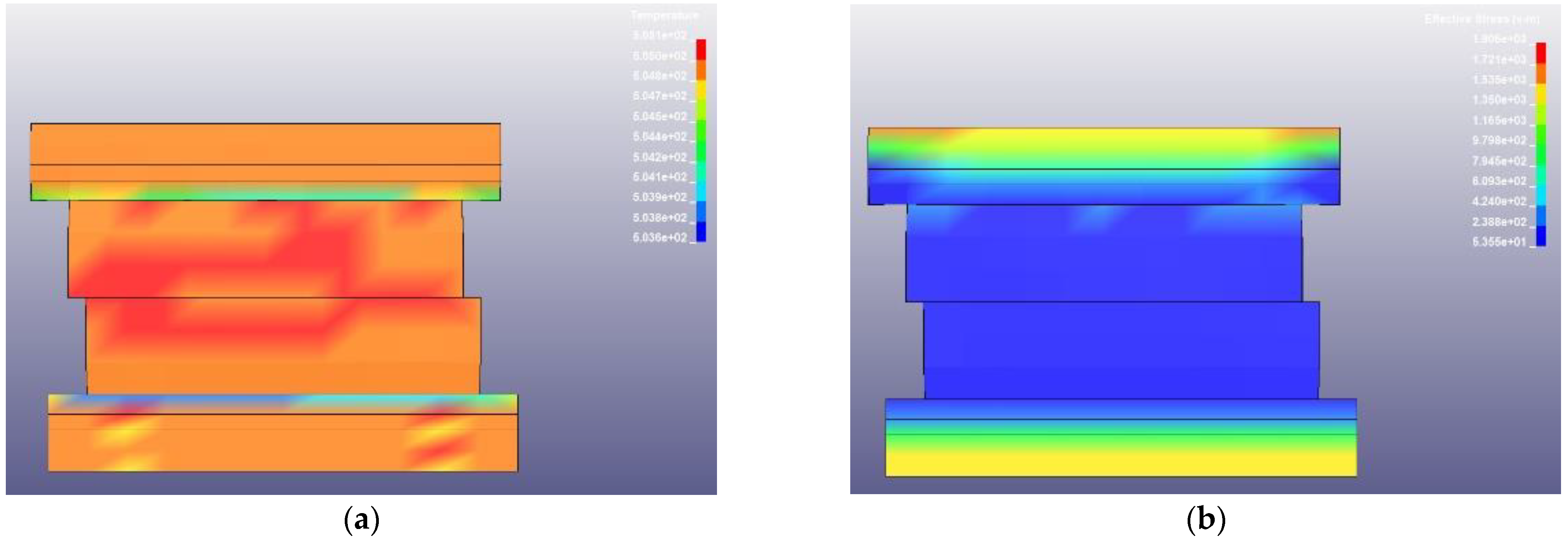
3. Results and Discussion
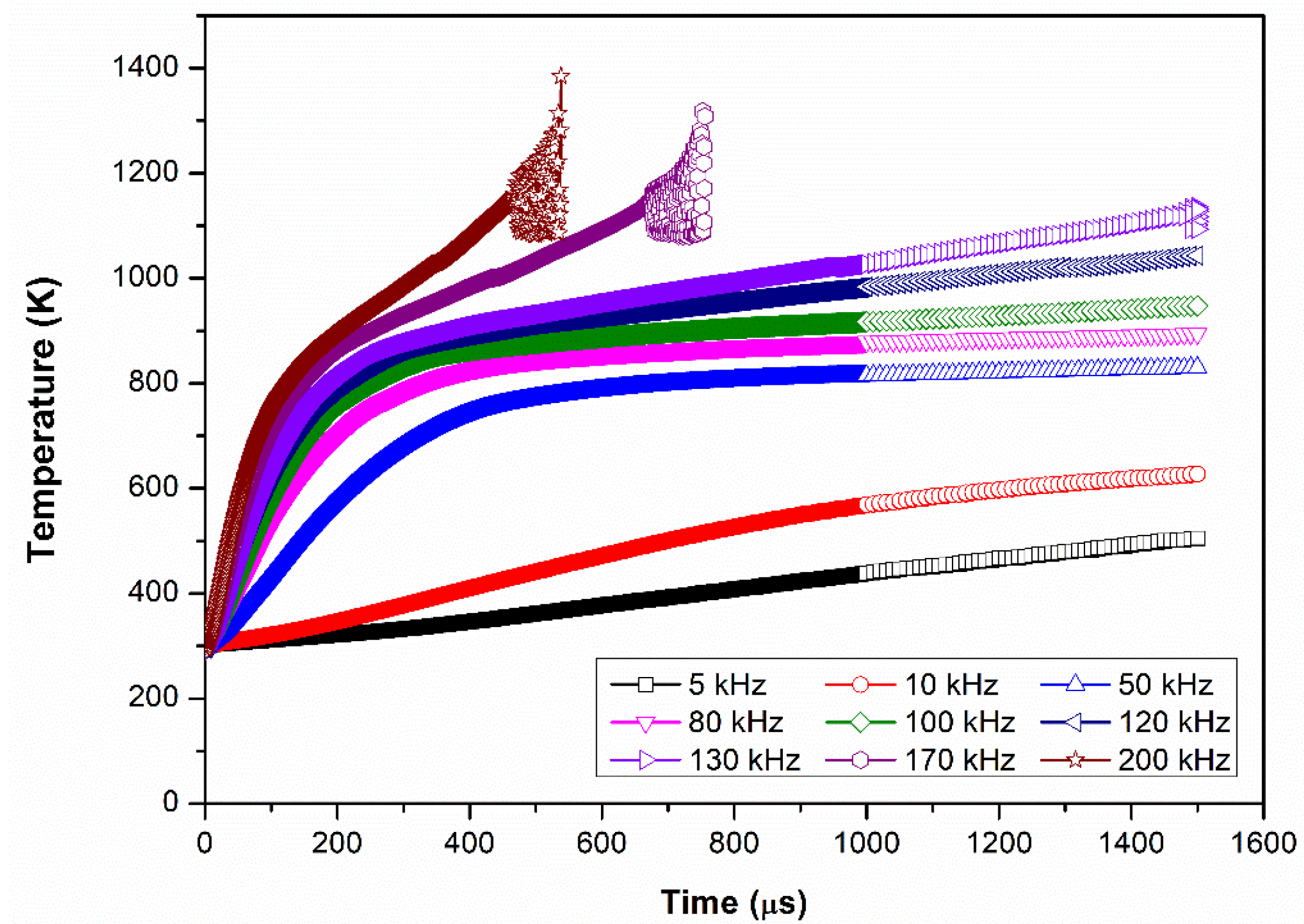
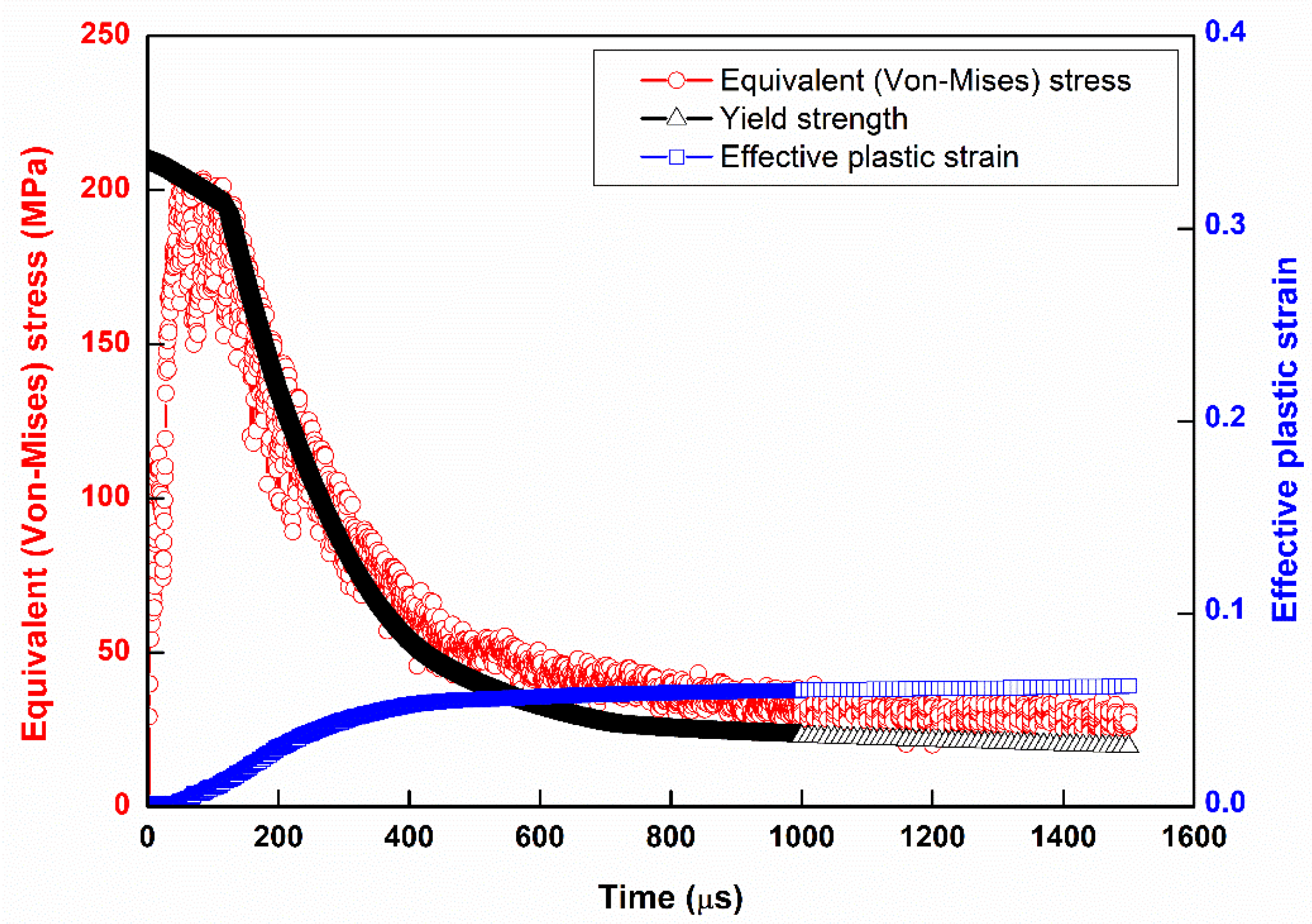
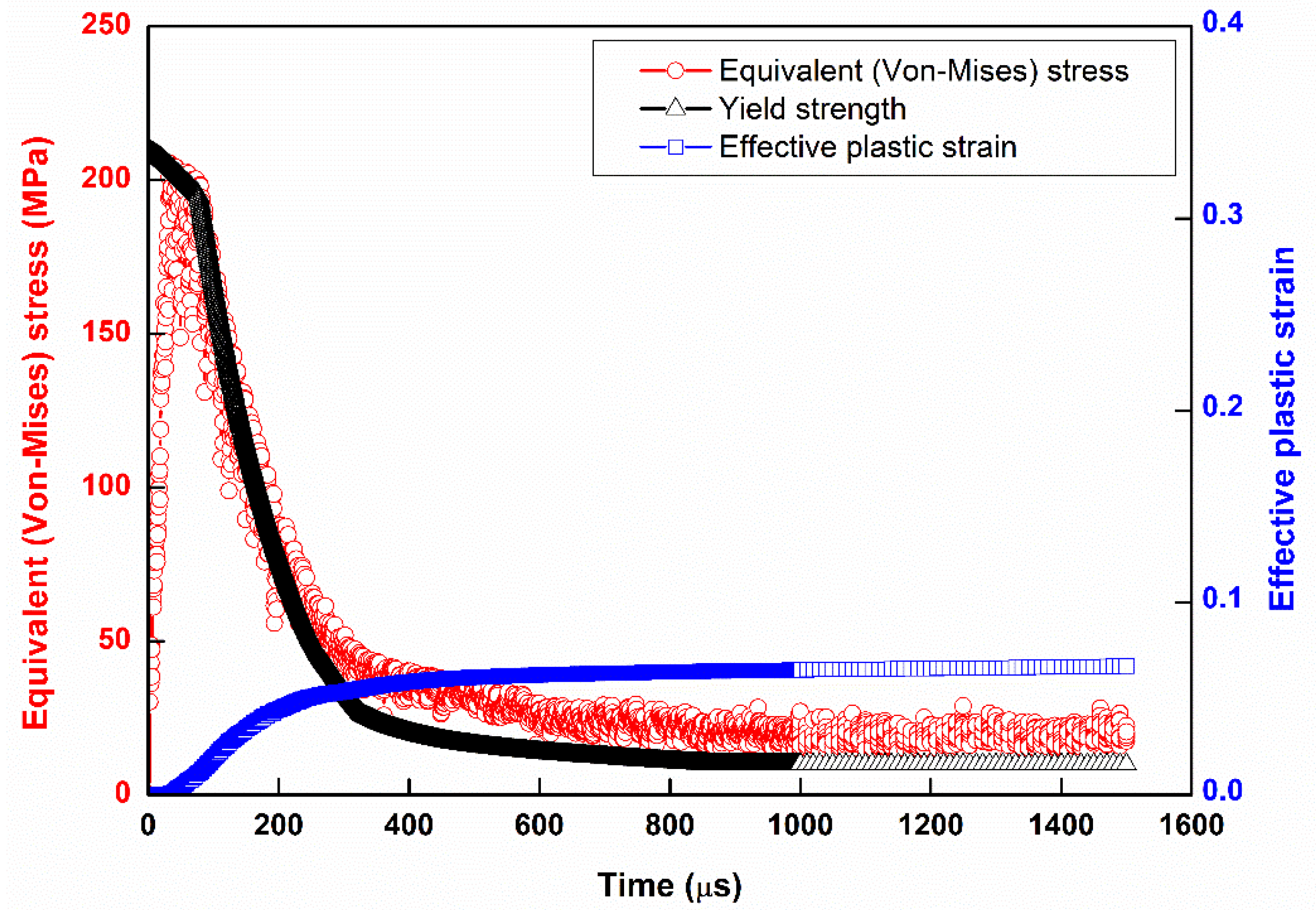
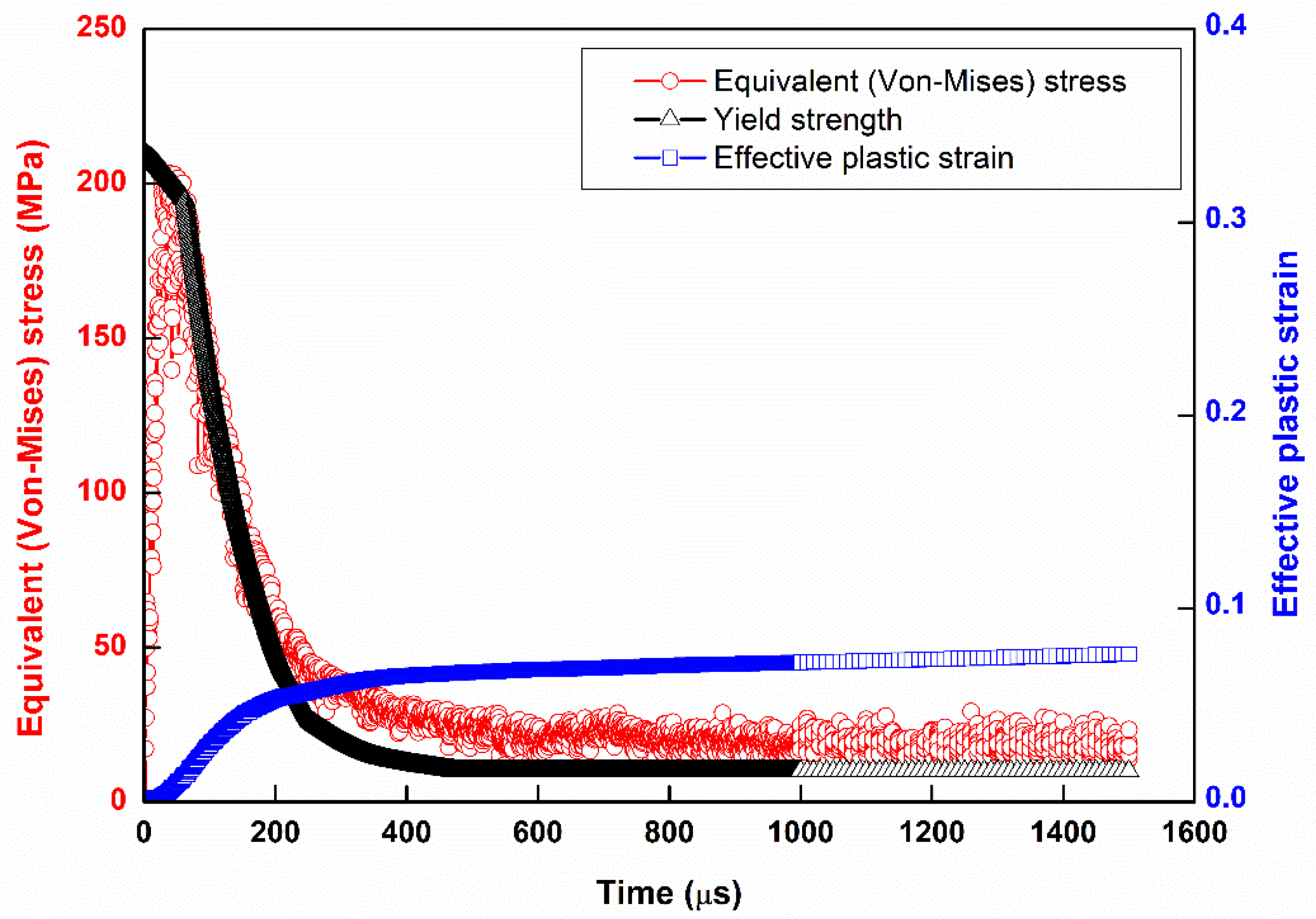
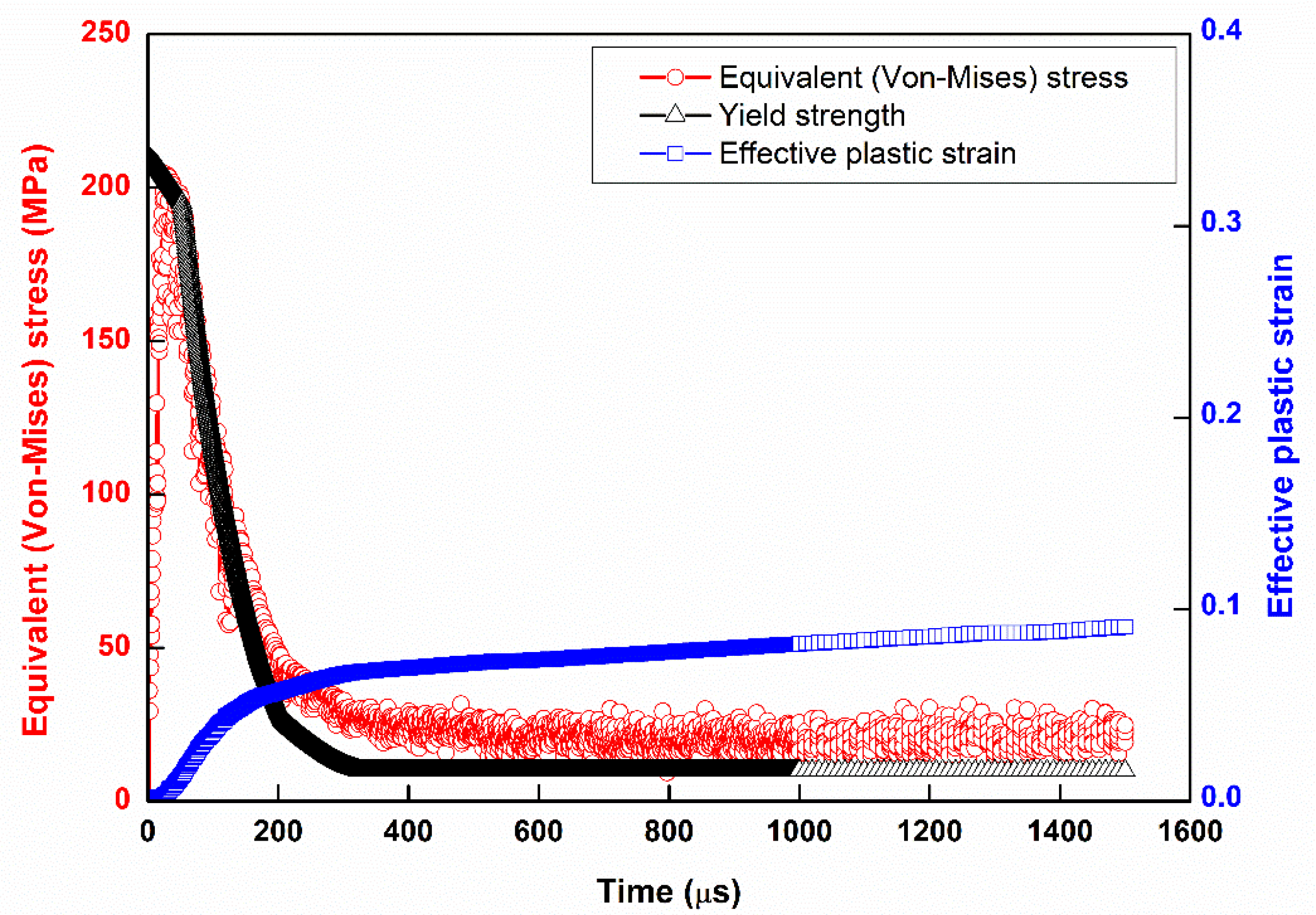
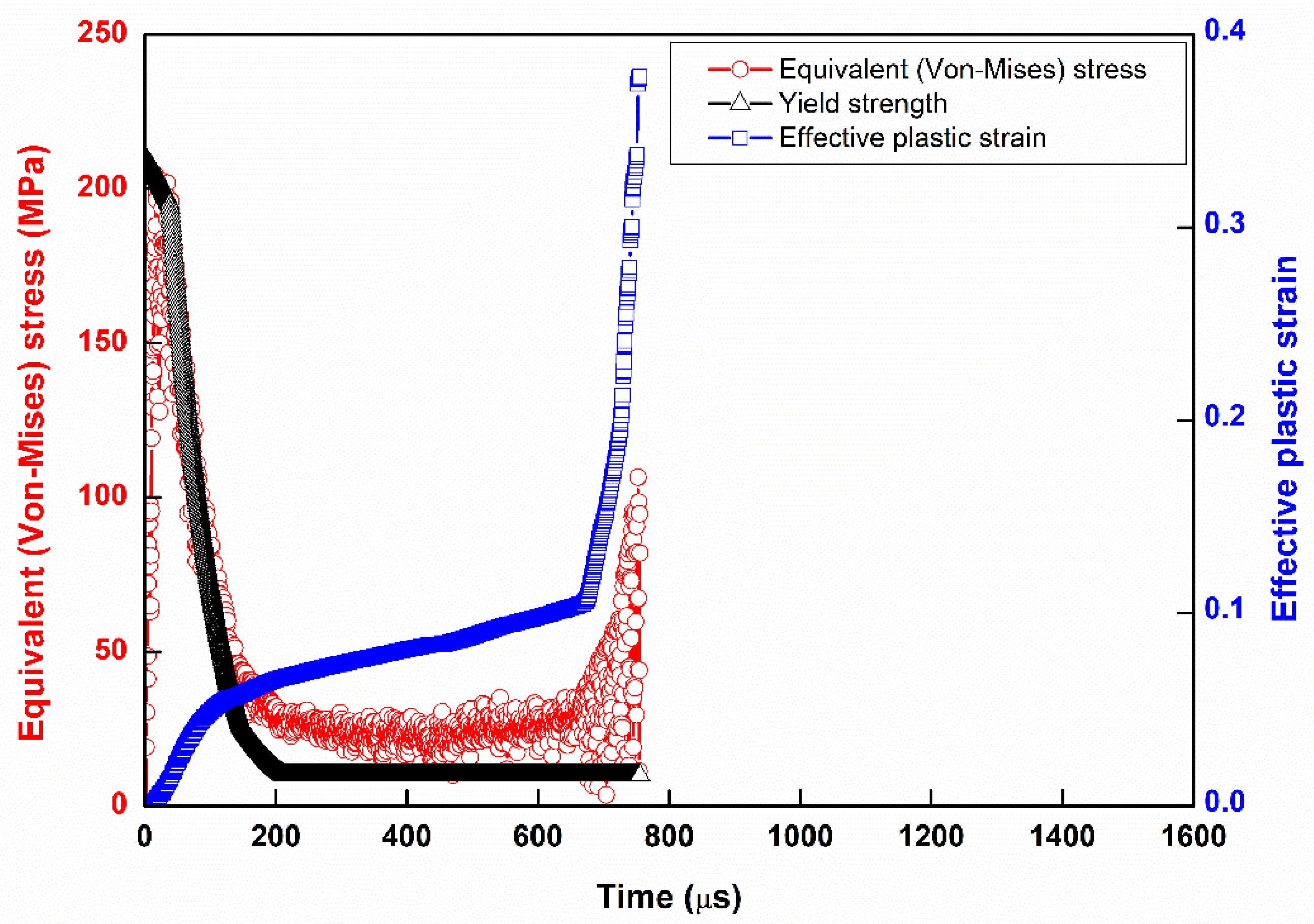
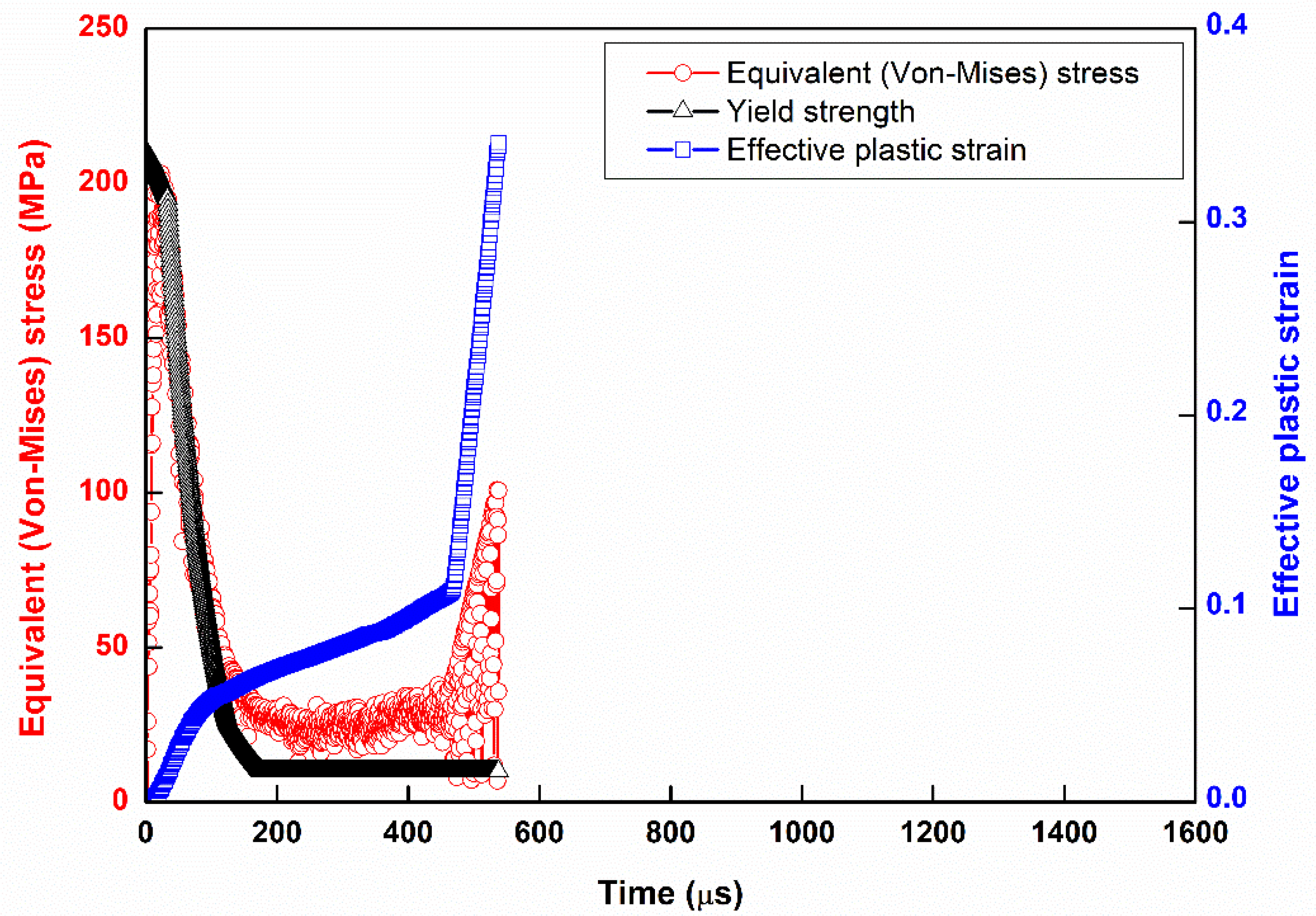
3.1. The Yield Strength Depends on the Temperature Result for Each Frequency
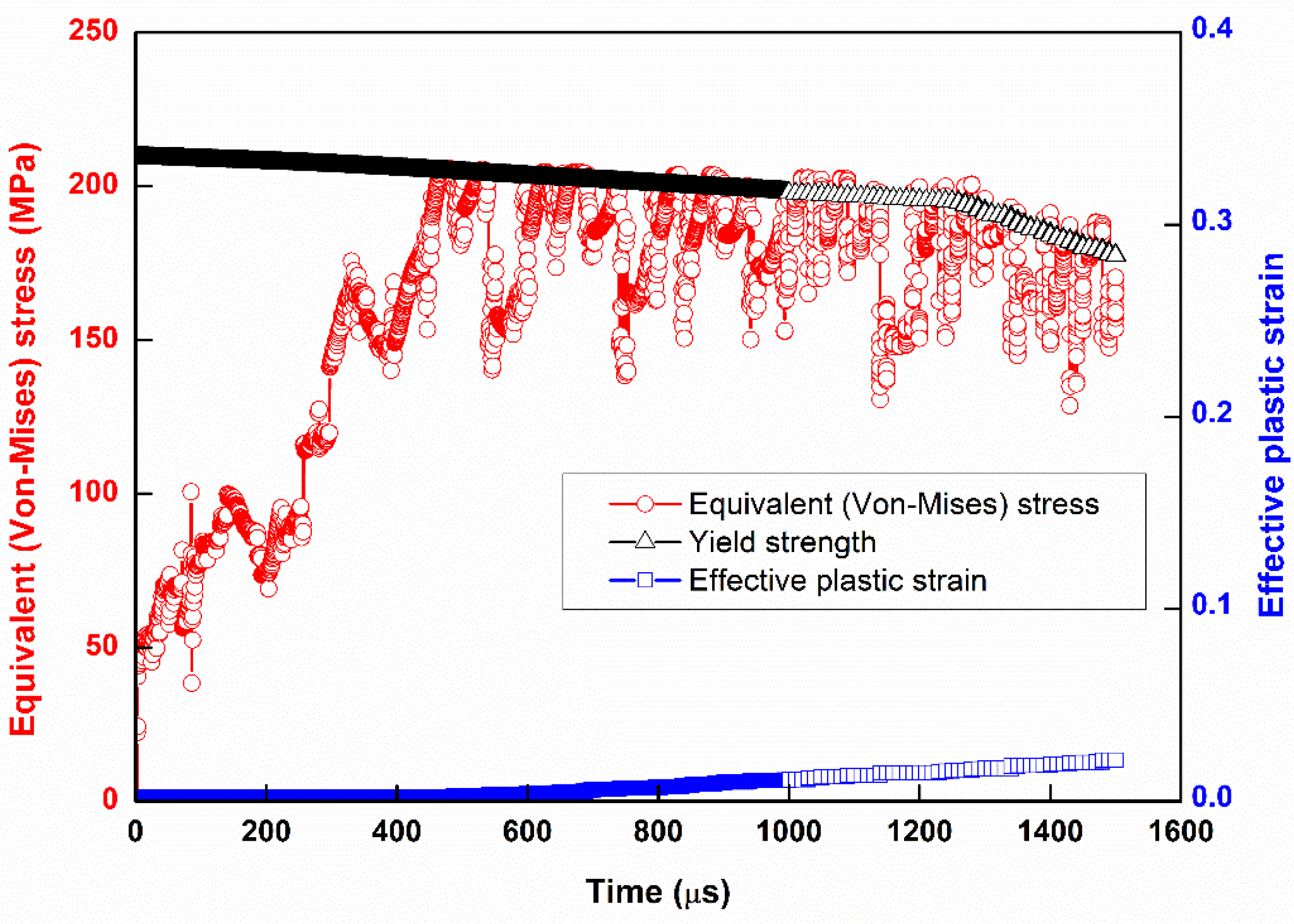
3.2. Strain Softening
3.3. Strain Hardening
3.4. Solid Solution State
3.5. Solid Solution Time Point Advances with Frequency
4. Conclusions
- By using other frequencies to compare with the simulation results of 50 kHz, it can be found that the bonding phenomenon will not occur in the simulation time of 1500 μs if the frequency is lower than 50 kHz.
- The low temperature copper-to-copper bonding technology requires lower temperature (573 K) and a shorter bonding time (100 s), establishing the effectiveness of this better bonding method by improving the reduction of temperature and time with the TCB by 100 times. This research will have a major impact on the industry.
- From the high frequency simulation, it was found that the end of the curve was in the solid solution phase. Near the end of the simulation, it can be found that the trend of the amplitude of the vibration (similarly to the temperature curve) becomes larger from the stress distribution. That is, the materials structure at this stage is not very stable. For this phenomenon, it is called a solid solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Topol, A.W.; La Tulipe, D.C.; Shi, L.; Frank, D.J.; Bernstein, K.; Steen, S.E.; Kumar, A.; Singco, G.U.; Young, A.M.; Guarini, K.W.; et al. Three-dimensional integrated circuits. IBM J. Res. Dev. 2006, 50, 491–506. [Google Scholar] [CrossRef]
- Patti, R.S. Three-dimensional integrated circuits and the future of system-on-chip designs. Proc. IEEE Inst. Electr. Electron. Eng. 2006, 94, 1214–1224. [Google Scholar] [CrossRef]
- Ruythooren, W.; Beltran, A.; Labie, R. Cu-Cu bonding alternative to solder based micro-bumping. In Proceedings of the 2007 9th Electronics Packaging Technology Conference, Singapore, 10 December 2007; pp. 315–318. [Google Scholar]
- Tu, K.N. Reliability challenges in 3D IC packaging technology. Microelectron. Reliab. 2011, 51, 517–523. [Google Scholar] [CrossRef]
- Motoyoshi, M. Through-silicon via (TSV). Proc. IEEE Inst. Electr. Electron. Eng. 2009, 97, 43–48. [Google Scholar] [CrossRef]
- Hu, Y.H.; Liu, C.S.; Lii, M.J.; Manna, A.L.; Rebibis, K.J.; Zhao, M.; Beyne, E.; Yu, C.H. 3D stacking using Cu-Cu direct bonding for 40um pitch and beyond. In Proceedings of the 2012 4th Electronic System-Integration Technology Conference (ESTC 2012), Amsterdam, The Netherlands, 17–20 September 2012; pp. 1–5. [Google Scholar]
- Daily, R.; Teng, W.; Capuz, G.; Miller, A. Microscrubbing: An alternative method for 3D thermocompression bonding CuCu bumps and high bump density devices with low force, time and temperature. In Proceedings of the 2013 IEEE 63rd Electronic Components and Technology Conference, Las Vegas, NV, USA, 28–31 May 2013; pp. 255–259. [Google Scholar]
- Chen, K.N.; Fan, A.; Tan, C.S.; Reif, R. Temperature and duration effect on microstructure evolution during copper wafer bonding. J. Electron. Mater. 2003, 32, 1371–1374. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.K.; Wang, M.J.; Yeh, C.Y.; Chang, H.M.; Liu, Y.C. High-strength and thermal stable Cu-to-Cu joint fabricated with transient molten Ga and Ni under-bump-metallurgy. J. Alloys Compd. 2017, 702, 561–567. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, S.; Wang, F.; Chen, Z. Micro copper pillar interconnection using thermosonic flip chip bonding. J. Electron. Packag. 2018, 140, 044502. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Zhang, H.; Chen, Z.; Zhou, C.; Liu, X.; Zhu, W. The thermal cycling reliability of copper pillar solder bump in flip chip via thermal compression bonding. Microelectron. Reliab. 2020, 104, 113543. [Google Scholar] [CrossRef]
- Srinivasan, V.P.; Balamurugan, S.; Balakarthick, B.; Devva Darshan, S.; Dhanush Prabhu, A.B. Experimental investigation on ultrasonic metal welding of copper sheet with copper wire using Taguchi method. Mater. Today Proc. 2020, in press. [Google Scholar] [CrossRef]
- Watanabe, N.; Asano, T. Room-temperature Cu-Cu bonding in ambient air achieved by using cone bump. Appl. Phys. Express 2010, 4, 016501. [Google Scholar] [CrossRef]
- Iwanabe, K.; Shuto, T.; Noda, K.; Nakai, S.; Asano, T. Room-temperature microjoining using ultrasonic bonding of compliant bump. In Proceedings of the 2012 3rd IEEE International Workshop on Low Temperature Bonding for 3D Integration, Tokyo, Japan, 22–23 May 2012; pp. 167–170. [Google Scholar]
- Chang, J.Y.; Cheng, R.S.; Kao, K.S.; Chang, T.C.; Chuang, T.H. Reliable microjoints formed by solid-liquid interdiffusion (SLID) bonding within a chip-stacking architecture. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 979–984. [Google Scholar] [CrossRef]
- Klumpp, A.; Merkel, R.; Ramm, P.; Weber, J.; Wieland, R. Vertical system integration by using inter-chip vias and solid-liquid interdiffusion bonding. Jpn. J. Appl. Phys. 2004, 43, L829. [Google Scholar] [CrossRef]
- Pan, C.T.; Yang, H.; Shen, S.C.; Chou, M.C.; Chou, H.P. A low-temperature wafer bonding technique using patternable materials. J. Micromech. Microeng. 2002, 12, 611. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Thanh, L.Q.; Loc, N.H.; Huu, M.N.; Nguyen Van, A. Effects of Different Roller Profiles on the Microstructure and Peel Strength of the Ultrasonic Welding Joints of Nonwoven Fabrics. Appl. Sci. 2020, 10, 4101. [Google Scholar] [CrossRef]
- Ng, R.; Nai, M.L.S.; Chan, H.L.I.; Shi, C.W.P.; Song, B. Comparative eco-efficiency analyses of copper to copper bonding technologies. Procedia CIRP 2014, 15, 96–104. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.C.; Yang, T.F.; Wu, C.S.; Kao, K.S.; Cheng, R.C.; Chen, T.H. Reliability estimation and failure mode prediction for 3D chip stacking package with the application of wafer-level underfill. Microelectron. Eng. 2013, 107, 107–113. [Google Scholar] [CrossRef]
- Gao, J.; Kelly, R.; Yang, Z.; Chen, X. An investigation of capillary vibration during wire bonding process. In Proceedings of the 2008 International Conference on Electronic Packaging Technology & High Density Packaging, Shanghai, China, 28–31 July 2008; pp. 1–6. [Google Scholar]
- Sahani, P.; Mula, S.; Roy, P.K.; Kang, P.C.; Koch, C.C. Structural investigation of vacuum sintered Cu-Cr and Cu-Cr-4% SiC nanocomposites prepared by mechanical alloying. Mater. Sci. Eng. A 2011, 528, 7781–7789. [Google Scholar] [CrossRef]
- White, G.K.; Collocott, S.J. Heat Capacity of Reference Materials: Cu and W. J. Phys. Chern. Ref. Data 1984, 13. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Miller, T.J.; Zinkle, S.J.; Chin, B.A. Strength and Fatigue of Dispersion-Strengthened Copper. J. Nucl. Mater. 1991, 178–181, 263–266. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005; pp. 12–108. [Google Scholar]
- Liu, T. Sliding friction of copper. Wear 1964, 7, 163–174. [Google Scholar] [CrossRef]
- Li, J.; Fuliang, W.; Han, L.; Zhong, J. Theoretical and experimental analyses of atom diffusion characteristics on wire bonding interfaces. J. Phys. D Appl. Phys. 2008, 41, 135303. [Google Scholar] [CrossRef]
- Rusinko, A. Analytical description of ultrasonic hardening and softening. Ultrasonics 2011, 51, 709–714. [Google Scholar] [CrossRef] [PubMed]
- Murali, S.; Srikanth, N.; Vath III, C.J. Grains, deformation substructures, and slip bands observed in thermosonic copper ball bonding. Mater. Charact. 2003, 50, 39–50. [Google Scholar] [CrossRef]
- Srikanth, N.; Murali, S.; Wong, Y.M.; Vath, C.J., III. Critical study of thermosonic copper ball bonding. Thin Solid Films 2004, 462–463, 339–345. [Google Scholar] [CrossRef]
- Levine, L. The ultrasonic wedge bonding mechanism: Two theories converge. Proc. SPIE 1995, 2649, 242. [Google Scholar]
- Wang, F.; Han, L.; Zhong, J. Stress-induced atom diffusion at thermosonic flip chip bonding interface. Sens. Actuator A Phys. 2009, 149, 100–105. [Google Scholar] [CrossRef]
- Wang, F.; Han, L. Ultrasonic effects in the thermosonic flip chip bonding process. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 336–341. [Google Scholar] [CrossRef]
- Li, J.H.; Han, L.; Duan, J.A.; Zhong, J. Microstructural characteristics of Au/Al bonded interfaces. Mater. Charact. 2007, 58, 103–107. [Google Scholar] [CrossRef]
- Siddiq, A.; Ghassemieh, E. Thermomechanical analyses of ultrasonic welding process using thermal and acoustic softening effects. Mech. Mater. 2008, 40, 982–1000. [Google Scholar] [CrossRef]


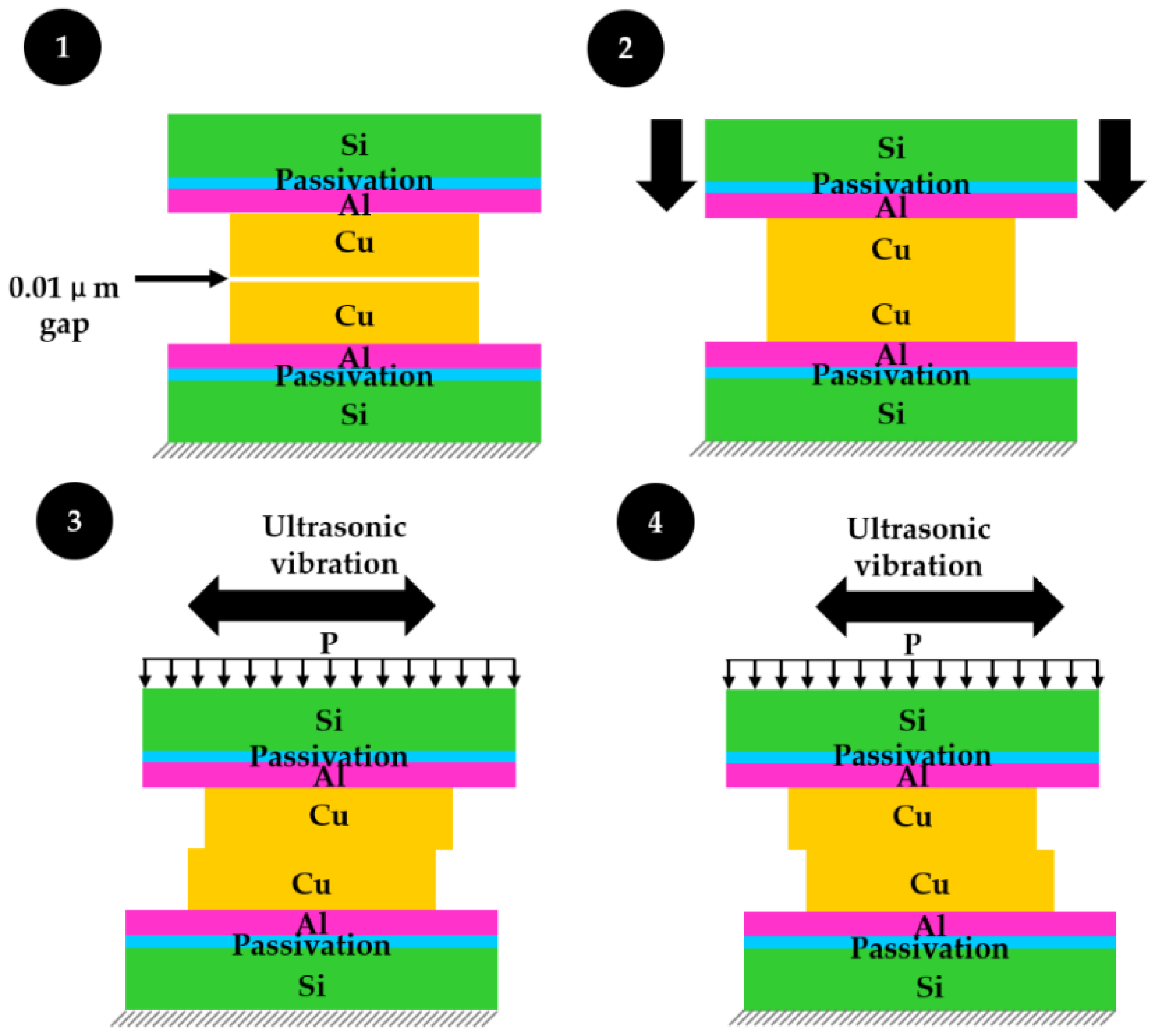


| Material | Length (μm) | Width (μm) | Height (μm) |
|---|---|---|---|
| Copper (Small) | 12 | 12 | 1.0 |
| Copper (Big) | 20 | 20 | 5.0 |
| Aluminum Pad | 24 | 24 | 1.0 |
| Passivation | 24 | 24 | 0.8 |
| Silicon | 24 | 24 | 2.1 |
| Total Elements | Max. Von-Mises Stress (MPa) | Max. Temperature (K) |
|---|---|---|
| 10,336 | 202.0 | 823.5 |
| 1836 | 204.0 | 830.0 |
| Deviation value (%) | 0.98% | 0.78% |
| Property | Copper | Aluminum | Passivation | Silicon |
|---|---|---|---|---|
| Density (kg/m3) | 8910 | 2710 | 1310 | 2330 |
| Young’s Modulus (GPa) | 130 | 69 | 32 | 180 |
| Poisson’s Ratio | 0.38 | 0.33 | 0.24 | 0.30 |
| Yielding Strength (GPa) | 0.21 | 0.40 | 0.35 | - |
| Tangent Modulus (GPa) | 0.60 | 1.38 | 3.20 | - |
| Specific Heat (J/Kg·K) | 383 | 900 | 940 | 702 |
| Thermal Conductivity (W/m·K) | 400 | 300 | 0.2 | 148 |
| Coefficient of thermal expansion, CTE (ppm/K) | 15.4 | 23.4 | 3.2 | 28.0 |
| Temperature (K) | Young’s Modulus (GPa) | Yielding Strength (GPa) | Tangent Modulus (GPa) | CTE (ppm/K) |
|---|---|---|---|---|
| 293 | 130.0 | 0.210 | 0.600 | 15.40 |
| 473 | 94.5 | 0.195 | 0.436 | 16.60 |
| 573 | 88.0 | 0.140 | 0.408 | 17.49 |
| 800 | 73.2 | 0.026 | 0.339 | 19.32 |
| 873 | 68.4 | 0.010 | 0.391 | 20.00 |
| 973 | 68.4 | 0.010 | 0.271 | 20.00 |
| 1358 1 | 68.4 | 0.010 | 0.271 | 20.00 |
| Temperature (K) | Specific Heat (J/Kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|
| 293 | 383 | 400 |
| 373 | 394 | 395 |
| 473 | 405 | 388 |
| 573 | 414 | 381 |
| 800 | 422 | 374 |
| 873 | 429 | 367 |
| 973 | 447 | 354 |
| 1358 1 | 447 | 354 |
| Frequency (kHz) | Von Mises Stress (MPa) | Effective Strain | Temperature (K) |
|---|---|---|---|
| 5 | 165.27 | 0.02 | 505 |
| 10 | 125.48 | 0.04 | 627 |
| 50 | 27.31 | 0.06 | 830 |
| 80 | 20.44 | 0.07 | 894 |
| 100 | 17.94 | 0.08 | 947 |
| 120 | 24.73 | 0.09 | 1043 |
| 130 | 28.04 | 0.11 | 1131 |
| 170 | 81.94 | 0.37 | 1307 |
| 200 | 100.65 | 0.34 | 1384 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, Y.-M.; Pan, C.-T.; Chen, B.-S.; Jian, S.-R. Numerical Analysis of the Welding Behaviors in Micro-Copper Bumps. Metals 2021, 11, 460. https://doi.org/10.3390/met11030460
Hwang Y-M, Pan C-T, Chen B-S, Jian S-R. Numerical Analysis of the Welding Behaviors in Micro-Copper Bumps. Metals. 2021; 11(3):460. https://doi.org/10.3390/met11030460
Chicago/Turabian StyleHwang, Yeong-Maw, Cheng-Tang Pan, Bo-Syun Chen, and Sheng-Rui Jian. 2021. "Numerical Analysis of the Welding Behaviors in Micro-Copper Bumps" Metals 11, no. 3: 460. https://doi.org/10.3390/met11030460
APA StyleHwang, Y.-M., Pan, C.-T., Chen, B.-S., & Jian, S.-R. (2021). Numerical Analysis of the Welding Behaviors in Micro-Copper Bumps. Metals, 11(3), 460. https://doi.org/10.3390/met11030460







