Numerical Modeling of Plasticity-Induced Fatigue Crack Growth Retardation Due to Deflection in the Near-Tip Area
Abstract
:1. Introduction
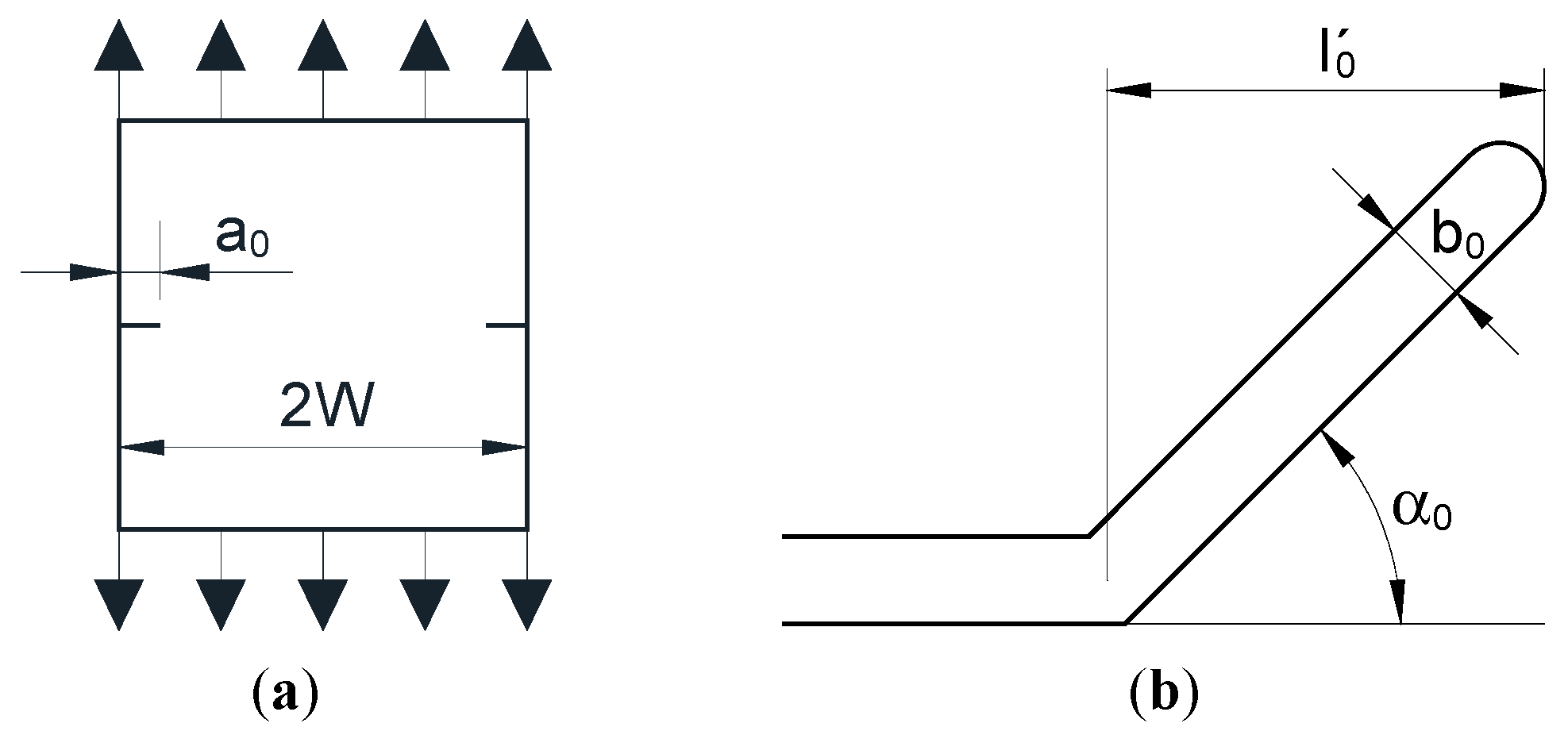
2. Numerical Procedure
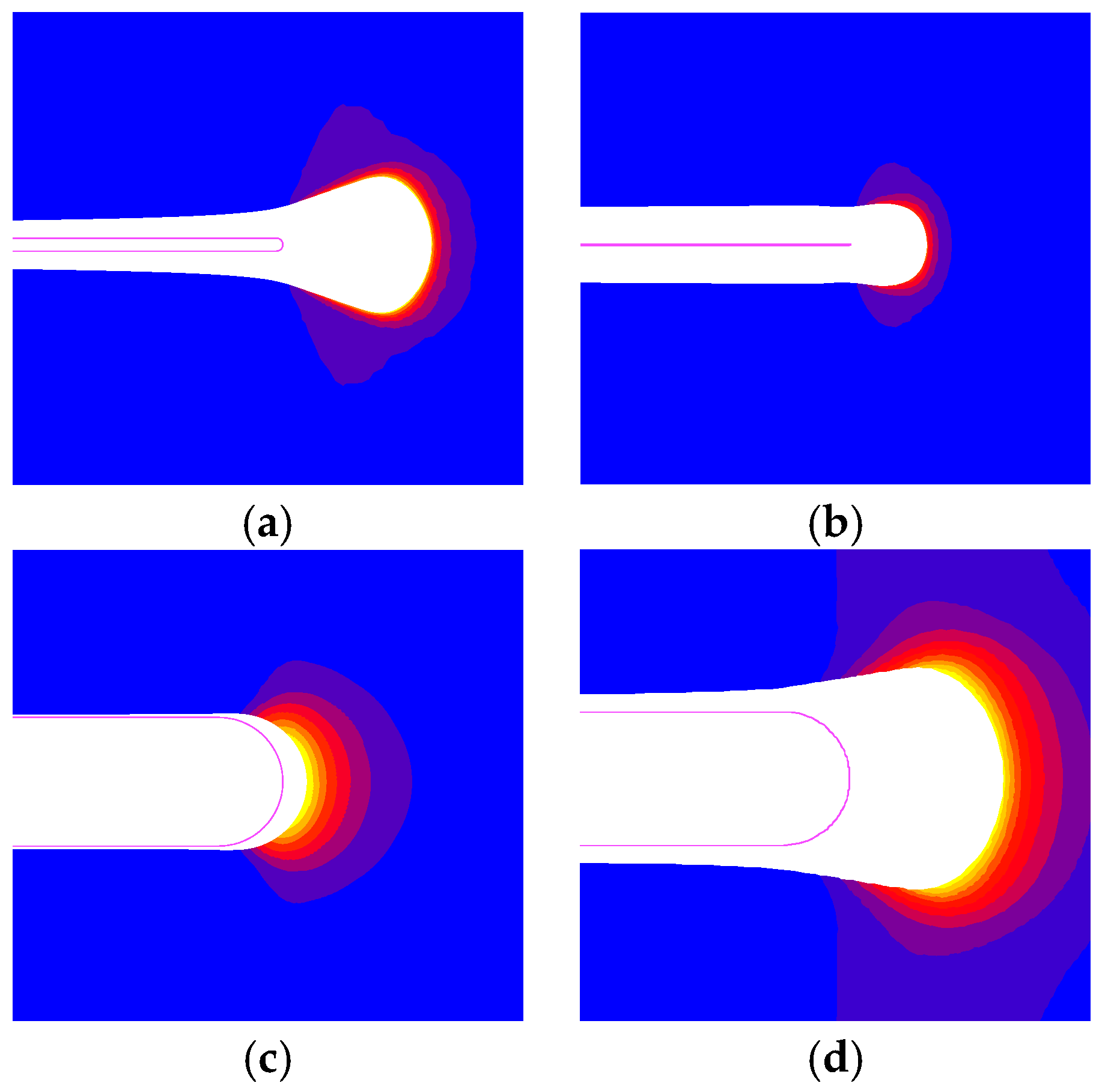
3. Fatigue Propagation Curve
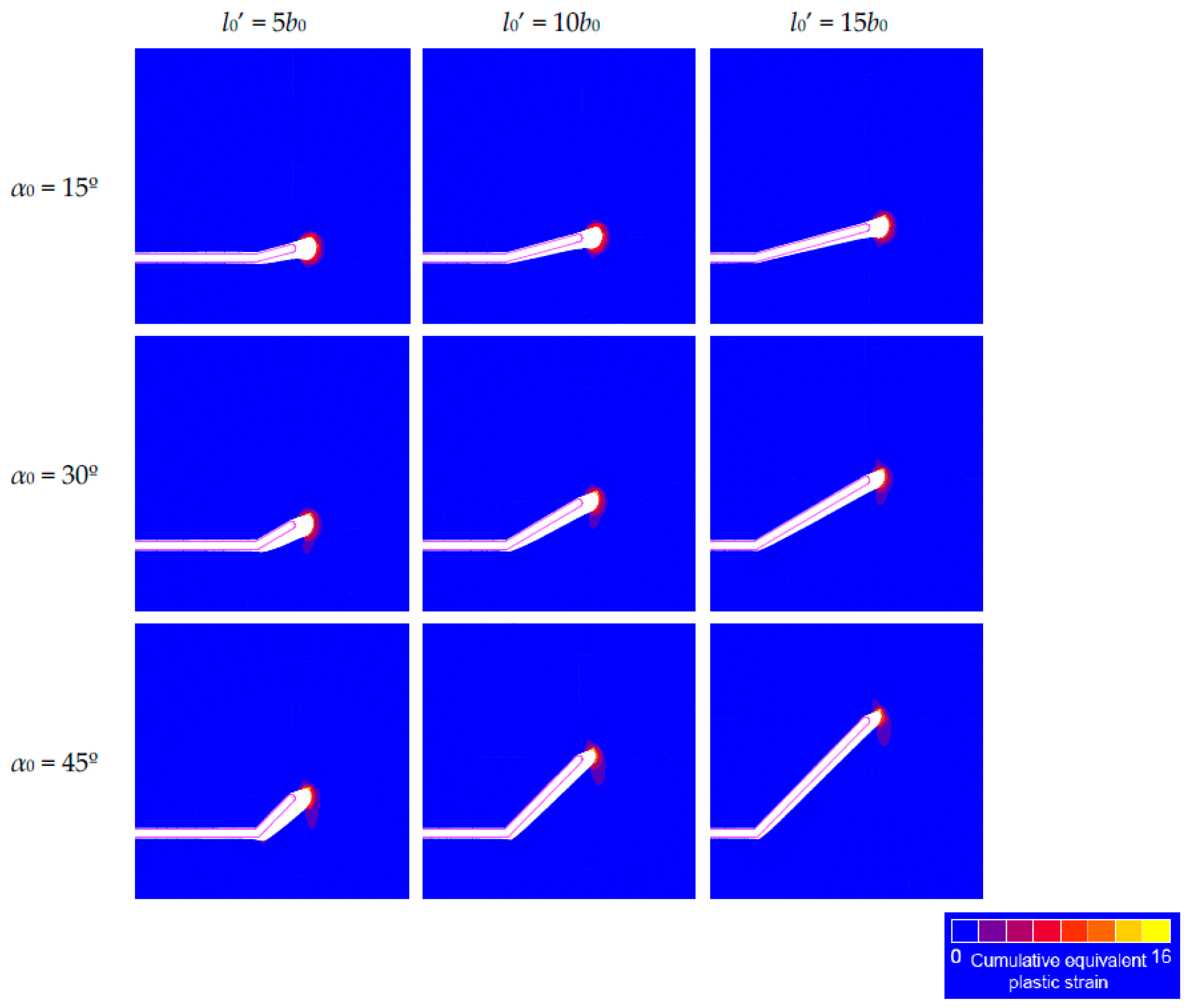
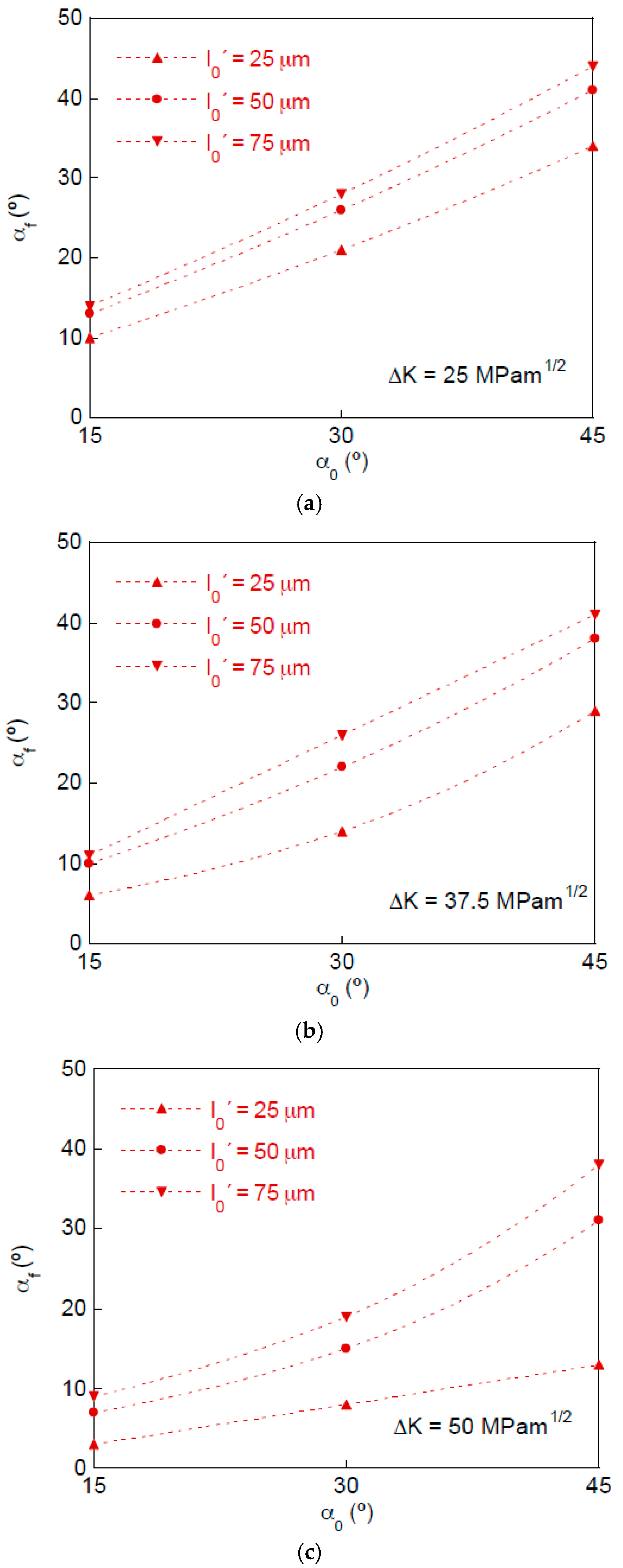
4. Kinked Crack Tip
5. Conclusions
- (i)
- Cracks with a kinked tip in a plate subjected to remote mode I (opening) fatigue tensile loading exhibit a plastic crack advance tending towards a global mode I in spite of the initial locally-multiaxial mixed-mode.
- (ii)
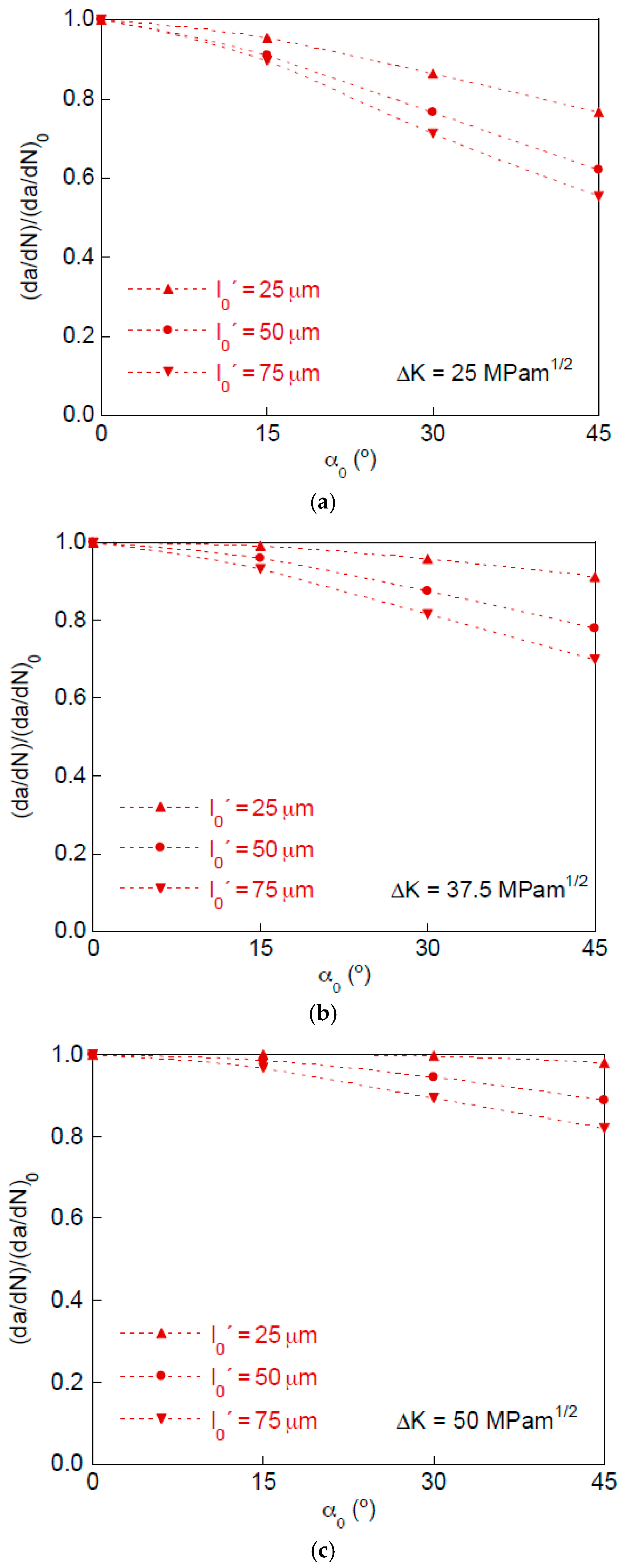
- The deflection of the crack tip produced a retardation effect (that could be easily quantified through the retardation factor) on the fatigue crack growth, when compared to a fully straight crack.
- (iii)
- The retardation effect increased with the initial kinked crack tip angle and with the initial projected kinked crack tip length, while it decreased with the stress intensity factor range.
- (iv)
- A lower retardation effect could be associated with the decrease in the angle of propagated deflected crack tip, with respect to the initial deflected crack tip, and with an increase in the crack opening displacement (COD) in the deflected crack tip.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Toribio, J.; Matos, J.C.; González, B. A macro- and micro-approach to the anisotropic fatigue behaviour of hot-rolled and cold-drawn pearlitic steel. Eng. Fract. Mech. 2014, 123, 70–76. [Google Scholar] [CrossRef]
- Kitagawa, H.; Yuuki, R.; Ohira, T. Crack-morphological aspects in fracture mechanics. Eng. Fract. Mech. 1975, 7, 515–529. [Google Scholar] [CrossRef]
- Suresh, S. Crack deflection: Implications for the growth of long and short fatigue cracks. Metall. Mater. Trans. A 1983, 14, 2375–2385. [Google Scholar] [CrossRef]
- Laird, C.; Smith, G.C. Crack propagation in high stress fatigue. Philos. Mag. 1962, 8, 847–857. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V. Simulations of fatigue crack growth by blunting–re-sharpening: Plasticity induced crack closure vs. alternative controlling variables. Int. J. Fatigue 2013, 50, 72–82. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V. Finite-deformation analysis of the crack-tip fields under cyclic loading. Int. J. Solids Struct. 2009, 46, 1937–1952. [Google Scholar] [CrossRef] [Green Version]
- Levkovitch, V.; Sievert, R.; Svendsen, B. Simulation of fatigue crack propagation in ductile metals by blunting and re-sharpening. Int. J. Fract. 2005, 136, 207–220. [Google Scholar] [CrossRef] [Green Version]
- Toribio, J.; Kharin, V. Large crack tip deformations and plastic crack advance during fatigue. Mater. Lett. 2007, 61, 964–967. [Google Scholar] [CrossRef]
- Tvergaard, V. Effect of underloads and overloads in fatigue crack growth by crack-tip blunting. Eng. Fract. Mech. 2006, 73, 869–879. [Google Scholar] [CrossRef]
- Hunnell, J.M.; Kujawski, D. Numerical simulation of fatigue crack growth behavior by crack-tip blunting. Eng. Fract. Mech. 2009, 76, 2056–2064. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V.; Ayaso, F.J.; González, B.; Matos, J.C.; Vergara, D.; Lorenzo, M. Numerical and experimental analyses of the plasticity-induced fatigue crack growth in high-strength steels. Constr. Build. Mater. 2011, 25, 3935–3940. [Google Scholar] [CrossRef]
- McClung, R.C.; Thacker, B.H.; Roy, S. Finite element visualization of fatigue crack closure in plane stress and plane strain. Int. J. Fract. 1991, 50, 27–49. [Google Scholar]
- Tvergaard, V. On fatigue crack growth in ductile materials by crack–tip blunting. J. Mech. Phys. Solids 2004, 52, 2149–2166. [Google Scholar] [CrossRef]
- Toribio, J.; Kharin, V. Comments on simulations of fatigue crack propagation by blunting and re-sharpening: The mesh sensitivity. Int. J. Fract. 2006, 140, 285–292. [Google Scholar] [CrossRef]
- Tvergaard, V. Mesh sensitivity effects on fatigue crack growth by crack-tip blunting and re-sharpening. Int. J. Solids Struct. 2007, 44, 1891–1899. [Google Scholar] [CrossRef] [Green Version]
- Benedetti, M.; Fontanari, V.; Monelli, B.D.; Beghini, M. A fully parametric weight function for inclined edge cracks with a kink. Eng. Fract. Mech. 2015, 136, 195–212. [Google Scholar] [CrossRef]
- Li, Y.; Sun, T.; Gao, Q.; Tan, C. A stress intensity factor estimation method for kinked crack. Eng. Fract. Mech. 2018, 188, 202–216. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S.; Viappiani, D. Influence of the crack morphology on the fatigue crack growth rate: A continuously-kinked crack model based on fractals. Eng. Fract. Mech. 2008, 75, 579–589. [Google Scholar] [CrossRef]
- Suresh, S. Micromechanisms of fatigue crack growth retardation following overloads. Eng. Fract. Mech. 1983, 18, 577–593. [Google Scholar] [CrossRef] [Green Version]
- Handerhan, K.J.; Garrison Jr., W. M. A study of crack tip blunting and the influence of blunting behavior on the fracture toughness of ultra high strength steels. Acta Metall. Mater. 1992, 40, 1337–1355. [Google Scholar] [CrossRef]
- Castro, J.T.P.; Meggiolaro, M.A.; Miranda, A.C.O. Singular and non-singular approaches for predicting fatigue crack growth behaviour. Int. J. Fatigue 2005, 27, 1366–1388. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. Computational Fracture Mechanics. In Numerical and Computer Methods in Structural Mechanics; Academic Press: New York, NY, USA, 1973; pp. 585–623. [Google Scholar]
- McMeeking, R.M. Finite deformation analysis of crack-tip opening in elastic-plastic materials and implications for fracture. J. Mech. Phys. Solids 1977, 25, 357–381. [Google Scholar] [CrossRef]
- Savruk, M.P. Stress Intensity Factors in Solids with Cracks; Naukova Dumka: Kiev, Ukraine, 1988. (In Russian) [Google Scholar]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Fleck, N.A. Finite element analysis of plasticity-induced crack closure under plane strain conditions. Eng. Fract. Mech. 1986, 25, 441–449. [Google Scholar] [CrossRef]
- Paris, P.C.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85D, 528–534. [Google Scholar] [CrossRef]
- Toribio, J.; Matos, J.C.; González, B. Influence of crack micro-roughness on the plasticity-induced fatigue propagation in high strength steel. Frat. Integrità Strutt. 2017, 41, 62–65. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toribio, J.; Matos, J.-C.; González, B. Numerical Modeling of Plasticity-Induced Fatigue Crack Growth Retardation Due to Deflection in the Near-Tip Area. Metals 2021, 11, 541. https://doi.org/10.3390/met11040541
Toribio J, Matos J-C, González B. Numerical Modeling of Plasticity-Induced Fatigue Crack Growth Retardation Due to Deflection in the Near-Tip Area. Metals. 2021; 11(4):541. https://doi.org/10.3390/met11040541
Chicago/Turabian StyleToribio, Jesús, Juan-Carlos Matos, and Beatriz González. 2021. "Numerical Modeling of Plasticity-Induced Fatigue Crack Growth Retardation Due to Deflection in the Near-Tip Area" Metals 11, no. 4: 541. https://doi.org/10.3390/met11040541
APA StyleToribio, J., Matos, J.-C., & González, B. (2021). Numerical Modeling of Plasticity-Induced Fatigue Crack Growth Retardation Due to Deflection in the Near-Tip Area. Metals, 11(4), 541. https://doi.org/10.3390/met11040541






