Hot Deformation Constitutive Equation and Plastic Instability of 30Cr4MoNiV Ultra-High-Strength Steel
Abstract
:1. Introduction
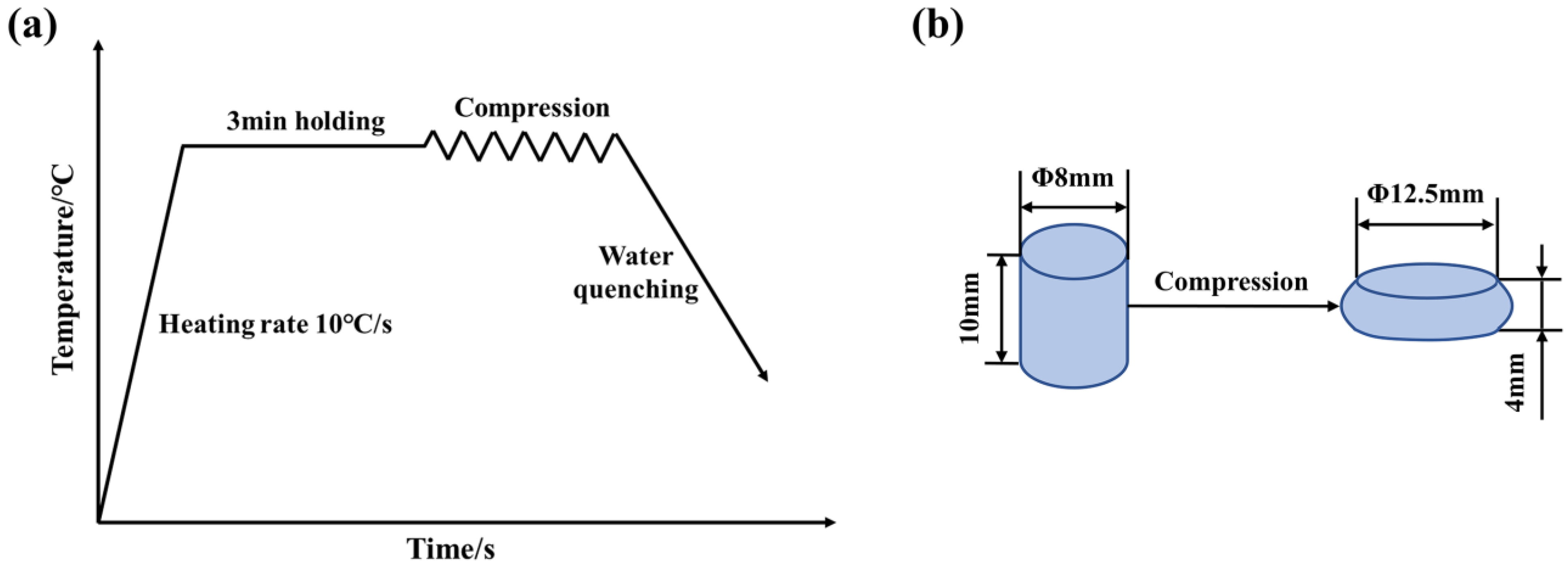
2. Materials and Methods
3. Results and Discussion
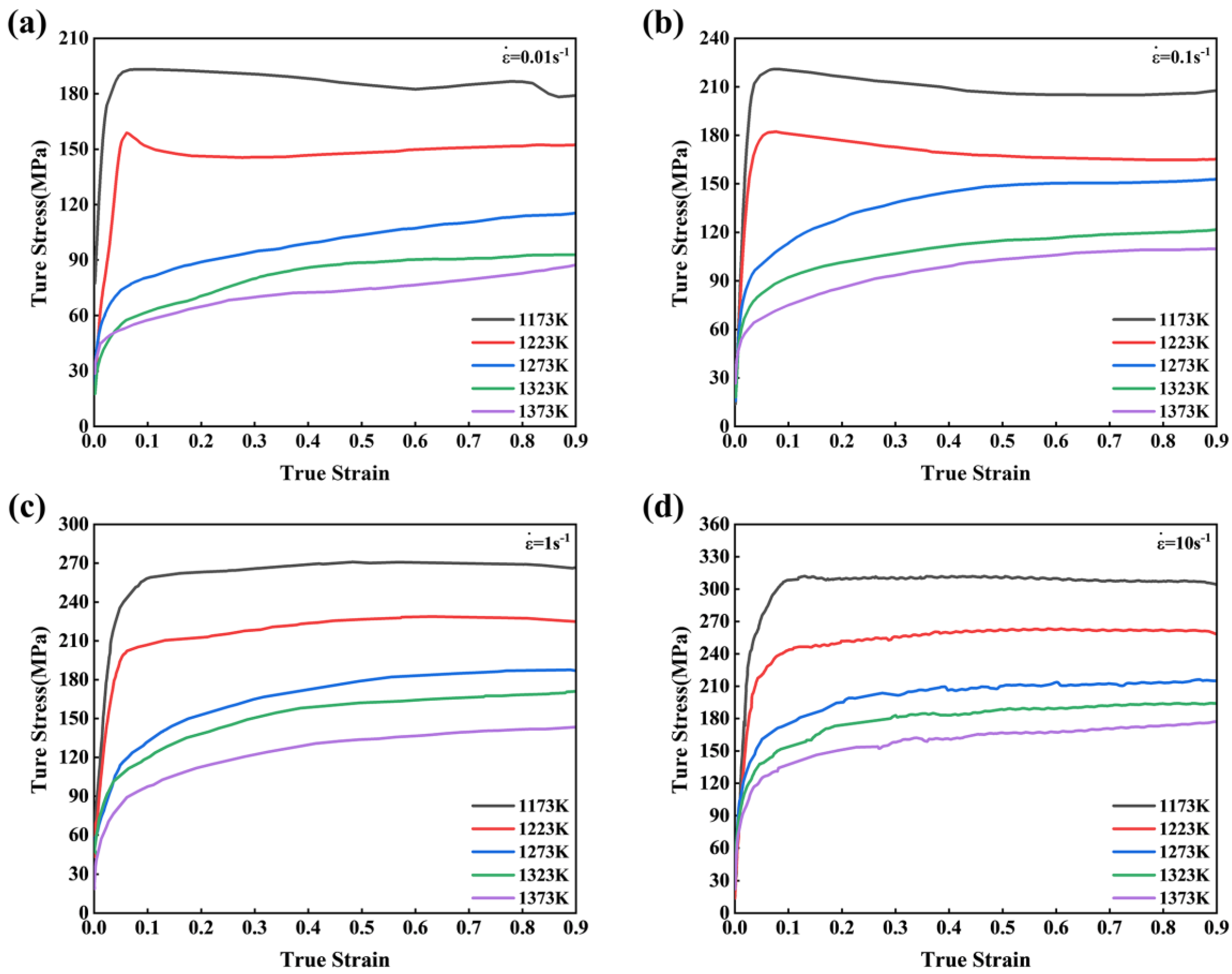
3.1. Stress-Strain Curves
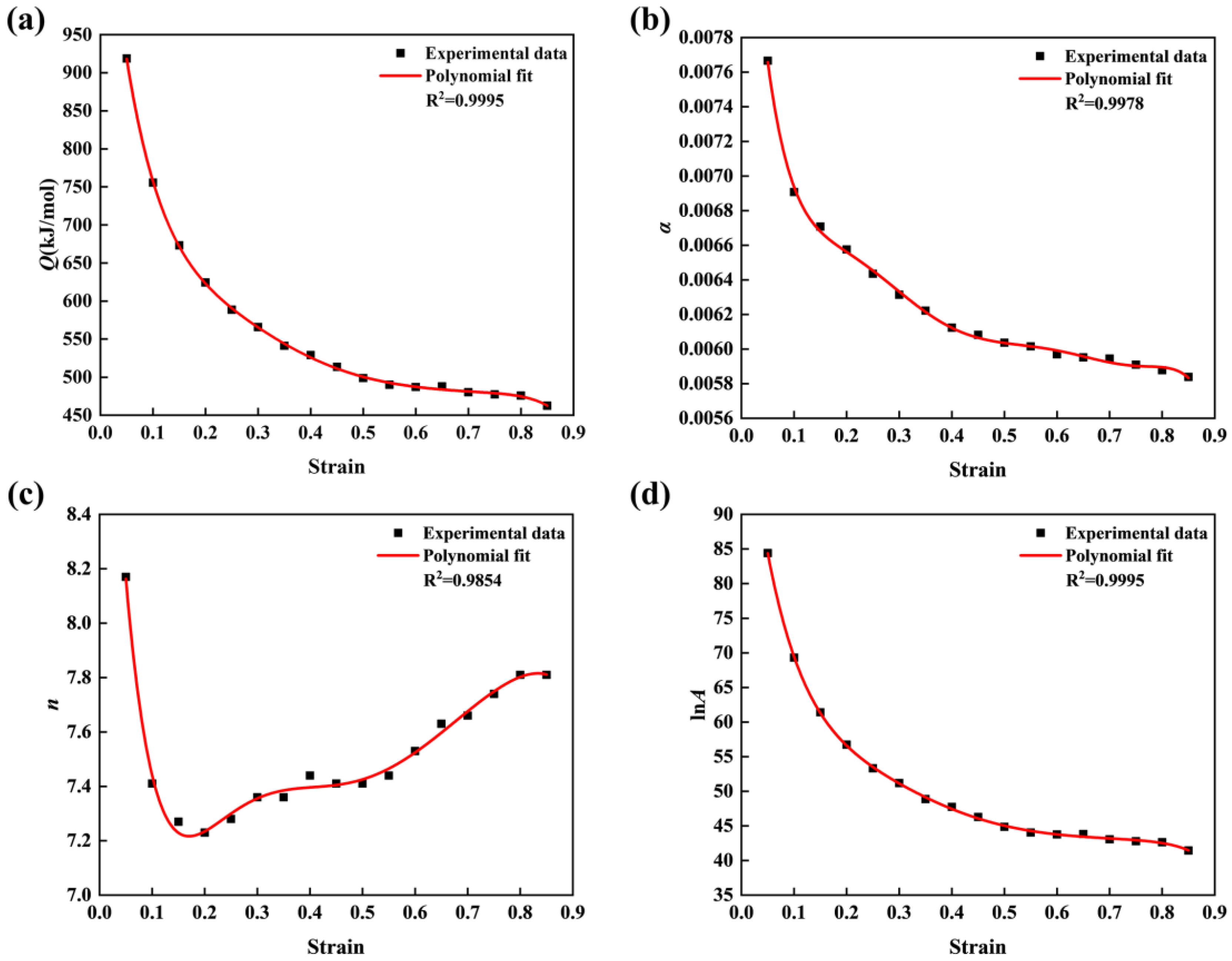
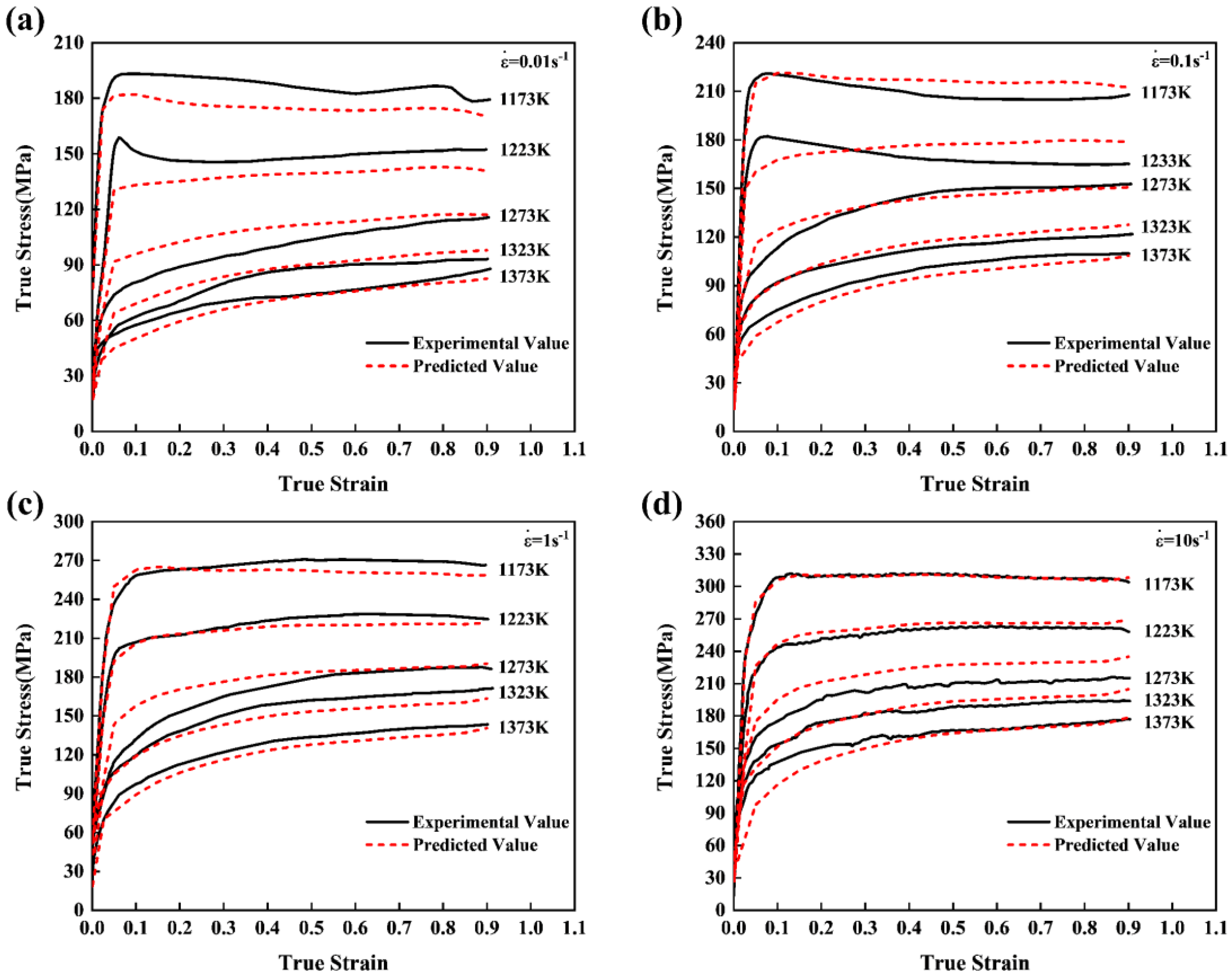
3.2. Constitutive Equation
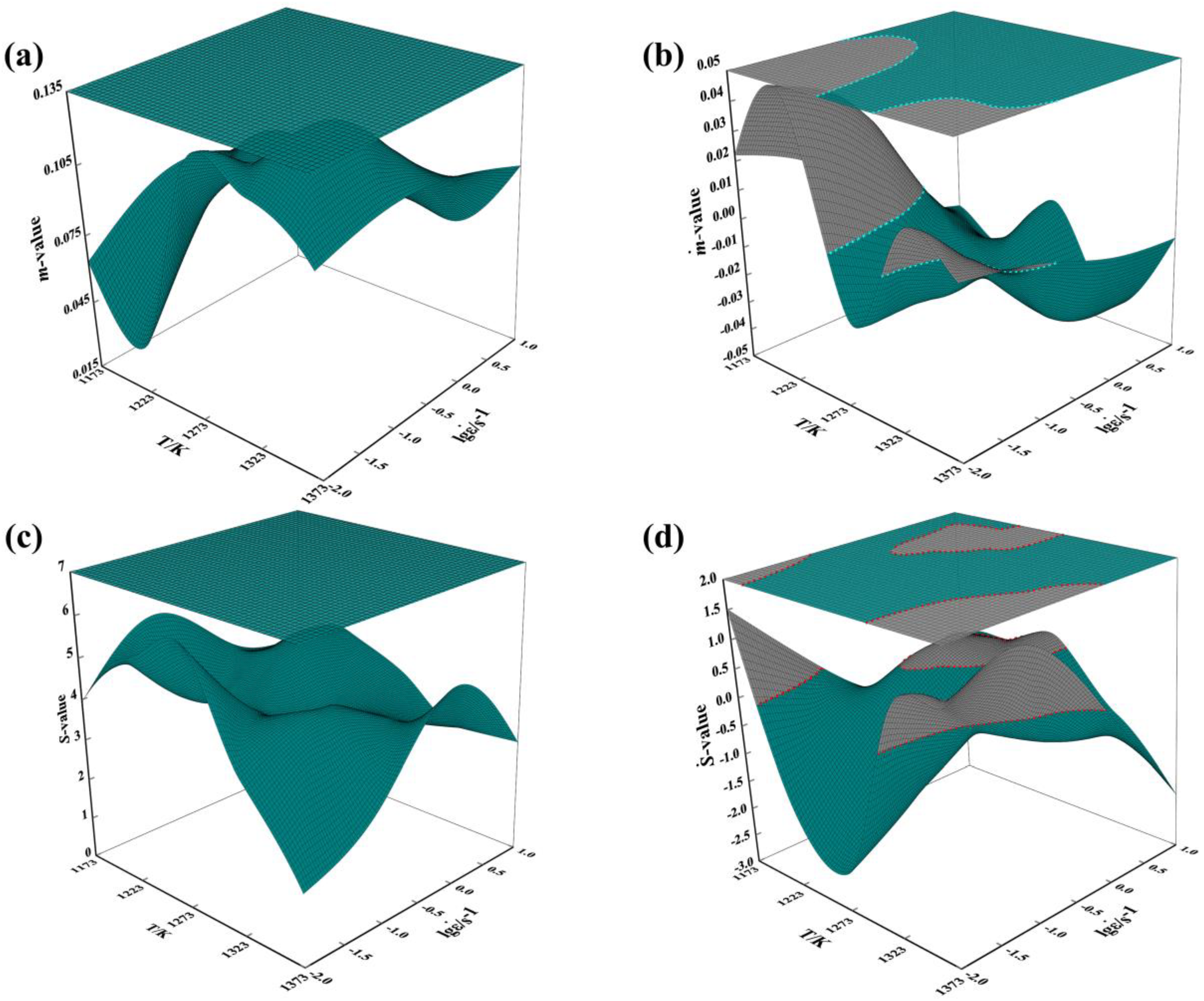
3.3. Processing Maps and Plastic Instability
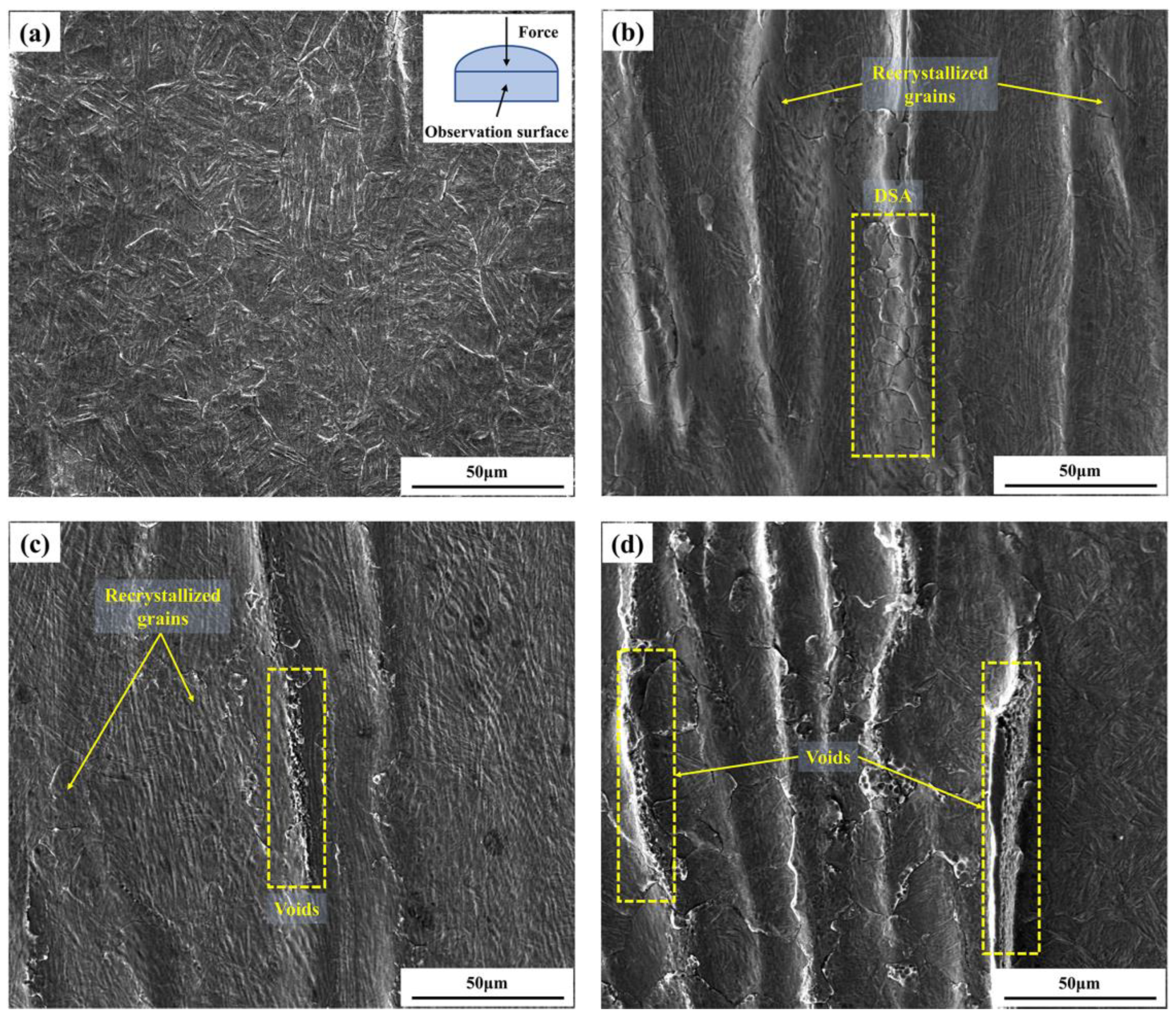
3.4. Microstructure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schiesaro, I.; Anzellini, S.; Loria, R.; Torchio, R.; Spina, T.; Flükiger, R.; Irifune, T.; Silva, E.; Meneghini, C. Anomalous Behavior in the Atomic Structure of Nb 3 Sn under High Pressure. Crystals 2021, 11, 331. [Google Scholar] [CrossRef]
- Errandonea, D.; Meng, Y.; Somayazulu, M.; Häusermann, D. Pressure-induced α→ω transition in titanium metal: A systematic study of the effects of uniaxial stress. Phys. B Phys. Condens. Matter 2005, 355, 116–125. [Google Scholar] [CrossRef] [Green Version]
- MacLeod, S.G.; Errandonea, D.; Cox, G.A.; Cynn, H.; Daisenberger, D.; Finnegan, S.E.; McMahon, M.I.; Munro, K.A.; Popescu, C.; Storm, C.V. The phase diagram of Ti-6Al-4V at high-pressures and high-temperatures. J. Phys. Condens. Matter 2021, 33, 154001. [Google Scholar] [CrossRef] [PubMed]
- Sellars, C.M.; Mctegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.-S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Lei, B.; Chen, G.; Liu, K.; Wang, X.; Jiang, X.; Pan, J.; Shi, Q. Constitutive Analysis on High-Temperature Flow Behavior of 3Cr-1Si-1Ni Ultra-High Strength Steel for Modeling of Flow Stress. Metals 2019, 9, 42. [Google Scholar] [CrossRef] [Green Version]
- Rao, K.P.; Prasad, Y.K.D.V. Hot deformation studies on a low-carbon steel: Part 1—Flow curves and the constitutive relationship. J. Mater. Process. Technol. 1996, 56, 897–907. [Google Scholar] [CrossRef]
- Jha, J.S.; Toppo, S.P.; Singh, R.; Tewari, A.; Mishra, S.K. Flow stress constitutive relationship between lamellar and equiaxed microstructure during hot deformation of Ti-6Al-4V. J. Mater. Process. Technol. 2019, 270, 216–227. [Google Scholar] [CrossRef]
- Xiong, W.; Song, R.; Yu, P.; Liu, Z.; Qin, S.; Zhang, Y.; Quan, S.; Huo, W.; Zhao, Z.; Su, S.; et al. Hot Deformation Behavior of V–Ti Microalloy Steels. Steel Res. Int. 2020, 92, 2000225. [Google Scholar] [CrossRef]
- Chen, Z.; Nash, P. Hot Deformation Behavior and Processing Maps for a Large Marine Crankshaft S34MnV Steel. Steel Res. Int. 2018, 89, 1700321. [Google Scholar] [CrossRef]
- Babaniaris, S.; Ramajayam, M.; Jiang, L.; Varma, R.; Langan, T.; Dorin, T. Effect of Al3(Sc,Zr) dispersoids on the hot deformation behaviour of 6xxx-series alloys: A physically based constitutive model. Mater. Sci. Eng. A 2020, 793, 139873. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Guo, C.; Guo, X.Y. Constitutive modeling of hot deformation behavior of H62 brass. Mater. Sci. Eng. A 2011, 528, 6510–6518. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X. Microstructure and plastic instability criteria of Mg-Gd-Y-Zr alloy during hot compression. Chin. J. Nonferrous Met. 2014, 24, 2961–2968. [Google Scholar]
- Ahamed, H.; Senthilkumar, V. Hot deformation behavior of mechanically alloyed Al6063/0.75Al2O3/0.75Y2O3 nano-composite—A study using constitutive modeling and processing map. Mater. Sci. Eng. A 2012, 539, 349–359. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K. Modeling of Dynamic Material Behavior in Hot Deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15A, 1883–1892. [Google Scholar] [CrossRef]
- Quan, G.Z.; Zhao, L.; Chen, T.; Wang, Y.; Mao, Y.P.; Lv, W.Q.; Zhou, J. Identification for the optimal working parameters of as-extruded 42CrMo high-strength steel from a large range of strain, strain rate and temperature. Mater. Sci. Eng. A 2012, 538, 364–373. [Google Scholar] [CrossRef]
- Zhai, R.; Wang, W.; Ma, R.; Zhang, S.; Ma, S.; Li, L.; Gong, S.; Zhang, H. Hot Deformation Behavior and Processing Map of As-Cast 40CrNiMo Alloy Steel. J. Mater. Eng. Perform. 2020, 29, 964–974. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, R.; Li, J.; Kou, H.; Li, H.; Chang, H.; Fu, H. Characterization of hot deformation behavior of Haynes230 by using processing maps. J. Mater. Process. Technol. 2009, 209, 4020–4026. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, F.; Shuang, Y.; Ma, L.; Chu, Z.; Zhao, C. Characterization of hot deformation behavior of as-extruded AZ31 alloy through kinetic analysis and processing maps. J. Mater. Process. Technol. 2020, 276, 116325. [Google Scholar] [CrossRef]
- Murty, S.V.S.N.; Rao, B.N.; Kashyap, B.P. On the hot working characteristics of 2014 Al–20 vol% Al2O3 metal matrix composite. J. Mater. Process. Technol. 2005, 166, 279–285. [Google Scholar] [CrossRef]
- Poletti, C.; Six, J.; Hochegger, M.; Degischer, H.P.; Ilie, S. Hot Deformation Behaviour of Low Alloy Steel. Steel Res. Int. 2011, 82, 710–718. [Google Scholar] [CrossRef]
- Rajput, S.K.; Chaudhari, G.P.; Nath, S.K. Characterization of hot deformation behavior of a low carbon steel using processing maps, constitutive equations and Zener-Hollomon parameter. J. Mater. Process. Technol. 2016, 237, 113–125. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K. Modelling of hot deformation for microstructural control. Int. Mater. Rev. 1998, 43, 243–258. [Google Scholar] [CrossRef]
- Xu, L.W.; Li, H.B.; Jiang, Z.H.; Cai, M.H.; Jiao, W.C.; Feng, H.; Zhang, S.C.; Lu, P.C. Hot Deformation Behavior of P550 Steels for Nonmagnetic Drilling Collars. Steel Res. Int. 2020, 91, 2000035. [Google Scholar] [CrossRef]
- Chen, L.; Xue, H.; Ma, X.; Jin, M.; Long, H.; Mao, T.; Wang, J. Processing Map and Hot Deformation Characteristics of 21Cr-11Ni-N-RE Lean Austenitic Heat-Resistant Steel. Steel Res. Int. 2015, 86, 1583–1593. [Google Scholar] [CrossRef]
- Ivanchenko, M.; Nevdacha, V.; Yagodzinskyy, Y.; Hänninen, H. Internal friction studies of carbon and its redistribution kinetics in Inconel 600 and 690 alloys under dynamic strain aging conditions. Mater. Sci. Eng. A 2006, 442, 458–461. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Prado, J.M.; Najafizadeh, A. Hot deformation behavior of a medium carbon microalloyed steel. Mater. Sci. Eng. A 2011, 528, 3876–3882. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A.; Moazeny, M. Flow curve analysis of 17-4 PH stainless steel under hot compression test. Metall. Mater. Trans. A 2009, 40, 2950–2958. [Google Scholar] [CrossRef]
- McQueen, H.J. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Cai, D.; Xiong, L.; Liu, W.; Sun, G.; Yao, M. Characterization of hot deformation behavior of a Ni-base superalloy using processing map. Mater. Des. 2009, 30, 921–925. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.; Yu, J.; Zhang, W. Constitutive analysis of homogenized 7005 aluminum alloy at evaluated temperature for extrusion process. Mater. Des. 2015, 66, 129–136. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Wang, J.G.; Wang, H.P.; Hu, Y.; Rao, H.D. Characterization of hot deformation behavior of 30Si2MnCrMoVE low-alloying ultra-high-strength steel by constitutive equations and processing maps. J. Iron Steel Res. Int. 2020, 27, 807–819. [Google Scholar] [CrossRef]
- Dong, J.; Li, C.; Liu, C.; Huang, Y.; Yu, L.; Li, H.; Liu, Y. Hot deformation behavior and microstructural evolution of Nb–V–Ti microalloyed ultra-high strength steel. J. Mater. Res. 2017, 32, 3777–3787. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti–6Al–4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Li, M.; Duan, Y.; Yao, D.; Guan, Y.; Yang, L. Constitutive Model and Flow Behavior of B1500HS High-Strength Steel during the Hot Deformation Process. Metals 2019, 10, 64. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Zhang, J.; Yang, B.; Li, Y.F.; Huang, J.F.; Lian, Y. Hot Deformation Characteristics and Processing Map of 1Cr12Ni2Mo2WVNb Martensitic Stainless Steel. Steel Res. Int. 2020, 91, 2000020. [Google Scholar] [CrossRef]





| C | Si | Mn | Cr | Ni | Mo | V | Al | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.30 | 0.24 | 0.94 | 3.85 | 0.67 | 1.31 | 0.35 | 0.05 | Bal. |
| Strain Rate [s−1] | Deformation Temperature [K] | ||||
|---|---|---|---|---|---|
| 1173 | 1223 | 1273 | 1323 | 1373 | |
| 0.01 | 193.24 | 158.85 | 115.62 | 93.17 | 87.91 |
| 0.1 | 221.00 | 182.26 | 152.81 | 121.79 | 109.83 |
| 1 | 270.99 | 228.80 | 187.61 | 171.35 | 143.43 |
| 10 | 311.71 | 263.33 | 215.62 | 194.19 | 177.01 |
| Polynomial Coefficients | The Material-Dependent Constants | |||
|---|---|---|---|---|
| Q [kJ/mol] | α | n | ln A | |
| B0 | 1219.831 | 0.00949 | 9.893 | 111.708 |
| B1 | −8053.152 | −0.0543 | −49.28 | −722.781 |
| B2 | 48,062.003 | 0.43802 | 350.185 | 4164.055 |
| B3 | −168,839.713 | −1.90727 | −1248.333 | −14,174.679 |
| B4 | 350,611.446 | 4.63567 | 2480.95 | 28,607.488 |
| B5 | −424,298.811 | −6.31237 | −2796.554 | −33,725.332 |
| B6 | 277,595.681 | 4.50402 | 1684.091 | 21,550.56 |
| B7 | −76,115.557 | −1.31131 | −424.078 | −5790.606 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Yao, Y.; Jia, Y.; Su, B.; Liu, G.; Zeng, B. Hot Deformation Constitutive Equation and Plastic Instability of 30Cr4MoNiV Ultra-High-Strength Steel. Metals 2021, 11, 769. https://doi.org/10.3390/met11050769
Chen G, Yao Y, Jia Y, Su B, Liu G, Zeng B. Hot Deformation Constitutive Equation and Plastic Instability of 30Cr4MoNiV Ultra-High-Strength Steel. Metals. 2021; 11(5):769. https://doi.org/10.3390/met11050769
Chicago/Turabian StyleChen, Gang, Yuanchao Yao, Yuzhen Jia, Bin Su, Guoyue Liu, and Bin Zeng. 2021. "Hot Deformation Constitutive Equation and Plastic Instability of 30Cr4MoNiV Ultra-High-Strength Steel" Metals 11, no. 5: 769. https://doi.org/10.3390/met11050769






