A Mixed Numerical-Experimental Method to Characterize Metal-Polymer Interfaces for Crash Applications
Abstract
:1. Introduction
2. Materials and Methods
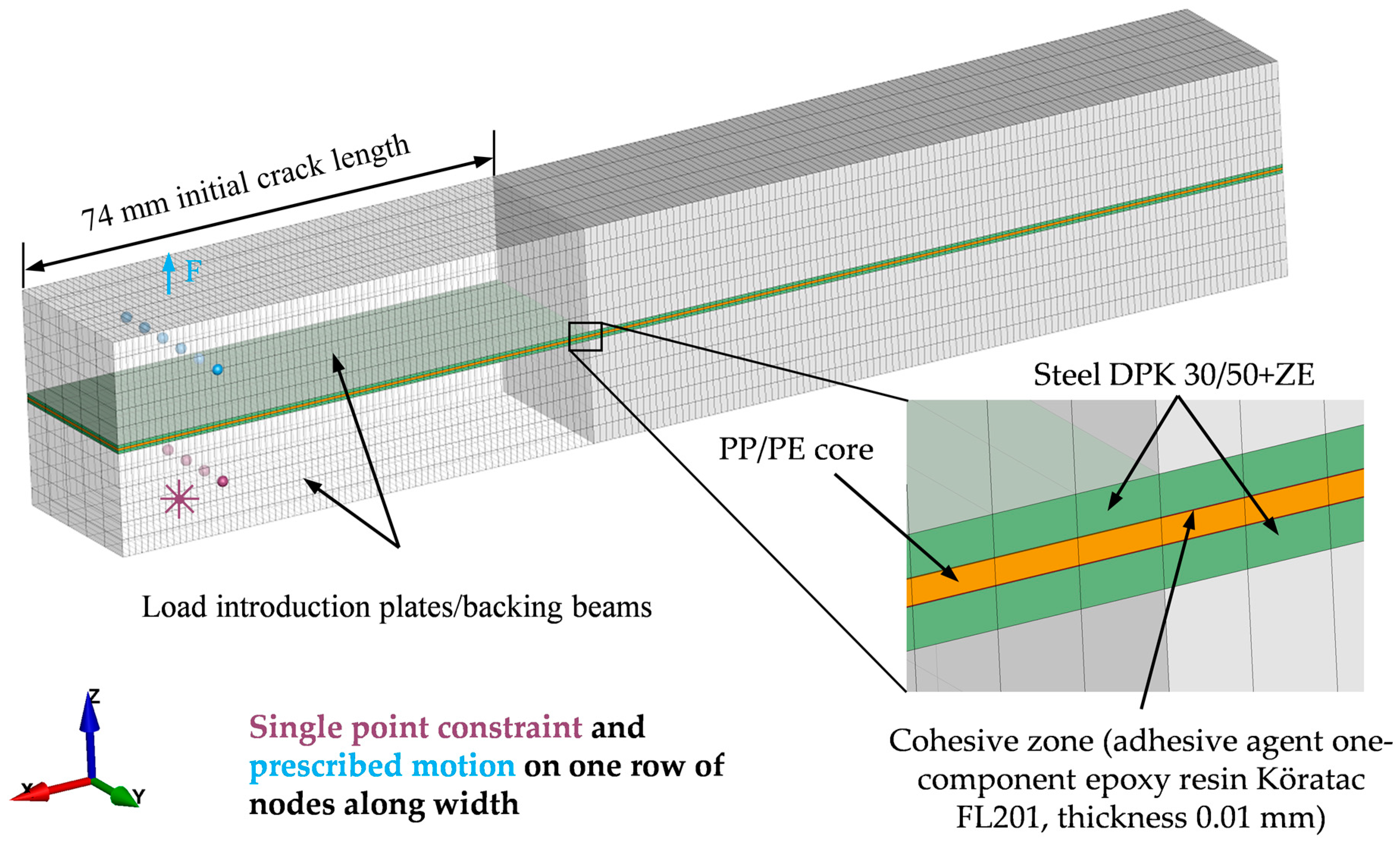
2.1. Mixed Numerical-Experimental Characterization Method
2.2. Investigated Material Configurations
2.3. Experimental Data Analysis
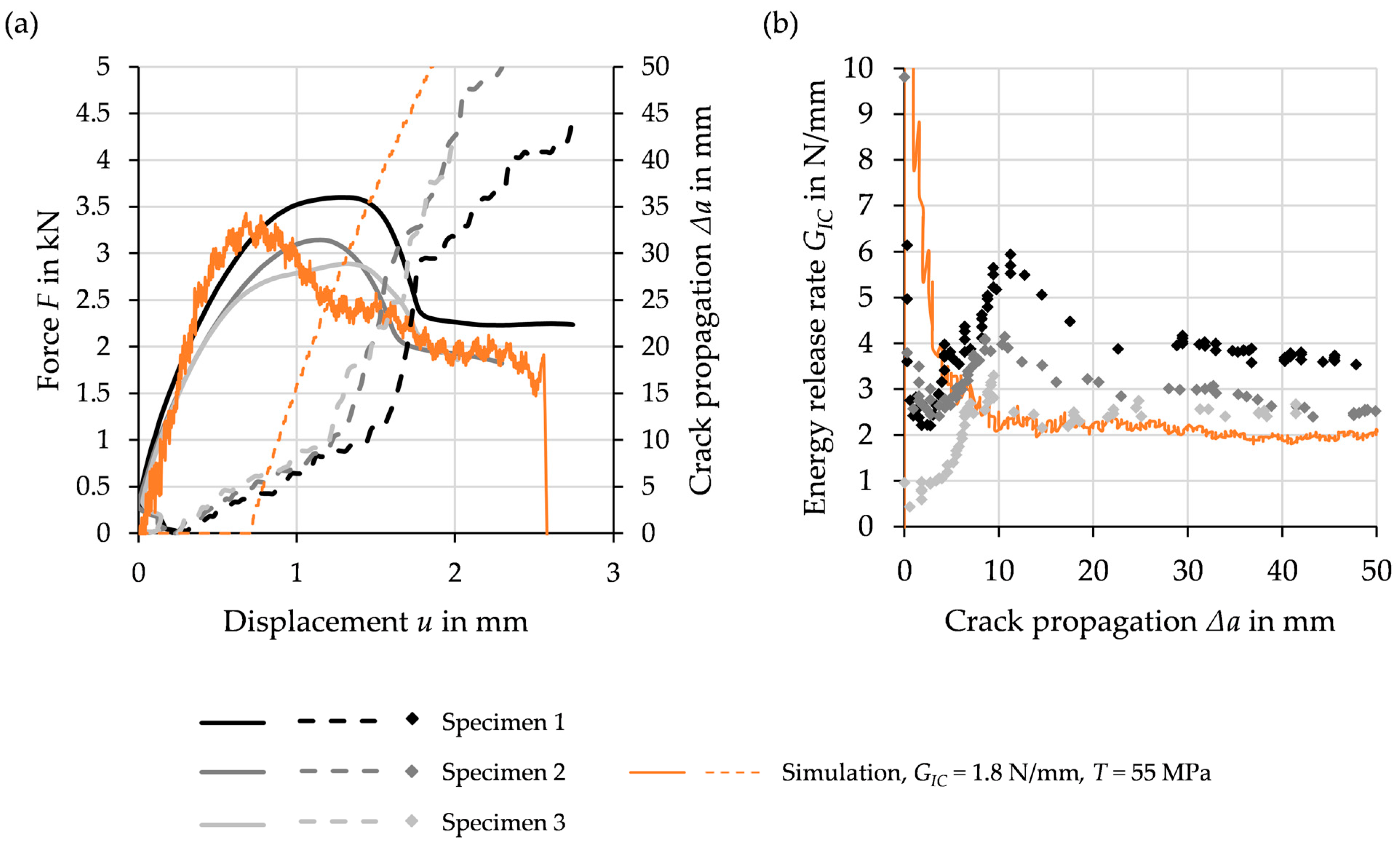
3. Results
3.1. Sepcimen Development
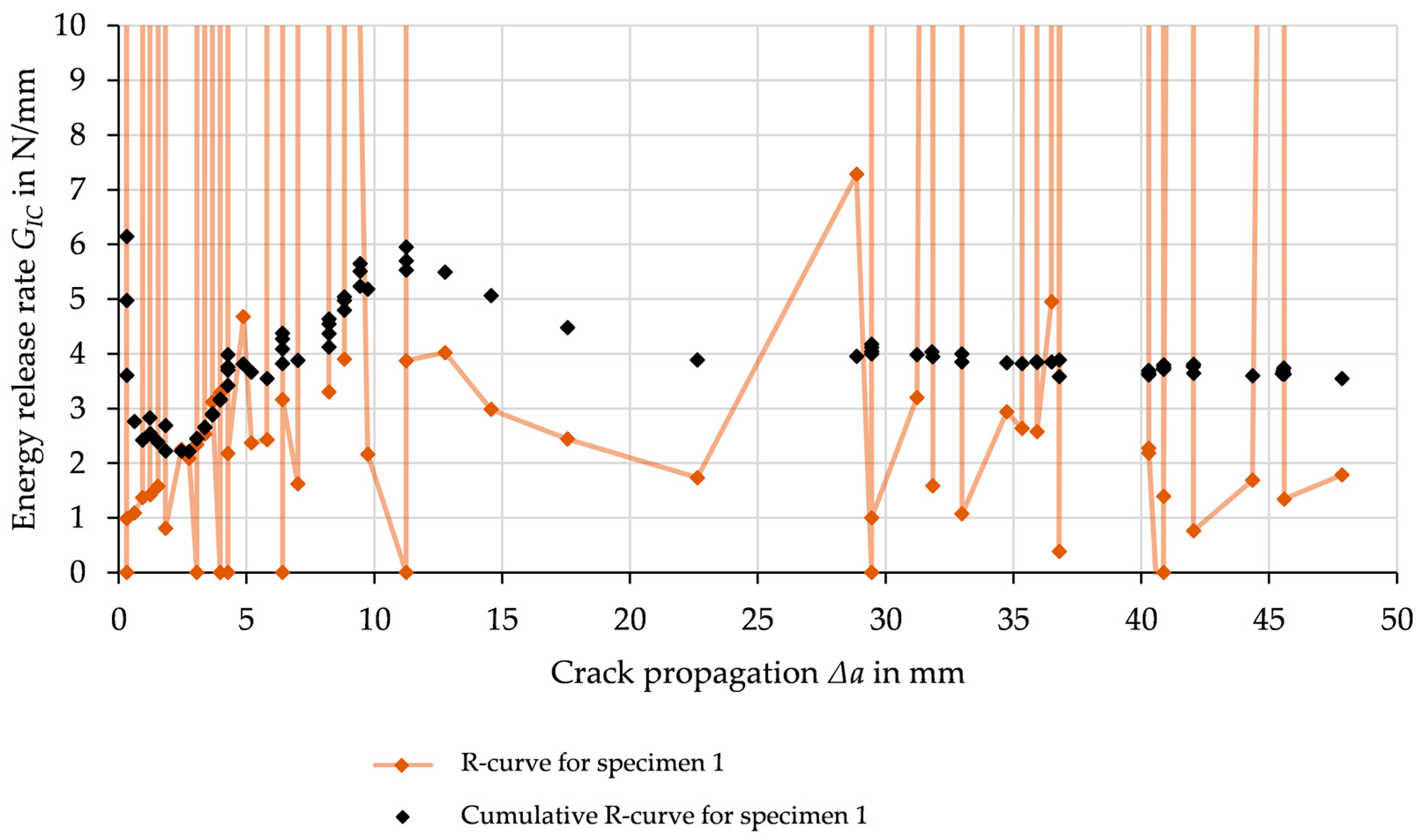
3.2. DCB Experiments
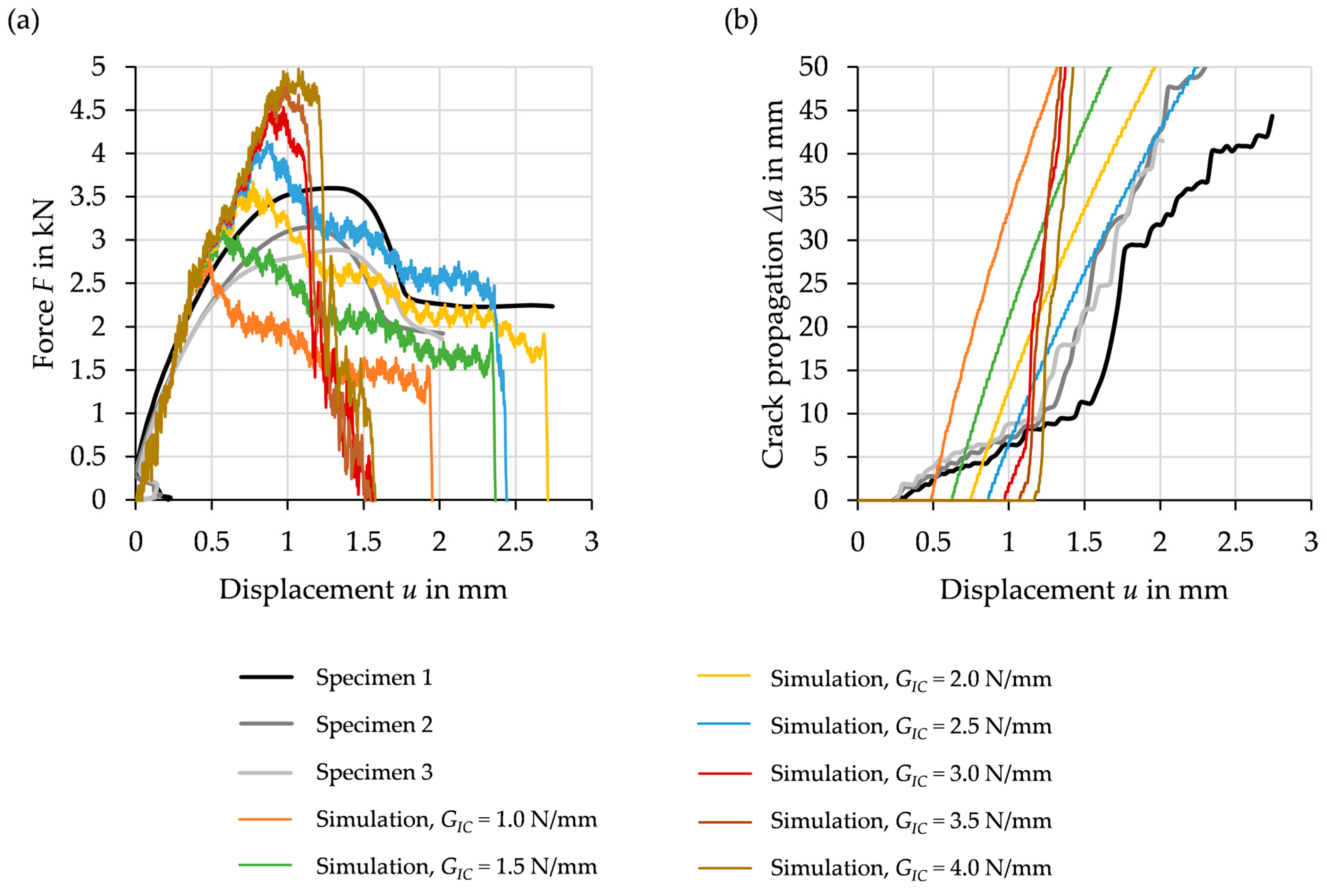
3.3. Simulation Methodology and Initial CZM
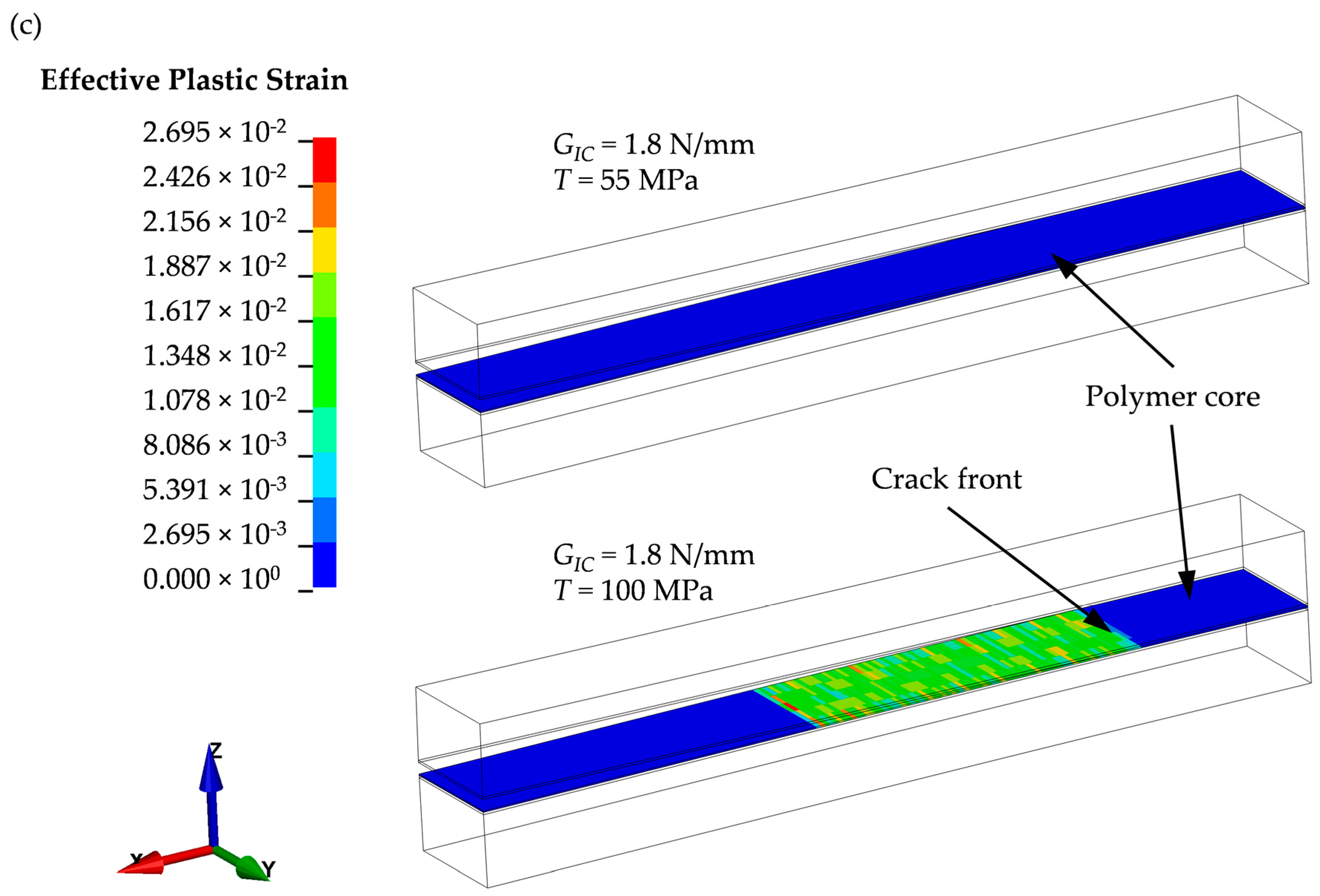
3.4. Recalibarion of the CZM
4. Discussion
4.1. Discussion on Experimental Results
4.2. Discussion on Numerical-Experimental Recalibration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hufenbach, W.; Jaschniski, J.; Weber, T.; Weck, D. Numerical and experimental investigations on HYLITE sandwich sheets as an alternative sheet metal. Arch. Civ. Mech. Eng. 2008, 8, 67–80. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, H.; Luo, J.; Li, N. A review on forming technologies of fibre metal laminates. Int. J. Lightweight Mater. Manuf. 2021, 4, 110–126. [Google Scholar] [CrossRef]
- ThyssenKrupp Steel Europe AG. BONDAL® Composite Material with Structure-Borne Sound Damping Properties. Available online: https://www.thyssenkrupp-steel.com/en/products/composite-material/overview-composite-material.html (accessed on 3 March 2021).
- 3A Composites GmbH. ALUCOBOND® for Transport and Industry. Available online: https://alucobond.com/alucobond-technical-data.html (accessed on 3 March 2021).
- Harhash, M.; Sokolova, O.; Carradò, A.; Palkowski, H. Mechanical properties and forming behaviour of laminated steel/polymer sandwich systems with local inlays-Part 1. Compos. Struct. 2014, 118, 112–120. [Google Scholar] [CrossRef]
- Kuhtz, M.; Buschner, N.; Henseler, T.; Hornig, A.; Klaerner, M.; Ullmann, M.; Jäger, H.; Kroll, L.; Kawalla, R. An experimental study on the bending response of multi-layered fibre-metal-laminates. J. Compos. Mater. 2019, 53, 2579–2591. [Google Scholar] [CrossRef] [Green Version]
- Harhash, M.; Kuhtz, M.; Richter, J.; Hornig, A.; Gude, M.; Palkowski, H. Trigger geometry influencing the failure modes in steel/polymer/steel sandwich crashboxes: Experimental and numerical evaluation. Compos. Struct. 2021, 262, 113619. [Google Scholar] [CrossRef]
- Ning, H.; Li, Y.; Hu, N. Improvement of interlaminar mechanical properties of CARALL based on nanofiller interface reinforcement and other fabrication techniques. In Proceedings of the 13th International Conference on Fracture, Beijing, China, 16–21 June 2013; pp. 1–11. [Google Scholar]
- Manikandan, P.; Chai, G.B. Mode-I Metal-Composite Interface Fracture Testing for Fibre Metal Laminates. J. Adv. Mater. Sci. Eng. 2018, 2018, 4572989. [Google Scholar] [CrossRef] [Green Version]
- Linde, P.; Pleitner, J.; de Boer, H.; Sinke, J. Numerical and experimental simulation of damage behaviour of fibre metal laminates. In Proceedings of the ICAS 2004-24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004; pp. 1–9. [Google Scholar]
- Hader-Kregl, L.; Wallner, G.M.; Kralovec, C.; Eyßell, C. Effect of inter-plies on the short beam shear delamination of steel/composite hybrid laminates. J. Adhes. 2019, 95, 1088–1100. [Google Scholar] [CrossRef]
- Uzay, C.; Bayramoglu, M.; Boztepe, M.H.; Necdet, G. Adhesion Surface Bonding Capability of Different Metal Sheets for Fiber Metal Laminate (FML) Applications. In Proceedings of the 1st International Mediterranean Science and Engineering Congress (IMSEC 2016), Adana, Turkey, 26–28 October 2016; pp. 1–9. [Google Scholar]
- Abdullah, M.R.; Prawoto, Y.; Cantwell, W.J. Interfacial fracture of the fibre-metal laminates based on fibre reinforced thermoplastics. Mater. Des. 2015, 66, 446–452. [Google Scholar] [CrossRef]
- Guillen, J.F.; Cantwell, W.J. The influence of cooling rate on the fracture properties of a glass reiforced/nylon fiber-metal laminate. Polym. Compos. 2002, 23, 839–851. [Google Scholar] [CrossRef]
- ASTM D 5379. Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- ASTM D 5528. Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM D 7291. Test Method for Through-Thickness Flatwise Tensile Strength and Elastic Modulus of a Fiber-Reinforced Polymer Matrix Composite Material; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Ostapiuk, M.; Bieniaś, J.; Surowska, B. Analysis of the bending and failure of fiber metal laminates based on glass and carbon fibers. Sci. Eng. Compos. Mater. 2018, 25, 1095–1106. [Google Scholar] [CrossRef]
- Wollmann, T.; Hahn, M.; Wiedemann, S.; Zeiser, A.; Jaschinski, J.; Modler, N.; Ben Khalifa, N.; Meißen, F.; Paul, C. Thermoplastic fibre metal laminates: Stiffness properties and forming behaviour by means of deep drawing. Arch. Civ. Mech. Eng. 2018, 18, 442–450. [Google Scholar] [CrossRef]
- Loutas, T.; Tsokanas, P.; Kostopoulos, V.; Nijhuis, P.; van den Brink, W.M. Mode I fracture toughness of asymmetric metal-composite adhesive joints. Mater. Today Proc. 2021, 34, 250–259. [Google Scholar] [CrossRef] [Green Version]
- Boeman, R.G.; Erdman, D.L.; Klett, L.B.; Lomax, R.D. A Practical Test Method for Mode I Fracture Toughness of Adhesive Joints with Dissimilar Substrates. In Proceedings of the SAMPE-ACCE-DOE Advanced Composites Conference, Detroit, MI, USA, 27–28 September 1999; pp. 1–9. [Google Scholar]
- Yousefi Kanani, A.; Green, S.; Hou, X.; Ye, J. Hybrid and adhesively bonded joints with dissimilar adherends: A critical review. J. Adhes. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Kuhtz, M.; Hornig, A.; Gude, M.; Jäger, H. A method to control delaminations in composites for adjusted energy dissipation characteristics. Mater. Des. 2017, 123, 103–111. [Google Scholar] [CrossRef]
- Tsartsaris, N.; Meo, M.; Dolce, F.; Polimeno, U.; Guida, M.; Marulo, F. Low-velocity impact behavior of fiber metal laminates. J. Compos. Mater. 2011, 45, 803–814. [Google Scholar] [CrossRef]
- Dogan, F.; Hadavinia, H.; Donchev, T.; Bhonge, P. Delamination of impacted composite structures by cohesive zone interface elements and tiebreak contact. Cent. Eur. J. Eng. 2012, 2, 612–626. [Google Scholar] [CrossRef] [Green Version]
- DIN EN 10346:2009-07. Continuously Hot-Dip Coated Steel Flat Products-Technical Delivery Conditions; German Version; Beuth Verlag GmbH: Berlin, Germany, 2009. [Google Scholar]
- Harhash, M. Forming Behaviour of Multilayer Metal/Polymer/Metal Systems. Ph.D. Thesis, TU Clausthal, Clausthal-Zellerfeld, Germany, 2017. [Google Scholar]
- Gajewski, T.; Garbowski, T. Mixed experimental/numerical methods applied for concrete parameters estimation. In Recent Advances in Computational Mechanics, Proceedings of the 20th International Conference on Computer Methods in Mechanics (CMM2013), Poznań, Poland, 27–31 August 2013; Łodygowski, T., Rakowski, J., Litewka, P., Eds.; CRC Press/Balkema: Leiden, The Netherlands, 2014; pp. 293–301. ISBN 978-1-138-02482-3. [Google Scholar]
- Garbowski, T.; Maier, G.; Novati, G. On calibration of orthotropic elastic-plastic constitutive models for paper foils by biaxial tests and inverse analyses. Struct. Multidisc. Optim. 2012, 46, 111–128. [Google Scholar] [CrossRef] [Green Version]


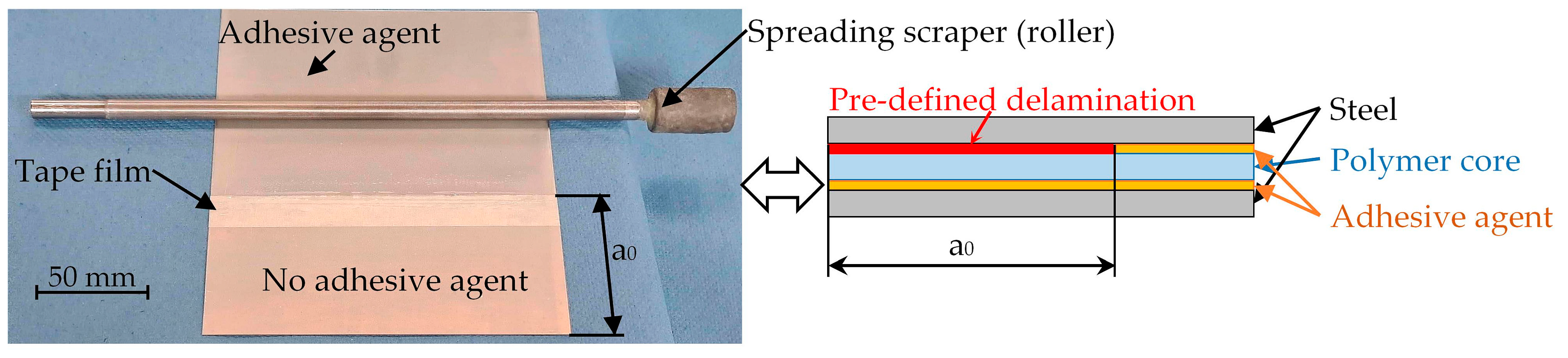
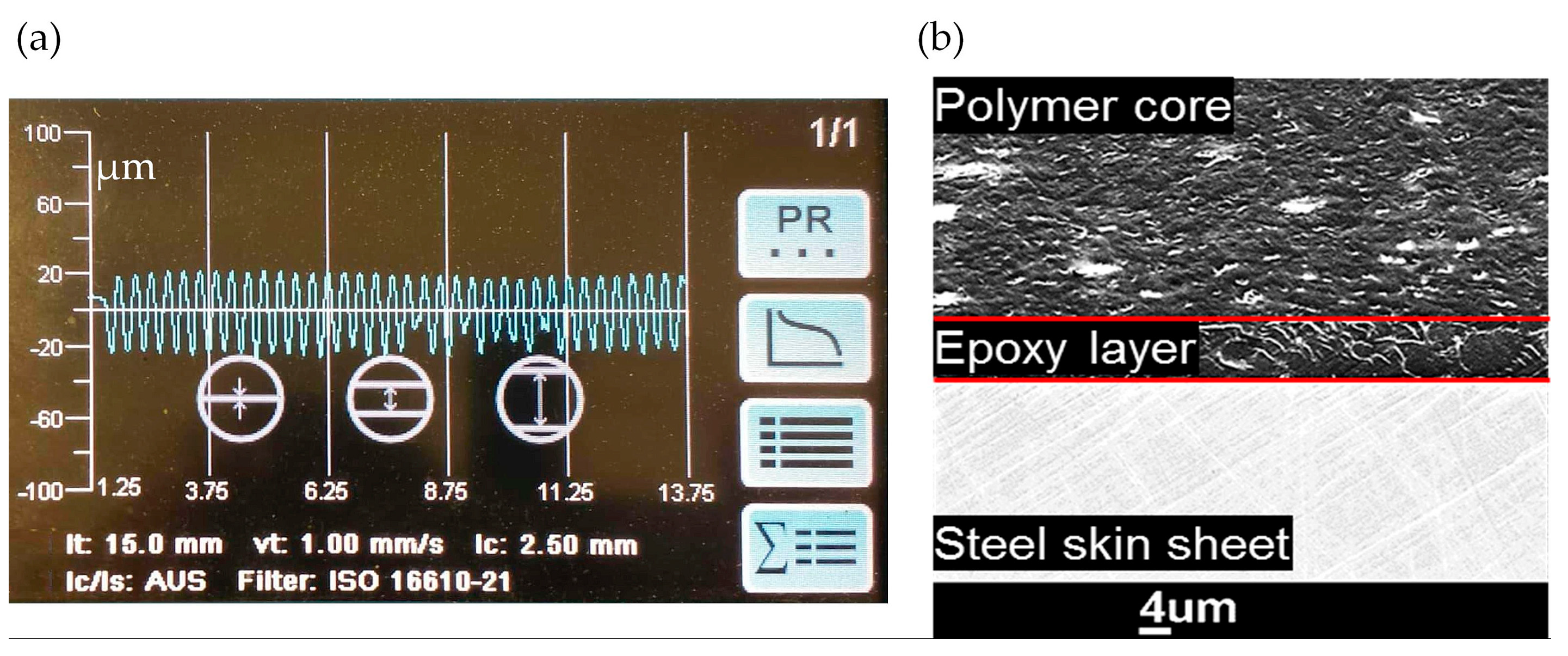

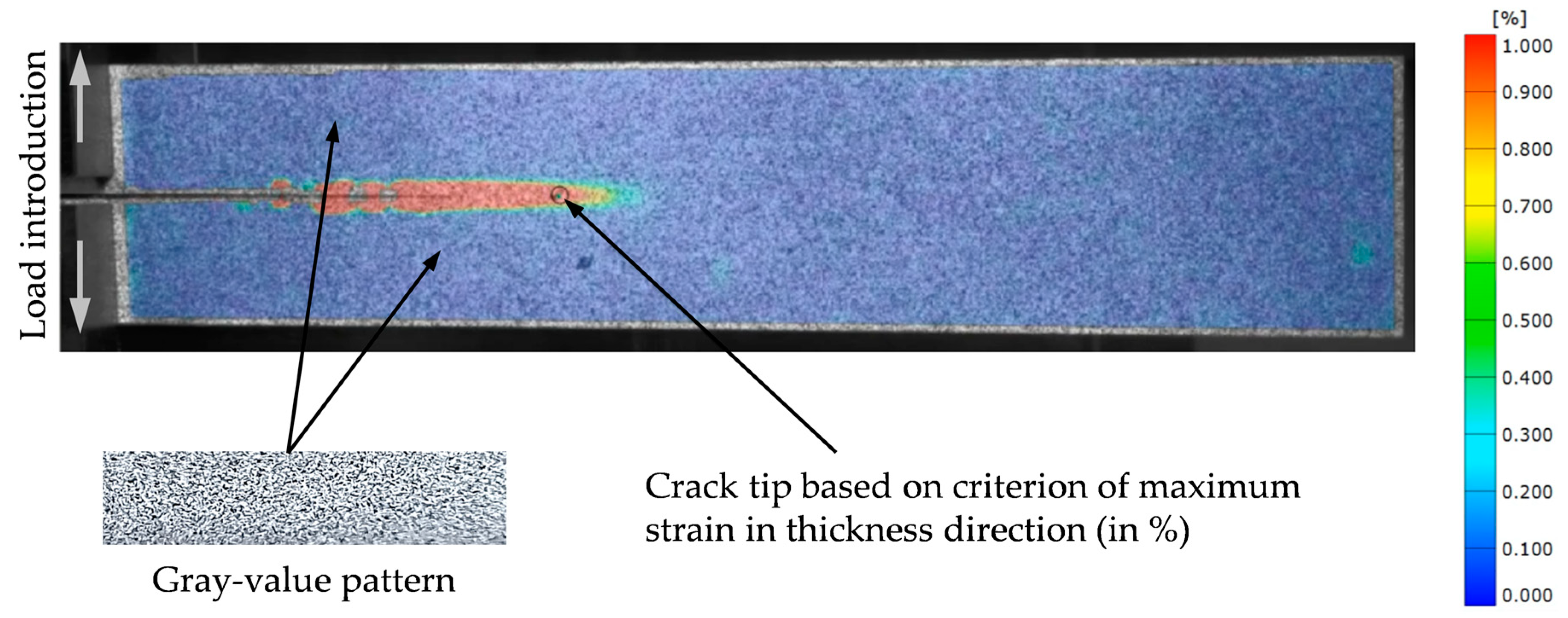



| Element | C, max. | Si, max. | Mn, max. | P, max. | S, max. | Al, total | Cr + Mo, max. | Nb + Ti, max. | V, max. | B, max. |
|---|---|---|---|---|---|---|---|---|---|---|
| Wt. % | 0.14 | 0.8 | 2.0 | 0.080 | 0.015 | ≤2.00 | 1.00 | 0.15 | 0.20 | 0.005 |
| Property | Value | Unit |
|---|---|---|
| Layer thickness, wet | 35 | µm |
| Layer thickness, dry | 7–15 | µm |
| Peak metal temperature | 216–241 | °C |
| Fraction of solid material | 30.9 | wt. % |
| Fraction of dissolvent | 69.1 | wt. % |
| *MAT_138/*MAT_COHESIVE_MIXED_MODE for MPM Interface before Recalibration | ||||||
|---|---|---|---|---|---|---|
| RO | EN | ET | GIC | GIIC | T | S |
| g/cm3 | GPa/mm | GPa/mm | N/mm | N/mm | MPa | MPa |
| 1.2 | 300 | 100 | 3 | 5 | 80 | 100 |
| *MAT_138/*MAT_COHESIVE_MIXED_MODE for MPM Interface after Recalibration | ||||||
|---|---|---|---|---|---|---|
| RO | EN | ET | GIC | GIIC | T | S |
| g/cm3 | GPa/mm | GPa/mm | N/mm | N/mm | MPa | MPa |
| 1.2 | 300 | 100 | 1.8 | 5 | 55 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richter, J.; Kuhtz, M.; Hornig, A.; Harhash, M.; Palkowski, H.; Gude, M. A Mixed Numerical-Experimental Method to Characterize Metal-Polymer Interfaces for Crash Applications. Metals 2021, 11, 818. https://doi.org/10.3390/met11050818
Richter J, Kuhtz M, Hornig A, Harhash M, Palkowski H, Gude M. A Mixed Numerical-Experimental Method to Characterize Metal-Polymer Interfaces for Crash Applications. Metals. 2021; 11(5):818. https://doi.org/10.3390/met11050818
Chicago/Turabian StyleRichter, Jonas, Moritz Kuhtz, Andreas Hornig, Mohamed Harhash, Heinz Palkowski, and Maik Gude. 2021. "A Mixed Numerical-Experimental Method to Characterize Metal-Polymer Interfaces for Crash Applications" Metals 11, no. 5: 818. https://doi.org/10.3390/met11050818
APA StyleRichter, J., Kuhtz, M., Hornig, A., Harhash, M., Palkowski, H., & Gude, M. (2021). A Mixed Numerical-Experimental Method to Characterize Metal-Polymer Interfaces for Crash Applications. Metals, 11(5), 818. https://doi.org/10.3390/met11050818








