A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata
Abstract
1. Introduction
2. Theoretical Model
2.1. Kinematics Model
2.2. Hardening Mechanism
2.3. Transformation Criterion
3. Implementation Process
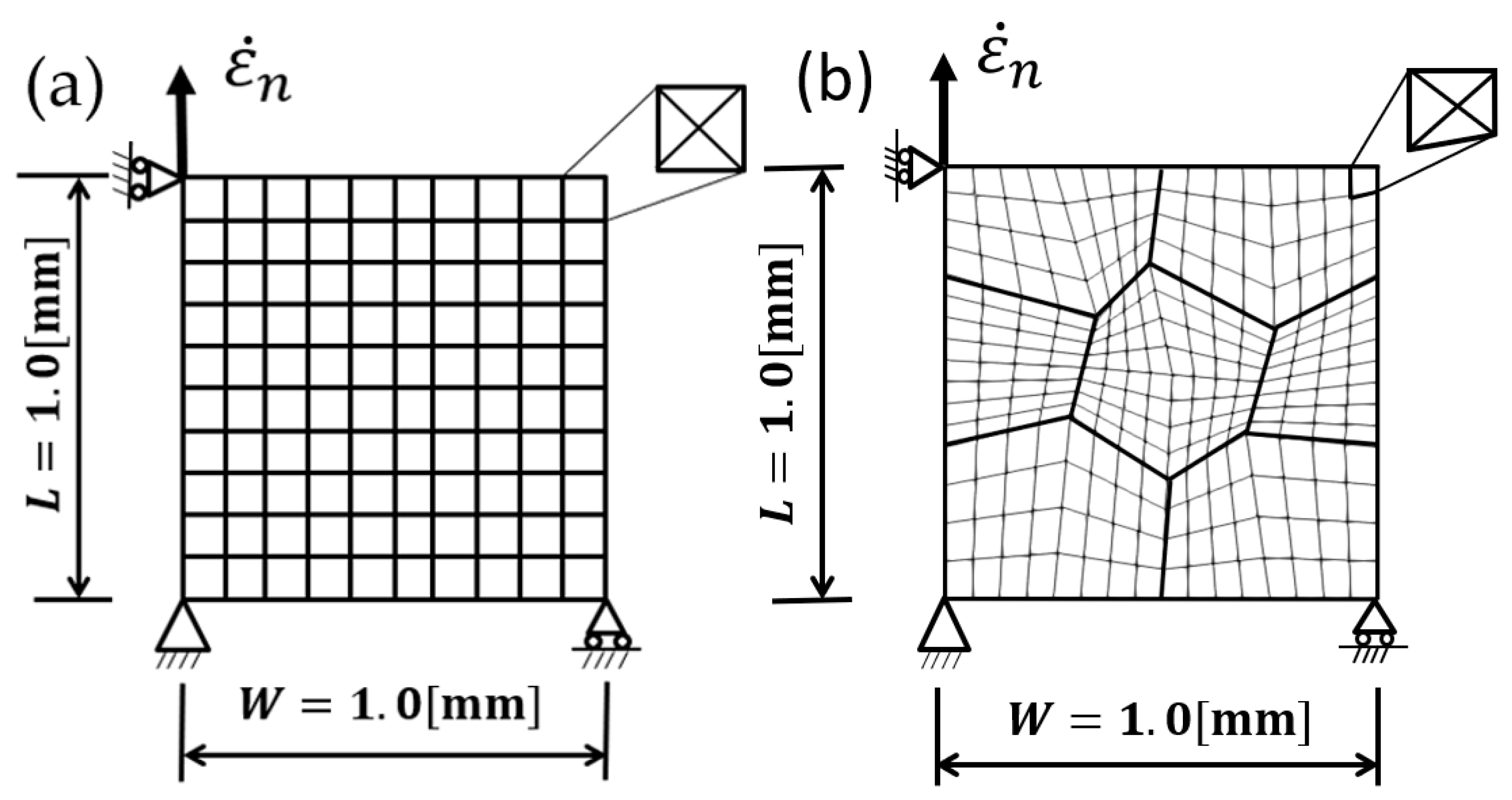
3.1. Finite Element Model and Boundary Conditions
3.2. Cellular Automata Approach
3.3. Material Constants and Parameters
4. Numerical Simulation and Discussion
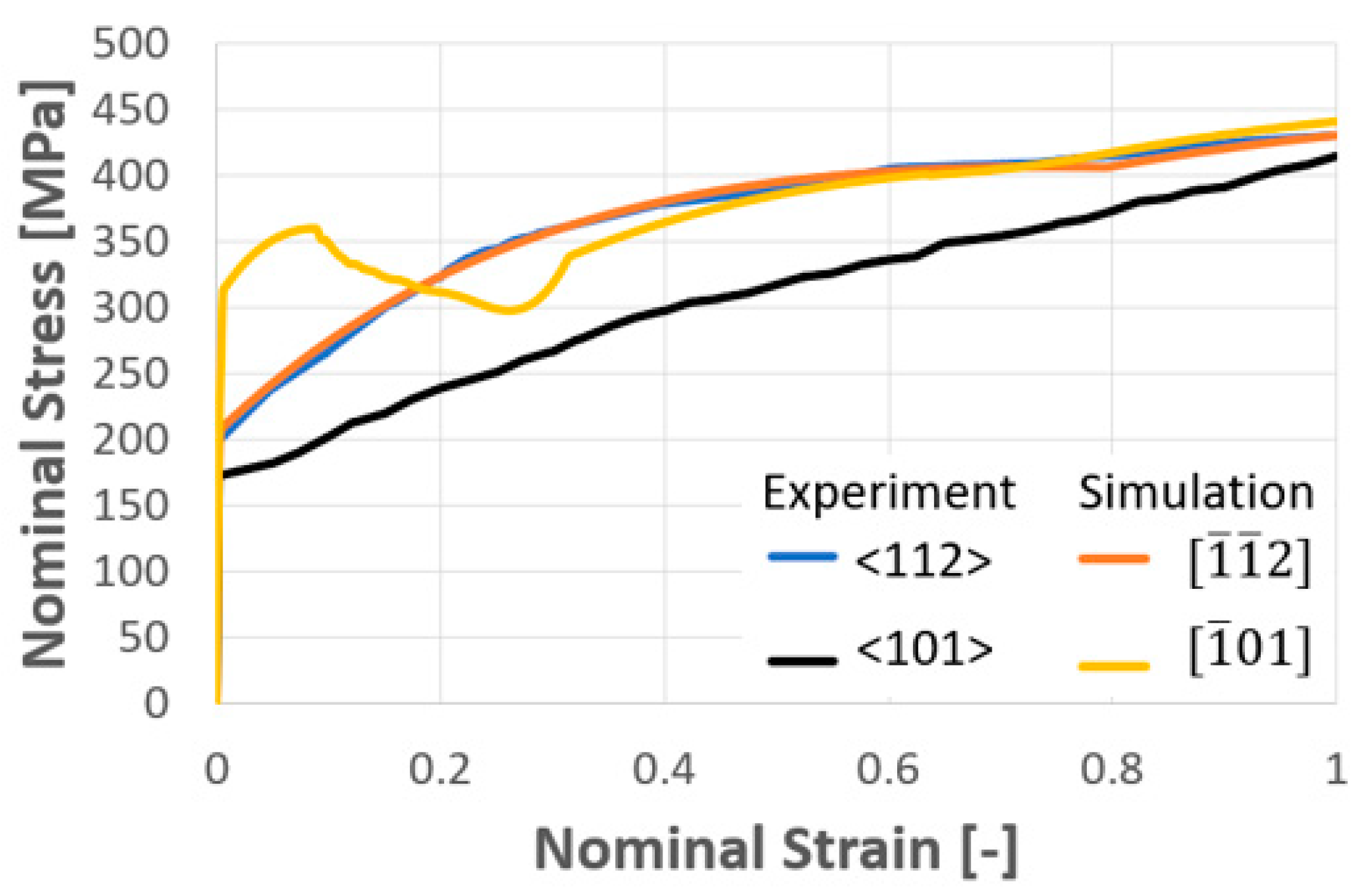
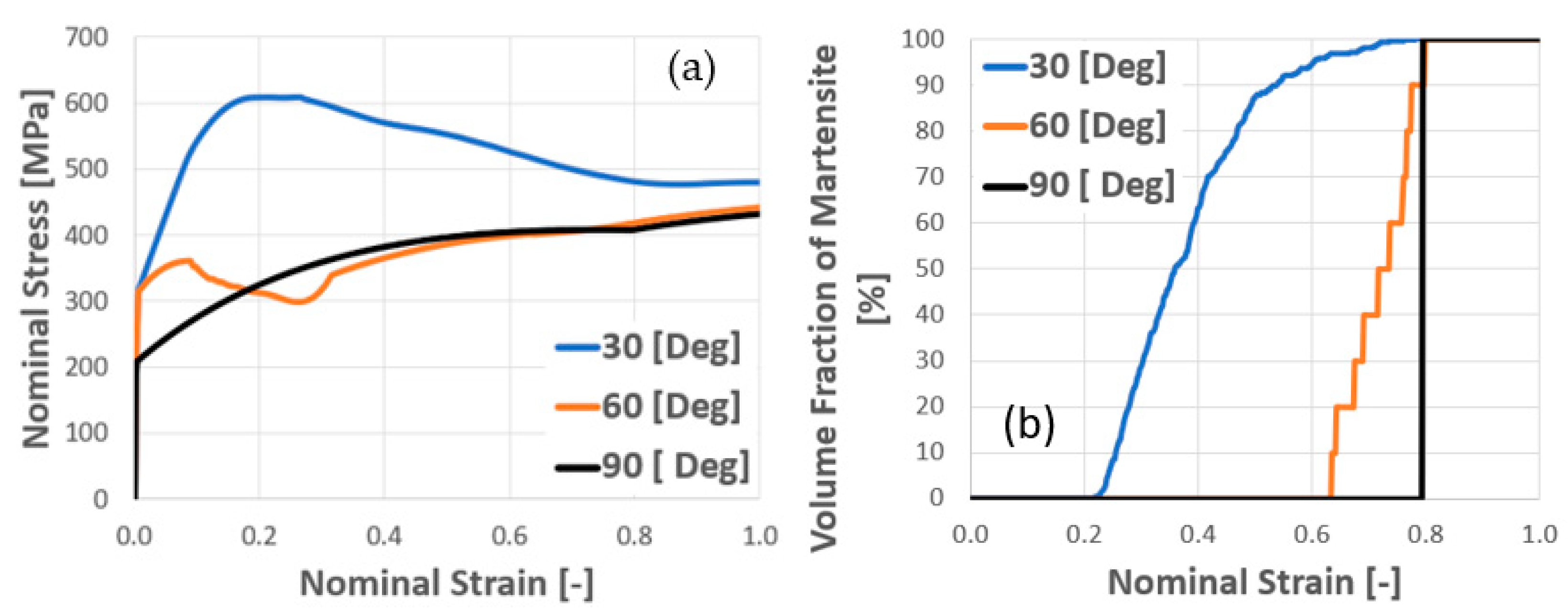
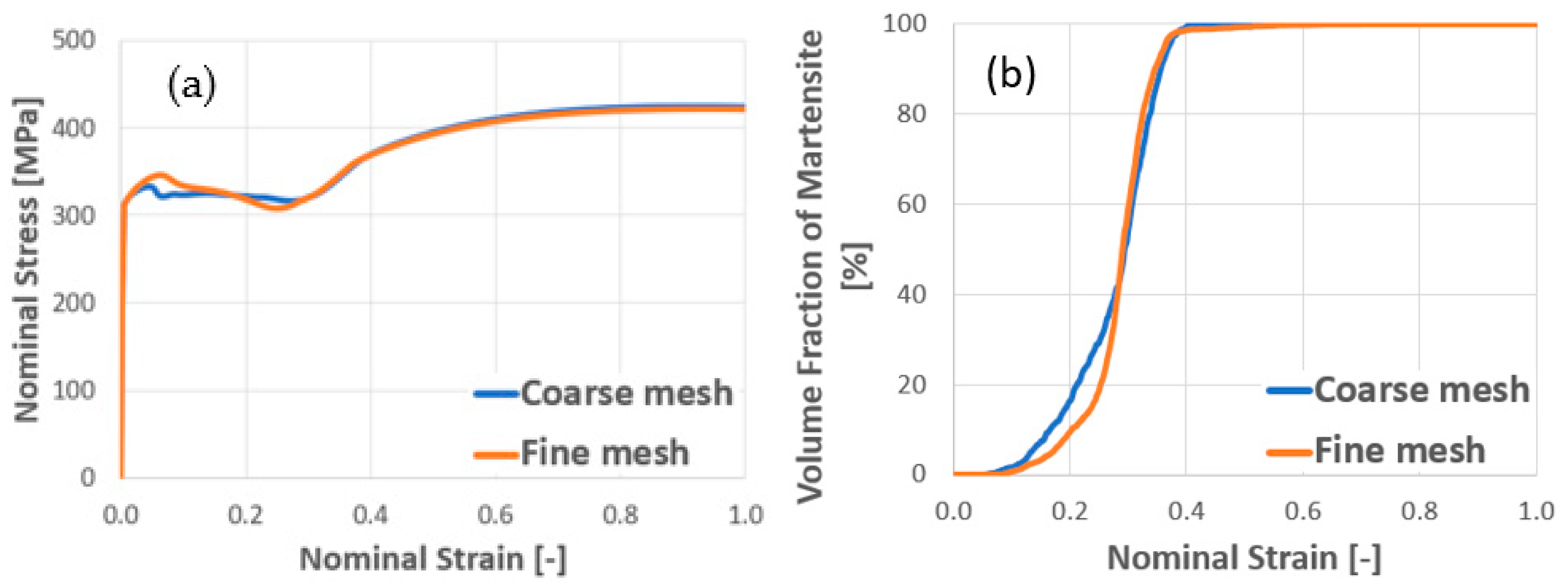
4.1. Calibration and Experimental Validation of Computational Results
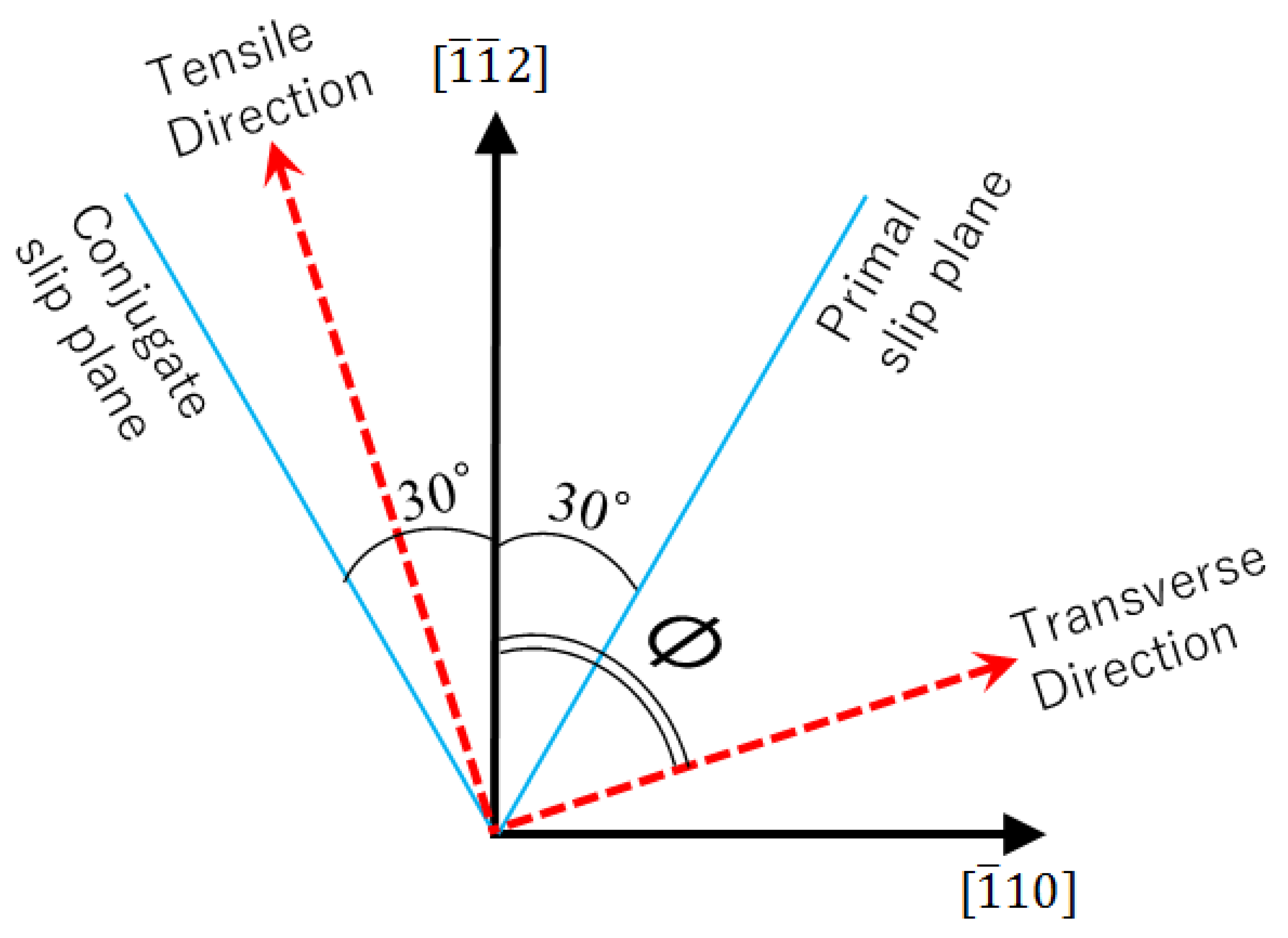
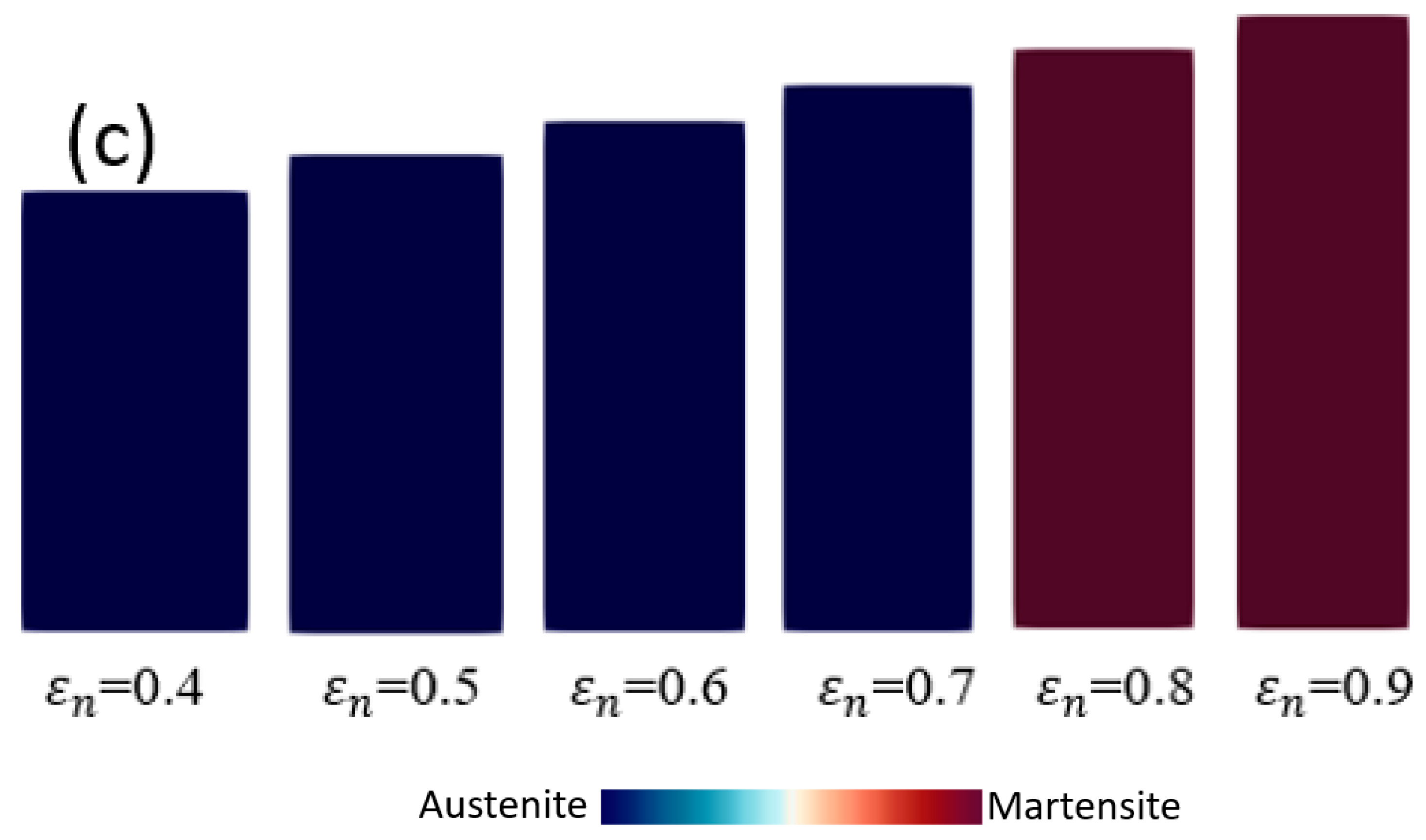
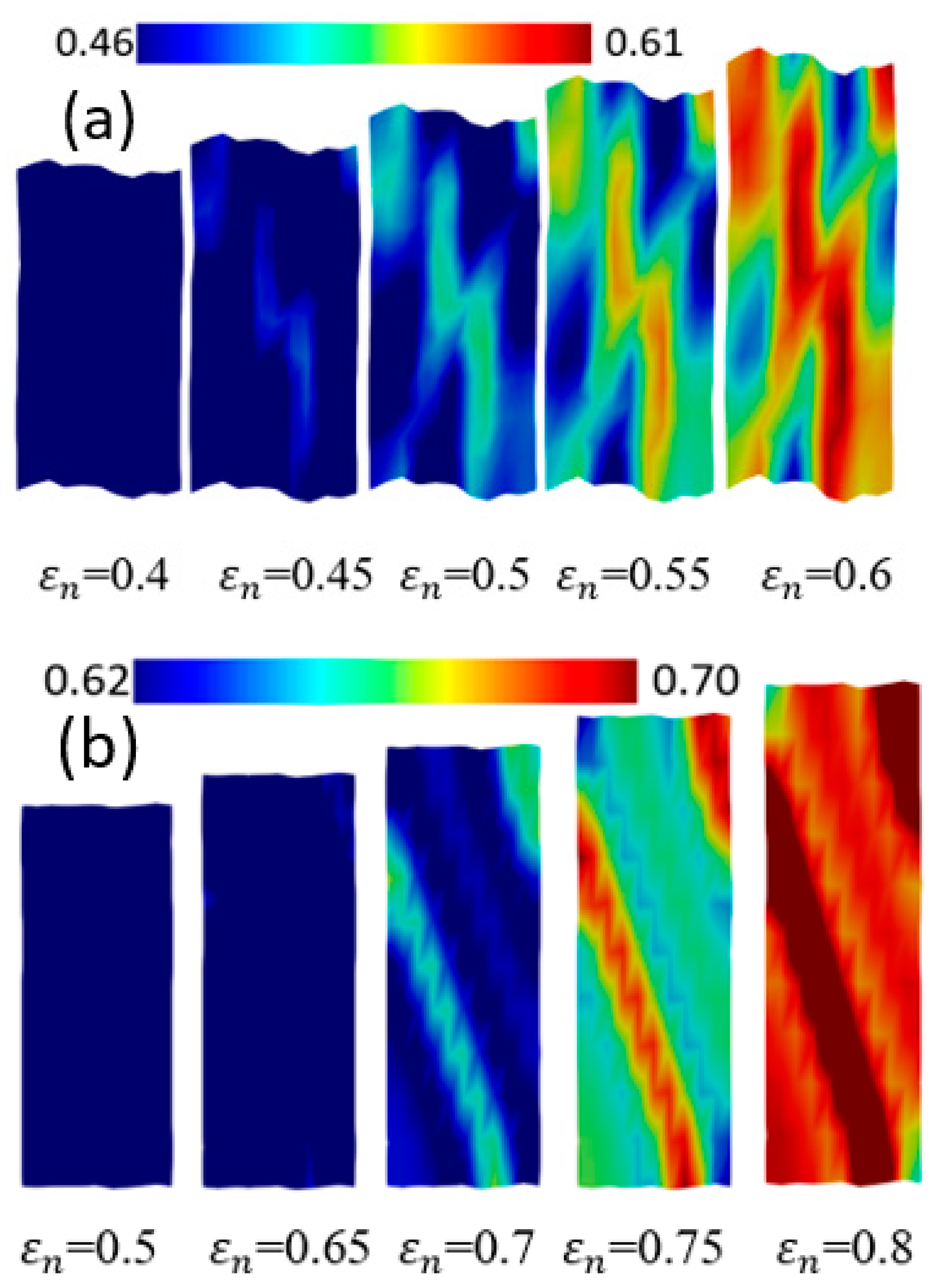
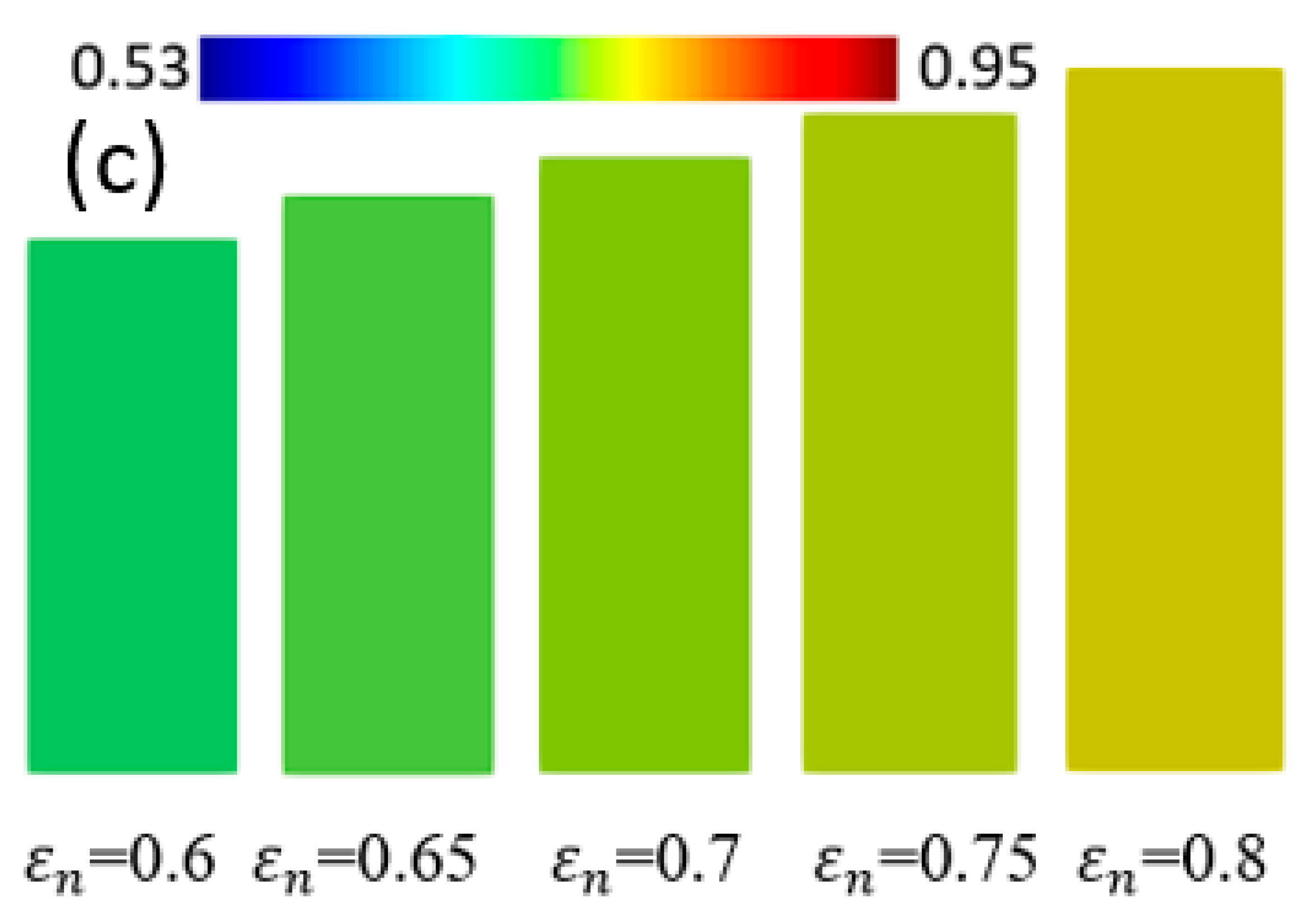
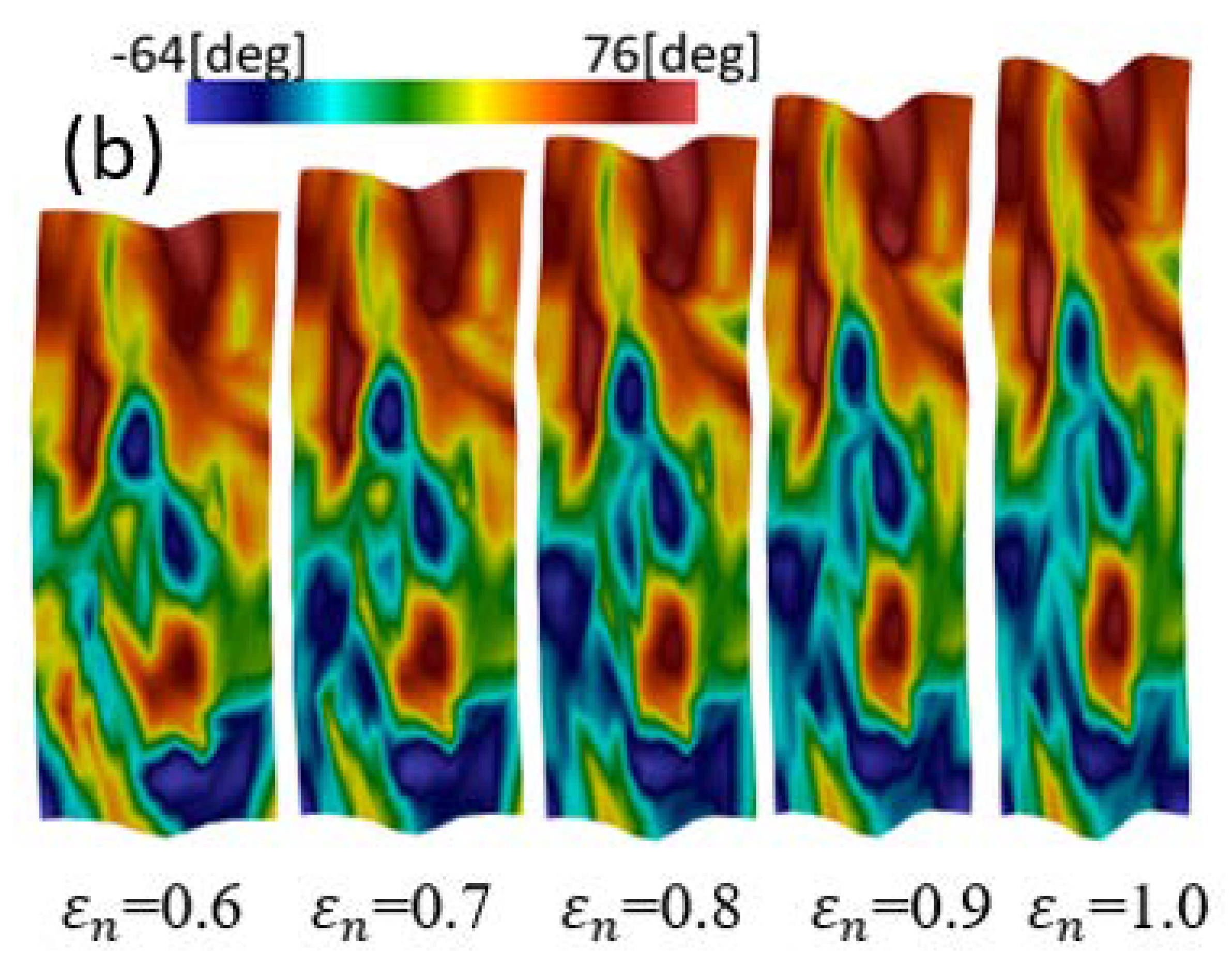
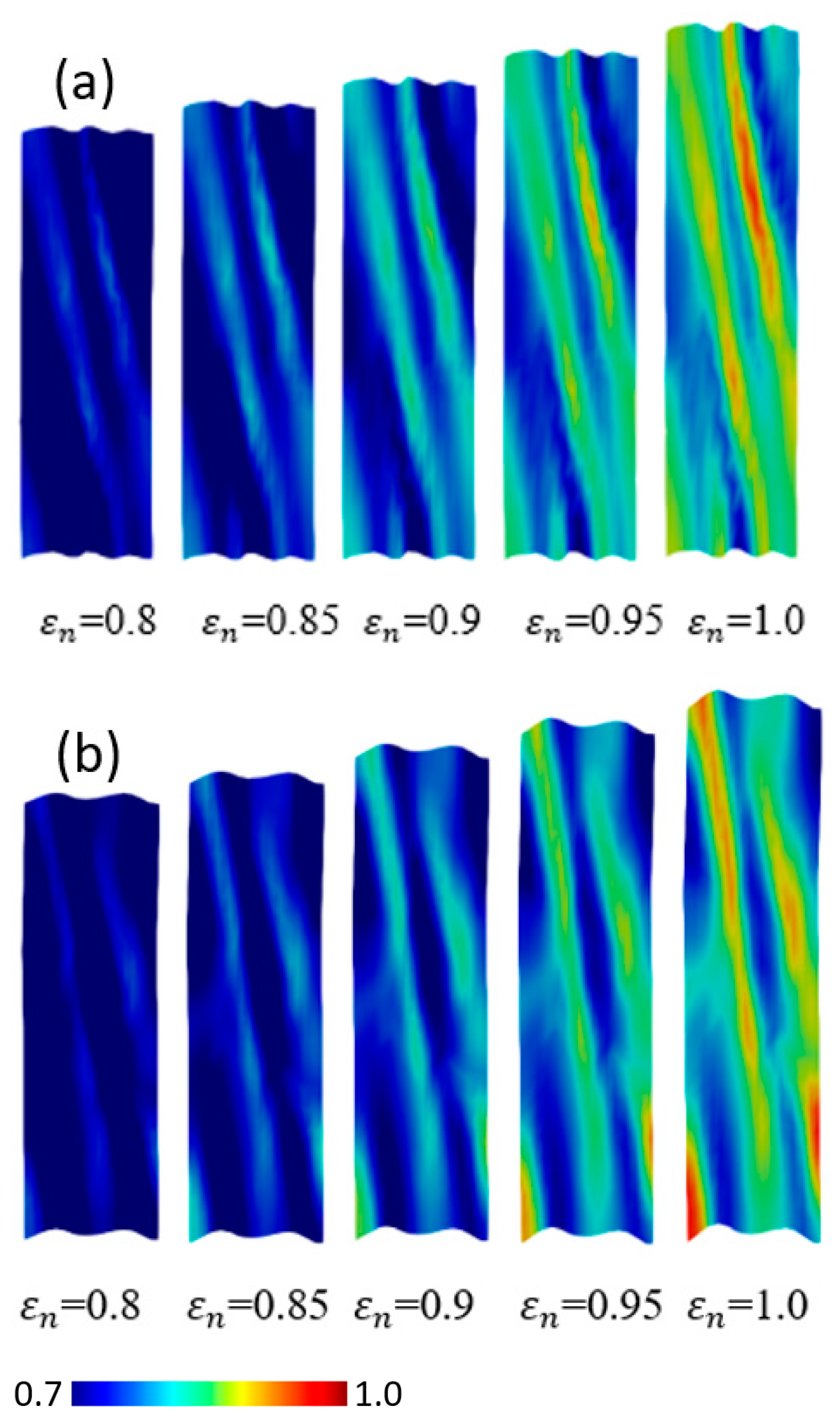
4.2. Monocrystal TRIP Steel
4.3. Polycrystal TRIP Steel
4.4. An Analysis of the Size of the Martensitic Embryo
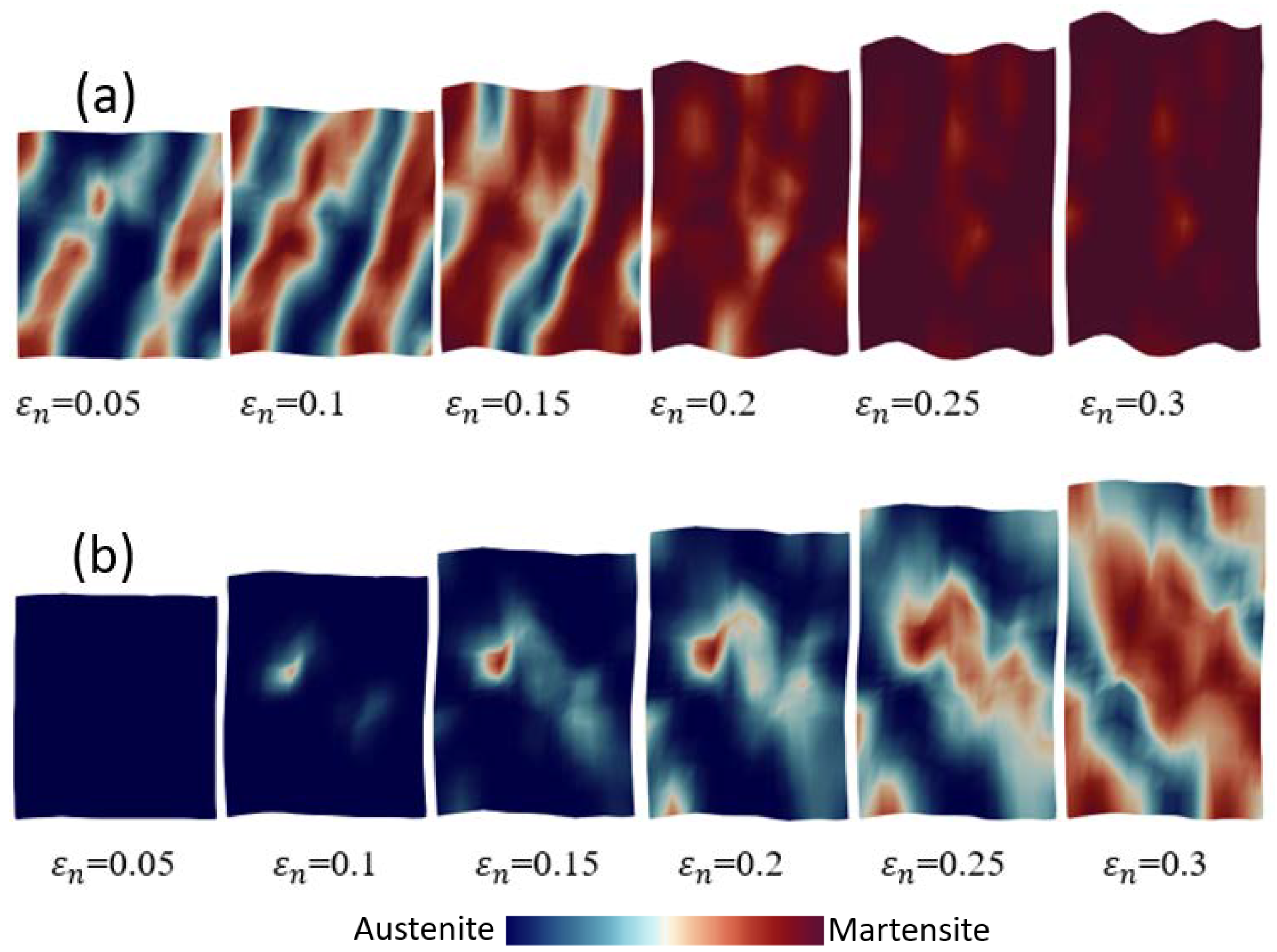
4.4.1. Single Crystal TRIP Steel
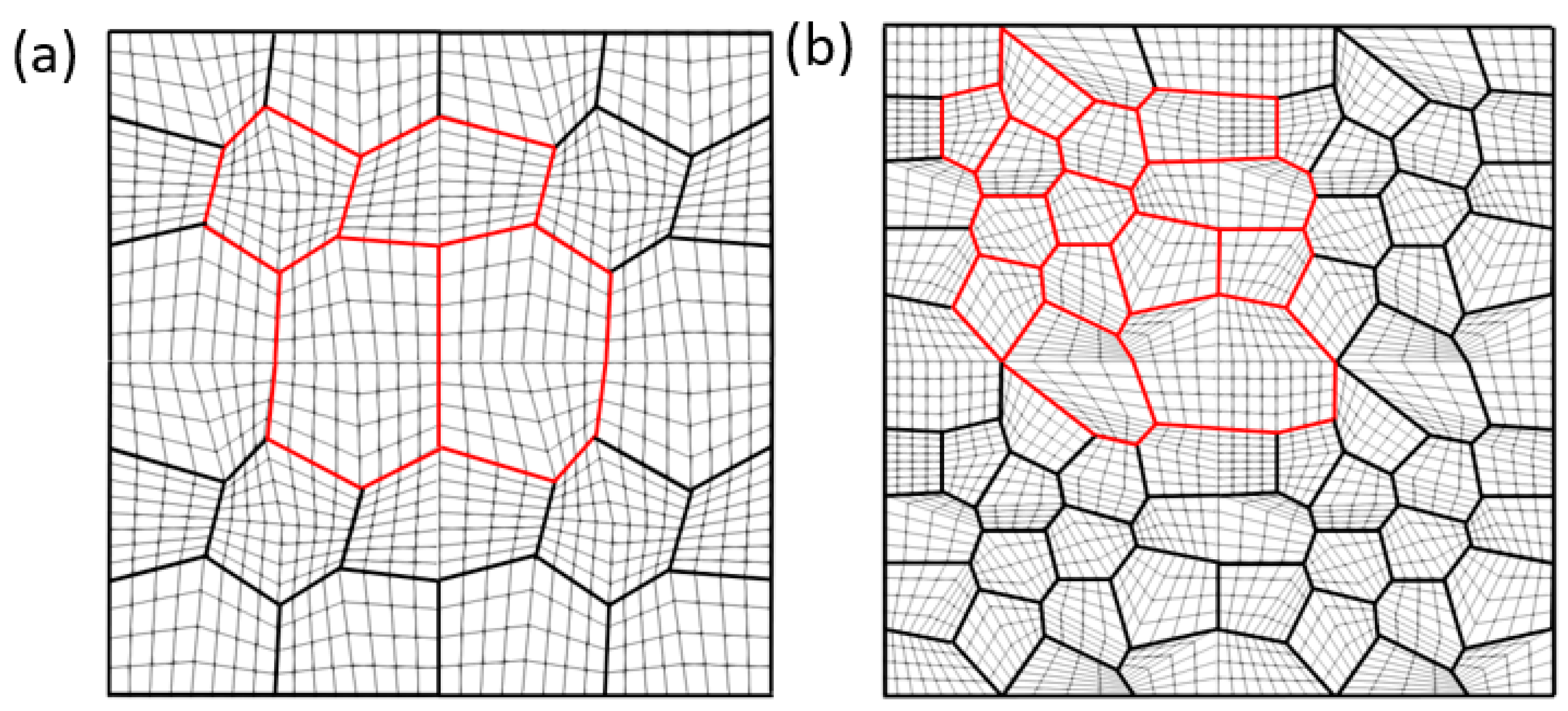
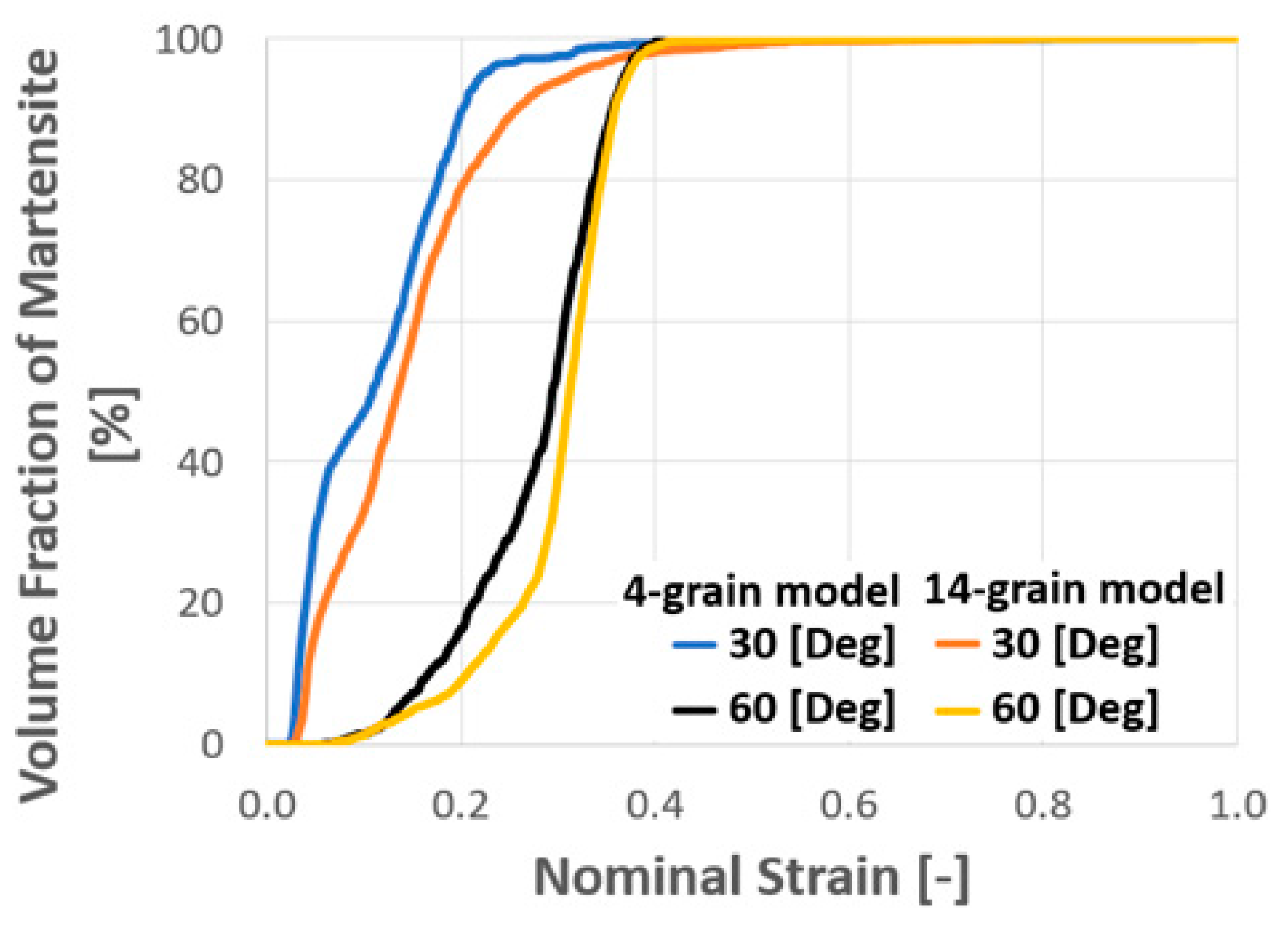
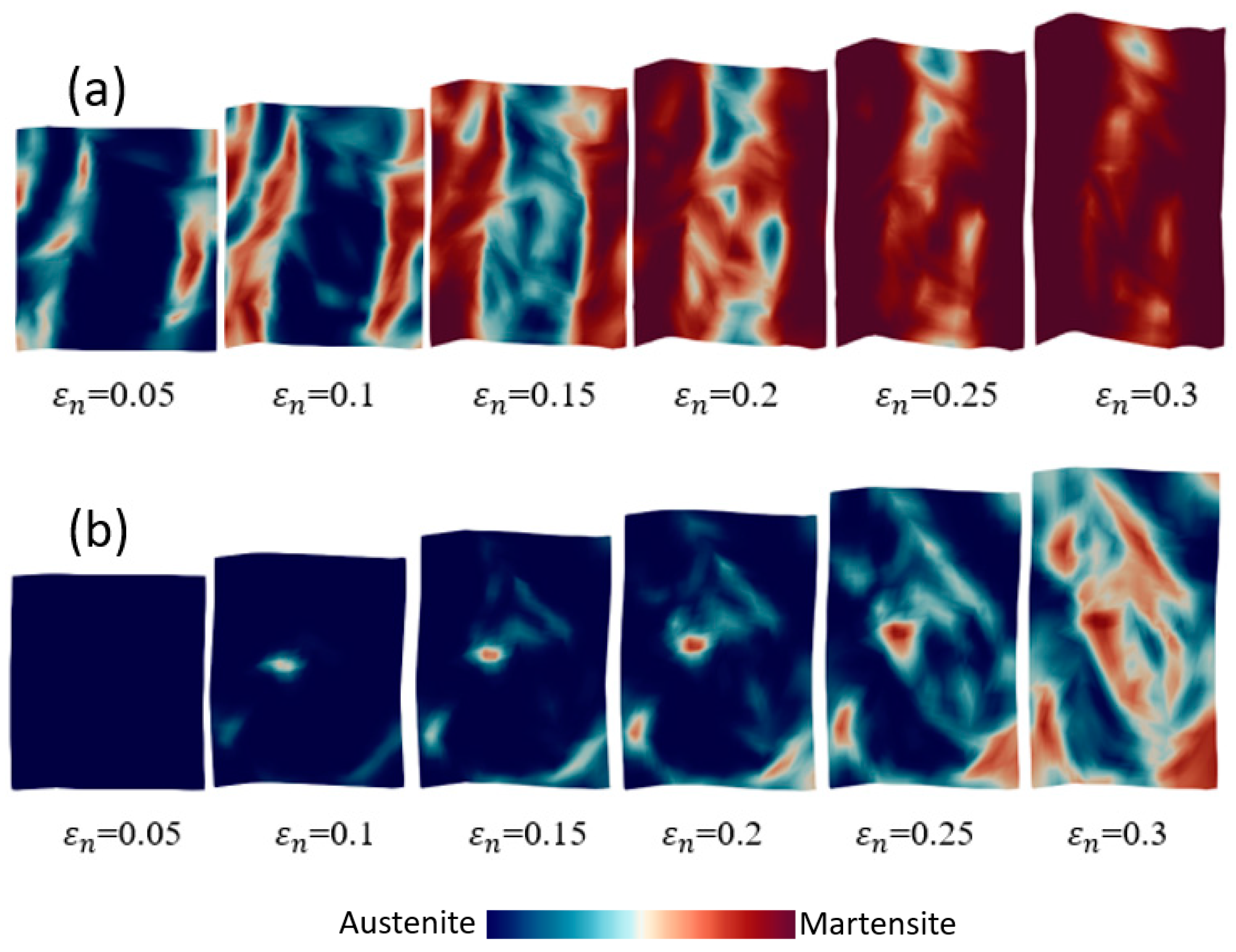
4.4.2. Polycrystal TRIP Steel
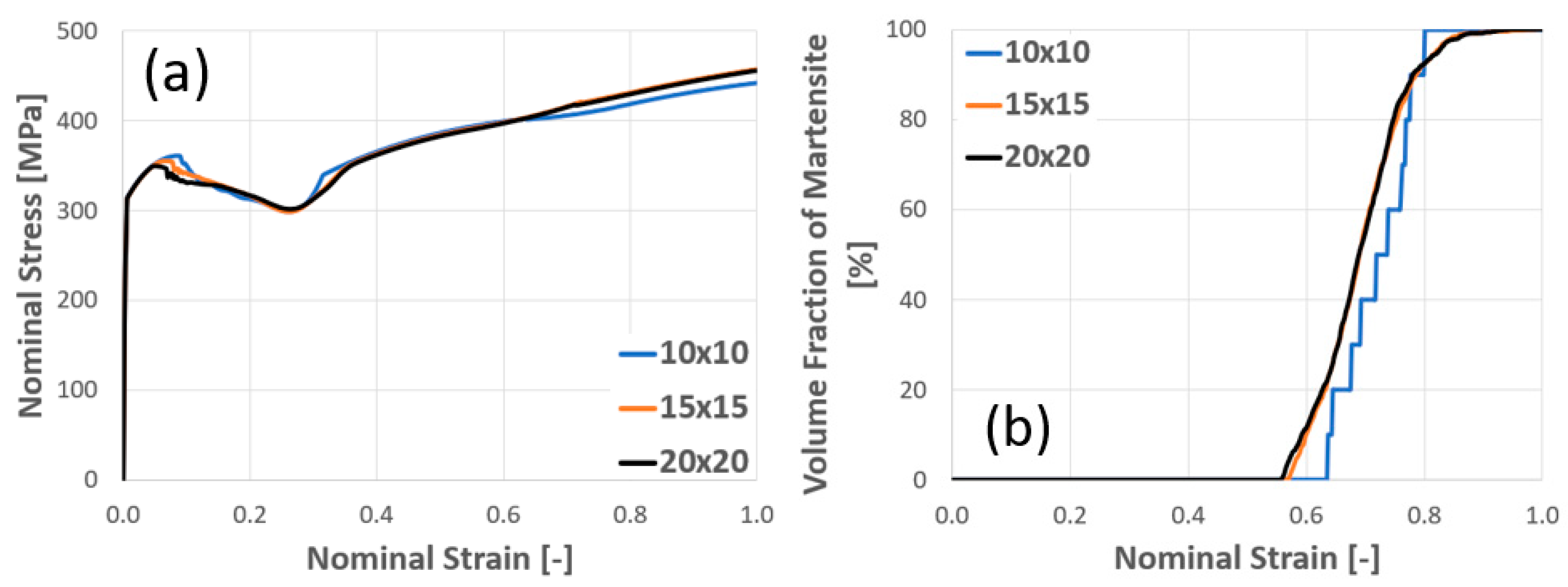
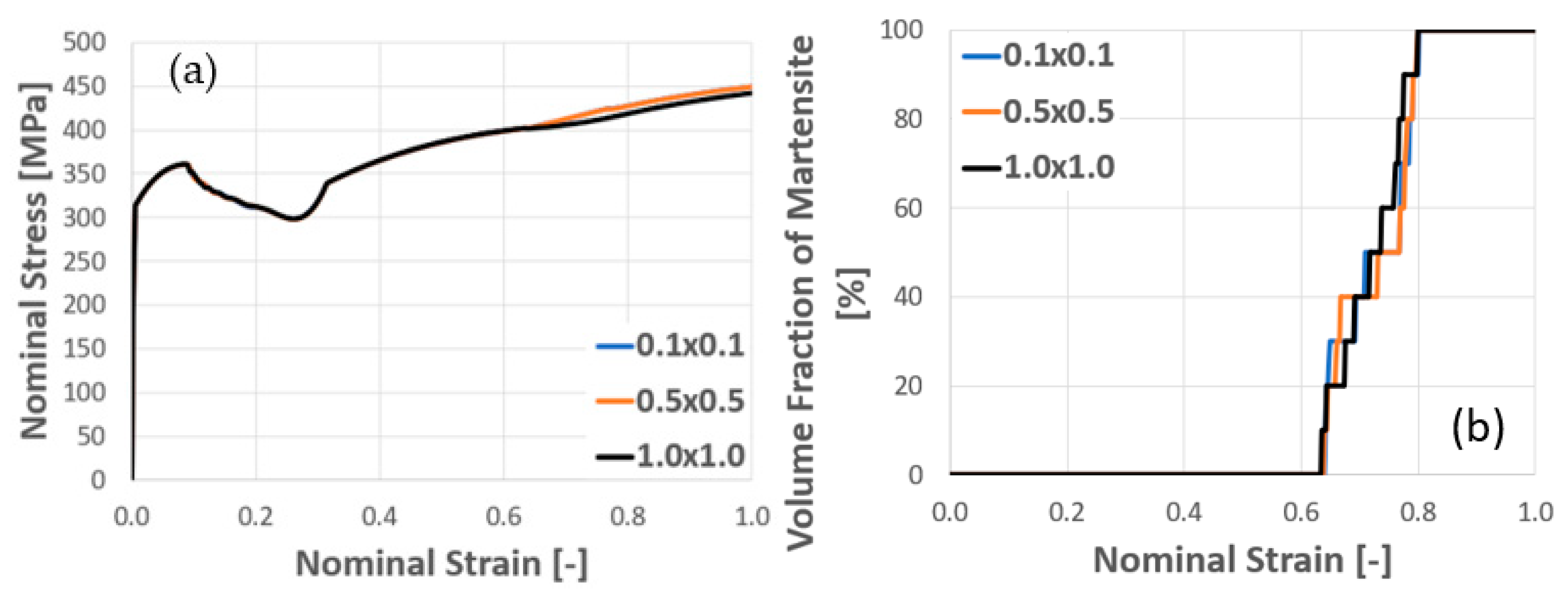
4.5. Discussion on Size Dependency
5. Concluding Remarks
- The numerical model, which combines the CPFEM and CA approaches in this study, is applied efficiently to describe the basic features of SIMT in crystalline TRIP steel.
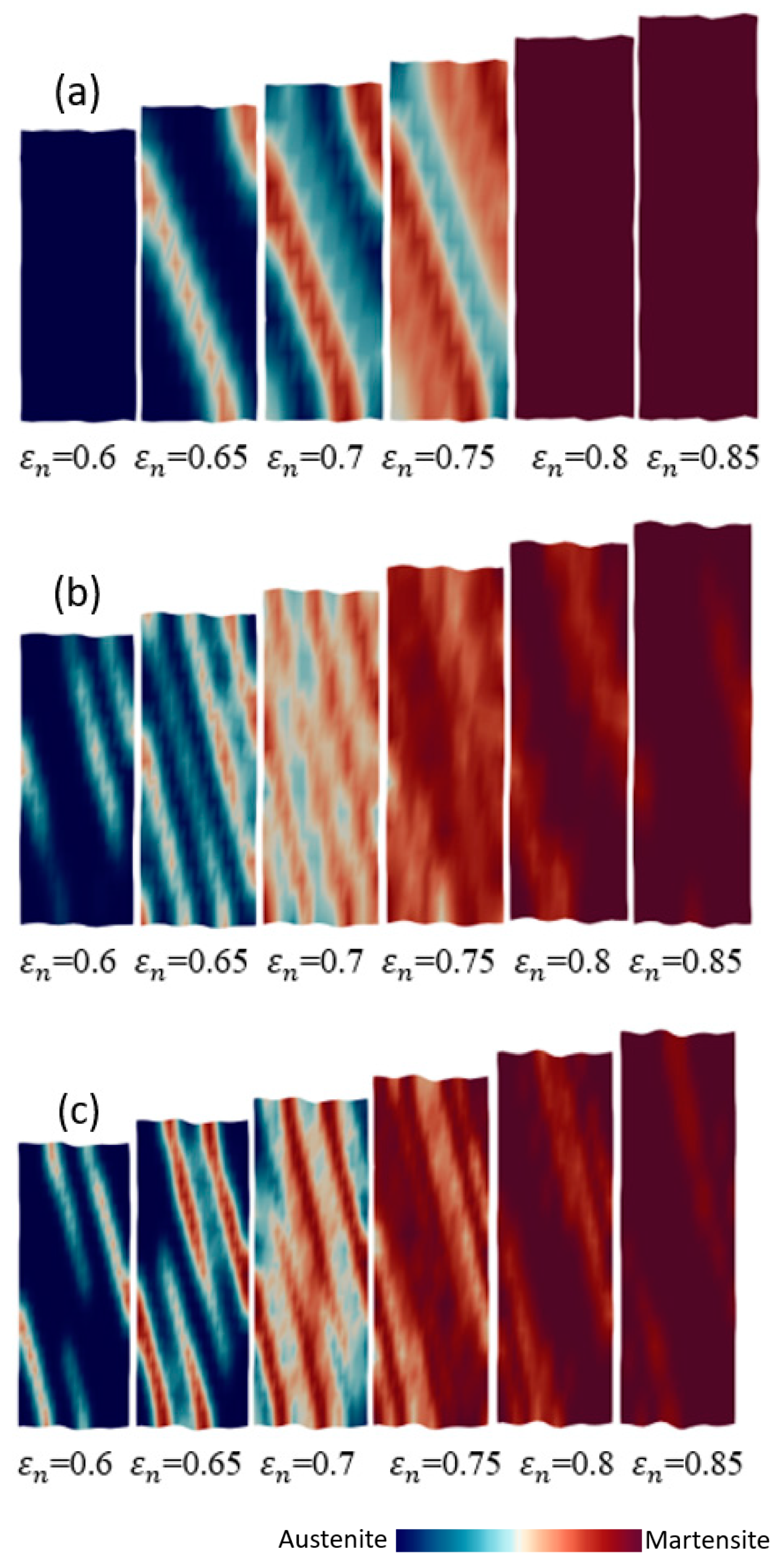
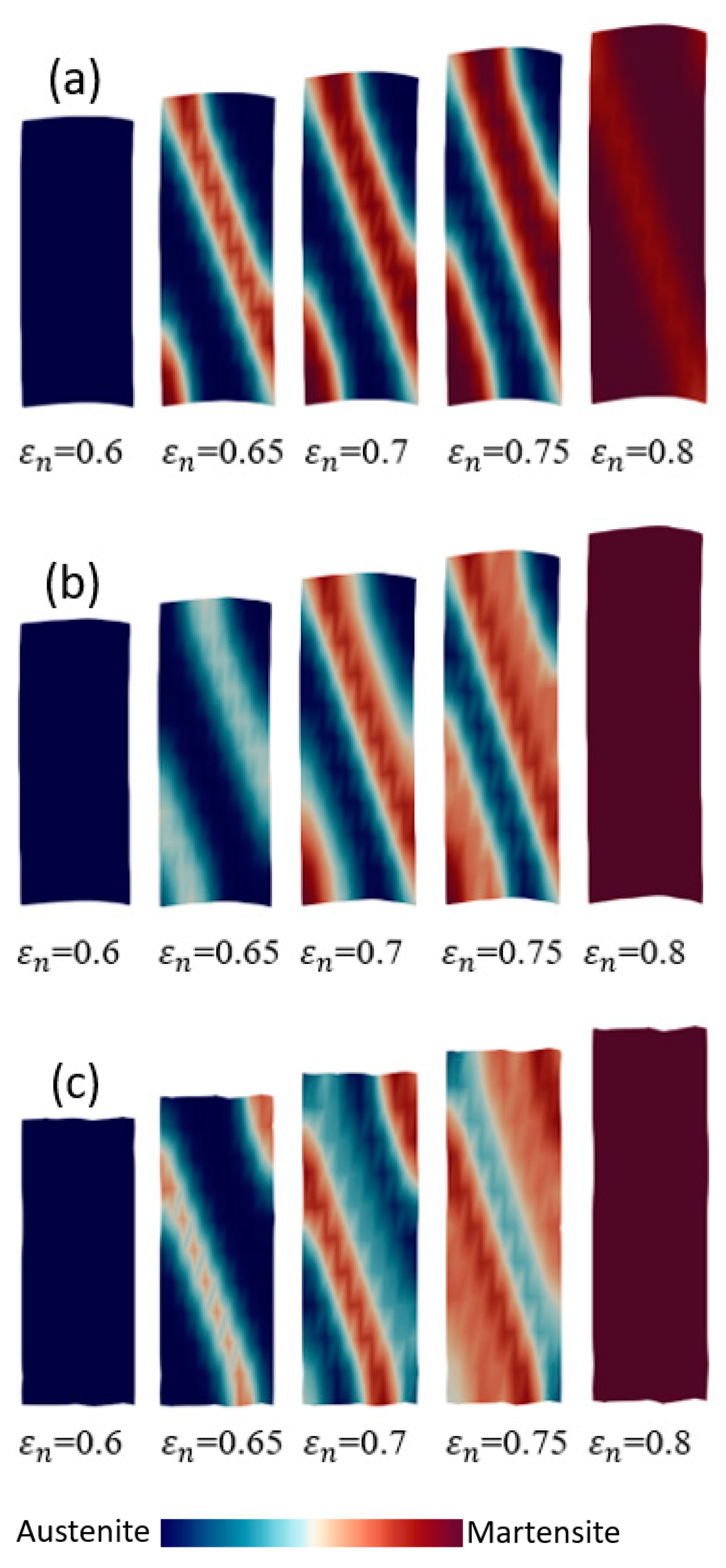
- The distributions of plastic strain and the martensitic phase are similar and explicitly formed as a shear band structure. The regions of the shear band structure, and their intersection, are thus effective sites for the nucleation of -martensite.
- The numbers, width, and direction of the bands, in the formation of the band structures, are significantly affected by the crystal orientations.
- In polycrystal models, the numbers of grains can greatly influence the strength, SIMT behavior and the formed microstructures of the crystalline TRIP steel.
- By analyzing the cell size and the mesh size in single and polycrystal models, the results show that the sizes of embryos and cells strongly influence the shear band formation and the martensitic volume fraction of crystal TRIP steel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Tangent Modulus Method
References
- Fischer, F.D.; Reisner, G.; Werner, E.; Tanaka, K.; Cailletaud, G.; Antretter, T. A new view on transformation induced plasticity (TRIP). Int. J. Plast. 2000, 16, 723–748. [Google Scholar] [CrossRef]
- Bowles, J.S.; Mackenzie, J.K. The crystallography of martensite transformations I. Acta Metal. 1954, 2, 129–137. [Google Scholar] [CrossRef]
- Nishiyama, Z. Martensitic Transformation; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Olson, G.B.; Cohen, M. Kinetics of strain-induced martensitic nucleation. Metall. Trans. A 1975, 6, 791–795. [Google Scholar] [CrossRef]
- Talonen, J.; Hänninen, H. Formation of shear bands and strain-induced martensite during plastic deformation of metastable austenitic stainless steels. Acta Mater. 2007, 55, 6108–6118. [Google Scholar] [CrossRef]
- Wu, R.; Tüzes, D.; Ispánovity, P.D.; Groma, I.; Hochrainer, T.; Zaiser, M. Instability of dislocation fluxes in a single slip: Deterministic and stochastic models of dislocation patterning. Phys. Rev. B 2018, 98, 054110. [Google Scholar] [CrossRef]
- Paul, H.; Morawiec, A.; Driver, J.H.; Bouzy, E. On twinning and shear banding in a Cu–8at.% Al alloy plane strain compressed at 77K. Int. J. Plast. 2009, 25, 1588–1608. [Google Scholar] [CrossRef]
- Jia, N.; Raabe, D.; Zhao, X. Texture and microstructure evolution during non-crystallographic shear banding in a plane strain compressed Cu–Ag metal matrix composite. Acta Mater. 2014, 76, 238–251. [Google Scholar] [CrossRef]
- Malik, A.; Amberg, G.; Borgenstam, A.; Ågren, J. Phase-field modelling of martensitic transformation: The effects of grain and twin boundaries. Model. Simul. Mater. Sci. Eng. 2013, 21, 085003. [Google Scholar] [CrossRef]
- Sierra, R.; Nemes, J.A. Investigation of the mechanical behavior of multi-phase TRIP steels using finite element methods. Int. J. Mech. Sci. 2008, 50, 649–665. [Google Scholar] [CrossRef]
- Sidhoum, Z.; Ferhoum, R.; Almansba, M.; Bensaada, R.; Habak, M.; Aberkane, M. Experimental and numerical study of the mechanical behavior and kinetics of the martensitic transformation in 304L TRIP steel: Applied to folding. Int. J. Adv. Manuf. Technol. 2018, 97, 2757–2765. [Google Scholar] [CrossRef]
- Levitas, V.I.; Idesman, A.V.; Olson, G.B. Continuum modeling of strain-induced martensitic transformation at shear-band intersections. Acta Mater. 1999, 47, 219–233. [Google Scholar] [CrossRef]
- Dan, W.J.; Li, S.H.; Zhang, W.G.; Lin, Z.Q. The effect of strain-induced martensitic transformation on mechanical properties of TRIP steel. Mater. Des. 2008, 29, 604–612. [Google Scholar] [CrossRef]
- Kubler, R.; Berveiller, M.; Buessler, P. Semi phenomenological modelling of the behavior of TRIP steels. Int. J. Plast. 2011, 27, 299–327. [Google Scholar] [CrossRef][Green Version]
- Beese, A.M.; Mohr, D. Effect of stress triaxiality and Lode angle on the kinetics of strain-induced austenite-to-martensite transformation. Acta Mater. 2011, 59, 2589–2600. [Google Scholar] [CrossRef]
- Cao, J.; Jin, J.; Wang, L.; Li, S.; Zong, Y. Modeling for onset strain of deformation-induced martensite transformation in Q&P steel by a mean-field Eshelby approach. Model. Simul. Mater. Sci. Eng. 2019, 27, 085002. [Google Scholar]
- Stringfellow, R.; Parks, D.; Olson, G. A constitutive model for transformation plasticity accompanying strain-induced martensitic transformations in metastable austenitic steels. Acta Metall. Mater. 1992, 40, 1703–1716. [Google Scholar] [CrossRef]
- Iwamoto, T.; Tsuta, T.; Tomita, Y. Investigation on deformation mode dependence of strain induced martensitic transformation in TRIP steels and modeling of transformation kinetics. Int. J. Mech. Sci. 1998, 40, 173–182. [Google Scholar] [CrossRef]
- Turteltaub, S.; Suiker, A. A multiscale thermomechanical model for cubic to tetragonal martensitic phase transformations. Int. J. Solids Struct. 2006, 43, 4509–4545. [Google Scholar] [CrossRef]
- Lai, Q.; Brassart, L.; Bouaziz, O.; Goune, M.; Verdier, M.; Parry, G.; Perlade, A.; Brechet, Y.; Pardoen, T. Influence of martensite volume fraction and hardness on the plastic behavior of dual-phase steels: Experiments and micromechanical modeling. Int. J. Plast. 2016, 80, 187–203. [Google Scholar] [CrossRef]
- Asaro, R. Crystal plasticity. Trans. ASME J. Appl. Mech. 1983, 50, 921–934. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metal. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Iwamoto, T.; Tsuta, T. Finite element simulation of martensitic transformation in single crystal TRIP steel based on crystal plasticity theory with cellular automata approach. Key Eng. Mater. 2004, 274–276, 679–684. [Google Scholar] [CrossRef]
- Xiao, N.; Tong, M.; Lan, Y.; Li, D.; Li, Y. Coupled simulation of the influence of austenite deformation on the subsequent isothermal austenite–ferrite transformation. Acta Mater. 2006, 54, 1265–1278. [Google Scholar] [CrossRef]
- Wang, H.; Capolungo, L.; Clausen, B.; Tome, C. A crystal plasticity model based on transition state theory. Int. J. Plast. 2017, 93, 251–268. [Google Scholar] [CrossRef]
- Trinh, T.D.; Iwamoto, T. A computational simulation of martensitic transformation in polycrystal TRIP steel by crystal plasticity FEM with voronoi tessellation. Key Eng. Mater. 2019, 794, 71–77. [Google Scholar] [CrossRef]
- Tjahjanto, D.D.; Turteltaub, S.; Suiker, A.S.J.; van der Zwaag, S. Modelling of the effects of grain orientation on transformation-induced plasticity in multi-phase steels. Model. Simul. Mater. Sci. Eng. 2006, 14, 617–636. [Google Scholar] [CrossRef]
- Hatem, T.M.; Zikry, M.A. Dislocation density crystalline plasticity modeling of lath martensitic in steel alloys. Philos. Mag. A 2009, 89, 3087–3109. [Google Scholar] [CrossRef]
- Lee, M.G.; Kim, S.J.; Han, H.N. Crystal plasticity finite element modeling of mechanically induced martensitic transformation (MIMT) in metastable austenite. Int. J. Plast. 2010, 26, 688–710. [Google Scholar] [CrossRef]
- Zecevic, M.; Upadhyay, M.V.; Polatidis, E.; Panzner, T.; Van Swygenhoven, H.; Knezevic, M. A crystallographic extension to the Olson-Cohen model for predicting strain path dependence of martensitic transformation. Acta Mater. 2019, 166, 386–401. [Google Scholar] [CrossRef]
- Levitas, V.I.; Javanbakht, M. Interaction between phase transformations and dislocations at the nanoscale. Part1. General phase field approach. J. Mech. Phys. Solids 2015, 82, 287–319. [Google Scholar] [CrossRef]
- Raabe, D. Cellular Automata in Materials Science with Particular Reference to Recrystallization Simulation. Annu. Rev. Mater. Res. 2002, 32, 53–76. [Google Scholar] [CrossRef]
- Yang, H.; Wu, C.; Li, H.; Fan, X. Review on cellular automata simulations of microstructure evolution during metal forming process: Grain coarsening, recrystallization and phase transformation. Sci. China Technol. Sci. 2011, 54, 2107–2118. [Google Scholar] [CrossRef]
- Pourian, M.H.; Bridier, F.; Pilvin, P.; Bocher, P. Prediction of crack initiation sites in alpha Ti-alloys microstructures under dwell-fatigue using Cellular Automaton simulation method. Int. J. Fatigue 2016, 85, 85–97. [Google Scholar] [CrossRef]
- Zheng, C.; Raabe, D. Interaction between recrystallization and phase transformation during intercritical annealing in a cold rolled dual-phase steel: A cellular automaton model. Acta Mater. 2013, 61, 5504–5517. [Google Scholar] [CrossRef]
- Smit, R.J.M.; Brekelmans, W.A.M.; Meijer, H.E.H. Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput. Methods Appl. Mech. Eng. 1998, 155, 181–192. [Google Scholar] [CrossRef]
- Levitas, V.I. Thermomechanical theory of martensitic phase transformations in inelastic materials. Int. J. Solids Struct. 1998, 35, 889–940. [Google Scholar] [CrossRef]
- Cherkaoui, M.; Berveiller, M.; Saber, H. Micromechanical modeling of martensitic transformation induced plasticity (TRIP) in austenitic single crystals. Int. J. Plast. 1998, 14, 597–626. [Google Scholar] [CrossRef]
- Kitajima, Y.; Sato, N.; Tanaka, K.; Nagaki, S. Crystal based simulations in transformation thermomechanics of shape memory alloys. Int. J. Plast. 2002, 18, 1527–1559. [Google Scholar] [CrossRef]
- Tanaka, K.; Tobushi, H.; Miyazaki, S. Mechanical Properties of Shape Memory Alloys; Yokendo Ltd.: Tokyo, Japan, 1993; pp. 7–61. [Google Scholar]
- Trinh, T.D.; Iwamoto, T. A Review on Numerical Analyses of Martensitic Phase Transition in Mono and Polycrystal Transformation-induced Plasticity Steel by Crystal Plasticity Finite Element Method with Length Scales. In State of the Art and Future Trends in Material Modeling; Altenbach, H., Öchsner, A., Eds.; Advanced Structured Materials; Springer: Cham, Switzerland, 2019; Volume 100, pp. 401–420. [Google Scholar]
- Ledbetter, H.M. Monocrystal elastic constants of 304-type stainless steel. Physica B+C 1985, 128, 1–4. [Google Scholar] [CrossRef]
- Ledbetter, H.M. Predicted single-crystal elastic constants of stainless steel 304. In Materials Studies for Magnetic Fusion Energy Applications at Low Temperatures-IV; Reed, R.P., Simon, N.J., Eds.; NBSIR: Boulder, CO, USA, 1981; Volume 12, pp. 227–236. [Google Scholar]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook; MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Tsurui, T.; Inoue, S.; Matsuda, K.; Ishigaki, H.; Murata, K.; Koterazawa, K. Effect of tensile axis on α′ martensitic formation of SUS304 stainless steel single crystals. J. Soc. Mater. Sci. 2001, 50, 1115–1119. [Google Scholar] [CrossRef][Green Version]
- Ganghoffer, J.F.; Simonsson, K. A micromechanical model of the martensitic transformation. Mech. Mater. 1998, 27, 125–144. [Google Scholar] [CrossRef]
- Cohen, M. Nucleation of solid state transformations. Trans. TMS-AIME 1958, 212, 171. [Google Scholar]


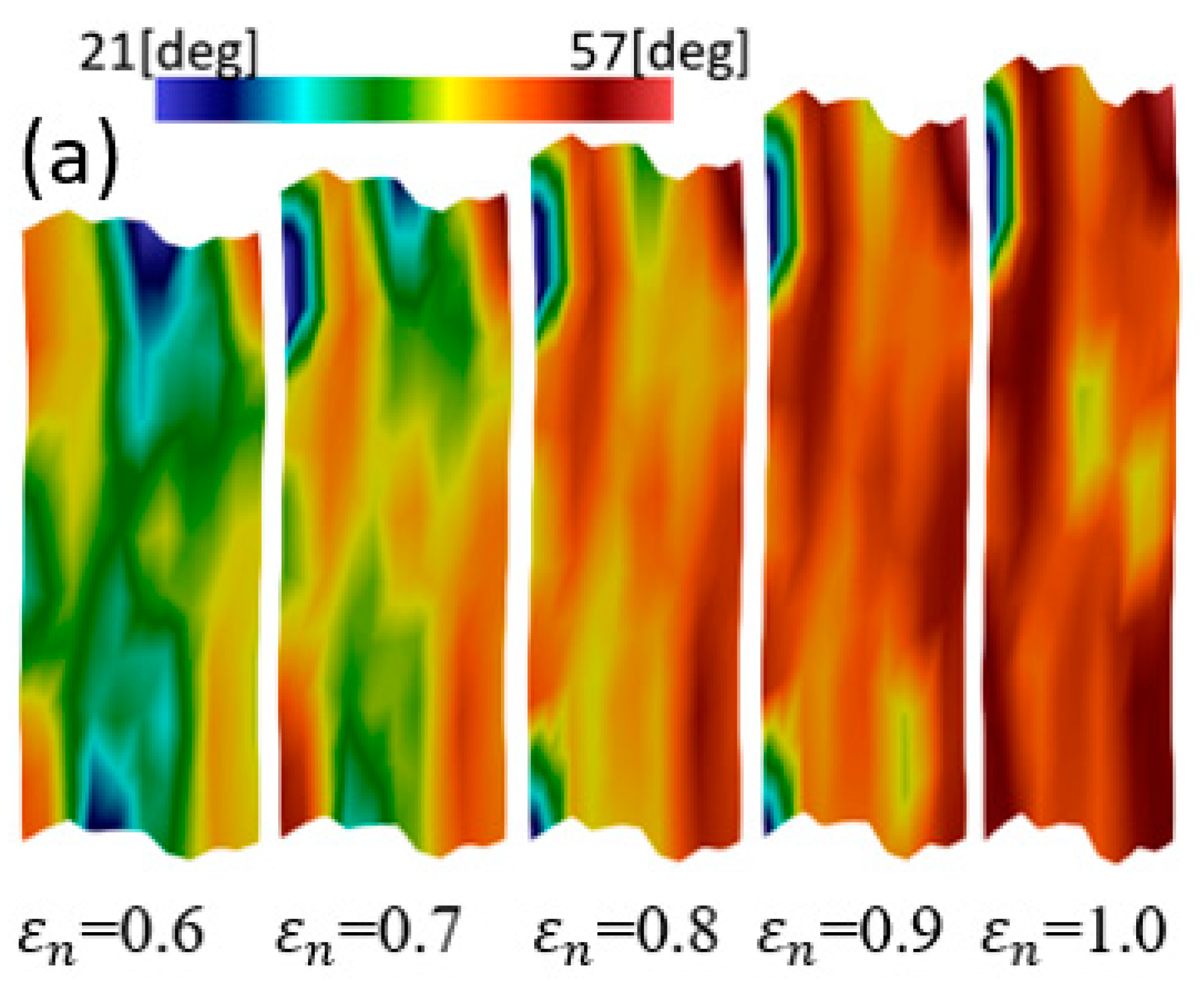
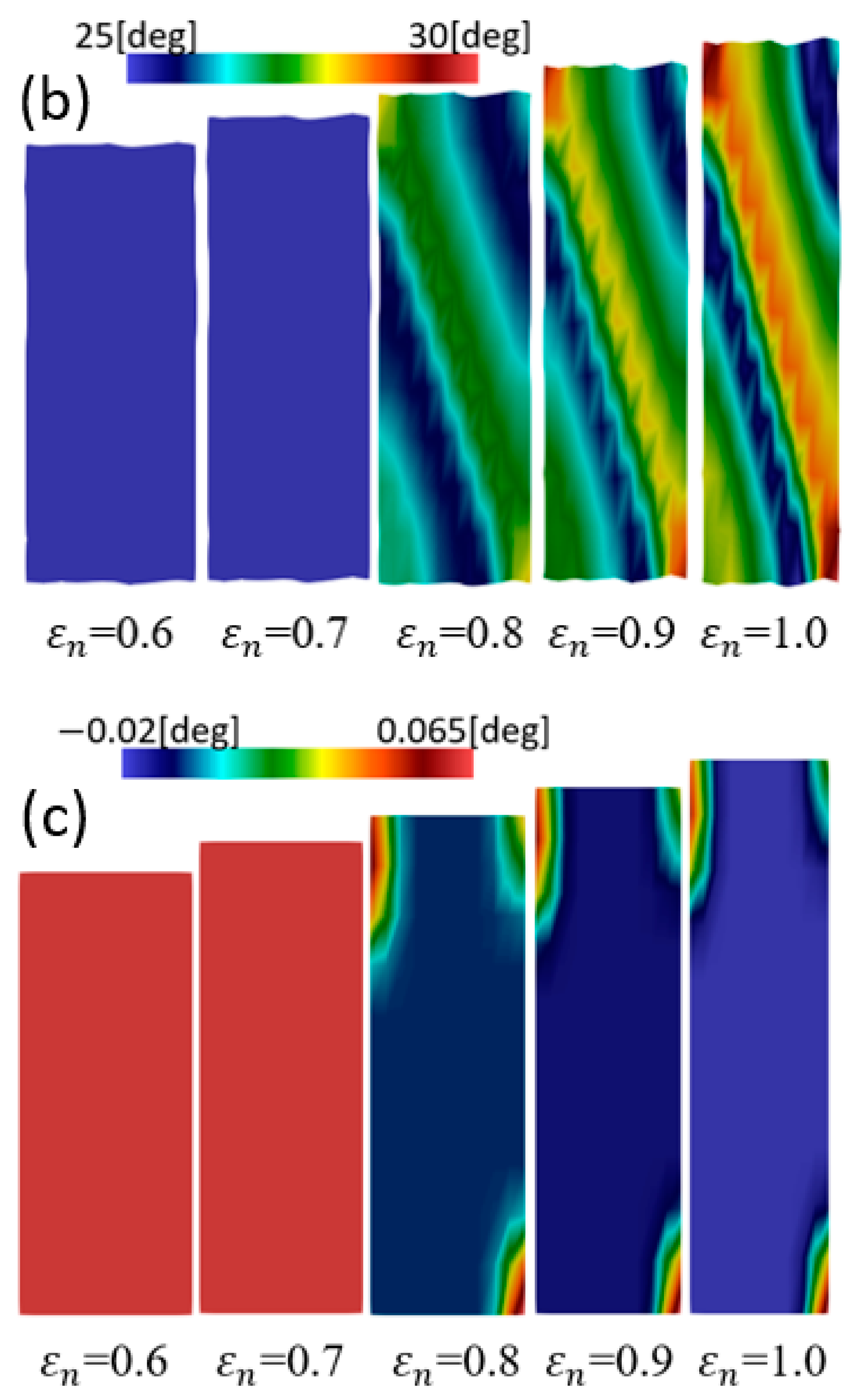

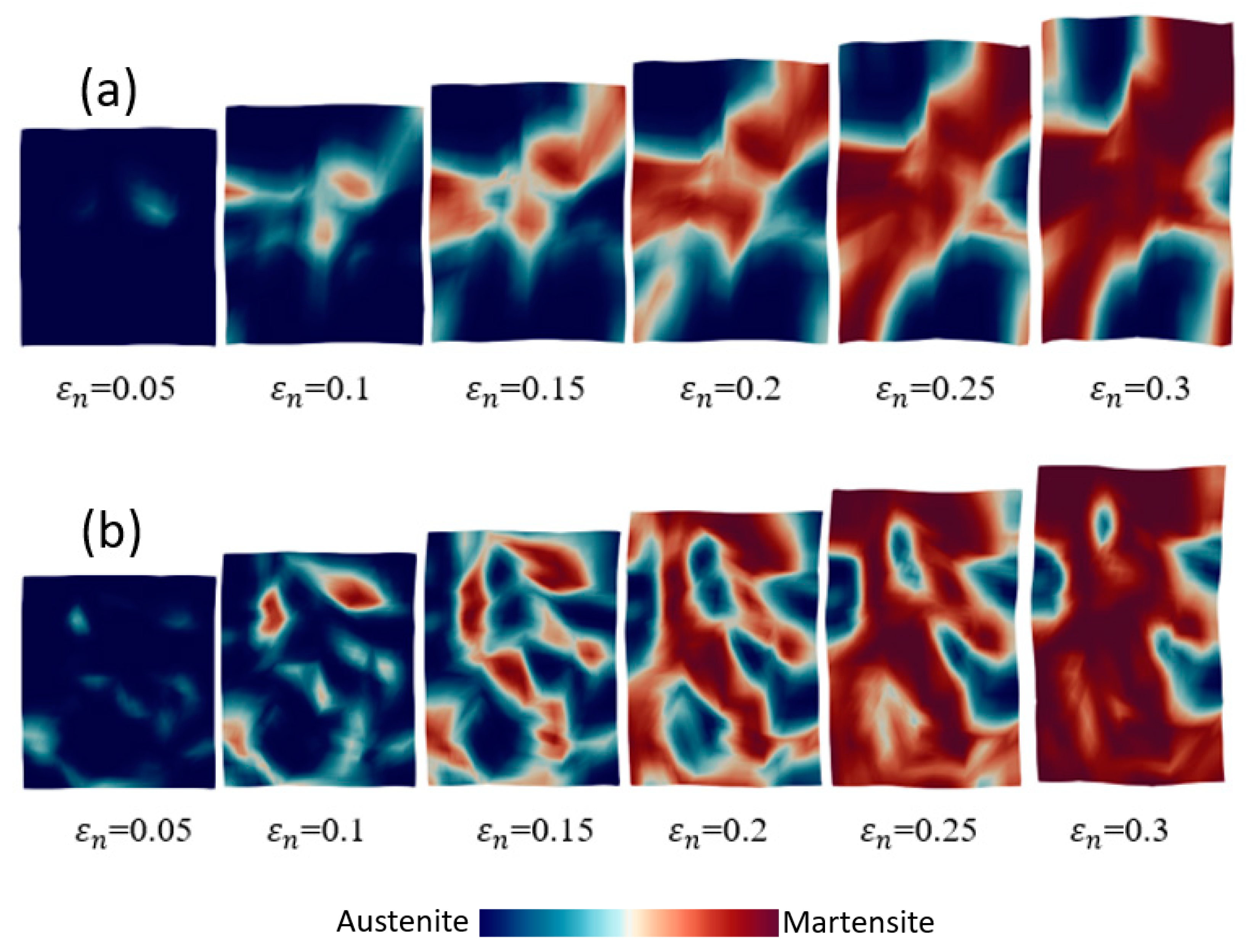
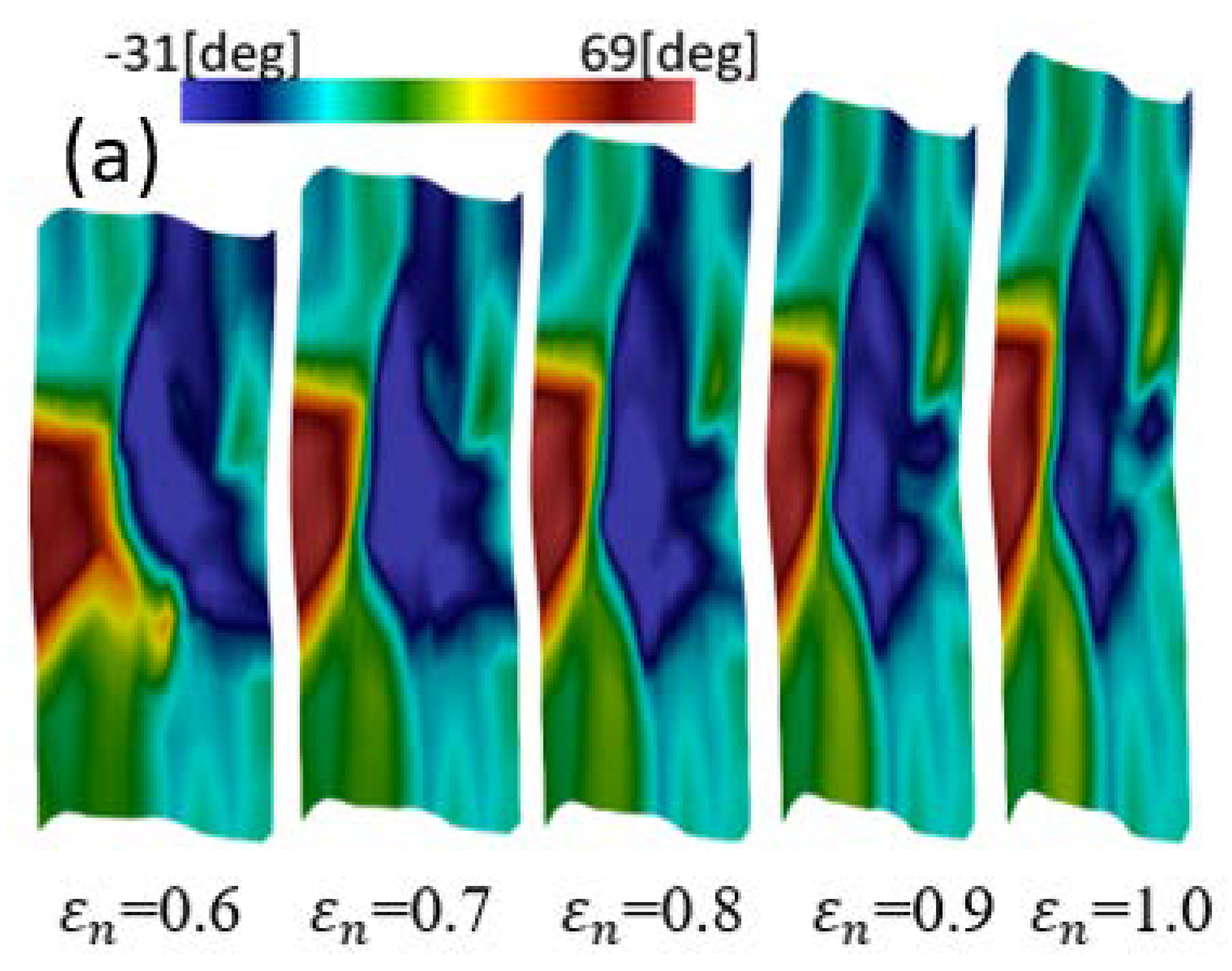
| Parameter(s) | Nomenclatures | Austenite | Martensite |
|---|---|---|---|
| Elastic moduli (GPa) | C11 C12 C44 | 209.0 133.0 121.0 | 236.9 140.6 116.0 |
| Slip resistance (MPa) | 89.71 | 114.65 | |
| Strain rate sensitivities | 0.01 | ||
| Reference strain rate () | |||
| Latent hardening ratio | 1.2 | ||
| Critical resolved shear stress (MPa) | |||
| Saturation resolved shear stress (MPa) | 5.05 | 4.08 | |
| Initial hardening rate in Equations (24) and (25) (MPa) | 1.85 | 1.95 | |
| Initial temperature (K) | 293 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trinh, T.D.; Iwamoto, T. A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata. Metals 2021, 11, 1316. https://doi.org/10.3390/met11081316
Trinh TD, Iwamoto T. A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata. Metals. 2021; 11(8):1316. https://doi.org/10.3390/met11081316
Chicago/Turabian StyleTrinh, Truong Duc, and Takeshi Iwamoto. 2021. "A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata" Metals 11, no. 8: 1316. https://doi.org/10.3390/met11081316
APA StyleTrinh, T. D., & Iwamoto, T. (2021). A Crystal Plasticity Simulation on Strain-Induced Martensitic Transformation in Crystalline TRIP Steel by Coupling with Cellular Automata. Metals, 11(8), 1316. https://doi.org/10.3390/met11081316







